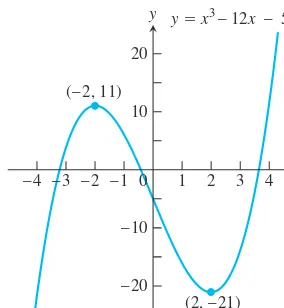
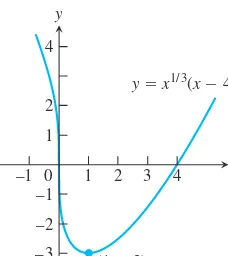
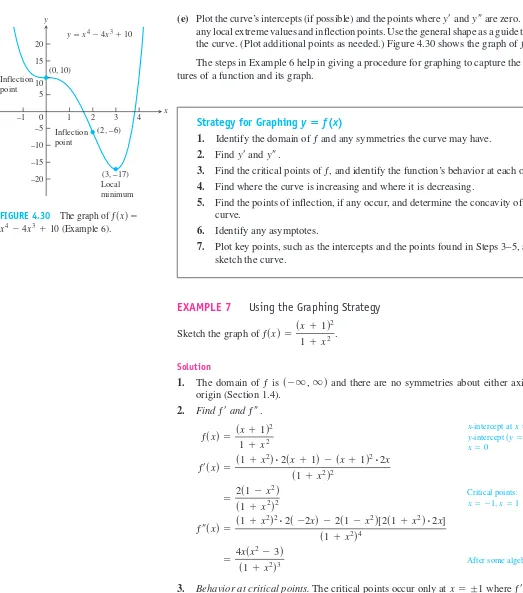
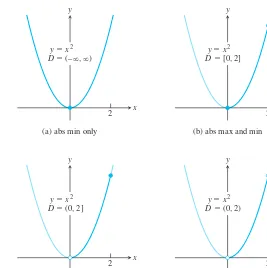
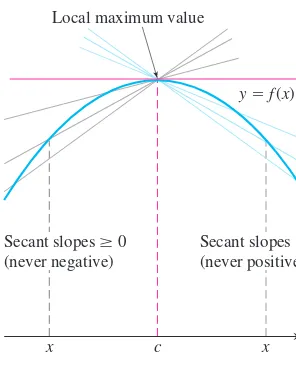
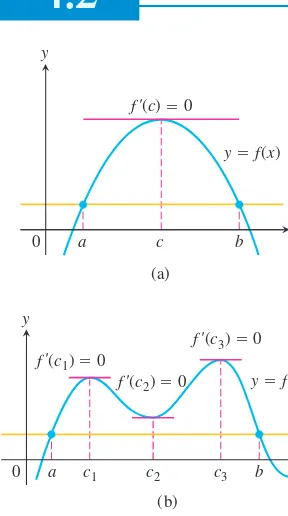
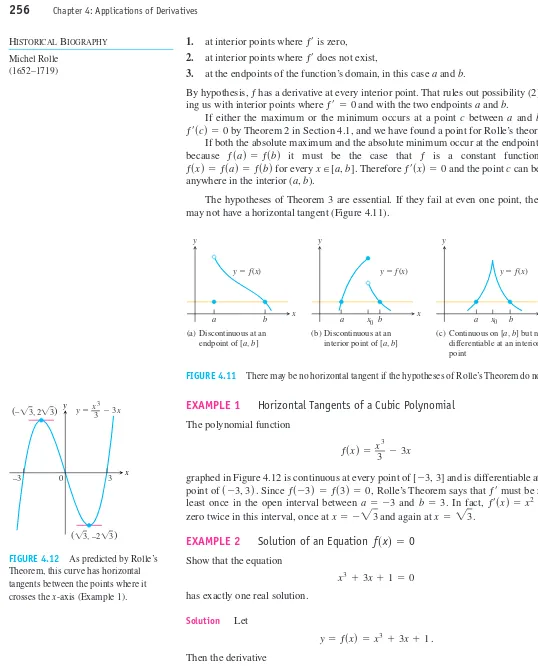
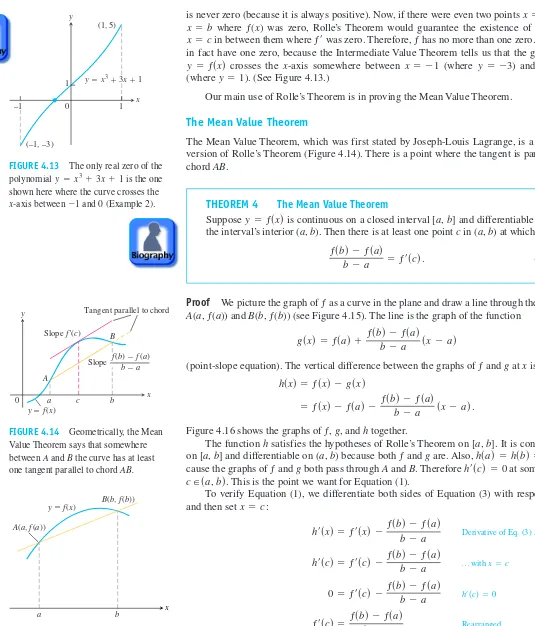
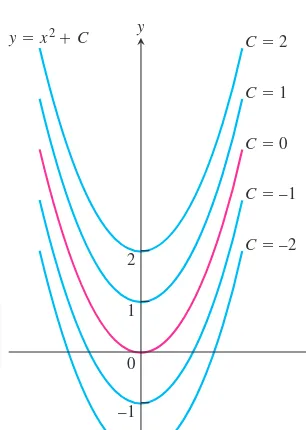
OVERVIEW This chapter studies some of the important applications of derivatives. We learn how derivatives are used to find extreme values of functions, to determine and ana- lyze the shapes of graphs, to calculate limits of fractions whose numerators and
Teks penuh
Gambar
Dokumen terkait
Penelitian tindakan kelas adalah strategi pengembangan profesi guru karena (a) menempatkan guru sebagai peneliti, bukan sebagai informan pasif, (b) menempatkan guru
Buol Tahun Anggaran 2013 akan melaksanakan Seleksi Sederhana dengan Prakualifikasi untuk Pekerjaan Jasa Konsultansi sebagai berikut :.. Paket
Metode pemberian tugas dengan sendirinya menuntut tanggung jawab guru yang sangat besar untuk memeriksa dan memberikan umpan balik terhadap tugas-tugas yang
Kajian Efektifitas Anggaran Kementerian/Lembaga dalam Pembangunan Infrastruktur Ekonomi dan Kesra di Kawasan
Pengadaan Peralatan Ranjang Tidur BPPTD Palembang Tahun Anggaran 2017 dengan nilai HPS.. sebesar
Karya ilmiah yang berjudul: Total Bakteri Asam Laktat dan Escherichia coli pada Ayam Broiler yang Diberi Campuran Herbal Dalam Ransum , penelitian yang terkait dengan
Organisasi : 1.18.01. - Dinas Pemuda, Olah Raga, Pariwisata dan Ekonomi Kreatif 1.18.. Program upaya pencegahan.
Pembuatan dan Penyelidikan Perilaku Mekanik Material Polymeric Foam Diperkuat Serat Tandan Kosong Kelapa Sawit (TKKS) Akibat Beban Statik dan Impak, Laporan Penelitian
![FIGURE 4.21The function ismonotonic on the intervals andbut it is not monotonic ons[0, - qq, dq, d.s- qƒsxd, 0] = x2](https://thumb-ap.123doks.com/thumbv2/123dok/3402711.1762577/24.684.54.210.178.342/figure-the-function-ismonotonic-intervals-andbut-monotonic-qfsxd.webp)