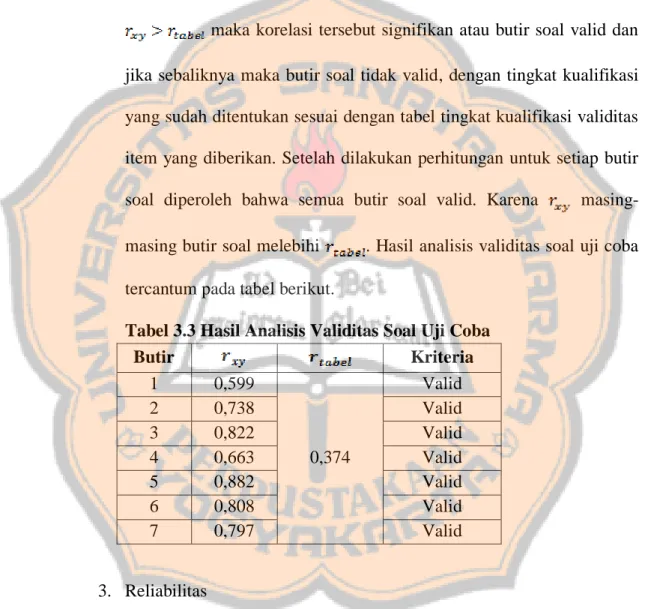
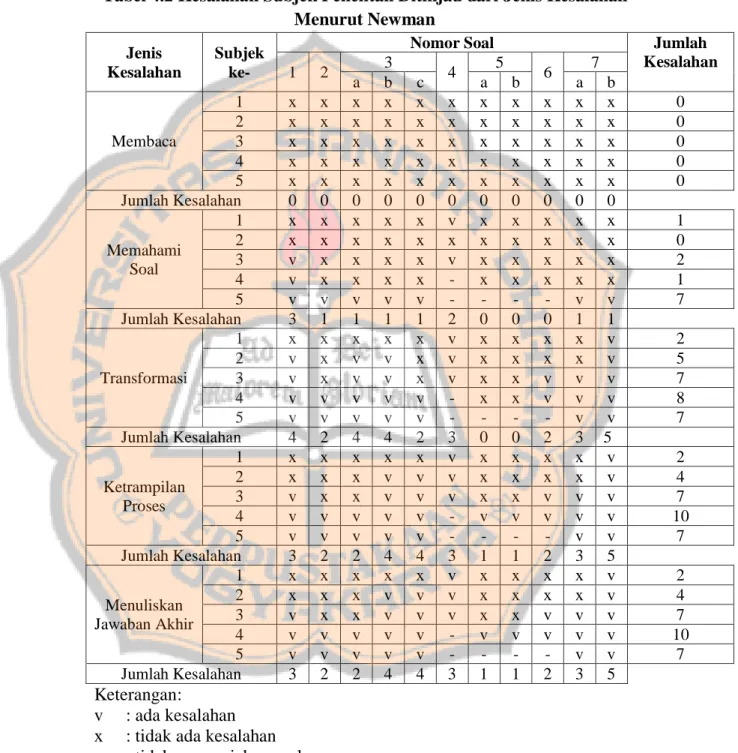
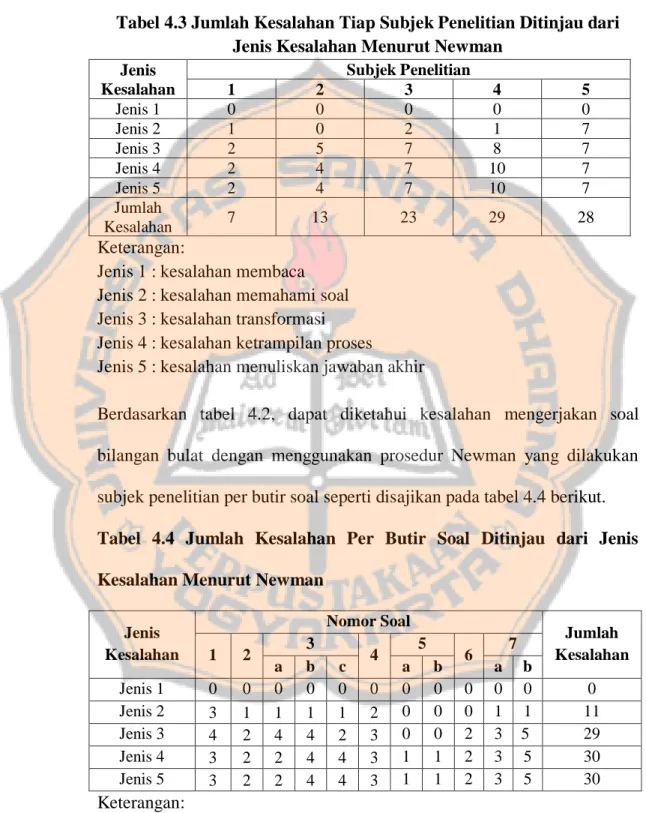
Analisis kesalahan siswa di kelas VII SMP Aloysius Turi tahun ajaran 2015/2016 dalam menyelesaikan soal cerita Matematika pada topik bilangan bulat berdasarkan metode analisis kesalahan newman
Teks penuh
Gambar




Garis besar
Dokumen terkait
perbuatan tersebut kadang-kadang amat tergantung pada pendapat umum pada waktu dan tempat itu, hal penting yang perlu dilihat adalah sejauh mana pelanggaran
[r]
sekalipun Anggaran DAU mengalami pengurangan yang sangat berarti, sebagai akibat berkurangnya wilayah Pemerintah Kabupaten Maluku Tengah yang diakibatkan oleh ketentuan pasal 7
- Jumlah dan jenis alat tangkap lemuru tahun 2010 - Hasil tangkapan masing-masing alat tangkap tahun 2010 - Upaya penangkapan (trip) masing-masing alat tangkap untuk
• Perlu dilaksanakannya Operational Level Agreement antara unit pengelola TI dengan unit-unit internal Ditjen Migas, namun kesepakatan itu harus disesuaikan dengan kapabilitas
Peristia dan0 adalah mutually exclusive $disjoint events& jika terjadinya salah satu peristia tersebut dalam sebuah eksperimen probabilitas men%egah
Berdasarkan latar belakang tersebut, penelitian ini bertujuan untuk mengetahui secara lebih pasti dan terperinci analisis faktor-faktor yang mempengaruhi pengungkapan
WAN (Wide Area Network) adalah kumpulan dari LAN dan atau Workgroup yang dihubungkan dengan menggunakan alat komunikasi modem dan jaringan Internet, dari/ke