Gelombang: distribusi lebar (broad) dari energi, mengisi ruang yang dilaluinya gangguan yang menjalar (bukan medium).

Gelombang

Gelombang

Gelombang

g

Partikel:

konsentrasi materi, dapat

mentransmisikan energi

mentransmisikan energi.

Gelombang:

distribusi lebar (broad) dari

energi, mengisi ruang yang dilaluinya →

gangguan yang menjalar (bukan medium).

Mekanika Kuantum:

gelombang materi

(matter waves)

(

)

Tipe Gelombang

p

g

Contoh gelombang:

Gelombang air

(air bergerak naik & turun)

Gelombang air

(air bergerak naik & turun)

Gelombang bunyi

(udara bergerak maju & mundur)

Gelombang stadium

(orang bergerak naik & turun)

Tiga tipe gelombang:

g

(

g

g

)

Gelombang cahaya

(apa yang bergerak??)

Tiga tipe gelombang:

Gelombang Mekanik (bunyi, air, perlu medium untuk menjalar)

Gelombang Elektromagnetik (cahaya, radio, tidak perlu medium)

G l b M t i

Tipe Gelombang

p

g

Menurut arah gangguan relatif terhadap arah propagasi:

Gelombang Transversal:

P i d h di ⊥ Perpindahan medium ⊥

Arah jalar gelombang

Gelombang Longitudinal: Perpindahan medium //

Arah jalar gelombang Arah jalar gelombang

Tipe Gelombang

p

g

Gelombang Longitudinal

Tipe Gelombang

p

g

Gelombang Air Gelombang Air

Tipe Gelombang

p

g

Sifat Gelombang

g

z Panjang Gelombang: Jarak λ antara titik-titik identik pada gelombang.

A li d P i d h k i A d i b h i ik

z Amplitudo: Perpindahan maksimum A dari sebuah titik pada gelombang. λ Panjang gelombang λ Amplitudo A A

z Perioda: Waktu T dari sebuah titik pada gelombang untuk melakukan satu osilasi secara komplit.

+A y 0 = t λ

Sifat Gelombang

+A -A T t = x

g

z Laju: Gelombang bergerak satu panjang gelombang λ

d l t i d T hi +A -A 4 T t = x dalam satu perioda T sehingga

lajunya v = λ / T.

λ

=

v

T

v

=

λ/

T

=

λ

f

+A 4 2T t = x f = 1/T : Frekuensi, jumlah

perioda per detik (Hertz, Hz)

-A +A 4 3T t = x -A +A T t = x

Contoh

z Sebuah kapal melempar sauh pada suatu lokasi dan diombang-ambingkan gelombang naik dan turun. Jika jarak antara puncak gelombang adalah 20 meter dan laju jarak antara puncak gelombang adalah 20 meter dan laju gelombang 5 m/s, berapa lama waktu Δt yang

dibutuhkan kapal untuk bergerak dari puncak ke dasar

lembah gelombang? t

lembah gelombang? t

t + Δt

z Diketahui v =

λ

/ T, maka T =

λ

/ v. Jika

λ

= 20 m dan v = 5 m/s, maka T = 4 sec

z Waktu tempuh dari puncak ke lembah adalah setengah

z Waktu tempuh dari puncak ke lembah adalah setengah perioda, jadi Δt = 2 sec

Contoh

z Laju bunyi di udara sedikit lebih besar dari 300 m/s, dan laju cahaya di udara kira-kira 300,000,000 m/s.

z Misal kita membuat gelombang bunyi dan gelombang

cahaya yang keduanya memiliki panjang gelombang 3 m. ÍBerapa rasio frekuensi gelombang cahaya terhadap ÍBerapa rasio frekuensi gelombang cahaya terhadap

gelombang bunyi?

Solusi

z Diketahui v = λ / T = λf (karena f = 1 / T )

Jadi f = v

λλ

Karena λ sama untuk kedua gelombang, maka

1 000 000

v

f

_{light light}

≅

1,000,000

v

f

g g

=

≅

Contoh …

z Berapakah frekuensi tersebut???

f v 300m s 100 H

Untuk bunyi dengan λ = 3m :

(low hum)

f v 300m s

3m 100 Hz

= ≈ =

λ

Untuk cahaya dengan λ = 3m :

(low hum) f v 3 10 m s 3m 100 MHz 8 = ≈ × = λ

Untuk cahaya dengan λ 3m :

(radio FM)

3m λ

Contoh

z Panjang gelombang microwave yang dihasilkan oleh oven microwave kira-kira 3 cm. Berapa frekuensi yang

dihasilkan gelombang ini yang menyebabkan molekul air dihasilkan gelombang ini yang menyebabkan molekul air makanan anda bervibrasi?

z Ingat v = λf z Ingat v = λf. f v 3 10 m s .03m 10 Hz 10GHz 8 10 = = × = = λ 1 GHz = 109 _siklus/sec Laju cahaya c = 3x108 _m/s 03 λ H H H H

Membuat molekul air bergoyang Membuat molekul air bergoyang

Koefisien

absorbsi dari air sebagai fungsi dari frekuensi. _{f = 10 GHz} Visible “ ater “water hole” 14

Fungsi Gelombang

g

g

• Kita menggunakan fungsi sinusoid untuk menggambarkan berbagai gelombang

y(x,t) = y

_m

sin(kx-

ω

t)

y :

amplitudo

Jika ∆

x

=

λ

fasa

y

_m

:

amplitudo

kx-

ω

t :

fasa

Jika ∆

x

=

λ

, fasa

bertambah 2

π

k:

bilangan

gelombang

k

=

2

π

λ

bertambah 2

Jika ∆

t

=

T

, fasa

π

gelombang

ω

:

frekuensi angular

ω

=

2

π

T

= 2

π

f

Contoh

(a) Tuliskan persamaan yang gelombang sinusoidal transversal yang menjalar pada tali dalam arah +y dengan bilangan

gelombang 60 cm-1 _{perioda 0 20 s dan amplitudo 3 0 mm}

gelombang 60 cm , perioda 0.20 s, dan amplitudo 3.0 mm. Ambil arah z sebagai arah transversal. (b) Berapa laju

transversal maksimum dari titik pada tali? (a)

k

= 60 cm-1,

T

=0.2 s,

z

_m=3.0 mm

z

(

y,t

)=

z

_msin(

ky

-

ωt

)

ω

= 2π/T = 2π/0.2 s =10πs-1

z

(

y, t

)=(3.0mm)sin[(60 cm-1₎

_y

_-(10πs-1₎

_t

_] u_z = ∂z(y,t) ∂t = −ωzm cos ky

(

− ωt

)

⎛ _⎞ (b) Laju 16 = −ωz_m sin π 2 − (ky − ωt) ⎛ ⎝ ⎞ ⎠

u

z,max=

ωz

m = 94 mm/s

Soal

Gelombang sinusoidal dengan frekuensi 500 Hz menjalar

dengan laju 350 m/s. (a) Berapa jarak dua titik yang berbeda fasa /3 rad? (b) Berapa beda fasa antara dua pergeseran fasa π/3 rad? (b) Berapa beda fasa antara dua pergeseran pada suatu titik dengan perbedaan waktu 1.00 ms ?

f

= 500Hz

v

=350 _{y(x t) = y sin(kx-}

ω

_t)

f

500Hz,

v

350 mm/s

φ

( )

x,t

= kx −

ω

t

(a) Fasa

_k

₌

2π

λ

y(x,t) = y_msin(kx-

ω

t)

φ

( )

x,t

=

2

π

f

v

x

− 2

π

ft

λ

v

=

λ

f

=

ω

k

Δ

φ

=

2

π

f

v

Δx

⎛ ⎞

k

ω

= 2π

f

Δx =

v

2

π

f

Δ

φ

=

350m/s

2

π

(

500Hz

)

π

3

⎛

⎝

⎞

⎠ = 0.117 m

3 (b)

Δ

φ

= 2

π

_f

Δt = 2

π

(

_{500 Hz}

)

_(1.00

×10

−3

₎

=

π

_rad.

Mengapa sinusoid?

g p

Komposisi Fourier dari gelombang square

Komposisi Fourier dari gelombang square

Mengapa sinusoid?

g p

Gelombang gigi gergaji

Laju Gelombang

j

g

„ Seberapa cepat bentuk gelombang menjalar?

Pilih sebuah perpindahan tertentu ⇒ fasa tertentu

kx-

ω

t = konstan v = dx dt =

ω

k y(x,t) = y_msin(kx-

ω

t) v>0 y(x,t) = y_msin(kx+

ω

t) _v<0

„ Laju gelombang adalah konstanta yang bergantung hanya

τ

Gelombang Transversal (Tali):

j g g y g g g y

pada medium, bukan pada amplitudo, panjang gelombang atau or perioda (seperti OHS)

v =

τ

μ

Gelombang Transversal (Tali):

Gelombang pada tali

Gelombang pada tali

„ Apa yang menentukan laju gelombang?

„ Tinjau sebuah pulsa yang menjalar pada sebuah tali: „ Tinjau sebuah pulsa yang menjalar pada sebuah tali:

v

Mi lk

z Tegangan tali adalah F

( / )

Misalkan:

z Massa per satuan panjang adalah μ (kg/m)

z Bentuk tali pada daerah maksimum pulsa adalah lingkaran dengan jari-jari R

R μ

F lingkaran dengan jari-jari R

R μ

Gelombang pada tali ...

g p

z Tinjau gerak bersama dengan pulsa

z Gunakan F = ma pada segmen kecil tali di “punck” pulsa

z Gaya total F_NET adalah jumlah tegangan F pada ujung-ujung segmen tali.

z Gunakan F ma pada segmen kecil tali di punck pulsa

g

z Total gaya pada arah-y

v θ θ F F y F_NET = 2F θ x y

Gelombang pada tali ...

z Massa m dari segmen adalah panjangnya (R x 2θ)

dikalikan massa per satuan panjang μ

g p

dikalikan massa per satuan panjang μ.

m = R 2θ μ 2θ μ R θ θ y x

Gelombang pada tali ...

z Percepatan a dari segmen adalah v 2_{/ R (sentripetal)}

dalam arah-y.

g p

v a R y x

Gelombang pada tali ...

z Jadi F_NET = ma menjadi:

R v 2 R F 2 2 ⋅ θμ = θ

g p

R F_TO T m a 2

v

F

=

μ

μ = F v v tegangan F

Gelombang pada tali ...

J di did t F

g p

z Jadi didapat: μ = F v v tegangan F

z Jika tegangan makin besar laju bertambah g g

massa per satuan panjang μ z Jika tegangan makin besar, laju bertambah. z Jika tali makin berat, laju berkurang.

z Seperti disebutkan sebelumnya, ini y bergantung hanya pada g g y sifat alami medium, bukan pada amplitudo, frekuensi, dst. dari gelombang.

Daya Gelombang

y

g

„ Gelombang menjalar karena tiap bagian dari medium

meng-komunikasikan geraknya pada bagian di sekitarnya. … Energi di transfer karena ada kerja ang dilak kan!

… Energi di-transfer karena ada kerja yang dilakukan!

„ Berape energi yang bergerak pada tali per satuan waktu.

(atau berapa

daya

-nya

?)

Daya Gelombang ...

y

g

„ Bayangkan tali bagian kiri digerakkan naik dan turun dalam arah y.

„ Anda pasti melakukan kerja karena F.dr > 0 saat tangan

anda bergerak naik dan turun.

„ Energi pasti bergerak menjauh dari tangan anda (ke „ Energi pasti bergerak menjauh dari tangan anda (ke

kanan) karena energi kinetik (gerak) dari tali tetap sama.

Bagaimana energi bergerak?

g

g

g

„ Tinjau sembarang posisi x pada tali. Tali di

bagian kiri x melakukan kerja pada tali di bagian kanan x, sama seperti yang dilakukan tangan anda: x θ x Daya P = F

.

v _x F Daya P F v

Daya sepanjang tali

y

p

j

g

„ Karena v hanya dalam arah sumbu y, untuk menghitung

Daya = F

.

v kita hanya perlu mencari F_y = -F sin θ

≈

-F θ

Daya F v kita hanya perlu mencari F_y F sin θ F θ

jia θ kecil.

„ Kecepatan v dan sudut θ y

pada sembarang titik pada tali dapat dicari dengan mudah:

θ x F _v F_y „ Jika F _v

( )

x t dy A sin

(

kx t

)

v = = ω − ω ) t kx cos( A ) t , x ( y = − ω θ dy dx

( )

A sin

(

kx t

)

dt t , x v _y = = ω − ω

(

− ω

)

≈ θ − = = θ kA sin kx t d dy tan Ingat sin θ ≈ θ _{tan θ ≈ θ}

(

)

dx _{cos θ ≈ 1} untuk θ kecil

Daya ...

y

v _y

( )

x,t = ωAsin

(

kx − ωt

)

„ Jadi: ) t (k i kFA F F t) P( F θ 2 2

(

kx t

)

kAsin − ω − ≈ θ

z Tapi kita telah tunjukkan and

k v = ω F = μv 2 ) t (kx sin kFA F F t) P(x, = F ⋅ v = _yv_y ≈ − θv_y = ω 2 2 −ω k

(

x ,t

)

v A sin

(

kx t

)

P = μ ω2 2 2 − ω (kx t ) cos − ω (kx t ) sin 2 ( − ω )

Daya Rata-rata

y

„ Kita baru saja menunjukkan bahwa daya yang mengalir melalui titik x pada tali pada waktu t diberikan oleh:

( )

x t v A

(

kx t

)

P , = μ ω 2 2 sin 2 − ω

z Sering kali kita hanya tertarik pada daya rata-rata pada tali. Dengan mengingat bahwa nilai rata-rata dari fungsi

sin2 _{(kx -} ωt) is 1_/

2 , maka dapat dituliskan:

P = 1 v A

2

2 2

μ ω 2

z Secara umum, daya gelombang sebanding dengan laju gelombang v dan amplitudo kuadrat A2_.

Energi Gelombang

g

g

„ Telah ditunjukkan bahwa energi “mengalir” sepanjang tali.

… Sumber energi ini (dalam contoh kita) adalah tangan yang menggoyang tali naik dan turun. … Tiap segmen dari tali mentransfer energi

… Tiap segmen dari tali mentransfer energi pada (melakukan kerja pada) segmen

berikutnya dengan menggerakkannya, sama ti t seperti tangan.. P =1 A v 2 2 2 μω z Kita dapatkan d E 1 d x 1 d E d t A d x d t = 1 2 2 2 μω d E = 1 A d x 2 2 2 μω

J di d E 1 2 A2 adalah energi rata-rata

Jadi adalah energi rata rata per satuan panjang

d E

A = 1 μω 2 2

Contoh Daya:

y

„ Sebuah tali dengan massa μ = 0.2 kg/m diletakkan di atas lantai licin. Salah satu ujungnya anda pegang dan

digoyangkan ke kanan dan kiri dua kali per detik dengan digoyangkan ke kanan dan kiri dua kali per detik dengan amplitudo of 0.15 m. Anda melihat bahwa jarak antara dua perut dari gelombang adalah 0.75 m.

B t t d d b ik d t li?

… Berapa rata-rata daya yang anda berikan pada tali? … Berapa energi rata-rata per satuan panjang dari tali? … Berapa tegangan tali?

… Berapa tegangan tali?

λ = 0 75 m f = 2 Hz

A = 0.15 m λ = 0.75 m

Contoh Power ...

P = 1 v A

2

2 2

μ ω

„ Diketahui A, μ dan ω = 2πf. Ditanya v! „ Ingat v = λf = (.75 m)(2 s-1) = 1.5 m/s . Jadi: „ Jadi:

(

) (

2

)

2 m 15 0 Hz 2 2 s m 5 1 m kg 2 0 2 1 P . . ⎟ ⋅ . ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ = π P = 0 533. W Daya rata-rata

Contoh Daya ...

y

d E 1 2 2 d E d x = A 1 2 2 2 μω „ Jadi: d E

(

)

(

)

d x k g m H z m = 1 ⎛_⎝⎜ ⎞_⎠⎟ ⋅ 2 0 2 2 2 0 1 5 2 2 . π .

Energi rata-rata per satuan panjang

dE

Contoh Daya ...

y

„ Diketahui bahwa tegangan tali bergantung pada laju gelombang dan rapat massa:

2 2 m 5 1 kg 2 0 v F = μ = ⎜⎛ ⎟⎞⎜⎛ ⎟⎞ s 5 . 1 m 2 . 0 v F ⎟ ⎠ ⎜ ⎝ ⎟ ⎠ ⎜ ⎝ = μ = Tegangan tali: F = 0.45 N

Contoh : Daya Gelombang

y

g

z Sebuah gelombang menjalar pada tali. Jika amplitudo dan panjang gelombang dibuat menjadi dua kali, berapa kali per bahan da a rata rata ang diba a oleh gelombang? perubahan daya rata-rata yang dibawa oleh gelombang? (Laju gelombang tidak berubah).

(a) 1 (b) 2 (c) 4

P_i

P P_f

Contoh : Daya Gelombang …

z Telah ditunjukkan bahwa daya rata-rata P = 1 A v 2 2 2 μω A v 1 _{2 2} 2 2 μω

y

g

P P A v A v A A f i f f i i f f i i = 2 = 1 2 2 2 2 2 2 2 μω μω ω ω Jadi

ω

λ

2

z Tapi karena v = λf = λω / 2π konstan,

ω

ω

λ

λ

f i i f

=

i e menlipatduakan panjang gelomang sama dengan i.e. menlipatduakan panjang gelomang sama dengan membuat frekuensi menjadi separuh dari awalnya.

P_{f f} A_f ⎛ _i A_f ⎜ ⎞⎟ ⎛⎜ ⎞⎟ ω 2 2 λ 2 2 So P _A A f i f f i i i f f i = = ⎝ ⎜ ⎠ ⎟ ⋅ ⎝ ⎜ ⎠ ⎟ ω 2 2 λ So ⎛⎜ ⎞⎟ ⎛⎜ ⎞⎟1 2 1 2 2 D = ⎛ ⎝⎜ ⎞⎠⎟ ⋅ ⎛⎝⎜ ⎞⎠⎟ = 1 Daya sama

Superposisi

p

p

„

„ Q:Q: Apa yang terjadi saat dua gelombang “bertabrakan?”

g g

„

„ A:A: Keduanya DIJUMLAHKAN! … Kita katakan gelombang

Prinsip Superposisi

p

p

p

Gelombang yang overlapping dijumlahkan

untuk menghasilkan gelombang resultan

untuk menghasilkan gelombang resultan

’( t) =

( t) +

( t)

y’(x,t) = y

₁

(x,t) + y

₂

(x,t)

Catatan: Gelombang yang overlapping tidak

Mengapa superposisi bekerja

g p

p

p

j

„ Dapat ditunjukkan bahwa persamaan gelombang adalah linier.

… Persamaan tidak memiliki suku dimana variabel dikuadratkan.

„ Untuk persamaan linier, jika terdapat dua (atau lebih) l i b b d f d f k Bf + Cf j b h solusi berbeda, f₁ dan f₂ , maka Bf₁ + Cf₂ juga sebuah solusi! (B dan C adalah konstanta sembarang.)

„ Ini dapat dilihat pada kasus osilasi harmonik sederhana:

x x

d2 _{= ω2}

„ Ini dapat dilihat pada kasus osilasi harmonik sederhana:

linier dalam x! x dt2 = −ω x = B sin(ωt) + C cos(ωt) linier dalam x! x = B sin(ωt) + C cos(ωt)

Penjumlahan Fasor

j

FASOR

: vektor dengan amplitudo y dari

FASOR

: vektor dengan amplitudo y

_m

dari

gelombang dan bergerak rotasi terhadap titik

asal dengan laju angular

g

j

g

ω

dari gelombang

g

g

Penjumlahan Fasor dapat digunakan jika:

„

Gelombang yang akan disuperposisi memiliki

laju angular

ω

yang sama

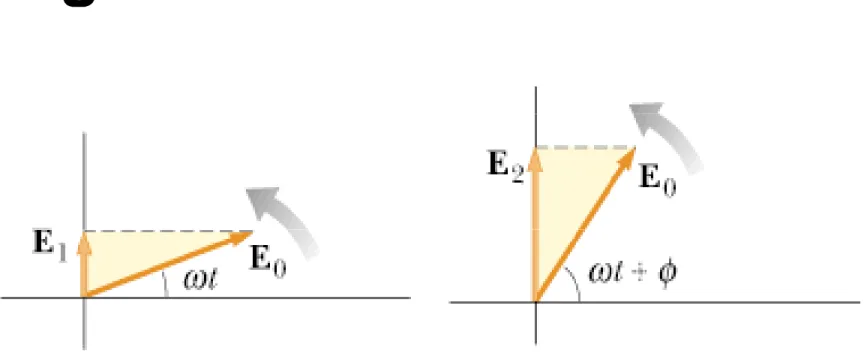
Diagram Fasor

g

Fungsi gelombang diberikan oleh proyeksi fasor (vektor E₀ dalam diagram) pada sumbu vertikal.

Penjumlahan fasor 2 gelombang

j

g

g

α

Penjumlahan dua gelombang dengan beda fasa φ secara grafis. Gelombang resultan E_P (proyeksi dari fasor E_R pada sumbu vertikal) adalah: vertikal) adalah:

(

ω +α

)

= _R t P E sin E

Penjumlahan fasor N gelombang

j

g

g

(

ω

+

α

)

=

E

sin

t

E

_P

=

E

_R

sin

(

ω

t

+

α

)

Interferensi

sinα + sinβ = 2sin1

2

(

α + β

)

cos 1

2

(

α − β

)

te e e s

2 2

• Dua gelombang, dengan amplitudo, panjang gelombang, laju yang sama, tapi berbeda fasa

y

₁

( )

t

= y

_m

sin kx

(

−

ω

t

)

_y

₂

( )

_t

= y

_m

_{sin kx}

(

−

ω

_t

+

φ

)

j y g

( )

⎟

⎠

⎞

⎜

⎝

⎛

₋

₊

⎥⎦

⎤

⎢⎣

⎡

=

+

=

′

_φ

_ω

_φ

2

1

sin

2

1

cos

2

2 1

y

y

kx

t

y

t

y

_m

Konstruktif:

φ

= m 2

( )

π

Amplitudo=2y_m

m

=0 1 2

Destruktif:

( )

π

φ

2

2

1 ⎟

⎠

⎞

⎜

⎝

⎛ +

= m

_Amplitudo=0

m

0,1,2,

⎝

2

⎠

Soal

Dua gelombang identik yang bergerak searah, memiliki perbedaan fasa sebesar π/2 rad. Berapa amplitudo

gelombang resultan dinyatakan dalam amplitudo y dari

y

₁

( )

t

= y

_m

sin kx

(

−

ω

t

)

gelombang resultan dinyatakan dalam amplitudo y_m dari masing-masing gelombang?

1

⎡

⎤

⎛

1

⎞

y

₁

( )

t

y

_m

s

(

kx

ω

t

)

y

₂

( )

t

= y

_m

sin kx

(

−

ω

t

+

φ

)

′

y t

( )

= 2y

_m

cos

1

2

φ

⎡

⎣

⎤

⎦

sin kx

−

ω

t

+

1

2

φ

⎛

⎝

⎞

⎠

π

φ

2

π

φ

=

Untuk

A

2

cos

1

φ

2

cos

π

1 4

A

= 2y

_m

cos

2

φ

= 2y

m

cos

4

= 1.4y

m

Superposisi & Interferensi

p

p

„ Telah kita lihat jika gelombang saling bertabrakan

(dijumlahkan), hasilnya dapat lebih besar atau lebih kecil dibandingkan aslinya

dibandingkan aslinya.

„ Ini disebut penjumlahan “konstruktif” atau “destruktif” bergantung pada tanda relatif dari masing-masing gelombang

gelombang.

penjumlahan konstruktif penjumlahan destruktif

Superposisi & Interferensi

p

p

„ Tinjau dua gelombang harmonik A dan B yang bertemu pada x=0.

… Amplitudo sama, tapi ω₂ = 1.15 x ω₁. … Amplitudo sama, tapi ω₂ 1.15 x ω₁.

„ Perpindahan terhadap waktu untuk masing-masing sbb:

A(ω t) A(ω₁t) B(ω₂t)

Bagaimana bentuk C(t) = A(t) + B(t) ??

INTERFERENSI

52

INTERFERENSI DESTRUKTIF

Pelayangan

y

g

z Dapatkan pola ini diprediksi secara matematik? ÍTentu!

(

t

)

cos

(

t

)

cos A 2 ) t cos( A ) t cos( A ω + ω = ω ω

z Jumlahkan dua kosinus dan ingat identitas:

(

t

)

cos

(

t

)

cos A 2 ) t cos( A ) t cos( A ω₁ + ω₂ = ω_L ω_H

(

)

ω_L = 1 ω − ω 2 1 2 H 2

(

1 2

)

1 ω + ω = ω where and cos(ω t)

Refleksi

„ Saat gelombang menjalar dari satu batas ke batas lainnya, terjadilah refleksi. Beberapa gelombang berbalik kembali (mundur) dari batas

(mundur) dari batas

… Menjalar dari cepat ke lambat -> terbalik

… Menjalar dari lambat ke cepat -> tetap tegak

μ

=

F

Refleksi

From high speed to

low speed (low

From low speed to

high speed (high

(

density to high

density)

g

( g

density to low

density)

Gelombang Tegak

sinα + sinβ = 2sin1

2(α + β)cos 1

2(α −β)

g

g

Dua

gelombang sinusoidal dengan

AMPLITUDO

dan

PANJANG GELOMBANG

sama

menjalar

2 2

dan

PANJANG GELOMBANG

sama

menjalar

dalam

ARAH BERLAWANAN

berinterferensi untuk

menghasilkan gelombang berdiri

g

g

g

( )

[

]

y

₁

( )

t

= y

_m

sin kx

(

−

ω

t

)

y

₂

( )

t

=

y

_m

sin

(

kx

+

ω

t

)

′

y x,t

( )

= y

₁

+ y

₂

= 2y

[

_m

sin kx

]

cos

ω

t

Gelombang tidak menjalar Amplitudo bergantung

pada posisi tidak menjalar

sin n( )π = 0 sin n + 1 2 ⎛ ⎝ ⎞ ⎠ π ⎡ ⎣ ⎤ ⎦ = 1

Gelombang Tegak…

′

y x,t

( )

= 2y

[

_m

sin kx

]

cos

ω

t

2 ⎝ ⎠ ⎣ ⎦

g

g

NODES

: titik-titik dengan amplitudo nol

n

λ

2π

kx

= n

π

, or x

=

n

λ

2

n

= 0,1,2,...

k =

2π

λ

ANTINODES

: titik-titik dengan amplitudo

maksimum (2y

_m

)

kx

= n +

1

2

⎛

⎝

⎞

⎠

π

, or x

= n +

1

2

⎛

⎝

⎞

⎠

λ

₂

n

= 0,1,2,...

Gelombang Tegak pada Tali

g

g

p

SYARAT BATAS

menentukan bagaimana

gelombang direfleksikan.

gelombang direfleksikan.

Ujung terikat

: y = 0, node pada ujung

Gelombang yg direfleksikan memiliki

tanda terbalik

Ujung bebas

: antinode pada ujung

tanda terbalik

Gelombang yg direfleksikan memiliki

tanda yang sama

tanda yang sama

Kasus: Kedua Ujung Terikat

j

g

y x,t

( )

= 2y

[

_m

sin kx

]

cos

ω

t

y x

(

= 0

)

= 0

y x

(

= L

)

= 0

i kL

( )

0

k

n

π

1 2 3

sin kL

( )

= 0

k

=

L

, n

= 1,2,3,....

k

hanya dapat memiliki nilai berikut

λ

=

2 L

n

ATAU

k = 2_λπ berikut f = v λ

f

=

nv

2L

ATAU

dimana

v

=

τ

_μ

_λ

2L

μ

Gelombang Tegak

g

g

„ Fundamental n=1 „ λ_nn = 2L/n/

Frekuensi Resonansi

n

τ

2 L

Resonansi:

saat terbentuk gelombang berdiri.

f

=

n

2L

τ

μ

λ

=

2 L

n

H

ik f

d

t l t

t

Harmonik fundamental atau pertama

1

λ

=

L

f

=

1

τ

2

=

L

μ

L

f

2

1

=

Harmonik ke dua atau overtone pertama

Harmonik ke dua atau overtone pertama

2

λ

=

L

f

₂

=

2 f

₁