Analisa Simulasi Dan Penentuan Parameter Sistem Pengendali PID Pada Pelontar Peluru Plastik Dua Sumbu Putar - ITS Repository
Teks penuh
Gambar
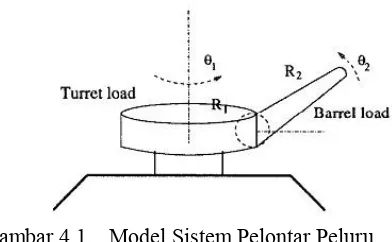
![Gambar 2.1 Sistem Turret dan gun[2]](https://thumb-ap.123doks.com/thumbv2/123dok/1810150.2099721/22.420.95.270.321.402/gambar-sistem-turret-dan-gun.webp)
![Gambar 2.2 Contoh respon sistem stabil[7]](https://thumb-ap.123doks.com/thumbv2/123dok/1810150.2099721/24.420.72.335.173.483/gambar-contoh-respon-sistem-stabil.webp)
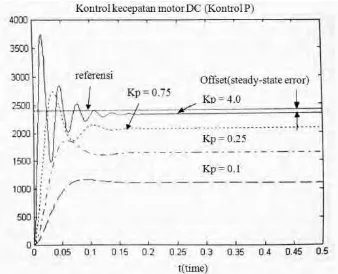
![Gambar 2.10 Respon kontroler PD [3]](https://thumb-ap.123doks.com/thumbv2/123dok/1810150.2099721/29.420.125.304.304.462/gambar-respon-kontroler-pd.webp)
Dokumen terkait
Dengan bauran promosi pengaruh yang diberikan terhadap keputusan pembelian sangat besar, karena perusahaan dapat memperkenalkan produk-produknya, membujuk dan menyarankan
Hasil penelitian ini menunjukkan pentingnya pemeriksaan sitogenetik pada penderita ambigus genitalia, tetapi adanya abnormalitas kromosom Y berupa aberasi
keseluruhan lampiran sebagaimana dimaksud pada huruf a harus sesuai dengan Peraturan Pemerintah Nomor 5 Tahun 2009 tentang Bantuan Keuangan Kepada Partai Politik dan
Bank Kustodian akan menerbitkan Surat Konfirmasi Transaksi Unit Penyertaan yang menyatakan antara lain jumlah Unit Penyertaan yang dijual kembali dan dimiliki serta Nilai
Diberikan kepada anak Paud setiap hari ……… 2.. Bahan dasar makanan tambahan adalah
Pada saat penghentian pengakuan atas aset keuangan secara keseluruhan, maka selisih antara nilai tercatat dan jumlah dari (i) pembayaran yang diterima, termasuk aset baru
o TL0 dapat berfungsi sebagai counter maupun timer 8 bit dengan sumber detak yang dapat dipilih yaitu sumber detak yang berasal dari P3.4 (T0) atau dari osilator/12. o
Untuk fungsi-fungsi yang sederhana dimana grafik fungsinya dapat digambarkan dengan mudah, ada dua metode grafik yang dapat dilakukan untuk mendapatkan tebakan
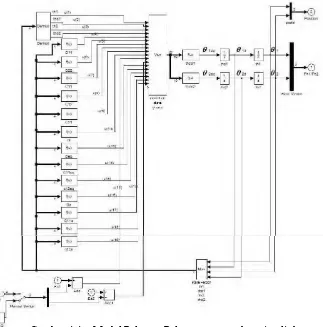
![Gambar 2.11 Diagram kontrol PID untuk motor DC [3]](https://thumb-ap.123doks.com/thumbv2/123dok/1810150.2099721/30.420.115.278.394.531/gambar-diagram-kontrol-pid-untuk-motor-dc.webp)
![Gambar 2.13 Interest Point[8]](https://thumb-ap.123doks.com/thumbv2/123dok/1810150.2099721/31.420.126.308.259.451/gambar-interest-point.webp)