PROFIL KOMUNIKASI MATEMATIS SISWA DALAM MENYELESAIKAN SOAL CERITA OPERASI PENJUMLAHAN DAN PENGURANGAN PECAHAN DI KELAS VIII SMP NEGERI 14 PALU
Teks penuh
Gambar

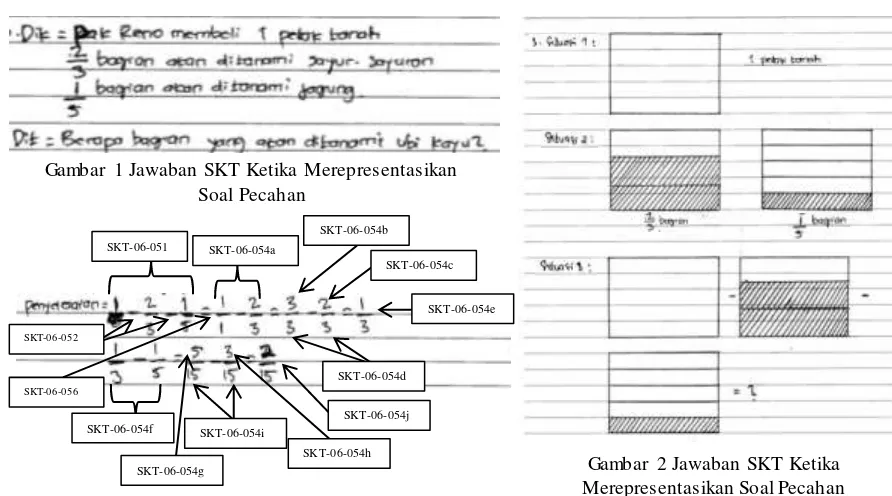

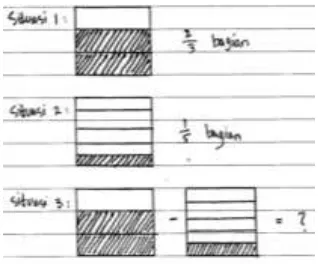
Dokumen terkait
The Paradox of Freedom in Modern Art (ed. Lavrijsen, 1998, hal 43-48) berpendapat mengenai hal senada melalui pandangan- nya pada keberadaan infrastruktur seni
Bentuk apresiasi tersebut salah satunya dapat diwujudkan dengan tetap menjaga eksistensi batik Indonesia, menciptakan motif-motif baru yang sebelumnya belum pernah dibuat dan
Rumusan masalah dalam penelitian ini adalah apakah inovasi pembelajaran dengan kombinasi metode konvensional dengan strategi mind mapping dapat meningkatkan hasil belajar siswa
(10) Hasil penelitian Hovanec dan DeLong (1996) mengungkapkan bahwa ditemukan beberapa jenis mikroba yang berperan dalam proses nitrifikasi, baik sebagai pengoksidasi amonia
MENEGASKAN SEMULA komitmen ASEAN terhadap penggalakan dan perlindungan hak asasi manusia dan kebebasan asasi serta tujuan dan prinsip yang termaktub dalam Piagam
Banyaknya objek pariwisata yang bisa digunakan untuk menambah devisi negara membutuhkan sebuah sistem dalam membantu pengguna dalam mencari objek yang dimiliki oleh pengguna.. Dalam
Upaya orangtua dalam meningkatkan motivasi intrinsik belajar Al- Quran pada usia anak-anak di TPQ agar anak tersebut memiliki rasa senang yang timbul dari dalam dirinya,
Metode analis yang digunakan dalam penelitian ini adalah regresi linier berganda.Analisis linier berganda ini digunakan untuk mengetahui adanya pengaruh antara