Pendahuluan Untuk mengetahui stabilitas suatu sistem, kita tidak perlu mencari lokasi aktual

Pendahuluan

Untuk mengetahui stabilitas suatu sistem, kita tidak perlu mencari lokasi aktual pole, namun cukup dengan melihat sign-nya, yang akan menunjukkan apakah pole berada di RHP (right-half-plane) atau LHP (left-halp-plane).

Kriteria Hurwitz dapat digunakan untuk mengetahui instabilitas sistem, tapi tidak cukup untuk memastikan stabilitas sistem.

Kriteria Routh-Hurwitz adalah metode yang efektif untuk menguji kestabilan

sistem. Kriteria ini juga dapat menunjukkan jumlah pole pada RHP atau pada sumbu imajiner.

Tes stabilitas yang handal untuk segala bentuk kasus dapat digunakan dalam proses disain untuk memastikan kestabilan sistem, misalnya untuk memantau kapan sistem mulai tidak stabil jika gain terus ditingkatkan.

6.5 Kriteria Stabilitas Routh-Hurwitz

6.5.1 Larik Routh (Routh Array)

Gambar berikut adalah sebuah sistem (sebagai contoh kasus) :

Persamaan karakteristik closed-loop-nya adalah :

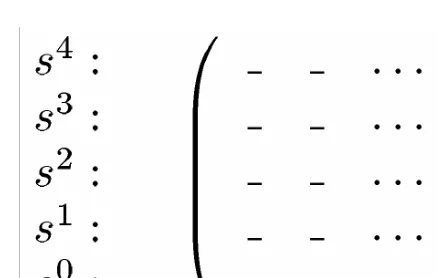
Langkah selanjutnya adalah menginsialisasi Routh array dengan mengisi dua baris pertama dengan koefisien polinom karakteristik sbb. :

1. Untuk baris s4_{, elemen pertamanya adalah a}

4, yaitu koefisien s4. Elemen berikutnya adalah a2 _{dan elemen terakhir adalah a}

0. Jadi, baris pertama adalah : s4 _{: a}

4 a2 a0

Perhatikan bahwa pada langkah ini, s4 _{hanya diisi oleh koefisien genap, karena} n = 4 (genap). Jika n ganjil, maka baris diisi dengan koefisien ganjil.

2. Untuk baris ke dua (s3_{), dilakukan pengisian elemen yang tersisa. Jadi} s3 _{: a}3 _a1 ₀

Angka 0 digunakal untuk menyamakan jumlah kolom.

Langkah berikutnya adalah mengisi baris yang tersisa pada matriks. Baris ke-3 diisi melalui pengoperasian baris ke-1 dan ke-2. Baris ke-4 diisi melalui pengoperasian baris ke-2 dan ke-3. Demikian seterusnya hingga seluruh baris terisi.

1. Dimulai dengan pembentukan matriks 2 x 2 dengan mengambil elemen kiri-atas dari matriks. Matriks 2 x2 ini dinamakan matriks R₁.

Elemen pertama dari baris ke-3 Routh Array dinamakan b₁, dimana b₁ = -det(R₁)/R₁(1,2)

2. Elemen ke-2 dari baris ke-3, b₂, dihitung dengan cara yang sama. R₂ dibuat dengan mengganti elemen kolom-2 dengan elemen kolom-3, sementara elemen kolom-1 dibiarkan tetap.

3. Langkah ini diteruskan hingga determinan bernilai nol, dimana selanjutnya elemen baris-3 diisi dengan nilai 0.

6.5.2 Tes Routh-Hurwitz

Dengan kriteria Routh-Rouwitz dapat dilakukan pengujian terhadap sistem, yang karakteristik closed-loop-nya telah lulus uji kriteria Hurwitz.

Kriteria Routh-Hurwitz :

Jumlah akar polinom karakteristik yang berada pada right-half-plane sama dengan jumlah perubahan sign pada kolom pertama Routh Array

Contoh 6.1

Jawab :

Karena koefisien persamaan sudah lengkap, maka sistem lulus tes Hurwitz. Dilakukan pengujian lebih lanjut dengan kriteria Routh-Hurwitz. Hasil inisialisasi adalah sbb. :

Kemudian dilakukan langkah-langkah untuk melengkapi isi tabel. Hasilnya sbb. :

Jadi matriksnya adalah dan isi kolom ke-1 adalah

6.6 Kasus-kasus khusus

Dua kasus khusus dapat terjadi pada saat pembuatan Routh array. • Nilai nol bisa muncul pada kolom pertama array.

• Seluruh elemen pada satu baris bernilai nol.

6.6.1 Nilai nol di kolom pertama

Jika kolom pertama memiliki elemen bernilai nol, maka akan terjadi operasi "pembagian dengan nol" pada langkah pencarian elemen untuk baris berikutnya. Untuk menghindari-nya, digunakan satu nilai kecil e (epsilon) sebagai pengganti nilai nol di kolom pertama. Contoh 6.2

Diketahui sebuah sistem kontrol memiliki fungsi transfer closed-loop sebagai berikut :

Jawab :

Polinom karakteristiknya adalah

sehingga Routh array-nya menjadi seperti yang terlihat pada tabel kiri. Pada tabel kanan, terlihat hasil analisis perubahan sign.

6.6.2 Seluruh elemen pada baris bernilai nol Hal ini bisa terjadi untuk polinom genap

Contoh 6.3

Buat Routh array untuk sistem dengan fungsi transfer closed-loop sbb. :

Jawab :

Selanjutnya, dilakukan diferensiasi Q(s) terhadap s :

dan baris ke-3 diganti dengan koefisien hasil derivatif (setelah disederhanakan melalui pembagian dengan 4), seperti terlihat pada tabel kiri di bawah ini.

Baris-baris lain dibuat dengan cara biasa, yang hasilnya terlihat di atas pada tabel kanan.

6.6.3 Interpretasi baris nol

Baris nol akan muncul pada Routh array jika polinom genap murni merupakan faktor dari polinom karakteristik. Sebagai contoh, polinom s4 _{+ 5s}2 _{+ 7 adalah polinom genap} murni, yang hanya memiliki pangkat genap untuk s. Polinom genap memiliki akar-akar simetris terhadap sumbu imajiner. Beberapa kondisi simetri dapat terjadi :

1. akar-akar real dan simetris terhadap sumbu imajiner (A)

2. akar-akar imajiner dan simetris terhadap sumbu real (B), atau

3. akar-akar bersifat kuadrantal (C)

Adalah polinom genap yang menimbulkan baris nol pada Routh array. Dengan demikian, baris nol mengindikasikan adanya akar-akar simetris terhadap origin. Beberapa akar dapat berada pada sumbu imajiner (simetri jenis B). Sebaliknya, jika kita tidak mendapatkan baris nol, kemungkinan kita tidak memiliki akar pada sumbu jω.

Karakteristik lain dari Routh array untuk kasus di atas yang masih perlu diperta-nyakan adalah apakah baris sebelum baris nol mengandung polinom genap, yang merupakan faktor polinom asalnya. Pada contoh yang lalu, polinom s4 _{+ 6s}2 _{+ 8} adalah faktor dari polinom asal. Akhirnya, uji Routh, dari baris yang

mengan-dung polinom genap hingga baris terakhir, hanya menguji pole pada polinom genap. Contoh berikut dapat menjelaskan hal ini.

Contoh 6.4

Jawab :

Dari persamaan dapat dibuat Routh array sbb. :

Untuk mempermudah, baris s6 _{dikalikan dengan 1/10 dan baris s}4 _{dikali 1/20. Terdapat} baris nol pada baris s3_{. Kembali ke baris s}4_{, ekstraksi polinom genap dan}

Baris nol diganti dengan 4, 6, 0 = 2, 3, 0 dan Routh array dapat dilengkapi :

Interpretasi

Kesimpulan yang bisa diambil adalah tidak ada perubahan sign dari bariss4 _{hingga s}0

sehingga tidak ada pole pada RHP (berarti tidak ada pole pada sumbu real dan kuadrantal). Tapi karena harus ada pole-pole yang simetris, maka pasti ada 4 pole pada sumbu jω.

Soal Latihan

6.7 Contoh Penggunaan Kriteria Routh-Hurwitz pada Disain Sistem Kontrol Contoh 6.5

Untuk sistem tertutup pada gambar di bawah ini, tentukan rentang nilai parameter gain K, dimana sistem closed-loop bersifat stabil.

Jawab : Fungsi transfer closed-loop adalah

Jika K = 1386, maka baris s1 _{menjadi baris nol. Baris sebelumnya adalah}

Q(s) = 18s2 _{+ 1386 dan derivatifnya adalah 36s, sehingga Routh array barunya} adalah :

Untuk polinom Q(s) tidak terdapat perubahan sign dari s1 _{hingga s}0_{, sehingga} pasti ada dua akar imajiner dan sistem bersifat stabil marginal.

Contoh 6.6

Contoh 6.6

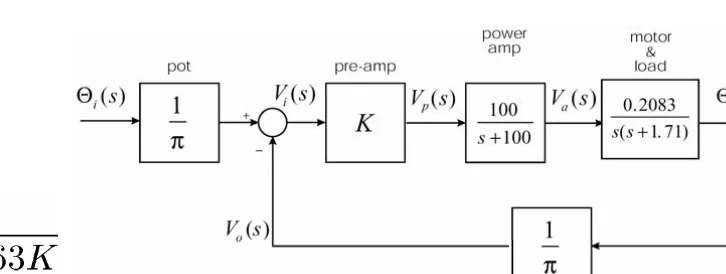
Fungsi transfer Untuk kontrol azimuth antena pada gambar di bawah ini adalah :

6.8 Stabilitas Relatif

Pengujian stabilitas sistem kontrol berdasarkan sejumlah parameter adalah hal yang sangat penting. Namun dalam perancangan sistem kontrol, stabilitas absolut bukan-lah sesuatu yang menarik.

Pada contoh sebelumnya, gain K maksimum yang diperoleh adalah 2623.29. Jika kita menginginkan "margin of safety" (margin aman) untuk memastikan bahwa sistem tidak akan pernah instabil. Sebagai contoh, untuk kasus di atas kita bisa batasi gain K maksimum sebesar 2620.29, yang berarti kita memberikan margin untuk gain sebesar 3.