III. METODE PENELITIAN
3.1. Jenis dan Sumber Data
Penelitian ini menggunakan data sekunder, yang meliputi data kuantitatif tahunan dan sekunder pada rentang waktu antara tahun 1980-2008. Data dalam penelitian ini adalah data dari negara-negara berkembang dan maju. Negara-negara berkembang yang dimaksud dalam studi empiris ini adalah 10 Negara-negara berkembang yaitu Indonesia, Thailand, Cina, India, Brasil, Argentina, Meksiko, Mesir, Afrika Selatan, dan Turki. Sedangkan, untuk negara-negara maju yang dimaksud dalam studi empiris ini adalah 10 negara maju yaitu Amerika Serikat, United Kingdom, Kanada, Jepang, Korea Selatan, Australia, Selandia Baru, Spanyol, Italia, dan Perancis. Pengolahan data dilakukan dengan perangkat lunak
Microsoft Excel 2007, Minitab dan Eviews 6.
Tabel 3.1. Data, Satuan, Simbol, dan Sumber Data
Variabel Satuan Simbol Sumber
GDP Pertanian Juta US$ GDPP WDI
GDP Industri Juta US$ GDPI WDI
CO2 Kilotonne CO2 WDI
CH4 Kilotonne CH4 EDGAR
N2O Kilotonne N2O EDGAR
Keterangan: WDI (World Development Indicator)
EDGAR (Emission Database for Global Atmospheric Research)
3.2. Metode Analisis Data
Metode analisis yang digunakan adalah metode deskriptif dan kuantitatif. Metode deskriptif adalah metode yang berkaitan dengan pengumpulan dan penyajian gugus data sehingga memberikan informasi yang berguna. Proses deskripsi data pada dasarnya meliputi upaya penelusuran dan pengungkapan
informasi yang lebih relevan yang terkandung di dalam data dan penyajian hasilnya dalam bentuk yang lebih ringkas dan sederhana, sehingga pada akhirnya mengarah pada keperluan adanya penjelasan dan penafsiran.
Metode penelitian ini juga mengandalkan proses kuantitatif untuk mendapatkan gambaran yang terstruktur dan jelas mengenai fenomena perekonomian yang terjadi. Penelitian kuantitatif berlandaskan interpretasi terhadap hasil olahan model dengan metode analisis panel data.
3.2.1. Metode Analisis Regresi dan Panel Data
Ketersediaan data untuk mewakili variabel yang akan digunakan dimana kondisinya yaitu data time series pendek dan unit cross section terbatas dapat diatasi dengan menggunakan metode panel data (pooled data). Penggunaan model panel data tersebut digunakan dengan tujuan agar diperoleh hasil estimasi yang lebih baik (efisien) dengan meningkatnya jumlah observasi yang berimplikasi pada meningkatnya derajat kebebasan (degree of freedom).
Penggunaan data panel telah memberikan banyak keuntungan secara statistik maupun teori ekonomi. Manfaat penggunaan panel data adalah sebagai berikut:
1. Mampu mengontrol heterogenitas individu
2. Mengurangi kolinearitas antar variabel, meningkatnya degree of freedom, lebih bervariasi dan lebih efisien
3. Mampu mengidentifikasi dan mengukur efek yang secara sederhana tidak dapat diperoleh dari data cross section murni atau time series murni
5. Lebih baik untuk study of dynamic adjustments
Model analisa data panel memiliki tiga macam pendekatan, yaitu pendekatan kuadrat terkecil (pooled least square), pendekatan efek tetap (fixed
effect), dan pendekatan efek acak (random effect). Selain itu, di dalam melakukan
pengolahan data panel terdapat juga kriteria pembobotan yang berbeda-beda yaitu
No weighting (semua observasi diberi bobot sama), Cross section weight (GLS
dengan menggunakan estimasi varians residual cross section, digunakan apabila ada asumsi terdapat cross section heteroskedasticity), dan Seemingly
Uncorrelated Regression/SUR (GLS dengan menggunakan covariance matrix cross section). Metode ini mengoreksi baik heteroskedastisitas maupun
autokorelasi antar unit cross section.
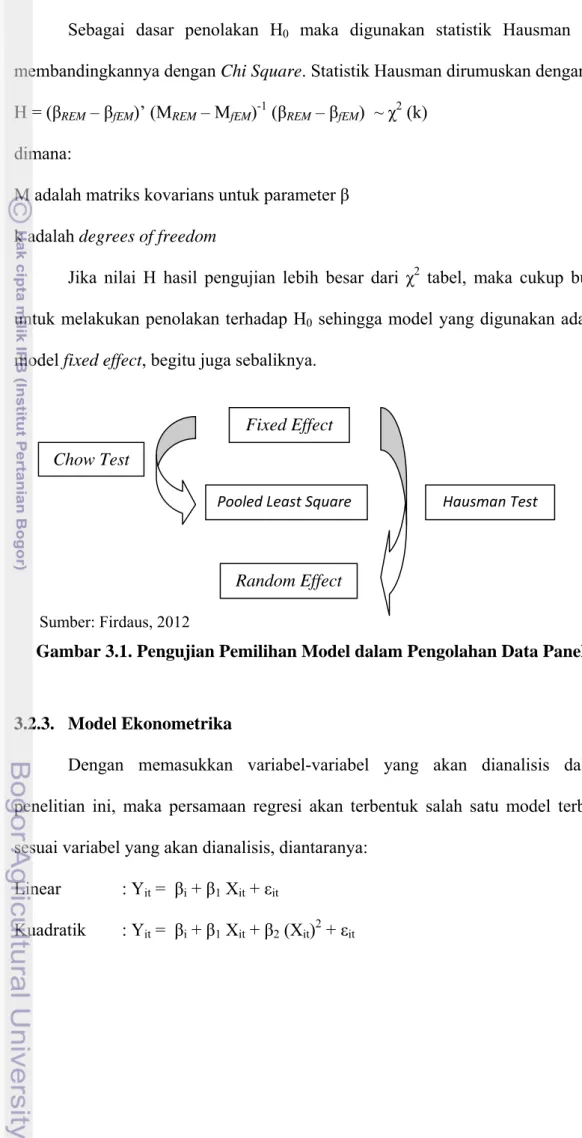
3.2.2. Pemilihan Pendekatan: Uji Hausman
Alur pengujian statistik untuk memilih pendekatan yang digunakan dapat diperlihatkan pada Gambar 3.1. Penggunaan pendekatan Pooled Least Square dirasakan kurang sesuai dengan tujuan digunakannya data panel maka dalam penelitian ini hanya mempertimbangkan pendekatan fixed effect dan random
effect. Dalam memilih apakah fixed atau random effect yang lebih baik, dilakukan
pengujian terhadap asumsi ada tidaknya korelasi antara regresor dan efek individu. Untuk menguji asumsi ini dapat digunakan Hausman Test. Dalam uji ini dirumuskan hipotesis sebagai berikut:
H0 : Model Random Effect
Sebagai dasar penolakan H0 maka digunakan statistik Hausman dan
membandingkannya dengan Chi Square. Statistik Hausman dirumuskan dengan: H = (βREM – βfEM)’ (MREM – MfEM)-1 (βREM – βfEM) ~ χ2 (k)
dimana:
M adalah matriks kovarians untuk parameter β k adalah degrees of freedom
Jika nilai H hasil pengujian lebih besar dari χ2 tabel, maka cukup bukti
untuk melakukan penolakan terhadap H0 sehingga model yang digunakan adalah
model fixed effect, begitu juga sebaliknya.
Fixed Effect Chow Test
Pooled Least Square Hausman Test
Random Effect
Sumber: Firdaus, 2012
Gambar 3.1. Pengujian Pemilihan Model dalam Pengolahan Data Panel
3.2.3. Model Ekonometrika
Dengan memasukkan variabel-variabel yang akan dianalisis dalam penelitian ini, maka persamaan regresi akan terbentuk salah satu model terbaik sesuai variabel yang akan dianalisis, diantaranya:
Linear : Yit = βi + β1 Xit + εit
Syarat: β2 ≠0, Jika β1 > 0 dan β2 < 0 maka membentuk kurva-U
terbalik (EKC), sedangkan jika β1 < 0 dan β2 > 0 maka
membentuk kurva-U.
Turning point = , jika β1 > 0 dan β2 > 0 atau β1 < 0
dan β2 < 0 maka tidak ada Turning point karena X > 0.
∆Y/∆X ≈ β1+ 2β2
Kubik : Yit = βi + β1 Xit + β2 (Xit)2 + β3 (Xit)3 + εit
Syarat: β3 ≠ 0, Jika β3 < 0 maka membentuk kurva-N terbalik,
sedangkan jika β3 > 0 maka membentuk kurva-N.
Turning point 1 = ²
Turning point 2 = ²
dimana:
Yit : emisi gas rumah kaca (CO2, N2O, dan CH4) untuk negara i pada
tahun t
Xit : GDP riil sektor industri atau pertanian untuk negara i pada tahun t
βi : konstanta
β1, β2, β3 : koefisien regresi
εit : error term untuk negara i pada tahun t
3.2.4. Perumusan Model
Setelah melewati tahapan uji pemilihan pendekatan analisis pada data panel dengan memasukkan variabel-variabel yang dianalisis dalam penelitian ini,
maka penelitian ini menggunakan pendekatan fixed effect cross section SUR sebagai analisis data panel terbaik. Dengan pendekatan fixed effect cross section SUR, maka terbentuk model terbaik sesuai variabel-variabel yang dianalisis. Adapun 6 model persamaan yang digunakan dalam penelitian ini adalah sebagai berikut: Sektor Pertanian: CO2 = βi + β1 GDPP + β2 (GDPP)2 + εit... (1) N2O = βi + β1 GDPP + β2 (GDPP)2 + εit... (2) CH4 = βi + β1 GDPP + β2 (GDPP)2 + εit... (3) Sektor Industri: CO2 = βi + β1 GDPI + β2 (GDPI)2 + εit... (4) N2O = βi + β1 GDPI + εit... .... (5) CH4 = βi + β1 GDPI + β2 (GDPI)2 + εit... .... (6) dimana: CO2 = karbondioksida (kilotonne)
N2O = nitrogen oksida (kilotonne)
CH4 = metana (kilotonne)
GDPP = Pertumbuhan ekonomi di sektor pertanian (US$) GDPI = Pertumbuhan ekonomi di sektor industri (US$)
3.2.5. Uji Beda (Uji-t)
Uji beda disebut pula dengan uji t karena merupakan huruf terakhir dari nama pencetus uji ini yaitu, Grosett. Sesuai dengan namanya, uji beda, maka uji
ini dipergunakan untuk mencari perbedaan, baik antara dua sampel data atau antara beberapa sampel data. Dalam kasus tertentu, juga bisa mencari perbedaan antara suatu sampel dengan nilai tertentu. Terdapat jenis uji beda lain selain berdasarkan jumlah kelompok sampel yang diuji. Misalnya jumlah sampel pada masing-masing kelompok juga menentukan jenis uji beda yang digunakan. Jika dua kelompok mempunyai anggota yang sama dan mempunyai korelasi maka dipergunakan uji sampel berpasangan (paired test), dan jika jumlah anggota kelompok berbeda maka memerlukan uji beda, misalnya Uji Wilcoxon, atau Mann-Whitney U-Test.
Beberapa ahli beranggapan bahwa uji beda merupakan uji statistik non parametrik dan ada pula yang beranggapan uji statistik parametrik. Uji t dengan distribusi normal maka tetap merupakan statistik parametrik, akan tetapi jika distribusi data tidak normal, barulah merupakan statistik non parametrik. Jadi penentuan parametrik atau bukan, tidak didasarkan pada jenis uji tetapi tergantung dari distribusi data, apakah normal atau tidak.
3.2.6. Pengujian Kriteria Ekonomi dan Statistik
Setelah mendapatkan parameter estimasi, langkah selanjutnya adalah melakukan berbagai macam pengujian terhadap parameter estimasi tersebutserta pengujian terkait model terbaik mana yang akan dipilih diantara pooled, fixed, dan random. Pengujian tersebut bisa berupa pengujian ekonomi, statistik, dan ekonometrik.
Pengujian dapat dilakukan dengan kriteria ekonomi dan statistik. Pengujian ekonomi dilakukan untuk melihat besaran dan tanda parameter yang
akan diestimasi, apakah sesuai dengan teori atau tidak. Sedangkan uji kriteria statistik dilakukan dengan uji koefisien regeresi secara individual (uji t), uji sihgnifikansi simultan (uji F), dan uji koefisien determinasi (R2)
3.2.6.1. Uji Koefisien Regresi Secara Individual (Uji t)
Uji t – statistik dilakukan untuk menguji apakah variabel independen secara individu mempunyai pengaruh yang signifikan terhadap variabel dependennya. Pengujian ini dilakukan untuk mengetahui sacara parsial variabel independen berpengaruh secara signifikan atau tidak terhadap variabel dependen. Dalam pengujian ini dilakukan uji dua arah dengan hipotesa :
H0: βi = 0 (tidak ada pengaruh variabel independen terhadap variabel dependen)
H1: βi ≠ 0 (ada pengaruh variabel independen terhadap variabel dependennya)
Kriteria pengujian :
1. Ho diterima dan Ha ditolak apabila t tabel > t hitung < t tabel, artinya variabel independen tidak berpengaruh secara signifikan terhadap variabel dependen.
2. Ho ditolak dan Ha diterima apabila t tabel < t hitung > t tabel, artinya variabel independen berpengaruh secara signifikan terhadap variabel dependen.
Sedangkan nilai t hitung adalah : T hitung = βi
3.2.6.2. Uji Signifikansi Simultan (Uji f)
Uji F statistik digunakan untuk menguji apakah keseluruhan variabel independen secara simultan berpengaruh terhadap variabel dependen. Pengujian ini dilakukan dengan hipotesa :
H0 = β1 = β2 = β3 = β4 = 0
(variabel independen secara bersama – sama tidak berpengaruh secara signifikan terhadap variabel dependen).
H1 ≠ β1 ≠ β2 ≠ β3 ≠ β4 ≠ 0
(variabel independen secara bersama – sama berpengaruh secara signifikan terhadap variabel dependen).
Atau dengan kata lain, dalam penelitian ini bila hasil F hitung menunjukkan hasil yang signifikan berarti variabel pertumbuhan ekonomi, aglomerasi dan variabel moderat secara bersama – sama berpengaruh terhadap kualitas lingkungan.
Untuk menghitung F hitung digunakan rumus (Gujarati, 1995) F hitung = R2 / (k-1)
(1 – R2) / (n-k) Dimana :
R2 = koefisien determinasi n = jumlah observasi
k = jumlah variabel independen termasuk konstanta Kriteria Pengujian:
1. H0 diterima dan H1 ditolak apabila F hitung < F tabel, artinya variabel
independen secara bersama – sama tidak berpengaruh secara signifikan terhadap variabel dependen.
2. H0 ditolak dan H1 diterima apabila F hitung > F tabel, artinya variabel
independen secara bersama – sama berpengaruh secara signifikan terhadap variabel dependen.
3.2.6.3. Uji Koefisien Determinasi (R2)
Koefisien determinasi (R2) digunakan untuk mengetahui besarnya daya menerangkan dari variabel independen terhadap variabel dependen pada model tersebut. Nilai R2 berkisar antara 0 < R2 < 1 sehingga kesimpulan yang diambil adalah:
• Nilai R2 yang kecil atau mendekati nol, berarti kemampuan
variabel-variabel bebas dalam menjelaskan variabel-variabel-variabel-variabel tak bebas sangat terbatas.
• Nilai R2 mendekati satu, berarti variabel-variabel bebas memberikan
hampir semua informasi untuk memprediksi variasi variabel tak bebas. Dalam penelitian ini berarti, bila nilai R2 memberikan hasil yang mendekati angka 1 , artinya kualitas lingkungan yang ditinjau dari tingkat emisi CO2, CH4, dan N2O dapat dijelaskan dengan baik oleh variasi variabel independen
GDPI dan atau GDPI2,GDPP dan atau GDPP2. Sedangkan sisanya (100% - nilai
R2) dijelaskan oleh sebab-sebab lain diluar model.
3.2.7. Uji Ekonometrika 3.2.7.1. Uji Autokorelasi
Istilah autokorelasi bisa didefinisikan sebagai korelasi di antara anggota observasi yang diurut menurut waktu (seperti data deret berkala) atau ruang
(seperti data lintas sektoral). Autokorelasi biasanya berhubungan dengan data deret berkala (time series) walaupun memungkinkan terdapat pada data cross
section.
Uji yang paling dikenal untuk pendeteksian autokorelasi adalah uji yang dikembangkan oleh Durbin dan Watson, yang populer dikenal sebagai statistik d Durbin-Watson (DW Test). Pengujian dengan DW Test hanya digunakan untuk autokorelasi tingkat satu (first order autocorrelation) dan mensyaratkan adanya
intercept (konstanta) dalam model regresi dan tidak ada variabel lag diantar
variabel independen.
Hipotesis yang akan diuji adalah: H0 : tidak ada autokorelasi (r = 0)
H1 : ada autokorelasi (r ≠ 0)
Tabel 3.2. Uji d Durbin-Watson: Aturan Keputusan
Hipotesis nol Keputusan Nilai DW
Tidak ada autokorelasi positif Tidak ada autokorelasi positif Tidak ada autokorelasi negatif Tidak ada autokorelasi negatif Tidak ada autokorelasi positif
atau negatif
Tolak
Tidak ada keputusan Tolak
Tidak ada keputusan Tidak ditolak 0 < d < dL dL ≤ d ≤ dU 4 - dL < d < 4 4 - dU ≤ d ≤ 4 - dL dU < d < 4 - dU Sumber: Gujarati, 2003 3.2.7.2. Uji Heterokedastisitas
Suatu asumsi kritis dari model regresi linear klasik adalah bahwa gangguan ui semuanya mempunyai varians yang sama. Jika asumsi ini tidak
sifat ketidakbiasan dan konsistensi dari penaksir OLS. Tetapi penaksir ini tidak lagi mempunyai varians minimum atau efisien . Dengan perkataan lain, sehingga tidak lagi memenuhi asumsi BLUE.
Untuk mendeteksi ada tidaknya pelanggaran ini dengan menggunakan
White Heterocdasticity Test (Gujarati, 2003). Nilai probabilitas Obs*R-squared
dijadikan sebagai acuan untuk menolak atau menerima H0. Hipotesis yang akan
diuji:
H0 : homoskedastisitas
H1 : heteroskedastisitas
Kriteria pengujiannya adalah:
1. Probabilitas Obs*R-squared < taraf nyata , maka tolak H0
2. Probabilitas Obs*R-squared > taraf nyata , maka terima H0
Uji heteroskedastisitas dapat dilakukan dengan uji grafik plot dan uji statistik. Uji grafik plot yang digunakan dengan melihat grafik plot antara nilai prediksi variabel terikat yaitu ZPRED dengan residualnya SRESID. Deteksi ada tidaknya heteroskedastisitas dapat dilakukan dengan melihat ada tidaknya pola tertentu pada scatterplot antara SRESID dan ZPRED.
Uji statistik yang digunakan adalah uji Glejser. Uji Glejser dilakukan dengan meregresikan nilai absolute residualnya terhadap variabel independen (Gujarati, 2003). Jika variabel independen signifikan secara statistik mempengaruhi variabel dependen, maka ada indikasi terjadi heteroskedastisitas.
3.2.7.3. Uji Normalitas
Uji normalitas digunakan untuk mengetahui apakah data berdistribusi normal atau tidak. Dalam penelitian ini menggunakan Jarque-Bera test (J-B test) untuk melihat apakah data terdistribusi normal atau tidak. Uji ini menggunakan hasil residual dan chi-square probability distribution, hipotesis yang akan diuji adalah:
H0 : Sampel berasal dari populasi yang berdistribusi normal
H1 : Sampel berasal dari populasi yang tidak berdistribusi normal
Kriteria pengujian adalah:
1. Bila nilai JB hitung > nilai X2tabel, maka H0 yang menyatakan residual, ut
adalah berdistribusi normal ditolak.
2. Bila nilai JB hitung < nilai X2tabel, maka H
0 yang menyatakan residual, ut
adalah berdistribusi normal diterima.
3.3. Definisi Operasional
Untuk memahami secara jelas variabel-variabel yang dituliskan dalam Tabel 3.1, maka definisi operasional variabel-variabel tersebut adalah:
1. Pertumbuhan Ekonomi di Sektor Pertanian (GDPP)
Variabel ini diperoleh dari Gross Domestic Product (GDP) riil di sektor pertanian dengan menggunakan tingkat harga konstan tahun dasar 2000 yang dinyatakan dalam US$. GDP pertanian merupakan penjumlahan total terhadap barang-barang dan jasa akhir pada sektor pertanian yang mencakup pertanian dalam arti sempit yaitu pertanian rakyat, kehutanan, perkebunan, perikanan, dan peternakan.
2. Pertumbuhan Ekonomi di Sektor Industri (GDPI)
Variabel ini diperoleh dari Gross Domestic Product (GDP) riil di sektor industri dengan menggunakan tingkat harga konstan tahun dasar 2000 yang dinyatakan dalam US$. GDP industri merupakan penjumlahan total terhadap barang-barang dan jasa akhir pada sektor industri yang mencakup manufaktur, pertambangan, konstruksi, listrik, air, dan gas.
3. Emisi Karbondioksida (CO2)
Variabel ini diperoleh dari emisi karbondioksida (CO2) yang dinyatakan
dalam kilotonne. Karbondioksida adalah gas rumah kaca yang penting karena ia menyerap gelombang inframerah dengan kuat. Karbondioksida dihasilkan oleh semua makhluk hidup pada proses respirasi dan digunakan oleh tumbuhan pada proses fotosintesis. Oleh karena itu, karbondioksida merupakan komponen penting dalam siklus karbon. Karbondioksida juga dihasilkan dari hasil samping pembakaran bahan bakar fosil. Karbondioksida anorganik dikeluarkan dari gunung berapi dan proses geotermal lainnya seperti pada mata air panas.
4. Emisi Metana (CH4)
Variabel ini diperoleh dari emisi metana (CH4) yang dinyatakan dalam kilotonne. Metana merupakan komponen utama gas alam yang termasuk gas
rumah kaca. Ia merupakan insulator yang efektif, mampu menangkap panas 20 kali lebih banyak bila dibandingkan karbondioksida. Metana dilepaskan selama produksi dan transportasi batu bara, gas alam, dan minyak bumi. Metana juga dihasilkan dari pembusukan limbah organik di tempat
pembuangan sampah (landfill), bahkan dapat keluarkan oleh hewan-hewan tertentu, terutama sapi, sebagai produk samping dari pencernaan.
5. Emisi Nitrogen Oksida (N2O)
Variabel ini diperoleh dari emisi nitrogen oksida (N2O) yang dinyatakan
dalam kilotonne. Nitrogen oksida adalah gas insulator panas yang sangat kuat. Ia dihasilkan terutama dari pembakaran bahan bakar fosil dan oleh lahan pertanian. Nitrogen oksida dapat menangkap panas 300 kali lebih besar dari karbondioksida. Nitrogen Oksida (N2O) dapat dihasilkan melalui penggunaan
pupuk pada pertanian dan dari industri nilon dan asam nitrat serta pembakaran bahan bakar pada mesin pembakaran internal.