RANCANGAN DAN PENGEMBANGAN
MODUL ELEKTRONIK MATERI TURUNAN FUNGSI
DENGAN PROGRAM
GEOGEBRA
SKRIPSI
Diajukan Untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Pendidikan
Program Studi Pendidikan Matematika
Disusun oleh :
Andreas Ricky Proklamanto
NIM : 0914141047
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
i
RANCANGAN DAN PENGEMBANGAN
MODUL ELEKTRONIK MATERI TURUNAN FUNGSI
DENGAN PROGRAM
GEOGEBRA
SKRIPSI
Diajukan Untuk Memenuhi Salah Satu Syarat
Memperoleh Gelar Sarjana Pendidikan
Program Studi Pendidikan Matematika
Disusun oleh :
Andreas Ricky Proklamanto
NIM : 091414047
PROGRAM STUDI PENDIDIKAN MATEMATIKA
JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN
UNIVERSITAS SANATA DHARMA
YOGYAKARTA
iv
HALAMAN PERSEMBAHAN
Dengan Gembira Penuh Syukur Skripsi Ini
Kuupersembahkan untuk :
Tuhanku Tercinta Yesus Kristus dan Bundaku Tersayang
Bunda Maria
Bapak dan Ibuk yang Selalu Mendukung Sepenuh Jiwa
dan Raga
Kakekku yang juga selalu Mendukungku
Adikku yang Aneh
Saudara-saudaraku yang Terkasih
vi
Abstraks
Andreas Ricky Proklamanto. 2013. Rancangan dan Pengembangan Modul Elektronik Materi Turunan Fungsi dengan Program Geogebra. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengeatahuan Alam, Fakultas Keguruan dan Ilmu Pengetahuan, Universitas Sanata Dharma.
Penelitian ini bertujuan untuk menghasilkan elektronik modul matematika dengan pendekatan konstruktivisme sebagai perangkat pembelajaran siswa kelas XI IPA 5 SMA Kolese de Britto tahun ajaran 2012/2013 pada materi Tafsiran Geometris Turunan Fungsi. Elektronik modul ini menggunakan software Geogebra dandikemas secara website offline.
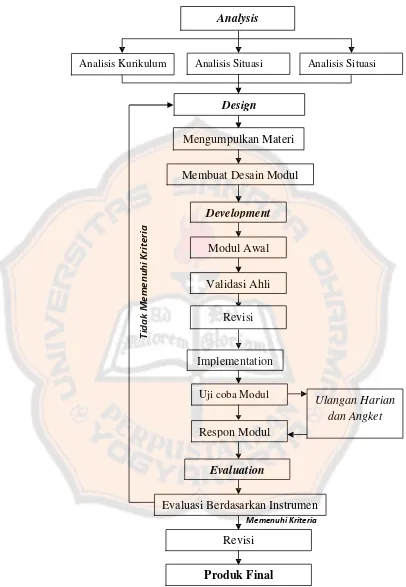
Langkah-langkah penelitian pengembangan ini menggunakan model ADDIE, Analysis, Design, Development, Implementation, dan Evaluation. Analysis (analisis) adalah analisis awal sebelum dilakukan pengembangan, mulai dari analisis awal, analisis kurikulum, dan analisis situasi, dilanjutkan dengan design (perancangan), adalah menyusun dan mengumpulkan materi, membuat desain. Kemudian development (pengembangan) melakukan pengembangan produk dari desain yang sudah dibuat, dan validasi ahli dengan menggunakan instrumen penelitian oleh ahli media dan ahli materi. Setelah divalidasi ahli dilanjutkan dengan pengemasan untuk selanjutnya dilakukan implementasi. Tahap berikutnya implementasi yang diikuti oleh 30 siswa sebagai kelas uji coba lapangan dan pengisian angket kualitas teknis. Ada pula lembar observasi yang diisi oleh 2 guru matematika dan 1 dosen pengamat sebagai penilaian kepraktisan pengguna guru saat pembelajaran. Tahap terakhir adalah evaluasi, dari semua tahapan dan masukan pada saat implementasi dievaluasi dan direvisi kembali, agar mendapat produk akhir.
Penilaian kualitas elektronik modul matematika berdasarkan aspek kevalidan, menunjukkan skor ideal 60,33 untuk aspek pendidikan dan skor ideal 38,50 untuk aspek tampilan, dengan persentase keidealan 80,84% untuk aspek pendidikan menunjukkan nilai sangat baik, sedangkan pada aspek tampilan dengan persentase keidealan 77,00% menunjukkan penilaian baik. Aspek kualitas teknis dengan pengguna guru matematika memperoleh skor ideal 40 dengan persentase keidealan 88,89% yang menunjukkan penilaian sangat baik. Aspek kualitas teknis dengan pengguna siswa memperoleh skor ideal 13,34 dengan persentase keidealan 77,11% yang menunjukkan penilaian baik. Pada aspek keefektifan ditunjukkan berdasarkan ketuntasan hasil belajar siswa sebesar 73,34%, berdasarkan pedoman ketuntasan maka dapat disimpulkan tingkat ketuntasannya tinggi, sehingga dapat dikatakan efektif. Berdasarkan tiga kriteria penilaian kualitas produk menurut Nieveen:(1999), yakni kevalidan, kepraktisan dan keefektifan, maka dapat disimpulkan bahwa elektronik modul yang dikembangkan berhasil dengan memperoleh penilaian baik.
vii
Abstract
Andreas Ricky Proklamanto. 2013. Designing And Developing Of Electronic Module In Derivatif Function Material Using Geogebra Program. Mathematics Education Studies Program, Department of Mathematics and Natural Science, Faculty of Teacher of Training and Education, Sanata Dharma University.
This research aimed to create an electronic mathematics module using constructivism approach as a students’ learning device in class XI IPA 5 SMA Kolese de Britto academic year 2012/2013 in subject geometric interpretation derivative function. This electronic module used GeoGebra software and offline website.
The development research step used ADDIE model, Analysis, Design, Development, Implementation, and Evaluation. Analysis was a preliminary analysis which was done before doing development, started from the initial analysis, curriculum analysis, and situation analysis, followed by design which prepared and gathered materials, making design. Then, development was developing products which had been created and validating the product using research instruments from media specialists and experts. After validation, the step was continued with packaging and implementation. The implementation was done in 30 students as the field trial and filling up technical quality of the questionnaire. There was also observation sheets, which were filled in by two mathematics teachers and a lecturer as an observer, as teacher’s practical rating during learning process. The last step was evaluation of all steps and comments during the implementation which were evaluated and revised in order to get the final product. Electronic quality assessment module, which was based on aspects of mathematical validity, showed ideal score was 60.33 for the educational aspect and 38.50 for the ideal score of display aspect, with ideal percentage 80.84% for the education aspect, it showed an excellent score, while the display aspect with an ideal percentage of 77.00% showed a good score. Technical quality in which mathematics teacher as a user got an ideal score 40 with an ideal percentage 88.89%, it showed anexcellent score. Technical quality in which the students as the users got an ideal score ideal score of 13.34 with an ideal percentage 77.11% indicated a good score. In effectiveness aspect which was showed during student learning outcomes was 73.34%,it was based on the standard score guidelines, it can be concluded that the level of thoroughness was high in other words it was
effective. According to the three criteria of product quality assessment by Nieveen : (1999), namely validity, practicality and effectiveness, it can be concluded that the electronics module which had been developed could successfully got a good score.
ix
KATA PENGANTAR
Puji syukur penulis haturkan pada Tuhan Yang Maha Esa, yang telah melimpahkan rahmatnya sehingga penulis dapat menyelesaikan skripsi ini dengan baik dan lancar. Tujuan skripsi ini dibuat yaitu untuk memenuhi salah satu syarat untuk memperoleh gelar Sarjana Pendidikan pada Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.
Seiring dalam penyusunan skripsi ini, penulis mendapat bantuan, dukungan, bimbingan, nasehat, motivasi, dan masukan-masukan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada :
1. Bapak Rohandi, Phd. selaku Dekan FKIP yang telah menyediakan sarana dan prasarana pada penulis selama menempuh studi.
2. Drs. A. Atmadi. M.Si. selaku Ketua Jurusan PMIPA yang telah memberikan dukungannya dalam perijinan ini sehingga penelitian dapat berjalan lancar. 3. Bapak Dr. M. Andy Rudhito, S.Pd. selaku Kaprodi Pendidikan Matematika
sekaligus dosen pembimbing yang telah sabar membimbing, meluangkan waktu, tenaga, pikiran, serta memberi nasehat dan masukan yang bermanfaat kepada penulis dalam penyusunan skripsi dari awal hingga akhir penulisan skripsi ini dapat terselesaikan dengan baik dan lancar.
4. Bapak Dominikus Arif Budi Prasetyo, M.Si selaku dosen pembimbing akademik yang telah mendukung dan membimbing selama penulis menempuh studi di Universitas Sanata Dharma.
5. Bapak Dr. M. Andy Rudhito, S.Pd., Bapak Dominikus Arif B . P, S.Si., M.Si, dan Ibu Elisabet Ayunika Permata Sari, S.Pd., M.Sc selaku penguji yang telah memberikan masukan yang bermanfaat demi perbaikan dan penyempurnaan skripsi ini.
x
7. Bapak HJ Sriyanto S.Pd. selaku guru kelas XI IPA 5 SMA Kolese de Britto yang telah membimbing dan memberikan masukan kepada penulis demi kelancaran penelitian.
8. Segenap dosen dan karyawan Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas Sanata Dharma yang telah membimbing, mendidik, serta memberikan ilmunya yang berharga selama menempuh studi di Universtas Sanata Dharma.
9. Bapak, Ibu, dan adikku tercinta yang selalu mendukung siang dan malam terutama pada masa-masa kritis dalam penyusunan skripsi ini.
10.Pak Catur, Nono, Mbak Wiwik, Merry, Kribo, Blur, Awang, Yulius, Helen,dan Kokoh yang telah membantu penulis selama melakukan penelitian.
11.Semua pihak yang yang telah mendukung dari penyusunan hingga terselesaikannya skripsi ini yang tidak dapat penulis sebutkan satu persatu.
.
Yogyakarta, 2 4 Juli 2013 Penulis,
xi
DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN PERSETUJUAN PEMBIMBING ... ii
HALAMAN PENGESAHAN ... iii
HALAMAN PERSEMBAHAN ... iv
PERNYATAAN KEASLIAN KARYA ... v
ABSTRAK ... vi
ABSTRACT ... vii
LEMBAR PERNYATAAN PERSETUJUAN ... viii
KATA PENGANTAR ... ix
DAFTAR ISI ... xi
DAFTAR TABEL ... xiv
DAFTAR GAMBAR ... xvi
DAFTAR LAMPIRAN ... xviii
BAB I PENDAHULUAN 1 A. Latar Belakang Masalah ... 1
B. Identifikasi Masalah ... 7
xii
D. Tujuan Penelitian ... 8
E. Sistematika Penyajian ... 9
F. Ruang Lingkup ... 10
G. Manfaat Penelitian ... 10
BAB II LANDASAN TEORI 12 A. Kajian Teori ... 12
1. Pembelajaran Matematika ... 12
2. Pendekatan Konstruktivisme ... 17
3. Pembelajaran Berbantukan Komputer ... 19
4. Modul ... 21
5. Modul Elektronik ... 26
6. Kualitas Perangkat Pembelajaran ... 27
7. Materi Ajar ... 29
8. GeoGebra ... 33
B. Hasil Penelitian yang Relevan ... 36
C. Kerangka Berpikir ... 38
BAB III METODE PENELITIAN 41 A. Jenis Penelitian ... 41
B. Subjek Penelitian ... 47
C. Objek Penelitian ... 47
D. Waktu Peneltian ... 47
E. Instrumen Penelitian ... 48
xiii
BAB IV HASIL PENELITIAN DAN PEMBAHASAN ... 59
A. Hasil Rancangan dan Penelitian Program ... 59
1. Analisis ... 59
2. Design ... 61
3. Development ... 68
4. Implementasi ... 79
5. Evaluasi ... 91
B. Kualitas Modul Matematika ... 100
1. Kevalidan ... 101
2. Kepraktisan ... 103
3. Keefektifan ... 104
C. Pembahasan ... 107
D. Keterbatasan Penelitian ... 114
BAB V KESIMPULAN DAN SARAN ... 115
A. Kesimpulan ... 115
B. Saran ... 116
DAFTAR PUSTAKA ... 118
xiv
DAFTAR TABEL
Tabel 3.1 Kisi-Kisi Lembar Penilaian Modul Kriteria Kevalidan ... 50
Tabel 3.2 Kisi-kisi Angket untuk Observer ... 51
Tabel 3.3 Kisi – kisi Angket untuk Siswa ... 52
Tabel 3.4.1 Aturan Pemberian Skala pada Angket Kevalidan dan Observasi ... 55
Tabel 3.4.2 Aturan Pemberian Skala pada angket siswa ... 55
Tabel 3.5 Kriteria Penilaian ... 56
Tabel 3.6 Kategori Presentasi Penilaian Ideal ... 57
Tabel 3.7 Kriteria Efektivitas Hasil Belajar Secara Kuantitatif ... 58
Tabel 4.1 Masukkan dan Saran dan Tindak Lanjut Aspek Pendidikan ( Ahli Materi ) ... 72
Tabel 4.2 Masukkan dan Saran dan Tindak Lanjut Aspek Tampilan ( Ahli Media ) ... 75
Tabel 4.3 Masukkan dan Saran dan Tindak Lanjut Aspek Kepraktisan ( Pengguna Siswa ) ... 95
Tabel 4.4 Hasil Perhitungan Penilaian Aspek Pendidikan ... 100
Tabel 4.5 Kriteria Kategori Penilaian Ideal untuk Aspek Pendidikan ... 100
Tabel 4.6 Kategori Presentase Penilaian Ideal ... 101
Tabel 4.7 Hasil Perhitungan Penilaian Aspek Tampilan ... 101
xv
Tabel 4.9 Kategori Presentase Penilaian Ideal ... 102
Tabel 4.10 Hasil Perhitungan Penilaian Aspek Kepraktisan (Pengguna Siswa) ... 106
Tabel 4.11 Kriteria Kategori Penilaian Ideal untuk Aspek Kepraktisan ... 106
Tabel 4. 12 Kategori Presentase Penilaian Ideal ... 104
Tabel 4.13 Hasil Perhitungan Penilaian Aspek Keefektifan (Pengamatan Observer) ... 104
Tabel 4.14 Kriteria Kategori Penilaian Ideal untuk Aspek Keefetifan (Pengamatan Observer) ... 105
Tabel 4.15 Kategori Presentase Penilaian Ideal ... 105
Table 4.16 Perhitungan Kualitas Modul dengan Pengguna Guru ... 107
xvi
DAFTAR GAMBAR
Gambar 2.1Bagan Hubungan Komponen Pembelajaran ... 35
Gambar 3.1 Model Pengembangan ADDIE ... 42
Gambar 3.2 Desain Penelitian Modul ... 49
Gambar 4.1 Kerangka Modul Matematika ... 62
Gambar 4.2 GeoGebra Gradien Garis Singgung ... 64
Gambar 4.3 GeoGebra Komonotonan Fungsi... 64
Gambar 4.4 GeoGebra Kecekungan Fungsi ... 65
Gambar 4.5 GeoGebra Titik-titik Stasioner ... 66
Gambar 4.6 GeoGebra Sketsa Grafik ... 67
Gambar 4.7 GeoGebra Aplikasi Turunan ... 67
Gambar 4.8 Tampilan Layout E-modul ... 70
Gambar 4.9 StoryBoard Modul Matematika ... 78
Gambar 4.10.1 LKS 1 ... 81
Gambar 4.10.2. LKS 1 ... 82
Gambar 4.11.1 LKS 2 ... 84
Gambar 4.11.2 LKS 2 ... 85
Gambar 4.12 LKS 3 ... 87
Gambar 4.13.1 LKS 4 ... 89
xvii
LAMPIRAN
Lampiran 1: Pra Penelitian
1.1Kisi-kisi wawancara ... 121
1.2Pedoman Wawancara ... 122
1.3Hasil Wawancara ... 123
1.4Lembar Kerja Siswa ... 126
1.5Kisi-kisi Angket Penilaian (untuk ahli materi, ahli media, dan kualitas teknis) ... 134
1.6Instrumen Penelitian ... 135
1.7Kisi-kisi soal tes pengukuran (ulangan harian) ... 152
1.8Soal soal tes pengukuran (ulangan harian) 153 1.9Kunci jawaban dan pedoman penskoran pre-tes dan post-tes ... 155
1.10. Kunci jawaban dan pedoman penskoran pre-tes dan post-tes ... 155
1.11Hasil validasi (materi dan media) ... 182
1.12 Surat ijin penelitian ... 197
Lampiran 2: Pasca Penelitian 2.1. Hasil Pengisian Instrumen Penelitian obesrvasi ... 198
2.2. Hasil Pengisian Instrumen Penelitian untuk angket Siswa ... 204
2.3. Rekapitulasi Hasil Ulangan Siswa ... 206
2.4. Daftar validator (ahli materi, media, observer dan siswa pada uji coba lapangan) ... 207
2.5. Dokumentasi Pelaksanaan Uji Coba ... 209
2.6. Surat Sudah Melakukan Penelitian dari sekolah... 210
1
BAB I
PENDAHULUAN
A. LATAR BELAKANG
Pendidikan memegang peran penting dalam menciptakan dan
membentuk generasi muda yang maju, tangguh, terampil, dan terpelajar.
Pendidikan adalah suatu proses transformasi anak didik agar mencapai
hal-hal tertentu sebagai akibat proses pendidikan yang diikutinya. Seiring
perkembangan sains dan teknologi di era globalisasi, pendidikan di
Indonesia perlu berinovasi termasuk dalam strategi pelaksanaan
pembelajaran yang didukung dengan sarana dan prasarana yang memadai
untuk melakukan kegiatan pembelajaran di sekolah.
Pendidikan Indonesia telah mengalami perbaikan secara kontinu,
mulai dari kurikulum yang terus diperbaiki tiap periode hingga metode
pembelajaran yang di-update dengan pengadaan seminar bagi guru-guru
sekolah. Selain itu pengadaan fasilitas, sarana, dan prasarana sekolah juga
semakin diperhatikan oleh pemerintah. Hal ini tidak akan memberikan efek
yang signifikan jika tidak didukung oleh unit program pengajaran yang
sesuai dengan perkembangan pendidikan dan psikologi perkembangan
siswa, khususnya pada pelajaran matematika.
Revolusi menuju pendidikan matematika yang lebih bermakna saat ini
menjadi arah baru pendidikan matematika di Indonesia. Semakin disadari
pendidikan lanjut tidak lepas dari pemahaman bahwa matematika memiliki
potensi besar mendukung pengembangan pribadi anak. Arti penting di atas
telah diterima secara nyata hampir semua pihak, bahkan matematika
menempati posisi vital dalam sistem pendidikan. Secara kuantitas, alokasi
waktu pelajaran matematika setiap jenjang pendidikan selalu besar. Ruang
yang tersedia ini diharapkan dapat lebih dimanfaatkan untuk menggali
dan memberdayakan potensi pelajaran matematika.(Sumaryanta, 2010 :74)
Pembelajaran matematika selama ini kurang memberikan perhatian
terhadap pengembangan kemampuan berpikir tingkat tinggi seperti
kemampuan berpikir kreatif dan pemecahan masalah secara sistematis dan
bernalar. Padahal kemampuan ini sangat penting, karena dalam kehidupan
sehari-hari setiap orang selalu dihadapkan pada berbagai masalah yang
harus dipecahkan dan menuntut pemikiran kreatif untuk menemukan solusi
dari permasalahan yang dihadapi. Saat ini berbagai macam inovasi baru
di dalam dunia pendidikan terutama pada proses pembelajaran. Salah
satunya pembelajaran konstruktivisme. Pemilihan pendekatan ini lebih
membuat siswa antusias terhadap persoalan dalam berpikir secara
nalar, kreatif, dan sistematis sehingga mereka mau mencoba
memecahkan masalah dalam mengkonstruksi pengetahuannya sendiri.
Menurut Sutrisno (1998), permasalahan yang timbul dalam proses
belajar mengajar matematika antara lain: pertama, pembelajaran konsep dan
prosedur dalam matematika yang dipraktekkan di sekolah pada umumnya
menemukan strategi pemecahan masalah sehingga siswa hanya menghafal
rumus atau konsep tanpa memahami maknanya tidak mampu menerapkan
dalam masalah problem solving.
Kedua selama ini guru dipandang sebagai pusat pembelajaran artinya
guru dipandang sebgai satu-satunya sumber pembelajaran. Hal ini membuat
situasi belajar sangat membosankan. Siswa hanya diperlakukan sebagai
obyek sehingga kreatifitas siswa menjadi tidak maksimal.
Ketiga adanya tuntutan masa depan dimana dimana diperlukan
pendekatan dalam pembelajaran yang menghasilkan output pendidikan yang
berkualitas sehingga mampu berkompetisi positif dalam menghadapi
tuntutan masa depan.(Siti Juraidah,2012 )
Pada sisi lain tersedianya unit program pengajaran yang berkualitas
masih sangat kurang. Buku pegangan yang notabene sebagai unit program
pengajaran paling familiar masih dinilai kurang memotivasi siswa karena
sebagian para pengarang buku pegangan kurang memikirkan bagaimana
buku tersebut agar mudah dipahami oleh siswa. Kaidah-kaidah psikologi
pembelajaran dan teori-teori desain suatu buku teks kurang diaplikasikan
dalam penyusunan buku teks secara optimal. Akibatnya, siswa sulit
memahami buku yang dibacanya dan sering buku- buku teks tersebut
membosankan. Gejala tidak efisien, tidak efektif dan kurang relevan tampak
dari beberapa indikator seperti, kurangnya motivasi belajar siswa,
penyelesaian tugas siswa tidak sesuai waktu yang ditentukan, dan hasil tes
demikian maka sulit diharapkan pencapaian tujuan pembelajaran secara
optimal.(Made Wina, 2009:229)
Melihat kondisi tersebut, pengembangan unit program pengajaran
matematika dengan pendekatan konstrutivisme merupakan suatu solusi
untuk membantu siswa dan guru dalam pembelajaran matematika yang
bertujuan meningkatkan kemampuan siswa dalam memahami materi
tertentu. Tanpa adanya unit program pengajaran siswa akan mengalami
kesulitan dalam belajarnya, apalagi jika guru menjelaskan materi
pembelajaran kurang jelas dan tidak sesuai dengan kecepatan pemahaman
siswa.
Pengalaman belajar siswa dapat diperoleh tidak hanya dari kelas,
siswa dapat belajar dari lingkungan sekitar kapanpun dan dimanapun ia
berada, tetapi belajar dengan fokus materi tertentu biasa didapatkan siswa
dari buku pelajaran dengan fasilitas seorang guru. Untuk membawa dua
hal tersebut kapanpun dan dimanapun tidaklah mungkin, karena itu perlu
dibuat unit program pengajaran yang dapat menggabungkan materi dan
pengajaran komunikatif untuk memberikan pengalaman belajar pada
masing-masing siswa.
Unit program pengajaran diharapkan dapat memenuhi kebutuhan
belajar siswa dan dapat menyesuaikan dengan kecepatan pemahaman
masing-masing siswa. Unit program pengajaran tersebut paling tidak
memuat materi matematika tertentu, memuat kegiatan pembelajaran, lembar
pengajaran tersebut dalam pembelajaran.
Modul merupakan suatu unit program pengajaran yang disusun
dalam bentuk tertentu untuk keperluan belajar. Menurut makna istilah
asalnya modul adalah alat ukur yang lengkap, merupakan unit yang dapat
berfungsi secara mandiri, terpisah, tetapi juga dapat berfungsi sebagai
kesatuan dari seluruh unit lainnya. Pada kenyataannya modul merupakan
jenis kesatuan kegiatan belajar yang terencana, dirancang untuk membantu
para siswa secara individual dalam mencapai tujuan-tujuan belajarnya.(Nana
Sudjana dan ahmad Rivai, 1989:132)
Penyajian modul secara menarik dengan konsep konstruktivisme, dan
bersumber oleh buku-buku konstekstual membuat modul bisa membawa
siswa pada kondisi yang sebenarnya dan membuat matematika menjadi
menarik. Dengan menggunakan media elektronik, permasalahan yang rumit
dan abstrak dapat tervisualisasi secara konkrit sehingga modul lebih
menarik. Hal ini didukung berdasarkan pengamatan peneliti semasa PPL
adanya kecenderungan siswa lebih tertarik pada hal yang baru serta
didukung oleh visualisasi.
Matematika yang mempunyai banyak cabang yaitu aljabar, aritmatika,
geometri, teori bilangan, trigonometri, kalkulus, statistika, dan lain-lain.
Terlebih materi kalkulus sangatlah abstrak untuk dipahami. Padahal
kalkulus adalah salah satu cabang dari matematika yang terpenting dan
banyak diterapkan secara luas pada cabang-cabang ilmu pengetahuan yang
perekonomian, dan sebagainya. Secara garis besar, kalkulus dapat kita
kelompokkan menjadi dua cabang besar, yakni kalkulus diferensial dan
kalkulus integral.
Di jenjang pendidikan SMA materi kalkulus dibagi menjadi 3
bagian yaitu limit fungsi, turunan fungsi ,dan integral fungsi. Ketiga materi
ini sangatlah penting bagi siswa SMA karena merupakan materi-materi
matematika tersebut akan terus diterapkan pada jenjang perguruan tinggi
bahkan dunia kerja. Sehingga materi tersebut sangat dibutuhkan pemahaman
lebih. Namun siswa hanya mengetahui rumus operasi limit, kalkulus
diferensial dan kalkulus integral secara langsung. Mereka tidak mengetahui
dari mana asal rumus operasi limit, kalkulus diferensial dan kalkulus
integral. Kedua menurut pengalaman peneliti, peneliti mengalami kesulitan
dalam memahami konsep dasar pada materi ajar limit yang akan berdampak
pada materi selanjutnya yaitu kalkulus diferensial dan kalkulus integral.
Salah satu media elektronik yang dapat digunakan dalam proses
pembelajaran adalah GeoGebra. Dengan menggunakan software GeoGebra
ini siswa diharapakan mampu untuk memahami materi secara geometri
khususnya materi kalkulus difrensial dengan baik. Hal ini karena dalam
software GeoGebra, bangun dimensi dua maupun tiga dikemas dalam
bantuk yang lebih menarik dan bangun dapat terlihat lebih nyata. Sehingga
proses pembelajaran dapat berjalan dengan lancar dan efektif dan
mempercepat proses pembelajaran sehingga semua materi pelajaran dapat
melalui suatu media yang interaktif yang berbasis multimedia khususnya
e-modul.
Berdasarkan permasalahan-permasalahan di atas, peneliti termotivasi
untuk mengembangkan unit program pengajaran yang dapat meminimalkan
suasana kurang kondusif dalam pembelajaran. Unit program pengajaran
yang dapat melibatkan semua siswa secara aktif mengikuti kegiatan
pembelajaran matematika. Unit program pengajaran tersebut memberikan
penjelasan bertahap secara konstruktif yang akan dilakukan selama
pembelajaran. Pengembangan modul matematika merupakan salah satu
langkah untuk meningkatkan kemampuan berpikir tingkat tinggi siswa yang
sangat penting untuk membangun fondasi bagi keilmuan matematika dan
keilmuan lain yang dipelajari siswa pada tahap lebih lanjut.
Bertolak dari latar belakang tersebut diatas dapat dirumuskan dalam
bentuk penelitian skripsi dengan judul“Rancangan dan Pengembangan
Modul Elektronik Materi Turunan Fungsi dengan Program Geogebra”.
B. IDENTIFIKASI MASALAH
Berdasarkan latar belakang diatas, dapat diidentifikasi beberapa masalah,
antara lain:
1. Kurangnya perhatian terhadap pengembangan kemampuan berpikir
kreatif, nalar ,dan sistematis dalam pembelajaran matematika.
2. Kurangnya pengembangan unit program pengajaran dalam mengatasi
variasi pembelajaran matematika.
pegangan siswa dalam penerapannya di berbagai bidang.
4. Kurangnya pengembangam modul sebagai unit program pengajaran
matematika dalam upaya melatih siswa dalam berpikir secara
konstruktif.
C. RUMUSAN MASALAH
Berdasarkan uraian diatas, dapat dirumuskan beberapa masalah, antara lain:
1. Bagaimana rancangan dan pengembangan Elektronik Modul Materi
Turunan dengan penggunaan program GeoGebra ?
2. Bagaimanakah keefektifan penggunaan elektronik modul GeoGebra
untuk memfasilitasi pembelajaran matematika pokok bahasan Turunan
Fungsi di sekolah menengah ditinjau dari hasil ulangan siswa?
D. TUJUAN PENELITIAN
Tujuan dari penelitian ini adalah
1. Rancangan dan pengembangan Elektronik Modul Materi Turunan
dengan penggunaan program GeoGebra .
2. Analisa keefektifan penggunaan elektronik modul GeoGebra untuk
memfasilitasi pembelajaran matematika pokok bahasan Turunan Fungsi
di sekolah menengah ditinjau dari hasil ulangan siswa.
E. SISTEMATIKA PENYAJIAN
Untuk memudahkan dan memberikan gambaran yang lebih jelas secara
menyeluruh mengenai penelitian isi penelitian ini, maka dibuat website
Bab I Pendahuluan
Mencakup Latar Belakang Masalah, Identifikasi Masalah, Rumusan
Masalah, Tujuan Penelitian, Sistematika Penyajian, Ruang Lingkup, dan
Manfaat Penelitian.
Bab II Landasan Teori
Berisikan beberapa teori- teori yang mencakup tentang pembelajaran
matematika, pendekatan konstruktivisme, pembelajaran berbantukan
computer, modul, e-modul, kualitas perangkat pembelajaran, materi ajar,
geogebra, tinjauan pustaka, dan kerangka berpikir .
Bab III Metode Penelitian
Berisikan metode- metode yang digunakan dalam penelitian yang
mencakup: jenis penelitian, subjek penelitian, objek penelitian, waktu
penelitian, instrument penelitian, teknik dan analisis data.
Bab IV Hasil Penelitian dan Pembahasan
Berisikan tentang analisis data yang telah diolah untuk menjawab
pertanyaan dalam rumusan masalah dalam penelitian, serta berisikan
pembahasan dan keterbatasan dari penelitian ini.
Bab V Kesimpulan dan Saran
Berisikan tentang kesimpulan dari hasil penelitian secara menyeluruh yang
F. RUANG LINGKUP
Permasalahan yang akan dikaji dalam skripsi ini adalah:
1. Materi matematika dalam media pembelajaran yang akan dikembangkan
hanya menyangkut mata bab turunan fungsi dengan subbab tafsiran
geometris turunan fungsi.
2. Mengingat keterbatasan dan kemampuan yang dimiliki peneliti, maka
penelitian difokuskan pada pengembangan modul pembelajaran
matematika dengan pendekatan kostruktivisme dalam pembelajaran
Tafsiran Geometris Turunan Fungsi SMA kelas XI. Pengujian kualitas
modul berdasarkan kriteria kevalidan, kepraktisan, dan kefektifan.
3. Modul Elektronik yang dibuat, hanya untuk pengujian kualitas modul
saja bukan untuk pengujian teori.
G. MANFAAT PENELITIAN
1. Bagi peneliti
Sebagai calon guru peneliti dapat mengetahui bahwa pembelajaran
menggunakan media yang interaktif dapat membuat pembelajaran lebih
menyenangkan dan dapat meningkatkan prestasi siswa.
2. Bagi guru
a. Memberi variasi cara mengajar guru, agar pembelajaran dapat
berlangsung secara efektif, dan dapat mencapai tujuan pembelajaran
yang optimal.
b. Mampu memvisualisasikan hal-hal yang masih abstrak dalam
c. Sebagai pelengkap media pembelajaran dalam materi Turunan
Fungsi.
d. Menjadi perangkat bantu dan alternative dalam pembelajaran materi
Turunan Fungsi.
e. Diharapkan dapat digunakan sebagai bahan acuan pengembangan
media pembelajaran interaktif guna meminimalisasi kejenuhan dan
kebosanan dalam pembelajaran konvensional di kelas yang
mengakibatkan motivasi belajar siswa menjadi berkurang untuk
memahami materi yang diberikan guru.
3. Bagi siswa
12
BAB II
LANDASAN TEORI
A. KAJIAN TEORI
1. Pembelajaran Matematika
Belajar merupakan aktivitas yang disengaja dan dilakukan oleh
individu agar terjadi perubahan kemampuan diri, dengan belajar anak yang
tadinya tidak mampu melakukan sesuatu, menjadi mampu melakukan
sesuatu, atau anak yang tadinya tidak terampil menjadi terampil.
1 Menurut Hilgard dan Bower, belajar (to learn) memiliki arti : 1) to
gain knowledge, comprehenson, or mastery of trough experience or study;
2) to fix in the mind or memory; memorize; 3) to acquire trough
experience; 4) to become in forme of to find out. Menurut definisi tersebut,
belajar memiliki pengertian memperoleh pengetahuan atau menguasai
pengetahuan melalui pengalaman, mengingat, menguasai
pengalaman, dan mendapatkan informasi atau menemukan. Dengan
demikian, belajar memiliki arti dasar adanya aktivitas atau kegiatan dan
penguasaan tentang sesuatu.2
Antony Robbins, mendefinisikan belajar sebagai proses menciptakan
hubungan antara sesuatu (pengetahuan) yang sudah dipahami dan sesuatu
(pengetahuan) yang baru. Dari definisi ini dimensi belajar memuat
1
Tim Pengembang MKDP Kurikulum dan Pembelajaran, Kurikulum & Pembelajaran, (Cet.1; Jakarta: Rajagrafindo Persada, 2011), hlm. 124.
beberapa unsur, yaitu : (1) penciptaan hubungan, (2) sesuatu hal
(pengetahuan) yang sudah dipahami, dan (3) sesuatu (pengetahuan) yang
baru. Pandangan Antony Robbins senada dengan apa yang dikemukakan
oleh Jerome Brunner, bahwa belajar adalah suatu proses aktif di mana
siswa membangun (mengkonstruk) pengetahuan baru berdasarkan pada
pengalaman/pengetahuan yang sudah dimilikinya.3 Berdasarkan
pengertian belajar maka belajar merupakan proses aktif individu dalam
membangun pengetahuan baru berdasarkan pada pengalaman/pengetahuan
yang sudah dimilikinya agar terjadi perubahan kemampuannya.
Proses belajar terjadi melalui banyak cara baik disengaja maupun
tidak disengaja dan berlangsung sepanjang waktu dan menuju pada suatu
perubahan pada diri pembelajar. Perubahan yang dimaksud adalah
perubahan perilaku berupa pengetahuan, pemahaman, keterampilan, dan
kebiasaan yang baru diperoleh individu. Terkait dengan proses belajar
sangat lekat dengan istilah mengajar.
Unsur terpenting dalam mengajar ialah merangsang serta mengarahkan
siswa belajar. Mengajar pada hakikatnya tidak lebih dari sekedar
menolong para siswa untuk memperoleh pengetahuan, ketrampilan, sikap,
serta ide dan apresiasi yang menjurus kepada perubahan tingkah laku dan
pertumbuhan siswa (Subiyanto, 1988:30). Cara mengajar yang baik
merupakan kunci dan prasyarat bagi siswa untuk dapat belajar dengan
baik. Salah satu tolak ukur bahwa siswa telah belajar dengan baik adalah
jika siswa itu dapat mempelajari apa yang yang harus dipelajari, sehingga
indikator hasil belajar yang diinginkan siswa dapat tercapai.4 Terkait
dengan cara mengajar hal ini sangatlah erat dengan istilah pembelajaran.
Menurut Suparni pembelajaran sebagai suatu proses kerjasama, tidak
hanya menitik beratkan pada kegiatan guru atau kegiatan siswa saja, akan
tetapi guru dan siswa secara bersama-sama berusaha mencapai tujuan
pembelajaran yang telah ditentukan.5 Pembelajaran dapat diartikan
sebagai proses kerja sama antara guru dan siswa dalam memanfaatkan
segala potensi dan sumber yang ada baik potensi, bakat, minat, dan
kemampuan dasar yang dimiliki termasuk gaya belajar maupun potensi
yang ada di luar diri siswa, termasuk lingkungan, sarana, dan sumber
belajar sebagai upaya untuk mencapai tujuan tertentu.6
Pembelajaran adalah suatu kombinasi yang tersusun meliputi unsur-unsur
manusiawi, material, fasilitas, perlengkapan, dan prosedur yang saling
mempengaruhi mencapai tujuan pembelajaran. Manusia yang terlibat
dalam sistem pengajaran terdiri dari siswa, guru, dan tenaga lainnya, misalnya
tenaga laboratorium. Material, meliputi buku-buku, papan tulis, dan kapur,
fotografi, slide dan film, audio, dan video tape. Fasilitas dan perlengkapan,
terdiri dari ruangan kelas, perlengkapan audio visual, juga komputer. Prosedur,
4 Trianto, Mendesain Model Pembelajaran Inovatif-Progresif, (Cet.2; Jakarta: Kencana Prenada Media Group, 2010), hlm.17.
5 Suparni, Perencanaan Pembelajaran Matematika (Handout),(Yogyakarta, UIN Sunan Kalijaga Yogyakarta, 2009), hlm. 4.
meliputi jadwal dan metode penyampaian informasi, praktik, belajar, ujian dan
sebagainya.7
Matematika berasal dari bahasa Latin manthanein atau mathema yang
berarti belajar atau hal yang dipelajari. Matematika dalam bahasa Belanda
disebut wiskunde atau ilmu pasti, yang kesemuanya berkaitan dengan
penalaran. Ciri utama matematika adalah penalaran deduktif, yaitu
kebenaran suatu konsep atau pernyataan diperbolehkan sebagai akibat
logis dari kebenaran sebelumnya sehingga kaitan konsep atau pernyataan
dalam matematika bersifat konsisten.8
Matematika berfungsi untuk mengembangkan kemampuan
menghitung, mengukur, menurunkan dan menggunakan rumus matematika
dalam pemecahan masalah pada kehidupan sehari-hari. Sesuai dengan
tujuan pembelajaran matematika:9
1. Melatih cara berfikir dan bernalar dalam menarik kesimpulan,
misalkan melalui kegiatan penyelidikan eksplorasi, eksperimen,
menunjukkan persamaan dan perbedaan.
2. Mengembangkan aktivitas kreatif yang melibatkan imajinasi, intuisi,
dan penemuan dengan mengembangkan pemikiran divergen, orisinil,
rasa ingin tahu, membuat prediksi dan dugaan, serta mencoba-coba.
3. Mengembangkan pemecahan masalah.
7 Oemar Hamalik, Kurikulum dan Pembelajaran, (Cet 6; Jakarta : Bumi Aksara, 2007),hlm. 57.
8 Depdiknas, Standar Kompetensi Mata Pelajaran Matematika Sekolah Menengah Pertama dan Madrasah Tsanawiyah (Jakarta:Depdiknas, 2003), hlm. 1.
4. Mengembangkan kemampuan menyampaikan informasi atau
mengkomunikasikan gagasan seperti melalui pembicaraan lisan,
catatan, grafik, peta, diagram, dalam menjelaskan gagasan.
Berdasarkan uraian di atas maka pembelajaran Matematika adalah
proses kerja sama antara guru dan siswa dalam memanfaatkan segala
potensi dan sumber yang ada baik potensi, bakat, minat, dan kemampuan
dasar yang dimiliki termasuk gaya belajar maupun potensi yang ada di
luar diri siswa, termasuk lingkungan, sarana, dan sumber belajar
sebagai upaya untuk mencapai tujuan melatih cara berfikir dan
bernalar dalam menarik kesimpulan, misalkan melalui kegiatan
penyelidikan eksplorasi, eksperimen, menunjukkan persamaan dan
perbedaan. Mengembangan aktivitas kreatif yang melibatkan imajinasi,
intuisi, dan penemuan dengan mengembangkan pemikiran divergen,
orisinil, rasa ingin tahu, membuat prediksi dan dugaan, serta
mencoba-coba, sehingga dapat menyampaikan informasi atau mengkomunikasikan
gagasan seperti melalui pembicaraan lisan, catatan, grafik, peta, diagram,
dalam menjelaskan gagasan dalam kemampuannya dalam menghitung,
mengukur, menurunkan dan menggunakan rumus matematika. Dengan
menitik beratkan pada proses belatih penalaran dalam hal pembelajaran
matematika maka hal ini terkait dengan metode pendekatan
2. Pendekatan Konstruktivisme
Bagi konstruktivisme, kegiatan belajar adalah kegiatan yang aktif,
yang memungkinkan pelajar membangun sendiri pengetahuannya. Pelajar
mencari arti sendiri hal-hal yang mereka pelajari. Ini adalah suatu proses
menyesuaikan konsep dan ide-ide baru dengan kerangka berpikir
yang telah ada dalam pikiran mereka (Bettemcourt, 1989;
Shymansky,1992; Watts dan Pope, 1989). Menurut konstruktivisme,
pelajar sendirilah yang bertanggung jawab terhadap hasil belajarnya.
Mereka membawa pengertiannya yang semula dalam situasi belajar yang
baru. Mereka sendiri yang membuat penalaran terhadap hal-hal yang
dipelajarinya dengan cara mencari makna, membandingkan dengan
yang telah diketahui dengan pengalaman baru, dan menyelesaikan
ketegangan antara yang telah ia ketahui dengan yang ia perlukan
dalam pengalaman yang baru.
Menurut kaum konstruktivis, belajar adalah suatu proses organik untuk
menemukan sesuatu, lebih daripada suatu proses mekanik untuk
mengumpulkan sesuatu. Belajar bukanlah suatu kegiatan mengumpulkan
fakta-fakta, tetapi suatu perkembangan pemikiran yang berkembang
dengan membuat kerangka pengertian yang berbeda. Pelajar harus punya
pengalaman dengan membuat hipotesa, prediksi mengetes hipotesa,
memanipulasi objek, memecahkan persoalan, mencari jawaban,
menggambarkan, meneliti, berdialog, mengadakan refleksi,
membentuk konstruksi yang baru. Belajar yang berarti terjadi melalui
suatu refleksi, pemecahan konflik pengertian, dan dalam proses selalu
memperbaharui tingkat pemikiran yang tidak lengkap (Fosnot, 1989).
Setiap pelajar mempunyai cara untuk mengerti sendiri. Maka,
penting bahwa setiap pelajar mengerti kekhasannya dan juga keunggulan
dan kelemahannya dalam mengerti sesuatu. Mereka perlu menemukan cara
belajar yang tepat bagi mereka sendiri. Setiap pelajar mempunyai cara
yang cocok untuk mengkonstruksikan pengetahuannya yang kadang
sangat berbeda dengan teman-teman yang lain.10
Dari semua itu hanya ada satu prinsip yang paling penting adalah guru
tidak boleh hanya semata-mata memberikan pengetahuan kepada siswa .
Siswa harus membangun pengetahuan didalam benaknya sendiri. Seorang
guru dapat membantu proses ini dengan cara-cara mengajar yang membuat
informasi menjadi sangat bermakna dan sangat relevan bagi siswa, dengan
memberikan kesempatan kepada siswa untuk menemukan atau
menerapkan sendiri ide-ide dan dengan mengajak siswa agar menyadari
dan menggunakan strategi-strategi mereka sendiri untuk belajar. Guru
dapat memberikan tangga kepada siswa yang mana tangga itu nantinya
dimaksudkan dapat membantu mereka mencapai tingkat pemahaman yang
lebih tinggi , tetapi harus diupayakan agar siswa itu sendiri yang
memenemukan kebenarannya.
Sehingga pembelajan matematika dengan pendekatan konstrutivisme
ialah proses kerja sama antara guru dan siswa dalam memanfaatkan segala
potensi dan sumber yang ada sebagai upaya untuk mencapai tujuan
melatih cara berfikir dan bernalar dalam menarik kesimpulan, dengan
cara membantu dan memberikan kesempatan kepada siswa untuk
menemukan atau menerapkan sendiri ide-ide serta mengajak siswa agar
menyadari dan menggunakan strategi-strategi mereka sendiri untuk
belajar. Sehingga nantinya dimaksudkan dapat membantu mereka
mencapai tingkat pemahaman yang lebih tinggi.
3. Pembelajaran Berbantukan Komputer
Pembelajaran Komputer-Assisted Instruction atau Pembelajaran
Berbantuan Komputer atau (PBK) sebagai proses mengajar yang
dilakukan secara langsung yang melibatkan komputer untuk
mempresentasikan bahan ajar dalam suatu model pembelajaran yang
interaktif untuk memberikan dan mengendalikan lingkungan belajar
secara individual pada masing-masing peserta didik (Splittgerber dan
Stirzaker,1984). Definisi ini selaras dengan Steinberg yang menyatakan
bahwa PBK merupakan semua penerapan komputer untuk pembelajaran
yang memiliki aspek individual, interaktif, dan arahan (Steinberg,1991).
Makna PBK sebagai pembelajaran individual, karena komputer
memberikan layanan sebagai seorang tutor bagi seorang peserta didik
daripada sebagai seorang instruktor untuk suatu kelompok peserta
arah secara intensif antara siswa dengan sistem komputer. Ini dimaknai
sebagai PBK interaktif. Selain ini, dengan PBK memungkinkan
peserta didik dapat mengajukan pertanyaan, memberi respon dan sistem
komputer menyajikan umpan balik secepat mungkin setelah peserta
didik memberi respon. Umpan balik yang diberikan komputer
diharapkan agar mahasiswa selalu dapat mendorong dan meningkatkan
kemampuan. Prosedur stimuli yang disajikan melalui layar monitor,
respon mahasiswa melalui papan ketik dan umpan balik yang berbentuk
teks, suara atau gambar diarahkan berdasarkan struktur program yang
dirancang oleh pengembang PBKI. Ditinjau dari peran apa yang
diperankan program komputer, Merrill (1996) secara spesifik
menyatakan bahwa PBKI merupakan penggunaan komputer untuk
membantu dalam aktivitas pembelajaran. Pada umumnya digunakan
dengan mengacu penerapan tutor, seperti misalnya memberi drill and
practice, tutorials, simulation, and games. Definisi ini selaras dengan
Tailor dalam Merrill (1996), yang menyatakan bahwa semua aplikasi
komputer dalam pendidikan dapat diklasifikasi sebagai tutor, tool atau
tutee.
Berdasarkan uraian diatas dapat disimpulkan bahwa Pembelajaran
berbantukan Komputer secara sederhana yaitu penggunaan Komputer
sebagai alat bantu dalam dunia pendidikan dan pengajaran. Penggunaan
Komputer secara langsung denga peserta didik untuk menyampaikan isi
peserta didik. Materi pembelajaran dibuat dalam bentuk powerpoint atau
CD pembelajaran interaktif.
4. Modul
Modul merupakan unit pengajaran yang terkecil dan lengkap, yang
memuat rangkaian kegiatan belajar yang direncanakan secara sistematis,
memuat tujuan belajar yang dirumuskan secara eksplisit dan spesifik,
merupakan realisasi pengakuan individual yang memungkinkan
untuk siswa belajar secara mandiri. Rumusan tujuan pengajaran yang
spesifik dalam modul dapat diubah menjadi item-item tes untuk
mengevaluasi hasil belajar siswa. Dengan mengubah tujuan pengajaran
menjadi item-item tes itu dapat ditentukan dengan pasti apakah yang
seharusnya dikuasai oleh siswa apabila mereka telah menyelesaiakan
modul yang bersangkutan. 11
Di Indonesia, istilah modul untuk pertama kali dikumandangkan
dalam suatu forum rapat antara 8 Proyek Perintis Sekolah
Pembangunan di Cibulan, Bogor pada bulan Februari 1974.12 Modul
yang dikembangkan pada saat itu berbentuk buku kecil.
Penggunaan modul untuk keperluan belajar pada dasarnya untuk
membantu siswa secara mandiri untuk mencapai tujuan belajarnya. Hal
ini sesuai dengan pendapat Nana Sudjana dan Ahmad Rivai dalam Departeman Pendidikan Nasional “modul merupakan jenis kesatuan
11 St.Vembriarto, PengantarPengajaran Modul, (Yogyakarta:Yayasan Pendidikan Paramita, 1985), hlm. 12.
kegiatan belajar yang terencana, dirancang untuk membantu siswa secara mandiri dalam mencapai tujuan belajarnya”. Modul mempunyai
beberapa karakteristik tertentu, misalnya :13
a. Berbentuk unit pengajaran terkecil dan lengkap
b. Berisi rangkaian kegiatan belajar yang dirancang secara sistematis
c. Berisi tujuan belajar yang dirumuskan secara jelas dan khusus
d. Memungkinkan siswa belajar mandiri
Modul bisa dipandang sebagai paket program pengajaran yang
terdiri dari komponen-komponen yang berisi tujuan belajar, bahan
pelajaran, metode belajar, alat atau media, serta sumber belajar dan
sistem evaluasinya.
Menurut Nana Sudjana dan Ahmad Rivai modul didefinisikan
sebagai satu unit program belajar mengajar terkecil yang secara rinci
menggariskan :14
a. Standar kompetensi dan kompetensi dasar yang inigin dicapai
b. Pokok-pokok materi yang dipelajari
c. Kedudukan dan fungsi modul dalam kesatuan program yang
lebih luas
d. Peran guru dalam proses belajar mengajar
e. Alat-alat dan sumber yang akan digunakan
13Departemen Pendidikan Nasional Direktorat Jenderal Pendidikan Dasar dan Menengah, Direktorat Pendidikan menengah Umum, Pedoman Khusus Penyusunan Modul Sekolah Menengah Atas, 2004, hlm. 28-29.
f. Kegiatan-kegiatan belajar yang harus dilakukan dan harus
dihayati siswa secara berurutan
g. Lembaran kerja yang harus diisi siswa
h. Program evaluasi yang akan dilaksanakan
Sebuah modul bisa dikatakan baik dan menarik apabila terdapat
karakteristik sebagai berikut. 15
a. Self Instructional, yaitu melalui modul tersebut seseorang atau
peserta belajar mampu membelajarkan diri sendiri, tidak
tergantung pada pihak lain. Untuk memenuhi karakter self
instructional, maka dalam modul harus; 1) berisi tujuan yang
dirumuskan dengan jelas; 2) berisi materi pembelajaran yang
dikemas ke dalam unit-unit kecil atau spesifik sehingga
memudahkan belajar secara tuntas; 3) menyediakan contoh dan
ilustrasi yang mendukung kejelasan pemaparan materi
pembelajaran; 4) menampilkan soal-soal latihan, tugas dan
sejenisnya yang memungkinkan pengguna memberikan respon
dan mengukur tingkat penguasaannya; 5) kontekstual yaitu
materi-materi yang disajikan terkait dengan suasana atau konteks
tugas dan lingkungan penggunanya; 6) menggunakan bahasa
yang sederhana dan komunikatif; 7) terdapat rangkuman materi
pembelajaran; 8) terdapat instrumen penilaian, yang
memungkinkan penggunaan melakukan ‘self assessment’; 9)
terdapat instrumen yang dapat digunakan penggunanya
mengukur atau mengevaluasi tingkat penguasaan materi; 10)
terdapat umpan balik atas penilaian, sehingga penggunanya
mengetahui tingkat penguasaan materi; dan 11) tersedia
informasi tentang rujukan referensi yang mendukung materi
pembelajaran dimaksud.
b. Self Contained, yaitu seluruh materi pembelajaran dari satu unit
kompetensi atau sub kompetensi yang dipelajari terdapat di
dalam satu modul secara utuh. Tujuan dari konsep ini adalah
memberikan kesempatan pembelajar mempelajari materi
pembelajaran yang tuntas, karena materi dikemas ke dalam satu
kesatuan yang utuh. Jika harus dilakukan pembagian atau
pemisahan materi dari satu unit kompetensi harus dilakukan
dengan hati-hati dan memperhatikan keluasan kompetensi yang
harus dikuasai.
c. Stand Alone (berdiri sendiri), yaitu modul yang dikembangkan
tidak tergantung pada media lain atau tidak harus digunakan
bersama-sama dengan media pembelajaran lain. Dengan
menggunakan modul, pebelajar tidak tergantung dan harus
menggunakan media yang lain untuk mempelajari dan atau
mengerjakan tugas pada modul tersebut. Jika masih
yang digunakan, maka media tersebut tidak dikategorikan
sebagai media yang berdiri sendiri.
d. Adaptive, modul hendaknya memiliki daya adaptif yang
tinggi terhadap perkembangan ilmu dan teknologi. Dikatakan
adaptif jika modul dapat menyesuaikan perkembangan ilmu
pengetahuan dan teknologi, serta fleksibel digunakan. Dengan
memperhatikan percepatan perkembangan ilmu dan teknologi pengembangan modul multimedia hendaknya tetap “up to date”.
Modul yang adaptif adalah jika isi materi pembelajaran dapat
digunakan sampai dengan kurun waktu tertentu.
e. User Friendly, modul hendaknya bersahabat dengan
pemakainya.
Setiap instruksi dan paparan informasi yang tampil bersifat
membantu dan bersahabat dengan pemakainya, termasuk kemudahan
pemakai dalam merespon, mengakses sesuai dengan keinginan.
Penggunaan bahasa yang sederhana, mudah dimengerti serta
menggunakan istilah yang umum digunakan.
Sebuah modul dapat bermakna kalau peserta didik dapat dengan
mudah menggunakannya. Pembelajaran dengan modul memungkinkan
seorang peserta didik yang memiliki kecepatan tinggi dalam belajar akan
lebih cepat menyelesaikan satu atau lebih kompetensi dasar
dibandingkan dengan peserta didik lainnya.16
Modul matematika yang disusun dapat mendekatkan materi yang
diajarkan dengan kehidupan sehari-hari siswa yang sebenarnya, seperti
memberikan contoh peristiwa sehari-hari yang ada kaitannya dengan
materi pembelajaran, misalnya simulasi melukis sketsa grafik fungsi
aljabar. Dengan demikian modul yang dikembangkan dapat digunakan
oleh guru sebagai bahan ajar ataupun siswa sebagai sumber belajar.
Agar pembelajaran matematika berbantukan komputer dapat
mencapai tujuan yang diiinginkan, maka diperlukan perangkat
pembelajaran yang berkaitan dengan perangkat komputer pula. Maka
perangkat pembelajaran yang dikembangkan berupa e-modul.
5. Modul Elektronik
Menurut Nurma (2010) dalam (http://nurma.staff.uns.ac.id)
mengatakan: Modul Elektronik (E-Modul) merupakan alat atau sarana
pembelajaran yang berisi materi, metode, batasan-batasan, dan cara
mengevaluasi yang dirancang secara sistematis dan menarik untuk
mencapai kompetensi yang diharapkan sesuai dengan tingkat
kompleksitasnya secara elektronik (bagian dari e-learning).
E-modul dalam penelitian ini digunakan sebagai bahan ajar pada
mata pelajaran Matematika bab Turunan Fungsi dengan pokok bahasan
Tafsiran Geometris Turunan sebagai Gradien garis Singgung dengan
program aplikasi Geogebra jenjang Sekolah Menengah Atas (SMA)
kelas XI (sebelas) semester II (dua). Penggunaan e-modul sebagai
digunakan juga sebagai bahan ajar. Pengembangan e-modul sebagai
bahan ajar elektronik itu sendiri tidak jauh berbeda dengan modul,
hanya saja e-modul dirancang menggunakan sebuah software dan
dioperasikan menggunakan sebuah personal komputer. Sehingga pada
e-modul ini secara karakteristik memeliki karakteristik yang sama
dengan modul yaitu self instruksional, self contained, stand alone,
adaptive, dan user friendly.
6. Kualitas Perangkat Pembelajaran
Untuk memperoleh hasil pengembangan yang berkualitas
diperlukan penilaian. Untuk menentukan kualitas hasil pengembangan
model dan perangkat pembelajaran diperlukan tiga kriteria:
kevalidan, kepraktisan, dan keefektifan. Ketiga kriteria ini mengacu
pada kriteria kualitas hasil penelitian pengembangan yang dikemukakan
oleh Van den Akker dalam Rochmad (2011) dan kriteria kualitas produk
yang dikemukakan oleh Nieveen dalam Rochmad (2011). Van den
Akker dalam Rochmad (2011) dan Nieveen dalam Rochmad (2011)
menyatakan, bahwa dalam penelitian pengembangan model
pembelajaran perlu kriteria kualitas yaitu kevalidan (validity),
kepraktisan (practically), dan keefektifan (effectiveness).
Dalam penelitian ini, kualitas perangkat e-modul dinilai dari:
a. Aspek Kevalidan
E-modul pembelajaran Turunan Fungsi dikatakan valid jika
bahwa media pembelajaran Turunan Fungsi dikatakan valid dengan
revisi atau tanpa revisi, didasarkan pada landasan teoritik yang
kuat. Pengembangan sumber belajar Turunan Fungsi berbasis
e-modul memenuhi kriteria atau aspek yang terkandung dalam
media pembelajaran Turunan Fungsi. Aspek yang harus dipenuhi
dalam media ini adalah (1) Kualitas materi ( isi dan tujuan,) (2)
Kualitas tampilan (instruksional dan teknik).
b. Aspek Kepraktisan
E-modul Turunan Fungsi dikatakan praktis jika memenuhi
kriteria yaitu:
1) Para responden menyatakan bahwa media pembelajaran
Turunan Fungsi dapat diterapkan di kelas dan bermanfaat.
2) Tingkat keterlaksanaan penggunaan media pembelajaran
Turunan Fungsi termasuk tinggi dengan meninjau aktivitas
siswa dan guru.
c. Aspek Keefektifan
Aspek keefektifan biasanya berkaitan erat dengan
perbandingan antara tingkat pencapaian tujuan dengan rencana
yang telah disusun sebelumnya, atau perbandingan antara hasil
nyata dengan hasil yang direncanakan (Mulyasa, 2003: 82). Uno
(2008: 138) menyatakan bahwa keefektifan pengajaran biasanya
diukur dengan tingkat pencapaian siswa pada tujuan pembelajaran
menyatakan bahwa keterlaksanaan model dikatakan efektif dilihat dari
komponen- komponen: (1) hasil belajar siswa, (2) aktivitas siswa dan
(3) respon siswa. Hal ini berdasarkan pada tingkatan pengalaman dan
hasil intervensi konsisten dengan tujuan yang dimaksud. Tingkatan
pengalaman ini dengan adanya respon positif dari siswa yang
ditunjukkan melalui angket yang diberikan sedangkan intervensi
konsisten dengan tujuan yang dimaksud ditunjukkan dengan tes hasil
belajar. Sehingga pada e-modul pembelajaran Turunan Fungsi ini
dikatakan efektif jika memberikan hasil yang sesuai harapan dengan
ditunjukkan oleh tes hasil belajar.
7. Materi Ajar
Dalam subbab sebelumnya telah diketahui bahwa turunan sebuah
fungsi merupakan bentuk secara umum dari laju perubahan jarak
terhadap waktu. Dinyatakan dalam 𝑓(𝑥) dalam bentuk
, lalu apakah arti turunan fungsi 𝑓(𝑥) pada 𝑥 = 𝑎 secara geometris?
Secara geometris turunan fungsi dapat ditafsirkan sebagai gradient
garis singgung kurva di titik 𝑃(𝑥1, 𝑦1) terletak pada kurva 𝑦 = 𝑓(𝑥) maka persamaan garis singgung kurva yang melalui titik 𝑃(𝑥1, 𝑦1) adalah :
Dengan gradient 𝑚 = 𝑓’(𝑥1).
Tafsiran turunan turunan Fungsi secara geometris tidak
berhenti pada gradient garis singgung saja melainkan berlanjut pada
kemonotonan dan kecekungan kurva, nilai ekstrim, hingga menggambar
grafik fungsi aljabar. Berikut ini akan diuraikan secara singkat keempat
pokok bahasan tersebut.
a. Kemonotonan dan Kecekungan Kurva
Fungsi naik atau fungsi turun disebut sebagai Fungsi monoton
sedangkan fungsi naik atau turun didefinisikan sebagai berikut:
1) Fungsi dikatakan naik pada interval 𝐼 jika
𝑓(𝑥1) < 𝑓(𝑥2) bilamana 𝑥1< 𝑥2 pada interval 𝐼 dan secara
penerapan turunan dikatakan jika 𝑓(𝑥) naik jika 𝑓’(𝑥) > 0. 2) Fungsi dikatakan turun pada interval I jika
𝑓(𝑥1) > 𝑓(𝑥2) bilamana 𝑥1< 𝑥2 pada interval 𝐼 dan secara
penerapan turunan dikatakan jika 𝑓(𝑥) naik jika 𝑓’(𝑥) < 0. Maka kecekungan fungsi dapat dinyatakan sebagai berikut. Jika 𝑓(𝑥) terdifrensial pada selamg terbuka 𝐼
1) 𝑓’(𝑥) naik pada interval 𝐼, 𝑥 ∈ 𝐼, maka 𝑓(𝑥) cekung ke atas pada interval 𝐼, atau secara penerapan turunan dapat diuji dengan turunan kedua 𝑓(𝑥) yaitu 𝑓’’(𝑥) > 0 .
2) 𝑓’(𝑥) turun pada interval 𝐼, 𝑥 ∈ 𝐼, maka 𝑓(𝑥) cekung ke atas pada interval 𝐼, atau secara penerapan turunan dapat diuji
3) Hal yang terkait pada kecekungan adalah titik belok Titik 𝑃 pada kurva disebut titik belok jika kurva berubah dari cekung
ka atas menjadi cekung ke bawah atau dari cekung ke bawah
menjadi cekung ke atas pada 𝑃 sehingga secara penerapan turunan dapat diuji menggunakan turunan kedua
yaitu 𝑓’’(𝑥) = 0 .
b. Nilai Ekstrim
Misal diketahui kurva 𝑦 = 𝑓(𝑥) dengan titik (𝑎, 𝑏) merupakan titik puncak (titik maksimum atau titik minimum). Garis singgung
kurva di titik (𝑎, 𝑏) akan sejajar sumbu x atau mempunyai gradient 0
(𝑚 = 𝑓’(𝑎) = 0). Titik(𝑎, 𝑏) disebut titik ekstrim, nilai 𝑥 = 𝑎
disebut titik stasioner, sedangkan nilai 𝑦 = 𝑏 disebut nilai ekstrim.
Definisi:
Nilai 𝑓(𝑎) disebut nilai maksimum pada interval 𝐼 jika 𝑓(𝑎) >
𝑓(𝑥) untuk setiap 𝑥 ∈ 𝐼, sedangkan nilai 𝑓(𝑎) disebut nilai
minimum pada interval 𝐼 jika 𝑓(𝑎) < 𝑓(𝑥) untuk setiap 𝑥 ∈ 𝐼. Untuk menentukan jenis nilai ekstrim (maksimum atau
minimum) fungsi 𝑓(𝑥) dapat dilakukan dengan uji turunan kedua sebagai berikut.
1) Tentukan turunan pertama dan kedua fungsi 𝑓(𝑥), yaitu 𝑓’(𝑥) dan 𝑓’’(𝑥)
2) Tentukan titk stasioner, yaitu pembuat nol dari turunan pertama
3) Nilai 𝑓(𝑎) adalah nilai maksimum jika pada uji turunan kedua
nilai 𝑓’’(𝑎) < 0 sedangkan nilai 𝑓(𝑎) adalah nilai minimum jika pada uji turunan kedua nilai 𝑓’’(𝑎) > 0.17
c. Menggambar grafik Fungsi Aljabar
Dengan mempelajari turunan fungsi, menentukan, fungsi naik
dan fungsi turun, kemonotonan dan keckungan kurva, nilai ekstrim
maka kita dapat menggambar grafik fungsi fungsi aljabar secara
mudah. Berikut adalah langkah-langkah menggambar grafik fungsi
aljabar.
1) Tentukan titik-titik potong kurva dengan subu koordinat (jika ada
dan mudah ditentukan)
a. Titik potong kurva dengan 𝑠𝑢𝑚𝑏𝑢 𝑌, syarat 𝑥 = 0
b. Titik potong kurva dengan 𝑠𝑢𝑚𝑏𝑢 𝑋, 𝑠𝑦𝑎𝑟𝑎𝑡 𝑦 = 0 2) Tentukan nilai-nilai ekstrim
3) Tentukan interval dimana fungsi naik dan interval dimana fungsi
turun
4) Tentukan interval dimana fungsi cekung ke atas dan interval
dimana fungsi cekung ke bawah.
5) Tentukan nilai fungsi 𝑓(𝑥) untuk 𝑥 positif besar dan 𝑥 negative besar.
6) Tentukan titik bantu sejauh dibutuhkan.18
17 Sriyanto, Catur Supatmono, Matematika Kontektual Untuk SMA/MA Kelas XI Program Studi IPA (Intan Pariwara: Klaten:2011)hlm 306.
d. Aplikasi Turunan Fungsi
Aplikasi turunan fungsi yang sederhana ada pada model
matematika yang berkaitan dengan nilai ekstrim, fungsi dapat ditentukan
dengan berbagai persoalan kontekstual. Langkah-langkah umum
penyelesaiannya sebagai berikut.
1) Tentukan variabel yang terlibat dalam soal. Jika soal berbentuk soal
cerita, terlebih dahulu lakukan pemisalan.
2) Tentukan mana yang akan dicari nilai ekstrim maximum dan
minimumnya. Umumnya hal ini dilakukan membuat persamaan agar
fungsi yang dicari minimum atau maximumnya menjadi satu
variabel. Jika diperlukan pada proses ini menggunakan cara subtitusi
atau elimanasi.
3) Tentukan nilai stationer untuk menentukan nilai minimum atau nilai
maximum fungsi.
4) Jika soal berbentuk cerita, tafsiran jawaban yang diperoleh sehingga
sungguh-sungguh menjawab persoalan yang terkandung dari soal
cerita tersebut.
8. GeoGebra
GeoGebra adalah salah satu program komputer yang dapat
dimanfaatkan sebagai media pembelajaran matematika adalah
program GeoGebra. GeoGebra dikembangkan oleh Markus
GeoGebra adalah prgram komputer untuk membelajarkan matematika
khususnya geometri dan aljabar. Program ini dapat dimanfaatkan
secara bebas yang dapat diunduh dari www.geogebra.com. Website
ini rata-rata dikunjungi sekira 300.000 orang tiap bulan. Hingga saat
ini, program ini telah digunakan oleh ribuan siswa maupun guru dari
sekira 192 negara.
Program GeoGebra melengkapi berbagai program komputer untuk
pembelajaran aljabar yang sudah ada, seperti Derive, Maple, MuPad,
maupun program komputer untuk pembelajaran geometri, seperti Geometry’s Sketchpad atau CABRI. Menurut Hohenwarter (2008),
bila program-program komputer tersebut digunakan secara spesifik
untuk membelajarkan aljabar atau geometri secara terpisah, maka
GeoGebra dirancang untuk membelajarkan geometri sekaligus aljabar
secara simultan.
Berdasarkan penjelasan di atas modul elektronik dengan materi
tafsiran geometris turunan fungsi akan dikembangkan menggunakan
program GeoGebra versi 4.2 yang telah diperkenalkan oleh
Hohenwarter sejak November 2012.
a. Area Kerja
1) Tampilan Aljabar (Algebra View) - deskripsi objek pada tampilan
grafik yang ditampilkan.
2) Tampilan Grafik (Graphics View)- tempat untuk kontruksi,
3) CAS (Komputer Algebra System) merupakan fasilitas yang mulai
dimasukkan pada GeoGebra Versi 4.2 Beta. Fitur ini digunakan
untuk melakukan perhitungan aljabar.
4) Graphics 2D – mirip tampilan Graphics View, bedanya untuk
tampilan Graphics 2D ini apabila diaktifkan akan memunculkan
jendela baru. Setiap kali kita memasukkan persamaan atau perintah
pada Inbut Bar maka hasil grafiknya akan muncul pada jendela ini.
b. Menu, Toolbar Dan Tool
Gambar 1 Jendela Kerja GeoGebra
Seperti pada aplikasi lain, menu bar GeoGebra berada pada bagian
atas terdiri atas menu File, Edit Options, Tools, Window dan Help.
Di bawahnya terdapat Toolbar yang berisi menu untuk membangun,
menggambar, mengukur dan memanipulasi objek. Pada setiap
kategori yang ada di Toolbar terdapat beberapa Tool lain yang
tersembunyi, untuk menampilkannya kita dapat mengklik tanda
panah kecil di bagian kanan bawah setiap kotak Tool yang ada di
1) Menu Bar - digunakan untuk mengelola file, edit file dan pengaturan modifikasi.
2) Toolbar – alat-alat yang digunakan untuk menggambar, membangun, mengukur dan memanipulasi objek.
Tool yang sedang aktif ditandai dengan adanya kotak biru pada Tool
tersebut. Selama Tool itu sedang aktif kita bisa menggunakannya untuk
melakukan tugasnya dan tidak perlu mengklik lagi untuk membuat
objek yang sama. Setiap Tool yang ada dan sedang aktif akan
dijelaskan nama Tool disamping kanan dari Toolbar itu sendiri.
B. HASIL PENELITIAN YANG RELEVAN
1. Penelitian yang dilakukan oleh Ratini (2006) yang berjudul
"Pengembangan Media Pembelajaran Matematika Berbasis
Edutainment untuk Siswa SMP Kelas VIII pada Pokok Bahasan
Persamaan Garis Lurus". Beberapa hasil penelitian tersebut antara
lain bahwa penyusunan CD media pembelajaran matematika
mengikuti langkah-langkah sebagai berikut: 1) pembuatan
konsep, 2) desain, 3) pengumpulan materi, 4) assembly, 5) uji coba.
Selain itu pada penilitian tersebut juga disimpulkan bahwa media
pembelajaran yang dihasilkan mampu menumbuhkan motivasi
75% dari 36 siswa yang mengikuti uji coba media pertama.
Jadi, media pembelajaran matematika berbasis edutainment
yang dikembangkan dapat menumbuhkan motivasi belajar siswa