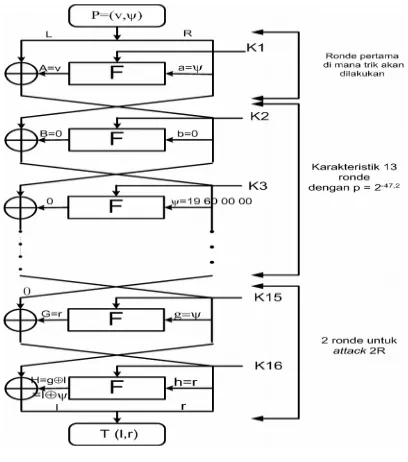
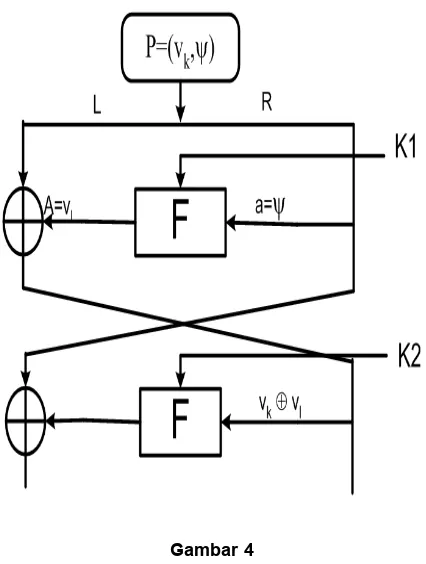
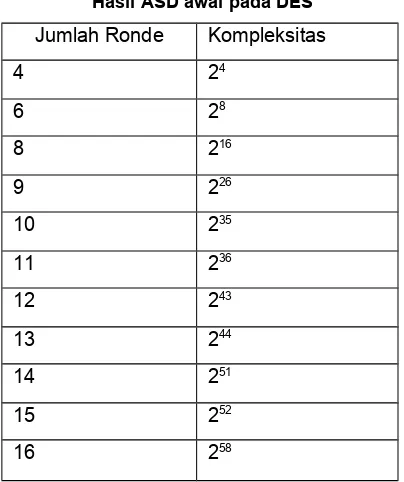
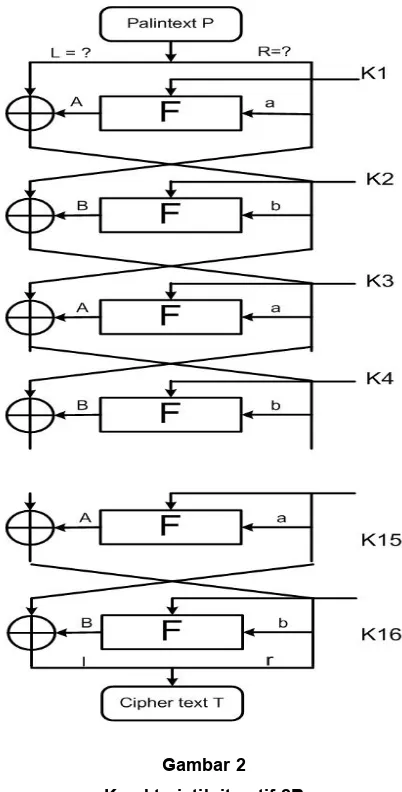
Abstrak : Pada umumnya komponen yang membentuk mekanisme dimodelkan sebagai batang kaku. Anggapan ini tidak berlaku terutama apabila gaya yang bekerja pada komponen tersebut sangat besar dan deformasi yang terjadi tidak dapat diabaikan. Makalah ini membah
Teks penuh
Gambar


Dokumen terkait
Indonesia sebagai penghasil minyak setengah jadi kelapa sawit (CPO) dengan jumlah yang sangat besar. Produk CPO Indonesia menjadi komoditas unggulan Indonesia yang memenuhi
Analitycal Hierarchy Process (AHP) Adalah metode untuk memecahkan suatu situasi yang komplek tidak terstruktur kedalam beberapa komponen dalam susunan yang hirarki, dengan
Kebijakan puritanisme oleh sultan Aurangzeb dan pengislaman orang-orang Hindu secara paksa demi menjadikan tanah India sebagai negara Islam, dengan menyerang berbagai praktek
Selain itu, perhitungan harga pokok produksinya pun masih belum tepat karena biaya bahan baku langsung belum dihitung berdasarkan standar yang spesifik dan
[r]
Pada tahap pertama dari penelitian ini adalah uji distribusi untuk data permintaan, data penjualan, data demand untuk kategori the celup dengan menggunakan uji
Perkembangan masyarakat Indonesia pada saat ini dalam menghadapi era globalisasi yang penuh dengan tantangan dan kemungkinan yang bisa terjadi seakan-akan masyarakat Indonesia
;< Calon Kepala Desa Suradita .ang memperoleh suara sah terban.ak ditetapkan sebagai Calon Calon Kepala Desa Suradita .ang memperoleh suara sah terban.ak ditetapkan sebagai