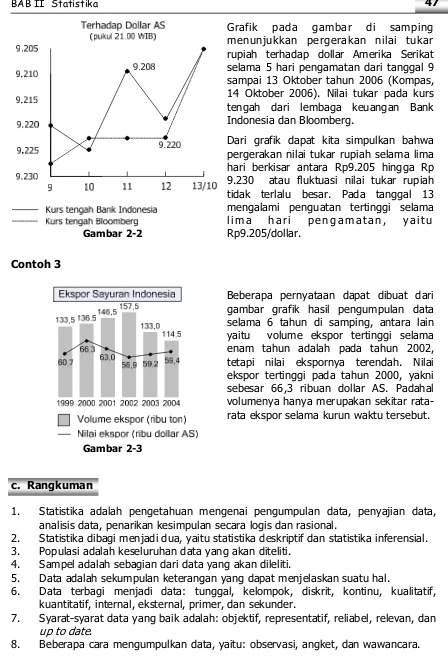
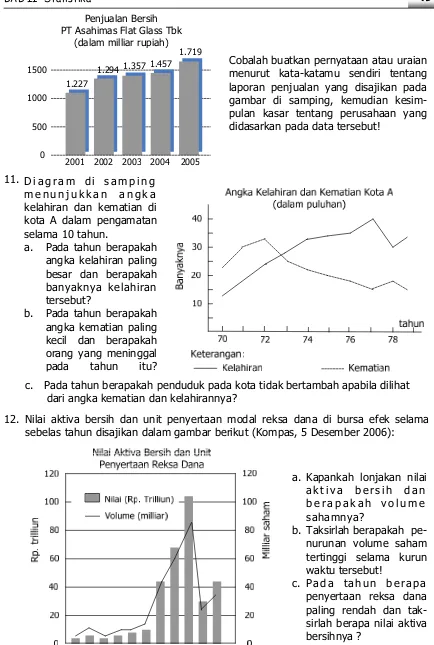
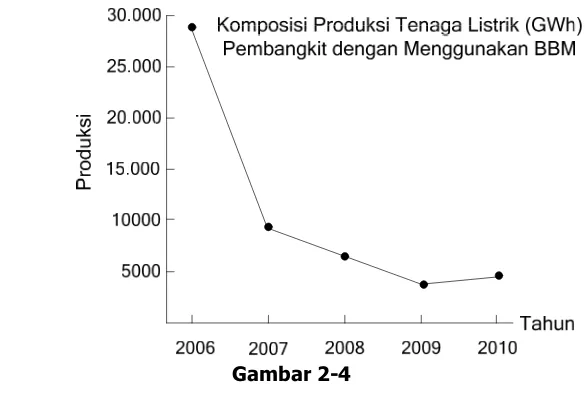
smk12 MudahBelajarMatematika Toali
Teks penuh
Gambar


Garis besar
Dokumen terkait
Menentukan salah satu ukuran sisi yang belum diketahui pada dua bangun yang sebangun.. Syarat dua segitiga
Jika dua buah segitiga memiliki sudut-sudut yang bersesuaian sama besar maka kedua segitiga tersebut sebangun dan mengakibatkan sisi-sisi yang bersesuaian adalah
Dalam melukis segitiga samasisi, kamu harus ingat sifat-sifat pada segitiga samasisi, yaitu mempunyai tiga sisi yang sama panjang dan ketiga sudutnya sama ukuran?. Untuk
Apabila diketahui panjang dua sisi suatu segitiga siku-siku, maka panjang sisi yang ketiga dapat dihitung menggunakan teorema Pythagoras.. Panjang hipotenusa sama
Perhatikan gambar berikut.. Hitunglah panjang AD. Hubungan antara kesebangunan dengan kekongruenan adalah: untuk dua segitiga yang kongruen sudah pasti sebangun, akan tetapi untuk
Disajikan gambar dua segitiga sebangun yang salah satu sudutnya berhimpit dan ukuran yang diperlukan diketahui (tidak memiliki sisi sejajar), peserta didik dapat menentukan
ketiga titik sudut A,B dan C, masing- masing ditarik garis yang tegak lurus terhadap sisi segitiga AB, BC dan CA sehingga terbentuk segitiga baru. Diketahui ∆ABC sebangun
segitiga yang ketiga sisinya. Segitiga adalah bangun datar yang dibatasi oleh tiga buah sisi dan mempunyai tiga buah titik sudut. Jenis-Jenis Segitiga Berdasarkan Panjang