PENERAPAN MODEL SEARCH, SOLVE, CREATE, AND SHARE DENGAN PENDEKATAN PROBLEM POSING UNTUK MENINGKATKAN KEMAMPUAN PENALARAN DAN KOMUNIKASI MATEMATIS SISWA SMP.
Teks penuh
Gambar

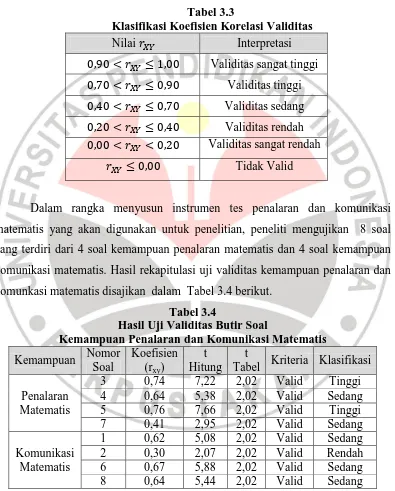
Dokumen terkait
Pelaksanaan pembinaan berjalan cukup lancar dengan dilakukannya pembagian tugas adanya koordinasi dari setiap elemen sekolah serta dukungan dari orang tua meskipun
[r]
Asesmen portofolio berdampak positif terhadap sikap siswa pada.
Tujuan umum penelitian ini adalah untuk memberikan usulan rancangan perbaikan produk spring bed yang dapat memenuhi kebutuhan konsumen dengan menggunakan metode
itu, spora tumbuh dengan ukuran yang lebih panjang karena akan berfungsi. sebagai
Sebagaimana penjelasan pada ayat (1), Transmigrasi Swakarsa Mandiri yang dilaksanakan oleh masyarakat baik secara kelompok maupun perseorangan maupun kelompok yang
Penelitian ini bertujuan untuk menganalisis pengaruh simultan antara variabel-variabel eksogen terhadap variabel-variabel endogen, yakni PDRB perkapita, indeks curah hujan,
Penelitian ini dilakukan untuk mengukur Kepuasan konsumen Depot Soto Gebraak Cak Anton di lihat dari Segi Pelayanan,Segi Rasa,Segi Harga,Segi CiriKhas,Segi Lokasi dan