PERBANDINGAN KEMAMPUAN KONEKSI MATEMATIKA
DALAM MEMECAHKAN MASALAH
DITINJAU DARI DOMINASI
OTAK KIRI ATAU OTAK KANAN
SKRIPSI
Oleh:
IRSYA NOURUZAMAN ASSIDIK D74212074
UNIVERSITAS ISLAM NEGERI SUNAN AMPEL SURABAYA FAKULTAS TARBIYAH DAN KEGURUAN
JURUSAN PENDIDIKAN MATEMATIKA DAN IPA PROGRAM STUDI PENDIDIKAN MATEMATIKA
PERBANDINGAN KEMAMPUAN KONEKSI MATEMATIKA
DALAM MEMECAHKAN MASALAH
DITINJAU DARI DOMINASI
OTAK KIRI ATAU OTAK KANAN
SKRIPSI
Diajukan kepada Universitas Islam Negeri Sunan Ampel Surabaya untuk memenuhi salah satu persyaratan dalam menyelesaikan Program Sarjana
Pendidikan (S.Pd)
Oleh:
Irsya Nouruzaman Assidik NIM. D74212074
UNIVERSITAS ISLAM NEGERI SUNAN AMPEL SURABAYA FAKULTAS TARBIYAH DAN KEGURUAN
JURUSAN PENDIDIKAN MATEMATIKA DAN IPA PROGRAM STUDI PENDIDIKAN MATEMATIKA
v
PERBANDINGAN KEMAMPUAN KONEKSI MATEMATIKA DALAM MEMECAHKAN MASALAH DITINJAU DARI DOMINASI OTAK KIRI
ATAU OTAK KANAN
Oleh:
Irsya Nouruzaman Assidik ABSTRAK
Salah satu dari lima tujuan matematika diajarkan pada jenjang pendidikan sekolah adalah memahami konsep matematika, menjelaskan keterkaitan antar konsep atau algoritma secara luwes, akurat, efisien. Tujuan tersebut secara sederhana bisa disebut dengan koneksi matematika. Koneksi matematika merupakan keterkaitan antar konsep dalam matematika, keterkaitan matematika dengan bidang studi yang lain dan aplikasi matematika dalam kehidupan sehari-hari. Tujuan penelitian ini adalah untuk mengetahui perbedaan kemampuan koneksi matematika siswa dalam memecahkan masalah dibedakan dari dominasi otak kiri atau otak kanan.
Penelitian ini merupakan penelitian komparatif dengan pendekatan kuantitatif. Populasi dalam penelitian ini adalah siswa kelas XI MIPA SMA Negeri 1 porong, dengan menggunakan kelas XI MIPA 5 sebagai sampel penelitian. Sampel akan dibagi menjadi dua kategori, yaitu siswa yang dominan otak kiri dan siswa yang dominan otak kanan dengan membandingkan kemampuan koneksi matematika tiap kategori. Data hasil kemampuan koneksi matematika siswa dianaisis dengan menggunakan uji kesamaan dua rata-rata (uji-t untuk mengetahui adanya perbedaan kemampuan koneksi matematika siswa yang dominan otak kiri dan siswa yang dominan otak kanan.
Hasil penelitian kemampuan koneksi matematika dalam memecahkan masalah ditinjau dari dominasi otak kiri atau otak kanan menggunakan uji hipotesis kesamaan dua rata-rata (uji-t) didapat bahwa nilai �ℎ� �� sebesar 2, , sedangkan ttabel sebesar 2,0 . Hasil tersebut menunjukkan bahwa nilai thit > ttab, sehingga dapat diketahui bahwa cukup untuk menolak H0, yang berarti ada perbedaan yang signifikan kemampuan koneksi matematika dalam memecahkan masalah antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan.
ix
DAFTAR ISI
HALAMAN JUDUL... i
LEMBAR PERSETUJUAN PEMBIMBING ... ii
LEMBAR PENGESAHAN TIM PENGUJI ... iii
LEMBAR PERNYATAAN KEASLIAN ... iv
HALAMAN PERSEMBAHAN ... v
ABSTRAK ... vi
KATA PENGANTAR ... vii
DAFTAR ISI ... ix
DAFTAR TABEL ... xi
DAFTAR GAMBAR ... xii
DAFTAR LAMPIRAN ... xiii
BAB I PENDAHULUAN A. Latar Belakang Masalah ... 1
B. Rumusan Masalah ... 6
C. Tujuan Penelitian ... 6
D. Manfaat Penelitian ... 6
E. Definisi Operasional Variabel ... 7
F. Batasan Penelitian ... 8
G. Sistematika Pembahasan ... 8
BAB II KAJIAN PUSTAKA A. Kemampuan Koneksi Matematika Siswa dalam Memecahkan Masalah ... 9
B. Dominasi Otak Kiri dan Dominasi Otak Kanan... 17
C. Keterkaitan Antara Kemampuan Koneksi Matematika dalam Memecahkan Masalah dengan Dominasi Otak Kiri atau Otak Kanan ... 28
D. Hipotesis Penelitian ... 29
BAB III METODE PENELITIAN A. Jenis dan Pendekatan Penelitian ... 30
B. Tempat dan Waktu Penelitian ... 30
C. Desain Penelitian ... 31
D. Populasi, Sampel dan Teknik Sampling... 32
E. Variabel Penelitian ... 33
F. Teknik dan Instrumen Penelitian ... 34
G. Teknik Analisis Data... 36
x
B. Analisis data Perbedaan Kemampuan Koneksi Matematika
dalam Memecahkan Masalah ... 45
C. Pembahasan Hasil Penelitian ... 52
BAB V PENUTUP A. Kesimpulan ... 55
B. Saran ... 55
DAFTAR PUSTAKA ... 56
xi
DAFTAR TABEL
2.1 Indikator Kemampuan Koneksi Matematika dalam Memecahkan
Masalah ... 16
2.2 Kriteria Penilaian Angket ... 23
2.3 Perbandingan Mode Kiri vs Mode Kanan ... 26
3.1 Desain Penelitian ... 31
3.2 Daftar Nama Validator ... 36
3.3 Contoh Tabel Uji Kolmogorov-Smirnov ... 37
3.4 Contoh Tabel Uji Bartlett ... 38
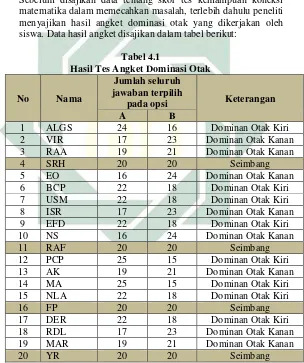
4.1 Hasil Tes Angket Dominasi Otak ... 41
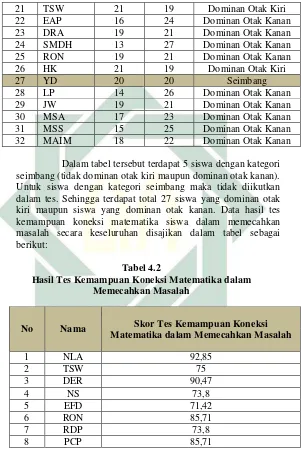
4.2 Hasil Tes Kemampuan Koneksi Matematika dalam Memecahkan Masalah ... 42
4.3 Hasil Tes Kemampuan Koneksi Matematika dalam Memecahkan Masalah Untuk Menghitung Rata-rata, Varians, dan Stadar Deviasi ... 43
4.4 Hasil Perhitungan Uji Normalitas dalam Tabel Kolmogorov-Smirnov ... 46
4.5 Hasil Tes Kemampuan Koneksi Matematika dalam Memecahkan Masalah Siswa yang Dominan Otak Kiri untuk Menghitung Rata-rata dan Varians ... 47
4.6 Hasil Tes Kemampuan Koneksi Matematika dalam Memecahkan Masalah Siswa yang Dominan Otak Kanan untuk Menghitung Rata-rata dan Varians ... 48
xii
DAFTAR GAMBAR
xiii
DAFTAR LAMPIRAN
LAMPIRAN A (BAHAN PENELITIAN)
1. Angket Dominasi Otak ... 60
2. Kisi-kisi Soal Tes Kemampuan Koneksi Matematika ... 64
3. Tes Kemampuan Koneksi Matematika ... 67
4. Kunci Jawaban dan Pedoman Penskoran Tes Kemampuan Koneksi ... 69
5. Lembar Validasi Tes Kemampuan Koneksi ... 77
LAMPIRAN B (HASIL PENELITIAN) 1. Salah Satu Hasil Tes Kemampuan Koneksi Matematika Siswa Dominan Otak Kiri ... 81
2. Hasil Tes Kemampuan Koneksi Matematika Siswa Dominan Otak Kanan ... 83
3. Tabel Nama Siswa Kategori Dominan Otak Kiri dan Dominan Otak Kanan ... 85
LAMPIRAN C (SURAT DAN LAIN-LAIN) 1. Surat Ijin Penelitian ... 86
2. Surat Keterangan Pelaksanaan Penelitian ... 87
3. Form Bimbingan ... 88
BAB I
PENDAHULUAN
A. Latar Belakang Masalah
Matematika merupakan salah satu ilmu yang sangat bermanfaat dalam kehidupan sehari-hari untuk menunjang kemajuan teknologi.1 Matematika juga menjadi salah satu sarana berpikir yang dapat menumbuhkembangkan cara berpikir logis, sistematis, dan kritis. Mengingat begitu pentinganya matematika, maka kurikulum di Indonesia mengatur bahwa pada mata pelajaran matematika di sekolah perlu membekali siswanya dengan kemampuan berpikir logis, analitis, sistematis, kritis dan kreatif serta kemampuan bekerja sama.
Pemerintah melalui Permendikbud No.58 Tahun 2014 menyusun kompetensi inti dan kompetensi dasar matematika sebagai landasan pembelajaran untuk mengembangkan kemampuan berpikir seperti yang telah dijelaskan di atas.2 Lebih lanjut, dalam lampiran ketiga peraturan tersebut juga dijelaskan tentang tujuan pembelajaran matematika agar setiap peserta didik memiliki kemampuan sebagai berikut3: (a) memahami konsep matematika, menjelaskan keterkaitan antar konsep atau algoritma secara luwes, akurat, efisien, dan tepat dalam pemecahan masalah; (b) Menggunakan pola sebagai dugaan dalam penyelesaian masalah, dan mampu membuat generalisasi berdasarkan fenomena atau data yang ada; (c) Menggunakan penalaran pada sifat, melakukan manipulasi matematika baik dalam penyederhanaan, maupun menganalisa komponen yang ada dalam pemecahan masalah dalam konteks matematika maupun di luar matematika (kehidupan nyata, ilmu, dan teknologi) yang meliputi kemampuan memahami masalah, membangun model matematika, menyelesaikan model dan menafsirkan solusi yang diperolehtermasuk dalam rangka memecahkan masalah dalam kehidupan sehari-hari (dunia nyata);
1Sri Wahyuni, Tesis : “Kemampuan Koneksi Matematika siswa SMP dalam Memecahkan Masalah Terbuka Ditinjau dari Kemampuan Matematika”. (Surabaya: Univ Negeri Surabaya, 2015), hal. 1
2Permendikbud No.58 Tahun 2014 Lampiran III Matematika SMP/MTs, hal 325-327
(d) Mengkomunikasikan gagasan, penalaran serta mampu menyusun bukti matematika dengan menggunakan kalimat lengkap, simbol, tabel, diagram, atau media lain untuk memperjelas keadaan atau masalah; (e) Memiliki sikap menghargai kegunaan matematika dalam kehidupan, yaitu memiliki rasa ingin tahu, perhatian, dan minat dalam mempelajari matematika, serta sikap ulet dan percaya diri dalam pemecahan masalah.
Salah satu dari kelima tujuan tersebut, yaitu “memahami konsep matematika, menjelaskan keterkaitan antar konsep atau algoritma secara luwes, akurat, efisien“. Tujuan yang pertama ini secara tidak langsung adalah tentang koneksi matematika. Kalimat tersebut juga menunjukkan bahwa kemampuan koneksi matematika merupakan salah satu dari lima tujuan yang harus dicapai oleh peserta didik dalam mata pelajaran matematika. Pada pelajaran matematika, konsep yang baru selalu terkait dengan konsep yang lama atau konsep sebelumnya, oleh karena itu dibutuhkan kemampuan koneksi matematika untuk mengaitkan tiap konsep yang dipelajari.
Istilah koneksi matematika pertama kali dimunculkan oleh NCTM (National Council of Teachers of Mathematics) yang merupakan sebuah perkumpulan guru matematika di Amerika. Koneksi matematika merupakan keterkaitan antara konsep-konsep matematika secara internal maupun keterkaitan secara eksternal. Maksud dari koneksi secara internal dalam hal ini yaitu keterkaitan antar konsep dalam matematika, dan koneksi secara eksternal yang berarti keterkaitan antara matematika dengan bidang studi yang lain maupun aplikasi matematika dengan kehidupan sehari-hari. Berdasarkan penjelasan tersebut dapat diketahui bahwa koneksi matematika memiliki tiga aspek, yaitu koneksi antar konsep dalam matematika, koneksi dengan disiplin ilmu yang lain dan koneksi matematika dengan aplikasinya dalam kehidupan sehari-hari.4
Salah satu karakteristik dalam mempelajari matematika adalah dengan menerapkan penalaran deduktif.5
4
Mujiyem Sapti, “Kemampuan Koneksi Matematis (Tinjauan Terhadap Pendekatan Pembelajaran Savi)”. Jurnal Pendidikan Matematika. - : 11, (2010), hal. 62
5Rochmad, “Proses Berpikir Induktif dan Deduktif dalam Mempelajari Matematika“.
Penalaran deduktif dalam matematika merupakan pola penalaran dalam menilai suatu kebenaran didasarkan pada definisi, teorema, maupun konsep-konsep sebelumnya. Berdasarkan penjelasan tersebut, maka koneksi antar konsep dalam matematika akan sangat membantu pola bernalar deduktif dalam belajar matematika.
Kemampuan koneksi matematika merupakan salah satu faktor penting dalam melakukan pemahaman konsep matematika. Dengan melakukan koneksi, konsep-konsep matematika yang telah dipelajari tidak ditinggalkan begitu saja sebagai bagian yang terpisah, tetapi digunakan sebagai pengetahuan dasar untuk memahami konsep yang baru.6 Koneksi matematika juga tidak terpartisi dalam berbagai topik yang saling terpisah, namun merupakan satu kesatuan.7
Koneksi matematika juga sangat berperan pada proses pemecahan masalah. Sebagaimana Hodgson menyatakan bahwa “Mathematical connections serve as tools in the problem-solving process.”8
Pernyataan tersebut bisa dimaknai bahwa koneksi matematika berfungsi sebagai alat dalam proses pemecahan masalah.
Pemecahan masalah adalah suatu aktivitas intelektual untuk mencari solusi masalah yang dihadapi dengan menggunakan bekal pengetahuan yang sudah dimiliki.9 Pemecahan masalah juga merupakan proses menerapkan pengetahuan yang telah diperoleh sebelumnya pada situasi baru dan berbeda. Berdasarkan kedua definisi tersebut dapat diketahui bahwa, pemecahan masalah membutuhkan bekal pengetahuan yang sudah dimiliki dalam proses penyelesaiannya. Oleh karena
6Nila Kurniasari – Budiyono - Teguh Wibowo, “Kemampuan Koneksi Matematika pada Kompetensi Dasar Menghitung Luas Permukaan dan Volume Kubus, Balok, Prisma, dan Limas”. Jurnal Pendidikan Matematika, 2 : 1, (2013), hal. 45
7Sugiman, “Koneksi Matematika dalam Pembelajaran Matematika di Sekolah Menengah Pertama”. Jurnal Pendidikan Matematika UNY, 4 : 1 (Juni, 2008), hal. 57
8Hodgson, “Connecting Mathematics across the Curriculum”. (USA The NCTM, 1995), hal. 21
9
itu koneksi matematika akan sangat membantu siswa dalam meningkatkan kemampuan pemecahan masalah.10
Koneksi matematika juga memiliki keterkaitan erat dengan proses pemecahan masalah. Ini dibuktikan dengan beberapa pernyataan dari para ahli. Krulik dan Rudnick mengatakan bahwa “problem solving shows the interconnections among mathematicial ideas”. Pernyataan tersebut memiliki arti bahwa pemecahan masalah menunjukkan keterhubungan/koneksi antar ide-ide matematika. Sedangkan Drew dan Rankin mengatakan bahwa “children learn best in open-ended explorations when teachers help them make connections”. Pernyataan tersebut berarti bahwa koneksi matematika dapat membantu anak-anak dalam mengeksplorasi masalah terbuka.11
Salah satu faktor yang memengaruhi kemampuan koneksi matematika adalah keterampilan berpikir. Hal tersebut dikarenakan koneksi matematika menjadi salah satu dari lima keterampilan dasar pembelajaran di Amerika. Lima keterampilan itu adalah sebagai berikut: komunikasi matematika (communication), berfikir secara matematika (reasoning), koneksi matematika (connection), pemecahan masalah (problem solving), pemahaman matematika (undersatanding).12 Faktor yang berperan penting dalam berpikir adalah otak.
Otak adalah organ tubuh yang mengatur segala aktivitas manusia.13 Berdasarkan teori Split-Brain Roger Sperry, bahwa otak besar (cerebrum) merupakan bagian terbesar dari otak manusia. Otak besar adalah bagian yang memproses semua kegiatan intelektual kecerdasan otak manusia, pada teori tersebut juga dikemukakan bahwa otak besar dibagi menjadi dua, belahan
10Saiful Bahri. “Peningkatan Kemampuan Pemecahan Masalah dan Koneksi Matematika
Siswa dengan Pendekatan Kontekstual (Contextual Teaching And Learing) di SMA Swasta Al-Azhar Medan”.Universitas Muslim Nusantara Al Washliyah (2012).
11Fikri Apriono, Tesis : “Profil Kemampuan Koneksi Matematika Siswa SMP dalam memecahkan masalah ditinjau dari Perbedaan Gender”. (Surabaya: Univ Negeri Surabaya, 2015), hal. 5
12
Asep Jihad. Pengembangan Kurikulum Matematika (Tinjauan Teoritis dan Historis). (Bandung: Multipressindo, 2008), hal. 148
13
otak kiri (brain's left hemisphere) dan belahan otak kanan (brain's right hemisphere).
Belahan otak kiri cenderung memproses informasi berupa kata, angka, logika, analisis, daftar dan kemampuan menghitung. Belahan otak kanan cenderung memproses informasi berupa pemikiran konseptual, warna, irama, musik, visual-spasial, gambar dan imajinasi serta kemampuan untuk menghasilkan ide-ide kreatif. Belahan otak kanan berfungsi menguasai bagian sebelah kiri anggota badan, dan sebaliknya belahan otak kanan berfungsi menguasai bagian sebelah kanan anggota badan.14
Belahan otak kiri dan belahan otak kanan ini sangat memengaruhi gaya pemikiran setiap manusia. Setiap manusia memiliki gaya pemikiran yang berbeda, ada pemikirannya lebih dipengaruhi oleh belahan otak kiri dan begitu juga sebaliknya. Gaya pemikiran belahan otak kanan adalah lebih bebas dan acak, lebih menyeluruh, menekankan pada intuisi, subjektif, sintesis dan abstrak, sedangkan gaya pemikiran belahan otak kiri lebih kepada logis, rasional, analitik, objektif, berurutan dan spesifik. Gaya pemikiran inilah yang akan menyebabkan proses penerimaan informasi dari setiap manusia berbeda, termasuk dalam proses pembelajaran, khususnya dalam hal matematika.
Dalam proses penerimaan informasi dan berpikir oleh otak dalam kehidupan sehari-hari, ada kecenderungan bahwa manusia lebih sering menggunakan salah satu belahan otaknya. Hal ini oleh para ahli disebut dengan dominasi otak (brain dominance). Mengacu pada karakteristik otak kanan dan otak kiri yang telah dijelaskan sebelumnya, peneliti tertarik untuk melihat adanya perbedaan kemampuan koneksi matematika siswa dalam memecahkan masalah dibedakan berdasarkan dominasi otaknya. Berdasarkan uraian tersebut, maka peneliti mengajukan skripsi yang berjudul “Perbandingan Kemampuan Koneksi Matematika dalam Memecahkan Masalah Ditinjau dari Dominasi Otak Kiri atau Otak Kanan”.
14
B. Rumusan Masalah
Berdasarkan latar belakang yang telah dijelaskan di atas, maka rumusan masalahnya adalah adakah perbedaan yang signifikan kemampuan koneksi matematika dalam memecahkan masalah antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan?
C. Tujuan Penelitian
Berdasarkan rumusan masalah maka tujuan penelitian ini adalah untuk mengetahui perbedaan kemampuan koneksi matematika dalam memecahkan masalah antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan.
D. Manfaat Penelitian
Hasil dari penelitian ini, peneliti berharap dapat memberikan manfaat bagi:
1. Siswa yang diteliti
Dapat menjadi bahan evaluasi bagi siswa, agar dapat meningkatkan meningkatkan kemampuan koneksi matematika dalam memecahkan masalah.
2. Bagi Guru
Sebagai informasi mengenai hasil perbandingan kemampuan koneksi matematika siswa dalam memecahkan masalah, sehingga dapat digunakan guru sebagai pertimbangan untuk merancang pembelajaran yang sesuai untuk siswa yang dominan otak kiri dan siswa yang dominan otak kanan dalam upaya perbaikan pengajaran di lembaga pendidikan yang diajar.
3. Bagi Peneliti
Dapat membandingkan kemampuan koneksi matematika siswa dalam memecahkan masalah, mana yang lebih baik, antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan.
4. Bagi Peneliti yang lain
E. Definisi Operasional Variabel
Agar tidak terjadi kesalahan penafsiran dalam memahami judul penelitian, maka peneliti perlu membuat definisi operasional sebagai berikut:
1. Kemampuan (Kamus Besar Bahasa Indonesia) adalah kesanggupan atau kecakapan dalam melaksanakan sesuatu.
2. Koneksi matematika merupakan keterkaitan antara konsep-konsep matematika secara internal maupun keterkaitan secara eksternal, yang meliputi tiga aspek penting yaitu, keterkaitan antar konsep dalam matematika, keterkaitan antara matematika dengan disiplin ilmu yang lain dan keterkaitan antara matematika dengan kehidupan sehari-hari.
3. Kemampuan koneksi matematika merupakan kecakapan dalam mengetahui keterkaitan keterkaitan antar konsep dalam matematika, keterkaitan antara matematika dengan disiplin ilmu yang lain dan keterkaitan antara matematika dengan kehidupan sehari-hari.
4. Masalah matematika adalah sesuatu soal matematika yang belum memiliki prosedur pasti serta membutuhkan bekal pengetahuan baru dan pengetahuan lama untuk menyelesaikannya.
5. Pemecahan masalah merupakan suatu aktivitas intelektual untuk mencari penyelesaian masalah yang dihadapi dengan menggunakan bekal pengetahuan yang sudah dimiliki.
6. Kemampuan koneksi matematika dalam memecahkan masalah adalah kecakapan yang dimiliki dalam mengetahui keterkaitan antara tiga aspek, yaitu koneksi antar topik matematika, koneksi dengan disiplin ilmu yang lain, dan koneksi dalam kehidupan sehari-hari, dalam pemecahan masalah.
memiliki fungsi yang saling melengkapi.
F. Batasan Penelitian
Berdasarkan rumusan masalah yang telah dijelaskan sebelumnya serta agar penelitian dapat terfokus, maka perlu adanya batasan penelitian. Pada penelitian ini, adapun batasan yang digunakan peneliti dalam pengkajian masalah tentang kemampuan koneksi matematika, adalah pada materi turunan SMA kelas XI kurikulum 2013 mata pelajaran matematika (wajib).
G. Sistematika Pembahasan
Sistematika pembahasan dalam penelitian ini adalah sebagai berikut :
BAB I Pendahuluan. Pada bab ini terdiri dari tujuh sub bab, yaitu latar belakang masalah, rumusan masalah, tujuan penelitian, manfaat penelitian, devinisi operasional variabel, batasan penelitian dan sistematika pembahasan.
BAB II Kajian pustaka. Kajian Pustaka yang merupakan dasar teori dalam penelitian ini terdiri dari empat sub bab, yaitu kemampuan koneksi matematika dalam memecahkan masalah, dominasi otak kanan dan otak kiri, keterkaitan antara kemampuan koneksi matematika dalam memecahkan masalah dengan dominasi otak, serta hipotesis penelitian.
BAB III Metode Penelitian. Pada bab ini terdiri dari tujuh sub bab, yaitu jenis dan pendekatan penelitian; tempat dan waktu penelitian; desain penelitian; populasi, sampel dan teknik sampling; variabel penelitian; teknik dan instrumen penelitian; teknik analisis data. BAB IV Hasil Penelitian. Hasil penelitian merupakan bagian
yang membahas tentang hasil penelitian. Dalam penelitian ini, penulis membahas tentang perbedaan kemampuan koneksi matematika siswa dalam memecahkan masalah sesuai dengan rumusan dan tujuan penelian.
BAB II
KAJIAN PUSTAKA
A. Kemampuan Koneksi Matematika dalam Memecahkan Masalah
1. Kemampuan Koneksi Matematika
Kemampuan menurut Kamus Besar Bahasa Indonesia berasal dari kata mampu yang berarti kuasa atau sanggup, sedangkan kemampuan yang berarti kesanggupan atau kecakapan dalam melaksanakan sesuatu. Koneksi menurut Kamus Besar Bahasa Indonesia adalah hubungan yang dapat memudahkan atau melancarkan segala urusan (kegiatan). Dalam hubungannya dengan matematika disebut dengan koneksi matematika.
Koneksi matematika merupakan dua kata yang berasal dari bahasa inggris yaitu mathematical connection.1 Istilah koneksi matematika pertama kali dimunculkan oleh NCTM (National Council of Teachers of Mathematics). NCTM merupakan sebuah perkumpulan guru matematika di Amerika. NCTM juga menjadikan koneksi matematika sebagai standar kurikulum pembelajaran matematika sekolah dasar dan menengah.2
Koneksi yang berasal dari bahasa Inggris connection yang berarti hubungan atau keterkaitan, oleh karena itu koneksi matematika merupakan keterkaitan antara konsep-konsep dalam matematika yang secara internal saling berhubungan, ataupun keterkaitan secara eksternal, yaitu matematika dengan bidang lain baik bidang studi lain maupun dengan kehidupan sehari-hari.3
1
Arif Widarti. “Kemampuan Koneksi Matematis Dalam Menyelesaikan Masalah Kontekstual Ditinjau dari Kemampuan Matematis Siswa”. Jurnal Pendidikan Matematika. 1:3, (2013), hal 4
2
Nuriana Rachmani Dewi, “Peningkatan Kemampuan Koneksi Matematis Mahasiswa Melalui Brain-Based Learning Berbantuan Web”.Prosiding SNMPM Universitas Sebelas Maret, 1 : 4, (2013 ) hal. 284
3Mujiyem Sapti, “Kemampuan Koneksi Matematis (Tinjauan Terhadap Pendekatan
Pembelajaran Savi)”. Jurnal Pendidikan Matematika. - : 11, (2010), hal. 62
Ada tiga aspek dari koneksi matematika dalam standar NCTM, yaitu koneksi antar topik dalam matematika, koneksi matematika dengan disiplin ilmu lain, dan koneksi dengan dunia nyata atau koneksi dengan kehidupan sehari-hari.4 Koneksi matematika juga merupakan jembatan dimana pengetahuan sebelumnya atau pengetahuan yang baru digunakan untuk membangun atau memperkuat pemahaman tentang hubungan antar ide-ide matematika.5
Mengacu pada penjelasan NCTM, aspek kemampuan koneksi matematika terbagi dalam tiga hal sebagai berikut:
i)
Aspek koneksi antar topik dalam matematika Matematika adalah ilmu yang memiliki banyak topik yang saling terkait. Dalam matematika antara satu konsep dengan konsep yang lain saling memiliki hubungan yang cukup erat, tidak hanya dari segi konten atau isi namun juga rumus yang saling terkait. Berdasarkan hal tersebut, aspek yang pertama ini akan sangat membantu siswa dalam mengenali dan menghubungkan antar konsep dalam matematika untuk memecahkan suatu masalah.6 Sebagai contoh koneksi antar topik dalam matematika, yaitu dalam mempelajari tentang segitiga Pascal. Topik ini memiliki koneksi dengan topik himpunan dalam mencari himpunan bagian beserta anggotanya, atau bisa memiliki koneksi dengan topik polinomial untuk menentukan koefisien dan pangkatnya.7ii)
Aspek koneksi antara matematika dengan disiplin ilmu yang lainMatematika merupakan suatu disiplin ilmu yang mampu mengembangkan disiplin ilmu yang lain.
4Nuriana Rachmani Dewi, Op. Cit., hal 285 5
Elly Susanti. Proses Koneksi Produktif dalam Menyelesaikan Masalah Matematika. (Surabaya: Direktorat Jendral Pendidikan Tinggi Islam, 2013) hal.14-16
6Sri Wahyuni, Tesis : “
Kemampuan Koneksi Matematika siswa SMP dalam Memecahkan Masalah Terbuka Ditinjau dari Kemampuan Matematika”. (Surabaya: Univ Negeri Surabaya, 2015), hal.15
7
Selain itu, matematika juga mampu untuk saling terkait dengan disiplin ilmu lain dalam memecahkan suatu masalah tertentu. Sebagai contoh ialah dalam pemecahan masalah peluruhan dalam mata pelajaran kimia, maka siswa harus juga memahami dan mengerti tentang konsep pangkat dalam matematika.
iii)
Aspek koneksi antara matematika dengan kehidupannyata.8
Tidak dapat dipungkiri bahwa matematika telah menjadi bagian nyata dalam kehidupan sehari-hari. Kegiatan jual beli dan keuangan adalah salah satu contoh kecil kegiatan matematika dalam kehidupan sehari-hari. Ini menunjukkan bahwa matematika bisa sangat bermanfaat dalam menyelesaikan suatu permasalahan dalam kehidupan sehari-hari.9
Berdasarkan ketiga aspek koneksi yang telah dijelaskan sebelumnya, maka perlu adanya indikator terhadap pencapaian kemampuan koneksi matematika. Indikator kemampuan koneksi matematika mengacu pada standar NCTM adalah sebagai berikut.
i) Recognize and use connections among mathematical ideas
ii) Understand how mathematical ideas interconnect and build on one another to produce a coherent whole, and
iii) Recognize and aplly mathematics in contexs outside of mathematics10
Dari ketiga penjelasan tersebut dapat diketahui bahwa indikator koneksi matematika yang dikemukakan oleh NCTM meliputi:
i) Mengenali dan menggunakan koneksi antar ide-ide dalam matematika
8
Karunia Eka Lestari. “Implementasi Brain-Based Learning Untuk Meningkatkan Kemampuan Koneksi Dan Kemampuan Berpikir Kritis Serta Motivasi Belajar Siswa SMP”. Jurnal Pendidikan Matematika-Fkip Unsika.2 : 1, (November, 2014), hal.36 9
Sri Wahyuni, Op. Cit., hal.16 10
ii) Memahami bagaimana ide-ide matematika dihubungkan dan dibangun satu sama lain saling berkaitan
iii) Mengenali dan mengaplikasikan matematika pada konteks di luar matematika
Pada penelitian ini, siswa akan menjadi sampel, sehingga dalam konteks ini, kemampuan koneksi matematika adalah kecakapan atau kesanggupan siswa dalam mengetahui keterkaitan keterkaitan antar konsep dalam matematika, keterkaitan antara matematika dengan disiplin ilmu yang lain dan keterkaitan antara matematika dengan kehidupan sehari-hari.
2. Pemecahan Masalah Matematika
Masalah dalam konteks matematika merupakan suatu soal matematika yang belum memiliki prosedur pasti serta membutuhkan bekal pengetahuan baru dan pengetahuan lama untuk menyelesaikannya. Dalam penelitian ini yang dimaksud dengan pemecahan masalah adalah proses menerapkan pengetahuan yang telah diperoleh sebelumnya pada situasi baru dan berbeda.11 Definisi lain menjelaskan bahwa, pemecahan masalah adalah suatu aktivitas intelektual untuk mencari penyelesaian masalah yang dihadapi dengan menggunakan bekal pengetahuan yang sudah dimiliki.12 Sedangkan, dalam konteks matematika yang dimaksud dengan pemecahan masalah adalah proses untuk memahami, merencanakan, dan melaksanakan rencana pemecahan dari masalah yang berkaitan dengan pola dan aturan sebagaimana aturan itu digunakan sebagai solusi untuk menyelesaikan bermacam permasalahan dalam matematika.13
11
Husna - M. Ikhsan - Siti Fatimah.“Peningkatan Kemampuan Pemecahan Masalah Dan Komunikasi Matematis Siswa Sekolah Menengah Pertama Melalui Model Pembelajaran Kooperatif Tipe Think-Pair-Share (TPS)”. Jurnal Peluang, 1 : 2, (April, 2013), hal. 82 12
Nilam Sari. “Peningkatan kemampuan Pemecahan Masalah Matematis Melalui Pembelajaran Berbasis Masalah dan Konvensional pada Mahasiswa STMIK di Kota Medan”. Jurnal Saintech, 6 : 4 (Desember, 2014), hal. 107
13
Tujuan pemecahan masalah dalam pembelajaran matematika adalah untuk: (1) membangun pengetahuan matematika baru, (2) memecahkan masalah yang muncul dalam matematika dan di dalam konteks-konteks lainnya, (3) menerapkan dan menyesuaikan bermacam strategi yang sesuai untuk memecahkan permasalahan dan (4) memantau dan merefleksikan proses dari pemecahan masalah matematika.14 Pemecahan masalah matematika memiliki dua makna, yaitu pertama pemecahan masalah sebagai suatu pendekatan pembelajaran yang digunakan kembali dalam menemukan kembali dan memahami materi konsep dan prinsip matematika. Kedua, pemecahan masalah sebagai suatu kegiatan yang terdiri atas mengidentifikasikan data untuk memecahkan masalah, membuat model matematika dari suatu masalah dalam kehidupan sehari-hari, memilih dan menerapkan strategi untuk menyelesaikan masalah.15
Dalam memecahkan masalah, setiap individu memerlukan waktu yang berbeda. Hal ini disebabkan oleh motivasi dan strategi yang digunakan dalam menyelesaikan masalah yang sedang dihadapinya. Terdapat beberapa faktor yang dapat memengaruhi kemampuan pemecahan masalah matematika, yaitu: i) Pengalaman awal
Pengalaman terhadap tugas-tugas menyelesaikan soal cerita atau soal aplikasi. Pengalaman awal seperti ketakutan (pobia) terhadap matematika dapat menghambat kemampuan siswa dalam memecahkan masalah.
ii) Latar belakang matematika
Kemampuan terhadap konsep-konsep matematika yang berbeda-beda tingkatannya dapat memicu
14
Husna - M. Ikhsan - Siti Fatimah, Op. Cit., hal. 82 15
perbedaan kemampuan siswa dalam memecahkan masalah.
iii) Keinginan dan motivasi.
Dorongan yang kuat dari dalam diri (internal), seperti menumbuhkan keyakinan bahwa akan mampu menyelesaikan soal yang sulit sekalipun.
Langkah yang harus dilakukan dalam memecahkan masalah berdasarkan pada teori problem solving Polya, yaitu (1) memahami masalah; (2) merencanakan penyelesaian; (3) menyelesaikan rencana penyelesaian; (4) memeriksa kembali. Memahami masalah merujuk pada pemahaman terhadap apa yang diketahui, apa yang ditanyakan. Membuat rencana merujuk pada bagaimana strategi penyelesaian yang terkait. Menyelesaikan rencana penyelesaian merujuk pada penyelesaian strategi penyelesaian yang telah disusun. Sedangkan memeriksa kembali berkaitan dengan pengecekan jawaban serta pembuatan kesimpulan akhir.16
3. Kemampuan Koneksi Matematematika dalam Memecahkan Masalah
Kemampuan koneksi merupakan kemampuan yang dasar yang harus dikuasai oleh siswa dalam belajar matematika. Jika memiliki kemampuan koneksi matematika maka siswa akan mampu melihat bahwa matematika itu suatu ilmu yang memiliki topik yang saling terkait, serta bermanfaat dalam penyelesaian masalah matematika.17 Dalam konteks tersebut, kemampuan koneksi matematika dalam memecahkan masalah adalah kemampuan yang dimiliki siswa dalam mengetahui keterkaitan antara tiga aspek, yaitu koneksi antar topik matematika, koneksi dengan disiplin ilmu yang lain, dan koneksi dalam kehidupan sehari-hari, dalam pemecahan masalah.
16
Berdasarkan Peraturan Menteri Pendidikan dan Kebudayaan No. 58 Tahun 2014 salah satu tujuan mata pelajaran matematika adalah agar siswa memiliki kemampuan memahami konsep matematika, menjelaskan keterkaitan antar konsep atau algoritma secara luwes, akurat, efisien, dan tepat dalam pemecahan masalah. Hal tersebut secara tidak langsung adalah tujuan agar setiap pesserta didik memiliki kemampuan koneksi matematika dalam memecahkan masalah. Dalam tujuan yang selanjutnya juga dijelaskan, agar peserta didik memiliki kemampuan memecahkan masalah yang meliputi kemampuan memahami masalah, merancang model matematika, menyelesaikan model dan menafsirkan solusi yang diperoleh.18
Koneksi matematika dan pemecahan masalah merupakan dua dari lima keterampilan yang dikembangkan dalam pembelajaran matematika di Amerika. Lima keterampilan itu adalah sebagai berikut: komunikasi matematika (communication), berfikir secara matematika (reasoning), koneksi matematika (connection), pemecahan masalah (problem solving), pemahaman matematika (undersatanding).19 Koneksi matematika juga sangat berperan pada proses pemecahan masalah. Sebagaimana Hodgson menyatakan bahwa
“Mathematical connections serve as tools in the
problem-solving process.”20
Pernyataan tersebut bisa dimaknai bahwa koneksi matematika berfungsi sebagai alat dalam proses pemecahan masalah.
Koneksi matematika juga memiliki keterkaitan erat dengan proses pemecahan masalah. Ini dibuktikan dengan beberapa pernyataan dari para ahli. Krulik dan Rudnick mengatakan bahwa “problem solving
shows the interconnections among mathematicial ideas”. Pernyataan tersebut memiliki arti bahwa pemecahan
18 Ibid, 59 19
Asep Jihad. Pengembangan Kurikulum Matematika (Tinjauan Teoritis dan Historis). (Bandung: Multipressindo, 2008), hal 148
masalah menunjukkan keterhubungan/koneksi antar ide-ide matematika. Sedangkan Drew dan Rankin mengatakan bahwa “children learn best in open-ended explorations when teachers help them make connections”. Pernyataan tersebut berarti bahwa koneksi matematika dapat membantu anak-anak dalam mengeksplorasi masalah terbuka.21
Tujuan koneksi matematika diberikan pada siswa sekolah menengah diharapkan agar dapat: (1) mengenali representasi yang ekuivalen dari suatu konsep yang sama, (2) mengenali hubungan prosedur satu represantasi ke prosedur representasi yang ekuivalen, (3) menggunakan dan menilai koneksi beberapa topik matematika, (4) menggunakan dan menilai koneksi antara matematika dan disiplin ilmu lain.22 Dengan adanya tujuan tersebut, maka membangun koneksi matematika akan berdampak baik, sehingga dapat membantu siswa dalam mengaplikasikan pemikiran matematika dan membuat model matematika untuk memecahkan masalah yang terkait dengan disiplin ilmu lain seperti seni, musik, psikologi, sains, dan bisnis.
Mengacu pada tahap-tahap pemecahan masalah Polya dan aspek koneksi matematika yang dikemukakan oleh NCTM, maka perlu adanya indikator yang mampu mengukur kemampuan koneksi matematika siswa dalam memecahkan masalah. Peneliti mengadaptasi indikator yang telah digunakan sebelumnya dan menyajikannya dalam tabel sebagai berikut.
Tabel 2.1
Indikator Kemampuan Koneksi Matematika dalam memecahkan Masalah
Tahap pemecahan Masalah Polya
Indikator Koneksi Matematika dalam memecahkan Masalah Memahami Menyebutkan konsep matematika
21Fikri Apriono, Tesis : “Profil Kemampuan Koneksi Matematika Siswa SMP dalam memecahkan masalah ditinjau dari Perbedaan Gender”. (Surabaya: Univ Negeri Surabaya, 2015), hal. 5
22
Masalah yang terdapat pada soal atau yang diketahui
Menjelaskan keterkaitan antar konsep matematika dalam soal atau yang diketahui
Membuat model matematika sesuai dengan masalah yang diberikan
Merencanakan Pemecahan
Masalah
Menjelaskan langkah-langkah penyelesaian masalah matematika dari apa yang ditanyakan
Melaksanakan Pemecahan
Masalah
Menyelesaikan pemecahan masalah matematika sesuai dengan langkah-langkah yang telah dibuat.
Memeriksa Kembali
Menyelidiki kesesuaian antara yang diketahui, yang ditanyakan.
Menyelidiki kesesuaian antara langkah-langkah penyelesaian dengan proses penyelesaian
B. Dominasi Otak Kiri dan Dominasi Otak Kanan
Otak manusia bertanggung jawab terhadap pengaturan seluruh tubuh dan cara berpikir. Otak pada dasarnya berfungsi untuk mengatur dan mengkoordinasikan sebagian besar gerakan, perilaku, dan fungsi homeostasis tubuh.23 Para ahli neusosains membahas tentang cara kerja otak manusia. Ada dua teori tentang otak yang cukup terkenal tentang otak manusia, yaitu teori Splitt-Brain yang dikemukakan oleh Roger Sperry dan teori empat kuadran otak yang dikembangkan oleh Ned Hermann. Roger Sperry mengatakan bahwa secara umum otak dibedakan menjadi dua, yaitu otak kiri dan otak kanan. Sedangkan Ned Hermann, membagi otak menjadi empat, yaitu belahan otak kiri, sistem limbik kiri, sistem limbik kanan dan belahan otak kanan. Dari dua teori tersebut peneliti lebih tertarik meneliti tentang teori Splitt-Brain Roger Sperry yang
23
membahas mengenai seorang yang dominan otak kiri maupun dominan otak kanannya.
1. Definisi dan Struktur Otak Manusia
Otak manusia adalah struktur pusat pengaturan yang memiliki volume sekitar 1.350cc dan terdiri atas 100 juta sel saraf atau neuron. Pada waktu embrio, otak manusia dibedakan menjadi 3 bagian yaitu otak depan, otak tengah, dan otak belakang. Seiring dengan pertumbuhan dan perkembangan manusia, otak pun berkembang. Otak depan berkembang menjadi otak besar (cerebrum) dan diensefalon, otak tengah yang berukuran kecil dan merupakan penghubung antara otak depan dan otak belakang. Otak belakang terdiri atas otak kecil (cerebelum) dan sumsum lanjutan.
Gambar 2.1 Struktur Otak
a. Otak Depan
i) Otak Besar (Cerebrum)
dan lapisan dalam.24 Lapisan luar (korteks) berwarna abu-abu. Permukaan lapisan ini berlipat-lipat, hingga permukaannya luas. Pada lapisan ini berisi badan sel saraf dan berbagai macam pusat saraf. Lapisan dalam berwarna putih dan banyak mengandung serabut saraf yaitu dendrit dan neurit. Fungsi otak besar yaitu untuk berfikir, pusat kesadaran dan kemauan, pusat ingatan, serta pengendalian ingatan, misal bergerak, mendengar, dan membau.
ii) Diensefalon
Diensefalon adalah bagian otak yang terdiri dari mid-diencephalic territory, pretalamus, zona limitan intratalamika, talamus yang berfungsi menghubungkan komunikasi antar belahan otak besar, hipotalamus sebagai pusat pengendalian waktu biologis, suhu tubuh dan sekresi hormon, epitalamus, dan pretektum.25
b. Otak Belakang
Bagian dari otak belakang terbagi menjadi 3 meliputi jembatan Varol, sumsum lanjutan (medulla oblongata), dan otak kecil (cerebellum).26
i) Otak Kecil (Cerebelum)
Serebelum terdiri atas 2 belahan, yaitu belahan kanan dan belahan kiri yang dihubungkan oleh jembatan varol yang terletak di bagian depan otak kecil. Otak kecil berfungsi untuk mengatur keseimbangan tubuh dan mengkoordinasikan otot-otot sebagai alat gerak. Benturan pada otak kecil dapat mengganggu keseimbangan tubuh. Jika otak kecil terpukul, keseimbangan tubuh akan terganggu.
ii) Sumsum Lanjutan (Medula Oblongata)
Sumsum lanjutan atau sumsum penghubung merupakan penghubung antara otak kecil dengan
24
Tri Widodo dkk. Ilmu Pengetahuan Alam 9. (Jakarta: Depdikbud, 2008) hal.31 25Beatty, J. “The Human Brain: Essentials of Behavioral Neuroscience.“
Thousand Oak, CA: Sage Publicaion diakses dari http://id.wikipedia.org/wiki/Otak pada taggal 25 Oktober 2015.
sumsum tulang belakang. Sumsum ini terletak di depan otak kecil dan di bawah otak besar. Berfungsi untuk mengatur pernapasan, denyut jantung, suhu tubuh, tekanan darah, dan kegiatan tubuh lain yang tak sadar.27
iii) Jembatan Varol
Jembatan Varol berisi serabut saraf yang menghubungkan lobus kiri dan kanan otak kecil, serta menghubungkan otak kecil dengan korteks otak besar.
iv) Otak Tengah (mesencephalon)
Otak tengah (mesencephalon) adalah bagian otak yang mempunyai dua struktur yaitu tektum dan cerebral peduncle. Tektum terlibat pada proses pendengaran dan kendali gerakan mata. Cerebral peduncle terdiri dari tegmentum, crus cerebri, dan substantia nigra.
2. Pengertian Dominasi Otak (Brain Dominance)
Dominasi otak dalam bahasa inggris dikenal dengan istilah brain dominance. Mengacu pada pendapat Hilda Rammer Ross, dalam disertasinya dijelaskan bahwa, Brain dominance is identified as the tendency for one hemisphere to control the processing of Information in a particular task.Hemispheric dominance refers to the brain hemisphere more likely to be used when a person is faced with the need to solve a problem.28 Berdasarkan penjelasan tersebut dapat diketahui bahwa, dominasi otak merupakan kecenderungan salah satu belahan otak untuk mengontrol pengolahan informasi dalam tugas tertentu. Dominasi belahan otak mengacu pada salah satu belahan otak yang lebih mungkin untuk digunakan ketika seseorang dihadapkan dengan kebutuhan untuk memecahkan masalah.
27
Tri Widodo dkk. Ilmu Pengetahuan Alam 9. (Jakarta: Depdikbud, 2008) hal.32 28
Selain Hilda Rammer Ross, ada pendaapat lain tentang dominasi otak dari dari Jacolyn B. Girolamo, dia mengatakan bahwa,
Brain dominance is A normal condition in which one hemisphere or one quadrant of the brain is better suited than the others for performing certain information processing functions. Sometimes also referred to as cerebral dominance or lateralization. (Lateralization is Left-right assymetry in brain functioning). Brain dominance has been studied in connection with numerous individual characteristics..29
Berdasarkan penjelasan tersebut dapat diketahui bahwa, dominasi otak adalah sebuah kondisi normal di mana salah satu belahan atau satu belahan otak lebih baik daripada yang lain untuk melakukan fungsi pengolahan informasi tertentu. Biasa disebut sebagai dominasi otak, atau lateralisasi. (Lateralisasi adalah penyeimbangan belahan otak kiri kiri dan belahan otak kanan dalam fungsi otak).
Berdasarkan disertasi yang ditulis Jacolyn B Girolamo, dia juga membahas tentang definisi dominan belahan otak kiri dan dominan belahan otak kanan. Dia mengatakan bahwa,
Right Brain Dominant is An individual who prefers to utilize the right hemisphere of the brain when thinking and learning. And Left Brain Dominant is An individual who prefers to utilize the left hemisphere of the brain when thinking and learning.30
Pernyataan tersebut memiliki arti, bahwa dominan otak kanan adalah seorang individu yang lebih suka memanfaatkan belahan kanan otak ketika berpikir dan belajar. Sedangkan dominan otak kiri adalah seorang
29
Jacolyn B Girolamo. Disertasi : “The relationship of brain dominance to attitude, achievement, and creativity among Atwater High School students”. (Brigham Young University, 1988), hal.7
individu yang lebih suka memanfaatkan otak kiri otak ketika berpikir dan belajar.
Berdasarkan pengertian dominasi otak yang sudah dijelaskan pada paragraf sebelumnya, dapat diketahui bahwa individu yang dominan otak kanan dan yang dominan otak kiri memang berbeda. Kontrol fungsi otak yang menyebabkan adanya dominan pada salah satu belahan tertentu. Individu dengan otak kanan cenderung lebih kreatif dan intuitif, baik dibidang seni yang kreatif, maupun di bidang-bidang lainnya. Individu tersebut memiliki waktu yang tepat untuk memprioritaskan hal-hal yang sulit, karena sebagian keputusan yang dibuat pada saat akhir. 31
Pada umumnya setiap orang biasanya memiliki kecenderungan untuk dominan pada salah satu belahan otak tersebut. Ada yang dominan otak kiri, ada yang dominan otak kanan. Dominasi peran belahan otak dapat terjadi karena dipengaruhi oleh lingkungan yang melingkupi orang tersebut, misalnya: sistem pendidikan di keluarga, di sekolah, dan di masyarakat. Kondisi yang merugikan adalah apabila dominasi itu menyebabkan fungsi belahan otak lainnya menjadi lemah. Kalau hal ini terjadi, maka akan membuat kemampuan berpikir kita menjadi tidak optimal. Dominasi belahan otak kiri dan otak kanan akan berpengaruh terhadap kemampuan seseorang dalam menyerap informasi, dalam belajar, dalam memecahkan masalah, dan dalam proses berpikir.32
Dalam penelitian ini, untuk menentukan sampel dominan otak kiri atau dominan otak kanan, peneliti menggunakan metode angket yang terdapat dalam buku “13 Wasiat Terlarang Dahsyat dengan Otak Kanan” karya Ippho Santosa seorang penulis yang ahli dalam bidang Psikologi yang juga dikenal sebagai pakar otak kanan.
31Erlin Ladyawati –Prayogo, “Jurnal Pembelajaran tematik untuk Menyeimbangan Kerja Otak Kanan dan Otak Kiri”. Univ PGRI Adi Buana Surabaya. 61 : 2 (Desember, 2013), hal 36
Angket tersebut berjumlah 40 butir pertanyaan hanya dengan 2 opsi jawaban A dan B. Kriteria seseorang yang dominan otak kanan dan seseorang yang dominan kiri sesuai dengan angket tersebut adalah sebagai berikut:
Tabel 2.2
Kriteria Penilaian Angket
Keterangan Kriteria
Dominan Otak Kiri Jika jumlah opsi jawaban A lebih banyak daripada jumlah opsi jawaban B (A > B)
Seimbang Jika jumlah opsi jawaban A sama dengan jumlah opsi jawaban B (A =
B)
Dominan Otak
Kanan
Jika jumlah opsi jawaban B lebih banyak daripada jumlah opsi jawaban A (B > A)
Siswa dengan kategori seimbang tidak diikutsertakan untuk melaksanakan soal tes kemampuan koneksi. Hal tersebut dikarenakan siswa tersebut tidak masuk kategori dominan otak kanan maupun dominan otak kiri sesuai dengan penelitian.
3. Otak Kiri dan Otak Kanan
Otak besar (Cerebrum) merupakan bagian terbesar dari otak manusia. Otak besar juga merupakan bagian yang memproses semua kegiatan intelektual, seperti kemampuan berpikir, penalaran, mengingat, membayangkan, serta merencanakan masa depan. Otak besar dibagi menjadi belahan kanan dan belahan kiri, atau lebih dikenal dengan otak kanan dan otak kiri. Masing– masing belahan mempunyai fungsi berbeda.
jenis-jenis kegiatan tertentu seperti pemikiran konseptual dan gagasan-gagasan abstrak mengenai cinta, keindahan, dan kesetiaan. Sedangkan otak kiri adalah otak yang bekerja untuk menganalisis dan diperuntukkan bagi aspek-aspek pertimbangan yang diperuntukkan bagi aspek-aspek pembelajaran akademik. Daya ingat otak kiri bersifat pendek (short term memory).33
Secara fungsi, otak kiri bekerja untuk berpikir, menganalisis, menghitung, menulis, membaca, menghafal, yang kesemua bagian tersebut bersifat akademik. Otak kanan lebih cenderung berfungsi dalam kreativitas yang dihasilkan dari emosi, kreasi, imajinasi, pemikiran, daya ingat, kepribadian, pengamatan. Perbedaan otak kiri dan otak kanan terletak pada penggunaannya, akan tetapi kalau keduanya digabungkan maka akan menghasilkan kekuatan besar yang mendorong pencapaian keberhasilan dalam hidup manusia.
Otak kanan dan otak kiri mempunyai fungsi yang berbeda-beda. Sebenarnya kedua belahan otak kiri dan kanan sama penting dan sama kuatnya. Mereka saling melengkapi satu dengan yang lain. Pada saat otak kanan sedang bekerja, otak kiri cenderung lebih tenang. Dan sebaliknya, pada saat otak kiri aktif bekerja, maka otak kanan cenderung diam. Walaupun setiap belahan otak tidak saling bersama-sama dalam aktif bekerja, akan tetapi keduanya terlibat sama dalam proses pemikiran. Otak manusia terlalu rumit dan kompleks untuk dikategorikan secara ketat seperti itu, tetapi pada kenyataannya kedua belahan iru secara terus menerus tetap saling berkomunikasi.
Sebagai contoh sederhana, seumpama kita melihat raut wajah orang yang sedang murung, maka kita tidak akan melihat menggunakan otak kanan mengapa ia murung. Ketika kita mendengar sebuah percakapan, maka otak kiri sedang berkonsentrasi pada apa yang
33
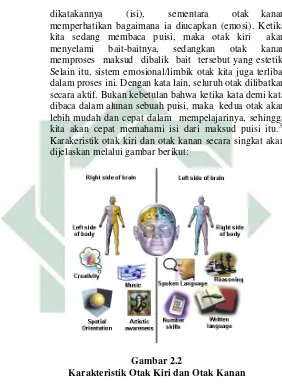
dikatakannya (isi), sementara otak kanan memperhatikan bagaimana ia diucapkan (emosi). Ketika kita sedang membaca puisi, maka otak kiri akan menyelami bait-baitnya, sedangkan otak kanan memproses maksud dibalik bait tersebut yang estetik. Selain itu, sistem emosional/limbik otak kita juga terlibat dalam proses ini. Dengan kata lain, seluruh otak dilibatkan secara aktif. Bukan kebetulan bahwa ketika kata demi kata dibaca dalam alunan sebuah puisi, maka kedua otak akan lebih mudah dan cepat dalam mempelajarinya, sehingga kita akan cepat memahami isi dari maksud puisi itu.34 Karakeristik otak kiri dan otak kanan secara singkat akan dijelaskan melalui gambar berikut:
Gambar 2.2
Karakteristik Otak Kiri dan Otak Kanan
Pada gambar sedikit dijelaskan karakteristik otak kanan dan otak kiri. Gambar tersebut juga menjelaskan bahwa belahan otak kanan mengontrol tubuh sebelah kiri sedangkan belahan otak kiri mengontrol
34
angota tubuh bagian kanan. Para ilmuwan telah menemukan bahwa pada hampir semua orang, belahan otak kiri (sebagai pengendali sisi kanan tubuh) memproses informasi dalam sekuensial, linear, dan tertib. Otak kiri ini memainkan peran utama dalam kegiatan seperti membaca, menulis, dan komputasi. Belahan kanan otak (sebagai
pengendali sisi kiri tubuh) cenderung untuk
[image:38.420.74.371.57.464.2]mengkhususkan diri dalam pendekatan nonverbal, simultan, dan holistik untuk informasi.35 Penggolongkan karakteristik belahan otak kanan dan belahan otak kiri pada tabel berikut. 36
Tabel 2.3
Perbandingan Karakteristik Mode Kiri dan Mode Kanan
*) yang di dalam kurung itu opsi pemilihan kata lainnya
Mode Kiri Mode Kanan
Verbal: menggunakan kata-kata untuk menamai, mendeskripsikan, mendefinisikan
Analitis: menggambarkan (membayangkan) hal-hal secara langkah demi langkah, dan bagian demi bagian
Simbolis: Menggunakan suatu simbol untuk menunjukkan suatu benda. Misalnya, gambar bentuk mata menunjukkan mata, tanda + untuk
menunjukkan proses
Nonverbal: Mengetahui beberapa hal, namun minim koneksi dengan kata-kata.
Sintentis: Menempatkan sesuatu bersama-sama untuk membentuk keseluruhan hal (sesuatu yang menyeluruh/ utuh/ lengkap) Konkrit: Mengaitkan sesuatu apa adanya, pada saat ini saja
Analogis: Melihat kemiripan antara beberapa hal, memahami hubungan metafora (kiasan)
Nontemporal (tidak sementara): tanpa rasa (kepekaan) terhadap waktu Tidak rasional:Tidak memerlukan dasar (tidak berdasar) alasan atau
35
Jacolyn B Girolamo. Disertasi : “The relationship of brain dominance to attitude, achievement, and creativity among Atwater High School students”. (Brigham Young University, 1988), hal.14
36Hilda Rammer Ross. Disertasi: “
penjumlahan Abstrak: Mengambil sedikit informasi dan menggunakannya untuk merepresentasikan (menggambarkan) keseluruhan hal (informasi).
Temporal (sementara) : Menjaga (menuruti/ menepati/ mengikuti) jalan waktu (maksudnya itu semacam timeline), mengurutkan suatu hal setelah hal lainnya: mengerjakan hal pertama pada waktu yang pertama, hal kedua pada waktu yang kedua, dll.
Rasional: Menarik kesimpulan berdasarkan alasan dan fakta. Digital: Menggunakan bilangan-bilangan dalam perhitungan
Logis: Menarik
kesimpulan berdasarkan logika: suatu hal berkaitan dengan lainnya dalam urutan yang logis, misalnya, suatu teorema matematis atau suatu argumen yang tertata dengan baik
Linear: Berpikir dalam artian ide-ide yang saling berkaitan, satu gagasan secara langsung berkaitan dengan yang lainnya,
fakta, kesediaan (keinginan) untuk menangguhkan penilaian
Spasial: melihat (tempat) dimana suatu hal berhubungan dengan hal lainnya, dan bagaimana bagian-bagian bersatu untuk membentuk suatu keseluruhan
Intuitif: Membuat lompatan
wawasan, seringkali berdasarkan pola yang tidak lengkap, dugaan, perasaan atau citra visual
sering kali mengarahkan ke suatu kesimpulan yang konvergen
C. Keterkaitan Antara Kemampuan Koneksi Matematika dalam Memecahkan Masalah dengan Dominasi Otak Kiri atau Otak Kanan
Koneksi matematika merupakan keterkaitan antara konsep-konsep dalam matematika yang secara internal saling berhubungan, ataupun keterkaitan secara eksternal, yaitu matematika dengan bidang lain baik bidang studi lain maupun dengan kehidupan sehari-hari.37 Ada tiga aspek dari koneksi matematika dalam standar NCTM, yaitu koneksi antar topik dalam matematika, koneksi matematika dengan disiplin ilmu lain, dan koneksi dengan dunia nyata atau koneksi dengan kehidupan sehari-hari.38 Sedangkan dominasi otak merupakan kecenderungan salah satu belahan otak untuk mengontrol pengolahan informasi dalam tugas tertentu. Dominasi belahan otak mengacu pada salah satu belahan otak yang lebih mungkin untuk digunakan ketika seseorang
dihadapkan dengan kebutuhan untuk memecahkan masalah.39
Menurut Jacolyn B Girolamo, yang dimaksud dengan dominan otak kanan adalah seorang individu yang lebih suka memanfaatkan belahan kanan otak ketika berpikir dan belajar. Sedangkan dominan otak kiri adalah seorang individu yang lebih suka memanfaatkan otak kiri otak ketika berpikir dan belajar.40 Berdasarkan pengertian pengertian tersebut, dapat diketahui bahwa individu yang dominan otak kanan dan yang dominan otak kiri memiliki cara berpikir yang berbeda. Kontrol fungsi otak yang menyebabkan adanya dominan pada salah satu belahan tertentu. Dominasi belahan otak kiri dan otak kanan akan berpengaruh terhadap kemampuan seseorang dalam menyerap informasi, dalam belajar, dalam memecahkan masalah, dan dalam proses
37
Mujiyem Sapti, Op. Cit. hal. 62
38Nuriana Rachmani Dewi, Op. Cit., hal 285 39
Hilda Rammer Ross. Op. Cit. hal. 3 40
berpikir.41 Dominasi belahan otak kiri dan otak kanan tentunya juga akan berpengaruh terhadap kemampuan koneksi matematika pemecahan masalah.
D. Hipotesis Penelitian
Hipotesis merupakan jawaban sementara terhadap rumusan masalah penelitian, di mana rumusan masalah penelitian telah dinyatakan dalam bentuk pertanyaan. Dikatakan sementara karena jawaban yang diberikan baru didasarkan pada teori. Hipotesis dirumuskan atas dasar kerangka pikir yang merupakan jawaban sementara atas masalah yang dirumuskan.42 Berdasarkan rumusan masalah serta kajian pustaka di atas ,hipotesis yang diajukan peneliti adalah:
“Ada perbedaan yang signifikan pada kemampuan koneksi matematika siswa dalam memecahkan masalah, antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan.”
41
Rudi Santoso Yohanes, Op. Cit. hal 752 42
BAB III
METODE PENELITIAN
A. Jenis dan Pendekatan Penelitian
Jenis penelitian ini merupakan penelitian komparatif atau komparasi, hal tersebut dikarenakan tujuan dari penelitian ini adalah membandingkan kemampuan koneksi matematika dalam memecahkan masalah antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan. Kata ‘komparasi’ dalam bahasa Inggris comparation, yaitu perbandingan. Makna dari kata tersebut menunjukkan bahwa dalam penelitian ini peneliti bermaksud mengadakan perbandingan kondisi yang ada di dua tempat, apakah kedua kondisi tersebut sama, atau ada perbedaaan dan kalau ada perbedaaan, kondisi di tempat mana yang lebih baik.1
Penelitian ini menggunakan pendekatan penelitian kuantitiatif. Pendekatan kuantitatif adalah penelitian yang analisisnya lebih fokus pada data-data numerikal (angka) yang diolah dengan menggunakan metode statistika. Pada umumnya penelitian menggunakan pendekatan kuantitatif merupakan penelitian sampel besar, karena pada pendekatan kuantitatif dilakukan pada penelitian inferensial yaitu dalam rangka pengujian hipotetsis dan menyandarkan kesimpulan pada suatu probabilitas kesalahan penolakan hipotesis nihil. Melalui pendekatan ini, maka akan diperoleh signifikansi hubungan antar variabel yang diteliti.2
B. Tempat dan Waktu Penelitian 1. Tempat Penelitian
Tempat penelitian adalah tempat dimana peneliti melaksanakan penelitian dan mendapatkan data penelitian. Penelitian ini dilaksanakan bertempat di SMA Negeri 1 Porong Kabupaten Sidoarjo.
2. Waktu Penelitian
1Suharsimi Arikunto, Prosedur Penelitian (Jakarta: Rineka Cipta, 2010), hal. 6 2
Saifudin Azwar, Metode Penelitian, (Yogyakarta : Pustaka Pelajar, 2011), hal. 5
Waktu penelitian adalah waktu saat penelitian sedang berlangsung, atau pada saat peneliti mengambil data penelitian menggunakan metode angket maupun tes. Penelitian ini dilaksanakan pada hari kamis tanggal 26 Mei 2016, tahun pelajaran 2015/2016.
C. Desain Penelitian
[image:43.420.92.365.146.438.2]Agar suatu penelitian dapat memberikan hasil yang sesuai dengan tujuan yang telah ditetapkan, maka perlu adanya desain penelitian. Dalam melakukan penelitian, terlebih lagi untuk penelitian kuantitatif, salah satu langkah yang penting ialah membuat desain penelitian. Desain penelitian pada hakikatnya merupakan suatu strategi untuk mencapai tujuan penelitian yang telah ditetapkan dan berperan sebagai pedoman atau penuntun peneliti pada seluruh proses penelitian.3 Penelitian ini akan membandingkan dan melihat perbedaan kemampuan koneksi matematika antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan. Untuk sampel dengan kategori seimbang, maka sampel tersebut tidak diambil karena tidak masuk sebagai kriteria sampel. Desain penelitian ini digambarkan pada tabel berikut:
Tabel 3.1 Desain Penelitian
XI MIPA 5 X1 T1 Y1
XI MIPA 5 X1 T
XI MIPA 5 X1 T2 Y1
Keterangan:
X1 : Pemberian angket untuk membagi sampel menjadi 3 kelompok
T1 : Sampel yang dominan otak kiri
T : Sampel kategori seimbang (tidak dominan otak kiri dan tidak dominan otak kanan)
3
T2 : Sampel yang dominan otak kanan
Y1 : Tes Kemampuan Koneksi matematika dalam memecahkan masalah
D. Populasi, Sampel dan Teknik Sampling 1. Populasi
Populasi adalah keseluruhan gejala atau satuan yang ingin diteliti.4 Sedangkan menurut Ahmad Tanzeh populasi penelitian adalah seluruh data yang menjadi perhatian penelitian kita dalam suatu ruang lingkup dan waktu yang kita tentukan.5 Jadi dapat disimpulkan bahwa populasi adalah keseluruhan objek yang diteliti. Sehingga, pada penelitian ini populasinya adalah siswa kelas XI MIPA SMAN 1 Porong Kabupaten Sidoarjo tahun pelajaran 2015/2016.
2. Sampel
Sampel adalah sebagian atau wakil populasi yang diteliti.6 Sampel dalam penelitian ini adalah seluruh siswa kelas XI MIPA 5. Data hasil penelitian tersebut menunjukkan bahwa, dari 32 siswa secara keseluruhan dalam satu kelas, terdapat 10 siswa dominan otak kiri, 17 siswa dominan otak kanan, dan 5 siswa dengan kategori seimbang, yaitu tidak dominan otak kiri maupun dominan otak kanan (data terlampir). Sesuai dengan rumusan masalah penelitian, maka untuk 5 sampel kategori seimbang tidak diikutsertakan dalam tes kemampuan koneksi matematika. Sehingga sampel penelitian ini secara keseluruhan adalah 27 siswa.
3. Teknik Sampling
Teknik sampling adalah cara untuk menentukan sampel yang jumlahnya sesuai dengan ukuran sampel yang akan dijadikan sumber data sebenarnya, dengan memperhatikan sifat-sifat dan penyebaran populasi agar
4Bambang Prasetyo, Metode Penelitian Kuantitatif (Jakarta: PT. Raja Grafindo Persada. 2008) hal.119
diperoleh sampel yang representatif.7 Teknik pengambilan sampel pada penelitian ini adalah teknik simple random sampling. Sampel diambil satu kelas secara acak yang mewakili populasi pada sekolah yang menjadi tempat penelitian. Alasan penulis menggunakan cara ini karena penulis memperoleh informasi dari guru mata pelajaran bahwa pembagian kelas tidak berdasarkan tingkat kepandaian siswa, sehingga antara kelas satu dengan yang lainnya bersifat homogen. Pengambilan sampel dilakukan dengan memperhatikan ciri-ciri sebagai berikut:
a) Siswa mendapat materi yang berdasarkan kurikulum yang sama.
b) Siswa diampu oleh guru yang sama. c) Siswa yang duduk di kelas yang sama.
E. Variabel Penelitian
Variabel penelitian dapat didefinisikan segala sesuatu yang dapat mengelompokkan objek pengamatan atau penelitian ke dalam dua atau lebih kelompok.8Dalam definisi lain juga dijelaskan bahwa variabel penelitian adalah objek penelitian yang bervariasi.9 Dalam penelitian ini terdapat dua variabel, yaitu variabel bebas dan variabel terikat.
Variabel bebas (independent variable), adalah variabel yang menjadi sebab timbulnya atau berubahnya variabel dependen (variabel terikat).10 Variabel bebas dalam penelitian ini adalah siswa yang dominan otak kanan dan siswa yang dominan otak kiri.
Variabel terikat (dependent variable) merupakan variabel yang dipengaruhi atau yang menjadi akibat, karena adanya variabel bebas.11 Variabel terikat dalam penelitian ini adalah kemampuan koneksi matematika dalam memecahkan masalah.
7
S Margono, Metodologi Penelitian Pendidikan, (Jakarta: Rineka Cipta, 2004) hal 125. 8
Budiyono, Metodologi Penelitian Pendidikan. (Surakarta: UNS Press, 2003), hal.27 9
Suharsimi Arikunto, Op. Cit., hal.159 10
Sugiyono, Statistika untuk Penelitian, (Bandung: Alfabeta, 2006), hal.3 11
F. Teknik dan Instrumen Penelitian 1. Teknik Pengumpulan Data
Dalam penelitian ini teknik pengumpulan data menggunakan metode angket dan tes. Metode angket digunakan untuk memperoleh memilih sampel secara keseluruhan yang nantinya sampel dikategorikan berdasarkan dominasi otaknya. Sampel tersebut berasal dari siswa dengan kategori dominan otak kiri, siswa dengan kategori seimbang (tidak dominan otak kiri dan tidak dominan otak kanan) dan siswa dengan kategori dominan otak kanan. Untuk siswa dengan kategori seimbang maka tidak diikutsertakan mengikuti tes kemampuan koneksi matematika dalam memecahkan masalah.
Setelah metode angket, metode tes digunakan untuk memperoleh data yang berupa skor tes kemampuan koneksi matematika siswa dalam memecahkan masalah. Data ini berskala rasio yang akan diolah untuk mengetahui perbedaan kemampuan koneksi matematika dalam memecahkan masalah antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan.
2. Instrumen Penelitian
Dalam kamus Besar Bahasa Indonesia instrumen memiki arti sarana penelitian (berupa seperangkat tes, dll) untuk mengumpulkan data sebagai bahan pengolahan. Definisi yang lain juga menjelaskan bahwa instrumen pengumpulan data adalah alat bantu yang dipilih dan digunakan oleh peneliti dalam kegiatan mengumpulkan data penelitian secara sistematis.12 Instrumen yang digunakan dalam penelitian ini yaitu angket dan soal tes kemampuan koneksi matematika dalam memecahkan masalah.
Angket dalam penelitian ini berfungsi untuk mengetahui tingkat dominasi otak siswa, jumlah siswa yang dominan otak kanan dan siswa yang dominan otak kiri. Angket dalam penelitian ini bersifat tertutup, jadi siswa diberi angket yang berupa pilihan ganda yang bisa langsung dipilih. Peneliti mengambil angket yang ditulis
12
Ippho Santosa, seorang penulis yang dikenal publik sebagai pakar otak kanan. Angket tersebut berjumlah 40 butir pertanyaan hanya dengan 2 opsi jawaban A dan B, dengan tanpa mengubah isi dari instrumen aslinya maka peneliti tidak melakukan validasi terhadap angket.
Tes adalah serentetan pertanyaan atau latihan serta alat lain yang digunakan untuk mengukur ketrampilan, pengetahuan intelegensi, kemampuan atau bakat yang dimiliki oleh individu atau kelompok.13 Pada penelitian ini untuk mengetahui kemampuan koneksi matematika siswa dalam memecahkan masalah, maka instrumen yang digunakan adalah soal tes kemampuan koneksi matematika dalam memecahkan masalah yang berupa soal tes essay yang telah divalidasi sebelumnya kepada para ahli. Tes harus memenuhi konten tolak ukur kemampuan koneksi matematika sesuai dengan indikator yang telah dibuat. Dalam penelitian ini, peneliti menggunakan dua orang validator untuk memvalidasi instrumen soal tes kemampuan koneksi matematika, sehingga instrumen peneliti dapat dikatakan valid. Valid berarti instrumen dapat digunakan untuk mengukur apa yang seharusnya diukur. Setelah divalidasi, dilakukan perbaikan berdasarkan saran dan pendapat validator agar masalah yang akan diberikan layak, valid, dan sesuai sehingga dapat digunakan untuk mengetahui skor kemampuan koneksi matematika siswa dalam memecahkan masalah. Setelah dilakukan revisi, maka instrumen tersebut dapat diberikan kepada subjek atau sampel penelitian.14 Adapun nama-nama validator dalam penelitian ini adalah sebagai berikut:
13Ibid,hal. 193
14Zainullah Zuhri, Skripsi : “
Tabel 3.2 Daftar Nama Validator
No Nama Jabatan
1 Ahmad Hanif Ahsyar, S.Pd., M.Si.
Dosen Pendidikan Matematika UINSA Surabaya
2 Imam Rofiki, M.Pd. Dosen Pendidikan Matematika UINSA Surabaya
G. Teknik Analisis Data
Data yang diperoleh peneliti merupakan data primer yang diperoleh langsung dari sampel melalui tes. Data skor hasil tes kemampuan koneksi matematika dalam memecahkan masalah tersebut berskala rasio. Setelah data tersebut dikumpulkan, maka tahap selanjutnya peneliti akan melaksanakan analisis data. Analisis data ini dalam penelitian ini menggunakan analisis data dengan pendekatan kuantitatif. Teknik yang digunakan untuk mengetahui adanya perbedaan kemampuan koneksi matematika dalam memecahkan masalah antara siswa yang dominan otak kiri dan siswa yang dominan otak kanan adalah dengan menggunakan analisis uji-t (t-T