ANALISIS REGRESI KOMPONEN UTAMA UNTUK
MENGATASI MASALAH MULTIKOLINIERITAS DALAM
ANALISIS REGRESI LINIER BERGANDA
Haris Bhakti Prasetyo, Dian Handayani, Widyanti Rahayu
1JURUSAN MATEMATIKA
FMIPA-UNIVERSITAS NEGERI JAKARTA
hariz_oke@yahoo.com
Abstraksi
Multikolinieritas adalah suatu kondisi dalam regresi linier berganda dimana antar variabel bebas saling berkorelasi. Masalah multikolinieritas pada regresi linier berganda mengakibatkan pengujian hipotesis parameter berdasarkan metode kuadrat terkecil memberikan hasil yang tidak valid. Indikasi masalah multikolinieritas dapat dideteksi dengan faktor inflasi ragam. Analisis komponen utama bertujuan menghasilkan variabel-variabel baru (komponen utama) yang saling ortogonal dan mereduksi dimensi data. Teknik yang digunakan untuk meregresikan komponen utama dengan variabel tak bebas melalui metode kuadrat terkecil disebut regresi komponen utama.
Kata kunci : multikolinieritas, regresi linier berganda, analisis komponen utama, regresi komponen utama.
1. PENDAHULUAN
Analisis regresi linier adalah teknik statistika yang dapat digunakan untuk menjelaskan pengaruh variabel bebas (independent variable) terhadap variabel tak bebas (dependent variable). Salah satu asumsi yang harus dipenuhi untuk melakukan pengujian hipotesis terhadap parameter pada analisis regresi linier berganda adalah tidak terjadinya korelasi antar variabel bebas (multikolinier).
Jika antarvariabel saling berkorelasi tinggi, pengujian hipotesis parameter berdasarkan metode kuadrat terkecil (least square method) memberikan hasil yang tidak valid, diantaranya variabel-variabel bebas yang seharusnya berpengaruh signifikan terhadap variabel tak bebas akan dinyatakan sebaliknya (tidak nyata secara statistik), tanda koefisien regresi dugaan yang dihasilkan bertentangan dengan kondisi aktual, penduga koefisien regresi bersifat tidak stabil sehingga mengakibatkan sulitnya menduga nilai-nilai variabel tak bebas yang tentunya akan mengakibatkan tidak akuratnya pada peramalan (Myers, 1991).
Kondisi ini mendorong untuk dikembangkannya suatu cara atau teknik yang dapat digunakan untuk mengatasi masalah multikolinieritas pada analisis regresi linier berganda. Salah satu solusi yang dapat digunakan adalah dengan menggunakan analisis komponen utama (principal component analysis). Melalui penggunaan analisis komponen utama ini akan dihasilkan variabel-variabel baru yang merupakan kombinasi linier dari variabel-variabel bebas asal dan antarvariabel baru ini bersifat saling bebas. Variabel-variabel yang baru ini disebut komponen utama, dan selanjutnya diregresikan dengan variabel tak bebas.
Tujuan dari penulisan paper ini yaitu Mengkaji analisis regresi komponen utama sebagai salah satu solusi untuk menangani multikolinieritas antar variabel bebas pada analisis regresi linier berganda, dan memberikan ilustrasi penerapan analisis regresi komponen utama.
2. LANDASAN TEORI
2.1 Review Matriks
Definisi 2.1 Matriks X berukuran p×p dikatakan matriks ortogonal jika X X XX′ = ′=I
Definisi ini mempunyai dua akibat. Pertama, bentuk matriks ortogonal adalah persegi (square). Kedua, karena X X′ =XX′=I , maka suatu matriks X dikatakan matriks ortogonal jika X−1=X . ′
Definisi 2.2 Misal matriks A berukuran p×p, dan elemen dari A untuk baris i dan kolom j dinyatakan
dalam a . Trace dari matriks ij A ; tr A adalah jumlah dari elemen diagonalnya yang didefinisikan ( )
=1
tr( ) =A
∑
ip aiiMisal A adalah matriks berukuran p×p dan x adalah vektor tak nol berukuran p×1. Nilai eigen
dari matriks A yang dinotasikan oleh λ adalah suatu nilai yang memenuhi persamaan berikut :
|A−λI|= 0. Untuk menentukan vektor eigen yang bersesuaian dengan suatu nilai eigen, maka nilai eigen yang telah diperoleh disubtitusi ke persamaan Ax=λx.
Definisi 2.4 Misal A adalah matriks simetrik berukuran p×p, maka dekomposisi spektral matriks ri A
diberikan oleh : =1 = = p i i i i λ ′ ′
∑
A e e PΛP (1) dengan λi adalah nilai eigen ke-i, dan ei adalah vektor eigen ke-i dari matriks A berukuran p×1, Padalah suatu matriks yang elemen-elemennya vektor eigen berukuran p×p, dan Λ adalah matriks diagonal
yang memiliki nilai eigen pada diagonal utamanya.
Definisi 2.5 Misal matriks A berukuran m×p, maka singular value decomposition untuk A didefinisikan sebagai berikut :
(m p) (m m)(m p)(p p)
= ′
× U× × V×
A Λ
dengan U adalah matriks berukuran m m× yang kolom-kolomnya adalah vektor eigen yang saling ortogonal
dari AA′, V adalah matriks berukuran p×p yang kolom-kolomnya adalah vektor eigen yang saling ortogonal dari A A′ , dan Λ adalah matriks diagonal berukuran m×p dengan elemen diagonal utama
0
i
λ ≥ ; i= 1, 2,…, min( , )m p pada sel ( , )i i , dan elemen pada selain diagonal bernilai nol.
2.2 Analisis Regresi Linier Berganda
Analisis regresi linier berganda merupakan analisis regresi yang melibatkan lebih dari satu variabel bebas (X X1, 2,…,Xp) dan mempunyai hubungan linier dengan variabel tak bebas ( )Y . Model regresi linier
berganda yang melibatkan p buah variabel bebas adalah :
Y =β0+β1X1+β2X2+ +⋯ βpXp+ε (2)
Dalam notasi matriks menjadi :
Y=Xβ+ε (3)
dengan Y adalah vektor berukuran n×1 yang elemen-elemennya merupakan nilai-nilai amatan dari variabel
tak bebas, X adalah matriks rancangan (design matrix) yang berukuran n× +(p 1), β adalah vektor yang berukuran (p+ ×1) 1 yang elemen-elemennya berupa parameter (koefisien) regresi, ε adalah vektor galat berukuran n×1, dimana galat diasumsikan E( ) = 0εi , dan var( ) =εi σ2; i= 1, 2,…,n.
Pendugaan parameter regresi β dengan menggunakan metode kuadrat terkecil berdasarkan model
= +
Y Xβ ε adalah dengan meminimumkan jumlah kuadrat galat (JKG) dimana JKG dirumuskan sebagai
berikut :
JKG=ε ε′ = (Y−Xb) (′Y−Xb)
Jika X adalah matriks rancangan berukuran n× +(p 1) yang bersifat full rank dengan p+ ≤1 n, maka penduga kuadrat terkecil untuk b adalah
ˆ = = ( 1
)−
β b X'X X'Y
Rumusan hipotesis untuk menguji parameter regresi secara parsial adalah sebagai berikut :
0: j = 0
H β artinya koefisien regresi ke- j tidak signifikan atau variabel bebas ke- j tidak berpengaruh nyata terhadap Y
1: j 0
H β ≠ artinya koefisien regresi ke- j signifikan atau variabel bebas ke- j berpengaruh nyata terhadapY
Statistik uji yang digunakan untuk menguji parameter regresi secara parsial adalah : hitung ˆ ˆ ( ) = ˆ var( ) j j j t β β β (4)
terhadap
Y
.Selang kepercayaan untuk βj dengan tingkat kepercayaan 100(1−α)% adalah
βˆj±t(n p− −1); /2α var(βˆj) (5)
2.3 Multikolinieritas
Multikolinieritas adalah suatu kondisi dimana terjadi korelasi antara variabel bebas atau antar variabel bebas tidak bersifat saling bebas. Besaran (quantity) yang dapat digunakan untuk mendeteksi adanya multikolinier adalah faktor inflasi ragam (Variance Inflation Factor / VIF). VIF digunakan sebagai kriteria untuk mendeteksi multikolinier pada regresi linier yang melibatkan lebih dari dua variabel bebas. Nilai VIF lebih besar dari 10 mengindikasikan adanya masalah multikolinier yang serius (Ryan, 1998). VIF untuk koefisien regresi- j didefinisikan sebagai berikut :
2 1 VIF = 1 j j R − (6)
dengan : R2j adalah koefisien determinasi antara X dengan variabel bebas lainnya pada persamaan/model j
dugaan regresi; dimana j= 1, 2,…,p.
2.4 Analisis Komponen Utama
Analisis komponen utama merupakan teknik statistik yang dapat digunakan untuk menjelaskan struktur variansi-kovariansi dari sekumpulan variabel melalui beberapa variabel baru dimana variabel baru ini saling bebas, dan merupakan kombinasi linier dari variabel asal. Selanjutnya variabel baru ini dinamakan komponen utama (principal component). Secara umum tujuan dari analisis komponen utama adalah mereduksi dimensi data dan untuk kebutuhan interpretasi.
2.4.1 Komponen utama yang Dibentuk Berdasarkan Matriks Kovariansi
Misal Σ merupakan matriks kovariansi dari vektor acak X′= [X X1, 2,…Xp] dengan pasangan nilai eigen dan vektor eigen yang saling ortonormal adalah ( , ), (λ1 e1 λ2,e2),…, (λp,ep). dimana
1 2 p 0
λ λ≥ ≥⋯≥λ ≥ , maka komponen utama ke-i didefinisikan sebagai berikut :
Wi =e X′i =e Xi1 1+e Xi2 2+ +… e Xip p, i= 1, 2,…,p (7)
dimana W1 adalah komponen pertama yang memenuhi maksimum nilai e e1′Σ 1=λ1. W2 adalah komponen
kedua yang memenuhi sisa keragaman selain komponen pertama dengan memaksimumkan nilai e Σe2′ 2 =λ2.
p
W adalah komponen ke-p yang memenuhi sisa keragaman selain W W1, 2,…,Wp−1 dengan memaksimumkan
nilai e Σe′p p =λp. Urutan W W1, 2,…,Wp harus memenuhi persyaratan
1 2 p
λ λ≥ ≥…≥λ . Sementara itu, proporsi total variansi yang dijelaskan komponen utama ke-
k
adalah :
1 2
Proporsi total variansi populasi yang
= =
dijelaskan oleh komponen utama ke tr( )
k k p k λ λ λ λ λ − + + + Σ … (8) dengan k= 1, 2,…,p
2.4.2 Komponen utama yang Dibentuk Berdasarkan Matriks Korelasi
Selain berdasarkan matriks kovariansi, komponen utama juga dapat dibentuk berdasarkan matriks korelasi. Hal ini dilakukan jika variabel-variabel bebas yang diamati mempunyai perbedaan range yang sangat besar.
Komponen utama ke-i; Wi yang dibentuk berdasarkan variabel-variabel yang telah dibakukan
1 2 = ( , , , p)
Z′ Z Z … Z dengan cov( ) =Z ρ didefinisikan sebagai berikut :
Wi =e Zi1 1+e Zi2 2+ +… e Zip p i= 1, 2,…,p (9)
Sementara itu, proporsi total variansi yang dapat dijelaskan oleh komponen utama ke-k berdasarkan
variabel bebas yang telah dibakukan didefinisikan sebagai berikut :
Proporsi total variansi populasi yang = =
dijelaskan oleh komponen utama ke tr( )
k k k p λ λ − ρ (40)
2.4.3 Kriteria Pemilihan Komponen Utama
Salah satu tujuan dari analisis komponen utama adalah mereduksi dimensi data asal yang semula terdapat p variabel bebas menjadi k komponen utama (dimana k< p). Kriteria pemilihan k yaitu :
1. Proporsi kumulatif keragaman data asal yang dijelaskan oleh k komponen utama minimal 80% , dan proporsi total variansi populasi bernilai cukup besar (Johnson, 2002).
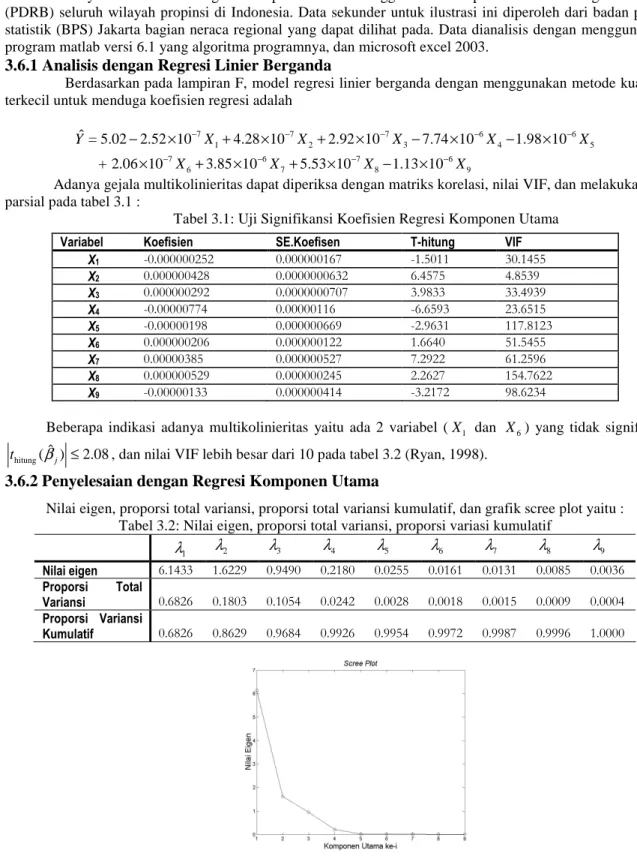
2. Dengan menggunakan scree plot yaitu plot antara i dengan λi, pemilihan nilai k berdasarkan scree plot
ditentukan dengan melihat letak terjadinya belokan dengan menghapus komponen utama yang menghasilkan beberapa nilai eigen kecil membentuk pola garis lurus (Rencher, 1998).
3. REGRESI KOMPONEN UTAMA
Cara pembentukan regresi komponen utama melalui analisis komponen utama ada dua cara. Pertama, pembentukan komponen utama berdasarkan matriks kovariansi (peragam). Kedua, pembentukan komponen utama berdasarkan matriks korelasi. Kedua cara tersebut digunakan tergantung pada kondisi range amatan pada variabel bebas.
3.1 Regresi komponen utama yang dibentuk berdasarkan matriks kovariansi
Misal matriks P adalah matriks ortogonal dengan memenuhi persamaan P P′ =PP′=I. Karena
= c
W X P, maka proses persamaan regresi linier berganda menjadi regresi komponen utama yaitu :
= = ' = c c + + + Y Xβ ε Y X PPβ ε Y Wα ε (51)
Model regresi komponen utama yang telah direduksi menjadi
k
komponen adalahY=α01 W+ kαk+ε (62)
dengan Xc merupakan matriks yang elemen-elemennya dikurang dengan rataannya (centered) yang
mensyaratkan rataan nol dan variansi σ2,
Y adalah variabel tak bebas, α0 adalah intersep, 1 adalah vektor
yang elemen-elemennya adalah 1 berukuran n×1, Wk adalah suatu matriks berukuran n k× yang
elemennya terdapat komponen utama, αk adalah vektor koefisien komponen utama berukuran k×1, dan
ε
adalah vektor galat berukuran n×1.
3.2 Regresi komponen utama yang dibentuk berdasarkan matriks korelasi
Persamaan regresi komponen utama berdasarkan matriks korelasi pada dasarnya hampir sama dengan persamaan regresi komponen utama berdasarkan matriks korelasi yaitu variabel X X1, 2,…,Xp
diganti dengan variabel baku Z Z1, 2,…,Zp. Umumnya proses untuk memperoleh persamaan regresi
komponen utama berdasarkan matriks korelasi mempunyai proses yang sama pada penurunan persamaan regresi komponen utama berdasarkan matriks kovariansi yaitu pada formula (11), dan (12), maka model regresi komponen utama berdasarkan matriks korelasi adalah sebagai berikut :
Y=α01+Wkαk+ε (73) dengan Y adalah variabel tak bebas, α0 adalah intersep, 1 adalah vektor yang elemen-elemennya adalah 1 berukuran n×1, Wk adalah suatu matriks berukuran n k× yang elemennya terdapat komponen utama, dimana Wk =ZPk, αk adalah vektor koefisien komponen utama berukuran k×1, dan ε adalah vektor galat berukuran n×1.
3.3 Pendugaan Koefisien Regresi Komponen Utama
Misal koefisien a a0, 1,…,ap merupakan penduga regresi komponen utama dari koefisien
0, 1, , p
α α …α . Pendugaan koefisien dengan maksimum likelihood menghasilkan dugaan yang sama pada
kuadrat terkecil, namun untuk memenuhi asumsi normal, pendugaan koefisien menggunakan maksimum likelihood. Prosedur menduga koefisien α' = (α α0, 1,…,αp) dengan metode maksimum likelihood yaitu dengan cara mengkalikan fungsi densitas f( )εi , mengambil nilai logaritma (ln ), dan diturunkan terhadap
0 1
= (a a, , ,ap)
′
a … , kemudian disamakan dengan nol. Pendugaan koefisien regresi komponen utama yang
diperoleh dari maksimum likelihood adalah sebagai berikut :
2 2 ( 1/2 1 2 =1 ln ( , , , ; ) 1 )[( ) ( )] ln = 0 2 n n i L e a a σ ε ε ε σ πσ − ∂ ∂ − ′ − ≡ ∂ ∂
∏
Y Wa Y Wa … (84) dan hasil dari (14) adalaha= (W W′ )−1W Y (95) ′
Misal ak = ( ,a a1 2,…,ak) merupakan penduga koefisien regresi komponen utama dengan k komponen, maka penyederhanaan pada (15) yaitu :
(
)
1 1 = ( ) = ( ) k k k k k c k − − ′ ′ ′ a W W W Y Λ X P Y (106)dengan Λ−1 merupakan matriks diagonal yang mempunyai elemen diagonal utama
1 1 1
1 2
((n−1) ) , ((λ − n−1)λ ) ,− …, ((n−1)λk)− , dan
k
P adalah matriks berukuran k k× yang elemen-elemennya merupakan vektor eigen, dimana masing-masing vektor eigen e e1, 2,…,ek berukuran k×1.
Jika menggunakan regresi komponen utama berdasarkan matriks korelasi, maka pendugaan parameter (koefisien) α adalah sebagai berikut :
k = k1
(
( k))
− ′
a Λ ZP Y dan a0 =Y (117)
3.4 Transformasi Komponen Utama
Transformasi komponen utama merupakan variabel baru (W) yang terdapat dalam regresi
komponen utama diubah sedemikian sehingga menjadi variabel asal ( )X . Hasil transformasi komponen utama menjadi variable Xc yang mempunyai koefisien regresi β* yaitu :
: f W→X c * 0 c = + + Y α 1 X β ε * 1 =1 = (( 1) ) k m m m c m n− λ − ′ ′
∑
b e e X Y dan b0 =YHasil transformasi variable Xc menjadi variable Xyang mempunyai koefisien regresi β* yaitu : : f Xc→X * * * 1 1 2 2 p p Y = +ξ β X +β X + +… β X * Y ξ = −β′X
Hasil transformasi komponen utama menjadi variable Zyang mempunyai koefisien regresi β* yaitu :
: f W→Z * 0 = + + Y α 1 Zβ ε * 1 =1 = (( 1) ) k m m m c m n− λ − ′ ′
∑
b e e Z Y dan b0 =YHasil transformasi veriabel Z menjadi variable Xyang mempunyai koefisien regresi γ yaitu :
:
f Z→X
1/ 2 *
=
g V b dan g0= −Y b V*′ 1/ 2X
3.5 Nilai Ekspektasi dan Variansi Penduga Koefisien Regresi Komponen Utama
Nilai ekspektasi bias penduga koefisien regresi komponen utama yaitu
1 = 1 (( 1) ) p m m m c m k n λ − + ′ ′ −
∑
e e X Y . Sementara itu, Nilai variansi regresi komponen utama adalah ˆ ((2 11) j) n
σ − λ −
dimana nilai cov(W Wi, j) = 0; i j, = 1, 2,…,p dan i≠ j. Sementara itu nilai variansi ˆ*
j
2 2 =1 ˆ 1 k mj m m e n σ λ −
∑
, dan nilai variansi penduga
γ
ˆ
j adalah2 2 =1 ˆ ˆ ( 1) k mj m jj m e n σ σ −
∑
λ .3.6 Ilustrasi Regersi Komponen Utama
Penyelesaian ilustrasi regresi komponen utama menggunakan data produk domestik regional bruto (PDRB) seluruh wilayah propinsi di Indonesia. Data sekunder untuk ilustrasi ini diperoleh dari badan pusat statistik (BPS) Jakarta bagian neraca regional yang dapat dilihat pada. Data dianalisis dengan menggunakan program matlab versi 6.1 yang algoritma programnya, dan microsoft excel 2003.
3.6.1 Analisis dengan Regresi Linier Berganda
Berdasarkan pada lampiran F, model regresi linier berganda dengan menggunakan metode kuadrat terkecil untuk menduga koefisien regresi adalah
7 7 7 6 6 1 2 3 4 5 7 6 7 6 6 7 8 9 ˆ = 5.02 2.52 10 4.28 10 2.92 10 7.74 10 1.98 10 + 2.06 10 3.85 10 5.53 10 1.13 10 Y X X X X X X X X X − − − − − − − − − − × + × + × − × − × × + × + × − ×
Adanya gejala multikolinieritas dapat diperiksa dengan matriks korelasi, nilai VIF, dan melakukan uji parsial pada tabel 3.1 :
Tabel 3.1: Uji Signifikansi Koefisien Regresi Komponen Utama
Beberapa indikasi adanya multikolinieritas yaitu ada 2 variabel (X1 dan X6) yang tidak signifikan
hitung(ˆj) 2.08
t β ≤ , dan nilai VIF lebih besar dari 10 pada tabel 3.2 (Ryan, 1998).
3.6.2 Penyelesaian dengan Regresi Komponen Utama
Nilai eigen, proporsi total variansi, proporsi total variansi kumulatif, dan grafik scree plot yaitu : Tabel 3.2: Nilai eigen, proporsi total variansi, proporsi variasi kumulatif
1 λ λ2 λ3 λ4 λ5 λ6 λ7 λ8 λ9 Nilai eigen 6.1433 1.6229 0.9490 0.2180 0.0255 0.0161 0.0131 0.0085 0.0036 Proporsi Total Variansi 0.6826 0.1803 0.1054 0.0242 0.0028 0.0018 0.0015 0.0009 0.0004 Proporsi Variansi Kumulatif 0.6826 0.8629 0.9684 0.9926 0.9954 0.9972 0.9987 0.9996 1.0000
Gambar 3.1: Scree plot komponen utama
Variabel Koefisien SE.Koefisen T-hitung VIF
X1 -0.000000252 0.000000167 -1.5011 30.1455 X2 0.000000428 0.0000000632 6.4575 4.8539 X3 0.000000292 0.0000000707 3.9833 33.4939 X4 -0.00000774 0.00000116 -6.6593 23.6515 X5 -0.00000198 0.000000669 -2.9631 117.8123 X6 0.000000206 0.000000122 1.6640 51.5455 X7 0.00000385 0.000000527 7.2922 61.2596 X8 0.000000529 0.000000245 2.2627 154.7622 X9 -0.00000133 0.000000414 -3.2172 98.6234
Berdasarkan tabel 3.2, komponen yang dapat mewakili dari 9 komponen ada 8 komponen utama sesuai dengan kriteria 80% dari proporsi kumulatif keragaman, akan tetapi kontribusi proporsi keragaman
5, 6, , 9
λ λ … λ hanya menjelaskan 0.28%, 0.18%, 0.15%, 0.09%, 0.04% . Ini berarti komponen ke-5 sampai ke-9
tidak ikut disertakan dalam model karena nilai keragaman data asal yang dapat dijelaskan oleh komponen utama bernilai relatif kecil (Johnson, 1998). Sesuai gambar scree plot pada gambar 3.1 menjelaskan bahwa komponen yang dilibatkan dalam model hanya 4 komponen karena setelah belokan ke-4, grafik scree plot membentuk pola linier yang artinya komponen yang membentuk pola tersebut tidak disertakan dalam model.
Uji hipotesis secara parsial penduga koefisien regresi komponen utama ke-1, 2,3, 4 sesuai formula
(
)
1 = ( 1) ( ) k n k k − ′ − a Λ ZP Y adalah :Tabel 3.3: Uji signifikansi koefisien regresi komponen utama
Komponen Utama Koefisien Standar Error T-hitung VIF
W1 -1.5360 0.2827 -5.4340 1
W2 1.2835 0.5499 2.3339 1
W3 -6.7530 0.7192 -9.3901 1
W4 -0.9504 1.5006 -0.6333 1
Komponen utama ke-4 tidak signifikan (thitung(α ≤ˆj) 2.05) pada tabel 3.5, sehingga hanya komponen
utama ke-1, 2,3 yang dilibatkan dalam model. Adapun model regresi komponen utama dengan
3
komponenadalah :
Yˆ = 8.4695 1.5360− W1+1.2835W2−6.7530W3
dimana a0 =Y = 8.4695
Model regresi linier berganda yang melibatkan variabel Z yang merupakan hasil transformasi dari
variabel W (pada 3.26) sebagai variabel bebas adalah :
1 2 3 4 5 6 7 8 9
ˆ = 8.4695 1.800 5.541 0.539 1.408 2.504 0.317 0.618 2.483 0.689
Y − Z + Z + Z − Z + Z − Z + Z + Z + Z dima na b0* =a0 = 8.4695, dan nilai Thitung dari masing=masing variabel bebas yaitu 5.4567, 8.3933, 2.6158 , -5.8600, 9.5653, -2.1774, 4.9688, 7.5615, 4.7619. Karena masing-masing nilai thitung(β ≤ˆ*j) 2.08, maka semua variabel bebas Z berpengaruh nyata terhadap Y .
Jika regresi linier berganda yang terdapat variabel Z ditransformasi menjadi variabel X sebagai
variabel bebasnya, maka model regresinya adalah :
6 6 6 6 6 6 1 2 3 4 5 6 6 6 6 7 8 9 ˆ = 4.68 0.16 10 0.50 10 0.02 10 0.97 10 0.44 10 0.02 10 0.13 10 0.14 10 0.08 10 Y X X X X X X X X X − − − − − − − − − − × + × + × − × + × − × + × + × + ×
dimana masing-masing penduga koefisien regresi (g g1, 2,…,gp) diperoleh dari formula g=V b , dan 1/2 *
* 1/2 0 =
g Y−b V X . ′
3.6.3 Perbandingan Regresi Linier Berganda dan Regresi Komponen Utama
Salah satu kriteria untuk membandingkan suatu model regresi adalah dengan menggunakan standar error (Fekedulegn, 2002). Untuk membandingkan model regresi linier berganda dan regresi komponen utama, akan dilihat nilai standar error penduga koefisien dari masing-masing model tersebut.
Nilai standar error dari metode kuadrat terkecil dan metode komponen utama adalah sebagai berikut: Tabel 3.8: Perbandingan standar error metode kuadrat terkecil dan komponen utama
Kuadrat Terkecil Komponen Utama
Variabel
Koefisien Standar Error Koefisien Standar Error
X1 -2.52x10-7 1.67x10-7 -0.16
×
10-6 2.86×
10-8 X2 4.28x10-7 0.63x10-7 0.50×
10-6 6.00×
10-8 X3 2.92x10-7 0.71x10-7 0.02×
10-6 8.37×
10-9 X4 -7.74x10-6 11.6x10-7 -0.97×
10-6 1.66×
10-7 X5 -1.98x10-6 6.69x10-7 0.44×
10-6 4.57×
10-8 X6 2.06x10-7 1.22x10-7 -0.02×
10-6 8.37×
10-9 X7 3.85x10-6 5.27x10-7 0.13×
10-6 2.65×
10-8 X8 5.29x10-7 2.45x10-7 0.14×
10-6 1.84×
10-8 X9 -1.33x10-6 4.14x10-7 0.08×
10-6 1.79×
10-8Berdasarkan tabel 3.8, nilai penduga koefisien standar error paling kecil adalah metode komponen utama pada regresi komponen utama daripada metode kuadrat terkecil pada regresi linier berganda.
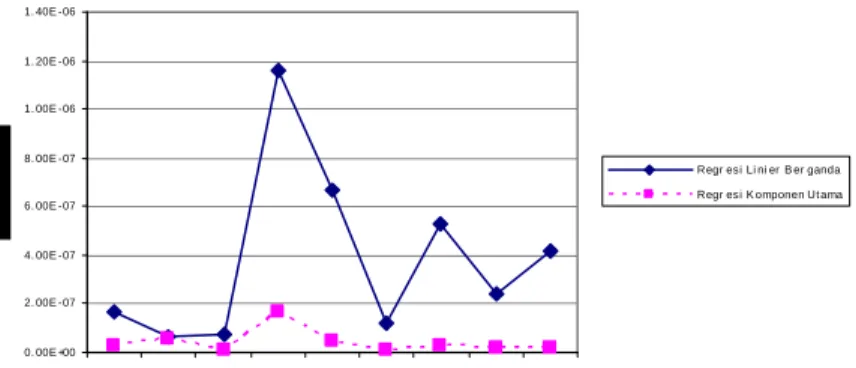
Secara visual, perbandingan standar error penduga koefisien regresi linier berganda dan regresi komponen utama adalah :
0. 00E +00 2. 00E -07 4. 00E -07 6. 00E -07 8. 00E -07 1. 00E -06 1. 20E -06 1. 40E -06 X 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 V a r i a b e l
Regr esi Li ni er B er ganda Regr esi K omponen Ut ama
Gambar 3.2: Grafik standar error regresi linier berganda dan regresi komponen utama
Berdasarkan gambar 3.2, plot standar error penduga koefisien regresi komponen utama berada di bawah plot standar error penduga koefisien regresi linier berganda. Hal ini dapat menunjukkan hasil prosedur untuk menduga komponen utama lebih tepat dan dipercaya (reliable) terhadap variabel-variabel bebas daripada metode kuadrat terkecil (Fekedulegn, 2002).
4. KESIMPULAN
Berdasarkan ilustrasi pada sub bab 3.6, analisis dengan regresi komponen utama cukup efektif dalam mengatasi multikolinieritas. Ini ditunjukkan pada tabel 3.1 dimana nilai VIF masing-masing komponen utama bernilai satu, dan jika dilakukan uji parsial pada tabel 3.3, nilai T-hitung masing-masing variabel Z lebih besar dari T-tabel (bernilai 2.08) artinya masing-masing variable berpengaruh nyata terhadap Y. Perbandingan regresi komponen utama dengan regresi linier berganda menggunakan kriteria standar error penduga koefisien. Karena standar error penduga koefisien regresi komponen utama bernilai kecil, maka hasil prosedur untuk menduga komponen utama pada regresi komponen utama lebih tepat dan dipercaya (reliable) daripada metode kuadrat terkecil.
5. DAFTAR PUSTAKA
Fekedulegn, B.D., Colbert,J.J., Hicks, Jr.R.R. & Schuckers, M.E. 2002. Coping with
Multicollinearity: An Example on Application of Principal Components Regression in Dendroecology.www.fs.fed.us/ne/morgantown/4557/dendrochron/rpne721.pdf. 13 September 2006, pkl 21.00 WIB.
Johnson, R.A. & Wichern, D.W. 2002. Applied Multivariate Statistical Analysis, 5th edition. Pearson
Education International.
Myers, R.H. & Milton, J.S. 1991. A First Course In The Theory Of Linier Statistical Models. PWS-KENT Publishing Company, Boston.
Rencher, A.C. 1998. Multivariate Statistical Inference and Application. Wiley-Interscience Publication, Brigham.