t mtk 0908354 chapter1
Teks penuh
Gambar
Garis besar
Dokumen terkait
Buku dokumen prosiding pemantauan, pengendalian, pelaksanaan dan hasil perencanaan pembangunan Kesos dan Pemerintahan meliputi Perumahan, Permukiman, Kebersihan, Penataan
Dalam menjalani usahataninya petani padi sawah umumnya menjumpai hambatan–hambatan seperti hambatan pada pemasaran, hambatan pada sumber daya manusia, hambatan pada kemitraan,
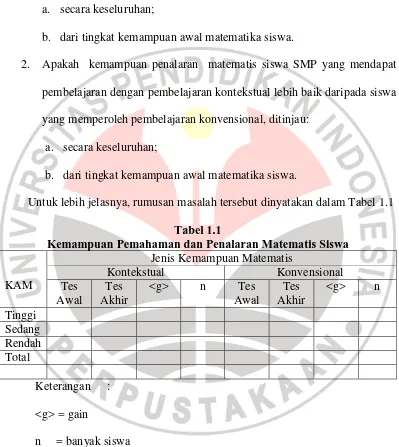
[r]
Maloklusi Klas II divisi 2 memiliki hubungan molar Klas II dengan karakteristik maloklusi ini adalah adanya inklinasi lingual atau linguoversi gigi insisivus sentralis rahang atas
bahwa berdasarkan pertimbangan sebagaimana dimaksud dalam huruf a, perlu menetapkan Keputusan Kepala Badan Karantina Ikan, Pengendalian Mutu dan Keamanan Hasil
PENGEMBANGAN PROGRAM PELATIHAN BATIK BERBASIS KEARIFAN LOKAL BAGI REMAJA D I INDUSTRI BATIK CIMAHI1. Universitas Pendidikan Indonesia | repository.upi.edu |
Penulisan ilmiah ini bertujuan untuk mengetahui bagaimana pentingnya suatu pemasaran guna meningkatkan hasil dari penjualan suatu produk barang yang diproduksi oleh perusahaan,
tidak mengetahui bahwa Salmah adalah Mas Merah yang disebut Salam