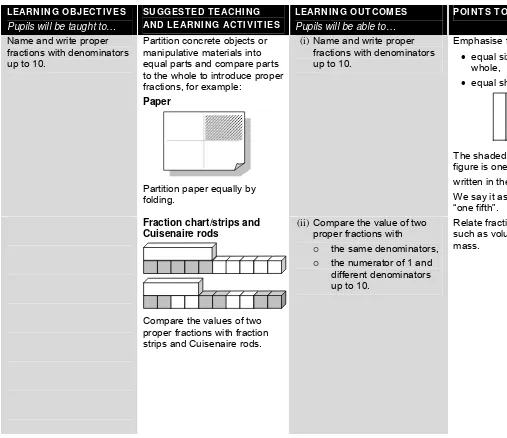
Learning Area 1: NUMBERS TO 100 000
Teks penuh
Gambar
Garis besar
Dokumen terkait
(Dalam
Setelah mencapai kesepakatan dengan para dosen yang akan mengajar pada Program Studi Doktor, maka KPS selanjutnya akan menyerahkan draft jadwal mata kuliah
PENGUMUMAN HASIL PENGADAAN LANGSUNG PENGADAAN BARANG/ JASA KEGIATAN APBD TAHUN ANGGARAN 2014.. DINAS PERTAMBANGAN DAN ENERGI KABUPATEN
Overview of Development Organization Senior Management Project Sponsor User Management Project Management Quality Assurance Project Development Project Team User Project Team
Memasuki tahun pelajaran 2016/2017, pemerintah telah mengupayakan berbagai perubahan dalam menciptakan karakter siswa yang positif sebagai bagian dari revolusi mental. Upaya
Dari hasil penelitian telah menunjukkan bahwa materi pelatihan (X 2 ) mempunyai pengaruh yang signifikan terhadap kompetensi (Y) hal ini, dapat diartikan bahwa
UU Perbankan menyebutkan bahwa, Pemegang saham yang dengan sengaja menyuruh Dewan Komisaris, Direksi, atau pegawai bank untuk melakukan atau tidak
Dalam satu sistem sungai ada perbedaan-perbedaan, kemiringan dasar, penampang sungai, dan material sungai (Kodoatie & Sjarief, 2010). Habitat air tawar menempati daerah