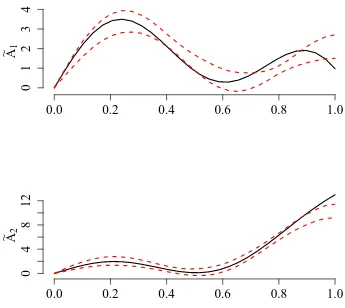
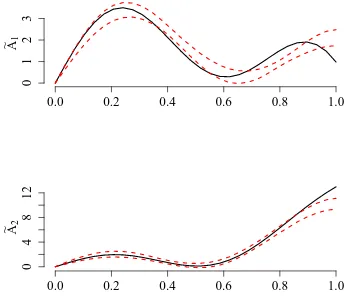
Statistics authors titles recent submissions
Teks penuh
Gambar
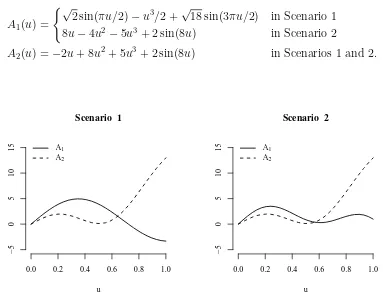
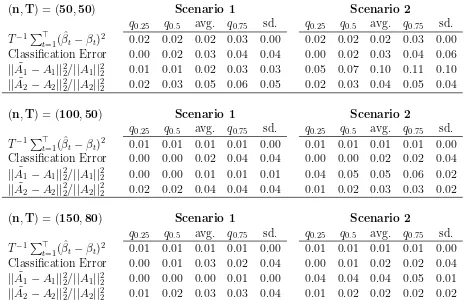
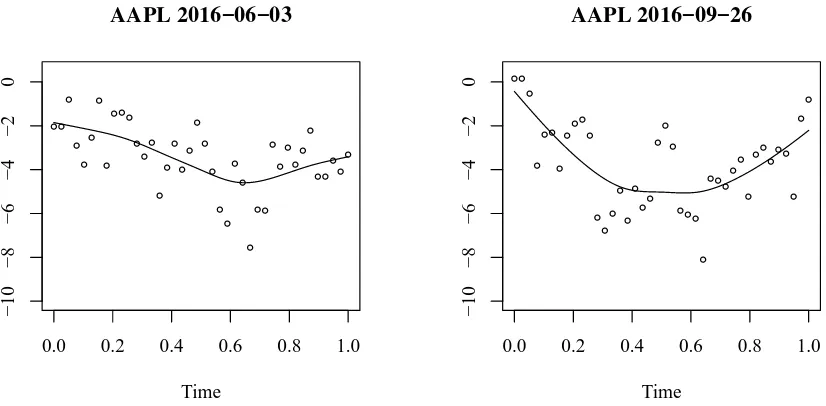
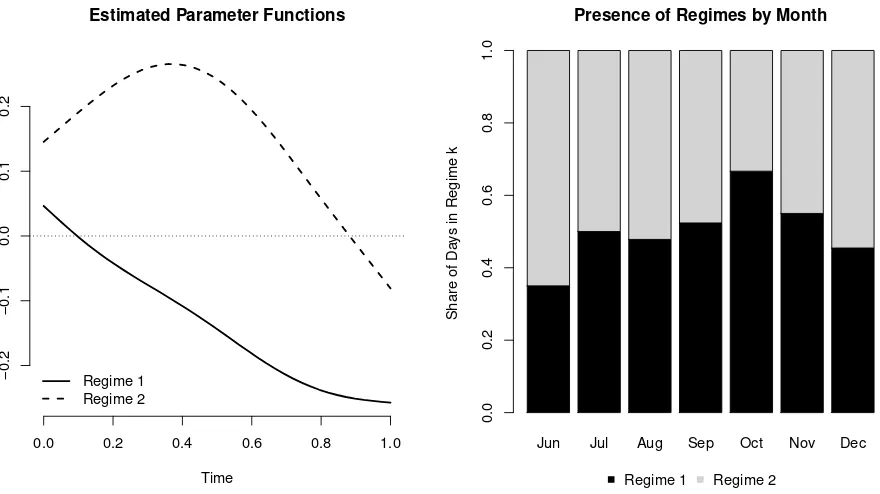
Garis besar
Dokumen terkait
Demikian Pengumuman Pemenang ini dibuat untuk diketahui, dan bagi Perusahan yang ditunjuk sebagai pemenang agar mempersiapkan untuk proses selanjutnya, atas perhatiannya
[r]
[r]
Meningkatnya Kapasitas Kemandirian Dan Produksi Dan Layanan Data/ Informasi Penginderaan Jauh Untuk Pengguna Berbagai Sektor Pembangunan Meningkatnya Kapasitas Produksi dan
Informasi hasil penelitian ini diharapkan dapat menjadi informasi serta masuka berharga bagi para guru dalam melakukan berbagai upaya untuk meningkatkan kualitas
Pembuktian Kualifikasi dilakukan oleh Direktur Utama / Pimpinan Perusahaan atau Penerima kuasa dari Direktur Utama / Pimpinan Perusahaan yang namanya tercantum
dengan membawa asli dan fotocopy seluruh dokumen yang sesuai dengan daftar isian dokumen. kualifikasi perusahaan saudara pada aplikasi SPSE, yang akan dilaksanakan
Sesuai ketentuan yang ber laku, maka Kelompok Ker ja (Pokja) IX (sembilan) KLP Bar ang/ Jasa Pemer intah Kabupaten Tapin akan melakukan kegiatan Pembuktian