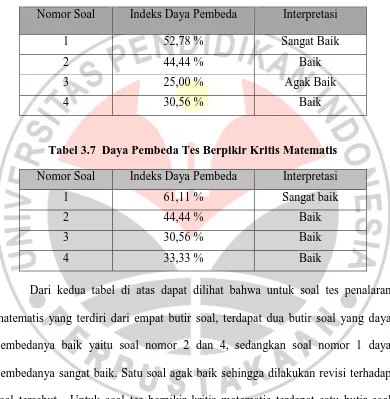
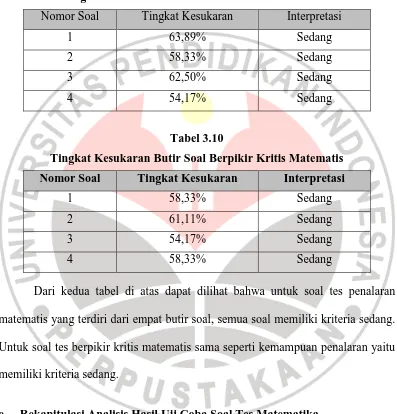
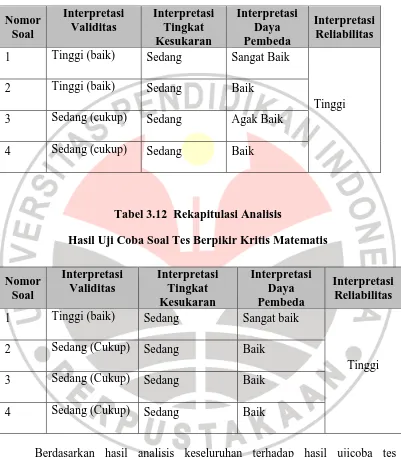
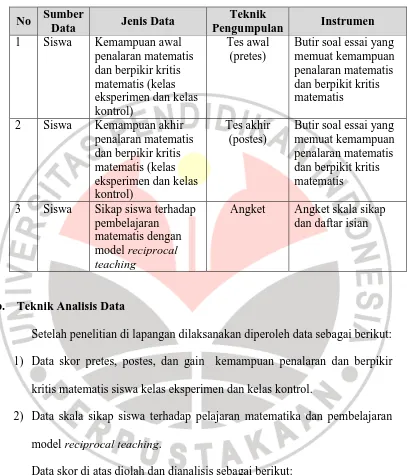
MENINGKATKAN KEMAMPUAN PENALARAN DAN BERPIKIR KRITIS MATEMATIS SISWA SMP MELALUI PEMBELAJARAN MODEL RECIPROCAL TEACHING.
Teks penuh
Gambar



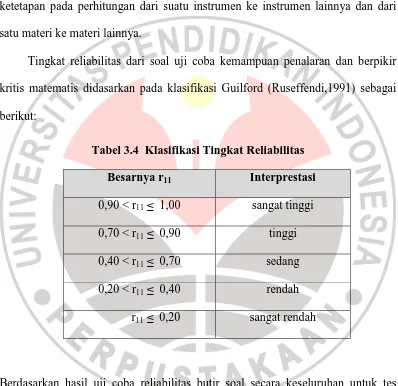
Dokumen terkait
[r]
Pada penelitian ini, digunakan 2 teori yang telah dijelaskan pada Bab II. yaitu teori keagenan (agency theory ) dan stewardship theory untuk
dimaksud pada ayat (2) huruf e memuat uraian tentang Rencana dan Pelaksanaan Program Bidang Pemberdayaan Masyarakat dengan mengacu pada Rencana Kerja Pemerintahan Desa
Bahwa dalam Produk tabungan dana haji pada Bank Panin dubai Syariah telah sesuai dengan Peraturan Menteri Agama No 24 tahun 2016 tentang perubahan atas Peraturan
Bukti fisik yang dilampirkan untuk komponen 2 (pendidikan dan . pelatihan) dan komponen 8 (keikutsertaan dalam
Alhamdulillah dan puji syukur tiada henti penulis panjatkan kepada Allah SWT serta Nabi Muhammad SAW, karena berkat rahmat dan hidayah-Nya penulis dapat menyelesaikan tugas
Biosaintropis Kajian Potensi Wisata dan Persepsi Wisatawan …Wisata Hutan 58 ( Calophyllum inophyllum L.), duwe’ atau juwet ( Syzygium cumini ) dan accem atau
Jika dalam sebuah masalah memuat kata-kata seperti di atas, maka hal ini merupakan indicator bahwa masalah tersebut dapat dipecahkan