PRINSIP MAKSIMUM PONTRYAGIN DALAM MODEL PENYEBARAN PENYAKIT SKRIPSI

i

PRINSIP MAKSIMUM PONTRYAGIN DALAM MODEL PENYEBARAN PENYAKIT

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh :

Yustina Astri Wijayanti NIM : 103114015

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA

FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

ii

PONTRYAGIN’S MAXIMUM PRINCIPLE

IN THE MODEL OF THE SPREAD OF DISEASE

A THESIS

Presented As Partial Fulfillment of the Requirements

To Obtain the Sarjana Sains Degree of

Mathematics Study Program

Written by: Yustina Astri Wijayanti

Student ID: 103114015

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

iii SKRIPSI

PRINSIP MAKSIMUM PONTRYAGIN DALAM MODEL PENYEBARAN PENYAKIT

Disusun oleh:

Yustina Astri Wijayanti

NIM : 103114015

Telah disetujui oleh:

Dosen Pembimbing Skripsi,

iv SKRIPSI

PRINSIP MAKSIMUM PONTRYAGIN DALAM MODEL PENYEBARAN PENYAKIT

Dipersiapkan dan ditulis oleh: Yustina Astri Wijayanti

103114015

Telah dipertahankan di depan Panitia Penguji pada tanggal 14 November 2014 dan dinyatakan telah memenuhi syarat

Susunan Panitia Penguji

Nama Lengkap Tanda

Tangan

Ketua Ir. Ig. Aris Dwiatmoko, M.Sc. ……….

Sekretaris Dr. rer.nat. Herry Pribawanto Suryawan, M.Si ……….

Anggota Hartono, S.Si., M.Sc., Ph.D ……….

Yogyakarta, 18 November 2014 Fakultas Sains dan Teknologi

Universitas Sanata Dharma Dekan,

v

HALAMAN PERSEMBAHAN

Karya ini sebagai bukti kasih setia Tuhan Yesus dalam hidupku.

“Oleh Dia kita juga beroleh jalan masuk oleh iman kepada kasih karunia ini. Di

dalam kasih karunia ini kita berdiri dan kita bermegah dalam pengharapan

menerima kemuliaan Allah”.

( Roma 5:2 )

“Janganlah hendaknya kamu kuatir tentang apapun juga, tetapi nyatakanlah

dalam segala hal keinginanmu kepada Allah dalam doa dan permohonan ucapan

syukur”.

(Filipi 4:6)

Karya ini aku persembahkan untuk :

Orang-orang terkasih: bapak, ibu, dan kakakku

vi

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan atau daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 3 November 2014

Penulis

vii ABSTRAK

Yustina Astri Wijayanti. 2014. Prinsip Maksimum Pontryagin dalam Model Penyebaran Penyakit. Skripsi. Program Studi Matematika, Jurusan Matematika, Fakultas Sains dan Teknologi, Universitas Sanata Dharma, Yogyakarta.

Topik yang dibahas dalam skripsi ini adalah aplikasi model SEIR dalam penyebaran penyakit, terutama penyakit menular. Penyakit menular merupakan suatu penyakit yang penyebarannya mempunyai dampak buruk bagi kehidupan individu dalam populasi. Tulisan ini akan membahas mengenai bagaimana mengurangi penyebaran penyakit dengan meminimalkan banyaknya individu yang terinfeksi. Untuk itu diperlukan suatu kontrol yaitu pemberian vaksin. Dalam hal ini, teori matematika yang digunakan adalah kontrol optimal dan model penyebaran penyakitnya adalah model SEIR. Model SEIR merupakan model penyebaran penyakit yang memperhatikan empat komponen, yaitu banyaknya individu yang rentan penyakit, banyaknya individu yang masuk dalam masa inkubasi, banyaknya individu yang terinfeksi penyakit, dan banyaknya individu yang sembuh dari penyakit. Keempat komponen tersebut diilustrasikan ke dalam model matematika berupa sistem persamaan diferensial dengan enam variabel dan lima persamaan.

Model SEIR akan diselesaikan menggunakan metode - metode kontrol optimal, yaitu prinsip maksimum Pontryagin dan metode sweep maju – mundur. Sedangkan system persamaan diferensial yang ada akan diselesaikan menggunakan metode Runga-Kutta orde-4. Selain itu, akan digunakan pula suatu teori matematika untuk linearisasi sistem persamaan diferensial untuk menyelesaikan model yang tidak memperhatikan kontrol.

Model SEIR yang disusun berdasarkan teori – teori matematika di atas dapat membantu mengambil keputusan untuk menurunkan penyebaran penyakit melalui pengendali anti virus, sehingga banyaknya individu yang terinfeksi pun juga akan mengalami penurunan.

viii ABSTRACT

Yustina Astri Wijayanti. 2014. Pontryagin Maximum Principle In Models Of Disease Spread. A Thesis. Mathematics Study Program, Departement of Mathematics, Faculty of Science and Technology, Sanata Dharma University, Yogyakarta.

The topic of this thesis is the application of SEIR model in diseases spread, especially for infectious diseases. Infectious diseases is a disease whose spreading has negative consequences for the individuals living in the population. This paper will discuss how to reduce the spread of disease by minimizing the number of infected individuals. So we need a control so called vaccine. In this case, the mathematical theory used is the optimal control and model of the spread of the disease is SEIR model. SEIR Model is a model of the spread of the disease which consider four components, namely the number of individuals who are susceptible, in the incubation period, infected, and recovering from disease. These four components are illustrated in the form of a mathematical model of the system of differential equations with six variables and five equations.

The SEIR model will be solved using optimal control method, namely the Pontryagin maximum principle and the forward - backward sweep method. The existing system of differential equations will be solved using Runga-Kutta method of order-4. Moreover, a mathematical theory for linearized system of differential equations will also be used to solve the model which does not consider control.

Model Seir based on the mathematical theory above can help take the decision to reduce the spread of disease through anti-virus control, so that the number of infected individuals will also decrease.

ix

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus yang

telah melimpahkan berkat dan kasihNya sehingga penulis dapat

menyelesaikan skripsi ini dengan baik.

Dalam penulisan skripsi ini penulis mendapatkan bantuan baik moril

maupun materiil dari berbagai pihak. Oleh karena itu, penulis ingin

mengucapkan terima kasih kepada :

1. Ibu Paulina Heruningsih Prima Rosa, S.Si., M.Sc., selaku Dekan

Fakultas Sains dan Teknologi, Universitas Sanata Dharma.

2. YG. Hartono, S.Si., M.Sc., Ph.D, selaku dosen pembimbing skripsi dan

Ketua Program Studi Matematika yang telah meluangkan banyak waktu

dan membimbing penulis dengan penuh kesabaran.

3. Ir. Ig. Aris Dwiatmoko, M.Sc., selaku dosen pembimbing akademik.

4. Bapak, Ibu, dan Romo, dosen-dosen yang telah memberikan ilmu yang

berguna kepada penulis.

5. Kedua orang tua, Bapak D. Suratija dan Ibu Suwarti, yang selalu

mendukung penulis dengan doa, semangat, dan materi.

6. Teman – temanku; Arga, Ratri, Ayu, Tika, Pandu, Sari, Dini, Celly, Leni, Agnes, Yohan, Roy, Marsel, dan Yosi, terima kasih untuk canda

x

7. Teman – teman adik tingkat 2012: Happy, Noni, Giri, terima kasih untuk doa, semangat, dan keceriaan yang selalu diberikan kepada

penulis.

8. Semua pihak yang telah ikut membantu penulis dalam menyelesaikan

skripsi ini.

Penulis menyadari bahwa skripsi ini masih jauh dari sempurna. Oleh

karena itu, penulis mengharapkan kritik dan saran yang dapat membangun

serta menyempurnakan skripsi ini. Akhirnya, penulis berharap semoga skripsi

ini dapat memberikan wawasan dan pengetahuan bagi pembaca.

Yogyakarta, 3 November 2014

xi

LEMBAR PERNYATAAN PERSETUJUAN

PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata

Dharma :

Nama : Yustina Astri Wijayanti

NIM : 103114015

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma, Karya Ilmiah saya yang berjudul :

Prinsip Maksimum Pontryagin dalam Model Penyebaran Penyakit

beserta perangkat-perangkat yang diperlukan (bila ada). Dengan demikian, saya memberikan kepada Universitas Sanata Dharma dan hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelola dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu minta ijin dari saya maupun memberi royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini saya buat sebenarnya.

Dibuat di Yogyakarta

Pada tanggal : 4 November 2014

Yang menyatakan

xii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ... iv

HALAMAN PERSEMBAHAN ... v

PERNYATAAN KEASLIAN KARYA ... vi

ABSTRAK ... vii

ABSTRACT ... viii

KATA PENGANTAR ... ix

PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH ... xi

DAFTAR ISI ... xii

DAFTAR GAMBAR ... xv

DAFTAR TABEL ... xvii

DAFTAR LAMPIRAN ... xviii

BAB I PENDAHULUAN ... 1

A.Latar Belakang ... 1

B.Rumusan Masalah ... 7

C.Batasan Masalah ... 7

D.Tujuan Penulisan ... 8

xiii

F. Metode Penulisan ... 8

G.Sistematika Penulisan ... 9

BAB II LANDASAN TEORI ... 11

A. Kontinu Sepotong - Sepotong ... 11

B. Deret Taylor ... 16

B.1. Definisi ... 16

B.2. Tingkat Keakuratan Hampiran ... 17

C. Metode Euler ... 19

D. Metode Runga - Kutta ... 20

E. Kestabilan Persamaan Diferensial ... 21

1. Pendahuluan... 21

2. Penyelesaian Umum Persamaan Diferensial ... 22

3. Titik Kesetimbangan... 23

4. Kestabilan ... 28

BAB III PRINSIP MAKSIMUM PONTRYAGIN ... 30

A. Kontrol Optimal ... 30

B. Contoh – Contoh Kontrol Optimal ... 31

C. Syarat Perlu Optimalitas ... 35

D. Langkah – Langkah Penyelesaian ... 48

BAB IV KONTROL YANG TERBATAS ... 61

A. Pendahuluan ... 61

B. Contoh – Contoh Soal ... 65

BAB V METODE SWEEP MAJU - MUNDUR ... 72

xiv

B. Metode Sweep Maju - Mundur ... 73

C. Contoh Masalah ... 76

BAB VI APLIKASI MODEL SEIR ... 91

A. Pendahuluan ... 91

B. Model SEIR Tanpa Kontrol dalam Penyebaran Penyakit ... 92

B.1. Pendahuluan ... 92

B.2. Penurunan Rumus ... 95

B.3. Pelinearan Sistem Secara Umum ... 96

B.4. Ilustrasi Linearisasi Sistem ... 101

B.5. Analisa Data ... 120

C. Model SEIR Dengan Kontrol dalam Penyebaran Penyakit ... 123

C.1. Pendahuluan ... 123

C.2. Penurunan Rumus ... 124

C.3. Analisa Data ... 127

BAB VII PENUTUP ... 130

A. Kesimpulan ... 130

B. Saran ... 131

DAFTAR PUSTAKA ... 132

xv

DAFTAR GAMBAR

Gambar 1.1 Diagram alur penyebaran penyakit ... 2

Gambar 2.1 Fungsi sepotong - sepotong ... 12

Gambar 2.2 Fungsi cekung ... 14

Gambar 2.3 Penyelesaian persamaan diferensial dengan titik sadle... 25

Gambar 2.4 Penyelesaian persamaan diferensial dengan titik nodal sink ... 25

Gambar 2.5 Penyelesaian persamaan diferensial dengan titik nodal source .. 26

Gambar 2.6 Penyelesaian persamaan diferensial dengan titik spiral sink ... 26

Gambar 2.7 Penyelesaian persamaan diferensial dengan titik spiral source .. 27

Gambar 2.8 Penyelesaian persamaan diferensial dengan titik center ... 27

Gambar 3.1 Peluncuran roket ... 33

Gambar 3.2 Grafik kontrol optimal ... 36

Gambar 3.3 Grafik tiga kondisi λ,x.u contoh 3.1 ... 51

Gambar 3.4 Grafik tiga kondisi λ,x.u contoh 3.2 ... 56

Gambar 3.5 Grafik 3 8 t 3 1 ) t ( λ _ 3 _ ... 59

Gambar 3.6 Grafik 18 17 ) t ln( 3 4 t 18 1 ) t ( x  3   ... 59

Gambar 3.7 Grafik _        3 t 3 8 t 2 1 ) t ( u 3 ... 60

Gambar 4.1 Grafik kondisi optimal λ(t) contoh 4.1... 70

Gambar 4.2 Grafik kondisi optimal u(t) contoh 4.1 ... 71

xvi

Gambar 5.1 Grafik tiga kondisi optimal λ,x.u contoh 5.2 ... 86

Gambar 5.2 Grafik tiga kondisi optimal λ,x.u contoh 5.3 ... 89

Gambar 6.1 Diagram alur model SEIR tanpa kontrol ... 93

Gambar 6.2 Grafik kasus 1 pada titik kesetimbangan yang pertama ...121

Gambar 6.3 Grafik kasus 1 pada titik kesetimbangan yang kedua ...122

Gambar 6.4 Diagram alur model SEIR dengan kontrol ...123

xvii DAFTAR TABEL

Halaman

xviii DAFTAR LAMPIRAN

Halaman

Lampiran 1 Program Metode Sweep Maju - Mundur ... 133

1 BAB I

PENDAHULUAN

A. LATAR BELAKANG

Setiap individu mempunyai tingkat kekebalan tubuh yang berbeda – beda. Ada individu yang tingkat kekebalan tubuhnya lemah dan ada pula yang tingkat

kekebalan tubuhnya kuat. Lemahnya kekebalan tubuh akan menimbulkan suatu

dampak yang cukup besar dalam kehidupan individu itu sendiri. Salah satu di

antaranya adalah individu itu akan mudah terserang penyakit, terutama untuk

penyakit menular. Dalam suatu populasi tertentu yang ditinggali oleh sebagian

besar individu dengan kekebalan tubuh yang lemah dan satu di antaranya sudah

terserang penyakit menular, maka akan dengan mudah penyakit tersebut

menyerang ke individu lainnya. Penyakit menular tersebut ada kemungkinan akan

menyerang banyak individu dan bisa saja melebihi batas normal atau melebihi

keadaan wajarnya. Penyebaran penyakit yang tidak wajar tersebut biasa disebut

dengan wabah.

Pada suatu saat t, model penyebaran penyakit biasanya

mempertimbangkan empat komponen, di antaranya banyaknya individu yang

rentan penyakit, banyaknya individu yang masih dalam masa inkubasi, banyaknya

individu yang terinfeksi penyakit, dan banyaknya individu yang sudah pulih /

sembuh dari penyakit. Keempat individu tersebut berturut - turut dinotasikan

keseluruhan dalam suatu populasi tertentu dinotasikan dengan N(t). Secara

umum, banyaknya individu keseluruhan pada saat t adalah

) t ( R ) t ( I ) t ( E ) t ( S ) t (

N     (Lenhart & Workman, 2007). Oleh karena itu,

model penyebaran penyakit tersebut dapat dirumuskan dengan model SEIR.

Model SEIR itu sendiri dapat digambarkan diagram alurnya sebagai berikut:

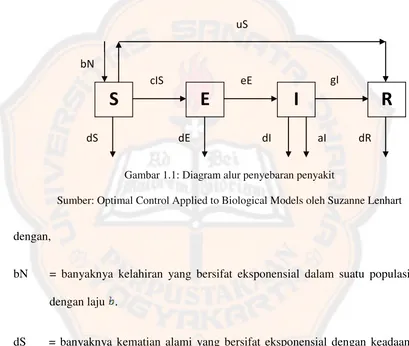
Gambar 1.1: Diagram alur penyebaran penyakit

Sumber: Optimal Control Applied to Biological Models oleh Suzanne Lenhart

dengan,

bN = banyaknya kelahiran yang bersifat eksponensial dalam suatu populasi

dengan laju .

dS = banyaknya kematian alami yang bersifat eksponensial dengan keadaan

individu yang rentan penyakit dengan laju

cIS = banyaknya kejadian penyakit yang timbul dengan laju

uS = banyaknya pemberian vaksin sebagai kontrol atas individu yang rentan

penyakit dengan laju

S

E

I

R

bN

cIS

dS dE

uS

eE

dI aI

gI

eE = banyaknya individu dalam masa peralihan, dari individu yang masih

tidak terlindungi menjadi individu yang terinfeksi dengan laju

dE = banyaknya kematian alami yang bersifat eksponensial dengan keadaan

individu yang tidak terlindungi dengan laju

gI = banyaknya individu terinfeksi penyakit yang sembuh dengan laju

dI = banyaknya kematian alami yang bersifat eksponensial dengan keadaan

individu yang masih terinfeksi penyakit dengan laju

aI = banyaknya kematian yang disebabkan oleh individu yeng terinfeksi

penyakit dengan laju

dR = banyaknya kematian alami yang bersifat eksponensial dengan keadaan

individu yang sudah sembuh dengan laju

Dari diagram alur di atas, dapat dijelaskan bahwa banyaknya individu

yang terlahir dalam suatu populasi tertentu pada awalnya individu tersebut masih

rentan terhadap penyakit. Kemudian, dari individu yang rentan tersebut apabila

diberikan vaksin maka individu itu dapat dikelompokkan ke dalam individu yang

sembuh. Selain itu, ada juga kemungkinan mulai muncul penyakit yang kemudian

individu tersebut masuk ke dalam masa inkubasi, yaitu masa di mana individu ada

kemungkinan muncul gejala-gejala terserang penyakit. Namun, dapat juga

individu rentan tersebut meninggal secara alami yang bersifat eksponensial

(membesar tanpa batas). Individu yang masih dalam masa inkubasi yang semula

terinfeksi penyakit, namun dapat juga individunya meninggal secara alami secara

eksponensial. Individu yang sudah terinfeksi mempunyai kemungkinan langsung

sembuh, namun dapat juga menyebabkan banyaknya individu yang meninggal

semakin besar. Kemudian, individu yang sudah sembuh dari penyakit akibat

infeksi dan awalnya dari individu yang rentan penyakit, dapat meninggal secara

alami secara eksponensial.

Dengan melihat uraian di atas yang diperoleh dari diagram sebelumnya,

secara matematis dapat dituangkan ke dalam suatu sistem persamaan diferensial

sebagai berikut:

,

Dalam kenyataannya, memang terdapat penyakit menular yang merambah

di daerah tertentu, seperti penyakit campak. Adanya penyakit tersebut dapat

membawa dampak negatif yang besar bagi kehidupan individu, maka seharusnya

diadakan pemberian vaksin. Vaksinasi tersebut diberikan untuk memberikan

kekebalan pada tubuh individu untuk mencegah terserangnya penyakit. Dengan

adanya pemberian vaksin tersebut diharapkan dapat meminimalkan banyaknya

individu yang terinfeksi. Pemberian vaksin ini berperan sebagai kontrol untuk

membantu mengurangi banyaknya individu yang terinfeksi.

Dengan adanya kontrol dalam permasalahan tersebut, maka permasalahan

Secara umum, kontrol optimal sendiri adalah suatu teori yang digunakan untuk

menyelesaikan permasalahan optimisasi dengan variabel kontrol. Dalam

optimisasi sendiri terdapat dua istilah, yaitu permasalahan maksimalisasi dan

permasalahan minimalisasi. Terdapat dua cara penyelesaian untuk masalah

kontrol optimal ini, yaitu secara analitik dan numerik. Secara analitik, kontrol

optimal dapat diselesaikan dengan beberapa metode, di antaranya adalah Prinsip

Maksimum Pontryagin, Regulator Linear Kuadratik, dan sebagainya. Sedangkan

salah satu metode yang digunakan untuk menyelesaikan secara numerik adalah

Sweep Maju-Mundur. Prinsip Maksimum Pontryagin adalah metode yang

ditemukan oleh seseorang yang berasal dari Uni Soviet yaitu Pontryagin. Prinsip

ini digunakan untuk menyelesaikan permasalahan kontrol optimal dengan variabel

kontrol yang bersifat deterministik dan kontinu terhadap fungsi . Sedangkan

Regulator Linear Kuadratik adalah metode yang digunakan untuk menyelesaikan

permasalahan kontrol optimal dengan variabel kontrol dan variabel keadaan awal

yang linear dan fungsi obyektifnya kuadrat. Permasalahan yang diselesaikan

menggunakan kontrol optimal dirumuskan dalam suatu fungsi obyektif. Fungsi

obyektif tersebut sebagai berikut:



f

t

t

u f t x t u t dt

0

)) ( ), ( , ( max

atau



f

t

t

u f t x t u t dt

0

di mana x(t) = variabel keadaan; t0 = batas awal

u(t) = variabel kontrol; tf = batas akhir

dengan kendala:

maks min

0 0

u ) t ( u u

awal keadaan x

) t ( x

dt )) t ( u ), t ( x , t ( g ) t ( ' x

 

  

Dengan mempertimbangkan variabel kontrol dalam permasalahan

penyebaran penyakit pada bagian terakhir dari dua paragraf sebelumnya, maka

permasalahan penyebaran penyakit dapat diselesaikan menggunakan Prinsip

Maksimum Pontryagin. Dalam hal ini, variabel kontrolnya kontinu terhadap

waktu (t).

Secara analitik, cukup menggunakan metode Prinsip Maksimum

Pontryagin sudah mendapatkan solusinya. Namun, dalam menyelesaikan masalah

secara numerik tidak cukup hanya menggunakan metode Prinsip Maksimum

Pontryagin melainkan harus menggunakan metode Sweep Maju-Mundur.

Permasalahan yang diselesaikan secara analitik akan menghasilkan penyelesaian

yang sebenarnya (sejati). Sedangkan masalah yang diselesaikan secara numerik

akan menghasilkan penyelesaian yang mendekati penyelesaian sejati, biasa

disebut dengan penyelesaian hampiran. Penyelesaian secara numerik digunakan

ketika masalah tidak dapat diselesaikan lagi secara analitik.

Tugas akhir ini akan membahas metode Prinsip Maksimum Pontryagin

Secara numerik akan digunakan metode Runga-Kutta 4 untuk menyelesaikan

persamaan diferensialnya. Dalam hal ini, digunakan metode Runga-Kutta orde 4

karena tingkat keakuratan (galat) yang dihasilkan kecil. Penyelesaian dikatakan

baik ketika galat yang dihasilkan adalah kecil.

Dengan demikian, Prinsip Maksimum Pontryagin dan metode Sweep

Maju-Mundur mempunyai peran yang penting untuk meminimalkan / mengurangi

banyaknya individu yang terinfeksi penyakit, sehingga diperoleh penyelesaian

yang optimal. Dalam tulisan ini, pembahasan permasalahannya hanya dibatasi

pada variabel kontrol yang bersifat deterministik dan kontinu. Untuk

memahaminya, maka diperlukan beberapa materi diantaranya fungsi kontinu,

turunan, persamaan diferensial, dll.

B. RUMUSAN MASALAH

Pokok permasalahan yang akan dibahas dalam tulisan ini yaitu:

1. Apa yang dimaksud dengan Prinsip Maksimum Pontryagin?

2. Apa yang dimaksud dengan metode Sweep maju - mundur?

3. Bagaimana meminimalkan banyaknya individu yang terserang penyakit

menggunakan Prinsip Maksimum Pontryagin dalam kontrol optimal?

C. BATASAN MASALAH

Pembahasan Prinsip Maksimum Pontryagin dalam tulisan ini hanya dibatasi

pada:

2. Tidak ada interaksi antar populasi, yaitu model dikembangkan hanya untuk

satu populasi tertentu.

3. Individu rentan terhadap penyakit.

4. Materi prasyarat hanya dibahas terbatas pada hal – hal pokok.

D. TUJUAN PENULISAN

Tujuan penulisan ini adalah untuk memahami Prinsip Maksimum

Pontryagin dan bagaimana cara menyelesaikan permasalahan kesehatan dalam

meminimalkan banyaknya individu yang terinfeksi penyakit.

E. MANFAAT PENULISAN

Manfaat yang didapat dari tulisan ini adalah untuk memperoleh

pengetahuan tentang Prinsip Maksimum Pontryagin dalam kontrol optimal

untuk menyelesaikan permasalahan kesehatan, yaitu dalam meminimalkan

banyaknya individu yang terinfeksi penyakit dengan variabel kontrol yang

kontinu.

F. METODE PENULISAN

Metode yang digunakan penulis adalah metode studi pustaka, yaitu

dengan mempelajari buku-buku yang berkaitan dengan kontrol optimal,

khususnya Prinsip Maksimum Pontryagin, metode Sweep Maju-Mundur, dan

G. SISTEMATIKA PENULISAN

BAB I PENDAHULUAN

A. Latar Belakang

B. Rumusan Masalah

C. Batasan Masalah

D. Tujuan Penulisan

E. Manfaat Penulisan

F. Metode Penulisan

G. Sistematika Penulisan

BAB II LANDASAN TEORI

A. Kontinu Sepotong - Sepotong

B. Deret Taylor

C. Metode Euler

D. Metode Runga - Kutta

E. Kestabilan Persamaan Diferensial

BAB III PRINSIP MAKSIMUM PONTRYAGIN

A. Kontrol Optimal

B. Contoh-Contoh Kontrol Optimal

C. Dasar dan Syarat Perlu

BAB IV KONTROL YANG TERBATAS

A. Pendahuluan

B. Contoh-Contoh Soal

BAB V METODE SWEEP MAJU-MUNDUR

A. Pendahuluan

B. Metode Sweep Maju-Mundur C. Contoh Masalah

BAB VII APLIKASI MODEL SEIR

A. Pendahuluan

B. Model SEIR tanpa Kontrol dalam Penyebaran Penyakit C. Model SEIR dengan Kontrol dalam Penyebaran Penyakit

BAB VII PENUTUP

A. Kesimpulan B. Saran

11 BAB II

LANDASAN TEORI

Pada bab ini akan dibahas mengenai dasar – dasar matematika yang menjadi dasar dalam pembahasan bab selanjutnya

A. KONTINU SEPOTONG - SEPOTONG Definisi 2.1

Misalkan I R _{adalah suatu selang/interval.} u:I R _{dikatakan kontinu} sepotong-sepotong jika fungsi tersebut kontinu di setiap tI, dengan pengecualian pada sejumlah berhingga titik t, dan jika u _{mempunyai nilai}

yang sama dengan salah satu nilai limit kiri atau limit kanan di setiap tI.

Contoh:

Sketsakan grafik fungsi f berikut dan tentukan apakah f kontinu, kontinu

sepotong-sepotong, atau tidak keduanya pada interval 1t 2 !

1 t , 1

t 

 ) t (

f 6t2, 1t 2

2 t , t

6 

Penyelesaian:

Fungsi f(t)t1 kontinu di (,1).

. 2 ) 1 ( 6 ) 1 ( f 4 2 t 6 lim

1 t

 

    

Kemudian nilai limit kiri saat t 2 untuk fungsi f(t)6t2 sama dengan nilai fungsi f(t)6t2 saat t2. Hal itu dapat ditunjukkan sebagai berikut:

. 2 ) 2 ( 6 ) 2 ( f 10 2 t 6 lim

2

t     

Sehingga, fungsi f(t)6t2 juga dikatakan kontinu di 1t2. Begitu juga untuk fungsi f(t)6t kontinu di (2,). Dengan demikian,

berdasarkan definisi 1.1 dapat disimpulkan bahwa fungsi tersebut kontinu

sepotong – sepotong. Untuk lebih jelasnya, fungsi tersebut dapat dituangkan dalam grafik berikut:

Definisi 2.2

Misalkan x:I R _{adalah kontinu di} I _{dan mempunyai turunan di setiap}

titik tI, dengan pengecualian pada sejumlah berhingga titik dari I.

Andaikan bahwa x' _{kontinu di mana-mana. Maka, dapat dikatakan bahwa} x

mempunyai turunan sepotong-sepotong.

Definisi 2.3

Misalkan k:I R. k _{dikatakan mempunyai turunan yang kontinu jika} k' ada dan kontinu di I .

Definisi 2.4

Suatu fungsi k(t) dikatakan cekung di

 

a,b jika

) t )

α

1 ( t

α

( k ) t ( k )

α

1 ( ) t ( k

α 1   2  1  2

untuk semua 0α1 dan untuk setiap at₁,t₂ b.

Definisi tersebut juga berlaku untuk kondisi sebaliknya, yaitu k(t) dikatakan

cembung di

 

a,b jika

). t )

α

1 ( t

α

( k ) t ( k )

α

1 ( ) t ( k

α 1   2  1  2

Definisi tersebut dapat diilustrasikan untuk fungsi yang cekung sebagai

berikut:

Misalkan diambil beberapa α untuk αk(t₁)(1α)k(t₂):

Untuk α0, maka

) t ( k ) t ( k ) 0 1 ( ) t ( k . 0 ) t ( k )

α

1 ( ) t ( k

Untuk α1, maka

) t ( k ) t ( k ) 1 1 ( ) t ( k 1 ) t ( k )

α

1 ( ) t ( k

α 1   2  1   2  1

Sedangkan, untuk 0α1 maka akan diperoleh suatu garis yang menghubungkan k(t₁)dengan k(t₂ ).

Selanjutnya, diambil beberapa α untuk k(αt₁ (1α)t₂):

Untuk α0, maka

) t ( k

) t ) 0 1 ( t. 0 ( k ) t )

α

1 ( t

α

( k

2

2 1

2 1



  

 

Untuk α1, maka





 

1

2 1

2 1

t k

t ) 1 1 ( t. 1 k ) t )

α

1 ( t

α

( k



  

 

Sedangkan, untuk 0α1 maka akan diperoleh suatu kurva yang menghubungkan k(t₁)dengan k(t₂ ).

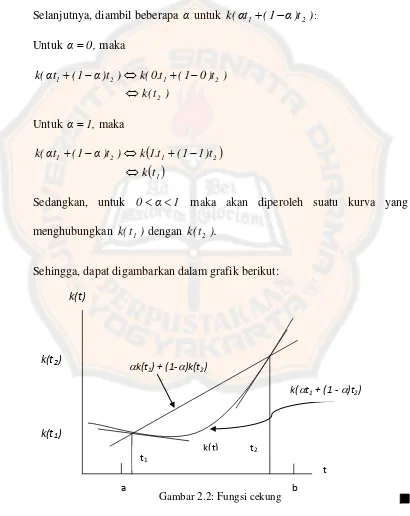
Sehingga, dapat digambarkan dalam grafik berikut:

Gambar 2.2: Fungsi cekung

k(t)

k(t2)

k(t1)

k(t)

k(t1) + (1-)k(t2)

k(t1 + (1 - )t2)

a b

t t1

untuk semua 0α1 dan semua (x₁,y₁),(x₂,y₂ ) dalam domain k. Kemudian apabila k adalah suatu fungsi yang cekung dan mempunyai turunan

di mana-mana, maka k mempunyai sifat garis singgung seperti berikut

)

B. DERET TAYLOR B.1. Definisi

terlebih dahulu dijelaskan mengenai deret Taylor dengan orde-2 yang dapat

dituliskan sebagai berikut:

n 2 n

n h x" 2 1 ' hx x ) h t (

x     (1.1)

dengan xn,x'n, dan x"n merupakan pendekatan terhadap x(tn),x'(tn ), dan

) t ( "

x _n . x"(t_n ) merupakan turunan kedua dari x(tn ).

Dari uraian singkat tersebut, dapat dituliskan bentuk umum metode deret

Taylor dengan orde-n pada x(th)sebagai berikut:

) 2 . 1 ( )

t ( R ) t ( x ! n h ... ) t ( " x ! 2 h ) t ( ' hx ) t ( x ) h t (

x n _n

n 2

 

 

  

dengan x (ξ)

)! 1 n (

h ) t (

R n 1

1 n

n

 



 adalah suku sisa (galat) dan ξ(t,th).

B.2. Tingkat Keakuratan Hampiran

Tingkat keakuratan suatu hampiran dapat dinyatakan dengan orde

hampiran yang biasanya dituliskan dengan O-besar. Orde hampiran juga

disebut sebagai orde galat. Misalkan bahwa x_k adalah nilai pendekatan dari

) t (

x _k . Apabila x_k menghampiri x(t_k ) dengan orde galatnya O(hn ), maka

dapat dinyatakan dalam persamaan berikut:

) h ( O x ) t (

x _k  _k  n

Dapat diartikan secara numeris bahwa jika semakin besar nilai n

berarti semakin kecil pula galat yang dihasilkan, sehingga nilai hampirannya

mempunyai tingkat keakuratan yang lebih tinggi / teliti dibandingkan dengan

suatu metode yang hanya mempunyai orde O(h).

Tingkat keakuratan hampiran sendiri didefinisikan sebagai berikut:

Definisi

Andaikan adalah fungsi bernilai riil yang didefinisikan pada kitar-δ

dengan pusat , ditulis sebagai , dengan .

Misal adalah fungsi yang didefinisikan dalam suatu domain

(daerah asal) yang memuat , maka

(i) , diartikan bahwa

terbatas. Jadi, terdapat bilangan dan , sehingga jika

, berakibat

(ii) , diartikan bahwa

M dalam definisi tersebut adalah suatu konstanta riil yang merupakan batas

dari x_k menghampiri x(t_k ).

Contoh:

Tunjukkan bahwa adalah .

Penyelesaian:

Akan ditentukan bilangan bulat positif dan sehingga untuk setiap ,

berlaku

Misal ambil , maka akan diperoleh

Dengan demikian, dari persamaan di atas diperoleh nilai dengan

.

C. METODE EULER

Metode Euler merupakan metode numerik paling sederhana yang

digunakan untuk menyelesaikan masalah nilai awal dengan bentuk

0 0 ) x t ( x )), t ( x , t ( f ) t ( '

x  

(c.1)

pada interval

Penyusunan metode Euler dengan membagi interval dalam N subinterval

nh t

t_n  ₀  untuk n0,1,2,...,N

dengan h adalah panjang langkah. Metode Euler diturunkan dari deret Taylor

pada x(th) yang dipotong sampai dengan suku kedua sebagai berikut:

) t ( R ) t ( hx ) t ( x ) h t (

x    '  ₁

(c.2)

dengan persamaan (d.1), maka persamaan (d.2) menjadi

) t ( R )) t ( x , t ( hf ) t ( x ) h t (

x     ₁

(c.3)

Kemudian saat t tn, maka persamaan (d.3) menjadi

) t ( R )) t ( x , t ( hf ) t ( x ) t (

x _n1  _n  _{n n}  _{1 n}

1 N ,..., 2 , 1 , 0

n 

Karena suku R₁(t_n) merupakan suku sisa (galat) dengan nilai yang

sangat kecil, maka suku tersebut dapat dibuang, sehingga dapat diperoleh untuk

bentuk umum metode Euler adalah

n n 1

n x hf

x _   untuk n0,1,2,...,N1

dengan x_n1 merupakan pendekatan terhadap x(t_n1),x_n merupakan pendekatan

D. METODE RUNGA-KUTTA

Metode Runga-Kutta merupakan metode yang digunakan untuk

menyelesaikan masalah nilai awal. Misalkan diketahui:

0 0 ) y t ( y ), y , t ( f '

y   (i)

pada interval t



tn,tn1



. Jika h adalah panjang langkah dan yn yang diketahui,

maka y y n1 f(t,y)dt

n

t

t n 1

n



  

 .

Untuk mendapatkan hasil pendekatan yang akurat, maka diperlukan

ukuran h yang sangat kecil. Oleh karena itu, penyelesaian masalah kontrol

optimal akan menggunakan metode Runga-Kutta 4, dengan tingkat keakuratannya

(galat) berorde 4 atau O(h4 ). Tingkat keakuratan tersebut sangat dipengaruhi

oleh panjang langkah yang diambil. Untuk memperolehnya dibutuhkan metode

Deret Taylor supaya penyelesaian hampirannya lebih akurat.

Metode Runga-Kutta merupakan penurunan metode Euler dengan

deret Taylor. Untuk metode Runga-Kutta orde 4, pada Deret Taylor dilakukan

pemotongan suku sampai suku ke keempat, yaitu

) h ( O ) t ( ' " y h 6 1 ) t ( " y h 2 1 ) t ( ' hy ) t ( y ) h t (

y     2  3  4

Secara umum, untuk skema numeris dari metode Runga-Kutta orde 4

dapat dituliskan sebagai berikut:



1 2 3 4



n 1

n K 2K 2K K

6 h y

dengan

) hK y , h t ( f K

) K 2 h y , 2 h t ( f K

) K 2 h y , 2 h t ( f K

) y , t ( f K

3 n n

4

2 n

n 3

1 n

n 2

n n 1

 



 



 

 

E. KESTABILAN PERSAMAAN DIFERENSIAL E.1. Pendahuluan

Dalam pembahasan mengenai kestabilan persamaan diferensial, akan

dimulai pembahasannya sebagai berikut.

Misalkan diberikan sistem persamaan diferensial yang sederhana,

yaitu

x A dt

x d

 (e.1)

dengan A adalah matriks konstanta 2x2 dan x adalah vektor 2x1

yang bersesuaian dengan matriks A. Apabila sistem tersebut mempunyai

solusi penyelesaian rt e v

x  dengan mensubstitusi x dalam persamaan (e.1),

maka dapat ditemukan persamaan

0 v ) rI A

(   (e.2)

di mana radalah nilai eigen dan v adalah vektor eigen dari matriks

0 ) rI A

det(   (e.3)

Sedangkan untuk vektor eigennya ditentukan dengan

mensubstitusikan nilai eigen yang didapat dari persamaan (e.3) ke dalam

persamaan (e.2). Penjelasan selanjutnya akan dibahas mengenai penyelesaian

umum persamaan diferensial dengan memperhatikan nilai eigen dan vektor

eigen yang sudah diperoleh tersebut.

E.2. Penyelesaian Umum Persamaan Diferensial

Nilai eigen yang dihasilkan tersebut di atas dibedakan dalam tiga

kasus, yaitu nilai eigen real beda, nilai eigen real sama, dan nilai eigen

kompleks. Penjelasan dari masing – masing nilai eigen tersebut adalah

1. Nilai Eigen Real Beda

Apabila r₁ r₂ ...r_n, maka penyelesaian umumnya adalah

t r n n t

r 2 2 t r 1 1

n 2

1 _{c v e ... c v e}

e v c

x     (e.4)

2. Nilai Eigen Real Sama

Apabila r₁ r₂ ...r_n, maka penyelesaian umunya adalah

t r 1 n n n t

r 2 3 3 t r 2 2 t r 1 1

n 3

2

1 _{c v te c v t e ... c v t e}

e v c

x       (e.5)

3. Nilai Eigen Kompleks

Apabila ada r₁,r₂,...,r_n yang bernilai kompleks dan misalkan

t r n n t

r 3 3 2

1

n 3 _{... c w e}

e w c ) t ( v c ) t ( u c

x     

dengan

) t

μ

sin b t

μ

cos a ( e ) t ( v

) t

μ

sin b t

μ

cos a ( e ) t ( u

t

λ

t

λ

 

 

E.3. Titik Kesetimbangan

Titik kesetimbangan adalah titik yang diperoleh ketika suatu sistem

berada pada keadaaan setimbang. Keadaan setimbang adalah keadaan di

mana perubahan suatu sistem sepanjang waktu adalah nol. Ada bermacam – macam tipe titik kesetimbangan, yaitu titik pelana (titik sadlle), nodal sink,

nodal source, spiral sink, spiral source, dan center. Sementara itu, titik

kesetimbangan tersebut diperoleh dengan membuat ruas kanan persamaan

(e.1) pada subbab sebelumnya sama dengan nol, yaitu Ax 0. Diasumsikan bahwa A adalah matriks tak singular atau det(A)0, sehingga titik

kesetimbangan pada persamaan (e.1) adalah x0.

Titik kesetimbangan suatu sistem disebut dengan titik sadlle apabila

nilai eigen yang diperoleh bernilai real dan berbeda tanda. Misalkan

penyelesaian umum dari suatu persamaan diferensial tertentu adalah

t r 2 2 t r 1 1

2 1 _{c v e}

e v c ) t (

x   

mempunyai titik kesetimbangan x(t)0. Sehingga ketika c₂ 0 dan t

berarti bahwa penyelesaiannya akan menjauhi titik setimbangnya. Dengan

demikian, titik kesetimbangan penyelesaiannya disebut titik sadlle.

Untuk nilai eigennya real dengan tanda yang sama akan mempunyai

dua titik kesetimbangan, yaitu nodal sink dan nodal source. Titik

kesetimbangan penyelesaian dikatakan nodal sink ketika nilai eigen realnya

bernilai sama – sama negatif. Sedangkan untuk nilai eigen realnya bernilai sama – sama positif titik kesetimbangannya adalah nodal source.

Hal yang serupa terjadi pada penyelesaian yang mempunyai nilai

eigen kompleks. Apabila matriks yang terbentuk dari persamaan

diferensialnya mempunyai nilai eigen kompleks, maka mempunyai dua

macam titik kesetimbangan, yaitu spiral sink dan spiral source. Titik

kesetimbangan penyelesaian dikatakan spiral sink apabila nilai dari bagian

real pada nilai eigennya negatif. Sedangkan apabila bagian realnya bernilai

positif, maka titik kesetimbangannya disebut spiral source.

Titik kesetimbangan yang terakhir adalah center. Titik

kesetimbangannya disebut dengan center ketika nilai eigen yang diperoleh

adalah kompleks murni, yaitu nilai eigen dengan bagian imajiner saja.

Titik – titik kesetimbangan tersebut akan ditunjukkan dalam sebuah grafik pada bidang fase menggunakan program MATLAB. Bidang fase

sendiri merupakan suatu bidang xy dari suatu sistem persamaan diferensial

untuk sumbu horizontal adalah x(t) sedangkan untuk sumbu vertikal adalah

). t (

y Berikut adalah ilustrasi – ilustrasinya:

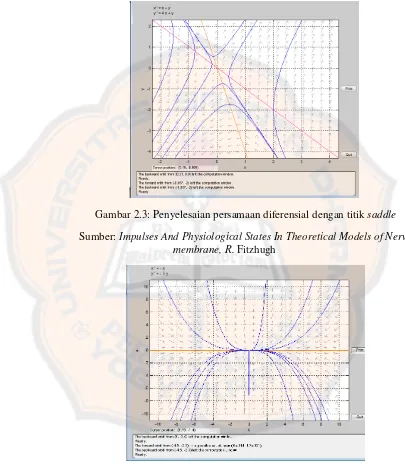
Gambar 2.3: Penyelesaian persamaan diferensial dengan titik saddle

Sumber: Impulses And Physiological States In Theoretical Models of Nerve membrane, R. Fitzhugh

Gambar 2.4: Penyelesaian persamaan diferensial dengan nodal sink

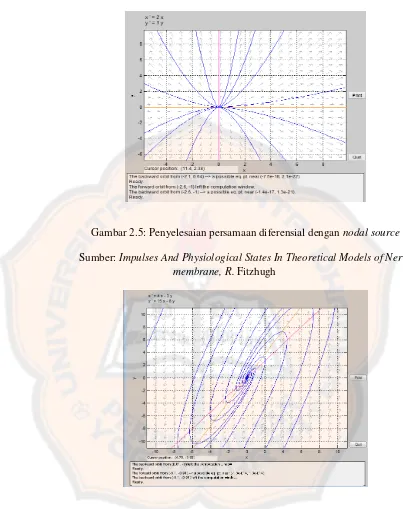
Gambar 2.5: Penyelesaian persamaan diferensial dengan nodal source

Sumber: Impulses And Physiological States In Theoretical Models of Nerve membrane, R. Fitzhugh

Gambar 2.6: Penyelesaian persamaan diferensial dengan spiral sink

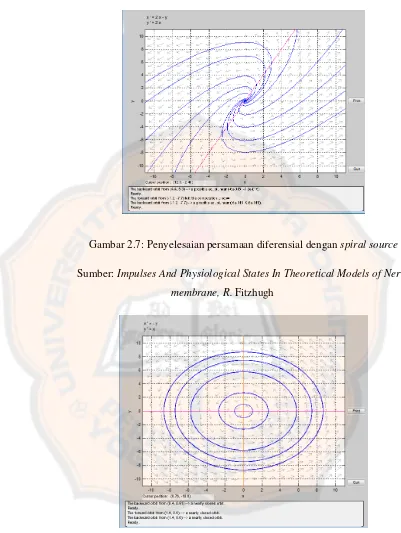
Gambar 2.7: Penyelesaian persamaan diferensial dengan spiral source

Sumber: Impulses And Physiological States In Theoretical Models of Nerve

membrane, R. Fitzhugh

Gambar 2.8: Penyelesaian persamaan diferensial dengan center

Sumber: Impulses And Physiological States In Theoretical Models of Nerve

E.4. Kestabilan

Suatu sistem dapat dikatakan stabil apabila sistem tersebut diberi

gangguan maka tidak akan mengubah sistemnya dengan seiring waktu yang

semakin meningkat. Kestabilan tersebut diperoleh dengan memperhatikan

nilai eigen dari persamaan diferensial yang diberikan. Persamaan diferensial

tersebut harus diubah terlebih dahulu ke dalam bentuk persamaan matriks

agar dapat ditemukan nilai eigennya, seperti persamaan (e.3) pada subbab

sebelumnya.

Sesuai dengan tipe dari titik kesetimbangan pada subbab

sebelumnya, sifat – sifat kestabilan suatu sistem (apabila dalam suatu persamaan diferensial diperoleh dua nilai eigen) dapat dirangkum dalam suatu

tabel seperti berikut:

Tabel 2.1. Sifat Kestabilan

Nilai Eigen

Tipe dari Titik

Kesetimbangan

Kestabilan

0

2

1  

 Node Tidak Stabil

0

2

1  

 Node Stabil Asimpotik

2

1 0 

   Titik Pelana Tidak Stabil

0

2

1  

 Proper atau improper

node

0

2

1  

 Proper atau improper

node

Stabil Asimpotik

  

₁, ₂  i

Titik Spiral Tidak Stabil

Stabil Asimtotik 0





0





μ λ

,

μ λ

i

μ λ

r , r

2 1

2 1

  

 

Center Stabil

Demikian dasar – dasar yang digunakan dalam pembahasan pada bab

31 BAB III

PRINSIP MAKSIMUM PONTRYAGIN

A. Kontrol Optimal

Kontrol optimal merupakan suatu model optimisasi yang digunakan

untuk mengoptimalkan suatu fungsi linear maupun nonlinear yang terbatas

oleh kendala-kendala berupa persamaan dan pertidaksamaan. Fungsi yang akan

dioptimalkan disebut dengan fungsi obyektif. Fungsi obyektif yang

dioptimalkan terdiri dari fungsi kontrol (u(t)) dan fungsi keadaan (x(t))yang

keduanya bergantung dengan waktu (t). Sifat waktu dalam masalah kontrol

optimal adalah kontinu dan diskret. Namun, dalam tulisan ini sifat waktu

kontrol optimalnya adalah kontinu. Fungsi kontrol sangat berperan untuk

mengoptimalkan suatu permasalahan. Penyelesaian optimalnya terletak pada

nilai yang optimal (terbaik) untuk kontrol (u*(t)) dan keadaannya (x*(t)).

Kontrol optimal dituangkan secara matematik dalam persamaan diferensial

biasa.

Secara umum, masalah kontrol optimal dapat dirumuskan sebagai

berikut (Suzanne Lenhart dan John T. Workman: 2007, 7):

yang mengoptimalkan (memaksimumkan atau meminimalkan):

, dt )) t ( u ), t ( x , t ( f min atau dt

)) t ( u ), t ( x , t ( f

max 1

0 1

0

t

t u t

t

u





(3.1)

dengan kendala:

bebas )

t ( x dan x

) t ( x

)) t ( u ), t ( x , t ( g ) t ( ' x

1 0

0  



(3.2)

Persamaan (3.1) menunjukkan fungsi obyektif, sedangkan persamaan

(3.2) menunjukkan fungsi kendalanya. Apabila fungsi kontrol diubah, maka

penyelesaian untuk persamaan differensial pada fungsi kendalanya juga akan

berubah. Hal ini menggambarkan bahwa terdapat hubungan antara kontrol dan

keadaannya (x(t)), yaitu sebagai pemetaan u(t)xx(u). Fungsi kendala

yang memenuhi persamaan differensial bergantung pada variabel kontrol dan

terdifferensial sepotong-sepotong. Seperti yang sudah dijelaskan sebelumnya,

variabel kontrol u(t) _{bersifat kontinu sepotong-sepotong. Oleh karena itu,}

fungsi obyektif dan fungsi kendala akan selalu fungsi yang terdiferensial secara

kontinu.

B. Contoh-Contoh Kontrol Optimal

Untuk memahami lebih lanjut tentang kontrol optimal, berikut akan

diberikan contoh-contohnya dalam kehidupan sehari-hari. Contoh-contohnya

adalah sebagai berikut:

1. Lintasan Roket (David Burghes, 2004, 197; 203)

Sebuah roket meluncurkan satelit ke orbit sekitar bumi. Dalam hal ini

konsumsi bahan bakar. Variabel kontrolnya memilih sudut gaya dorong (Φ)

dan laju pancaran gas (β). Sudut gaya dorong merupakan sudut yang terbentuk antara poros roket dengan garis horisontalnya (dasar tanah). Kontrol

dalam masalah ini adalah untuk mempengaruhi perpindahannya, sehingga

dapat dibentuk persamaan gerak roketnya:

ext F mF dt dv

m   (3.3)

dengan m= massa roket

v = kecepatan roket

F= gaya dorong

F_ext= gaya luar

Gaya dorong roket dirumuskan dengan:

β m

c

F  (3.4)

dengan c= kecepatan pembuangan gas

β= laju pembakaran

Persamaan (3.3) kedua ruas dibagi dengan m menjadi

m F F dt dv F

mF dt dv

m ext

ext   



 (3.5)

Kemudian gaya dorong pada persamaan (3.4) disubstitusikan ke

m F m

β

c dt dv m

F F dt

dv _{ext ext}

  



 (3.6)

Peluncuran roket dengan sudut gaya dorong (Φ), v (v₁,v₂ ) dan

) mg , 0 (

F_ext   dapat digambarkan sebagai berikut:

Gambar 3.1: Peluncuran Roket

Sumber: Control And Optimal Control Theories With Applications, D.

Burghes & Alexander Graham

Diketahui sudut gaya dorong (Φ)dan gaya dorong roket pada persamaan (3.4), maka persamaan perpindahan roket menjadi dua persamaan.

Kedua persamaan tersebut diturunkan dari sumbu horisontal (x) dan sumbu

vertikal (y) sebagai berikut:

Φ

cos m

β

c dt dv₁

 (3.7i)

g

Φ

sin m

β

c dt dv₂



Persamaan (3.7.i) merupakan persamaan yang bersesuaian dengan

sumbu horizontal, sedangkan persamaan (3.7.ii) adalah persamaan yang

bersesuaian dengan sumbu vertikal. Persamaan (3.7.ii) dipengaruhi oleh gaya

gravitasi bumi, sehingga terdapat pengurangan g.

Uraian di atas membawa permasalahan tersebut untuk dituangkan

dalam rumusan masalah kontrol optimal sebagai berikut:

Fungsi obyektif: 



T

0 β dt

min J

dengan kendala:

g Φ sin m

β c dt dv

Φ cos m

β c dt dv

2 1

 



2. Produksi Barang (Suresh P. Sethi & Gerald L. Thompson, 2000, 4)

Dalam suatu proses produksi baja, akan diambil untuk masalah

kontrol optimalnya adalah meminimalkan jumlah biaya penyimpanan dan

produksi. Dalam hal ini, meminimalkan jumlah biaya penyimpanan dan

produksi dapat dihitung dengan memaksimalkan negatif dari jumlahan kedua

biayanya dalam interval waktu

 

0,T . Untuk variabel kontrolnya sendiri adalah

laju produksinya P(t). Dalam masalah ini ada permintaan S(t). Oleh karena

dalam proses produksi juga memperhatikan penyimpanannya, maka variabel

keadaannya adalah banyaknya penyimpanan I(t), yaitu banyaknya ton baja

) t ( S ) t ( P ) t ( I

.

 

Persamaan tersebut menjelaskan bahwa persediaan baja berubah dari

waktu ke waktu. Agar permintaan selalu dipenuhi, maka tidak diizinkan

backlogging yaitu selalu ada persediaan, sehingga I(t)0. Sedangkan untuk

tingkat produksi diberikan batasannya antara batas bawah P_min dan batas atas

max

P . Misalkan biaya penyimpanan persediaan baja h(t) dan biaya produksi

baja yaitu c(P), maka uraian di atas dapat dituangkan ke dalam masalah

kontrol optimal sebagai berikut

Fungsi obyektif: 



T







0

P h(I(t)) c(P(t)) max

J

dengan kendala

min

max min

.

I ) T ( I

0 ) t ( I

P ) t ( P P 0

) t ( S ) t ( P ) t ( I

 

 



 

C. Syarat Perlu Optimalitas

Misalkan menyelesaikan masalah kontrol optimal untuk kasus

memaksimalkan J(u). Diberikan suatu grafik kontrol optimal u* _{dan keadaan}

*

Gambar 3.2: Grafik kontrol optimal

Sumber: Optimal Control Applied To Biological Models, S. Lenhart & John T.

Workman

Diasumsikan terdapat suatu kontrol optimal yang fungsinya kontinu

sepotong-sepotong dengan u* sebagai kontrolnya dan x* _{fungsi keadaan. Oleh}

karena itu J(u)J(u*) _{untuk semua kontrol} u. Misalkan terdapat pula

suatu fungsi variasi h(t)yang kontinu sepotong-sepotong dan suatu konstanta

. R

ε Maka, penjumlahan dari fungsi u*(t) _{dan perkalian antara konstanta}

εdengan fungsi h(t) _{juga suatu fungsi kontrol yang kontinu sepotong-sepotong,}

) t ( h ε ) t ( * u ) t (

uε   . Dimisalkan xε _{keadaan yang terkait dengan kontrol} uε, maka xε _{memenuhi persamaan differensial sebagai berikut:}

)) t ( u ), t ( x , t ( g ) t ( x dt

d _{ε ε ε}

Seperti yang terlihat dari grafik di atas bahwa jika semua lintasan

Misalkan diberikan fungsi obyektif di uε:



akan ditentukan menggunakan Teorema Fundamental Kalkulus,maka:



λ(t)x (t)



dt λ(t )x (t ) λ(t )x (t )

Dengan menambahkan persamaan (3.10) dan persamaan (3.9) maka:

Menggunakan aturan perkalian pada turunan dan persamaan (3.8): menggunakan limit sebagai berikut:

ε menjadi

0 persamaan integral yang terakhir, maka dapat diperoleh:

Menerapkan aturan rantai ke fungsi f dan g, diperoleh:

Untuk menyederhanakan persamaan (3.12), dengan menghilangkan koefisien dari

0

maka dipilih fungsi tambahan λ(t)untuk memenuhi





kondisi batas

)

Sehingga, penyederhanaan dari persamaan (3.12) menjadi:





sepotong, maka berlaku pula untuk

))

Sehingga menghasilkan





yang mengakibatkan diperolehnya kondisi optimalitasnya

f 0

u

u(t,x*(t),u*(t)) λ(t)g (t,x*(t),u*(t)) 0 untuk semuat t t

f    

Persamaan tersebut membentuk syarat perlu yang dibutuhkan kontrol

optimal. Syarat perlu yang dibutuhkan kontrol optimal dapat diperoleh dari

persamaan Hamilton H yang didefinisikan sebagai berikut

) dan λ kontinu, sedangkan u kontinu sepotong-sepotong. Dengan

memaksimalkan H yang sehubungan dengan u _di u*, kondisi-kondisi kontrol

Kondisi optimalitas:

Persamaan tambahan:

)

Kondisi transversal:

0 ) t (

λ 1 

Dan diberikan persamaan keadaan

0

Teorema 3.1

Andaikan bahwa f(t,x,u) _dan g(t,x,u) _{yang keduanya fungsi yang}

terdifferensial secara kontinu dalam t,x,u dan cekung di u. Misalkan u* _kontrol

optimal untuk masalah (3.1) dan (3.2), dengan keadaan x*, dan λ adalah fungsi

Bukti:

H merupakan turunan persamaan Hamilton terhadap u seperti pada pembahasan

sebelumnya. Persamaan terakhir tersebut diperoleh berdasarkan teorema 2.1.

Karena H(t,x,u,λ) f(t,x,u)λg(t,x,u) maka

Persamaan terakhir menjadi

)

singgung, yaitu “Jika k adalah fungsi cekung dan terdifferensialkan, maka fungsi

Teorema tersebut berlaku untuk masalah memaksimalkan fungsi

obyektif. Akan tetapi, teorema tersebut juga berlaku untuk masalah

meminimalkan fungsi obyektif. Namun, perbedaannya terletak pada ketaksamaan

Hamiltonnya, yaitu

)) t ( λ ), t ( * u ), t ( * x , t ( H )) t ( λ ), t ( u ), t ( * x , t (

H 

Jika penyelesaian yang diperoleh dari perhitungan fungsi obyektif

menghasilkan nilai  atau -, maka dikatakan bahwa masalah tersebut tidak

mempunyai penyelesaian. Berikut diberikan teorema yang menyatakan

ketunggalan dari penyelesaian masalah kontrol optimal.

Teorema 3.2

Diketahui 



1

0

t

t f(t,x(t),u(t))dt )

u ( J

dengan kendala x'(t) g(t,x(t),u(t)), x(t0) x0

Andaikan bahwa f(t,x(t),u(t))dan g(t,x(t),u(t)) keduanya fungsi

yang terdifferensial secara kontinu dalam t,x,u dan cekung di x dan u.

Andaikan u* adalah kontrolnya, dengan keadaannya x*, dan λ fungsi yang

terdifferensial sepotong-sepotong, sedemikian sehingga u*, x*, dan λ terletak

pada interval t0 t t1:

. 0 ) t (

λ

, 0 ) t (

λ

), g

λ

f ( '

λ

, 0 g

λ

f

1

x x u u

 

  

 

Maka untuk semua kontrol u

) u ( J *) u (

Bukti:

Menggunakan teorema 2.1 pada bab sebelumnya, hal tersebut memberikan

dt

Substitusikan

*)

Ke persamaan (3.13), sehingga diperoleh





Sehingga untuk perhitungan terakhir diperoleh sebagai berikut

dt

Hasil yang terpenting dalam kontrol optimal adalah prinsip

Teorema 3.3

Andaikan u* adalah kontrol optimal, dan menghasilkan keadaan x*,

untuk masalah



 1

0

t

t u

u J(u) max f(t,x(t),u(t))dt max

dengan kendala

. x ) t ( x )), t ( u ), t ( x , t ( g ) t ( '

x  ₀  ₀ (3.14)

Misalkan

^

t adalah titik tetap sedemikian sehingga t t t1. ^

0   Maka,

fungsi-fungsi terbatas

      

1 ^

t , t * ^

*

u

u ,

      

1 ^

t , t * ^

*

x

x , bentuk pasangan optimal untuk

masalah



 1

0

t

t u ^

u J(u) max f(t,x(t),u(t))dt

max

dengan kendala

). t ( x ) t ( x )), t ( u ), t ( x , t ( g ) t ( ' x

^ * ^



 (3.15)

Jika u* _{kontrol optimal tunggal untuk (3.14), maka}

^ *

u _kontrol

optimal tunggal untuk (3.15).

Bukti:

Diketahui bahwa u* kontrol optimal tunggal untuk (3.14). Akan dibuktikan

bahwa

^ *