LAPORAN PRAKTIKUM GELOMBANG LISSAJOUS

(1)

LAPORAN PRAKTIKUM GELOMBANG LISSAJOUS

Disusun oleh:

Nama : Ibnu Fitriatmoko (4201412101) Teman Kerja : 1. Erni Sri Purnami (4201412080) 2. Ida Sudarwati (4201412082) Dosen : Sarwi

Budi Astuti

JURUSAN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI SEMARANG

(2)

PERPADUAN GETARAN LISSAJOUS

A. TUJUAN

Eksperimen Lissajous ini bertujuan untuk:

1. Memperoleh berbagai macam bentuk kurva Lissajousdengan variasi frekuensi dan amplitudo

2. Membandingkan bentuk kurva Lissajous yang diperoleh dari eksperimen dengan bentuk kurva Lissajous teori

B. LANDASAN TEORI

Pada pertengahan abad 19, seorang fisikawan Perancis yang bernama Jules Antoine Lissajous (1822–1880) sangat tertarik pada bentuk persamaan parametrik berikut ini:

x(t) _{= A sin}

(

2π f_At+δ_A

₎

y(t)=Bsin

₍

2π f_Bt+δ_B)

Beliau mengembangkan fungsi tersebut pada suatu pembelajaran tentang getaran dengan menggabungkan dua gerakan sinusoidal yang saling tegak lurus. Persamaan diatas menggambarkan adanya getaran sinusoidal pada sumbu x dengan frekuensi a/2 π dan getaran sinusoidal pada sumbu y dengan frekuensi b/2 π. Jika nilai perbandingan antara a dengan b adalah bilangan rasional, maka akan menghasilkan efek getaran yang bergerak sepanjang lintasan kurva, yang dikenal dengan kurva Lissajous. Berikut ini akan diberikan perbandingan gambar kurva Lissajous dengan perbedaan konstanta a dan b sesuai dengan ilustrasi

(3)

Diperlukan variasi perbandingan konstanta, maupun parameter nilai lainnya (termasuk proses modifikasi persamaan parametrik) pada persamaan kurva Lissajous sehingga menghasilkan bentuk pola gambar yang cukup indah dan variatif.

Kurva Lissajous dapat dihasilkan dengan menggunakan osiloskop. Dua masukan sinusoida berbeda fase diterapkan pada osiloskop dalam mode XY dan hubungan antara fase dan sinyal disebut sebagai kurva Lissajous. Pada osiloskop, kita menganggap x dan y adalah channel 1 dan channel 2. Dimana A adalah amplitudo channel 1 dan B adalah amplitudo channel 2, fA adalah frekuensi channel 1 dan fB adalah frekuensi channel 2,

sehingga a: b adalah perbandingan frekuensi kedua saluran, dan δ adalah beda fase. Jika gambar Lissajous pada osiloskop, menampilkan 03:01 iniberarti hubungan antara frekuensi vertikal dan input sinusoidal horisontal.

(4)

Bila fA=fB dan δA=δB , maka kurva lissajous yang tampak akan memenuhi persamaan: y=B A x Bila

|

φA−φB

|

= π

2 maka akan berbentuk pola elips yang memenuhi persamaan

(

x A

)

2 +

(

y B

)

2 = 1 Bila

|

φA−φB

|

= π

2 dan A = B = R maka pola elips akan menjadi pola berbentuk lingkaran dengan persamaan

x2

+y2

=R2

Selain bentuk sederhana tersebut muncul pula banyak bentuk lain yang secara umum dapat dinyatakan dengan fungsi-fungsi sendiri.

Gambar. Pola Lissajous dengan f_y=2f_x, φ_A=φ_Bdan A=B

Untuk kasus dalam gambar di atas dapat dituliskan bentuk fungsinya adalah y=2

A x

2

−A

yang merupakan persamaan kuadrat.

(5)

Gambar 3. Berbagai pola lissajous

Keterangan: a = fy dan b = fx

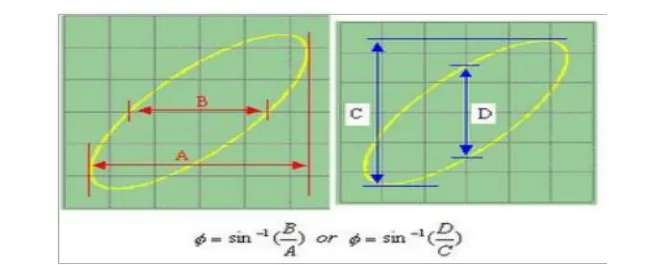
Beda fase antara dua getaran pembentuk kurva lissajous dapat ditentukan dengan persamaan berikut ini.

(6)

Persamaan tersebut adalah rumus untuk kurva yang lingkarannya serong ke kanan. Untuk kurva lissajous yang lingkarannya serong ke kiri, diperlihatkan pada gambar dibawah ini:

Gambar 5. Cara menghitung beda fase untuk kurva yang serong ke kiri

C. ALAT DAN BAHAN

Alat dan bahan yang digunakan dalam eksperimen Lissajous yaitu: 1. 1 buah Osiloskop

2. 2 buah Audio Frequency Generator (AFG) 3. 2 buah kabel probe

4. Transparansi 5. Spidol permanen D. LANGKAH KERJA

Langkah kerja pada eksperimen Lissajous yaitu: 1. Mengkalibrasi osiloskop

2. Menghubungkan AFG 1 pada channel Adan menghubungkan AFG 2 pada channel B menggunakan kabel probe

3. Mengatur AFG 1 dengan frekuensi sebesar 1 Hz dan amplitudo sebesar 2 Vpp danAFG 2 dengan frekuensi sebesar 1.5 Hz dan amplitudo sebesar 1 Vpp

(7)

5. Memvariasikan AFG 1 dan AFG 2 dengan nilai frekuensi dan amplitudo sebagai berikut: No AFG 1 AFG 2 f (Hz) A (Vpp) f (Hz) A (Vpp) 1 100 1 200 2 2 100 1 200 0.5 3 300 1 100 2 4 200 2 200 1.5 5 50 1.5 250 1.5 6 300 1.5 400 2 E. DATA PENGAMATAN F. ANALISIS DATA

(8)

G. PEMBAHASAN

Pada percobaan ini tujuannya adalah untuk memperoleh berbagai bentuk kurva lissajous dengan memvariasi frekuensi dan amplitude dan selanjutnya menggambar dengan cara manual dan membandingkan hasilnya dengan hasil yang diperoleh dari eksperimen. Lissajous adalah superposisi dari dua buah gelombang dengan syarat dua gelombang tersebut saling tegak lurus ( membentuk sudut 900_).

Dalam percobaan dengan memvariasikan frekuensi dan amplitude digunakan variasi data sebagai berikut :

(9)

2. fch2 : fch1 = 2 : 1 , Ach2 : Ach1 = 0.5 : 1 3. fch2 : fch1 = 1 : 3 , Ach2 : Ach1 = 2 : 1 4. fch2 : fch1 = 1 : 1 , Ach2 : Ach1 = 1.5 : 2 5. fch2 : fch1 = 5 : 1 , Ach2 : Ach1 = 1.5 : 1.5 6. fch2 : fch1 = 4 : 3 , Ach2 : Ach1 = 2 : 1.5

dari variasi di atas maka didapatkan bentuk kurva lissajous secara praktikum. Untuk membuktikan kebenaran dari bentuk lissajous secara praktikum maka dilakukan perbandingan bentuk dengan gambar lissajous dilukis secara manual. Untuk menghitung beda fase pada gambar lissajous digunakan rumus: jika kurva miring ke kanan besarnya

beda fase = arcsin x_x1

2 dan jika kurva miring ke kiri besarnya beda fase =

180−arcsinx1

x2 (jika perhitungan x sulit, gunakan y). Saat penggambaran secara manual

menempatkan lingkaran pada posisi kiri sebagai Ch 2 dan lingkaran pada posisi bawah sebagai Ch 1.

Untuk data pertama yaitu fch2 : fch1 = 2 : 1 , Ach2 : Ach1 = 2 : 1 , maka didapatkan hasil banyaknya gelombang pada sumbu y 1 gelombang atau tonjolan dengan panjang 4 cm dan pada sumbu x 2 gelombang atau tonjolan dengan panjang 2 cm. Dari bentuk lissajous yang kami dapat dari praktikum ternyata tedapat beda fase antara keduanya yaitu sebesar 1530_. Maka dari sini setelah dilakukan penggambaran secara manual didapatkan bentuk yang sama antara hasil praktikum dengan manual.

Untuk data yang kedua yaitu fch2 : fch1 = 2 : 1 , Ach2 : Ach1 = 0.5 : 1 , maka didapatkan hasil banyaknya gelombang pada sumbu y 1 gelombang atau tonjolan dengan panjang 1 cm dan pada sumbu x 2 gelombang atau tonjolan dengan panjang 2 cm. Dari bentuk lissajous yang kami dapat dari praktikum ternyata tedapat beda fase antara keduanya yaitu sebesar 190_{. Maka dari sini setelah dilakukan penggambaran secara manual didapatkan bentuk} yang sama antara hasil praktikum dengan manual.

Untuk data yang ketiga yaitu fch2 : fch1 = 1 : 3 , Ach2 : Ach1 = 2 : 1, maka didapatkan hasil banyaknya gelombang pada sumbu y 3 gelombang atau tonjolan dengan panjang 4 cm dan pada sumbu x 1 gelombang atau tonjolan dengan panjang 2 cm. Dari bentuk lissajous yang kami dapat dari praktikum ternyata tedapat beda fase antara keduanya yaitu sebesar 300_. Maka dari sini setelah dilakukan penggambaran secara manual didapatkan bentuk yang sama antara hasil praktikum dengan manual.

(10)

Untuk data yang keempat yaitu fch2 : fch1 = 1 : 1 , Ach2 : Ach1 = 1.5 : 2 , maka didapatkan hasil banyaknya gelombang pada sumbu y 1 gelombang atau tonjolan dengan panjang 3 cm dan pada sumbu x 1 gelombang atau tonjolan dengan panjang 4 cm. Dari bentuk lissajous yang kami dapat dari praktikum ternyata tedapat beda fase antara keduanya yaitu sebesar 1570_{. Maka dari sini setelah dilakukan penggambaran secara manual didapatkan bentuk} yang sama antara hasil praktikum dengan manual.

Untuk data kelima yaitu fch2 : fch1 = 5 : 1 , Ach2 : Ach1 = 1.5 : 1.5 , maka didapatkan hasil banyaknya gelombang pada sumbu y 1 gelombang atau tonjolan dengan panjang 3 cm dan pada sumbu x 5 gelombang atau tonjolan dengan panjang 3 cm. Dari bentuk lissajous yang kami dapat dari praktikum ternyata tedapat beda fase antara keduanya yaitu sebesar 1720_. Maka dari sini setelah dilakukan penggambaran secara manual didapatkan bentuk yang sama antara hasil praktikum dengan manual.

Untuk data keenam yaitu fch2 : fch1 = 4 : 3 , Ach2 : Ach1 = 2 : 1.5 , maka didapatkan hasil banyaknya gelombang pada sumbu y 3 gelombang atau tonjolan dengan panjang 4 cm dan pada sumbu x 4 gelombang atau tonjolan dengan panjang 3 cm. Dari bentuk lissajous yang kami dapat dari praktikum ternyata tedapat beda fase antara keduanya yaitu sebesar 360_. Maka dari sini setelah dilakukan penggambaran secara manual didapatkan bentuk yang sama antara hasil praktikum dengan manual.

Dari analisis bentuk lissajous di atas, maka pada intinya bentuk dari kurva lissajous dipengaruhi oleh 3 faktor yaitu frekuensi, amplitude, dan beda fase. Untuk faktor pertama yaitu frekuensi akan berpengaruh pada bentuk dari lissajous. Misal diketahui f1 : f2 = 2 : 3, maka bentuk dari lissajousnya pada sumbu y terdapat 3 gelombang atau tonjolan dan pada sumbu x terdapat 2 gelombang atau tonjolan. Untuk faktor yang kedua yaitu amplitude akan berpengaruh pada panjang dan lebar dari lissajous. Misal diketahui A1 : A2 = 3 : 4 , maka akan dihasilkan pada sumbu y lebarnya 6 cm dan pada sumbu x panjangnya 8 cm. Untuk beda fase akan berpengaruh pada letak perpotongan pada bagian tengah lissajous. H. KESIMPULAN

Dari hasil praktikum dapat disimpulkan sebagai berikut:

1. Bentuk dari kurva lissajous dipengaruhi oleh 3 faktor, yaitu frekuensi, amplitude dan beda fase. Frekuensi akan berpengaruh pada bentuk dari lissajous. Amplitudo akan berpengaruh pada panjang dan lebar dari lissajous. Untuk beda fase akan berpengaruh pada letak perpotongan pada bagian tengah lissajous.

(11)

DAFTAR PUSTAKA

Adiyasa, I Wayan.2011. Lissajous. http://project-electro.blogspot.com/2011/11/lissajous-ini-adalah-bagian-ke-dua-dari.html. 22 Maret 2014 (20:02 WIB)

Asari, Wachid. 2009. Generator Watermark yang Unik Berdasarkan Nomor Dokumen. Tesis. Program Pascasarjana Institut Teknologi Sepuluh Nopember. Surabaya

IOSR Journal of Engineering. 2012. Geometrical and Graphical Representations Analysis of Lissajous Figures in Rotor Dynamic System. 2(5): 971-977

(12)

Terr, David. -. Parametric Equations.

http://www.mathamazement.com/Lessons/Pre-Calculus/09_Conic-Sections-and-Analytic-Geometry/parametric-equations.html. 25 Maret 2014 (11:00 WIB)