Bab 1 Vektor
Dalam mempelajari kelistrikan dan kemagnetan, kita selalu bekerja dengan besaran-besaran yang perlu dideskripsikan dengan besar (magnitude) dan arahnya (direction). Besaran seperti ini disebut vektor. Terlebih dahulu kita akan meninjau sifat-sifatnya. Dengan menggunakan notasi dan termino-logi yang dibuat di sini, maka kita akan dapat menyatakan suatu hasil secara lebih kompak dan kita dapat memahami arti fisis dasarnya secara lebih mudah.
1-1 Definisi Vektor
Sifat-sifat pergeseran sebuah titik memberikan makna yang kita perlukan dalam mendefinisikan vektor. Jika kita bergerak dari suatu titik P1 melalui lintasan sembarang ke titik lain P2, maka seperti kita lihat pada Gambar 1-1 bahwa efek gerakan ini sama seperti jika titik tadi bergerak secara langsung menurut garis lurus D dari P1 ke P2 seperti ditunjukkan oleh arah anak panah. Garis D ini menyatakan pergeseran dan dicirikan oleh besarnya (panjang) dan arahnya (dari P1 ke P2). Jika kemudian kita menggeser titik tadi sepanjang E dari P2 ke titik lain P3, maka kita lihat pada Gambar 1-2 bahwa efek akhirnya sama seperti jika titik tersebut mengalami pergeseran tunggal F dari P1 ke P3. Dengan demikian, kita dapat menyatakan bahwa F sebagai resultan, atau jumlahan, dari pergeseran-pergeseran D dan E yang berurutan; jadi Gambar 1-2 menunjukkan cara yang mendasar bagaimana pergeseran-pergeseran digabungkan atau dijumlahkan untuk memperoleh resultannya.
Gambar 1-1. Garis berarah D adalah pergeseran titik dari P1 ke P2.
Gambar 1-2. Pergeseran F adalah resultan dari pergeseran D dan pergeseran E.
Gambar 1-3. Kedua vektor A dan A adalah sama.
Sebuah vektor merupakan perluasan dari tinjauan tersebut di atas, yaitu didefinisikan sebagai besaran yang memiliki sifat matematis yang sama seperti pergeseran sebuah titik. Jadi, sebuah vektor memiliki besar; vektor memiliki arah; dan penjumlahan dua vektor yang memiliki sifat intrinsik yang sama mengikuti aturan dasar yang diilustrasikan dalam Gambar 1-2. Dengan dua sifat pertama tersebut, kita dapat mewakilkan sebuah vektor dengan sebuah garis berarah seperti telah digunakan untuk pergeseran. Dalam buku ini, sebuah vektor dilambangkan oleh sebuah huruf dengan tanda anak panah di atasnya, seperti A; sedangkan besarnya dilambangkan oleh A atau A .
Sebuah skalar adalah besaran yang hanya memiliki besar. Sebagai contoh, massa suatu benda adalah sebuah skalar, sedangkan beratnya, yaitu gaya gravitasional yang bekerja pada benda, adalah sebuah vektor.
Karena sifat alami sebuah vektor sebagai besaran yang memiliki arah, maka pergeseran sejajar sebuah vektor tidaklah mengubah vektor tersebut. Dengan kata lain, dua buah vektor dikatakan sama jika keduanya memiliki besar dan arah yang sama. Hal ini diilustrasikan oleh Gambar 1-3 di mana A A. Sekarang kita dapat menyelidika operasi-operasi matematika apa saja yang dapat kita lakukan pada dan dengan besaran vektor.
Selanjutnya, kita dapat menyelidiki operasi matematis apa saja yang dapat kita lakukan dengan dan pada vektor.
I-2 Penjumlahan Vektor
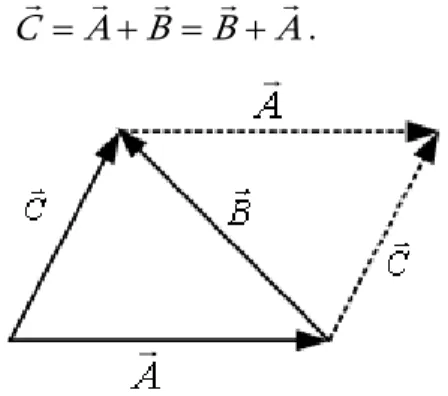
Berdasarkan pada aturan dasar di atas, jika kita punya vektor A dan dijumlahkan dengan vektor B, maka kita memperoleh vektor jumlahan C seperti ditunjukkan oleh garis utuh pada Gambar 1-4. Kita juga dapat melihat bahwa jika
memperoleh vektor C yang sama. Jadi, penjumlahan vektor-vektor memiliki sifat bahwa A B B A C . (1-1)
Gambar 1-4. Jumlahan dua vektor tidak bergantung pada urutan penjumlahan.
Dengan cara serupa seperti di atas, kita dapat memperoleh sifat asosiatif penjumlahan vektor:
A B
C A
B C
A C
BD , (1-2) dan seterusnya.
Jika kita membalik arah suatu pergeseran, seperti pergeseran D dalam Gambar 1-1 dengan menggambarnya lagi dalam arah berlawanan, maka efek akhirnya adalah tidak terdapat pergeseran. Dengan demikian, kita dapat men-definisikan negatif suatu vektor sebagai sebuah vektor yang memiliki besar yang sama tetapi berlawanan arah dengan vektor tadi, sehingga kita memper-oleh
A OA , seperti yang kita inginkan. Jadi kita dapat dengan mudah mengurangkan suatu vektor dengan vektor lain dengan cara menambahkannya dengan negatif vektor lain tersebut:
B AB
A (1-3)
Perkalian sebuah skalar s dengan sebuah vektor, kita tulis sebagai sA atau s
A , semata-mata adalah jumlahan s buah vektor A, atau merupakan sebuah vektor yang besarnya adalah s kali besar vektor A, dan memiliki arah yang sama dengan arah vektor A jika s positif, serta memiliki arah yang berlawanan dengan arah vektor A jika s negatif.
I-3 Vektor Satuan
Sebuah vektor satuan didefinisikan sebagai sebuah vektor yang besarnya sama dengan satu dan dilambangkan dengan sebuah huruf dengan tanda seperti “topi” di atasnya, misalnya eˆ . Vektor satuan tidak berdimensi se-
Gambar 1-5. Vektor satuan aˆ dalam arah vektor A.
Gambar 1-6. Vektor-vektor satuan dalam sistem koordinat tegak lurus.
hingga kita punya eˆ 1. Sebagai contoh, jika sebuah vektor satuan aˆ dipi-lih memiliki dalam arah vektor A, maka kita dapat menulis
aˆ A A dan A A aˆ . (1-4)
Hal ini diilustrasikan oleh Gambar 1-5.
Vektor-vektor satuan dalam sistem koordinat tegak lurus biasanya ditu-liskan sebagai xˆ , yˆ , dan zˆ , yang berturut-turut berkaitan dengan arah sumbu- sumbu x, y, dan z, seperti ditunjukkan oleh Gambar 1-6. Dengan kata lain, masing-masing vektor satuan tersebut memiliki arah sesuai pertambahan nilai koordinat yang bersangkutan. Ketiga vektor satuan ini saling tegak lurus satu dengan yang lainnya.
Sebagaimana akan kita lihat, kita perlu juga mendefinisikan vektor-vektor satuan lainnya sehingga lebih memudahkan dan menguntungkan.
I-4 Vektor Komponen dan Komponen Vektor
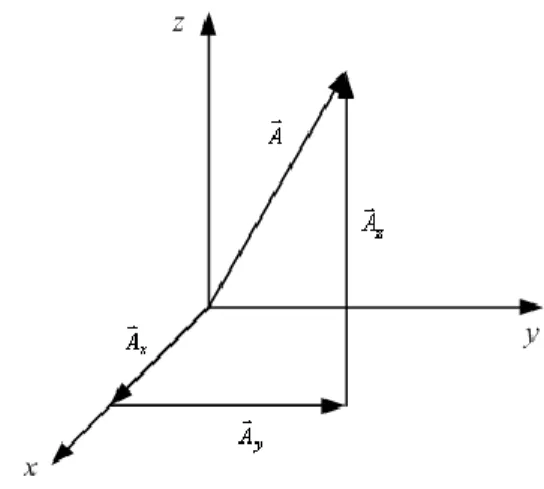
Untuk pembahasan lebih jauh, vektor akan lebih mudah jika dirujuk pada suatu sistem koordinat. Pada Gambar 1-7 kita dapat melihat bahwa kita dapat menulis sebuah vektor A sebagai jumlahan tiga buah vektor yang dipilih dengan benar, masing-masing sejajar dengan salah satu sumbu sistem koordi-
Gambar 1-7. Vektor A adalah jumlahan vektor-vektor komponen tegak lurus.
nat tegak lurus, yaitu A Ax Ay Az. Tetapi akan sangat berguna jika kita menuliskan tiap suku penjumlahan itu sebagai perkaian sebuah skalar dengan vektor-vektor satuan pada Gambar 1-6. Jadi kita menulis vektor komponen
x ˆ x x A
A dan seterusnya, dan ungkapan di atas tadi menjadi zˆ y ˆ x ˆ y z x A A A A . (1-5)
Ketiga skalar Ax, Ay, dan Az disebut komponen-komponen vektor A
; dan oleh karena itu sebuah vektor dapat dicirikan oleh tiga buah bilangan. Komponen vektor dapat positif maupun negatif; sebagai contoh, jika Ax negatif, maka vektor
x
A pada Gambar 1-7 akan memiliki arah menuju penurunan nilai x.
Pada Gambar 1-7 terlihat bahwa besar sebuah vektor dapat dinyatakan dalam komponen-komponennya sebagai
2 2 2 z y x A A A A A . (1-6)
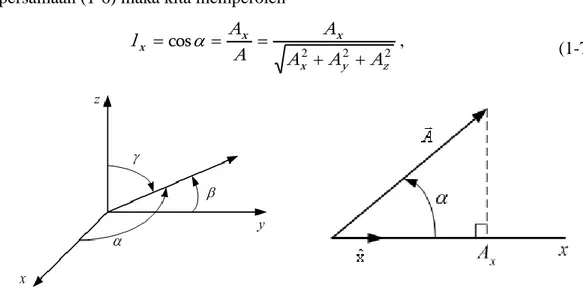
Gambar 1-8 melukiskan kenyataan bahwa vektor A membentuk sudut tertentu dengan tiap sumbu sistem koordinat; sudut-sudut ini , , dan disebut
sudut-sudut arah vektor A dan diukur dari arah positif sumbu-sumbu yang bersangkutan. Gambar 1-9 memperlihatkan bidang yang memuat A dan xˆ , dan kita lihat bahwa Ax A cos. Dengan menggabungkan ungkapan ini dengan persamaan (1-6) maka kita memperoleh
2 2 2 z y x x x x A A A A A A l cos , (1-7)
Gambar 1-8. Definisi sudut-sudut arah sebuah vector
Gambar 1-9. Skalar Ax adalah
komponen vektor A.
dengan lx disebut cosinus arah. Ungkapan yang serupa dengan ini juga berlaku
untuk kedua sudut arah dan serta cosinus arah yang terkait denganya yaitu ly
dan lz, sehingga kita lihat dari persamaan-persamaan (1-6) dan (1-7) bahwa jika
kita mengetahui komponen-komponen tegak lurus sebuah vektor, maka kita dapat menghitung besar vektor tersebut dan menentukan arahnya.
Jika kita menggabungkan persamaan-persamaan (1-4), (1-5) dan (1-7), maka kita temukan bahwa vektor satuan aˆ dapat juga ditulis sebagai
zˆ y ˆ x ˆ aˆlx ly lz , (1-8)
dan komponen-komponen dari suatu vektor satuan tidak lain adalah sudut-sudut arah vektor satuan tersebut. Jika sekarang kita menerapkan hasil umum persamaan (1-6) pada vektor khusus aˆ , maka kita memperoleh hubungan penting yang melibatkan cosinus arah, yaitu
1 2 2 2 z y x l l l (1-9)
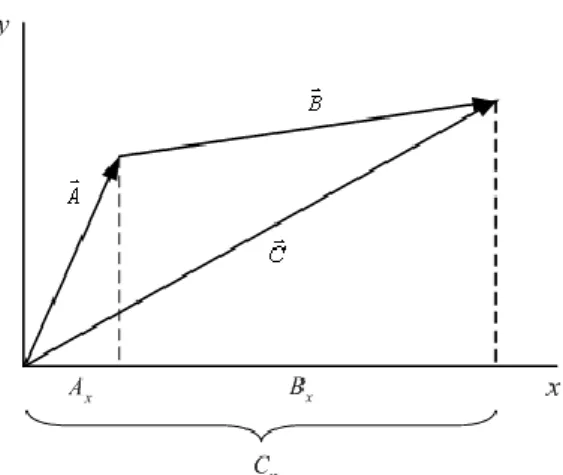
Penjumlahan vektor yang telah diilustrasikan oleh Gambar 1-4 dapat dengan mudah diungkapkan dalam komponen-komponen tegak lurusnya. Pada Gambar 1-10 kita dapat melihat bahwa sebuah komponen dari vektor jumlahan
B A
C diberikan oleh jumlahan komponen-komponen yang terkait, yaitu x
x
x A B
Gambar 1-10. Sebuah komponen dari suatu vektor jumlahan sama dengan jumlahan komponen-komponen yang bersangkutan dari vektor-vektor yang dijumlahkan.
I-5 Vektor Letak
Sekarang kita tinjau contoh sederhana suatu vektor. Seperti diperlihat-kan oleh Gambar 1-11, lokasi atau letak sebuah titk P di dalam ruang dapat dicirikan oleh vektor r yang dilukis dari titik asal sistem koordinat; vektor r ini disebut vektor letak titik. Dalam sistem koordinat tegak lurus pada Gambar 1-6, komponen-komponen vektor r tidak lain adalah koordinat (x, y, z) titik yang ditinjau; jadi kita punya
zˆ y ˆ x ˆ y z x r . (1-11)
Demikian pula, letak titik lain P dengan koordinat (x, y, z) ditunjukkan oleh vektor letak rxxˆyˆxzzˆ seperti pada Gambar 1-12. Sampai di
Gambar 1-11. Vektor r adalah vektor letak titik P.
Gambar 1-12. Vektor Radalah vektor letak relatif P terhadap P.
sini kita telah meyatakan letak dua titik secara sendiri-sendiri. Kita dapat juga menyatakan letak titik P relatif terhadap titik P dengan cara menggambar sebuah vektor dari P ke P; vektor R ini disebut vektor letak relatif titik P terhadap titik P. Kita lihat pada Gambar 1-12 bahwa rR r sehingga
r r
R . (1-12)
Dengan menggunakan persamaan-persamaan (1-10) dan (1-11) kita dapat menulis R dalam bentuk komponen sebagai
x x
xˆ
y y
yˆ
z z
zˆR (1-13)
dan oleh karena itu
2
2
2 z z y y x x R (1-14)karena persamaan (1-6). Kita akan cukup sering menggunakan hasil-hasil ini. Kita perlu catat bahwa letak relatif P terhadap P dinyatakan oleh vektor R yang dilukis dari P ke P, dan kenyataannya RR.
Meskipun kita tidak mencirikan sistem koordinat kita selain mengata-kan bahwa kita telah memilihnya secara sembarang dan untuk kemudahan, begitu suatu pilihan ini diambil untuk suatu kasus tertentu, maka sistem koordinat dikatakan “tetap di dalam ruang” dan vektor-vektor satuannya xˆ , yˆ, dan zˆ memiliki besar dan arah yang tetap. Dengan kata lain, sistem koordinat yang tetap yang kita gunakan singkatnya merupakan salah satu kerangka acuan inersial yang telah biasa kita gunakan dalam mekanika klasik.
1-6 Perkalian Skalar
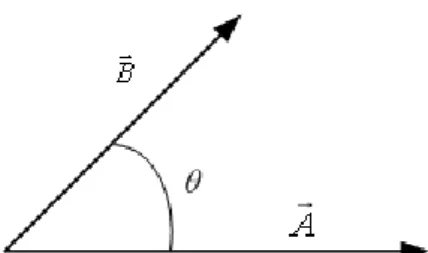
Kita mendefinisikan perkalian skalar (scalar product) antara dua buah vektor sebagai sebuah skalar yang sama dengan perkalian besar kedua vektor dan cosinus sudut antara kedua vektor tersebut, yaitu
cos AB B
A . (1-15)
Karena notasi yang digunakan, perkalian skalar disebut juga sebagai perkalian titik (dot product).
Kita lihat pada Gambar 1-13 bahwa kita dapat memperoleh interpretasi
Gambar 1-13. Sudut antara dua vektor yang dilibatkan dalam perkalian skalar AB.
dikalikan dengan besar vektor A, =
Acos
B = komponen A sepanjang B dikalikan dengan besar vektor B.Tampak jelas pada persamaan (1-15) bahwa perubahan urutan faktor perkalian skalar tidak mengubah hasil perkalian tersebut, yaitu
A B B
A (1-16)
dan jika kedua vektor saling tegak lurus maka AB0 dan sebaliknya. Selanjutnya, kuadrat suatu vektor dapat diinterpretasikan sebagai perkalian titik vektor tersebut dengan dirinya sendiri; hasilnya adalah kuadrat besar vektor tersebut dan kita dapat menulisnya sebagai
2 2 A A A
A . (1-17)
Jika kita telah mengetahui komponen-komponen tegak lurus dari A dan B, maka tidaklah nyaman bila kita menghitung AB dengan persamaan (1-15) karena kita harus mencari sudut antara A dan B. Untungnya, kita dapat mengungkapkan AB secara langsung dalam komponen-komponen tegak lurusnya. Karena sudut antara tiap pasang vektor satuan yang telah didefinisikan di dalam Gambar 1-6 adalah 90, maka dari persamaan (1-15) kita dapat dengan mudah memperoleh bahwa
0 yˆ yˆ zˆ zˆ xˆ x ˆ (1-18)
dan dari persamaan (1-17) bahwa
1 xˆ yˆ yˆ zˆ zˆ x ˆ . (1-19)
Dengan menulis masing-masing A dan B dalam bentuk persamaan (1-5), ma-ka kita dapat mengalikan keduanya suku per suku untuk memperoleh
Axˆx Ayyˆ Azzˆ
Bxˆx Byˆy Bzzˆ
BA
AxBxˆxˆxAxByxˆˆyAxBzˆxzˆ,
dan dengan menggunakan persamaan-persamaan (1-18) dan (1-19) untuk menyederhanakan kesembilan sukunya, maka kita dapat memperoleh bahwa
z z y y x xB A B A B A B A . (1-20)
Sekarang anggap eˆ adalah sebuah vektor satuan dalam suatu arah tertentu. Jika kita pilih Ae sebagai komponen A
sepanjang arah ini, maka tampak dari persamaan (1-15) bahwa eˆ A Ae . (1-21) 1-7 Perkalian Vektor
Perkalian vektor (vector product) disebut juga perkalian silang (cross product) dan ditulis sebagai AB. Hasil perkalian vektor jenis ini adalah sebuah vektor yang tegak lurus terhadap kedua vektor A dan B, besarnya didefinisika sebagai sin AB B A . (1-22)
Arah vektor ini ditentukan dengan aturan tangan kanan: jika jemari tangan kanan kita ditekuk dalam arah rotasi A melalui sudut kecil menujuB, maka jempol kita menunjuk arah AB. Aturan ini diilustrasikan oleh Gambar 1-14.
Jika kita memperhatikan bidang yang memuat A dan B yang ditun-jukkan oleh Gambar 1-15, maka kita dapat memperoleh interpretasi sederhana dari perkalian silang. Kita dapat melihat pada gambar tersebut dan persamaan (1-22) bahwa besar hasil perkalian silang sama dengan luas jajaran genjang dengan
A dan B sebagai sisi-sisinya.
Dari definisi arah vektor hasil perkalian silang yang ditunjukkan oleh Gambar 1-14, jelas bahwa urutan vektor-vektor yang diperkalikan adalah penting, karena tampak bahwa
A B
A
Gambar 1-14. Definisi arah vektor hasil perkalian silang dua vektor.
Gambar 1-15. Interpretasi besar vektor hasil perkalian silang dua vektor.
Jika A dan B sejajar, maka menurut persamaan (1-22) jelas bahwa 0 B
A , dan sebaliknya. Secara khusus,
0 A A . (1-24)
Untuk vektor-vektor satuan sepanjang sumbu-sumbu yang diperlihat-kan oleh Gambar 1-6, jika kita menggunakan persamaan (1-22), aturan tangan kanan, kenyataan-kenyataan bahwa vektor-vektor satuan tersebut saling tegak lurus, dan bahwa vektor hasil perkalian silang tegak lurus terhadap kedua vektor yang diperkalikan, maka kita memperoleh
zˆ y ˆ x
ˆ , yˆzˆˆx, zˆxˆyˆ, (1-25)
dan dengan persamaan (1-24) bahwa
0 xˆ yˆ yˆ zˆ zˆ x ˆ . (1-26)
Perkalian vektor dapat juga dengan baik ditulis dalam komponen-komponen tegak lurus. Dengan langkah yang serupa dengan yang telah kita lakukan dalam memperoleh persamaan (1-20), kita dapat menulis A dan B dalam bentuk ungkapan (1-5), kemudian mengalikan keduanya suku per suku, dan dengan menggunakan persamaan-persamaan (1-23), (1-25), dan (1-26) untuk menyederhanakan hasilnya. Kita memperoleh bahwa
AyBz AzBy
xˆ
AzBx AxBz
yˆ
AxBy AyBx
zˆ BA . (1-27)
Ungkapan ini dapat juga ditulis dalam bentuk sebuah determinan yang mudah diingat z y x z y x B B B A A A B A zˆ y ˆ xˆ . (1-28)
Dapat dibuktikan bahwa
z y x z y x z y x C C C B B B A A A C B A C B A (1-29) dan
B C
B A C C A B A . (1-30)Dalam persamaan (1-29) kita melihat bahwa tanda titik dan tanda silang dapat dipertukarkan tanpa mempengaruhi nilai perkalian skalar triple ini; oleh karena itu
rangkap tiga (triple) pada persamaan (1-30), tanda kurung menjadi penting karena
B C
A = C
AB
dengan menggunakan persamaan (1-23). Pembagian antara vektor tidak didefinisikan.1-8 Differensiasi Vektor terhadap Skalar
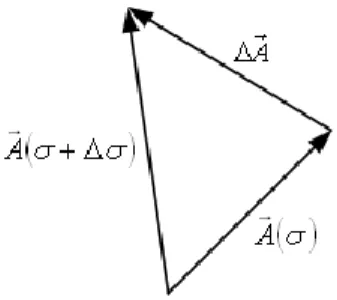
Anggap bahwa A merupakan fungsi kontinyu dari suatu variabel skalar sehingga kita dapat menulis AA
. Hal ini setara dengan ketiga persamaan skalar Ax Ax
, Ay Ay
, dan Az Az
. Jika berubah menjadi + , maka secara umum A berubah baik dalam arah maupun besarnya seperti ditunjukkan oleh Gambar 1-16. Perubahan A adalah AA
A
. Kemudian kita dapat mendefinisikan derivatif vektor A terhadap sebuah skalar sebagai berikut:
A A A d A d 0 lim 0 lim . (1-31)Proses ini telah menghasilkan vektor lain dari suatu vektor. Contoh-contoh untuk persamaan (1-31) yang telah akrab dengan kita adalah kecepatan dan percepatan sebuah partikel yang merupakan derivatif berurut vektor letak terhadap waktu.
Gambar 1-16. A adalah perubahan vektor A yang berkaitan dengan perubahan skalar .
Jika A ditulis dalam komponen-komponen tegak lurusnya seperti dalam persamaan (1-5), dan karena vektor-vektor satuannya tetap, maka dari persamaan (1-31) dapat terlihat bahwa komponen-komponen dari derivatif adalah derivatif-darivatif komponen yang bersangkutan, dan kita punya
zˆ y ˆ xˆ d dA d dA d dA d A d x y z . (1-32)
Begitu kita telah mendefinisikan derivatif A, maka kita dapat melangkah ke diferensial dA yang digunakan untuk mewakili perubahan infinitesimal pada A. Hal ini diperoleh dengan mengalikan persamaan (1-32) dengan d untuk menghasilkan zˆ y ˆ x ˆ y z x dA dA dA A d . (1-33)
Dengan menerapkan hasil ini pada vektor letak persamaan (1-11) maka kita memperoleh zˆ y ˆ x ˆ dy dz dx r d . (1-34) 1-9 Gradien Skalar
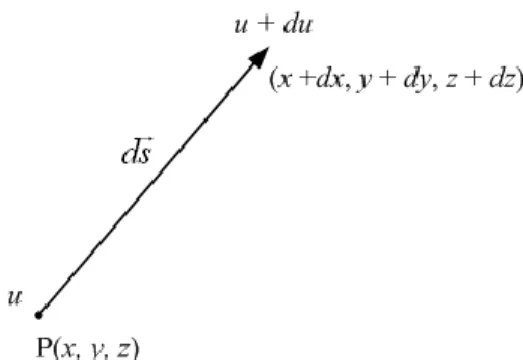
Anggap kita punya sebuah besaran skalar u yang merupakan fungsi letak sedemikian sehingga kita dapat menulis u u
x,y,z
. Situasi seperti ini disebut disebut medan skalar. Contoh medan skalar adalah suhu di tiap titik di dalam ruang. Pada suatu titik lain, yang digeser oleh ds dari suatu titik awal, nilai skalar dapat telah berubah sebesar udu (Gambar 1-17). Kenyataannya,dz z u dy y u dx x u u (1-35)
Gambar 1-17. Perubahan nilai fungsi skalar u akibat pergeseran sd.
dengan mengingat bahwa derivatif-derivatif dievaluasi pada titik awal, yaitu
u x
Px
u
, dan seterusnya. Meskipun kita telah menulis pergeseran sebagai ds, jelas pergeseran ini adalah perubahan vektor letak drsuatu titik, sehingga zˆ y ˆ x ˆ dy dz dx s d (1-36)
menurut persamaan 34). Dengan membandingkan persamaan-persamaan (1-35) dan (1-36) dengan persamaan (1-20), maka kita melihat bahwa kita juga dapat menulis du sebagai perkalian skalar ds dengan vektor
z u y u x u u xˆ yˆ zˆ (1-37) Sehingga u s d du . (1-38)
Vektor yang telah diperoleh dengan cara ini dan ditulis dalam komponen-komponen tegak lurus dalam persamaan (1-37) disebut gradien u dan sering juga ditulis sebagai grad u. Kita dapat memandang persamaan (1-38) sebagai definisi umum u karena ia ditulis dalam suatu bentuk yang tak bergantung pada sistem
koordinat tertentu. Dengan kata lain, gradien adalah suatu besaran yang akan memberikan perubahan suatu skalar bila ia dikalikan skalar dengan pergeseran.
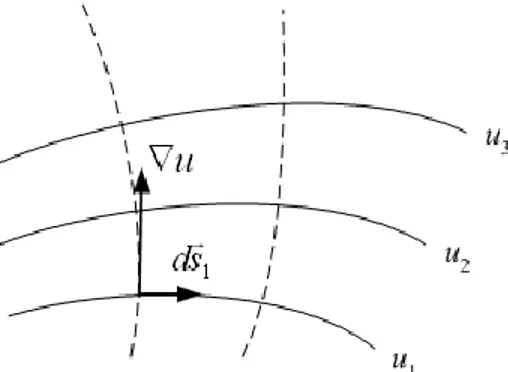
Untuk memahami makna gradien, kita tinjau Gambar 1-18 yang memperlihatkan sederetan permukaan yang masing-masing terbentuk dari titik-titik di mana u memiliki nilai yang sama; dengan kata lain, permukaan-permukaan ini adalah permukaan-permukaan dengan u tetap, berkaitan dengan nilai-nilai u1, u2, u3 … . Sekarang, suatu pergeseran seperti ds1
, yang memindahkan kita ke sebuah titik pada permukaan yang sama, tidak memin-
Gambar 1-18. Permukaan-permukaan dengan u tetap. Gradien u tegak lurus terhadap permukaan-permukaan seperti ini.
dahkan kita ke suatu titik dengan nilai u berbeda dari nilai u ditempat kita semula. Dengan demikian, du1ds1u 0. Dengan membandingkan hasil ini dengan persamaan (1-15), maka terlihat bahwa u dan ds1 saling tegak lurus; jadi u tegak lurus terhadap suatu permukaan dengan u tetap, sebagaimana ditunjukkan oleh Gambar 1-18.
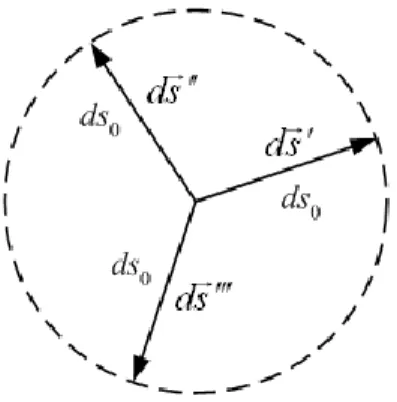
Sekarang kita tinjau pergeseran-pergeseran dengan besar ds0 yang tetap dari suatu titik tetapi dengan arah yang bervariasi seperti ds, ds, dan ds pada Gambar 1-19. Tampak dari persamaan-persamaan (1-38) dan (1-15) bah-wa perubahan u yang diakibatkan oleh pergeseran-pergeseran ini diberikan oleh
cos u ds
du 0 dan perbedaannya hanya karena perbedaan besar sudut antara pergeseran-pergeseran tersebut dengan arah tetapu. Seka-rang kita melihat bahwa du akan maksimum bila cos = 1 atau = 0 sehingga u sejajar
dengan pergeseran yang dimaksud. Dengan kata lain, arah gradien juga merupakan arah ke mana skalar memiliki laju perubahan maksimum.
Suatu vektor satuan nˆ yang tegak lurus terhadap suatu permukaan pada suatu titik di permukaan itu disebut vektor normal dan diilustrasikan oleh Gambar 1-20 untuk sebuah permukaan u = tetapan. Tetapi kita baru saja meli-
Gambar 1-19. Pergeseran-pergeseran dengan besar yang tetap tetapi berbeda arah.
Gambar 1-20. Definisi vektor satuan normal.
hat bahwa u juga tegak lurus terhadap permukaan tersebut sehingga nˆ dan u sejajar. Jadi, dengan menggunakan persamaan (1-4) kita dapat menulis
u u nˆ . (1-39)
Contoh
Anggap kita meninjau suatu kasus dua dimensi dengan u y2 kx
dengan k adalah tetapan. Jika kita menulis y2 kx u
, maka kita melihat bahwa permukaan-per-mukaan dengan u tetap adalah kurva-kurva pada bidang xy. Kenyataannya, permuka-an-permukaan ini berupa parabola-parabola seperti diperlihatkan oleh Gambar 1-21 untuk k = 1 dan nilai-nilai u tertentu. Dengan mensubstitusi ungkapan untuk u ini (dengan k = 1) ke dalam persamaan (1-37), maka kita memperoleh
y ˆ x ˆ y u 2
sehingga, dari persamaan (1-6), maka u 14y2 , dan dengan demikian
2 4y 1 y ˆ xˆ n ˆ 2y (1-40)
menurut persamaan (1-39). Dalam menggunakan hasil ini, tentu kita harus menggunakan nilai y yang berkaitan dengan sebuah titik pada kurva untuk u tertentu. Sebagai contoh, kita evaluasi nˆ untuk titik P pada Gambar 1-21 di tempat parabola yang terkait dengan u3 = 2 memotong sumbu y positif. Di sini xP = 0, dan yP2 xP u3 2 sehingga yP 2. Dengan mensubstitusikan ini ke persamaan (1-40), maka kita memperoleh nˆP ˆx 32 2yˆ
3 1
. Vektor ini dengan
komponen x negatif dan komponen y yang cukup besar diperlihatkan juga oleh Gambar 1-21.
Gambar 1-21. Permukaan-permukaan dengan u tetap untuk contoh Sub-Bab 1-9.
1-10 Operasi Differensial Lainnya
Komponen-komponen suatu vektor sangat mungkin juga bergantung pada letak, seperti misalnya Ax
x,y,z
dan lain sebagainya. Jadi, secara umum A berubah dari satu titik ke titik lain, baik besar maupun arahnya, dan kita menulis
x y z
A
r AA , , . Pada suku terakhir kita telah mengguna-kan penulisan yang ringkas dan memudahkan untuk menggungkapkan A se-bagai sebuah fungsi koordinat suatu titik dengan vektor letaknya. Suatu vektor yang nilai-nilainya dinyatakan pada setiap titik di dalam ruang disebut medan vektor. Sekarang kita tinjau suatu cara khusus ……….
Dengan memperhatikan kembali persamaan (1-37) maka terlihat bahwa u
dapat diinterpretasikan sebagai perkalian fungsi skalar u dengan operator del yang dinyatakan oleh
z y x xˆ yˆ zˆ . (1-41)
Dapat ditunjukkan bahwa operator yang agak abstrak ini memiliki sifat-sifat matematis yang sama seperti pergeseran sebuah titik dan oleh karena itu dapat diperlakukan sebagai vektor. Sekarang kita dapat melakukan dua operasi differensial dengan menggunakan kedua bentuk perkalian vektor.
Dengan menggunakan persamaan-persamaan (1-20) dan (1-41) maka kita dapat memperoleh z A y A x A A x y z . (1-42)
Perkalian skalar ini disebut sebagai divergensi A dan sering ditulis div A.
Dengan menggunakan persamaan-persamaan (1-27) dan (1-41) maka kita dapat memperoleh y A x A x A z A z A y A A xˆ z y yˆ x z zˆ y x . (1-43)
Perkalian vektor ini disebut rotasi A dan sering ditulis rot A (atau curl A). Perkalian vektor ini dapat juga dituliskan secara lebih mudah sebagai sebuah determinan seperti pada persamaan (1-28):
z y x A A A z y x A zˆ y ˆ xˆ . (1-44)
Makna dari nama divergensi dan rotasi akan menjadi lebih jelas saat kita menggunakannya dalam situasi di mana keduanya muncul secara alami.
Operator lainnya yang sangat penting dan berguna adalah Laplacian:
2 2 2 2 2 2 2 z y x . (1-45)
Sebagai contoh, jika kita terapkan pada sebuah skalar, 2 2 2 2 2 2 2 z u y u x u u , (1-46)
sedangkan ungkapan 2A mewakili tiga buah persamaan di mana 2 berope-rasi pada masing-masing dari ketiga komponen tegak lurus A, yaitu
2 2 2 2 2 2 2 z A y A x A A x x x x , (1-47)
dan ungkapan yang serupa dengannya untuk komponen-komponen y dan z.
Kita juga memiliki dua hasil yang bermanfaat yang melibatkan operator del. Karena persamaan (1-24), maka rotasi suatu gradien adalah nol:
0
u . (1-48)
Demikian juga, divergensi dari suatu rotasi adalah nol:
0 A (1-49)
karena persamaan-persamaan (1-29) dan (1-24).
Kita sekarang beralih ke integral yang melibatkan vektor. Walaupun banyak kemungkinan dapat dibayangkan, dua yang penting bagi kita dan kita akan membahasnya.
1-11 Intergral Garis
Dibayangkan kita bergerak dari suatu titik awal Pi
xi,yi,zi
ke suatu titik akhir Pf
xf ,yf ,zf
sepanjang sebuah kurva C tertentu (sebuah “garis” atau “lintasan”) seperti ditunjukkan oleh Gambar 1-22. Keseluruhan lintasan ini dapatdiperlakukan sebagai jumlahan vektor dari sederetan pergeseran infinitesimal ds sepanjang kurva C. Kita asumsikan bahwa terdapat suatu me-dan vektor A sedemikian sehingga nilai-nilainya dapat diperoleh di sepanjang lintasan tersebut. Kita evaluasi A pada setiap langkah, mengalikan kompo-nennya sepanjang ds dengan besar ds, dan menjumlahkan semuanya. Hasil-nya disebut sebagai integral garis A sepanjang kurva C dan ditentukan dengan
C C cos cos ds A ds A ds A f i . (1-50)Gambar 1-22. Hubungan-hubungan untuk perhitungan integral garis. Mungkin contoh yang paling akrab tentang integral garis adalah kerja (usaha) yang dilakukan pada sebuah partikel; dalam kasus tersebut, A merupakan se-buah vektor yang bekerja pada partikel.
Jika lintasan integrasi mengikuti sebuah kurva tertutup, seperti sebuah lingkaran, maka titik awal dan titik akhir akan berimpit. Kita menulis initegral garis untuk kasus ini sebagai
CA ds
.
Integral ini kadang-kadang disebut sirkulasi A; nilainya dapat nol atau tak nol bergantung pada A seperti yang akan kita lihat nanti.
C Axdx Aydy Azdz s d A C . (1-51)Dalam menggunakan persamaan (1-51) kita harus memperhatikan kenyataan bahwa dx, dy, dan dz tidak dapat bervariasi secara bebas karena koordinat-koordinat x, y, z dihubungkan oleh persamaan lintasan. Demikian juga, ung-kapan-ungkapan Ax Ax
x,y,z
dan seterusnya juga harus memperhatikan kesalingtergantungan ini. Pertimbangan-pertimbangan ini akan sangat baik diilustrasikan dengan memperhatikan sebuah kasus khusus.Contoh
Misalkan Ax2xˆy2yˆz2zˆ dan kita pilih bagian dari parabola y2 x antara titik asal (0, 0, 0) dan titik (2, 2,0) sebagai lintasan; kurva ini adalah parabola yang diilustrasikan oleh Gambar 1-21 untuk u2 = 0. Di sini z = tetapan, sehingga dz = 0 dan integran pada persamaan (1-51) menjadi
dy y dx x dy A dx Ax y 2 2 .
Kita dapat menulis ini sebagai fungsi sebuah variabel dengan menggunakan persamaan lintasan. Karena y2 x
, maka 2ydy dx atau dy dx 2 x dan
dy
y2 xdx
2
1 ; dengan demikian kita memperoleh
32
4 2
2 0 2 0 2 3 3 1 3 3 1 2 1 2
A ds x x dx x x C . 1.12 Vektor Elemen LuasanSebelum kita membahas tentang integral yang serupa dengan integral di atas tetapi merupakan jumlahan ke luasan tertentu, maka akan sangat membantu bila kita membahas terlebih dahulu secara rinci tentang wakilan suatu luasan dalam bentuk vektor. Gambar 1.23 memperlihatkan sebuah elemen luasan infinitesimal da yang
memiliki arah tertentu relatif terhadap sumbu-sumbu koordinat. Terlihat juga bahwa sebuah arah dapat dikaitkan dengan dengan luasan ini, yaitu vektor satuan
n
ˆ yang normal (tegak lurus) terhadap luasan, dan kita dapat menulisnya sebagai
da n a
d ˆ , (1-52)
dengan mengikuti bentuk umum persamaan (1-4). Tetapi, jelas bahwa terda-pat sifat mendua (ambiguitas) dari definisi ini kita dapat memilih nˆ memiliki arah yang berlawanan dengan pilihan semula dan ia juga masih tegak lurus terhadap elemen luasan da. Oleh karena itu, kita perlu melengkapi persamaan (1-52) dengan sebuah kesepakatan yang akan mengatakan kepada kita apa yang akan dilakukan; terdapat dua kasus.
Pertama, da merupakan bagian dari suatu permukaan terbuka, yaitu ia dibatasi oleh sebuah kurva tertutup C; sebuah halaman buku ini merupakan sebuah contoh permukaan terbuka tersebut. Dalam kasus ini, langkah pertama adalah memilih arah gerak (lintasan) mengelilingi kurva pembatas; setelah hal ini telah dilakukan, gulungkan jemari tangan kanan dalam arah lintasan tadi dan disepakati bahwa arah yang ditunjukkan oleh ibu jari sebagai arah nˆ . Aturan tangan kanan ini dilukiskan oleh Gambar 1-24; perhatikan bagaimana arah nˆ akan berbalik jika arah lintasan pada kurva C dibalik.
Gambar 1.23. Sebuah elemen luasan da pada permukaan S, vektor elemen lu-asan ini adalah danˆda,
Gambar 1.24. Arah vektor normal nˆ yang dipilih untuk pemukaan terbuka S yang dibatasi oleh kurva
dengan nˆ adalah vektor normal elemen luasan tersebut.
tertutup C dengan arah lintasan seperti terlihat pada gambar.
Gambar 1-25. Beragam vektor normal ke arah luar dari suatu permukaan tertutup.
Kedua, da merupakan bagian dari suatu permukaan tertutup. Dalam hal ini tidak ada kurva pembatas C tetapi permukaan ini membagi ruang menjadi ruang dalam dan ruang luar; permukaan sebuah bola merupakan sebuah contoh. Di sini arah nˆ senantiasa dipilih dari ruang dalam ke ruang luar. Hal ini diilustrasikan oleh Gambar 1-25 di mana arah-arah normal ke luar yang dimaksud di sini diperlihatkan untuk beberapa titik.
Bila persamaan (1-52) digabung dengan ungkapan untuk nˆ yang ber-bentuk persamaan (1-8), maka da dapat ditulis dalam bentuk komponen seba-gai
z da y da x da a d x ˆ y ˆ zˆ, (1-53) dengan da l dax x , day lyda , daz lzda (1-54)
dan l , x l , y l adalah komponen-komponen dari nˆ , yaitu cosinus arah. z Pengalaman kita dengan integral-integral rangkap telah membuat kita terbiasa dengan penggunaan dxdy sebagai sebuah elemen luasan di dalam bi-dang xy, dan jelas bahwa ungkapan ini berkaitan dengan salah satu komponen da. Untuk memperoleh hubungan ini, kita tinjau Gambar 1-26 yang memper-lihatkan sebuah elemen luasan da berbentuk segiempat siku-siku dengan sisi-sisi b dan c sehingga da = bc. Bidang luasan sejajar dengan sumbu y sehingga nˆ sejajar dengan bidang
xz dan membentuk sudut terhadap sumbu z; Gambar 1-27 memperlihatkan pandangan dari samping sepanjang sumbu y ke arah titik asal. Gambar-gambar tersebut juga memperlihatkan proyeksi luasan pada bidang xy dan bidang yz; proyeksi ini berupa persegiempat berturut-turut dengan luas dxdy dan dydz; dari gambar tersebut jelas juga bahwa dy = c. Proyeksi da pada bidang xz berupa garis yang ditandai dengan b di dalam Gambar 1-27. Dua sudut arah lainnya dari
n
ˆ diperoleh dengan membanding-kan kedua gambar ini dengan Gambar 1-8 dan terlihat bahwa = 90 dan = 90, sehingga cosinus-cosinus arah adalah
sin x
l , ly 0 dan lz cos .
Gambar 1-26. Penentuan komponen-komponen suatu vektor elemen luasan.
Dengan mensubstitusikan nilai-nilai ini ke dalam persamaan (1-54) dan dengan menggunakan Gambar 1-27, kita memperoleh bahwa daz dacos =
bcos
c dxdy , yang tidak lain adalah proyeksi luasan da pada bidang xy, yaitu proyeksi tegak lurus terhadap sumbu koordinat yang terkait. Demikian pula, kita akan memperoleh dax dydz , sedangkan day 0 untuk kasus khusus ini.Sekarang anggap bahwa n adalah negatif sehingga z > 90 sedangkan yang lainnya dibuat tetap sama; hal ini diilustrasikan oleh Gambar 1-28. Dengan membandingkannya dengan Gambar 1-26, terlihat bahwa proyeksi pada bidang xy dan bidang yz akan masih tetap persegiempat, berturut-turut dengan luas dxdy dan dydz. Tetapi, sekarang cos akan negatif sehingga da dacos = dxdy. Di
lain pihak, karena = 90 maka cos akan positif dan dax dydz seperti sebelumnya; da tetap nol. y
Gambar 1-27. Pandangan samping situasi dalam Gambar 1-26.
Gambar 1-28. Sebuah elemen luasan dengan sebuah komponen z negatif. Tinjauan-tinjauan ini dapat diperluas ke situasi di mana nˆ membentuk sudut sembarang terhadap semua sumbu. Besar suatu komponen dari da se-panjang sumbu tertentu akan sama dengan proyeksinya pada bidang koordinat yang tegak lurus terhadap sumbu tersebut dan, dalam koordinat tegak lurus, diberikan oleh oleh perkalian diferensial-diferensial yang bersangkutan. Kare-na kita selalu memperlakukan diferensial-diferensial ini sebagai besaran positif, maka komponen aktualnya akan diperoleh dengan mengalikan perkalian ini dengan tanda plus atan minus bergantung pada tanda komponen nˆ yang ber-sangkutan. Dengan demikian, kita telah memperoleh wakilan komponen-komponen tegak lurus dari suatu elemen luasan dan menulisnya sebagai
dydz
dax , day dzdx , daz dxdy (1-55)
di mana tanda plus digunakan untuk suatu komponen jika besar sudut arah nˆ terhadap sumbu yang bersangkutan adalah kurang dari 90, sedangkan tanda negatif digunakan bila sudut arah lebih besar dari 90.
1.13 Integral Permukaan
Tinjau sebuah permukaan S; seperti ditunjukkan oleh Gambar 1-29, kita dapat membagi S dalam vektor elemen-elemen luasan da seperti telah dibahas dalam subbab sebelumnya. Kita asumsikan kehadiran medan vektor A sedemikian sehingga nilainya dapat diperoleh di semua titik pada permukaan S. Pada tiap elemen luasan, kita mengevaluasi A, mengalikan komponennya dalam arah da dengan besar da, dan menjumlahkan semuanya. Hasilnya disebut sebagai integral permukaan A pada S dan dituliskan sebagai
S S SA da A nda A da ˆ cos . (1-56)Integral ini disebut juga fluks A yang melewati S. Kita telah menulis persamaan (1-56) dengan sebuah tanda integral tunggal untuk kemudahan, tetapi sebenarnya ia mewakili sebuah integral rangkap dua (ganda).
Jika permukaannya merupakan permukaan tertutup, maka akan sangat berguna bila hal ini ditandai secara eksplisit dengan menulis integral sebagai
SA da
. (1-56)
Nilai integral ini dapat nol ataupun tak nol, bergantung pada A, sebagaimana akan kita lihat nanti.
Gambar 1.29. Hubungan-hubungan yang digunakan untuk kalkulasi integral permukaan.
Dengan menggunakan persamaan-persamaan (1-20) dan (1-53), kita dapat menulis persamaan (1-56) dalam suku-suku koordinat tegak lurus sebagai
S x x y y z z SA da A da A da A da . (1-57)Dalam menggunakan persamaan 57), kita perlu menggunakan persamaan (1-55) dan kemudian pastikan memperhitungkan kenyataan bahwa dx, dy, dan dz tidak dapat bervariasi secara bebas karena koordinat-koodinat x, y, dan z dihubungkan oleh persamaan permukaan S. Kesalingtergantungan ini harus juga diperhitungkan dalam menentukan batas-batas integrasi dan dalam menulis komponen-komponen seperti Ax Ax
x,y,z
. Sekarang kita ilustrasikan hal ini dengan sebuah kasus khusus.Contoh
Anggap Ayzxˆzx yˆxy zˆ dan kita pilih permukaan S berupa bagian lingka-ran berjejari a yang berpusat di titik asal dan berada di kuadlingka-ran pertama pada bidang xy seperti ditunjukkan oleh Gambar 1.30; persamaan lingkaran adalah
2 2 2
a y
x . Di sini, luasan tegak lurus terhadap sumbu z sehingga nˆ dapat berupa zˆ ataupun zˆ . Misalnya kita pilih nˆ zˆ; maka satu-satunya komponen
a
d adalah daz dxdy se-perti diperoleh dari persamaan (1-55) dengan tanda plus karena sudut arah = 0, dan persamaan (1-57) menjadi
S SA da xydxdy . (1-58)Eleman luasan diperlihatkan sebagai daerah yang diarsir lebih gelap di dalam gambar. Kita memilih mengevaluasi integral dengan terlebih dahulu mengintegrasikannya ke variabel y sambil mempertahankan x tetap; hal ini akan menjumlahkan sumbangan
Gambar 1-30. Luasan integrasi untuk contoh dalam Subbab 1-13.
dari daerah pita yang diarsir kurang gelap; batas atas integrasi ke variabel y berkaitan dengan letak titik P dan diperoleh dari persamaan lingkaran untuk nilai x yang tetap ini, yaitu yP a2 x2 . Setelah hal ini dilakukan, selanjutnya kita mengintegrasi-kan ke seluruh variabel x yang mungkin, dengan menjumlahkan sumbangan dari pita-pita yang serupa, sehingga mencakup keseluruhan luasan S. Dengan demikan persamaan (1-58) menjadi
a a x a a x SA da xdx ydy 0xdx y 0 2 2 1 0 0 2 2 2 2
4 8 1 0 4 4 1 2 2 2 1 2 1 0 2 2 2 1 ax a x dx a x x a a
Sekarang kita beralih kepada dua teorema penting yang melibatkan je-nis-jenis integral yang telah dibahas di atas.
1.14 Teorema Divergensi
Teo-
V SA da Ad . (1-59)Integral dihitung untuk keseluruhan permukaan S dan volume V dengan elemen volume d . Demi kemudahan, kita telah menulis integral volume dengan sebuah tanda integral tunggal meskipun sesungguhnya ia merupakan integral rangkap tiga (tripel). Karena S merupakan permukaan tertutup, maka normal satuan nˆ yang digunakan untuk da adalah normal arah ke luar menu-rut kesepakatan kita dalam Subbab 1-12 seperti telah ditunjukkan oleh Gam-bar 1-25.
Teorema ini menghubungkan integral permukaan suatu medan vektor dengan integral volume dari divergensi medan vektor tersebut. Integral per-mukaan bergantung hanya pada nilai A di permukaan, sedangkan integral vo-lume memerlukan pengetahuan tentang A (tidak A) di seluruh volume.
Kita akan membuktikan teorema ini dengan evaluasi langsung. Dalam koordinat-koordinat tegak lurus, elemen volume adalah
dz dy dx
d (1-60)
dan, dengan menggunakan persamaan (1-42), kita dapat menulis integral volu-me sebagai suatu jumlahan:
V z V y V x dxdydz z A dz dy dx y A dz dy dx x A d A V . (1-61)Kita tinjau integral pertama. Langkah pertama kita adalah mengintegrasikan ke variabel x sambil mempertahankan y dan z tetap pada nilai-nilai y0 dan z . Jadi 0 kita akan menjumlahkan sumbangan dari sebuah batang dengan luas penampang dydz . Batang ini dan proyeksinya pada bidang yz diperlihatkan oleh Gambar 1-31. Batang ini memotong permukaan S pada titik P dan titk 1 P dan oleh karena 2 itu ia mendefinisikan dua elemen luasan da1 dan da2 pada permukaan S yang
arahnya diperlihatkan pada gambar. (Agar jelas, bagian sisa dari volume V dan luasan S tidak ditampilkan dalam di gambar.) Koordinat-
Gambar 1-31. Volume yang digunakan dalam memperoleh teorema divergensi. koordinat titik P dan titik 1 P berturut-turut adalah 2
x1,y0,z0
dan
x2,y0,z0
dengan x dan 1 x ditemukan sebagai nilai-nilai yang memenuhi persamaan 2permukaan S; jadi x dan 1 x merupakan batas integrasi untuk va-riabel x. 2 Dalam langkah ini, kemudian Ax x akan merupakan fungsi x saja karena y dan z tetap, sehingga
Ax x
dx dAx .Dengan demikian, integral pertama dalam persamaan (1-61) menjadi
dz dy z y x A z y x A dx x A dz dy x x x x x 0 0 1 0 0 2, , , , 2 1 . (1-62)Di dalam integran hasil ini, suku di dalam tanda kurung siku adalah selisih Ax bila dievaluasi pada titik-titik P dan 1 P , yang dapat ditulis sebagai 2
P2 A
P1Ax x . Dari persamaan (1-51) dan Gambar 1-31 tampak bahwa dz
dy
da2x sedangkan da1x dydz karena sudut yang dibentuk oleh luasan-luasan ini dengan sumbu x berturut-turut kurang dari 90 dan lebih dari 90. Jadi, integran di dalam persamaan (1-62) dapat ditulis sebagai
x x
x
x x x xx da A da A da A da
yang sama dengan sumbangan total pada integral permukaan Axdax yang ber-asal dari luasan-luasan da1 dan da2 pada permukaan S yang dipotong oleh ba-tang tersebut. Jadi, bila kita melakukan integrasi ke variabel-variabel y dan z dalam persamaan (1-62), maka kita akan menjumlahkan sumbangan-sum-bangan semua batang seperti ini; sumbangan tiap batang adalah Axdax dari luasan bagiannya, sehingga hasil akhir akan meupakan integral permukaan dari Axdax ke keseluruhan luasan S. Dengan kata lain, kita telah menemukan
S x x V x dxdydz A da x A . (1-64)Dengan cara serupa, dua integral terakhir dalam persamaan (1-61) akan diper-oleh berturut-turut sebagai
SAyday dan
SAzdazSehingga jika kita menambahkannya dengan persamaan (1-64), mensubstitusi-kannya ketiganya ke persamaan 61), dan dengan menggunakan persamaan (1-20), maka kita memperoleh
S S Axdax Ayday Azdaz A da d A V yang merupakan persamaan (1-59), dan ini membuktikan teorema tersebut.
Kita telah membuktikan teorema ini hanya untuk volume yang dibatasi oleh sebuah permukaan tunggal, tetapi kita dengan mudah dapat memperluas bukti yang berlaku juga pada wilayah yang dibatasi oleh beberapa permukaan, seperti sebuah bola berongga. Gambar 1-32 memperlihatkan sebuah volume V yang dikelilingi oleh dua permukaan S dan 1 S ; dua buah vektor normal ke arah 2 luar terhadap volume tersebut diperlihatkan sebagai nˆ dan nˆ. Sekarang kita bayangkan sebuah bidang memotong volume dan membaginya menjadi dua volume V dan 2 V ; jejak bidang ini ditunjukkan oleh garis putus-putus AB dan 1 CD. Volume V dikelilingi oleh sebuah permukaan tunggal yang me-rupakan
bagian dari S dan 1 S di sebelah bidang ditambah permukaan bidang 2 perpotongan yang ditunjukkan oleh AB dan CD; vektor normal ke arah luar terhadap permukaan batas yang baru diperlihatkan sebagai nˆ . Hal yang seru-pa 2 berlaku untuk V ; vektor normal yang terkait adalah 1 nˆ . Dengan mene-rapkan 1 persamaan (1-59) pada masing-masing volume ini dan kemudian men-jumlahkannya, maka kita memperoleh
V S S ABCD 2 ABCD 1 V1 2 1 2 nˆ nˆ da A da A a d A a d A d A Dalam dua integral terakhir, vektor-vektor normal saling berlawanan arah se-hingga tiap pada titik di bidang ABCD berlaku nˆ2 nˆ1 sedangkan nilai-nilai A dan da di bidang tersebut adalah sama; dengan demikian integral-integral ini saling meniadakan dan kita tinggal punya
V1V2Ad S1S2Ada yang sama dengan persamaan (1-59) karena volume total adalah V1 V2 dan permukaan batas total adalah S1S2.
Gambar 1-32. Sebuah volume yang dibatasi oleh dua permukaan.
Bukti ini jelas dapat diperluas ke sejumlah sembarang permukaan-per-mukaan batas dengan menggunakan banyak perpermukaan-per-mukaan-perpermukaan-per-mukaan perpo-tongan
Jika sekarang kita menerapkan teorema divergensi pada suatu situasi se-derhana khusus, maka kita dapat memperoleh sebuah hasil yang bermanfaat dan memperjelas maksudnya. Kita tinjau sebuah titik P di pusat sebuah volu-me kecil V. Jika V sangat kecil, maka A akan hampir konstan di seluruh volume sehingga dapat dilihat dengan mudah bahwa integral volume dalam persamaan (1-59) dapat ditulis sebagai
V A d A
V P dengan P A adalah nilai rerata A di sekitar titik P. Dengan meletakkan hasil ini ke dalam persamaan (1-59) dan membaginya dengan V , maka kita memperoleh
S P 1 a d A V A . (1-65)Jika sekarang kita gunakan V 0, sedangkan titip P tetap di pusat volume kecil, maka nilai rerata A di sekitar titik P menjadi nilai A di titik P; dengan menuliskannya hanya sebagai A maka kita punya
S 1 lim 0 V A da A V . (1-66)Ungkapan untuk A ini adalah dalam sebuah bentuk yang tak bergantung pada sistem koordinat tertentu, hal yang sebaliknya dengan persamaan (1-42), dan oleh sebab itu ia dapat digunakan sebagai sebuah definisi umum tentang divergensi sebuah vektor seperti halnya persamaan (1-38) sebagai cara umum pendefinisian sebuah gradien. Persamaan (1-66) juga memberik kita suatu pe-mahaman yang lebih baik tentang signifikasi divergensi karena tampak bahwa ia merupakan ukuran fluks keluar suatu vektor melalui suatu daerah kecil di sekitar titik yang ditinjau.
Adalah merupakan hal yang memungkinkan memulai dengan definisi persamaan (1-66) dan, dengan mengevaluasi fluks A yang melewati permuka-an yang mengelilingi sebuah volume xyz, memperoleh ungkapan untuk A dalam koordinat tegak lurus; hasilnya tentu saja persamaan (1-42).
1-15 Teorema Stokes
Kita tinjau sebuah permukaan S yang dibatasi oleh sebuah kurva C. Teorema Stokes menyatakan bahwa
S CA ds A da (1-67)dan ia menghubungkan integral garis suatu vektor pada suatu kurva tertutup dengan integral permukaan dari rotasi vektor tersebut pada luasan yang diling-kupi kurva tadi. Karena S merupakan permukaan terbuka, maka arah da da-lam persamaan (1-67) ditentukan dari pilihan arah gerak mengelilingi kurva C menurut persamaan (1-52) dan aturan tangan kanan yang telah diilustrasikan oleh Gambar 1-24; merupakan hal yang penting adalah bahwa kesepakatan tanda ini akan digunakan dalam banyak aplikasi dari persamaan (1-67).
Hal menarik untuk dicatat adalah bahwa persamaan (1-67) tidak men-syaratkan S memiliki bentuk tertentu kecuali bahwa ia dibatasi oleh C; oleh karena itu terdapat banyak kemungkinan dalam pemilihan permukaan. Secara umum, nilai integral
A
da akan berbeda di titik-titik pada semua permu-kaan ini, tetapi persamaan (1-67) menyatakan bahwa jumlahan semua suku ini akan sama, karena integral garis bergantung hanya pada nilai-nilai A sepan-jang garis yang sama. Hal ini diilustrasikan secara skematis oleh Gambar 1-33. Agar sederhana, anggap bahwa C adalah sebuah kurva tertutup yang terletak dalam sebuah bidang, seperti sebuah lingkaran. S dapat diambil sebagai daerah bidang yang dibatasi oleh lingkaran; bila dilihat dari samping, C dan S akan tampak sebagai garis, seperti terlihat pada gambar. Garis-garis putus-putus mewakilisemuanya memiliki C sebagai batas, dan integral
A
da ke masing-masing luasan tersebut akan memberikan hasil yang sama.Kita membuktikan teorema ini dengan evaluasi langsing integral per-mukaan dengan menggunakan ungkapan sebelumnya dalam koordinat tegak lurus. Dengan menggunakan persamaan (1-20) dan persamaan (1-43) kita da- pat memperoleh
Gambar 1-33. Permukaan-permukaan dengan kurva pembatas yang sama.
S S S z dax A da x A da y A da z A a d A x y x z y z y
S y z x z da x A da y A (1-68)di mana kita telah mengelompokkan suku-suku menurut komponen-kompo-nen A. Kita tinjau integral pertama dan kita namakan sebagai I . Kita eva-luasi x integral ini pertama-tama dengan mengintegralkannya ke sebuah pita dengan lebar dx yang sejajar dengan bidang yz dan berjarak x dari bidang ini. Kemudian, dengan mengintegralkan ke variabel x, kita jumlahkan sumbangan-sumbangan dari semua pita yang membagi-bagi permukaan S. Mula-mula kita asumsikan S cukup sederhana sehingga kita dapat memilih arah sumbu-sumbu sedemikian sehingga y dan z bertambah besar bersamaan dengan kita berge-rak dari pangkal ke ujung pita. Situasi ini diilustrasi oleh Gambar 1-34 yang juga memperlihatkan proyeksi pita pada bidang xz dan bidang xy sebagai ban-tuan untuk memahami orientasi permukaan. P dan 1 P berturut-turut adalah titik-titik awal dan akhir 2 integrasi, yaitu titik-titik perpotongan pita dengan kurva pembatas C dan koordinat-koordinatnya memenuhi persamaan kurva C. Elemen luasan da
diperlihatkan pada pertengahan langkah integrasi; tampak bahwa sudut arah da memiliki nilai-nilai yang sedemikian sehingga dan kurang dari 90, sedangkan > 90. (Sebuah pensil yang dipegang tegak lurus terhadap sebuah kertas karton yang memiliki orientasi sama seperti pita terar-
Gambar 1-34. Luasan yang digunakan untuk memperoleh teorema Stokes. sir akan membuat hal ini menjadi jelas.) Dengan demikian, menurut persama-an (1-55), day dxdz dan daz dxdy dan kita dapat menulis
2 1 P P pita z dz A dy y A dx Ix x x . (1-69)Di dalam suku yang berada di dalam tanda kurung, dy dan dz tidak saling be-bas karena y dan z dihubungkan oleh persamaan untuk S dan nilai x yang dili-batkan. Karena integran ini akan dievaluasi pada pita dengan x konstan, dan oleh sebab itu dx = 0, maka kita dapat menambahkan
Ax x
dx 0 padanya sehingga ia memiliki bentuk yang segera dapat dikenal:x x x dz dAx z A dy y A dx x A .
Sebagai hasilnya, persamaan (1-69) menjadi
pita 2 1 P P pita P P 2 1 dx A A dA dx Ix x x x . (1-70)Jika kita kembali lagi ke Gambar 1-34, dan meninjau pergeseran-pergeseran ds1 dan ds2 sepanjang C pada limit yang bersangkutan, maka di P tampak bahwa 1
1 s
d memiliki komponen x yang positif sehingga kita dapat menulis ds1x dx , sedangkan di P , 2 ds2 memiliki komponen x yang negatif sehingga ds1x dx . Konsekuensinya, integran persamaan (1-70) dapat ditulis sebagai
x
x
x
x x x xx ds A ds A ds A ds
A P2 2 P1 1 2 2 1 1
. (1-71)
yang sama dengan sumbangan total kepada integral garis Axdsx yang muncul dari pergeseran-pergeseran ds1 dan ds2 yang terpotong pada pita C oleh pita. Jadi, bila kita melakukan integrasi akhir ke variabel x di dalam persamaan (1-70), yaitu menjumlahkan sumbangan-sumbangan dari semua pita, maka sum-bangan tiap pita akan berupa Axdsx dari bagiannya dari kurva pembatas; hasil akhir akan berupa integral garis Axdsx ke keseluruhan kurva C. Dengan kata lain, kita telah menemukan bahwa
C S z x x x y x da A ds y A da z A . (1-72)Serupa dengan hasil di atas, dua integral akhir pada persamaan (1-68) berturut-turut dapat ditunjukkan memiliki nilai-nilai
Dengan mensubstitusikan hasil-hasil ini, bersama dengan persamaan (1-72), ke persamaan (1-68), maka kita dapat memperoleh
C C S A da Axdsx Aydsy Azdsz A ds (1-72)yang tepat sama dengan persamaan (1-67) dan ini membuktikan teorema terse-but.
Teorema ini dpat diperluas kepada kasus di mana sebuah permukaan di-batasi oleh lebih dari satu kurva dengan menggunakan metode yang serupa se-perti saat digunakan untuk teorema divergensi. Sebuah contoh situasi sese-perti ini diperlihatkan oleh Gambar 1-35. Perhatikan arah lintasan kurva pembatas sebelah dalam; this sense is chosen to keep the area of interest to one’s left as one moves
along the curve and is seen to be equivalent to the right-hand rule illustrated in
Figure 1-24. Kita akan membagi S menjadi permukaan-permukaan yang
masing-masing dibatasi oleh sebuah kurva dengan memperkenalkan pasangan-pasangan garis yang berimpitan sebanyak yang diperlukan; dua pasangan garis seperti ini diperlihatkan sebagai garis putus-putus pada gambar. Selanjutnya teorema Stokes dapat diterapkan pada masing-masing dari permukaan-permukaan ini dan hasilnya dijumlahkan. Sumbangan kepada integral garis dari garis-garis tadi akan saling meniadakan karena arah lintasannya saling berlawanan dan hasil akhirnya akan kembali berbentuk persamaan (1-67). Prosedur serupa juga akan meniadakan kekhawatiran berkaitan dengan asumsi kita bahwa permukaan dalam Gambar 1-34 cukup datar bagi kita untuk mengarahkan sumbu-sumbu kita sedemikian sehingga y dan z selalu bertambah besar bersamaan dengan saat kita menginte-grasikan sepanjang pita. Jika permukaannya cukup berkelok, maka kita dapat
Gambar 1-35. Sebuah luasan yang dibatasi oleh dua buah kurva.
membaginya menjadi potongan-potongan yang cukup datar sedemikian sehingga , jika perlu, kita dapat memilih himpunan berbeda dari sumbu-sumbu untuk masing-masing potongan yang akan memenugi persyaratan dari Gambar 1-34; pembagian seperti ini diilustrasikan oleh Gambar 1-36. Bila kita menerapkan teorema pada tiap potongan dan menjumlahkan hasil-hasilnya, maka sumbangan-sumbangan dari garis-garis pembagi akan saling meniadakan , dan kita akan memperoleh persamaan (1-67) lagi.
Kita tinjau sebuah titik P di pusat sebuah luasan kecil anˆ. Bila persa-maan (1-67) diterapkan pada kasus ini, maka
A
nˆ akan hampir konstan di seluruh luasan ini, sehingga kita dapat menulis
C P 1 nˆ A ds a A dengan ruas kiri adalah nilai rerata di dekat titik P dari komponen A da-lam arah nˆ menurut persamaan (1-21). Sekarang, jika kita gunakan a 0, maka nilai rerata di dekat titik P menjadi nilainya di titik P tersebut, atau
C P 1 lim nˆ 0 a A ds A a (1-73)yang memberikan komponen A dalam arah tertentu dalam bentuk inte-gral garis A di sekitar suatu luasan kecil yang norma (tegak lurus) terhadap arah ini. Jadi, kita dapat mengambil persamaan (1-73) sebagai definisi umum komponen suatu rotasi dalam suatu arah tertentu. Jika kita melakukan hal ini untuk tiga arah
yang saling tegak lurus (seperti xˆ , yˆ , dan zˆ ), maka kita akan memperoleh komponen A dalam tiap arah tersebut dan dengan demikian kita memperoleh juga vektor A. Bila prosedur ini digunakan untuk koor-dinat-koordinat tegak lurus, maka hasilnya tentu saja adalah persamaan (1-43).
Gambar 1-36. Pembagian sebuah luasan untuk bukti umum teorema Stokes. 1-16 Koordinat Silinder
Hingga di sini kita hanya telah menggunakan koordinat tegak lurus dengan vektor-vektor satuan yang tetap. Tetapi, banyak persoalan lebih mu-dah dinyatakan dan dikerjakan di dalam sistem koordinat lain, dan kita ingin melihat apa yang akan terjadi pada banyak hasil-hasil kita. Kita hanya perlu bekerja dengan dua sistem koordinat yang penting.
Yang pertama adalah koordinat silinder di mana letak titik P dicirikan oleh tiga besaran , , dan z yang definisinya dilukiskan oleh Gambar 1-37; gambar ini juga memperlihatkan vektor letak rsuatu titik bersama dengan ti-ga vektor satuan baru yang akan didefinisikan segera. Tampak bahwa bila r diproyeksikan pada bidang xy, maka adalah panjang proyeksi tersebut, se-dangkan adalah sudut yang dibentuk oleh proyeksi tadi dengan sumbu x po-sitif; z sama seperti halnya dalam koordinat tegak lurus. Hubungan antara ko-ordinat silinder dan koko-ordinat tegak lurus suatu titik P terlihat pada gambar sebagai
cos
sehingga 2 2 y x x y tan . (1-75)
Sekarang kita dapat mendefinisikan himpunan tiga buah vektor satuan yang saling tegak lurus sebagai berikut: pertama, zˆ sama seperti zˆ dalam koor-
Gambar 1-37. Definisi koordinat-koordinat silinder.
dinat tegak lurus; kedua, ρˆ dipilih dalam arah bertambahnya nilai variabel dan tegak lurus terhadap zˆ sehingga ρˆ sejajar dengan bidang xy; akhirnya, ˆ didefinisikan tegak lurus terhadap kedua vektor satuan sebelumnya dan arah-nya terlihat pada gambar. Tampak bahwa ˆ tegak lurus terhadap bidang = konstan, dan oleh sebab itu arahnya dalam arah bertambahnya nilai variabel . Vektor-vektor satuan ini diperlihatkan di lokasi titik P dengan maksud untuk menegaskan bahwa mereka merupakan fungsi titik P dalam arti bahwa jika titik P digeser maka ρˆ dan ˆ berubah arah, meskipun zˆ tidak berubah. Jadi, vektor-vektor satuan ini tidak semuanya konstan, tidak seperti xˆ , yˆ , dan zˆ .
Karena ρˆ , ˆ , dan zˆ merupakan vektor-vektor satuan yang saling tegak lurus, maka ketiganya memenuhi hubungan yang analog dengan persamaan-persamaan (1-18), (1-19), dan (1-25): 1 ˆ ˆ ˆ ˆ ˆ ˆ z z (1-76) 0 ˆ ˆ ˆ ˆ ˆ ˆ z z zˆ ˆ ˆ ˆzˆˆ zˆˆˆ.
Komponen-komponen tegak lurus dari ρˆ dan ˆ diperoleh dari peme-riksaan Gambar 1-37; akan sangat membantu bila membayangkan keduanya diproyeksikan pada bidang xy, dan hasilnya adalah
y xˆ sin ˆ cos
ˆ
ˆsin xˆcos yˆ. (1-77)
Persamaan-persamaan ini dapat dipecahkan untuk xˆ dan yˆ sehingga kompo-nen-komponennya dalam koordinat-koordinat silinder diperoleh sebagai
ˆ sin ˆ cos ˆ x yˆ sin ˆ cosˆ. (1-78)
Dengan mendiferensialkan persamaan (1-77), maka kita dapat menemukan se-cara eksplisit bagaimana ρˆ dan ˆ berubah saat P digeser:
ˆ ˆ d d dan ˆ ˆ d d . (1-79)
Karena ρˆ , ˆ , dan zˆ saling tegak lurus, maka kita dapat menyatakan sembarang vektor A dalam komponen-komponennya sepanjang arah-arah vektor-vektor satuan ini; analog dengan persamaan (1-5), kita dapat menulis A dalam bentuk
z A A A
A ˆ ˆ zˆ. (1-80)
Gambar 1-38. Elemen volume dalam sistem koordinat silinder.
Untuk kasus khusus yaitu vektor letak r, tampak pada Gambar 1-37 bahwa z
z
rˆ ˆ (1-81)
yang juga dapat diperoleh dari persamaan 11) dengan substitusi persamaan (1-74) dan menggunakan persamaan (1-77). Kita juga dapat memperoleh diferensial
r
d dari persamaan (1-81) dan persamaan (1-79):
z dz d d z dz d d r d ˆ ˆ ˆ ˆ ˆ ˆ (1-82)
sehingga komponen-komponennya dalam arah-arah pertambahan , , dan z berturut-turut adalah d, d, dan dz. Pergeseran-pergeseran komponen-komponen ini diperlihatkan oleh Gambar 1-38, dan tampak bahwa ketiganya berkaitan dengan jarak yang digeser oleh P akibat perubahan salah satu koor-dinat sedangkan dua yang lainnya tetap. Elemen volume yang diarsir memili-ki sisi-sisi yang tidak lain adalah komponen-komponen dari dr yang diberi-kan oleh persamaan (1-82). Oleh karena itu, elemen volume dalam koordinat silinder adalah