SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika.

(1)

ANALISIS PEMAHAMAN KONSEP MAHASISWA

PENDIDIKAN MATEMATIKA UNIVERSITAS SANATA DHARMA KELAS A PERSAMAAN DIFERENSIAL BIASA TAHUN AKADEMIK 2018/2019 PADA MATERI PERSAMAAN DIFERENSIAL ORDE SATU

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Disusun oleh:

Mateas Handy Wicaksono 151414046

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(2)

i

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Disusun oleh:

Mateas Handy Wicaksono 151414046

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN

UNIVERSITAS SANATA DHARMA YOGYAKARTA

(3)

ii

(4)

(5)

iv

HALAMAN PERSEMBAHAN

“Dalam hidup ini saya memiliki mental seperti orang yang

bermain sepeda, bila saya tidak mengayuh sepeda maka saya

akan jatuh

”

(B.J. Habbie)

Skripsi ini saya persembahkan untuk: Bapak Vitus Supardi dan Ibu Christina Sri Mulatsih Timotius Vivid Nugroho, Ludovikus Farrel Setiawan, Maria Setia Ifani Keluarga besar di Ketapang, Klaten, Gamping, dan Jakarta Keluarga besar Pendidikan Matematika Universitas Sanata Dharma

(6)

v

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam kutipan dan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 19 Juli 2019 Penulis,

(7)

vi

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIK

Yang bertanda tangan di bawah ini, saya mahasiswa Universitas Sanata Dharma: Nama : Mateas Handy Wicaksono

NIM : 151414046

Demi pengembangan ilmu pengetahuan, saya memberikan kepada Perpustakaan Universitas Sanata Dharma karya ilmiah saya yang berjudul:

Dengan demikian, saya memberikan kepada Perpustakaan Universitas Sanata Dharma hak untuk menyimpan, mengalihkan dalam bentuk media lain, mengelola dalam bentuk pangkalan data, mendistribusikan secara terbatas, dan mempublikasikannya di internet atau media lain untuk kepentingan akademis tanpa perlu meminta ijin dari saya maupun memberikan royalti kepada saya selama tetap mencantumkan nama saya sebagai penulis.

Demikian pernyataan ini yang dibuat dengan sebenarnya. Dibuat di Yogyakarta

Pada tanggal 19 Juli 2019 Yang menyatakan,

(8)

vii ABSTRAK

Mateas Handy Wicaksono. 2019. Analisis Pemahaman Konsep Mahasiswa Pendidikan Matematika Universitas Sanata Dharma Kelas A Persamaan Diferensial Biasa Tahun Akademik 2018/2019 pada Materi Persamaan Diferensial Orde Satu . Skripsi. Program Studi Pendidikan Matematika. Jurusan Pendidikan Matematika dan Ilmu Pengetahuan. Fakultas Keguruan dan Ilmu Pendidikan. Universitas Sanata Dharma, Yogyakarta.

Penelitian ini bertujuan untuk mendeskripsikan pemahaman konsep mahasiswa Pendidikan Matematika Universitas Sanata Dharma pada materi persamaan diferensial orde satu dan mengetahui faktor-faktor yang menyebabkan mahasiswa kesulitan dalam memahami konsep persamaan diferensial orde satu.

Jenis penelitian yang digunakan adalah penelitian deskriptif dengan pendekatan kualitatif. Subjek penelitian ini adalah 43 mahasiswa Pendidikan Matematika Universitas Sanata Dharma yang sedang menempuh perkuliahan Persamaan Diferensial Biasa pada tahun akademik 2018/2019 di kelas A. Metode pengambilan data berupa tes esai dan wawancara. Data yang diperoleh berupa lembar jawaban mahasiswa dan transkip wawancara. Teknik analisis data yang digunakan adalah reduksi data, penyajian data dan kesimpulan.

Hasil penelitian menunjukkan bahwa 23,36% mahasiswa mampu menggunakan prosedur atau operasi tertentu untuk memperlihatkan suatu fungsi merupakan solusi persamaan diferensial; 18,60% mahasiswa mampu mengklasifikasikan persamaan diferensial orde satu menurut sifat-sifat atau ciri-ciri tertentu; 4,65% mahasiswa mampu menggunakan prosedur atau operasi tertentu untuk menentukan penyelesaian umum persamaan diferensial orde satu; dan hanya 2,33% mahasiswa mampu mengaplikasikan konsep atau algoritma persamaan diferensial orde satu ke pemecahan masalah. Adapun faktor-faktor yang menyebabkan mahasiswa kesulitan dalam memahami konsep persamaan diferensial diantaranya faktor internal, yaitu: belum menguasai materi prasyarat yaitu turunan dan integral; terburu-buru dalam mengerjakan soal sehingga tidak membaca soal hingga tuntas; kurang memahami ciri-ciri dari jenis persamaan diferensial orde satu, cara memperlihatkan suatu fungsi merupakan solusi dari persamaan diferensial, langkah-langkah menentukan solusi dari persamaan diferensial orde satu, kurang memahami maksud soal; dan tidak teliti dalam melakukan perhitungan. Faktor eksternal yaitu: kurangnya diskusi dengan teman atau dosen di kelas ketika belum memahami materi, aktivitas yang tidak berhubungan dengan perkuliahan persamaan diferensial.

(9)

viii ABSTRACT

Mateas Handy Wicaksono. 2019. Analysis of Students’ Concept Understanding of Mathematics Education Sanata Dharma University in Class A Ordinary Differential Equation Academic Year 2018/2019 on First Order Differential Equations. Thesis. Mathematics Education Study Program. Faculty of Teacher Training and Education.

The research aimed to describe the concept understanding ability of Mathematics Education students of Sanata Dharma University on first order differential equations and knowing the factors those causes the students had trouble when they understood the first order differential equations.

The type of research is decriptive research with qualitative research. Subject of the research were 43 students of Mathematics Education of Sanata Dharma University on the course of Ordinary Differential Equation class A on academic year 2018/2019. The collecting data methods used an essay test and interviews. Data obtained were the students’ answer sheets and interviews transcipt. The analysis data technique used data reduction, display data, and conclusion.

The result of the research showed that 25,58% students could use the procedure or operation when they showed that a function is solution of differential equation; 18,60% students could classify first order differential equations into the characteristics; 4,65% students could use the procedure or operation to determine the general solution of the first order differential equations; and only 2,33% students could apply the concepts or algorithms of first order differential equations to solve problem. The factors those causes the students had trouble when they understood the first order differential equations were internal factors and external factors. Then internal factors were have not understood the previous materials yet (derivative and integral), answered the questions rashly so they did not read and understand the questions; have not understood characteristics of types of first order differential equations, the way to show that a function is general solution of differential equations, the procedure to determine a solution of first order differential equations, and the point of questions; answered the counting not carefully. External factors were less discussed with friends or lecture when have not understood the material and the activities that are not related to Ordinary Differential Equation class.

(10)

ix

KATA PENGANTAR

Puji syukur kepada Tuhan Yang Maha Esa atas rahmat-Nya yang melimpah. Oleh karena rahmat-Nya penulis dapat menyelesaikan skripsi ini dengan baik. Skripsi ini berjudul Analisis Pemahaman Konsep Mahasiswa Pendidikan Matematika

Universitas Sanata Dharma Kelas A Persamaan Diferensial Biasa Tahun Akademik 2018/2019 pada Materi Persamaan Diferensial Orde Satu. Skripsi ini disusun sebagai

pemenuhan salah satu syarat untuk memperoleh sarjana pendidikan Program Studi Pendidikan Matematika Fakultas Keguruan dan Ilmu Pendidikan Universitas Sanata Dharma.

Penulis menyadari bahwa dalam menyelesaikan skripsi ini, penulis mendapat banyak bimbingan, penilaian, saran, dan dukungan dari berbagai pihak. Oleh karena itu, penulis mengucapkan terima kasih kepada:

1. Bapak Febi Sanjaya, M.Sc. selaku dosen pembimbing sekaligus dosen pengampu mata kuliah Persamaan Diferensial Biasa kelas A tahun ajaran 2018/2019 yang telah memberikan kesempatan kepada peneliti untuk melakukan penelitian di kelas yang beliau ampu serta meluangkan waktu untuk membimbing, mengarahkan dan memberikan masukan sebagai penyempurnaan skripsi ini;

2. Bapak Dr. Yohanes Harsoyo, S.Pd., M.Si. selaku Dekan Fakultas Keguruan dan Ilmu Universitas Sanata Dharma Yogyakarta;

3. Bapak Beni Utomo, M.Sc. selaku Ketua Program Studi Pendidikan Matematika Universitas Sanata Dharma Yogyakarta;

4. Bapak Dominikus Arif Budi Prasetyo, M.Si dosen pendidikan matematika yang membantu dalam membuat instrumen yang digunakan, seluruh dosen dan karyawan Program Studi Pendidikan Matematika yang telah memberikan ilmu, bimbingan, dan pengalaman belajar yang memadai kepada penulis selama belajar di Universitas Sanata Dharma;

5. Mas Arif, Bu Tari dan Pak Sugeng selaku staf JPMIPA yang telah membantu segala hal terkait administrasi penulis selama kuliah;

(11)

x

6. Mahasiswa Progam Studi Pendidikan Matematika Universitas Sanata Dharma yang mengikuti perkuliahan Persamaan Diferensial Biasa kelas A tahun ajaran 2018/2019 yang telah bersedia menjadi subjek penelitian.

7. Sahabat dan teman-teman Pendidikan Matematika 2015 yang telah membuka diri untuk berdinamika, berbagi pengalaman, membantu, memberi semangat, dan menerima penulis selama empat tahun perkuliahan.

8. Semua pihak yang secara langsung ataupun tidak langsung sudah membantu selama perkuliahan.

Penulis menyadari bahwa skripsi ini belum sempurna. Penulis membuka diri untuk menerima kritik dan saran yang membangun demi pengembangan ke arah yang lebih baik. Semoga skripsi ini dapat menjadi referensi untuk keperluan studi dan penelitian lebih lanjut.

Yogyakarta, 19 Juli 2019

(12)

xi DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ... iv

PERNYATAAN KEASLIAN KARYA ... v

LEMBAR PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIK ... vi

ABSTRAK ... vii

ABSTRACT ... viii

KATA PENGANTAR ... ix

DAFTAR ISI ... xi

DAFTAR TABEL ... xiv

DAFTAR GAMBAR ... xv

DAFTAR BAGAN ... xix

DAFTAR LAMPIRAN ... xx

DAFTAR SIMBOL ... xxi

BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 4 C. Tujuan Penelitian ... 4 D. Pembatasan Masalah ... 4 E. Penjelasan Istilah ... 5 F. Manfaat Penelitian ... 5

BAB II LANDASAN TEORI ... 6

A. Pemahaman Konsep Matematis ... 6

B. Persamaan Diferensial... 10

(13)

xii

D. Penelitian yang Relevan ... 24

E. Kerangka Berpikir ... 25

BAB III METODOLOGI PENELITIAN ... 27

A. Jenis Penelitian ... 27

B. Subjek Penelitian ... 27

C. Bentuk Data ... 27

D. Waktu dan Tempat Pelaksanaan Penelitian ... 28

E. Metode Pengumpulan Data ... 28

F. Instrumen Pengumpulan Data ... 29

G. Teknik Analisis Data ... 31

H. Prosedur Pelaksanaan Penelitian Secara Keseluruhan ... 32

BAB IV HASIL DAN PEMBAHASAN ... 34

A. Deskripsi Hasil Tes ... 34

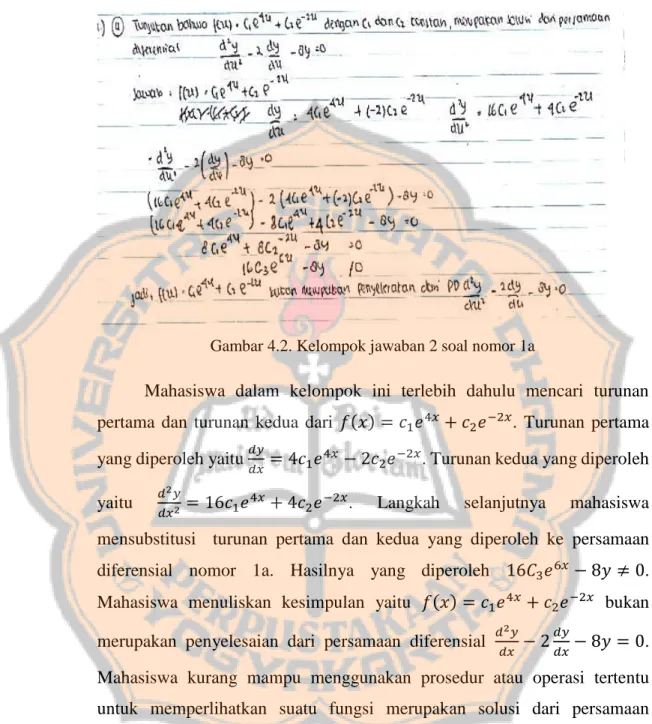
1. Jawaban Soal Nomor 1a ... 34

2. Jawaban Soal Nomor 1b ... 40

3. Jawaban Soal Nomor 2a ... 46

4. Jawaban Soal Nomor 2b ... 51

5. Jawaban Soal Nomor 2c ... 58

6. Jawaban Soal Nomor 2d ... 64

7. Jawaban Soal Nomor 3 ... 69

8. Jawaban soal Nomor 4... 79

B. Deskripsi Hasil Tes dan Wawancara ... 87

1. Subjek M32 ... 87 2. Subjek M41 ... 99 3. Subjek M9 ... 110 4. Subjek M24 ... 121 5. Subjek M15 ... 130 6. Subjek M18 ... 141

(14)

xiii

C. Pembahasan ... 151

1. Ketercapaian Indikator Pemahaman Konsep... 151

2. Faktor-faktor yang Menyebabkan Mahasiswa Kesulitan dalam Memahami Konsep Persamaan Diferensial Orde Satu ... 155

D. Keterbatasan Penelitian ... 155 BAB V PENUTUP ... 157 A. Kesimpulan ... 157 B. Saran ... 158 DAFTAR PUSTAKA ... 160 LAMPIRAN ... 162

(15)

xiv

DAFTAR TABEL

Tabel 3.1. Kategori Hasil Tes ... 28

Tabel 3.2. Kisi-Kisi Soal Tes Esai ... 29

Tabel 3.3. Pertanyaan Wawancara ... 30

Tabel 4.1. Kategori Nilai ... 87

(16)

xv

DAFTAR GAMBAR

Gambar 4.1. Kelompok jawaban 1 soal nomor 1a ... 35

Gambar 4.8. Kelompok jawaban 1 soal nomor 1b ... 41

(17)

xvi

Gambar 4. 28. Kelompok jawaban 7 soal nomor 2b ... 56

Gambar 4.31. Kelompok jawaban 1 soal nomor 2c ... 59

Gambar 4.40. Kelompok jawaban 1 soal nomor 2d ... 64

Gambar 4 44. Kelompok jawaban 5 soal nomor 2d ... 67

Gambar 4.48. Kelompok jawaban 1 soal nomor 3 ... 70

(18)

xvii

Gambar 4.62. Jawaban M32 untuk nomor 1a ... 88

Gambar 4.63. Jawaban M32 untuk nomor 1b ... 89

Gambar 4.66. Jawaban M32 untuk nomor 2c ... 93

Gambar 4.67. Jawaban M32 untuk nomor 2d ... 94

Gambar 4.68. Jawaban M32 untuk nomor 3 ... 96

(19)

xviii

(20)

xix

DAFTAR BAGAN

(21)

xx

DAFTAR LAMPIRAN

Lampiran 1. Surat Ijin ... 163

Lampiran 2. Soal Tes Esai ... 164

Lampiran 3. Kunci Jawaban... 165

Lampiran 4. Lembar Validasi ... 172

Lampiran 5. Nilai Tes Mahasiswa ... 174

Lampiran 6. Jawaban Subjek M32 ... 175

Lampiran 12. Transkip Wawancara Mahasiswa yang Pernah Mengambil Mata Kuliah Persamaan Diferensial Bisa ... 197

(22)

xxi

DAFTAR SIMBOL MATEMATIKA

Simbol Keterangan

𝑎𝑛(𝑥), 𝑓(𝑥), ℎ(𝑥), 𝑃(𝑥), 𝐹(𝑥),𝑄(𝑥) fungsi dalam variabel 𝑥

𝑔(𝑦) fungsi dalam variabel 𝑦

𝑔(𝑣) fungsi dalam variabel 𝑣

𝑓(𝑥, 𝑦), 𝐹(𝑥, 𝑦) 𝑀(𝑥, 𝑦), 𝑁(𝑥, 𝑦) fungsi dalam variabel 𝑥 dan 𝑦

𝑑𝑥 diferensial dari variabel 𝑥

𝑑𝑦 diferensial dari variabel 𝑦

𝑑𝑣 diferensial dari variabel 𝑣

𝑑𝑧 diferensial dari variabel 𝑧

𝜕𝑥 diferensial parsial dari variabel 𝑥 𝜕𝑦 diferensial parsial dari variabel 𝑦 𝜕𝑧 diferensial parsial dari variabel 𝑧

𝑑𝑦

𝑑𝑥 turunan pertama 𝑦 terhadap 𝑥

𝑑𝑣

𝑑𝑥 turunan pertama 𝑦 terhadap 𝑣

𝑑2_𝑦

𝑑𝑥2 turunan kedua 𝑦 terhadap 𝑥

𝑑𝑛_𝑦

𝑑𝑥𝑛 turunan ke-𝑛 dari 𝑦 terhadap 𝑥

𝜕𝑣

𝜕𝑠 turunan parsial pertama 𝑣 terhadap 𝑠 𝜕𝑣

𝜕𝑡 turunan parsial pertama 𝑣 terhadap 𝑡 𝜕𝑧

𝜕𝑥 turunan parsial pertama 𝑧 terhadap 𝑥 𝜕𝑧

𝜕𝑦 turunan parsial pertama 𝑧 terhadap 𝑦 𝜕2𝑧

𝜕𝑥2 turunan parsial kedua 𝑧 terhadap 𝑥 𝜕2𝑧

𝜕𝑦2 turunan parsial kedua 𝑧 terhadap 𝑦 ∫ 𝑓(𝑥)𝑑𝑥 integral tak tentu dari 𝑓(𝑥) terhadap 𝑥

∫ 𝑔(𝑦)𝑑𝑦 integral tak tentu dari 𝑔(𝑦) terhadap 𝑦

𝑒 konstanta Euler 𝑐, 𝑐₀, 𝑐₁, 𝑐₂ konstanta 𝜆 lambda 𝜖 anggota/elemen ℝ bilangan riil ln logaritma natural

(23)

xxii

𝜇(𝑥) faktor integral (fungsi dalam variabel 𝑥)

𝑥_𝑖 nilai mahasiswa

𝑥̅ rata-rata nilai mahasiswa

(24)

1 BAB I PENDAHULUAN A. Latar Belakang

Matematika berperan penting dalam perkembangan ilmu pengetahuan dan teknologi sehingga berpengaruh kepada kehidupan sehari-hari. Matematika merupakan ilmu dasar yang sebaiknya dipelajari oleh semua orang dari tingkat SD sampai SMA bahkan perguruan tinggi karena membantu seseorang dalam memperoleh, mengelola, dan memanfaatkan informasi secara logis, kritis dan kreatif untuk bertahan hidup pada keadaan yang selalu berubah-ubah dan kompetitif (Lestari, 2015). Pembelajaran matematika di perguruan tinggi bertujuan untuk mengembangkan segala kemampuan matematis mahasiswa dalam memperoleh hasil belajar yang maksimal. Salah satu kemampuan yang dikembangkan dalam pembelajaran matematika yaitu kemampuan pemahaman konsep. Pemahaman konsep merupakan kemampuan mengklasifikasikan dan menjelaskan informasi atau objek yang diperoleh berdasarkan karakteristiknya.

Kesumawati (dalam Ningsih, 2016), menyatakan bahwa landasan penting yang harus dimiliki oleh peserta didik dalam usahanya untuk berpikir menyelesaikan permasalahan matematika maupun permasalahan dalam kehidupan sehari-hari adalah kemampuan dalam memahami konsep matematika. Konsep-konsep membantu kita untuk mengidentifikasi objek-objek yang ada di sekitar kita dengan cara mengenali ciri-ciri masing-masing objek (Hamalik, 2001 : 16). Pentingya kemampuan pemahaman konsep juga disampaikan oleh National

Council of Teacher of Mathematics (2000: 11), yaitu peserta didik harus belajar

matematika dengan pemahaman, secara aktif membangun pengetahuan baru dari pengalaman dan pengetahuan sebelumnya. Prinsip ini didasarkan pada ide bahwa belajar matematika dengan pemahaman adalah penting. Belajar matematika tidak hanya terkait keterampilan menghitung tetapi juga memerlukan kemampuan untuk berpikir beralasan secara matematis untuk menyelesaikan masalah-masalah baru.

(25)

Mahasiswa pendidikan matematika juga sebagai calon guru matematika harus mengembangkan kemampuan pemahaman konsep karena menjadi tujuan pertama yang diharapkan dapat tecapai dalam pembelajaran matematika di sekolah. KTSP 2006 yang disempurnakan pada Kurikulum 2013 (Hendriana dan Soemarno, 2014 :7), mencantumkan tujuan pembelajaran matematika yang intinya terdiri dari kemampuan dalam: (1) memahami konsep matematika, (2) menggunakan penalaran, (3) memecahkan masalah, (4) mengomunikasikan gagasan, dan (5) memiliki sikap menghargai kegunaan matematika.

Salah satu mata kuliah yang ada di program studi pendidikan matematika adalah persamaan diferensial biasa. Menurut Ross (1984), persamaan diferensial adalah persamaan yang memuat turunan-turunan dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas. Persamaan diferensial seringkali muncul dalam model matematika yang mencoba menggambarkan dunia nyata, seperti laju perubahan suhu, konsentrasi zat, pertumbuhan penduduk dan bidang ilmu lainnya. Mallet (dalam Ningsih dan Rohana, 2018) berpendapat bahwa persamaan diferensial memfokuskan pada teknik algoritma untuk menentukan solusi dari beberapa tipe spesifik persamaan diferensial.

Berdasarkan pengalaman ketika belajar persamaan diferensial di semester VI, kemampuan pemahaman konsep sangat penting. Pada persamaan diferensial orde satu, mahasiswa harus mampu membedakan bentuk persamaan diferensial seperti persamaan diferensial separabel, homogen, eksak, linear dan Bernoulli. Berdasarkan hasil wawancara dengan 4 mahasiswa angkatan 2015 yang pernah mengambil mata kuliah persamaan diferensial biasa, letak kesulitan dalam menyelesaikan soal terkait persamaan diferensial orde satu diantaranya, kesulitan dalam memahami materi, menemukan ide awal dalam hal ini membedakan jenis-jenis persamaan diferensial orde satu, serta menyelesaikan turunan dan integral untuk mencari solusi dari persamaan diferensial orde satu.

(26)

Hasil penelitian yang dilakukan Oktavia dan Khotimah (2016 : 99 – 108) terkait analisis kesulitan mahasiswa dalam menyelesaikan persamaan diferensial tingkat satu adalah pertama, kesulitan pemahaman konsep yang meliputi kesulitan merumuskan ciri atau bentuk umum persamaan diferensial, kesulitan menentukan teknik penyelesaian persamaan diferensial. Kedua, kesulitan penerapan konsep yang terdiri terdiri kesulitan dalam langkah-langkah perhitungan, kesulitan dalam materi prasyarat. Sementara penelitian yang dilakukan Naisunis, Taneo, dan Daniel (2018: 107 – 119) terkait analisis kesalahan mahasiswa dalam pemecahan masalah persamaan diferensial memperlihatkan bahwa kesalahan yang paling banyak dilakukan mahasiswa dalam tahap pemecahan masalah adalah kesalahan konsep. Ningsih dan Rohana (2018: 168 – 176) melakukan penelitian terkait pemahaman mahasiswa terhadap persamaan diferensial biasa berdasarkan teori APOS (Action

– Process – Object – Schema). Hasil penelitian yang dilakukan memperlihatkan

bahwa sebagian besar mahasiswa hanya mampu memahami konsep pada tahap aksi. Pada teori APOS, seseorang yang memiliki kemampuan pemahaman konsep yang baik akan mencapai pada tahap skema.

Berdasarkan pengamatan yang dilakukan pada tanggal 15 Februari 2019 terhadap mahasiswa yang mengambil mata kuliah Persamaan Diferensial Biasa tahun akademik 2018/2019 di kelas A, peneliti menemukan masalah terhadap kemampuan pemahaman mahasiswa. Ketika dosen memberikan soal terkait integral, mahasiswa kesulitan dalam menyelesaikannya karena tidak mampu mengidentifikasi bentuk integral yang diberikan. Konsep integral sendiri sangat penting dalam pembelajaran persamaan diferensial. Penyelesaian pada persamaan diferensial berkaitan dengan teknik pengintegralan. Kemudian saat dosen memberikan contoh persamaan diferensial dan meminta mahasiswa memberikan contoh yang lain, mahasiswa mengalami kesulitan.

Dari uraian di atas, peneliti tertarik untuk mengetahui secara mendalam kemampuan pemahaman konsep mahasiswa Pendidikan Matematika Universitas

(27)

Sanata Dharma yang mengambil mata kuliah Persamaan Diferensial Biasa tahun akademik 2018 / 2019 di kelas A. Materi yang digunakan yaitu persamaan diferensial orde satu.

B. Rumusan Masalah

Berdasarkan latar belakang masalah di atas, peneliti merumuskan masalah sebagai berikut:

1. Bagaimana kemampuan pemahaman konsep mahasiswa Pendidikan Matematika Universitas Sanata Dharma yang mengambil mata kuliah Persamaan Diferensial Biasa tahun akademik 2018/2019 kelas A terhadap materi persamaan diferensial orde satu?

2. Faktor-faktor apa saja yang menyebabkan mahasiswa kesulitan dalam memahami konsep persamaan diferensial orde satu?

C. Tujuan Penelitian

Sesuai rumusan masalah di atas, penelitian ini bertujuan untuk:

1. mendeskripsikan kemampuan pemahaman konsep mahasiswa Pendidikan Matematika Universitas Sanata Dharma yang mengambil mata kuliah Persamaan Diferensial Biasa tahun akademik 2018/2019 kelas A pada materi persamaan diferensial orde satu.

2. mengetahui faktor-faktor yang menyebabkan mahasiswa kesulitan dalam memahami konsep persamaan diferensial orde satu.

D. Pembatasan Masalah

Batasan masalah pada penelitian ini adalah sebagai berikut.

1. Mahasiswa yang menjadi subyek penelitian ialah mahasiswa Pendidikan Matematika Universitas Sanata Dharma yang mengikuti mata kuliah Persamaan Diferensial Biasa di tahun akademik 2018/2019 kelas A.

(28)

E. Penjelasan Istilah

1. Pemahaman konsep adalah kemampuan seseorang untuk menerjemahkan, menjelaskan, menganalisis dan menyimpulkan informasi atau materi yang diperolehnya dalam bentuk ucapan maupun tulisan

2. Persamaan diferensial adalah persamaan yang memuat turunan-turunan dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas.

3. Persamaan diferensial orde satu adalah persamaan diferensial yang indeks tertinggi dari turunan yang terlibat dalam persamaannya yaitu satu.

F. Manfaat Penelitian 1. Bagi Dosen

a. Penelitian ini dapat memberikan informasi kepada dosen Program Studi Pendidikan Matematika mengenai kemampuan pemahaman konsep mahasiswa pada materi persamaan diferensial orde satu.

b. Informasi yang diperoleh dari penelitian ini dapat membantu dosen pengampu mata kuliah persamaan diferensial biasa untuk melakukan evaluasi pada sistem pembelajaran yang dilakukan.

2. Bagi Mahasiswa

Penelitian ini membantu mahasiswa mengetahui kemampuan pemahaman konsep mereka terkait persamaan diferensial orde satu dan memotivasi mereka untuk meningkatkan kemampuannya.

3. Bagi peneliti

Penelitian ini dapat menambah wawasan dan pengalaman baru dalam penelitian terkait kemampuan pemahaman konsep terhadap materi persamaan diferensial orde satu. Hasil penelitian ini dapat digunakan sebagai salah satu referensi para peneliti yang lain untuk mengetahui pemahaman mahasiswa.

(29)

6 BAB II

LANDASAN TEORI A. Pemahaman Konsep Matematis

1. Pengertian Pemahaman

Pemahaman menurut Bloom (Susanto, 2013: 6) diartikan sebagai kemampuan untuk menyerap arti dari materi atau bahan yang dipelajari. Maksud dari pemahaman Bloom ini adalah seberapa besar peserta didik mampu menerima, menyerap, dan memahami pelajaran yang diberikan oleh guru kepada peserta didik, atau sejauh mana peserta didik dapat memahami serta mengerti apa yang ia baca, yang dilihat, yang dialami, atau yang ia rasakan berupa hasil penelitian observasi langsung yang ia lakukan.

Susanto (2013: 7) sendiri mengkategorikan pemahaman dalam beberapa aspek dengan kriteria-kriteria sebagai berikut:

a. Pemahaman merupakan kemampuan untuk menerangkan dan menginterpretasikan sesuatu; ini berarti bahwa seseorang yang telah memahami sesuatu atau telah memperoleh pemahaman akan mampu menerangkan atau menjelaskan kembali apa yang telah ia terima. Selain itu, bagi mereka yang telah memahami tersebut, maka ia mampu memberikan interpretasi atau menafsirkan secara luas sesuai dengan keadaan yang ada di sekitarnya, ia mampu menghubungkan dengan kondisi yang ada saat ini dan yang akan datang.

b. Pemahaman bukan sekadar mengetahui, yang biasanya hanya sebatas mengingat kembali pengalaman dan memproduksi apa yang pernah dipelajari. Bagi orang yang benar-benar telah paham ia akan mampu memberikan gambaran, contoh, dan penjelasan yang lebih luas dan memadai.

c. Pemahaman lebih dari sekadar mengetahui, karena pemahaman melibatkan proses mental yang dinamis dengan memahami ia akan mampu memberikan

(30)

uraian dan penjelasan yang lebih kreatif, tidak hanya memberikan gambaran yang lebih luas dan baru sesuai dengan kondisi saat ini.

d. Pemahaman merupakan suatu proses bertahap yang masing-masing tahap mempunyai kemampuan tersendiri, seperti menerjemahkan, menginterpretasi, ekstrapolasi, aplikasi, analisis, sintesis, dan evaluasi.

Menurut Van De Walle (2008: 26), pemahaman dapat didefinisikan sebagai ukuran kualitas dan kuantitas hubungan suatu ide dengan ide yang telah ada. Tingkat kemampuan pemahaman peserta didik berbeda tergantung kemampuan awal yang dimilikinya. Pemahaman membantu peserta didik untuk melihat hubungan yang sederhana di antara fakta-fakta atau konsep. (Arikunto, 2012: 131)

2. Pengertian Konsep

Woolfolk (dalam Suradi, 2004) mendefinisikan konsep sebagai suatu kategori yang digunakan untuk mengelompokkan ide-ide, peristiwa-peristiwa, orang-orang, dan objek-objek yang similar atau serupa. Sementara Hulse, Egeth dan Deese (dalam Suharnan, 2005: 115) mendefinisikan konsep sebagai sekumpulan atau seperangkat sifat yang dihubungkan oleh aturan-aturan tertentu. Suatu sifat merupakan setiap aspek dari sesuatu objek, atau kejadian yang memiliki sifat-sifat yang sama dengan objek atau kejadian yang lain. Suatu aturan adalah instruksi untuk berbuat sesuatu.

Menurut Hamalik (2001: 162), suatu konsep adalah suatu kelas atau kategori stimuli yang memiliki ciri-ciri umum. Stimuli adalah objek-objek atau orang. Belajar konsep berguna dalam rangka pendidikan peserta didik atau paling tidak punya pengaruh tertentu. Orang yang telah memiliki konsep, berarti orang tersebut telah memiliki pemahaman jelas tentang suatu konsep atau citra mental tentang sesuatu. Sesuatu tersebut dapat berupa objek konkret ataupun gagasan yang abstrak.

(31)

Soedjadi (2000: 4) mendefinisikan konsep sebagai ide abstrak yang dapat digunakan untuk menggolongkan atau mengklasifikasikan sekumpulan objek. Kosep berhubungan erat dengan definisi. Definisi adalah ungkapan yang membatasi suatu konsep. Dengan adanya definisi orang dapat membuat ilustrasi atau gambar atau lambang dari konsep yang didefinisikan.

Berdasarkan pengertian-pengertian mengenai pemahaman dan konsep, dapat dikatakan pemahaman konsep adalah kemampuan seseorang untuk menerjemahkan, menjelaskan, menganalisis dan menyimpulkan informasi atau materi yang diperolehnya dalam bentuk ucapan maupun tulisan.

3. Pemahaman Konsep Matematis

Hudojo (2001 : 136) mendefinsikan konsep matematika merupakan suatu ide abstrak yang memungkinkan kita mengklasifikasikan objek-objek dan peristiwa-peristiwa ke dalam ide abstrak tersebut. Lebih lanjut Hudojo berpendapat bahwa belajar matematika berarti belajar tentang konsep-konsep dan struktur-struktur yang terdapat dalam bahasan yang dipelajari serta mencari hubungan-hubungan antara konsep-konsep dan struktur-struktur tersebut. Konsep dalam matematika biasanya dituliskan dalam bentuk definisi.

Dubinsky dan McDonald (dalam Ningsih dan Rohana, 2018: 169), berpendapat bahwa pemahaman terhadap suatu konsep matematika merupakan hasil konstruksi atau rekonstruksi dari objek-objek matematika. Proses konstruksi atau rekonstruksi konsep matematika tersebut terjadi melalui tahapan aksi, proses dan objek, yang tergabung membentuk suatu skema dalam menyelesaikan permasalahan matematika.

Menurut Lestari dan Yudhanegara (2015: 81), kemampuan pemahaman matematis adalah kemampuan menyerap ide-ide matematika. Sementara Skemp (dalam Hendriana dan Soemarmo, 2014: 20) menggolongkan pemahaman dalam dua tingkat, yaitu pemahaman instrumental dan pemahaman relasional. Pemahaman instrumental merupakan kemampuan menghafal dan memahami

(32)

konsep/prinsip secara terpisah, menerapkan rumus dalam perhitungan sederhana, dan mengerjakan perhitungan secara algoritmik. Pemahaman relasional merupakan kemampuan mengaitkan suatu konsep/prinsip lainnya.

Secara sederhana kemampuan pemahaman konsep matematis merupakan kemampuan untuk mengklasifikasikan dan menjelaskan ide-ide matematika. Untuk mencapai pemahaman yang bermakna maka pembelajaran matematika harus diarahkan pada pengembangan kemampuan koneksi matematik antar berbagai ide, memahami bagaimana ide-ide matematik saling terkait satu sama lain sehingga terbangun pemahaman menyeluruh, dan menggunakan matematika dalam konteks di luar matematika. (NCTM, 2000)

4. Indikator Pemahaman Konsep

Menurut Hamalik (2001: 166), untuk mengetahui apakah peserta didik mengetahui suatu konsep paling tidak ada empat hal yang dapat diperbuatnya, yaitu sebagai berikut.

a. Ia menyebutkan nama contoh-contoh konsep bila dia melihatnya. b. Ia dapat menyatakan ciri-ciri (properties) konsep tersebut.

c. Ia dapat memilih, membedakan antara contoh-contoh dari yang bukan contoh. d. Ia mungkin lebih mampu memecahkan masalah yang berkenaan dengan

konsep tersebut.

Sementara menurut Depdiknas (dalam Yunika dan Rohana, 2018) indikator pemahaman konsep antara lain yaitu:

1) Menyatakan ulang sebuah konsep;

2) Mengklasifikasikan objek-objek menurut sifat-sifat tertentu sesuai dengan konsepnya;

3) Memberikan contoh dan non-contoh dari konsep;

4) Menyajikan konsep dalam berbagai bentuk representasi matematis; 5) Mengembangkan syarat perlu atau syarat cukup suatu konsep;

(33)

7) Mengaplikasikan konsep atau algoritma ke pemecahan masalah. 5. Faktor- Faktor yang Mempengaruhi Kemampuan Pemahaman Konsep

Tinggi rendahnya kemampuan pemahaman konsep seseorang sangat berkaitan dengan faktor-faktor yang mempengaruhi proses belajar. Menurut Suradi (2002) mengemukakan beberapa faktor yang mempengaruhi mudah atau sulitnya orang belajar konsep, yaitu: (a) kejelasan dan kekonkretan ciri-ciri utama definisi; (b) tersedianya definisi; (c) penyajian contoh-contoh positif; (d) penyajian contoh-contoh negatif; dan (e) penyajiannya yang simultan dilawankan dengan penyajian yang sekuensial dari contoh-contoh positif dan contoh-contoh negatif.

Pemahaman konsep merupakan bagian dari hasil belajar. Menurut Susanto (2013: 12), faktor yang mempengaruhi hasil belajar peserta didik dibagi menjadi dua faktor internal dan eksternal.

a. Faktor internal

Faktor internal merupakan faktor yang bersumber dari dalam diri peserta didik, mempengaruhi kemampuan belajarnya. Faktor internal ini meliputi: kecerdasan, minat dan perhatian, motivasi belajar, ketekunan, sikap, kebiasaan belajar, serta kondisi fisik dan kesehatan.

b. Faktor eksternal

Faktor yang berasal dari luar diri peserta didik yang mempengaruhi hasil belajar . Faktor eksternal ini diantaranya teman belajar, guru, kejelasan materi, dan lingkungan sekitarnya.

B. Persamaan Diferensial

Berikut adalah penjelasan materi persamaan diferensial menurut Ross (1984). Definisi 1

Persamaan diferensial adalah persamaan yang memuat turunan-turunan dari satu atau lebih variabel tak bebas terhadap satu atau lebih variabel bebas.

(34)

Persamaan diferensial biasa adalah suatu persamaan yang memuat turunan-turunan dari satu atau lebih variabel tak bebas terhadap satu variabel bebas. Definisi 3

Persamaan diferensial parsial adalah suatu persamaan yang memuat turunan-turunan parsial dari satu atau lebih variabel tak bebas terhadap lebih dari satu variabel bebas.

Berikut adalah beberapa contoh untuk persamaan diferensial biasa atau parsial. Contoh 1 a. 𝑑𝑦_𝑑𝑥= 5𝑥 − 5 b. 𝑑 2_𝑦 𝑑𝑥2+ 3 𝑑𝑦 𝑑𝑥− 7𝑦 = 0 c. 𝜕𝑣_𝜕𝑠+𝜕𝑣_𝜕𝑡 = 𝑣 d. 𝜕 2_𝑧 𝜕𝑥2+ 𝜕2𝑧 𝜕𝑦2 = 𝑥2

Berdasarkan contoh (1) serta mengacu definisi (2) dan definisi (3), persamaan (a) dan (b) termasuk ke dalam persamaan diferensial biasa. Persamaan (c) dan (d) termasuk ke dalam persamaan diferensial parsial.

Tingkat turunan tertinggi yang muncul dalam persamaan diferensial disebut order Definisi 4.

Orde persamaan diferensial adalah tingkat tertinggi dari semua turunan yang terdapat pada persamaan diferensial tersebut.

Definisi 5.

Pangkat dari persamaan diferensial adalah pangkat dari turunan tingkat tertinggi setelah persamaan diferensial setelah persamaan diferensial tersebut ditulis dalam bentuk polinomial dalam turunan.

Contoh 2 a. 𝑑𝑦 𝑑𝑥 = 𝑥 + 2 b. (𝑑 4_𝑦 𝑑𝑥2) 2 + 5𝑑𝑦 𝑑𝑥+ 6 = 0

(35)

c. 𝜕𝑧

𝜕𝑥= 𝑧 + 𝑥 𝜕𝑧 𝜕𝑦

Pada contoh (2) persamaan (a) merupakan persamaan diferensial orde satu dan berpangkat satu. Persamaan (b) merupakan persamaan diferensial orde empat dan berpangkat dua. Persamaan (c) merupakan persamaan diferensial orde satu dan berpangkat satu.

Definisi 6

Persamaan diferensial orde 𝑛, dengan variabel tak bebas 𝑦 dan variabel bebas 𝑥, dapat dinyatakan dalam bentuk

𝑎₀(𝑥)𝑑_𝑑𝑥𝑛𝑦_𝑛+ 𝑎₁(𝑥)𝑑_𝑑𝑥𝑛−1_𝑛−1𝑦+ ⋯ + 𝑎_𝑛(𝑥)𝑦 = 𝑃(𝑥) (2.1) Dimana 𝑎₀ ≠ 0

Persamaan diferensial dikatakan memiliki bentuk linear jika memenuhi syarat-syarat berikut ini

1. Derajat dari variabel tak bebas dan turunan-turunannya adalah satu.

2. Tidak ada perkalian antara variabel bebas dan turunan-turunannya maupun perkalian antara turunan dengan turunannya.

3. Tidak ada fungsi transenden dari variabel-variabel tak bebas.

Jika tidak memenuhi syarat-syarat disebut persamaan diferensial tak linear. Penyelesaian Persamaan Diferensial

Definisi 7

Misalkan persamaan diferensial orde 𝑛

𝐹 (𝑑_𝑑𝑥𝑛𝑦_𝑛,_𝑑𝑥𝑑𝑛−1_𝑛−1, … ,𝑑𝑦_𝑑𝑥, 𝑥) = 0 (2.2) 1. Misal 𝑓 adalah fungsi 𝑥 real pada interval 𝐼 dan mempunyai turunan sampai

orde 𝑛 pada interval 𝐼. Fungsi 𝑓 disebut penyelesaian (solusi) eksplisit persamaan diferensial (2.2) jika memenuhi persamaan :

𝐹 (𝑑_𝑑𝑥𝑛𝑦_𝑛,_𝑑𝑥𝑑𝑛−1_𝑛−1, … ,𝑑𝑦_𝑑𝑥, 𝑥) = 0 Untuk setiap 𝑥 ∈ 𝐼

(36)

2. Fungsi implisit 𝑔(𝑥, 𝑦) = 0 disebut penyelesaian (solusi) implisit persamaan diferensial (2.2) apabila 𝑔 dapat mendefinisikan penyelesaian eksplisit persamaan diferensial.

3. Penyelesaian eksplisit dan implisit persamaan diatas disebut penyelesaian (solusi) persamaan diferensial.

Contoh 3

Diberikan sembarang persamaan diferensial 𝑑 2_𝑦 𝑑𝑥2− 4

𝑑𝑦

𝑑𝑥+ 4𝑦 = 0

Selidikilah apakah 𝑦 = 𝑒2𝑥_{, merupakan penyelesaian bagi persamaan diferensial}

diatas.

Penyelesaian:

Diketahui 𝑦 = 𝑒2𝑥 sehingga 𝑑𝑦_𝑑𝑥= 2𝑒2𝑥 , 𝑑 2_𝑦

𝑑𝑥2 = 4𝑒2𝑥, disubstitusikan pada ruas kiri persamaan diferensial semula dihasilkan

𝑑2_𝑦 𝑑𝑥2− 4

𝑑𝑦

𝑑𝑥+ 4𝑦 = 4𝑒

2𝑥_{− 4(2𝑒}2𝑥_{) + 4(𝑒}2𝑥_{) = 0}

Karena dihasilkan kesamaan identitas, maka dapat disimpulkan bahwa 𝑦 = 𝑒2𝑥 merupakan penyelesaian bagi persamaan diferensial 𝑑2𝑦

𝑑𝑥2− 4 𝑑𝑦

𝑑𝑥+ 4𝑦 = 0

Masalah Syarat Batas

Diberikan persamaan diferensial

𝑑𝑦

𝑑𝑥= 2𝑥 dengan syarat 𝑦(1) = 4

Tentukan penyelesaian persamaan diferensial tersebut. Penyelesaian:

Diketahui persamaan diferensial

𝑑𝑦

𝑑𝑥 = 2𝑥

𝑑𝑦 = 2𝑥 𝑑𝑥

dengan mengintegralkan kedua ruas didapatkan 𝑦 = 𝑥2_{+ 𝑐}

(37)

4 = 12_{+ 𝑐}

𝑐 = 3

Sehingga penyelesaian persamaan diferensial tersebut menjadi 𝑦 = 𝑥2_{+ 3}

Secara garis besar konsep penyelesaian persamaan diferensial dapat digolongkan menjadi:

1. Penyelesaian umum, bilamana penyelesaian persamaan diferensial memuat sembarang konstanta.

2. Penyelesaian khusus, bilamana konstanta dari penyelesaian umum persamaan diferensial diberikan oleh nilai tertentu. Penyelesaian khusus ini biasa dikenal dengan masalah syarat batas persamaan diferensial.

C. Persamaan Diferensial Orde Satu

Persamaan diferensial orde satu adalah persamaan yang dapat ditulis dalam bentuk

𝑑𝑦

𝑑𝑥= 𝑓(𝑥, 𝑦) (2.3)

atau dapat ditulis

𝑀(𝑥, 𝑦)𝑑𝑥 + 𝑁(𝑥, 𝑦)𝑑𝑦 = 0 (2.4) Contoh 4 𝑑𝑦 𝑑𝑥= 𝑥2+𝑦2 𝑥−𝑦

dapat ditulis dalam bentuk persamaan diferensial (2.4) menjadi (𝑥2_{+ 𝑦}2_{)𝑑𝑥 + (𝑦 − 𝑥)𝑑𝑦 = 0}

1. Persamaan Diferensial Separabel

Persamaan diferensial separabel adalah persamaan diferensial yang memiliki bentuk umum

𝑔(𝑦)𝑑𝑦_𝑑𝑥= 𝑓(𝑥) (2.5)

Persamaan diferensial (2.4) dapat ditulis menjadi 𝑔(𝑦)𝑑𝑦 = 𝑓(𝑥)𝑑𝑥

(38)

∫ 𝑔(𝑦)𝑑𝑦 = ∫ 𝑓(𝑥)𝑑𝑥

Jika fungsi-fungsi f dan g kontinu, maka nilai integralnya ada dan hasil integralnya merupakan penyelesaian persamaan diferensial tersebut.

Contoh 5

Tentukan penyelesaian persamaan diferensial 16𝑦𝑑𝑦_𝑑𝑥+ 9𝑥 = 0. Penyelesaian: 16𝑦𝑑𝑦_𝑑𝑥+ 9𝑥 = 0 16𝑦𝑑𝑦_𝑑𝑥= −9𝑥 16𝑦 𝑑𝑦 = −9𝑥 𝑑𝑥 ∫ 16𝑦 𝑑𝑦 = ∫ −9𝑥 𝑑𝑥 8𝑦2 _{= −}9 2𝑥 2_{+ 𝑐} 8𝑦2₊9 2𝑥 2 _{= 𝑐}

Jadi, penyelesaian persamaan diferensial di atas adalah 8𝑦2₊9 2𝑥

2 _{= 𝑐}

2. Persamaan Diferensial Homogen

Fungsi 𝐹(𝑥, 𝑦) disebut fungsi homogen bila terdapat 𝑛 ∈ ℝ sehingga berlaku 𝐹(𝜆𝑥, 𝜆𝑦) = 𝜆𝑛_{𝐹(𝑥, 𝑦), dengan 𝑛 order dari fungsi homogen 𝐹(𝑥, 𝑦).}

Ciri umum persamaan diferensial homogen adalah tiap suku derajatnya sama. Contoh 6

Diberikan 𝑓(𝑥, 𝑦) = 𝑥3− 2𝑥𝑦2+ 𝑦3, fungsi 𝑓 adalah fungsi homogen bederajat tiga karena berlaku

𝑓(𝜆𝑥, 𝜆𝑦) = (𝜆𝑥)3_{− 2(𝜆𝑥)(𝜆𝑦)}2_{+ (𝜆𝑦)}3

= 𝜆3_𝑥3 _{− 𝜆}3_2𝑥𝑦2_{+ 𝜆}3_𝑦3

= 𝜆3_(𝑥3_{− 2𝑥𝑦}2_{+ 𝑦}3₎

= 𝜆3_{𝑓(𝑥, 𝑦)}

Persamaan diferensial homogen adalah persamaan diferensial yang memiliki bentuk umum

(39)

𝑑𝑦 𝑑𝑥= 𝑔 (

𝑦

𝑥) (2.6)

Penyelesaian persamaan diferensial homogen.

Untuk menentukan penyelesaian umumnya, persamaan diferensial homogen direduksi menjadi persamaan diferensial separabel, dengan substitusi 𝑦 = 𝑣𝑥 Sehingga 𝑑𝑦

𝑑𝑥= 𝑣 + 𝑥 𝑑𝑣 𝑑𝑥

Persamaan (2.6) akan menjadi 𝑣 + 𝑥𝑑𝑣_𝑑𝑥= 𝑔(𝑣) [𝑣 − 𝑔(𝑣)]𝑑𝑥 + 𝑥 𝑑𝑣 = 0

Persamaan diferensial tersebut merupakan persamaan diferensial separabel. Dengan mengalikan _{[𝑣−𝑔(𝑣)]𝑥}1 diperoleh

𝑑𝑥 𝑥 +

𝑑𝑣

𝑣−𝑔(𝑣) = 0

Kemudian dengan pengintegralan akan didapatkan penyelesaiannya. Contoh 7

Tentukan penyelesaian persamaan diferensial (𝑥 − 𝑦)𝑑𝑥 = 𝑥 𝑑𝑦 . Penyelesaian : (𝑥 − 𝑦)𝑑𝑥 = 𝑥 𝑑𝑦 . 𝑥−𝑦 𝑥 = 𝑑𝑦 𝑑𝑥 1 −𝑦_𝑥 =𝑑𝑦_𝑑𝑥

Persamaan diferensial tersebut merupakan persamaan diferensial homogen, dengan memisalkan 𝑦 = 𝑣𝑥 atau 𝑦_𝑥= 𝑣, diperoleh

1 − 𝑣 = 𝑣 + 𝑥𝑑𝑣_𝑑𝑥 1 − 2𝑣 = 𝑥_𝑑𝑥𝑑𝑣 1 1−2𝑣𝑑𝑣 = 1 𝑥𝑑𝑥 ∫_1−2𝑣1 𝑑𝑣 = ∫1_𝑥𝑑𝑥

(40)

ln|1 − 2𝑣| = ln|𝑥| + 𝑐 ln |1 −2𝑦_𝑥| = ln|𝑥| + 𝑐

3. Persamaan Diferensial Eksak Persamaan diferensial orde satu

𝑀(𝑥, 𝑦)𝑑𝑥 + 𝑁(𝑥, 𝑦)𝑑𝑦 = 0

Dikatakan sebagai persamaan diferensial eksak jika persamaan itu mempunyai diferensial total dari 𝐹(𝑥, 𝑦) = 𝑐

𝑑𝐹(𝑥, 𝑦) =𝜕𝐹(𝑥,𝑦)_𝜕𝑥 𝑑𝑥 + 𝜕𝐹(𝑥,𝑦)_𝜕𝑦 𝑑𝑦 (2.7) dimana 𝜕𝐹(𝑥,𝑦) 𝜕𝑥 = 𝑀(𝑥, 𝑦) dan 𝜕𝐹(𝑥,𝑦) 𝜕𝑦 = 𝑁(𝑥, 𝑦). (2.8)

Andaikan 𝑀(𝑥, 𝑦) dan 𝑁(𝑥, 𝑦) memiliki turunan di semua titik maka dari persamaan (2.8) diperoleh 𝜕2_{𝐹(𝑥,𝑦)} 𝜕𝑦𝜕𝑥 = 𝜕𝑀(𝑥,𝑦) 𝜕𝑦 dan 𝜕2_{𝐹(𝑥,𝑦)} 𝜕𝑥𝜕𝑦 = 𝜕𝑁(𝑥,𝑦) 𝜕𝑥

karena 𝜕𝑀(𝑥,𝑦)_𝜕𝑦 dan 𝜕𝑁(𝑥,𝑦)_𝜕𝑥 kontinu, maka

𝜕2𝐹(𝑥,𝑦) 𝜕𝑦𝜕𝑥 = 𝜕2𝐹(𝑥,𝑦) 𝜕𝑥𝜕𝑦 Sehingga 𝜕𝑀(𝑥,𝑦) 𝜕𝑦 = 𝜕𝑁(𝑥,𝑦) 𝜕𝑥

merupakan syarat perlu dan syarat cukup agar 𝑀(𝑥, 𝑦)𝑑𝑥 + 𝑁(𝑥, 𝑦)𝑑𝑦 = 0. Penyelesaian persamaan diferensial eksak.

Fungsi 𝐹(𝑥, 𝑦) sebagai fungsi penyelesaian persamaan diferensial eksak diperoleh melalui operasi pengintegralan sebagai berikut.

a. Integralkan terhadap variabel 𝑥 sehingga diperoleh 𝐹(𝑥, 𝑦) = ∫ 𝑀(𝑥, 𝑦)𝑑𝑥 + 𝑔(𝑦)

(41)

𝑔(𝑦) adalah konstanta pengintegralan dan nilainya dapat ditentukan dengan

𝜕𝐹(𝑥,𝑦)

𝜕𝑦 = 𝑁(𝑥, 𝑦).

b. Integralkan terhadap variabel 𝑦, sehingga diperoleh 𝐹(𝑥, 𝑦) = ∫ 𝑁(𝑥, 𝑦)𝑑𝑦 + ℎ(𝑥)

ℎ(𝑥) adalah konstanta pengintegralan dan nilainya ditentukan dengan

𝜕𝐹(𝑥,𝑦)

𝜕𝑥 = 𝑀(𝑥, 𝑦).

Contoh 8

Tentukan penyelesaian persamaan diferensial (3𝑥 + 2𝑦)𝑑𝑥 + (2𝑥 + 𝑦)𝑑𝑦 = 0 Penyelesain:

Buktikan terlebih dahulu persamaan tersebut merupakan persamaan diferensial eksak. 𝑀(𝑥, 𝑦) = 3𝑥 + 2𝑦 𝑁(𝑥, 𝑦) = 2𝑥 + 𝑦 𝜕𝑀(𝑥,𝑦) 𝜕𝑦 = 2 𝜕𝑁(𝑥,𝑦) 𝜕𝑥 = 2 karena 𝜕𝑀(𝑥,𝑦) 𝜕𝑦 = 𝜕𝑁(𝑥,𝑦)

𝜕𝑥 , maka persamaan tersebut merupakan persamaan

diferensial eksak. 𝜕𝐹(𝑥,𝑦) 𝜕𝑥 = 𝑀(𝑥, 𝑦) = 3𝑥 + 2𝑦 𝐹(𝑥, 𝑦) = ∫ 3𝑥 + 2𝑦 𝑑𝑥 =3₂𝑥2 _{+ 2𝑥𝑦 + 𝑔(𝑦)} mencari nilai 𝑔(𝑦) 𝜕𝐹(𝑥,𝑦) 𝜕𝑦 = 𝑁(𝑥, 𝑦) 2𝑥 +𝑑𝑔(𝑦)_𝑑𝑦 = 2𝑥 + 𝑦 sehingga 𝑑𝑔(𝑦) 𝑑𝑦 = 𝑦 ∫ 𝑑(𝑔(𝑦)) = ∫ 𝑦 𝑑𝑦 𝑔(𝑦) =1₂𝑦2_{+ 𝑐} 0

(42)

Penyelesaian dari persamaan diferensial tersebut yaitu 𝐹(𝑥, 𝑦) = 𝑐₁ 3 2𝑥 2_{+ 2𝑥𝑦 +}1 2𝑦 2_{+ 𝑐} 0 = 𝑐1 3 2𝑥 2_{+ 2𝑥𝑦 +}1 2𝑦 2_{+ 𝑐} 0− 𝑐1 = 0 3 2𝑥 2_{+ 2𝑥𝑦 +}1 2𝑦 2_{+ 𝑐} 2 = 0 Faktor Integral

Persamaan 𝑀(𝑥, 𝑦)𝑑𝑥 + 𝑁(𝑥, 𝑦)𝑑𝑦 = 0 belum tentu eksak. Tetapi dengan mengalikannya dengan sebuah fungsi tertentu, persamaan diferensial tersebut menjadi eksak. Fungsi pengali itu disebut sebagai faktor integral.

Contoh 9

Persamaan diferensial (2𝑥2_{+ 𝑦)𝑑𝑥 + (𝑥}2_{𝑦 − 𝑥)𝑑𝑦 = 0 bukan merupakan}

persamaan diferensial eksak akan tetapi dengan mengalikan dengan faktor integral 1

𝑥2 maka persamaan diferensial menjadi (2𝑥_𝑥2₂+𝑦) 𝑑𝑥 + (𝑥2_𝑥𝑦−𝑥₂ ) 𝑑𝑦 = 0 (2 +_𝑥𝑦₂) 𝑑𝑥 + (𝑦 −1_𝑥) 𝑑𝑦 = 0 sehingga 𝑀(𝑥, 𝑦) = 2 +_𝑥𝑦₂ 𝑁(𝑥, 𝑦) = 𝑦 −1_𝑥 𝜕𝑀(𝑥,𝑦) 𝜕𝑦 = 1 𝑥2 𝜕𝑁(𝑥,𝑦) 𝜕𝑥 = 1 𝑥2

4. Persamaan Diferensial Linear Orde Satu

Persamaan linear orde satu memiliki bentuk umum

𝑑𝑦

𝑑𝑥+ 𝑃(𝑥)𝑦 = 𝑄(𝑥) (2.9)

Untuk menentukan penyelesaian umumnya, persamaan (2.9) dapat ditulis menjadi

[𝑃(𝑥)𝑦 − 𝑄(𝑥)]𝑑𝑥 + 𝑑𝑦 = 0 (2.10)

(43)

𝑀(𝑥, 𝑦) = 𝑃(𝑥)𝑦 − 𝑄(𝑥) 𝑁(𝑥, 𝑦) = 1

𝜕𝑀(𝑥,𝑦)

𝜕𝑦 = 𝑃(𝑥)

𝜕𝑁(𝑥,𝑦) 𝜕𝑥 = 0

Jika 𝑃(𝑥) ≠ 0 maka persamaan diferensial tersebut tidak eksak. Dibutuhkan faktor integral 𝜇(𝑥) supaya persamaan diferensial tersebut menjadi eksak. Persamaan (2.10) akan menjadi

[𝜇(𝑥)𝑃(𝑥)𝑦 − 𝜇(𝑥)𝑄(𝑥)]𝑑𝑥 + 𝜇(𝑥)𝑑𝑦 = 0 (2.11) karena persamaan (2.11) merupakan persamaan diferensial eksak maka

𝜕𝑀(𝑥,𝑦) 𝜕𝑦 = 𝜕𝑁(𝑥,𝑦) 𝜕𝑥 𝜕[𝜇(𝑥)𝑃(𝑥)𝑦−𝜇(𝑥)𝑄(𝑥)] 𝜕𝑦 = 𝜕[𝜇(𝑥)] 𝜕𝑥 𝜇(𝑥)𝑃(𝑥) =𝑑[𝜇(𝑥)]_𝑑𝑥 𝑑[𝜇(𝑥)] 𝜇(𝑥) = 𝑃(𝑥)𝑑𝑥

Kemudian dengan pengintegralan diperoleh ln|𝜇(𝑥)| = ∫ 𝑃(𝑥)𝑑𝑥

𝜇(𝑥) = 𝑒∫ 𝑃(𝑥)𝑑𝑥 _(2.12)

Karena 𝜇(𝑥) merupakan faktor integral maka persamaan (2.9) akan menjadi 𝑒∫ 𝑃(𝑥)𝑑𝑥 𝑑𝑦

𝑑𝑥+ 𝑒∫ 𝑃(𝑥)𝑑𝑥𝑃(𝑥)𝑦 = 𝑄(𝑥)𝑒∫ 𝑃(𝑥)𝑑𝑥 𝑑

𝑑𝑥[𝑒∫ 𝑃(𝑥)𝑑𝑥𝑦] = 𝑄(𝑥)𝑒∫ 𝑃(𝑥)𝑑𝑥

dengan pengintegralan diperoleh

𝑒∫ 𝑃(𝑥)𝑑𝑥_{𝑦 = ∫ 𝑒}∫ 𝑃(𝑥)𝑑𝑥_{𝑄(𝑥)𝑑𝑥 + 𝑐} _(2.13)

Contoh 10

Tentukan penyelesaian persamaan diferensial 𝑑𝑦_𝑑𝑥+ (1_𝑥) 𝑦 = 𝑒−2𝑥. Penyelesaian:

Bentuk tersebut merupakan persamaan diferensial orde satu tetapi tidak eksak maka terlebih dahulu dicari faktor integral

(44)

𝑃(𝑥) =1_𝑥

𝜇(𝑥) = 𝑒∫1𝑥𝑑𝑥 = 𝑒ln|𝑥| = 𝑥

Cara I

Kalikan persamaan diferensial dengan faktor integralnya akan menjadi 𝑥𝑑𝑦_𝑑𝑥+ 𝑦 = 𝑒−2𝑥_.

𝑑

𝑑𝑥(𝑥𝑦) = 𝑒 −2𝑥_.

dengan pengintegralan, diperoleh 𝑥𝑦 = −1₂𝑒−2𝑥_{+ 𝑐}

𝑦 = −_2𝑥1 𝑒−2𝑥₊𝑐 𝑥

Cara II

Karena ketika dikalikan dengan faktor integral persamaan tersebut menjadi persamaan diferensial eksak, maka penyelesaiannya menjadi

𝑥𝑑𝑦_𝑑𝑥+ 𝑦 = 𝑒−2𝑥_. 𝑥 𝑑𝑦 + 𝑦 𝑑𝑥 = 𝑒−2𝑥_𝑑𝑥 𝑥 𝑑𝑦 + 𝑦 𝑑𝑥 − 𝑒−2𝑥_{𝑑𝑥 = 0} 𝑥 𝑑𝑦 + (𝑦 − 𝑒−2𝑥_{) 𝑑𝑥 = 0} 𝑀(𝑥, 𝑦) = (𝑦 − 𝑒−2𝑥_{) dan 𝑁(𝑥, 𝑦) = 𝑥} 𝜕𝐹(𝑥,𝑦) 𝜕𝑥 = 𝑀(𝑥, 𝑦) = 𝑦 − 𝑒 −2𝑥 𝐹(𝑥, 𝑦) = ∫ 𝑦 − 𝑒−2𝑥_{𝑑𝑥 = 𝑥𝑦 +}1 2𝑒−2𝑥+ 𝑔(𝑦) mencari nilai 𝑔(𝑦) 𝜕𝐹(𝑥,𝑦) 𝜕𝑦 = 𝑁(𝑥, 𝑦) 𝑥 +𝑑𝑔(𝑦)_𝑑𝑦 = 𝑥 sehingga 𝑑𝑔(𝑦) 𝑑𝑦 = 0

(45)

∫ 𝑑(𝑔(𝑦)) = ∫ 0 𝑑𝑦 𝑔(𝑦) = 𝑐₀

Penyelesaian dari persamaan diferensial tersebut yaitu 𝐹(𝑥, 𝑦) = 𝑐1

𝑥𝑦 +1₂𝑒−2𝑥 _{+ 𝑐} 0 = 𝑐1 𝑥𝑦 = −1₂𝑒−2𝑥_{+ 𝑐} 1− 𝑐0 𝑦 = −_2𝑥1 𝑒−2𝑥₊𝑐1−𝑐0 𝑥 𝑦 = −_2𝑥1 𝑒−2𝑥₊𝑐 𝑥 dimana 𝑐 = 𝑐1− 𝑐0

5. Persamaan Diferensial Bernoulli

Persamaan diferensial Bernoulli memiliki bentuk umum

𝑑𝑦

𝑑𝑥+ 𝑃(𝑥)𝑦 = 𝑄(𝑥)𝑦

𝑛 _(2.14)

dengan 𝑛 ≠ 0 dan 𝑛 ≠ 1

Untuk menentukan penyelesaian umumnya, reduksilah persamaan Bernoulli menjadi persamaan diferensial linear orde satu.

Bagilah persamaan (2.14) dengan 𝑦𝑛_{maka diperoleh}

𝑦−𝑛 𝑑𝑦

𝑑𝑥+ 𝑃(𝑥)𝑦

1−𝑛 _{= 𝑄(𝑥)} _(2.15)

dengan memisalkan 𝑣 = 𝑦1−𝑛_sehingga

𝑑𝑣 = (1 − 𝑛)𝑦−𝑛_𝑑𝑦

𝑦−𝑛_{𝑑𝑦 =} 𝑑𝑣 1−𝑛

Substitusikan ke dalam persamaan (2.15)

𝑑𝑣 (1−𝑛)𝑑𝑥+ 𝑃(𝑥)𝑣 = 𝑄(𝑥) 𝑑𝑣 𝑑𝑥+ (1 − 𝑛)𝑃(𝑥)𝑣 = (1 − 𝑛)𝑄(𝑥) 𝑑𝑣 𝑑𝑥+ 𝑃1(𝑥)𝑣 = 𝑄1(𝑥) (2.16) dengan 𝑃₁(𝑥) = (1 − 𝑛)𝑃(𝑥) dan 𝑄1(𝑥) = (1 − 𝑛)𝑄(𝑥)

(46)

Contoh 11

Tentukan penyelesaian persamaan diferensial 𝑑𝑦_𝑑𝑥+ 𝑦 = 𝑥𝑦3 Penyelesaian:

Persamaan tersebut merupakan persamaan diferensial Bernoulli dimana 𝑛 = 3. Langkah pertama, bagi persamaan tersebut dengan 𝑦3_{, maka diperoleh}

𝑦−3 𝑑𝑦 𝑑𝑥+ 𝑦 −2 _{= 𝑥} _(2.17) Misalkan 𝑣 = 𝑦1−𝑛 _{= 𝑦}−2_sehingga 𝑑𝑣 = −2𝑦−3_𝑑𝑦 −1₂𝑑𝑣 = 𝑦−3_𝑑𝑦

Substitusikan ke persamaan (2.17) diperoleh −1₂_𝑑𝑥𝑑𝑣+ 𝑣 = 𝑥

𝑑𝑣

𝑑𝑥− 2𝑣 = −2𝑥 (2.18)

Persamaan (2.18) merupakan persamaan diferensial linear orde satu tetapi tidak eksak. Sehingga terlebih dahulu mencari faktor integral

𝜇(𝑥) = 𝑒∫ −2𝑑𝑥 _{= 𝑒}−2𝑥

Kalikan persamaan (2.18) dengan faktor integralnya sehingga menjadi 𝑒−2𝑥 𝑑𝑣

𝑑𝑥− 2𝑒−2𝑥𝑣 = −2𝑥𝑒−2𝑥 𝑑

𝑑𝑥(𝑒

−2𝑥_{𝑣) = −2𝑥𝑒}−2𝑥

dengan pengintegralan diperoleh 𝑒−2𝑥_{𝑣 =}1 2𝑒−2𝑥(2𝑥 + 1) + 𝑐 𝑣 = 𝑥 +1₂+ 𝑐𝑒2𝑥 Karena 𝑣 = 𝑦−2_{, maka} 1 𝑦2 = 𝑥 + 1 2+ 𝑐𝑒 2𝑥

(47)

D. Penelitian yang Relevan

1. Oktavia dan Khotimah (2016) melakukan penelitan yang bertujuan untuk menganalisis kesulitan dan faktor penyebab kesulitan mahasiswa dalam menyelesaikan persamaan diferensial orde satu. Subjek penelitian ini adalah mahasiswa program studi Pendidikan Matematika FKIP UMS yang berjumlah 7 orang. Metode pengumpulan data menggunakan wawancara dan dokumentasi. Jenis penelitian ini adalah deskriptif kualitatif. Teknik analisis data melalui tiga tahap: reduksi data, penyajian data, dan penarikan kesimpulan. Data yang dianalisis merupakan hasil Ujian Tengah Semester (UTS). Hasil penelitian menunjukkan jenis-jenis kesulitan yang dialami mahasiswa dalam menyelesaikan persamaan diferensial orde satu dibagi menjadi 2 kategori, yaitu pertama kesulitan pemahaman konsep yang meliputi: (1) kesulitan merumuskan ciri atau bentuk umum persamaan diferensial; (2) kesulitan menentukan teknik penyelesaian persamaan diferensial. Kedua kesulitan penerapan konsep yang terdiri dari: (1) kesulitan dalam langkah-langkah perhitungan; (2) kesulitan dalam materi prasyarat. Faktor penyebab mahasiswa mengalami kesulitan, pertama faktor intrinsik, yaitu: aktivitas belajar kurang, kurang mengingat rumus, kebiasaan yang kurang baik, kurang latihan soal, tidak adanya motivasi belajar, latar belakang pendidikan yang tidak sesuai. Kedua faktor ekstrinsik, yaitu aktif dalam kegiatan sosial di lingkungan masyarakat.

2. Naisunis, Taneo, dan Daniel (2018) melakukan penelitian yang bertujuan untuk mengetahui kesalahan apa saja yang dilakukan oleh mahasiswa dalam pemecahan masalah pada mata kuliah persamaan diferensial. Tempat penelitian di STKIP Soe pada semester genap tahun akademik 2016/2017 dengan subjek penelitan sebanyak 15 mahasiswa. Jenis penelitan ini merupakan penelitian deskriptif kualitatif dengan teknik pengumpulan datanya melalui observasi, analisis kerja dan wawancara. Teknik analisis data yang digunakan adalah teknik analisis Miles and Huberman yaitu reduksi data, penyajian data dan penarikan

(48)

kesimpulan. Hasil penelitiannya adalah kesalahan yang dilakukan mahasiswa pada tahap pertama (memahami) meliputi kesalahan fakta 7%, kesalahan konsep 13,33% dan kesalahan operasi 7%. Kesalahan tahap kedua (merencanakan) meliputi kesalahan fakta 13,33%, kesalahan konsep 13,33% dan kesalahan operasi 13,33%. Kesalahan tahap ketiga (menyelesaikan) adalah kesalahan fakta 12,22%, kesalahan konsep 50,56%, kesalahan prinsip 16,67% dan kesalahan operasi 15%. Seluruh mahasiswa tidak melakukan pengecekan kembali dalam tahapan masalah, sehingga seluruh mahasiswa melakukan kesalahan pada tahap ini.

3. Ningsih dan Rohana (2018) melakukan penelitian terkait pemahaman mahasiswa terhadap persamaan diferensial biasa berdasarkan teori APOS. APOS adalah singkatan dari Action – Process – Object – Schema yang dikemukan oleh Ed Dubinsky untuk mengetahui kemampuan pemahaman konsep seseorang. Subjek penelitian ini adalah 33 mahasiswa semester 5B Program Studi Pendidikan Matematika tahun akademik 2017/2018 pada salah satu Universitas Swasta di kota Palembang, Sumatera Selatan. Penelitian ini merupakan penelitian deskriptif. Data dikumpulkan melalui tes dan wawancara. Hasil penelitian memperlihatkan bahwa sebagian besar mahasiswa hanya mampu memahami konsep persamaan diferensial biasa pada tahap aksi. Padahal berdasarkan teori APOS, jika seseorang memahami konsep dengan baik, dia akan mampu mencapai tahap skema. Mahasiswa mampu menyelesaikan persamaan diferensial orde satu homogen yang sederhana, kesalahan terbanyak terletak pada penggunaan prinsip turunan dan pengintegralan dari suatu fungsi eksponen dan logaritma.

E. Kerangka Berpikir

Matematika merupakan ilmu dasar yang wajib dipelajari oleh semua orang dari tingkat SD sampai SMA bahkan perguruan tinggi. Pembelajaran matematika di perguruan tinggi bertujuan untuk mengembangkan segala kemampuan

(49)

matematis mahasiswa dalam memperoleh hasil belajar yang maksimal. Salah satu kemampuan yang dikembangkan dalam pembelajaran matematika yaitu kemampuan pemahaman konsep. Pemahaman konsep merupakan kemampuan mengklasifikasikan dan menjelaskan informasi atau objek yang diperoleh berdasarkan karakteristiknya. Kemampuan pemahaman konsep merupakan kemapuan yang sangat penting dalam menyelesaikan masalah dalam matematika.

Salah satu mata kuliah yang ada di program studi pendidikan matematika adalah persamaan diferensial biasa. Masalah-masalah yang ada dalam persamaan diferensial memerlukan kemampuan pemahaman konsep untuk menyelesaikannya. Salah satu materi persamaan diferensial biasa yaitu persamaan diferensial orde satu. Mahasiswa dalam belajar persamaan diferensial orde satu harus mampu membedakan jenis-jenisnya. Kemampuan pemahaman konsep mahasiswa pada materi persamaan diferensial orde satu dapat ditinjau dari beberapa indikator diantaranya: 1) mengklasifikasikan objek-objek menurut sifat-sifat tertentu., 2) menggunakan, memanfaatkan, dan memilih prosedur atau operasi tertentu dan 3) mengaplikasikan konsep atau algoritma ke pemecahan masalah.

Pentingnya dan Masalah Pemahaman Konsep Perkuliahan Persamaan Diferensial Biasa Materi Persamaan Diferensial Orde Satu Kemampuan pemahaman konsep mahasiswa ditinjau dari indikator. Faktor yang mempengaruhi kesulitan dalam memahami konsep persamaan diferensial orde satu Bagan 2. 1. Kerangka Berpikir Penelitian

(50)

27 BAB III

METODOLOGI PENELITIAN A. Jenis Penelitian

Jenis penelitian yang dilakukan oleh peneliti adalah penelitian deskriptif dengan pendekatan kualitatif. Penelitian deskriptif adalah penelitian yang bertujuan untuk menggambarkan atau mendeskripsikan suatu masalah atau objek apa adanya. Sedangkan penelitian kualitatif merupakan penelitian yang bermaksud memahami fenomena tentang apa yang dialami oleh subjek penelitian misalnya perilaku, persepsi, motivasi, tindakan dll., secara holistik dan dengan cara deskripsi dalam bentuk kata-kata dan bahasa, pada suatu konteks khusus yang alamiah dan dengan memanfaatkan berbagai metode alamiah (Moleong, 2008: 6).

Peneliti memilih penelitian kualitatif karena tujuan dari penelitian ini untuk mendeskripsikan kemampuan pemahaman konsep mahasiswa pada materi persamaan diferensial orde satu dan faktor-faktor yang menyebabkan mahasiswa kesulitan dalam memahami konsep persamaan diferensial orde satu.

B. Subjek Penelitian

Subjek dari penelitian ini adalah 43 mahasiswa Program Studi Pendidikan Matematika Universitas Sanata Dharma yang mengambil mata kuliah Persamaan Diferensial Biasa pada tahun ajaran 2018/2019 di kelas A.

C. Bentuk Data

Pada penelitian ini, bentuk data yang digunakan adalah data kuantitatif dan kualitatif. Pada penelitian ini yang termasuk data kuantitatif adalah hasil tes mahasiswa dan yang termasuk data kualitatif adalah hasil wawancara. Data yang diperoleh dalam penelitian akan dideskripsikan untuk menjawab rumusan masalah yang ditentukan

(51)

D. Waktu dan Tempat Pelaksanaan Penelitian

Penelitian ini dilakukan bulan Februari-April 2019. Penelitian ini dilaksanakan di Program Studi Pendidikan Matematika Universitas Sanata Dharma Yogyakarta.

E. Metode Pengumpulan Data

Metode pengumpulan data yang digunakan dalam penelitian ini : 1. Tes Esai

Tes dilakukan untuk mengetahui kemampuan pemahaman konsep mahasiswa pada materi persamaan diferensial orde satu. Tes dilakukan saat materi terkait persamaan diferensial orde satu telah selesai dipelajari yaitu pada bulan Maret.

2. Wawancara

Peneliti melakukan wawancara kepada mahasiswa dengan tujuan untuk mendalami hasil jawaban tes mahasiswa dan mengetahui faktor-faktor yang membuat mahasiswa kesulitan memahami konsep persamaan diferensial orde satu. Wawancara dilakukan setelah hasil tes dikoreksi. Peneliti mengelompokkan mahasiswa menjadi tiga kelompok berdasarkan hasil tes menurut Arikunto (2012: 299) dan memilih dua mahasiswa dari masing-masing kelompok untuk diwawancarai.

Tabel 3.1. Kategori Hasil Tes

Kategori Ketentuan Kelompok Tinggi 𝑥_𝑖 ≥ 𝑥̅ + 𝑠 Kelompok Sedang 𝑥̅ − 𝑠 < 𝑥_𝑖 < 𝑥̅ + 𝑠 Kelompok Rendah 𝑥_𝑖 ≤ 𝑥̅ − 𝑠 Keterangan : 𝑥_𝑖 : nilai mahasiswa

𝑥̅ : rata-rata nilai mahasiswa

(52)

F. Instrumen Pengumpulan Data

Instrumen penelitian yang akan digunakan oleh peneliti adalah sebagai berikut : 1. Lembar Tes Esai

Tes esai yang dibuat digunakan dalam ujian tengah semester berisikan pertanyaan mengenai solusi dari persamaan diferensial dan persamaan diferensial orde satu. Data yang diperoleh akan dianalisis untuk mengetahui kemampuan pemahaman konsep mahasiswa berdasarkan indikator.

Tabel 3.2. Kisi-Kisi Soal Tes Esai

Indikator Soal Indikator

Pemahaman Konsep Soal

Memperlihatkan bahwa suatu fungsi merupakan solusi dari persamaan diferensial.

Menggunakan prosedur atau operasi tertentu.

1. a. Tunjukkan bahwa 𝑓(𝑥) = 𝑐₁𝑒4𝑥_{+ 𝑐}

2𝑒−2𝑥 dimana 𝑐1 dan

𝑐2 konstan, merupakan solusi dari

persamaan diferensial

𝑑2_𝑦 𝑑𝑥2− 2

𝑑𝑦

𝑑𝑥− 8𝑦 = 0

b. Tentukan nilai m agar 𝑓(𝑥) = 𝑒𝑚𝑥 merupakan solusi dari persamaan diferensial 𝑑2_𝑦 𝑑𝑥2− 5 𝑑𝑦 𝑑𝑥+ 4𝑦 = 0 Menentukan jenis-jenis persamaan diferensial orde satu Mengklasifikasikan objek-objek menurut sifat-sifat tertentu

2. Tentukan jenis persamaan diferensial di bawah ini. (separabel/ homogen/ eksak/ linear/ Bernoulli). Berikan penjelasan secukupnya. a. [(𝑥 + 1)𝑒𝑥_{− 𝑒}𝑦_{]𝑑𝑥 − 𝑥𝑒}𝑦_{𝑑𝑦 = 0} b. (4𝑥2_{𝑦 + 3𝑦)𝑑𝑥 + (𝑥}4_{+ 1)𝑑𝑦 = 0} c. (3𝑥2_{− 2𝑦}2_{)𝑑𝑥 + (𝑥𝑦)𝑑𝑦 = 0} d. 𝑥4𝑑𝑦 + (2𝑥3𝑦 − 1)𝑑𝑥 = 0 Menentukan penyelesaian umum persamaan Menggunakan prosedur atau operasi tertentu.

3. Tentukan penyelesaian umum persamaan diferensial berikut