broughan16. 126KB Jun 04 2011 12:08:27 AM
Teks penuh
Gambar
Garis besar
Dokumen terkait
Then we state Theorem 2.2 presenting a list of equivalent assertions describing any equivariant weak n -equivalences by means of the Bredon homology with local coefficients..
We give upper and lower bounds for the largest integer not representable as a posi- tive linear combination of three given integers, disproving an upper bound conjectured by
Yamazaki that an upper and a lower bounds for the numerical radius of a geometrically weighted shift operator can be obtained from the numerical range of the Aluthge transformation
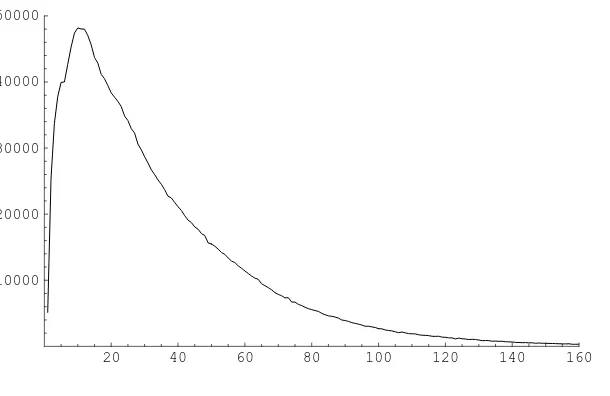
The main objective in this section is to prove the following theorem concerning the conditional distribution of the number of edges given the colouring..
In this paper, we prove upper and lower bounds on the free energy in the SK model with multidi- mensional spins in terms of variational inequalities involving the
The main lemma in the proof of Theorem 1.1 involves estimating the resistances. A combination of the above identities will then yield lower bounds for the hitting times. We then
To prove this theorem we extend the bounds proved in [ 2 ] for the continuous time simple random walk on (Γ , µ ) to the slightly more general random walks X and Y defined
The proof of Theorems 1.1-1.2 is obtained by getting first a lower bound, Proposi- tion 2.1, proved in Section 2, and then an upper bound on the minimal energy of J , Proposition