getdoc059a. 353KB Jun 04 2011 12:04:02 AM
Teks penuh
Gambar
Garis besar
Dokumen terkait
We start by reviewing facts about Brownian motion in a rectangle with the intent of using conformal invariance to relate these results to regions that are conformally equivalent to
It has been shown that certain types of random walks in random potentials and Brownian motion in Poissonian potentials undergo a phase transition from sub-ballistic to ballistic
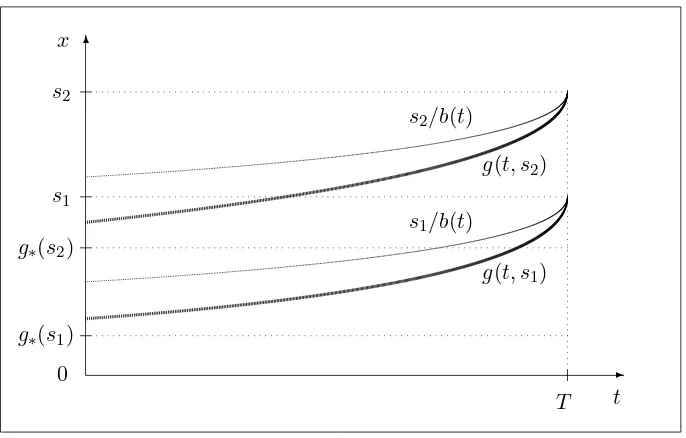
Indeed, necessary (and sufficient) conditions for the smooth fit to hold are found to be regularity of the diffusion process X , differentiability of the gain function at the
Keywords Brownian bridge, Brownian excursion, Brownian scaling, local time, Bessel process, zeros of Bessel functions, Riemann zeta function.. AMS subject classification 60J65,
In this section we prove the existence of a minimal stopping time which solves the Skorokhod embedding problem for random walk, and make some simple observations which show that
Keywords: Brownian motion, random time change, exit boundary, local time, additive func- tional, stochastic differential equation, Khas’minskii’s lemma, spectrally negative
We consider global geometric properties of a codimension one manifold embedded in Euclidean space, as it evolves under an isotropic and volume preserving Brownian flow
Key words: Exit place of Brownian motion, parabolic-type domain, horn-shaped domain, h - transform, Green function, harmonic measure.. AMS 2000 Subject Classification: