Beyond the Bell-Shaped Curve:

Beyond the Bell-Shaped Curve:

A New Universal Law

NZ Mathematics Research Institute Summer School

January 6—11, 2019 Craig A. Tracy

Department of Mathematics UC Davis

Lecture 1

• Stochastic growth & KPZ Universality

• Random Matrices, TW Distributions, ASEP to KPZ

• Stochastic Conservation Laws

• High dimensional statistical inference & TW distributions.

• Concluding Remarks

-4 -2 2 4 x

0.1 0.2 0.3 0.4

Normal Density

-4 -2 2 4 x

0.1 0.2 0.3 0.4 0.5

TW Densities

β = 1 β = 2 β = 4

➔

Outline

Stochastic Growth of an Interface

Want a “simple” model (but not this simple!)

Height in each

column is a sum of independent

random variables

CLT tells us the limiting fluctuations of the height in each column are Gaussian.

No spatial correlation.

KPZ Phenomenology

• Stochastic growth normal to the surface

• Kardar-Parisi-Zhang (1986)

• Basic object: (random) height function h(x,t)

• Satisfies the KPZ equation (nonlinear stochastic PDE):

•

@h

@t = ⌫ @²h

@x² +

✓ @h

@x

◆2

+ p

D ⌘(x, t) h ⇠ v₁t + ( t)^1/3 , t ! 1

Let’s see the experimental results first.

Work of K.Takeuchi & M.Sano

in 2010

Stochastic growth in liquid crystals: Droplet initial

condition

Stochastic growth in liquid crystals: Flat initial condition

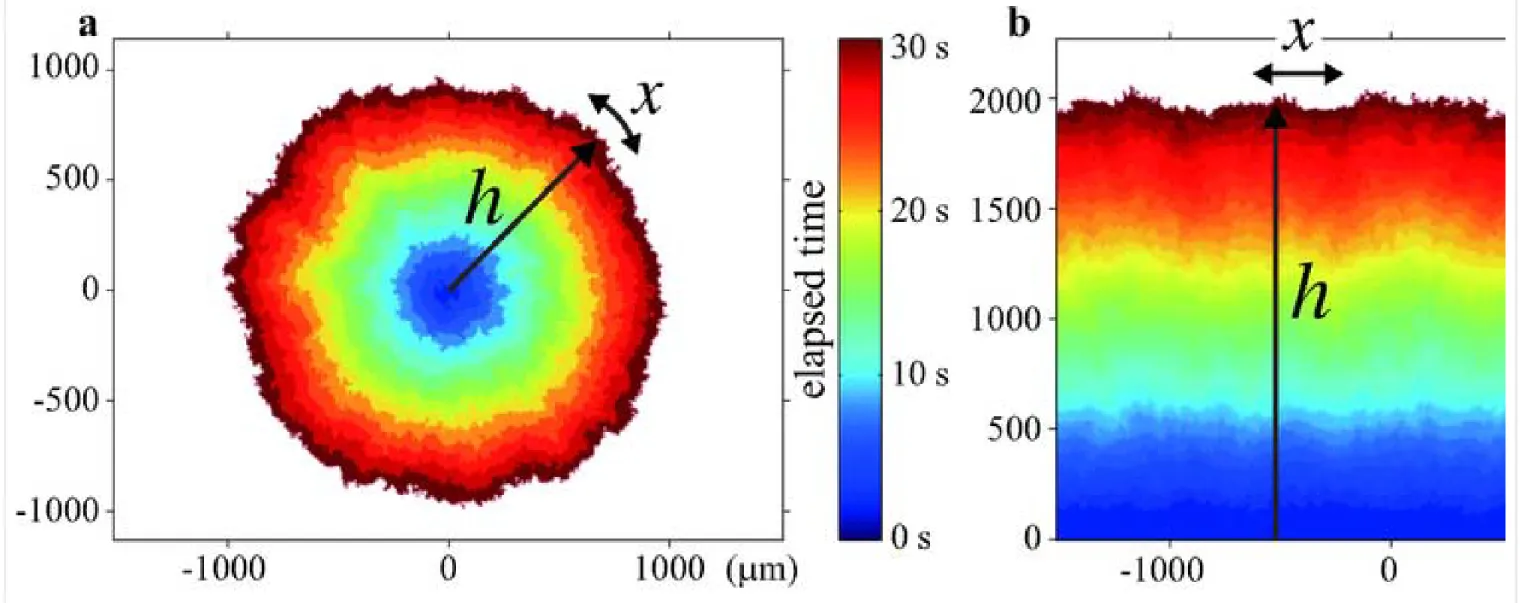
Growing DSM2 cluster with a circular (a) and flat (b) interface. : Growing interfaces uncover universal fluctuations behind scale invariance ...

file:///Volumes/CRAIG1/Conferences:Seminars/Saclay:SPA:Bielefeld/Takeuchi/srep00034_F1.html[7/11/11 2:44:49 PM]

nature.com ^Sitemap

back to article

back to article

Scientific Reports ISSN (online) 2045-2322

Figure 1: Growing DSM2 cluster with a circular (a) and flat (b) interface.

From

Growing interfaces uncover universal fluctuations behind scale invariance

Kazumasa A. Takeuchi Masaki Sano Tomohiro Sasamoto Herbert Spohn Scientific Reports 1, Article number: 34 doi:10.1038/srep00034

Figure 1: Growing DSM2 cluster with a circular (a) and flat (b) interface.

Binarised snapshots at successive times are shown with different colours. Indicated in the colour bar is the elapsed time after the laser emission. The local height h(x, t) is defined in each case as a function of the lateral coordinate x along the mean profile of the interface (a circle for a and a horizontal line for b). See also Supplementary Movies 1 and 2.

Log In Register

Home Search For Authors For Referees About Scientific Reports

Figures index Next figure

Figure 1 Article

$nPage.sectionPath

Height function h(x,t)

TW Distribution Functions F

1

and F

2

F₂(s) = exp

✓ Z ₁

s

(x s)q(x)² dx

◆

F₁(s) = exp

✓ 1 2

Z ₁

s

q(x) dx

◆

F₂(s)^1/2

d

²

q

dx

²

= xq + 2q

³

q (x) ⇠ Ai(x), x ! 1

Painlevé II equation

No adjustable parameters

-4 -2 2 x 0.1

0.2 0.3 0.4 0.5

f₄ f₂ f₁

f (x) = dF (x)

dx , = 1, 2, 4

Distribution Skewness Kurtosis

F1 0.293... 0.165...

F2 0.224... 0.093…!

F4 0.165... 0.049...!

F

0 20 40 -0.2

0 0.2 0.4 0.6 0.8

t (s)

〈χn 〉 c – 〈χ GUEn 〉 c

0 20 40 60 80

-0.2 0 0.2 0.4 0.6 0.8

t (s)

〈χn 〉 c –〈χ GOEn 〉 c

10⁰ 10¹ 10²

10^-1 10⁰

10⁰ 10¹ 10²

10^-1 10⁰

slope -1/3 slope -1/3

0 20 40 60

0 0.1 0.2 0.3

t (s)

amplitude ratios ^{GOE skew.}

GUE skew.

GOE kurt.

GUE kurt.

-5 0 5

10⁰

10^-2

10^-4

rescaled height χ

ρ(χ)

GUE

GOE

n = 1

n = 2 n = 3

n = 4 n = 1

n = 2 n = 3 n = 4

K. Takeuchi & M. Sano, “Evidence for geometry-dependent universal fluctuations!

of the Kardar-Parisi-Zhang interfaces in liquid-crystal turbulence”, Journal of Statistical Physics 147 (2012), 853-890. arXiv:1203.2530. (Earlier Phys. Rev. Lett.)

“Effects of Particle Shape on Growth

Dynamics at Edges of Evaporating Colloidal Drops”

P. Yunker, M. Lohr, T. Still, A. Borodin, D. Durian & A. Yodh arXiv:1209.4137

•

Resulting deposits of particles grow from the edge defining a growth line in space & time. Experiment varies ε=aspect ratio of major-minor diameters

•

For spherical particles (ε=1.0) growth is spatially

uncorrelated with β=0.48(4). Consistent with Poisson statistics “raining particles”.

•

For slightly anisotropic particles (ε=1.2), β=0.37(4) consistent with KPZ universality. Measured

skewness=0.20(6) & kurtosis=0.10(3). Recall for F2

numbers are 0.224… and 0.093…,respectively.

Experimental Results

Random Matrices

• GUE: N x N complex Hermitian matrices

• GOE: N x N real symmetric matrices

• Probability density exp[-Tr(A²)/2N]/Z

• Eigenvalues are random variables

• Largest eigenvalue ≃ 2N + N^{1/3 ξ}TW, N→∞

• ^ξ_TW has distribution F2 (F1) for GUE (GOE).

Universality in RMT

What is the connection of RMT distributions to stochastic growth processes?

• Kardar, Parisi and Zhang predicted the 1/3 exponent but made no prediction for the fluctuating quantity.

• The KPZ equation, as initially formulated, is ill-defined due to the square of the gradient term (see Martin Hairer for rigorous

account).

• Many discrete models of the determinantal class were solved exactly and were argued to be in the KPZ universality class.

• For example, Prähofer & Spohn introduced the Airy process whose 1-point function is the distribution F2. These same authors showed in various discrete models that flat initial conditions lead to F1 and droplet initial conditions leads to F2.

• However, all these models were of the determinantal class. KPZ equation not a determinantal process!

ASEP on Integer Lattice

⬅

⬅ _{q p}

Each particle has an alarm clock --

exponential distribution with parameter one

●

When alarm rings particle jumps to right with probability p and to the left with probability q

●

Jumps are suppressed if neighbor is occupied

●

p ≠ q

Initial Conditions

Step Initial Condition, q>p

Flat Initial Condition

Random: Product Bernoulli measure

Integrable Structure of ASEP

Hans Bethe!

1906-2005

We solve the Kolmogorov forward equation (“master equation”) for the

transition probability Y X:!

P

Y

(X;t) ^!

Main idea comes from the!

Bethe Ansatz (1931)

Universality Theorem

⌧ = p

q , = q p, = m

t , c₁ = 1 + 2p

, c₂ = ^1/6(1 p

)^2/3 Theorem (TW, 2009):

For ASEP with step initial condition and 0  p < q, we have

tlim!1 P

✓x_m(t/ ) c₁t

c₂t^1/3  s

◆

= F₂(s) uniformly for in a compact subset of (0, 1).

Remarks:

When p = 0 (only jumps to the left, = 1) the model is called TASEP for totally asymmetric . . . . TASEP is a determinantal process whereas ASEP is not. The above limit law for TASEP was proved by Johannson in 2000.

What does this have to do with KPZ Eqn?

KPZ & Stochastic Heat Equation

@h

@t = ⌫ @²h

@x² +

✓ @h

@x

◆2

+ W

Problem term

Bertini & Giacomin (1997) two essential insights:

Define the solution to the KPZ equation via a Hopf-Cole transformation:

h(t, x) = log Z(t, x)

where Z=Z(t,x) satisfies the stochastic heat equation

@Z

@t = 1 2

@²Z

@x² Z(t, x)W

Z(t,x) is obtained from ASEP in a particularly delicate asymptotic limit called WASEP (weakly asymmetric simple exclusion process)

KPZ Crossover Scaling Function

•

Amir, Corwin & Quastel and independently Sasamoto &

Spohn in 2010 analyzed the TW formula for Prob(xm(t)≤x) for step initial conditions in the WASEP limit.

•

This gives the KPZ crossover scaling function that interpolates between Gaussian for short times and F2

for large times.

•

These authors like to say they showed that the “KPZ equation is in the KPZ Universality Class!”

Further Remarks

• Hairer & Quastel (2015) have shown a large class of 1+1-dimensional continuous interface growth models

converge to the Hopf-Cole solutions to the KPZ equation

• This is the first time that an explicit formula has been

obtained for the solution to a nonlinear stochastic PDE.

• This has led (Quastel et al.) to study the “KPZ Fixed

Point” which is conjectured to describe the scaling limit of a large class of stochastic growth models.

Other Appearances

• Random tilings, e.g. Aztec diamond, Arctic circle theorem & fluctuations (Johansson)

• Directed polymers in a random environment (Johansson et al.)

• Longest increasing subsequences in random permutations (Baik-Deift-Johansson)

• Big data (see Professor Johnstone’s lectures)

Future Problems/Directions

• Extend universality theorems to stochastic growth processes.

• Formulate a ``central limit theorem’’ for TW distributions.

• Further study of the connection of RMT distributions and nonlinear SPDEs.

• KPZ growth in 2+1 dimensions (see numerical work of Halpin-Healy)

Amir-Corwin-Quastel: arXiv:1003.1885

Baik-Deift-Johansson: arXiv:math/9810105 Johansson: arXiv:math/9903234

Sasamoto-Spohn: arXiv:1002.1879; 1002.1973; 1002.1883 Praehofer-Spohn: arXiv:math/0105240

Tracy-Widom: arXiv:0704.2633; 0804.1379; 0807.1713; 1105.4906

A few references arXiv: https://arxiv.org/

Thank you for your

attention!