Digital Arithmetic: O ti d Operations and Circuits

Chapter-6p

Digital Arithmetic:

O ti d

Operations and Circuits

Circuits

Afroza Sultana

Binary Addition

• The addition of two binary number is performed in exactly the same manner as the addition of decimal numbers.

• Least-significant-digit first.

• “Carry” of 1 into the next position may be needed.

• 4 different cases for binary addition 0 + 0 = 0

1 0 1

1 + 0 = 1

1 + 1 = 10 = 0 + carry of 1 into next position

1 + 1 + 1 = 11 = 1 + carry of 1 into next position 1 + 1 + 1 = 11 = 1 + carry of 1 into next position

• The operations of subtraction, multiplication, and division actually use only addition as their basic operation

Examples

(3) 011

1001(9) 11.011(3.3 75)

110(6) (3) 0

+ ^1111(15)

00 (9)

+ 10.110(2.7 50)

75) .0 (3.3

+

) 9 (

1001 ^{11000 (24 ) 110 . 001 ( 6 . 125 )}

Review Question Review Question

• Add the following pairs of binary numbers.g p y – 10110 + 00111

ans.) 11101)

– 011.101 + 010.010 ans.) 101.111

– 10001111 + 00000001 ans.) 10010000

Representing signed numbers

Sign-magnitude system:

Calculator and Computer do not normally use it, because circuit implementation is more complex than other system. The

t l d t f ti i d bi

most commonly used system for representing signed binary numbers is the 2’s compliment system.

1’s Complement System

ƒ Change each 0 to 1, and each 1 to 0.

ƒ Examplep

(45) 1 0 1 1 0 1 original binary number

↓ ↓ ↓ ↓ ↓ ↓

(- 45) 0 1 0 0 1 0 complement each bit 1 0 1 1 0 1 ( 45)

1 0 1 1 0 1 ( 45) + 0 1 0 0 1 0 (-45)

1 1 1 1 1 1 1 1 1 1 1 1

Add one to this result, get zero.dd o e o s esu , ge e o.

2’s Complement System

ƒ Take the 1’s complement of the number

A 1 i ifi i i i

ƒ Add 1 to the least-significant-bit position

complement s

1' form to

bit each

complement

010010

45 of

equivalent binary

101101

number binary

original of

complement s

2' 010011

complement s

2' form to

1 add

1

complement s

1 form to

bit each

complement

010010

+

number binary

original of

complement s

2 010011

Representing signed numbers using 2’s complement form

• If the number is positive, the magnitude is represented p in its positional-weighted p g binary form, and a sign bit of 0 is placed in front of the MSB.

• If the number is negative, the magnitude is

represented in its 2’s complement form and

represented in its 2 s complement form, and

a sign bit of 1 is placed in front of the MSB.

Example p

Example

• Represent each of the following signed decimal numbers as a signed binary number in the 2’s- numbers as a signed binary number in the 2 s- complement system. Use a total of five bits including the sign bit.

(a) +13 (b) –9 (c) +3 (d) –2 (e) –8 Ans:

(a) 01101 (b) 10111 (c) 00011 (d)11110 (e) 11000

Negation

• Negation is the operation of converting a positive number to its negative equivalent or a negative number

t it iti i l t

to its positive equivalent.

• We negate a signed binary number by 2’s- complementing it.

• Example

– Each of the following numbers is a signed binary number in the 2’s-complement system Determine number in the 2 s complement system. Determine the decimal value in each case:

(a) 01100 (b)11010 (c)10001

Ans. (a) +12 (b) -6 (c) -15

Special case in 2’s-complement t ti

representation

• Whenever a signed number has a 1 in the sign bit and all 0s

f h i d bi i d i l i l i 2^N h

for the magnitude bits, its decimal equivalent is –2^N, where N is the number of bits in the magnitude.

• The complete range of values that can be represented in thep g p 2’s-complement system having N magnitude bits is –2^N to +(2^N - 1).

• The range of unsigned decimal values that can beThe range of unsigned decimal values that can be represented in a byte is 256 different values (0-255)

• The range of signed decimal values that can be represented in a byte is 256 different values ( 128 to +127)

in a byte is 256 different values (-128 to +127)

Review Questions

• Represent each of the following values as an eight-bit signed number in the 2’s-complementg g p system

(a) +13= 00001101 (b) –7 = 11111001 (c) –128 = 10000000

• Each of the following is a signed binary number in the 2’s-complement system. Determine the decimal equivalent for each

decimal equivalent for each.

(a) 100011= -29 (b) 1000000 = - 64 (c) 01111110 = +126

(c) 01111110 +126

Review Questions

• What range of signed decimal values can be represented in 12 bits (including the sign bit)?

represented in 12 bits (including the sign bit)?

Ans: -2048 to +2047

• How many bits are required to represent decimal

• How many bits are required to represent decimal values ranging from –50 to +50?

Ans: 7 Ans: 7

• What is the largest negative decimal value that can be represented by a two-byte number?

be represented by a two byte number?

Ans: -32768

Addition in 2’s-complement system

• Case I: Two Positive Numbers.

+9 : 0 1 0 0 1 (augend) 4 0 0 1 0 0 ( dd d) +4 : 0 0 1 0 0 (addend)

0 1 1 0 1 (sum = +13)

Sign bitsg

Addition

• Case II: Positive Number and Smaller Negative Number

+9 : 0 1001 (augend) ( g ) -4 : 1 1100 (addend)

1 0 0101 1 0 0101

Sign bitsg

This carry is disregarded;

The result is 00101 (sum =+5)

Addition

• Case III: Positive Number and Larger Negative

N b

Number

-9 : 1 0 1 1 1 +4 : 0 0 1 0 0 +4 : 0 0 1 0 0

1 1 0 1 1 (sum = -5)

Negative sign bit

Addition

• Case IV: two negative Numbers

-9 : 1 0 1 1 1 -9 : 1 0 1 1 1 -4 : 1 1 1 0 0

1 1 0 0 1 1

Sign bitg

This carry is disregarded;

The result is 10011(sum =-13)

Addition

• Case V: Equal and Opposite Numbers

-9 : 1 0 1 1 1 +9 : 0 1 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0

Sign bit Disregard;

The result is 00000 (sum = +0)

Subtraction in the 2’s-complement System

• TheThe procedureprocedure forfor subtractingsubtracting oneone binarybinary number (the subtrahend) from another binary number (the minuend)

– Negate the subtrahend. This will change the

bt h d t it i l t l f it

subtrahend to its equivalent value of opposite sign.

– Add this to the minuend. The result of this addition will represent the difference betweenp the subtrahend and the minuend.

Subtraction

• Subtract 4 from 9

• (+9) – (+4) =(+9) + (-4)= (+5) +9 : 0 1 0 0 1 (Minuend)

4 : 1 1 1 0 0 (Subtrahend) - 4 : 1 1 1 0 0 (Subtrahend)

1 0 0 1 0 1 (Difference = +5)

Disregard;

The result is 00101 (Difference = +5)

Subtraction

• Subtract 8 from -9

• (-9) – (+8) =(-9) + (-8)= (-17) -9 : 1 0 1 1 1 (Minuend)

8 : 1 1 0 0 0 (Subtrahend) - 8 : 1 1 0 0 0 (Subtrahend)

1 0 1 1 1 1 (Difference = -17)

Magnitude

Overflow Sign bit

Magnitude

The result is 101111 (Difference = -17)

Arithmetic Overflow

• When two positive or two negative numbers are being added, an overflow could occur if there is

h i t th i bit iti

a carry happening to the sign-bit position.

• Overflow can occur when the minuend and subtrahend have different signs.

BCD Addition

• Add using ordinary addition, the BCD code groups for each digit.

• If the Sum equals 9 or less than 9, no correction needed.

• Correction of 0110 is needed at the position where sum is greater than 9.

Examples

5 for

BCD

0101

5

←

9 for

BCD

1001

9

4 for

BCD

0100

4

←

← +

+

33 for

BCD

0011

0011

33

45 for

BCD

0101

0100

45

← +

+

←

78 for

BCD

1000

0111

78

33 for

BCD

0011

0011

33

←

← +

+

Examples

+275 = 0 0 1 0 0 1 1 1 0 1 0 1275 0 0 1 0 0 1 1 1 0 1 0 1 +641 = 0 1 1 0 0 1 0 0 0 0 0 1 +916 = 1 0 0 0 1 0 1 1 0 1 1 0

0 1 1 0

1 0 0 1 0 0 0 1 0 1 1 0

Invalid BCD in 2nd digit, needs correction in g , the 2^nd position.

The result is 1001 0001 0110 = BCD of 961

Hexadecimal Arithmetic

• Hex Addition

Add the two hex digits in decimal mentally – Add the two hex digits in decimal, mentally inserting the decimal equivalent for those digits larger than 9.

larger than 9.

– If the sum is 15 or less, it can be directly expressed as a hex digit.

e p essed s e d g .

– If the sum is greater than or equal to 16, subtract 16 and carry a 1 to the next digit position.y g p

Examples

58

• Add the hex numbers 58 and 24 58

24

7C Ans: Sum =7C

7C s: Su 7C

• Add the hex numbers 3AF and 23C

• Add the hex numbers 3AF and 23C 3AF

3AF 23C

5EB Ans: Sum = 5EB

Hex Subtraction

• How to get the 2’s-complement of a hex number?

• Convert to binary take the 2’s complement of the

• Convert to binary, take the 2’s complement of the binary equivalent, and then convert back to hex.

73A

0111 0011 1010

0111 0011 1010

1000

1000 1100 0101

+1 1’s complement

1000 1100 0110

8C6

Hex Subtraction

• A quicker procedure: subtract each hex digit from F; then add 1.

F F F

7 3 A

}

Subtract each digit from F

-7 -3 -A

8 C 5 1

}

^← Subtract each digit from F Add 1

+ 1

8 C 6

← ^{Add 1}

← Hex equivalent of 2’s complement

complement

Example

• Subtract 3A5 Subtract 3A5

₁₆₁₆

from 592 from 592

₁₆₁₆

. . 5 9 2

^{F F F}

5 9 2

+C 5 B

-3 -A -5 C 5 A

11 E D

_{+ 1}

C 5 B Disregard carry

C 5 B

ALU

Design of Full Adder

Logic circuit with 3 inputs and 2 outputs. The inputs are a bit from the augends, a bit from the addend and a bit from a carry C from a previous stage

C_IN from a previous stage_.

Truth table for a full-adder circuit

K Mappings for the full-adder outputs

Full-adder Outputs

) (

) (

) (

)

(BC BC A BC BC A B C A B C

A

S ⊕ ⊕

p

) (

) (

) (

)

(BC_IN BC_IN A BC_IN BC_IN A B C_IN A B C_IN A

S= + + + = ⊕ + ⊕

C B

A X

A X

A X

A S

C B

X

Let _IN

⊕

⊕

⊕

⊕

= ,

A AC

C C

C A

AC A

A C

C

C B

A X

A X

A X

A

S = + = ⊕ = ⊕ ⊕ _IN

) (

) (

) (

. .

AB AC

BC C

C AB B

B AC

A A

BC

C_Out = _IN( + )+ _IN( + )+ ( _IN + _IN) = _IN + _IN +

Complete circuitry for a FA

Parallel Binary Adder

Parallel Adder

• All the bits of the augend and the addend are fed into the adder ckt simultaneously.y

• Parallel addition is extremely fast.

Complete Parallel Adder With Registers

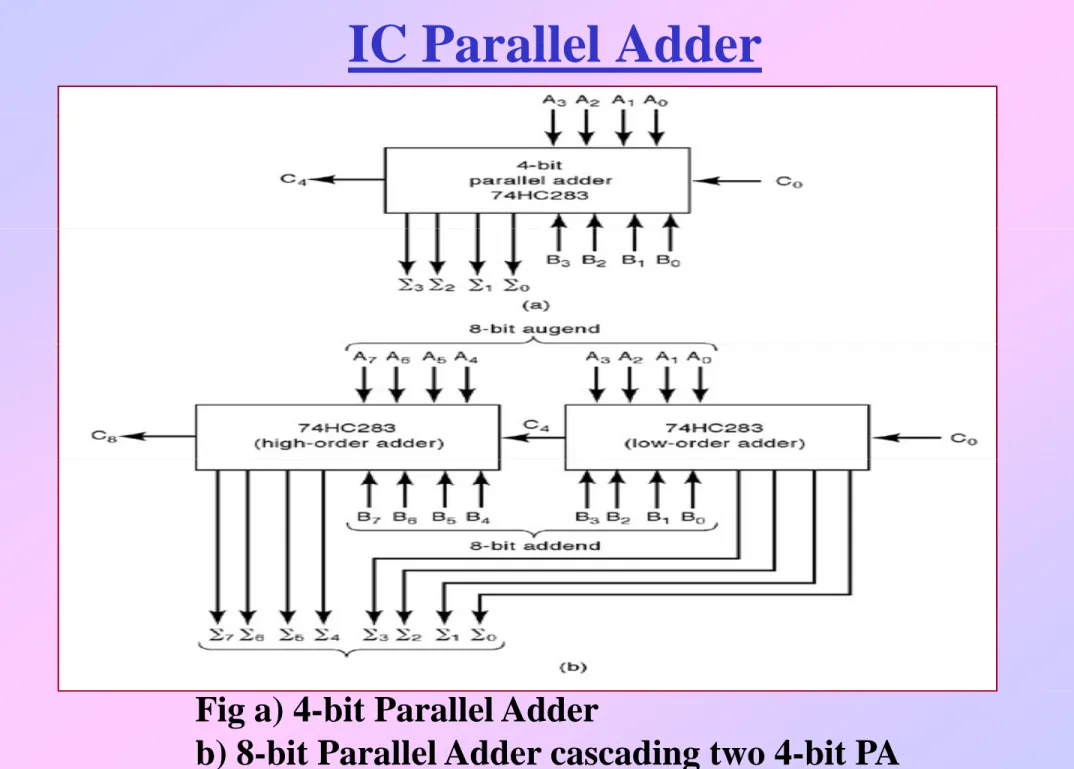
IC Parallel Adder

Fig a) 4-bit Parallel Adder

b) 8-bit Parallel Adder cascading two 4-bit PA

2’s Complement System p y

• The operations of addition and subtraction of signed numbers can be performed using only the addition operation if we use the 2’s complement form to represent negative numbers

numbers.

Addition

Subtraction

Combined Addition and Subtraction

Combined Addition and Subtraction

• The adder / subtractor ckt is controlled by twoThe adder / subtractor ckt is controlled by two control signals ADD and SUB.

• When ADD= 1 and SUB=0 the ckt performsp addition.

• When ADD=0 and SUB =1, the ckt performs a 2’s, p complement operation.

• The result of addition or subtraction appears at the outputs ∑₀ to ∑₃

BCD Adder

• Add the BCD code groups for each decimal digit position;

use ordinary binary addition.

• For those positions where the sum is 9 or less, the sum is in proper BCD form and no correction is needed

proper BCD form and no correction is needed

• When the sum of two digits is greater than 9, a correction of 0110 should be added to that sum to produce the proper BCD result. This will produce a carry to be added to the next decimal position.

decimal position.

A₃A₂A₁A₀ ← BCD code group B₃B₂B₁ B₀ ← BCD code group S₄S₃ S₂ S₁ S₀ ← straight binary sum

Formation of logic for 0110 correction

S₄ S₃ S₂ S₁ S₀

0 1 0 1 0 (10)

• Whenever S₄ =1 (sums greater than 15)

0 1 0 1 1 (11)

0 1 1 0 0 (12)

greater than 15)

• Whenever S₃ =1 and

0 1 1 0 1 (13)

0 1 1 1 0 (14)

3

either S₂ or S₁ or both are 1 (sums 10 to 15)

0 1 1 1 1 (15)

1 0 0 0 0 (16)

1 0 0 0 1 (17)

X=S₄+S₃(S₂+S₁) _{1 0 0 0 1 (17)}

1 0 0 1 0 (18)

X=S₄+S₃(S₂+S₁)

A BCD adder

Cascaded BCD Adder