TERPENDEK
FAJAR ADIYATNO
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Menentukan Jalur Distribusi Terpendek. Dibimbing oleh AMRIL AMAN dan TONI BAKHTIAR.
Supply chain management adalah sebuah proses pembuatan dan penyampaian barang kepada konsumen. Salah satu faktor utama dari supply chain management adalah supply chain networks.
Supply chain networks terdiri atas dua bagian utama yaitu lokasi produksi dan proses distribusi. Keduanya berkaitan dengan penentuan jalur distribusi atau rute optimum dari produsen ke konsumen yang berkaitan dengan waktu, jarak tempuh, dan kapasitas kendaraan. Masalah penentuan rute optimum ini disebut dengan Vehicle Routing Problem with Time Windows
(VRPTW).
Penelitian dilakukan di bagian supply chain CV KATRACO, sebuah perusahaan swasta yang bergerak dalam pendistribusian bahan bakar minyak ke SPBU dan beberapa perusahaan di wilayah Jawa Tengah dan sekitarnya. Penelitian ini bertujuan merancang supply chain network untuk kasus VRPTW untuk meminimumkan total jarak tempuh kendaraan. Metode yang digunakan adalah metode heuristic yaitu sweep heuristic, saving heuristic, dan nearest depot heuristic sebagai route constructing methods. Metode 2-opt, metode relocate, dan metode exchange digunakan sebagai
route improvement methods untuk menentukan rute yang lebih optimum bagi kendaraan.
Determine the Distribution of the Shortest Path. Supervised by AMRIL AMAN and TONI BAKHTIAR.
Supply chain management is a process of manufacture and delivery of goods to consumers. One of the main factors of supply chain management is supply chain networks. Supply chain networks consist of two main parts, i.e. , the location of production and the distribution process. Both are related to the determination of optimum distribution channels or routes from producers to consumers which are related to time, distance, and vehicle capacity. This problem is called with the Vehicle Routing Problem with Time Windows (VRPTW).
TERPENDEK
FAJAR ADIYATNO
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
NIM
: G54061594
Menyetujui
Tanggal Lulus:
Pembimbing I,
Dr. Ir. Amril Aman, M.Sc.
NIP. 19570330 198103 1 001
Pembimbing II,
Dr. Toni Bakhtiar, M.Sc.
NIP. 19720627 199702 1 002
Mengetahui:
Ketua Departemen,
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah SWT atas berkat, rahmat dan kasih sayang-Nya sehingga penulis mampu menyelesaikan karya ilmiah ini. Berbagai kendala dialami oleh penulis sehingga banyak sekali orang yang membantu dan berkontribusi dalam pembuatan karya ilmiah ini. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih kepada:
1. Sang pencipta, Tuhan semesta alam Allah SWT, atas maha karya-Nya yaitu bumi yang sempurna ini;
2. keluarga tercinta: bapak dan ibu, ibu sebagai pemberi motivasi dan bapak sebagai sumber inspirasi, untuk Itang, Opi, Amel yang selalu memberikan semangat dan doa.
3. Dr. Ir. Amril Aman, M.Sc. selaku dosen pembimbing I yang telah meluangkan waktu dan pikiran dalam membimbing, memberi motivasi, semangat dan doa;
4. Dr. Toni Bakhtiar, M.Sc. selaku dosen pembimbing II yang telah memberikan ilmu, kritik dan saran, motivasi serta doanya;
5. Drs. Siswandi, M.Si. selaku dosen penguji yang telah memberikan ilmu, saran dan doanya;
6. semua dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan;
7. staf Departemen Matematika: Bapak Yono, Bapak Hery, Bapak Deni, Ibu Ade, Bapak Epul, Bapak Bono dan Ibu Susi atas semangat dan doanya;
8. sahabat yang selalu memberi semangat: Nia, Apri, vera, Sofyan, Tami, Arum, Wira Fardan, Dandi, Slamet, dan Margi;
9. kawan yang selalu memberi inspirasi: Faisal, Dhia, Feni, Vivi;
10. keluarga besar H Khamsiah dan H Maliha yang selalu memberi motivasi dan doa; 11. semua teman Matematika 42 yang selalu menjadi contoh yang baik;
12. semua teman Matematika 43 yang selalu menjadi bagian dari keluarga; 13. semua teman Matematika 44 yang selalu mendukung agar terus berkembang; 14. perkumpulan perpustakaan: Ricken, Agnes, Ryu, Peny, Iput;
15. teman satu pembimbing: Mira, Fardan, Razono, Nurisma, Imam, Lili;
16. teman seperjuangan perwira 40: Ucok, Erwin, Satrio, Bayu, Ilman, Dandi, Anif, Hendra, Zul, Leo, Hesti, Sari;
17. teman seperjuangan 43 Banjarnegara: Galih, Heru, Jona, Ita, Vita, Bani, Arin, Revi, Okta, eny, Lia, Leli, Ayu, Anggi;
18. Gumatika dan Ikamahamas yang telah mengasah pribadi ini menjadi pribadi yang tangguh;
19. Guardian angel for being my special one;
20. semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.
Bogor, Desember 2010
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... viii
DAFTAR TABEL ... viii
DAFTAR LAMPIRAN ... ix
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan Penelitian ... 1
1.3 Manfaat ... 1
II LANDASAN TEORI 2.1 Supply Chain Management ... 1
2.2 Supply Chain Network ... 2
2.3 Distribusi ... 2
2.4 Graf ... 2
2.5 Traveling Salesman Problem ... 2
2.5.1 Traveling Salesman Problemwith Time Windows... 3
2.5.2 m-TSP ... 3
2.6 Vehicle Routing Problem ... 3
2.7 Vehicle Routing Problemwith Time Windows ... 4
2.8 Metode Heuristic ... 5
2.8.1 SavingHeuristic ... 5
2.8.2 SweepHeuristic ... 7
2.8.3 Nearestdepot Heuristic ... 8
2.8.4 Metode 2-opt ... 9
2.8.5 Metode Relocate ... 9
2.8.6 Metode Exchange ... 10
III DISTRIBUSIBAHANBAKARMINYAKDICVKATRACO 3.1 Ruang Lingkup ... 12
3.2 Pengolahan Data ... 12
3.3 Perumusan Masalah ... 13
3.4 Formulasi Masalah ... 13
3.5 Hasil dan Pembahasan ... 14
IV SIMPULAN ... 20
Simpulan ... 20
DAFTARPUSTAKA ... 20
LAMPIRAN ... 21
DAFTAR GAMBAR
Halaman
1 Peta Jalan Raya di Jawa Tengah ... 2
2 Rute dalam Traveling salesman Problem (TSP) ... 3
3 Ilustrasi Saving Heuristic ... 7
4 Ilustrasi Sweep Heuristic ... 8
5 Ilustrasi Nearestdepot Heuristic ... 8
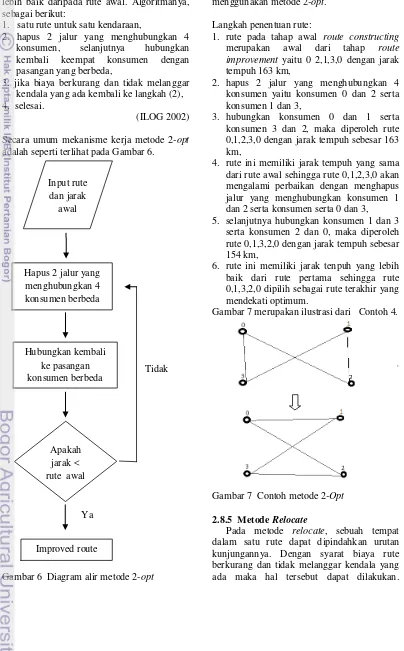
6 Diagram alir Metode 2-opt ... 9
7 Ilustrasi Metode 2-opt ... 9
8 Diagram alir Metode Relocate ... 10
9 Ilustrasi Metode Relocate ... 10
10 Diagram alir Metode Exchange ... 11
11 Ilustrasi Metode Relocate ... 12
DAFTAR TABEL
Halaman 1 Permintaan tiap TPS ... 52 Jarak antar-TPS ... 6
3 Nilai savings ... 6
4 Ranking nilai savings ... 7
5 Data permintaan dan waktu bongkar-muat tiap konsumen ... 13
6 Hasil simulasi tahap route constructing... 15
7 Hasil simulasi tahap route improvement ... 16
8 Hasil simulasi menggunakan metode savingsheuristic kendaraan pertama ... 16
9 Hasil simulasi menggunakan metode savingsheuristic kendaraan kedua ... 17
10 Hasil simulasi menggunakan metode savingsheuristic kendaraan ketiga ... 17
11 Hasil simulasi menggunakan metode sweepheuristic kendaraan pertama ... 17
12 Hasil simulasi menggunakan metode sweepheuristic kendaraan kedua ... 18
13 Hasil simulasi menggunakan metode sweepheuristic kendaraan ketiga ... 18
14 Hasil simulasi menggunakan metode nearestdepotheuristic kendaraan pertama ... 18
15 Hasil simulasi menggunakan metode nearestdepotheuristic kendaraan kedua ... 19
16 Hasil simulasi menggunakan metode nearestdepotheuristic kendaraan ketiga ... 19
17 Hasil rute saat ini kendaraan pertama ... 19
18 Hasil rute saat inikendaraan kedua ... 19
19 Hasil rute saat ini kendaraan ketiga ... 20
DAFTAR LAMPIRAN
Halaman
1 Hasil simulasi menggunakan metode savings heuristic pada kendaraan pertama sampai
kesembilan ... 21
2 Hasil simulasi menggunakan metode sweep heuristic pada kendaraan pertama sampai kesepuluh ... 23
3 Hasil simulasi menggunakan metode nearestdepot heuristic pada kendaraan pertama sampai kesepuluh ... 25
4 Hasil rute saat ini pada kendaraan pertama sampai keduabelas ... 27
5 Matrik jarak saaat ini (km) ... 30
6 M-File Mathlab ... 31
7 Input program (notepad) ... 33
8 Output program savings heuristic ... 34
9 Output program sweep heuristic ... 36
10 Output program nearestdepot heuristic ... 38
11 Skrip program savings heuristic ... 40
12 Skrip program sweep heuristic ... 43
13 Skrip program nearestdepot heuristic ... 46
14 Peta jalur distribusi (CV KATRACO) ... 49
RIWAYAT HIDUP
Penulis dilahirkan di Banjarnegara pada tanggal 23 Juni 1988 sebagai anak pertama dari empat bersaudara, anak dari pasangan Imam Sayoga dan Mafrukha.
Pada tahun 2000 penulis lulus dari SD Muhammadiyah I Banjarnegara kemudian tahun 2003 lulus dari SLTPN I Bawang. Tahun 2006 penulis lulus dari MAN 2 Banjarnegara dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur USMI (Undangan Seleksi Masuk IPB). Pada tahun 2007, penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
I PENDAHULUAN
Pada bagian awal bab ini, akan dijelaskanlatar belakang dan tujuan penelitian yang dilakukan. Sementara itu pada bagian akhir bab ini akan disajikan manfaat dari penelitian ini bagi perusahaan.
1.1 Latar belakang
Bahan bakar merupakan suatu komponen penting dalam proses produksi, terutama dalam hal pendistribusian barang. Harga bahan bakar yang tidak stabil mendorong perusahaan harus bisa membuat semua lini proses produksi berjalan secara efektif dan efisien. Perusahan harus mengintegrasikan semua arus informasi barang dan jasa, mulai dari pemasok atau agen hingga ke konsumen. Proses integrasi ini disebut dengan supply
chain management.
Supply chain management adalah sebuah proses di mana produk diciptakan dan disampaikan kepada konsumen. Salah satu faktor utama yang merupakan bagian dari
supply chain management adalah supply chain
networks. Supply chain networks terdiri dari dua bagian utama yaitu lokasi produksi dan proses distribusi. Penentuan lokasi produksi dan proses distribusi merupakan faktor yang sangat penting. Penentuannya akan berhubungan dengan proses pemasaran dan pelayanan terhadap permintaan konsumen. Lokasi produksi yang tepat akan dapat meningkatkan kinerja perusahaan, sedangkan proses distribusi berkaitan dengan pengiriman barang dan jasa dari produsen ke konsumen dengan tepat sasaran dan waktu yang cepat.
Proses distribusi harus memperhatikan penentuan jalur distribusi yang tepat.
Penentuan jalur distribusi berkaitan dengan jarak tempuh, waktu tempuh dan kendaraan yang dipakai. Masalah yang berkaitan dengan penentuan jalur distribusi dalam hal ini adalah penentuan rute yang optimum untuk kendaraan dari satu produsen untuk melayani banyak konsumen yang berkaitan dengan waktu dan jarak tempuh, masalah ini disebut dengan Vehicle Routing Problem with Time
Windows (VRPTW).
1.2 Tujuan Peneltian
Tujuan dari penelitian ini adalah merancang supply chain network untuk kasus VRPTW pada CV KATRACO yang bergerak pada pengiriman bahan bakar minyak. Metode yang digunakan adalah metode heuristic
seperti sweep heuristic, saving heuristic, nearest depot heuristic untuk menentukan rute yang optimum bagi kendaraan. Pemilihan metode yang tepat juga dapat bertujuan untuk meminimumkan biaya distribusi yang berdampak pada proses produksi dan kepuasan konsumen.
1.3Manfaat
Manfaat yang dapat diperoleh dari penelitian ini adalah perancangan supply
chain network yang dapat memberikan:
1. gambaran pemilihan rute optimum bagi kendaraan untuk mencapai lokasi tujuan dengan cepat dan tepat,
2. memaksimalkan barang bawaan,
3. meminimumkan jumlah kendaraan yang dipakai sehingga dapat memberi keuntungan yang lebih bagi perusahaan.
II LANDASAN TEORI
Dalam bab ini, akan dijelaskan beberapametode yang digunakan dalam penelitian. Pertama-tama akan dijelaskan pengertian
supply chain management, supply chain network, distribusi, graf, Traveling Salesman
Problem (TSP) yang merupakan dasar dari
Vehicle Routing Problem (VRP). Pada bagian
terakhir akan diperlihatkan penggunaan metode heuristic untuk mencari solusi dari kasus VRPTW yang dihadapi.
2.1 Supply Chain Management
Supply chain management adalah sebuah proses yang meliputi:
- kegiatan menentukan lokasi produksi dengan tepat
- kegiatan merancang produk baru (product development)
- kegiatan mendapatkan bahan baku (procurement)
- kegiatan merencanakan produksi dan persediaan
- kegiatan melakukan produksi
- kegiatan inventori (penyimpanan) barang-barang hasil produksi
- kegiatan melakukan pengiriman barang-barang hasil produksi (distribution)
- planning and control.
Brebes Tegal
Supply chain network merupakan sebuah
pilihan proses management yang melakukan fungsi dalam upaya mendapatkan bahan baku, transportasi bahan baku sampai pada tempat produksi dan distribusi hasil produksi kepada konsumen.
(Ganeshan & Harrison 1995)
Proses supply chain network akan menentukan kinerja suatu perusahaan dalam upaya meningkatkan keuntungan dan melayani kepuasan konsumen.
2.3 Distribusi
Distribusi ialah proses pengiriman barang dan jasa sampai ke konsumen pada waktu yang cepat dan tempat yang tepat. Proses distribusi dipengaruhi oleh keputusan transportasi yang digunakan. Untuk menciptakan proses distribusi yang efektif dan efisien maka perusahaan harus merancang jalur distribusi yang tepat. Jalur distribusi yang tepat dicapai dengan memilih rute yang paling optimum antara lokasi asal dan lokasi tujuan.
(Hugos 2003)
Pemilihan jalur distribusi yang tepat dapat meningkatkan kepuasan konsumen karena produk yang mereka inginkan bisa mereka terima tepat waktu, sedangkan bagi perusahaan tujuannya adalah mengefisienkan biaya dan meningkatkan kinerja sumber daya manusianya.
2.4 Graf
Suatu graf G adalah pasangan terurut (V,E) dengan V himpunan takkosong dan berhingga dan E himpunan pasangan takterurut yang menghubungkan elemen-elemen V. Graf G dinotasikan dengan
G=(V,E). Elemen V disebut verteks (node, simpul) sedangkan elemen E disebut sisi (edge).
(Foulds 1992)
Dalam masalah transportasi, himpunan simpul pada graf G dinotasikan V(G) yang merupakan representasi dari kota tujuan, sedangkan himpunan sisi pada graf G
dinotasikan E(G) merupakan representasi dari jalur penghubung antarkota tujuan. Gambar 1 merupakan ilustrasi sebuah graf yang menyatakan peta jaringan jalan raya yang menghubungkan sejumlah kota di Provinsi Jawa Tengah.
Gambar 1 Peta jalan raya di Jawa Tengah.
2.5 Traveling Salesman Problem
Traveling salesman problem adalah suatu permasalahan di mana seorang salesman akan mengunjungi seluruh kota yang ada dan diharuskan kembali ke kota awal pada akhir perjalanannya. Tujuannya adalah menentukan rute perjalanan yang melalui seluruh kota dan meminimumkan jarak tempuh. Permasalahan semacam ini merupakan suatu contoh dari permasalahan Traveling Salesman Problem
(TSP).
Fungsi objektif: meminimumkan jarak yang ditempuh dan mengunjungi setiap kota yang ada, dengan tidak terdapat subtour atau penumpukan kendaraan yang melayani rute dari kota ke-i
menuju kota ke-j yang hanya dilayani oleh satu kendaraan. L adalah banyaknya subtour
dari setiap rute dari kota-kota 1,2,...,m. Pada awal bagi salesman untuk mendistribusikan barang kepada konsumen melalui rute yang ada.
Gambar 2 Contoh rute dalam traveling
salesman problem (TSP).
Dalam perkembangannya TSP memiliki beberapa variasi, yaitu: Traveling Salesman
Problem with Time Windows (TSPTW) yang
merupakan TSP dengan tambahan waktu pelayanan di setiap kota dan m-Traveling
Salesman Problem (m-TSP) yang
menggunakan sejumlah salesman untuk mengunjungi seluruh kota.
2.5.1 Traveling Salesman Problem with Time Windows
Traveling salesman problem with time
windows merupakan pengembangan dari TSP.
Pada TSPTW rute yang ditempuh memiliki tambahan kendala waktu pelayanan (time windows) untuk setiap konsumen.
Time windows pada setiap konsumen dapat
berbeda satu sama lain, tetapi memiliki karekteristik yang sama yakni berupa selang waktu. Time windows , menunjukkan selang waktu pelayanan pada konsumen i, dengan sebagai batas awal dan sebagai batas akhir. Formulasi untuk TSPTW tidak berbeda dengan formulasi TSP di atas, dengan tambahan beberapa kendala. Misal � adalah waktu pelayanan pada kota ke-i, maka untuk setiap i haruslah berlaku:
� ; ∀= 1,2,… (6) � + , � ; ∀, = 1,2,… (7)
∀≠
Pada (6), waktu pelayanan � berada di antara batas awal dan batas akhir dari time
windows. Kendaraan harus melayani
konsumen tidak kurang dari waktu dan tidak lebih dari waktu , sedangkan pada persamaan berikutnya (7), dipastikan waktu pelayanan di kota j (�) adalah lebih besar
Salah satu variasi dari TSP adalah m-TSP, di mana terdapat m-salesman mengunjungi seluruh kota tetapi setiap kota hanya dapat dikunjungi oleh tepat satu salesman saja. Tiap
salesman berawal dari suatu depot dan pada akhir perjalannya juga harus kembali ke depot tersebut. Tujuannya adalah meminimumkan total jarak dari setiap rute.
Masalah m-TSP dikenal juga sebagai
vehicle routing problem (VRP), di mana
sebuah kota direpresentasikan sebagai sebuah konsumen dan tiap kendaraan memiliki kapasitas tertentu. Total jumlah permintaan dalam suatu rute tidak boleh melebihi kapasitas dari kendaraan yang beroperasi.
(Larsen 1999)
2.6 Vehicle Routing Problem
Vehicle Routing Problem (VRP)
dan berakhir di depot, setiap konsumen dikunjungi tepat satu kali oleh tepat satu kendaraan, jumlah permintaan tiap rute tidak melebihi kapasitas kendaraan dan meminimumkan biaya perjalanan.
(Cordeau et al 2002)
VRP adalah masalah optimisasi kombinatorial yang kompleks, karena merupakan gabungan dari masalah kapasitas (packing problem) dan masalah pencarian rute optimal kendaraan dari suatu depot dan melayani sejumlah konsumen (traveling
salesman problem). Dalam prakteknya VRP
banyak digunakan pada masalah distribusi logistik. Karakteristik dari formulasi VRP adalah satu depot (dilambangkan dengan O) yang memiliki sebanyak k kendaraan untuk melakukan pengiriman, di mana kapasitas setiap kendaraan sebesar � . Kendaraan tersebut mengirimkan permintaan sebesar � kepada konsumen ke-i, dengan i=1,2,3,…,n.
Jarak yang ditempuh setiap kendaraan adalah jarak yang paling minimum dengan , adalah
jarak yang ditempuh dari konsumen i ke yang tersedia dan permintaan yang dikirim tidak melebihi kapasitas kendaraan yang tersediauntuk setiap rute.
(Machado et al 2002)
Definisi variabel keputusan, konstanta, fungsi objektif dan fungsi kendala dalam VRP adalah sebagai berikut:
Variabel keputusan
, =
1, jika dikunjungi setelah oleh kendaraan 0, jika selainnya. Konstanta
� = permintaan konsumen ke− � = kapasitas maksimum kendaraan
, = jarak yang ditempuh dari konsumen i ke meminimumkan total jarak tempuh kendaraan, di mana , adalah jarak dari konsumen i kekontinuan rute dari setiap kendaraan yang beroperasi. Kendaraan yang telah selesai melayani konsumen ke-i diharuskan segera pergi untuk melayani konsumen berikutnya. Kendala (7) memastikan agar total permintaan (�) pada satu rute tidak melebihi kapasitas kendaraan (� ) yang beroperasi pada rute tersebut.
(Kritikos & Ioannou 2004)
2.7 Vehicle Routing Problem with Time Windows
VRP dengan tambahan kendala waktu pelayanan disebut sebagai Vehicle Routing
Problem with Time Windows (VRPTW).
pelayanan pada konsumen, biasanya selang waktu tersebut berbeda pada setiap konsumen. (Hideki et al 2006) Seperti halnya VRP, fungsi objektif bagi VRPTW adalah meminimumkan total jarak tempuh kendaraan. Kendala yang digunakan pun sama seperti formulasi VRP (2)-(8), tetapi perlu ditambahkan beberapa kendala yang berhubungan dengan time windows. Kendala tersebut, antara lain:
Konstanta
= waktu kedatangan pada tempat i
= waktu kedatangan pada tempat j
� = waktu servis di konsumen i Kendala (9) memastikan waktu kedatangan kendaraan di konsumen j ( ) selalu lebih besar dari kedatangan kendaraan di konsumen
i ( ), di mana � merupakan waktu service di sebaliknya. Kendala berikutnya (10) memastikan kedatangan kendaraan di konsumen i berada di antara selang waktu yang telah ditentukan, dengan batas awal dan batas akhir , sedangkan kendala terakhir (11) memastikan agar waktu kedatangan kendaraan ke setiap konsumen selalu positif.
(Larsen 1999)
2.8 Metode Heuristik
Penggunaan metode branch and bound
untuk mencari solusi VRP yang memiliki banyak kota (lebih dari 50 kota) memerlukan waktu komputasi yang lama. Alasan tersebut menjadi sebab dikembangkannya metode
heuristic. Metode heuristic dapat memberikan solusi lebih cepat daripada metode branch and bound, tetapi tidak ada jaminan solusi yang dihasilkan optimal. Solusi dari metode
heuristic didapat selain dengan cara trial and error juga dengan pendekatan secara intuitif.
(Winston 2004)
Untuk memecahkan masalah VRP dengan metode heuristic diperlukan dua tahap yaitu
route constructing sebagai tahap pertama dan
route improvement pada tahap kedua. Pada penelitian ini metode sweep heuristic, saving
heuristic, nearest depot heuristic akan
digunakan untuk mencari solusi pada tahap pertama. Selanjutnya metode 2-opt, metode
relocate dan metode exchange digunakan
untuk memperbaiki solusi yang telah ada.
2.8.1 Saving Heuristic
Metode savings heuristic membangun rute terpendek berdasarkan nilai saving yang diurutkan dari yang terbesar kemudian diakumulasikan berdasarkan permintaan tiap vertek tanpa melebihi kapasitas kendaraan, dinotasikan savings s(i,j). Algoritmanya
2. buat ranking dari perhitungan savings dan buat daftar dari hasil savings yang terbesar hingga terkecil,
3. akumulasikan tiap nilai savings dari yang paling besar hingga yang paling kecil berdasarkan permintaan tiap verteks, 4. apabila telah mencapai batas maksimum
kapasitas kendaraan, maka beralih ke nilai
savings terbesar kedua untuk memulai rute baru dengan kendaraan yang berbeda seterusnya hingga permintaan tiap konsumen terpenuhi.
(ILOG 2002)
Ilustrasi dari metode savings heuristic
diberikan dalam Contoh 1.
Contoh 1
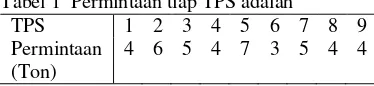
Sebuah kota kecil mempunyai dua truk pemungut sampah dengan kapasitas 23 ton. Truk tersebut harus mengangkut sampah di 9 titik tempat pembuangan sampah (TPS). Berikut data yang disajikan pada Tabel 1 yang merupakan permintaan tiap TPS, dan Tabel 2 merupakan jarak antar-TPS.
Tabel 1 Permintaan tiap TPS adalah
TPS 1 2 3 4 5 6 7 8 9 Permintaan
(Ton)
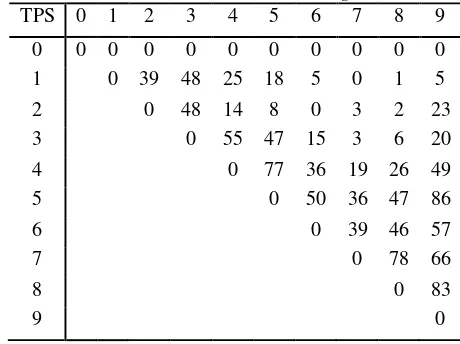
Tabel 2 jarak antar-TPS
TPS 0 1 2 3 4 5 6 7 8 9
0 0 25 43 57 43 61 29 41 48 71 1 0 29 34 43 68 49 66 72 91 2 0 52 72 96 72 81 89 114 3 0 45 71 71 95 99 108 4 0 27 36 65 65 65
5 0 40 66 62 46
6 0 31 31 43
7 0 11 46
8 0 36
9 0
Berikut adalah proses perhitungan nilai
savings:
1. bila kita akan menghitung s(0,1), dilihat pada Tabel 2 jarak dari depot ke node 0 adalah 0, kemudian jarak dari depot ke
node 1 adalah 25, dan jarak dari depot ke
node 1 adalah 25, maka:
s(0,1) = d(0,0) + d(0,1) –d(0,1) = 0 + 25 – 25 = 0,
2. sama seperti perhitungan pada s(0,1), bila kita menghitung s(1,2) maka langkah pertama yang harus kita lakukan adalah
mencari data jarak dari depot ke node 1, jarak dari depot ke node 2, dan jarak dari
node 1 ke node 2, sehingga:
s(1,2) = d(0,1) + d(0,2) –d(1,2) = 25 + 43 – 29 = 39.
Lakukan perhitungan savings terhadap semua kombinasi setiap node sehingga diperoleh nilai savings yang disajikan pada Tabel 3 dan urutkan nilai savings dari yang paling besar hingga yang paling kecil yang disajikan pada Tabel 4.
Tabel 3 Nilai savings
TPS 0 1 2 3 4 5 6 7 8 9
0 0 0 0 0 0 0 0 0 0 0 1 0 39 48 25 18 5 0 1 5 2 0 48 14 8 0 3 2 23 3 0 55 47 15 3 6 20 4 0 77 36 19 26 49 5 0 50 36 47 86
6 0 39 46 57
7 0 78 66
8 0 83
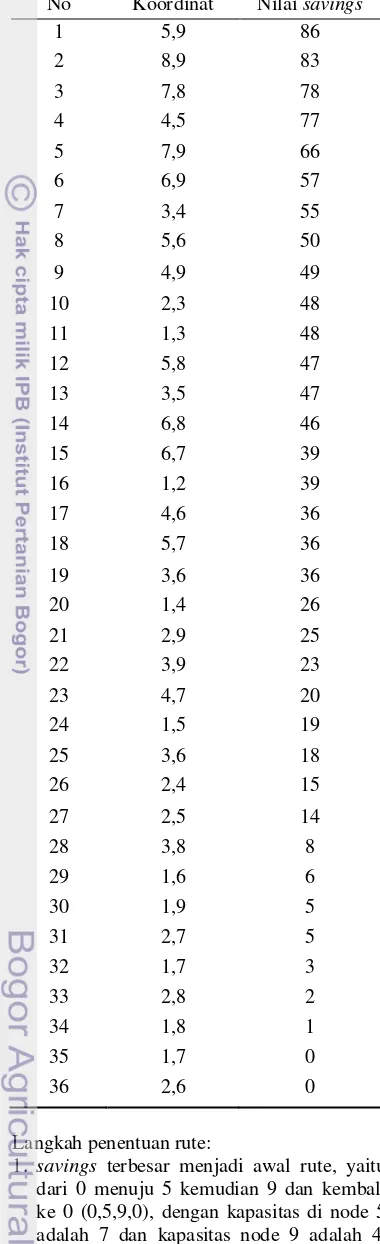
Urutkan berdasarkan nilai savings tertinggi Tabel 4 Ranking nilai savings
No Koordinat Nilai savings
1 5,9 86 selanjutnya dapat dibuat berdasarkan daftar ranking savings,
2. rute yang dapat digabungkan selanjutnya adalah (0,5,9,8,0) dengan kapasitas angkut adalah 15, rute ketiga yang dapat dibuat untuk satu kali perjalanan yaitu (0,5,9,8,7,0) dengan kapasitas 20 unit. Kapasitas per sekali angkut adalah 23 unit, berarti tersisa 3 unit yang dapat diangkut, 3. daftar savings ke-4 dicoba untuk penentuan
rute, bila dibuat rute (0,5,9,8,7,4,0) akan diperoleh kapasitas 24. Kapasitas sekali angkut yang diperbolehkan adalah 23, maka rute ini tidak dapat digunakan sehingga untuk savings (4,5) menjadi awal rute kedua yang terbesar,
4. kemudian dibuat rute dari data savings ke-5 sehingga diperoleh rute (0,5,9,8,7,6,0) dengan kapasitas adalah 23 unit. Rute ini memungkinkan karena kapasitas angkut per sekali distribusi sebanyak 23 unit, 5. penentuan rute selanjutnya sama halnya
dengan tahap awal dan dimulai dari daftar savings terbesar kedua,
6. dari perhitungan diperoleh rute pertama yaitu (0,5,9,8,7,6.0) dengan kapasitas adalah 23. Kemudian rute kedua (0,1,2,3,4,0) dengan kapasitas 19. Dua rute ini memiliki jarak total adalah 420 km, tetapi kedua rute ini belum merupakan rute yang optimum sehingga perlu melakukan perbaikan pada tahap improvement.
Gambar 3 merupakan ilustrasi dari Contoh 1
Gambar 3 Contoh savings heuristic
2.8.2 Sweep Heuristic
sampai seluruh lokasi dikunjungi oleh kendaraan yang tersedia di depot. Algoritmanya sebagai berikut:
1. sejumlah kendaran yang tersedia,
2. kendaraan memulai sebuah rute dari depot 3. temukan konsumen yang terdekat dari titik awal atau depot bagi kendaraan. Kemudian temukan konsumen yang terdekat dari titik sebelumnya. Jika tidak dimungkinkan untuk melakukan kunjungan tanpa melanggar kendala kapasitas kendaraan yang ada akhiri rute kendaraan, pilih kendaraan lain dan lakukan lagi langkah 2, 4. kendaraan yang akan dialokasikan untuk mengunjungi konsumen harus memenuhi semua kendala,
5. jika semua kendaraan telah digunakan dan telah mengunjungi semua konsumen maka selesai.
(ILOG 2002)
Ilustrasi dari metode sweep heuristic diberikan dalam Contoh 2.
Contoh 2
Dalam Contoh 2 dibahas penentuan rute pengambilan sampah seperti pada Contoh 1 dengan menggunakan metode sweep heuristic.
Rute pertama diawali dari depot kemudian menuju ke konsumen 1. Pemilihan konsumen 1 sebagai awal dari rute karena memiliki jarak yang paling dekat dengan depot yaitu 25 km. Selanjutnya, dilanjutkan ke konsumen 2 karena memiliki jarak yang paling dekat merupakan ilustrasi dari Contoh 2.
Gambar 4 Contoh sweep heuristic
2.8.3 Nearest Depot Heuristic
Metode nearest depot heuristic dimulai dengan menentukan banyaknya kendaraan di depot. Membangun rute dengan menelusuri tempat yang paling dekat dengan depot atau stasiun pertama, kemudian untuk rute
berikutnya juga diawali dengan lokasi yang paling dekat dengan depot. Perjalanan berhenti ketika kapasitas kendaraan atau time
windows terpenuhi untuk semua kendaraan.
Jika kapasitas kendaraan atau time windows
telah dicapai maka kendaraan tersebut harus kembali ke depot. Jalankan kendaraan berikutnya dengan aturan yang sama seperti kendaraan pertama, sampai seluruh lokasi dikunjungi oleh kendaraan yang tersedia di depot. Algoritmanya sebagai berikut:
1. sejumlah kendaraan yang tersedia,
2. mulai sebuah rute dari depot bagi kendaraan,
3. temukan konsumen yang terdekat dari titik awal atau depot bagi kendaraan. Jika tidak dimungkinkan untuk melakukan kunjungan tanpa melanggar kendala kapasitas kendaraan yang ada akhiri rute kendaraan, pilih kendaraan lain dan lakukan lagi langkah 2,
4. jika semua konsumen telah dikunjungi maka selesai.
(ILOG 2002)
Ilustrasi dari metode nearest depot heuristic
diberikan dalam Contoh 3.
Contoh 3
Dalam Contoh 3 dibahas penentuan rute pengambilan sampah seperti pada Contoh 1 dengan menggunakan metode nearest depot heuristic.
Rute pertama diawali dari depot kemudian menuju ke konsumen 1. Pemilihan konsumen 1 sebagai awal rute karena memiliki jarak yang paling dekat dengan depot yaitu 25 km. Selanjutnya, dilanjutkan ke konsumen 6 karena memiliki jarak terpendek kedua dengan depot yaitu 29 km dan seterusnya
2.8.4 Metode2-Opt
Pada dasarnya metode 2-opt ialah memindahkan dua jalur pada rute yang ada, kemudian menghubungkan kembali jalur tersebut dengan pasangan konsumen yang berbeda. Sebagai catatan, metode 2-opt hanya dapat dilakukan jika rute baru yang dihasilkan lebih baik daripada rute awal. Algoritmanya, sebagai berikut:
1. satu rute untuk satu kendaraan,
2. hapus 2 jalur yang menghubungkan 4 konsumen, selanjutnya hubungkan kembali keempat konsumen dengan pasangan yang berbeda,
3. jika biaya berkurang dan tidak melanggar kendala yang ada kembali ke langkah (2), 4. selesai.
(ILOG 2002)
Secara umum mekanisme kerja metode 2-opt
adalah seperti terlihat pada Gambar 6.
Gambar 6 Diagram alir metode 2-opt
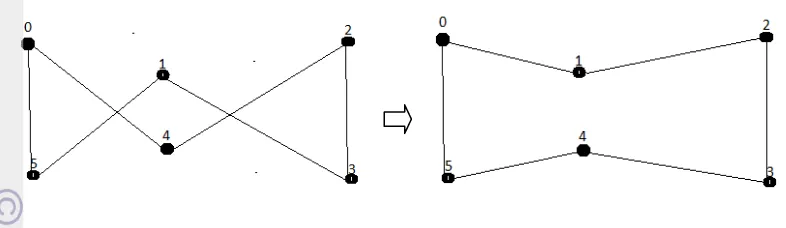
Ilustrasi dari metode 2-opt diberikan dalam menggunakan metode2-opt.
Langkah penentuan rute: 0,1,2,3,0 dengan jarak tempuh sebesar 163 km,
4. rute ini memiliki jarak tempuh yang sama dari rute awal sehingga rute 0,1,2,3,0 akan mengalami perbaikan dengan menghapus jalur yang menghubungkan konsumen 1 dan 2 serta konsumen serta 0 dan 3, 5. selanjutnya hubungkan konsumen 1 dan 3
serta konsumen 2 dan 0, maka diperoleh rute 0,1,3,2,0 dengan jarak tempuh sebesar 154 km,
6. rute ini memiliki jarak tenpuh yang lebih baik dari rute pertama sehingga rute 0,1,3,2,0 dipilih sebagai rute terakhir yang mendekati optimum.
Gambar 7 merupakan ilustrasi dari Contoh 4.
Gambar 7 Contoh metode 2-Opt
2.8.5 Metode Relocate
Metode relocate ini dapat memindahkan sebuah kunjungan pada rute yang sama ke posisi yang berbeda. Algoritmanya, sebagai berikut:
1. satu rute untuk satu kendaraan,
2. hapus 2 jalur yang menghubungkan 3 konsumen, selanjutnya hubungkan kembali keempat konsumen dengan pasangan yang berbeda,
3. jika biaya berkurang dan tidak melanggar kendala yang ada kembali ke langkah (2), 4. selesai.
(ILOG 2002)
Secara umum mekanisme kerja metode
relocate adalah seperti terlihat pada Gambar 6.
Gambar 8 Diagram alir metode relocate
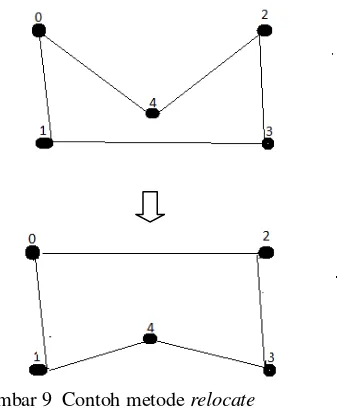
Ilustrasi dari metode relocate diberikan dalam Contoh 5
Contoh 5
Dalam Contoh 5 dibahas penentuan rute pengambilan sampah seperti pada Contoh 1 hanya pada konsumen 1,2,3,4 dengan menggunakan metode relocate.
Langkah penentuan rute:
1. rute pada tahap awal route constructing
merupakan awal dari tahap route improvement yaitu 0,3,4,2,1,0 dengan jarak tempuh 226 km,
2. hapus jalur yang menghubungkan antara konsumen 0 dan 3 serta konsumen 3 dan 4, 3. hubungkan konsumen 0 dan 4 serta konsumen 4 dan 2, maka diperoleh rute 0,4,2,3,1,0 dengan jarak tempuh 228 km, 4. rute ini memiliki jarak tempuh yang lebih
jelek dari rute awal sehingga rute 0,4,2,3,1,0 akan mengalami perbaikan dengan menghapus jalur yang menghubungkan konsumen 0 dan 4 serta konsumen serta 4 dan 2,
5. maka diperoleh rute 0,2,3,4,1,0 dengan jarak tempuh sebesar 190 km. Rute ini memiliki jarak tempuh yang lebih baik dari rute awal sehingga rute 0,4,2,3,1,0 dipilih sebagai rute terakhir yang mendekati optimum.
Gambar 9 merupakan ilustrasi dari Contoh 5
Gambar 9 Contoh metode relocate
2.8.6 Metode Exchange
yang dikeluarkan. Pada satu rute kendaraan, dua kunjungan yang berbeda dapat dipertukarkan urutannya. Algoritmanya, sebagai berikut:
1. satu rute untuk satu kendaraan,
2. hapus 4 jalur yang menghubungkan 6 konsumen, selanjutnya hubungkan kembali keempat konsumen dengan pasangan yang berbeda,
3. jika biaya berkurang dan tidak melanggar kendala yang ada kembali ke langkah (2), 4. selesai.
(ILOG 2002)
Secara umum mekanisme kerja metode
exchange adalah seperti terlihat pada Gambar
10.
Gambar 10 Diagram alir metode exchange
Ilustrasi dari metode exchange diberikan dalam Contoh 6
Contoh 6
Dalam Contoh 6 dibahas penentuan rute pengambilan sampah seperti pada Contoh 1 hanya pada konsumen 1,2,3,4,5 dengan menggunakan metode exchange.
Rute diawali dari depot 0 ke konsumen 4,2,3,1,5 dan kembali ke depot 0. memiliki jarak tempuh yang belum optimum yaitu 339 km maka rute perlu dilakukan perbaikan dengan metode exchange. Rute setelah mengalami perbaikan berubah menjadi depot 0 ke konsumen 1,2,3,4,5 dan berakhir di depot 0 dengan jarak tempuh 239 km.
Langkah penentuan rute:
1. rute pada tahap awal route constructing
merupakan awal dari tahap route improvement (metode exchange) yaitu dari 0 menuju 4,2,3,1 kemudian 5 dan kembali lagi ke 0 dengan jarak tempuh 339 km, 2. dari rute awal dapat dilakukan perbaikan
dengan cara menghapus 4 jalur yang menghubungkan 6 konsumen berbeda, 3. pada rute awal yaitu 0,4,2,3,1,5,0 akan
mengalami perbaikan dengan menghapus 2 jalur pertama yang menghubungkan antara konsumen 0 dan 4 serta konsumen 4 dan 2 selanjutnya hubungkan kembali pada pasangan konsumen yang berbeda. Penghapusan jalur kedua dilakukan pada jalur yang menghubungkan konsumen 3 dan 1 serta 1 dan 5 selanjutnya hubungkan kembali pada pasangan konsumen yang berbeda,
4. hubungkan konsumen 0 dan 1, 1 dan 2, 3 dan 4 serta konsumen 4 dan 5,
5. maka diperoleh rute 0,1,2,3,4,5,0 dengan jarak tempuh sebesar 239 km. Rute ini memiliki jarak tempuh yang lebih baik dari rute awal sehingga rute 0,4,2,3,1,5,0 dipilih sebagai rute terakhir yang mendekati optimum. Gambar 11 merupakan ilustrasi dari Contoh 6
Gambar 8 Contoh metode exchange
III DISTRIBUSI BAHAN BAKAR MINYAK DI CV KATRACO
Bab ini diawali dengan penjelasan tentangruang lingkup penelitian, pengolahan data, rumusan masalah yang terjadi di perusahaan tempat penelitian ini berlangsung dan formulasi secara matematis. Hasil dan pembahasan dari penelitian yang dilakukan terdapat pada bagian akhir bab ini.
3.1 Ruang Lingkup
Penelitian dilakukan di CV KATRACO pada bagian supply chain. CV KATRACO merupakan perusahaan swasta yang berlokasi di Banjarnegara dan bergerak dalam pendistribusian bahan bakar minyak ke SPBU dan beberapa perusahaan di wilayah Jawa Tengah dan sekitarnya. Data yang digunakan meliputi rute pengiriman bahan bakar minyak di wilayah Jawa Tengah dan sekitarnya yang dilakukan oleh CV KATRACO untuk masalah VRPTW. Menggunakan metode heuristic
untuk menentukan rute yang optimum bagi kendaraan. Dalam penelitian ini, pembahasan juga akan dibatasi pada proses distribusi untuk saluran SPBU di daerah Jawa Tengah dan sekitarnya. Saluran SPBU dipilih karena jumlahnya yang terbesar dibandingkan dengan saluran lain yang ada.
3.2 Pengolahan Data
Kombinasi antara data sekunder dan data primer digunakan untuk mendukung kesempurnaan dari penelitian ini. Pengumpulan data dilakukan melalui wawancara dengan pihak yang terkait untuk memahami tentang proses distribusi pada perusahaan tersebut. Setelah mendapatkan
informasi yang dibutuhkan, penelitian dilanjutkan dengan memformulasikan masalah distribusi yang ada sebagai sebuah formulasi VRPTW. Selanjutnya, digunakan program ILOG Dispatcher versi 2.1 dan ILOG Solver
versi 4.4, yang dijalankan dalam Microsoft Visual C++ versi 6.0, sebagai alat untuk mencari solusi dari formulasi VRPTW yang dihadapi.
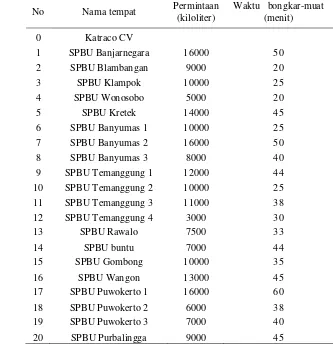
Data yang diperoleh dari kegiatan tersebut, antara lain: letak konsumen, permintaan konsumen waktu bongkar-muat di tempat konsumen, jumlah kendaraan, kapasitas kendaraan, jarak antarkonsumen dengan depot dan dengan konsumen lain. Sedangkan diasumsikan kecepatan kendaraan konstan, waktu buka - tutup gudang konsumen seragam yakni pada pukul 10.00 sampai dengan pukul 20.00, dimana pukul 10.00 dimisalkan sebagai 0 dan pukul 20.00 sebagai 600 dan kendaraan mampu memuat hingga 24.000 kiloliter. Langkah pertama adalah menentukan letak setiap konsumen dan mengetahui jarak dari setiap konsumen, seperti terlihat pada Lampiran 5.
Tabel 7 Data permintaan dan waktu bongkar-muat tiap konsumen
No Nama tempat Permintaan (kiloliter)
Perusahaan melakukan pengiriman bahan bakar minyak setiap harinya. Kemudian bahan bakar minyak tersebut akan didistribusikan ke SPBU di sekitar Jawa Tengah dan sekitarnya, sebelum sampai ke tangan konsumen. Permintaan SPBU tiap harinya telah diketahui sebelumnya. Pendistribusian akan dilakukan menggunakan satu jenis kendaraan, sehingga kapasitas setiap kendaraan seragam. Selain melakukan pengiriman bahan bakar minyak, petugas juga melakukan bongkat-muat dan memindahkan bahan bakar minyak pada tempat yang telah disediakan. Biaya tetap kendaraan akan muncul bila kendaraan tersebut dipakai dalam kegiatan distribusi. Masalah yang dihadapi adalah menetapkan jalur distribusi terpendek dengan biaya minimum dengan mempertimbangkan kendala kapasitas pada kendaraan dan untuk memenuhi setiap permintaan SPBU.
Asumsi yang digunakan, antara lain: semua pesanan SPBU dapat dipenuhi oleh perusahaan, kecepatan kendaraan konstan sehingga tidak ada satu hal pun yang dapat
mempercepat atau memperlambat kecepatan kendaraan. Kendaraan yang digunakan seragam, sehingga setiap kendaraan mempunyai kapasitas yang sama, jarak antar-SPBU diketahui dan permintaan tiap hari SPBU diketahui.
3.4 Formulasi Masalah
variabel keputusan
, =
1, jika dikunjungi setelah oleh kendaraan 0, jika selainnya
� =
1, jika kendaraan dioperasikan
0, jika selainnya Konstanta
� = permintaan dari konsumen ke− � = kapasitas k kendaraan
, = waktu yang dibutuhkan dari konsumen i ke konsumen dengan kendaraan
= kecepatan rata−rata kendaraan = waktu kedatangan pada tempat
= biaya bila kendaraan digunakan
Fungsi objektif (1) pada model di atas adalah meminimumkan banyaknya kendaraan yang berjumlah 12 dan meminimumkan jarak tempuh kendaraan untuk melayani 21 konsumen. Fungsi objektif tersebut
dihadapkan pada kendala-kendala, sebagai berikut: pada kendala (2) dan (3) dipastikan bahwa setiap konsumen yang ada akan dilayani oleh tepat satu kendaraan. Kendala (4) dan (5) akan memastikan tersedianya kendaraan untuk melayani rute yang ada dan juga untuk memastikan kendaraan pergi dan kembali dari depot. Pada kendala (6) akan dipastikan kontinuitas rute kendaraan artinya memastikan bahwa kendaraan yang masuk ke suatu kota harus meninggalkan kota tersebut, sedangkan kendala (7) menggambarkan bahwa jumlah permintaan untuk satu rute tidak melebihi kapasitas kendaraan yang beroperasi. Selanjutnya, pada kendala (8) dipastikan bahwa tidak akan nada konsumen yang dilayani oleh kendaraan yang tidak aktif. Kendala (9) memperlihatkan hubungan antara jarak, kecepatan dan waktu tempuh kendaraan, jarak dan waktu tempuh berbanding lurus. Kendala (10) menunjukkan bahwa jarak dari i ke j sama dengan jarak dari
j ke i, sedangkan kendala (11) memastikan tidak ada subtour pada formulasi yang ada. L
adalah subtour dari setiap rute dari kota-kota 1,2,...,21 Berikutnya, kendala (12) dan (13) berkaitan dengan waktu pelayanan. Pada kendala (12) dipastikan waktu kedatangan kendaraan di tempat konsumen berada di antara waktu buka dan tutup gudang, sedangkan pada kendala (13) memastikan kendaraan akan berada di j pada saat kendaraan berangkat dari i ditambah dengan waktu service pada i dan waktu tempuh dari i
ke j.
3.5 Hasil dan Pembahasan
Pada subbab ini akan diperlihatkan hasil simulasi dari masalah yang diteliti. Kemudian hasil tersebut akan dicari metode yang paling baik dan akan dibandingkan dengan keadaan yang terjadi di lapangan saat ini.
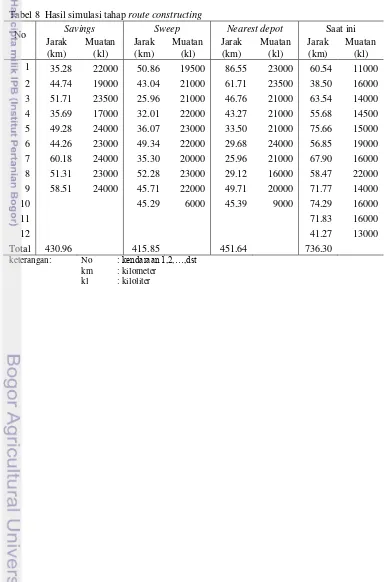
Dari Tabel 6 dan 7 dapat disimpulkan bahwa masing-masing rute pada hasil simulasi tahap
route constructing tiap metode memiliki jarak tempuh yang bebeda. Pada metode sweep heuristic memiliki total jarak tempuh lebih pendek pada kendaraan yang digunakan. Pada hasil simulasi total jarak yang ditempuh kesepuluh kendaran mencapai 415.8533 kilometer, sedangkan total jarak pada metode
memiliki total jarak tempuh terpendek. Jika dibandingkan dengan total jarak tempuh kendaraan saat ini, yaitu 736.2997 kilometer, metode sweep heuristic memiliki total jarak tempuh lebih pendek. Pada tahap route
constructing memiliki jarak tempuh yang
belum optimum maka perlu mengalami perbaikan pada tahap route improvement di mana pada savings heuristic menggunakan
relocate yang menghasilkan total jarak
tempuh 428.7705 kilometer, pada sweep
heuristic menggunakan 2-opt yang
menghasilkan total jarak tempuh 415.2911 kilometer, dan pada nearest depot heuristic
menggunakan exchange yang menghasilkan total jarak tempuh 450.6885 kilometer. Total jarak tempuh memiliki pengaruh besar terhadap pengeluaran perusahaan dalam proses distribusi, semakin pendek jarak tempuh maka biaya yang dikeluarkan dalam pendistribusian barang hasil produksi akan semakin kecil dan semakin panjang jarak tempuh maka biaya yang dikeluarkan semakin besar.
Tabel 8 Hasil simulasi tahap route constructing
No
Savings Sweep Nearest depot Saat ini
Jarak
keterangan: No : kendaraan 1,2,…,dst
km : kilometer
Tabel 9 Hasil simulasi tahap route improvement
Total 428.7705 415.2911 450.6885
keterangan: No : kendaraan 1,2,…,dst
km : kilometer
Dari Tabel 8,9,10 merupakan hasil simulasi menggunakan metode savings
heuristic kendaraan pertama, kedua dan
ketiga. Setiap kendaraan membawa sejumlah bahan bakar minyak sesuai dengan permintaan dari kapasitas maksimum 24000 kiloliter yang dapat dibawa dalam satu kali pengiriman. Pada kendaraan pertama rute yang dilalui meliputi depot, konsumen ke-10, konsumen ke-9 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 35.2833 kilometer dan banyaknya produk yang dibawa sebanyak 22000 kiloliter, serta waktu tiba kendaraan pertama di konsumen 10 yaitu antara 10.18
dan 18.33 satuan waktu dan seterusnya sampai kendaraan kembali ke depot. Sedangkan kendaraan kedua rute yang dilalui meliputi depot, konsumen ke-11, konsumen ke-8 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 44.7428 kilometer dan banyaknya produk yang dibawa sebanyak 19000 kiloliter. Kendaraan ketiga rute yang dilalui meliputi depot, konsumen ke-13, konsumen ke-7 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 51.7056 kilometer dan banyaknya produk yang dibawa sebanyak 23500 kiloliter dan seterusnya sampai kendaraan ke sembilan (Lampiran 1).
Tabel 10 Hasil simulasi menggunakan metode savings heuristic kendaraan pertama
Kode Nama
Tabel 11 Hasil simulasi menggunakan metode savings heuristic kendaraan kedua
Kode Nama Waktu tiba Jarak tempuh Permintaan (jam) (kilometer) (crate)
Tabel 12 Hasil simulasi menggunakan metode savings heuristic kendaraan ketiga
Kode Nama
Waktu tiba Jarak tempuh Permintaan (jam) (kilometer) (crate)
Dari Tabel 11,12,13 merupakan hasil simulasi menggunakan metode sweep heuristic
kendaraan pertama, kedua dan ketiga. Setiap kendaraan membawa sejumlah bahan bakar minyak sesuai dengan permintaan dari kapasitas maksimum 24000 kiloliter yang dapat dibawa dalam satu kali pengiriman. Pada kendaraan pertama rute yang dilalui meliputi depot, konsumen 2, konsumen ke-13, konsumen ke-12 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 50.2966 kilometer dan banyaknya produk yang dibawa sebanyak 19500 kiloliter, serta waktu tiba kendaraan pertama di konsumen 2 yaitu antara 10.13 dan 18.00 satuan waktu dan
seterusnya sampai kendaraan kembali ke depot. Sedangkan kendaraan kedua rute yang dilalui meliputi depot, konsumen ke-11, konsumen ke-3 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 43.0438 kilometer dan banyaknya produk yang dibawa sebanyak 21000 kiloliter. Kendaraan ketiga rute yang dilalui meliputi depot, konsumen ke-1, konsumen ke-4 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 25.9599 kilometer dan banyaknya produk yang dibawa sebanyak 21000 kiloliter dan seterusnya sampai kendaraan ke sepuluh (Lampiran 2).
Tabel 13 Hasil simulasi menggunakan metode sweep heuristic kendaraan pertama
Kode Nama
Tabel 14 Hasil simulasi menggunakan metode sweep heuristic kendaraan kedua
Kode Nama
Waktu tiba Jarak tempuh Permintaan (jam) (kilometer) (crate)
Tabel 15 Hasil simulasi menggunakan metode sweep heuristic kendaraan ketiga
Kode Nama Waktu tiba Jarak tempuh Permintaan (jam) (kilometer) (crate)
Dari Tabel 14,15,16 merupakan hasil simulasi menggunakan metode nearest depot heuristic
kendaraan pertama, kedua, ketiga. Setiap kendaraan membawa sejumlah bahan bakar minyak sesuai dengan permintaan dari kapasitas maksimum 24000 kiloliter yang dapat dibawa dalam satu kali pengiriman. Pada kendaraan pertama rute yang dilalui meliputi depot, konsumen ke-19, konsumen ke-14, konsumen ke-18, konsumen ke-12 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 85.595 kilometer dan banyaknya produk yang dibawa sebanyak 23000 kiloliter, serta waktu tiba kendaraan pertama di konsumen 19 yaitu antara 10.24 dan 16.26 satuan waktu dan seterusnya sampai
kendaraan kembali ke depot dan berlaku untuk kendaraan kedua sampai kendaraan kesepuluh. Sedangkan kendaraan kedua rute yang dilalui meliputi depot, konsumen ke-17, konsumen ke-13 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 61.7068 kilometer dan banyaknya produk yang dibawa sebanyak 23500 kiloliter. Kendaraan ketiga rute yang dilalui meliputi depot, konsumen ke-11, konsumen ke-10 dan kembali ke depot, dengan total jarak yang ditempuh sepanjang 46.755 kilometer dan banyaknya produk yang dibawa sebanyak 21000 kiloliter dan seterusnya sampai kendaraan ke sepuluh (Lampiran 3).
Tabel 16 Hasil simulasi menggunakan metode nearest depot heuristic kendaraan pertama
Kode Nama
Tabel 17 Hasil simulasi menggunakan metode nearest depot heuristic kendaraan kedua
Kode Nama
Waktu tiba Jarak tempuh Permintaan (jam) (kilometer) (crate)
0 Depot 0 0
17 SPBU Puwokerto 1
10.23 – 17.48 23.2961 120.000
13 SPBU Rawalo 11.37 – 19.02 36.6116 7500 0 Depot 12.34 - 20.00 61.7068 0
Tabel 18 Hasil simulasi menggunakan metode nearest depot heuristic kendaraan ketiga
Kode Nama
Waktu tiba Jarak tempuh Permintaan (jam) (kilometer) (crate)
0 Depot 0 0
11 SPBU Temanggung 3
10.21 – 18.32 21.4521 11000
10 SPBU Temanggung 2
11.07 – 19.17 29.1192 10000
0 Depot 11.49 - 20.00 46.755 0
Tabel 17,18,19 merupakan hasil rute saat ini kendaraan pertama, kedua dan ketiga. Kendaraan pertama akan menempuh jarak sepanjang 60.5436 kilometer dan membawa 14000 kiloliter dari 24000 kiloliter yang diperkenankan. Kendaraan pertama melayani rute depot, konsumen ke-2, konsumen ke-4 dan kembali ke depot. Rute untuk kendaraan kedua meliputi depot, konsumen ke-1 dan kembali ke depot. Dengan membawa 16000
kiloliter dan menempuh jarak sepanjang 38.495 kilometer untuk rute tersebut. Pada rute berikutnya, kendaraan ketiga dijadwalkan akan membawa sebanyak 14000 kiloliter dan menempuh perjalanan sepanjang 63.5430 kilometer. Rute tersebut meliputi depot, konsumen ke-12, konsumen ke-11 dan kembali ke depot dan seterusnya sampai kendaraan ke dua belas ( Lampiran 4).
Tabel 19 Hasil rute saat ini kendaraan pertama
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
2 SPBU Blambangan 42.7528 9000 4 SPBU Wonosobo 47.6032 5000
0 Depot 60.5436 0
Tabel 20 Hasil rute saat ini kendaraan kedua
Kode Nama
Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
1 SPBU Banjarnegara 38.4957 16000
Tabel 21 Hasil rute saat ini kendaraan ketiga
Kode Nama Jarak tempuh Permintaan (kilometer) (crate) Berdasarkan penelitian yang dilakukan dapat
diambil beberapa kesimpulan, antara lain: 1. formulasi VRPTW dalam matematika
dapat digunakan untuk menyelesaikan masalah penentuan rute distribusi, 2. penggunaan formulasi VRPTW dengan
metode heuristik memastikan semua konsumen dilayani permintaannya dan tidak ada keterlambatan dalam pengirimannya,
3. menetapkan bahwa metode Sweep Heuristic memiliki solusi paling baik pada kasus ini dibandingkan dengan metode Savings Heuristic dan Nearest
depot heuristic yaitu total jarak tempuh terpendek 415.2911 kilometer dan dibutuhkan minimal sepuluh kendaraan untuk menangani 21 SPBU dengan memenuhi semua syarat yang berlaku, 4. rute pengiriman hasil simulasi memiliki
total jarak tempuh lebih pendek daripada rute yang diterapkan pada saat ini,
5. lebih banyak konsumen yang dikunjungi dalam satu rute sehingga dapat memaksimumkan barang yang dibawa oleh kendaraan.
DAFTAR PUSTAKA
Ayers B. 2001. Handbook of Supply ChainManagement. USA : st.Lucie Press. Cordeau J-F, Gendreau M, Laporte G, Potvin
JY, Semet F. 2002. A Guide to Vehicle Routing Heuristics. Journal of Operation Research Soceity 53: 512-522
Hoffman K & Padberg M. 2009. Traveling Salesman Problem. http://iris.gmu.edu/ ~khoffman/papers/trav_salesman.html. [8 Feb 2009].
Hugos M. 2003. Essentials of Supply Chain Management. Canada : John Wiley & Sons,Inc
Kritikos MN & Ioannou G. 2004. A synthesis of assignment and heuristic solutions for vehicle routing with time windows. Journal of the Operational Research Society (2004) 55, 2–11.
Larsen Jesper. 1999. Vehicle routing with time windows finding optimal solutions efficiently. DORSnyt (engl.)(1999), no. 116
Machado P, Tavares J, Pereira BF, Costa E. 2002. Vehicle Routing Problem: Doing it The Evolution Way.
Raditya A. 2009. Penggunaan Metode Heuristik Dalam Vehicle Routing Problem Untuk Meminimumkan Jumlah Dan Jarak Tempuh Kendaraan (Implementasi di PT. Nippon Indosari Corpindo) [skripsi]. Bogor: Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.
Sutapa NI, Widyadana AGI, Christine. 2003. Studi tentang Traveling Salesman Problem dan Vehicle Routing Problem dengan Time windows. Jurusan Teknik Industri, Universitas Petra, Surabaya Winston WL. 2004. Operation Research
Application and Algorithm. Brooks/Cole-Thompson Learning.
LAMPIRAN
Tabel 7 Hasil simulasi menggunakan metode Savings Heuristic kendaraan pertama
Tabel 8 Hasil simulasi menggunakan metode Savings Heuristic kendaraan kedua
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0 0
11 Konsumen 11 21.4521 - 498.709 21.4521 11000 8 Konsumen 8 66.7454 - 544.003 28.7454 8000 0 Depot 122.743 - 600 44.7428 0
Tabel 9 Hasil simulasi menggunakan metode Savings Heuristic kendaraan ketiga
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0 0
13 Konsumen 13 25.0952 - 490.39 25.0952 7500 7 Konsumen 7 70.1456 - 535.44 37.1456 16000 0 Depot 134.706 - 600 51.7056 0
Tabel 10 Hasil simulasi menggunakan metode Savings Heuristic kendaraan keempat
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0 0
14 Konsumen 14 17.8421 - 513.156 17.8421 7000 6 Konsumen 6 65.3691 - 560.683 21.3691 10000 0 Depot 104.686 - 600 35.6864 0
Tabel 11 Hasil simulasi menggunakan metode Savings Heuristic kendaraan kelima
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0 0
15 Konsumen 15 24.6383 - 495.3 24.6383 10000 5 Konsumen 5 70.8836 - 541.603 35.8836 14000 0 Depot 129.281 - 600 49.2809 0
Tabel 12 Hasil simulasi menggunakan metode Savings Heuristic kendaraan keenam
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0 0
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0 0
16 Konsumen 16 20.635 - 506.376 20.635 13000 3 Konsumen 3 75.8034 - 561.544 30.8034 10000 0 Depot 114.259 - 600 44.2594 0
Tabel 13 Hasil simulasi menggunakan metode Savings Heuristic kendaraan ketujuh
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
12 Konsumen 12 23.3967 - 453.2 23.3967 3000 17 Konsumen 17 65.917 - 495.736 35.917 16000
4 Konsumen 4 137.603 - 567.422 47.6032 5000 0 Depot 170.181 - 600 60.1812 0
Tabel 14 Hasil simulasi menggunakan metode Savings Heuristic kendaraan kedelapan
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
19 Konsumen 19 24.0754 - 482.766 24.0754 7000 1 Konsumen 1 78.4957 - 537.186 38.4957 16000 0 Depot 141.309 - 600 51.3094 0
Tabel 15 Hasil simulasi menggunakan metode Savings Heuristic kendaraan kesembilan
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
18 Konsumen 18 22.644 - 463.32 22.644 6000 20 Konsumen 20 65.6123 - 506.291 27.6123 9000 2 Konsumen 2 125.753 - 566.431 42.7528 9000 0 Depot 159.321 - 600 56.3215 0
Tabel 16 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan pertama
Tabel 17 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan kedua
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
11 Konsumen 11 21.4521 - 515.408 21.4521 11000 3 Konsumen 3 67.5877 - 561.544 29.5877 10000 0 Depot 106.044 - 600 43.0438 0
Tabel 18 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan ketiga
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
1 Konsumen 1 12.8137 - 516.854 12.8137 16000 4 Konsumen 4 63.3819 - 567.422 13.3819 5000 0 Depot 95.9599 - 600 25.9599 0
Tabel 19 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan keempat
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
5 Konsumen 5 13.3973 - 496.391 13.3973 14000 8 Konsumen 8 61.0091 - 544.003 16.0091 8000 0 Depot 117.007 - 600 32.0065 0
Tabel 20 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan kelima
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
7 Konsumen 7 14.5599 - 484.494 14.5599 16.000 14 Konsumen 14 68.2239 - 538.158 18.2239 7000
0 Depot 130.066 - 600 36.066 0
Tabel 21 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan keenam Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
15 Konsumen 15 24.6383 - 496.301 24.6383 10000 9 Konsumen 9 70.5002 - 542.163 35.5002 12000 0 Depot 128.338 - 600 49.3377 0
Tabel 22 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan ketujuh
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
10 Konsumen 10 17.6358 - 532.336 17.6358 10000 6 Konsumen 6 45.9823 - 560.683 20.9823 10000 0 Depot 85.2996 - 600 35.2996 0
Tabel 23 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan kedelapan
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
17 Konsumen 17 23.2961 - 471.017 23.2961 16000 19 Konsumen 1 88.2032 - 535.925 28.2032 7000
0 Depot 152.279 - 600 52.2787 0
Tabel 24 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan kesembilan
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
16 Konsumen 16 20.635 - 484.921 20.635 13000 20 Konsumen 20 68.0183 - 532.304 23.0183 9000
0 Depot 135.714 - 600 45.7143 0
Tabel 25 Hasil simulasi menggunakan metode Sweep Heuristic kendaraan kesepuluh
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
18 Konsumen 18 22.644 - 539.356 22.644 6000
0 Depot 83.288 - 600 45.288 0
Tabel 26 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan pertama
Tabel 27 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan kedua
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
17 Konsumen 17 23.2961 - 468.589 23.2961 16000 13 Konsumen 13 96.6116 - 541.905 36.6116 7500
0 Depot 154.707 - 600 61.7068 0
Tabel 28 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan ketiga
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
11 Konsumen 11 21.4521 - 511.697 21.4521 11000 10 Konsumen 10 67.1192 - 557.364 29.1192 10000
0 Depot 109.755 - 600 46.755 0
Tabel 29 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan keempat
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
16 Konsumen 16 20.635 - 492.368 20.635 13000 8 Konsumen 8 72.2696 - 544.003 27.2696 8000 0 Depot 128.267 - 600 43.267 0
Tabel 30 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan kelima
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
9 Konsumen 9 13.8375 - 516.34 13.8375 12.000 2 Konsumen 2 63.9293 - 566.431 19.9293 9000 0 Depot 97.498 - 600 33.498 0
Tabel 31 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan keenam Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
6 Konsumen 6 14.3173 - 514.637 14.3173 10000 5 Konsumen 9 41.283 - 541.603 16.283 14000 0 Depot 99.6803 - 600 29.6803 0
Tabel 32 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan ketujuh
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
1 Konsumen 1 12.8137 - 516.854 12.8137 16000 4 Konsumen 4 63.3819 - 567.422 13.3819 5000 0 Depot 95.9599 - 600 25.9599 0
Tabel 33 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan kedelapan
Kode Nama
Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
7 Konsumen 7 14.5599 - 535.44 14.5599 16000 0 Depot 79.1199 - 600 29.1199 0
Tabel 34 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan kesembilan
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
15 Konsumen 16 24.6383 - 514.924 24.6383 10000 3 Konsumen 3 71.2586 - 561.544 36.2586 10000 0 Depot 109.715 - 600 49.7147 0
Tabel 35 Hasil simulasi menggunakan metode nearestdepot heuristic kendaraan kesepuluh
Kode Nama Waktu tiba Jarak tempuh Permintaan (menit) (kilometer) (crate)
0 Depot 0 0
Lampiran 4
Tabel 36 Hasil rute saat ini kendaraan pertama
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
2 Konsumen 2 42.7528 9000 4 Konsumen 4 47.6032 5000
0 Depot 60.5436 0
Tabel 37 Hasil rute saat ini kendaraan kedua
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
1 Konsumen 1 38.4957 16000
0 Depot 38.4957 0
Tabel 38 Hasil rute saat ini kendaraan ketiga
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
12 Konsumen 12 23.3967 3000 11 Konsumen 11 21.4521 11000
0 Depot 63.5430 0
Tabel 39 Hasil rute saat ini kendaraan keempat
Kode Nama
Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
13 Konsumen 13 25.0952 7500 14 Konsumen 14 17.8421 7000
0 Depot 55.6776 0
Tabel 40 Hasil rute saat ini kendaraan kelima
Kode Nama
Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
8 Konsumen 8 28.7454 8000 19 Konsumen 19 24.0754 7000
Tabel 41 Hasil rute saat ini kendaraan keenam
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
15 Konsumen 15 24.6383 10000 20 Konsumen 20 27.6123 9000
0 Depot 56.8467 0
Tabel 42 Hasil rute saat ini kendaraan ketujuh
Kode Nama
Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
18 Konsumen 18 22.644 6000 10 Konsumen 10 17.6358 10000
0 Depot 67.90 0
Tabel 43 Hasil rute saat ini kendaraan kedelapan
Kode Nama
Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
6 Konsumen 6 21.3691 10000 9 Konsumen 9 21.4458 12000
0 Depot 58.4734 0
Tabel 44 Hasil rute saat ini kendaraan kesembilan
Kode Nama
Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
5 Konsumen 5 35.8836 14000
0 Depot 71.7672 0
Tabel 45 Hasil rute saat ini kendaraan kesepuluh
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
7 Konsumen 7 37.1456 16000
0 Depot 74.2912 0
Tabel 46 Hasil rute saat ini kendaraan kesebelas
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
17 Konsumen 17 35.917 16000
Tabel 47 Hasil rute saat ini kendaraan keduabelas
Kode Nama Jarak tempuh Permintaan (kilometer) (crate)
0 Depot 0 0
16 Konsumen 16 20.635 13000