The Effects of Variance of Interest rate to Variance of Annuity Future Values

(1)

PENGARUH KERAGAMAN SUKU BUNGA TERHADAP

KERAGAMAN

FUTURE VALUE

SUATU ANUITAS

WINA FATMILA SARI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA

Dengan ini saya menyatakan bahwa tesis berjudul Pengaruh Keragaman Suku Bunga terhadap Keragaman Future Value suatu Anuitas adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam daftar pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, Juli 2013

Wina Fatmila Sari

(4)

RINGKASAN

WINA FATMILA SARI. Pengaruh Keragaman Suku Bunga terhadap Keragaman

FutureValue suatu Anuitas. Dibimbing oleh I GUSTI PUTU PURNABA dan

RETNO BUDIARTI.

Time value of money merupakan suatu konsep yang mengacu pada

perbedaan nilai uang yang disebabkan karena perbedaan waktu, bahwa nilai uang sekarang tidak akan sama dengan nilai uang yang akan datang. Nilai uang sekarang dinyatakan sebagai Present Value (PV) dari uang tersebut, sedangkan nilai uang di masa yang akan datang dinyatakan sebagai Future Value (FV) dari uang tersebut.

Penentuan nilai uang, baik nilai uang sekarang maupun nilai uang yang akan datang bergantung pada waktu dan tingkat pengembalian. Perubahan nilai uang dipengaruhi oleh beberapa faktor antara lain inflasi, perubahan suku bunga, kebijakan pemerintah dalam bidang sekuritas dan dalam hal perpajakan. Karena perubahan nilai uang tersebut maka dibutuhkan suatu perumusan FV, hal tersebut berguna untuk mengetahui apakah sebuah investasi dapat menguntungkan atau tidak, dan untuk analisis anggaran.

Anuitas didefinisikan sebagai rangkaian pembayaran dalam jumlah tertentu yang dilakukan secara berkala pada jangka waktu tertentu. Pembayaran dapat dilakukan pada awal atau pada akhir periode, dengan jumlah tetap atau bervariasi. Anuitas yang dibayarkan pada awal periode disebut anuitas awal dan yang dibayarkan pada akhir periode disebut anuitas pasti. Nilai akumulasi dari anuitas tersebut setelah beberapa tahun kemudian disebut nilai akhir atau future value.

Burnecki et al. (2003) telah membahas tentang FV suatu anuitas dengan suku bunga tetap yang pembayarannya mengikuti bentuk deret aritmatika atau deret geometri. Kemudian dikaji pula FV untuk anuitas yang pembayarannya mengikuti bentuk deret aritmatika atau deret geometri dengan suku bunga acak. Dalam tulisan ini dikaji FV anuitas awal yang pembayarannya mengikuti bentuk deret aritmatika dan deret geometri dengan suku bunga sebagai peubah acak yang menyebar normal



 ,



. Formula dari FV dinyatakan dalam bentuk rekursif.

Perhitungan FV dari anuitas awal yang pembayarannya mengikuti bentuk deret aritmatika dan deret geometri dengan suku bunga acak dilakukan secara teoritis maupun simulasi. Suku bunga acak dinotasikan dengan i_k  i _k di mana

k

i merupakan peubah acak independen, i adalah konstanta dan _k peubah acak yang menyebar normal



 ,



. Dengan parameter-parameter yang telah ditentukan, dibangkitkan satu barisan suku bunga acak untuk perhitungan secara teoritis, sedangkan untuk perhitungan secara simulasi dibangkitkan barisan suku bunga acak sebanyak 1000 kali. Perhitungan tersebut masing-masing akan mendapatkan nilai rata-rata, ragam dan simpangan baku. Kemudian akan dihitung galat dari nilai rata-rata, ragam dan simpangan baku hasil teoritis dan hasil simulasi. Perhitungan galat menggunakan Symmetric Mean Absolute Percentage

Error (SMAPE). Semakin kecil nilai SMAPE, maka semakin akurat nilai

(5)

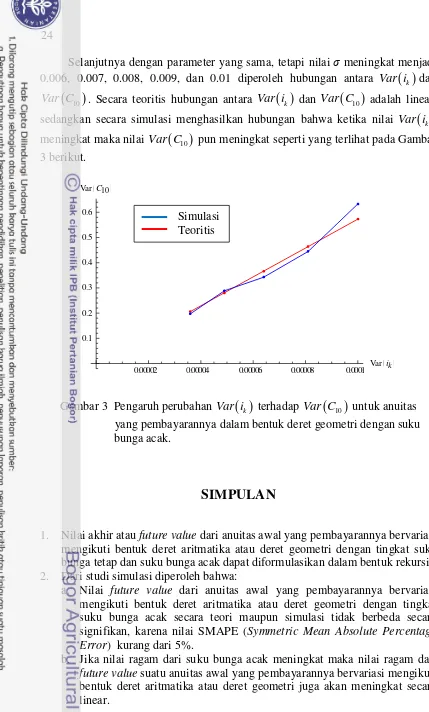
dari 0.000036 sampai 0.0001 diperoleh hubungan antara keragaman suku bunga dan keragaman FV.

Hasil perhitungan secara teoritis maupun simulasi menunjukkan bahwa ketika ragam dari barisan suku bunga acak meningkat maka ragam dari FV juga meningkat secara linear. FV dari anuitas awal yang pembayarannya bervariasi mengikuti bentuk deret aritmatika atau deret geometri dengan tingkat suku bunga acak secara teoritis maupun simulasi tidak berbeda secara signifikan, karena nilai SMAPE kurang dari 5%.

(6)

SUMMARY

WINA FATMILA SARI. The Effects of Variance of Interest rate to Variance of Annuity Future Values. Supervised by I GUSTI PUTU PURNABA and RETNO BUDIARTI.

Time value of money is a concept that refers to the difference of the value of money due to time difference. The value of money for present time would not be the same as the value of money in the future. The value of money for present time is called as Present Value (PV) of the money and the value of money for future time is called Future Value (FV) of the money.

Determination the value of money, for present and future time, depends on the time and rate of return. The value of money is determined by several factors such as inflation, fluctuation of interest rates, and government policy in securities and taxation. Due to fluctuation of the value of money we need a FV formulation, it is useful for knowing whether an investment can be profitable or not, and this information is useful also in budget analysis.

Annuity is defined as a series of payments made for a specific period. The payment, fixed or varied, can be made at the beginning or at the end of the period. Annuity paid at the beginning of the period is called annuity-due and annuity paid at the end of the period is called immediate annuity-certain. The accumulated value of the annuity after few years later is called as a final value or a future value.

Burnecki et al. (2003) have discussed about the FV of a fixed-rate annuity in which payments are made according to the arithmetic or geometric series. They have also examined FV for annuities in which payments are made according to arithmetic or geometric series with random rates of interest. This paper examines FV for annuity-due in which payments are made according to arithmetic or geometric series with interest rates as a random variable, which is normal distribution



 ,



. Future value formula is expressed in recursive form.

(7)

The theoretical and simulation results show that when the variance of random rates of interest increases, then the variance of FV increases linearly. FV of the annuity-due in which payments are made according to the arithmetic or geometric series, the random rates of interest in theory and simulation are not significantly different, because the value of SMAPE is less than 5%.

(8)

© Hak Cipta Milik IPB, Tahun 2013

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis ini

(9)

(10)

(11)

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

PENGARUH KERAGAMAN SUKU BUNGA TERHADAP

KERAGAMAN

FUTURE VALUE

SUATU ANUITAS

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2013

(12)

(13)

Judul Tesis : Pengaruh Keragaman Suku Bunga terhadap Keragaman Future

Value suatu Anuitas

Nama : Wina Fatmila Sari

NRP : G551090221

Disetujui oleh Komisi Pembimbing

Dr Ir I Gusti Putu Purnaba, DEA Ketua

Ir Retno Budiarti, MS Anggota

Diketahui oleh

Ketua Program Studi Matematika Terapan

Dr Ir Endar Hasafah Nugrahani, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

(14)

PRAKATA

Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Pebruari 2011 ini ialah

future value dari suatu anuitas, dengan judul Pengaruh Keragaman Suku Bunga

terhadap Keragaman Future Value suatu Anuitas.

Terima kasih penulis ucapkan kepada Bapak Dr Ir I Gusti Putu Purnaba, DEA dan Ibu Ir Retno Budiarti, MS selaku pembimbing, serta Ibu Dr Ir Endar Hasafah Nugrahani, MS yang telah banyak memberi saran. Ungkapan terima kasih juga disampaikan kepada Ayah (Alm), Emak (Alm), Ce’ Danil, adek Nathania serta seluruh keluarga, atas segala doa dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, Juli 2013

(15)

DAFTAR ISI

DAFTAR TABEL xiv

DAFTAR GAMBAR xiv

DAFTAR LAMPIRAN xiv

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 1

Sistematika Penulisan 2

LANDASAN TEORI 2

Percobaan Acak 2

Ruang Contoh dan Kejadian 2

Peubah Acak 2

Peubah Acak Diskret 3

Fungsi Sebaran 3

Fungsi Sebaran Bersama Dua Peubah Acak 3

Fungsi Kerapatan Peluang 3

Sebaran Normal 3

Nilai Harapan Peubah Acak Diskret 4

Teorema 1 (Sifat-sifat Nilai Harapan) 4

Simpangan Baku dan Ragam Peubah Acak Diskret 4

Suku Bunga 5

Anuitas dan Future Value 5

FUTURE VALUE SUATU ANUITAS 5

Anuitas dengan Suku Bunga Tetap 6

Anuitas Awal Sebesar 1 Satuan Selama k Tahun 6 Anuitas Awal Sebesar 1, 2, ,k Selama k Tahun 7 Anuitas Awal Sebesar 2 2

1, 2 , ,k Selama k Tahun 8

Anuitas Awal yang Menurun 9

Anuitas Awal dengan Pembayaran dalam Bentuk Deret Aritmatika 11 Anuitas Awal dengan Pembayaran dalam Bentuk Deret Geometri 12

Anuitas dengan Suku Bunga Acak 12

Anuitas dengan Pembayaran dalam Bentuk Deret Aritmatika 13 Anuitas dengan Pembayaran dalam Bentuk Deret Geometri 17

SIMULASI 20

Future Value Anuitas Awal dengan Pembayaran dalam

Bentuk Deret Aritmatika 21

Future Value Anuitas Awal dengan Pembayaran dalam

Bentuk Deret Geometri 23

SIMPULAN 24

DAFTAR PUSTAKA 25

LAMPIRAN 26

(16)

DAFTAR TABEL

1 Nilai galat dari nilai rata-rata, ragam dan simpangan baku untuk anuitas yang pembayarannya tetap tiga satuan dengan suku bunga acak 21 2 Nilai galat dari nilai rata-rata, ragam dan simpangan baku untuk anuitas

yang pembayarannya meningkat dengan suku bunga acak 22 3 Nilai galat dari nilai rata-rata, ragam dan simpangan baku untuk anuitas

yang pembayarannya mengikuti bentuk deret geometri dengan suku

bunga acak 23

DAFTAR GAMBAR

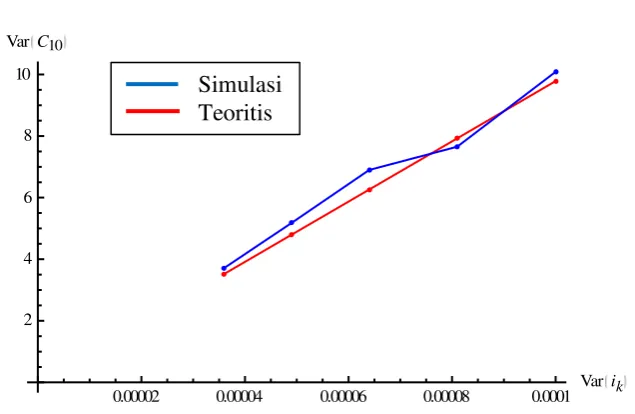
1 Pengaruh perubahan Var i

 

_k terhadap Var C

 

₁₀ untuk anuitas yang pembayarannya tetap tiga satuan dengan suku bunga acak 22 2 Pengaruh perubahan Var i

 

_k terhadap Var C

 

₁₀ untuk anuitas yang

pembayarannya meningkat dengan suku bunga acak 23 3 Pengaruh perubahan Var i

 

_k terhadap Var C

 

₁₀ untuk anuitas yang

pembayarannya mengikuti bentuk deret geometri dengan suku bunga

acak 24

DAFTAR LAMPIRAN

1 Bukti Teorema 1 (Sifat-sifat Nilai Harapan) 26

2 Pembuktian persamaan-persamaan pada anuitas dengan tingkat

suku bunga tetap 28

3 Pembuktian persamaan-persamaan pada anuitas yang pembayarannya dalam bentuk deret aritmatika dengan tingkat suku bunga acak 30 4 Pembuktian persamaan-persamaan pada anuitas yang pembayarannya

(17)

PENDAHULUAN

Latar Belakang

Time value of money atau dalam bahasa Indonesia disebut nilai uang

menurut waktu merupakan suatu konsep yang mengacu pada perbedaan nilai uang yang disebabkan karena perbedaan waktu. Jika seseorang diminta memilih untuk menerima 1 juta rupiah saat ini ataukah, misalnya 1 juta rupiah sepuluh tahun yang akan datang maka biasanya orang tersebut akan memilih untuk menerima 1 juta rupiah saat ini. Hal ini menunjukkan bahwa nilai uang 1 juta rupiah yang kita punya saat ini atau sekarang tidak sama dengan 1 juta rupiah pada sepuluh tahun yang lalu atau sepuluh tahun kemudian. Sehingga dapat disimpulkan bahwa nilai uang sekarang tidak akan sama dengan nilai uang yang akan datang. Nilai uang sekarang dinyatakan sebagai Present Value (PV) dari uang tersebut, sedangkan nilai uang di masa yang akan datang dinyatakan sebagai Future Value (FV) dari uang tersebut.

Penentuan nilai uang, baik nilai uang sekarang maupun nilai uang yang akan datang bergantung pada waktu dan tingkat pengembalian. Perubahan nilai uang dipengaruhi oleh beberapa faktor antara lain inflasi, perubahan suku bunga, kebijakan pemerintah dalam bidang sekuritas dan dalam hal perpajakan. Karena perubahan nilai uang tersebut maka dibutuhkan suatu rumusan FV, hal tersebut berguna untuk mengetahui apakah sebuah investasi dapat menguntungkan atau tidak, dan untuk analisis anggaran.

Pembahasan tentang FV sudah banyak dilakukan di antaranya oleh McCutcheon dan Scott (1986), Zaks (2001) membahas tentang FV suatu anuitas dengan suku bunga acak, sedangkan Burnecki et al. (2003) telah membahas tentang FV suatu anuitas dengan suku bunga tetap yang pembayarannya mengikuti bentuk deret aritmatika atau deret geometri. Kemudian dikaji pula FV

untuk anuitas yang pembayarannya mengikuti bentuk deret aritmatika atau deret geometri dengan suku bunga acak. Dalam tulisannya tersebut Burnecki et al.

(2003) juga mengoreksi hasil penelitian Zaks (2001).

Dalam penelitian ini dikaji FV anuitas awal yang pembayarannya mengikuti bentuk deret aritmatika dan deret geometri sebagai fungsi dari tingkat suku bunga dengan suku bunga sebagai peubah acak yang menyebar normal dengan parameter

 dan  .

Tujuan Penelitian Tujuan dari penelitian ini adalah sebagai berikut:

1. Mengkaji Future Value (FV) menggunakan formula rekursif dari suatu anuitas dengan suku bunga tetap dan suku bunga acak.

(18)

2

Sistematika Penulisan

Karya ilmiah ini terdiri atas lima Bab. Bab pertama merupakan pendahuluan yang berisi uraian mengenai latar belakang, tujuan penelitian, dan sistematika penulisan. Bab kedua berisi landasan teori yang menjadi konsep dasar dalam penyusunan pembahasan. Bab ketiga merupakan pembahasan secara teoritis mengenai future value suatu anuitas dengan tingkat suku bunga tetap dan suku bunga acak menggunakan formula rekursif. Bab keempat berisi simulasi future

value suatu anuitas yang pembayarannya mengikuti bentuk deret aritmatika dan

deret geometri dengan tingkat suku bunga acak. Bab terakhir pada tulisan ini berisi simpulan dari keseluruhan penulisan karya ilmiah ini.

LANDASAN TEORI

Landasan teori berikut merupakan beberapa landasan yang akan digunakan untuk menganalisis nilai akhir atau future value dari suatu anuitas dengan suku bunga acak. Di antara landasan tersebut ialah percobaan acak, ruang contoh, kejadian, peubah acak, fungsi sebaran, fungsi kerapatan peluang, sebaran normal, nilai harapan (expected value), simpangan baku (standard deviation), ragam

(variance), anuitas, bunga dan nilai yang akan datang (future value).

Percobaan Acak

Dalam suatu percobaan seringkali diperlukan pengulangan yang dilakukan dalam kondisi yang sama. Semua kemungkinan hasil yang akan muncul adalah diketahui, namun hasil dari percobaan berikutnya tidak dapat diduga dengan tepat. Percobaan semacam ini disebut percobaan acak (Hogg et al. 2005).

Ruang Contoh dan Kejadian

Himpunan semua hasil dari suatu percobaan acak disebut ruang contoh, dinotasikan dengan . Himpunan bagian dari suatu ruang contoh disebut kejadian (Grimmett dan Stirzaker 2001).

Peubah Acak

Misalnya



, ,P



adalah ruang peluang. Peubah acak (random variable) merupakan fungsi X:  di mana



:X

 

  x



untuk setiap

.

(19)

3 Peubah Acak Diskret

Peubah acak X disebut peubah acak diskret jika himpunan semua kemungkinan nilai



x x x₁, ₂, ₃,



dari peubah acak tersebut merupakan himpunan terhitung dari _{(Grimmett dan Stirzaker 2001).}

Catatan: Suatu himpunan bilangan C disebut terhitung jika C terdiri atas bilangan bulat terhingga atau anggota C dapat dikorespondensikan 1-1 dengan bilangan bulat positif.

Fungsi Sebaran

Fungsi sebaran (distribution function) dari suatu peubah acak X adalah fungsi F_X : 

 

0,1 yang diberikan oleh F_X

 

x P X



x



.

(Ghahramani 2005)

Fungsi Sebaran Bersama Dua Peubah Acak

Fungsi sebaran bersama dua peubah acak X dan Y merupakan suatu fungsi

 

2

: 0,1

F  yang didefinisikan oleh: F_XY

 

x y, P X



x Y, y



.

(Grimmett dan Stirzaker 2001)

Fungsi Kerapatan Peluang

Fungsi kerapatan peluang dari peubah acak diskret X adalah fungsi

 

: 0,1

p  yaitu p_X( )x P X



x



.

(Grimmett dan Stirzaker 2001)

Sebaran Normal

Peubah acak X dikatakan menyebar normal dengan parameter  dan  jika

X memiliki fungsi kepekatan peluang (probability density function) sebagai berikut:

 

1



 

₂



2

exp ,

2 2

x

f x 

  

 _ 

 

 

 

 

x

   .

(20)

4

Nilai Harapan Peubah Acak Diskret

Misalkan X adalah peubah acak diskret dengan himpunan nilai yang mungkin adalah A. Jika p_X

 

x adalah fungsi massa peluang dari X, maka nilai harapan (expected value) dari X didefinisikan sebagai:

 

X

 

x A

E X x p x

 



dan E X

 

dikatakan ada jika _X

 

x A

x p x





konvergen mutlak (Ghahramani 2005).

Teorema 1 (Sifat-sifat Nilai Harapan)

1. Jika X 0, maka E X

 

0.

2. Jika a b,  maka E aX



bY



aE X

 

bE Y

 

.

3. Jika X adalah peubah acak konstan, dengan P X



c



1 untuk suatu konstanta, maka E X

 

c.

4. Jika dan adalah independen maka E XY

 

E X E Y

   

. 5. Jika X dan Y dependen maka E XY

 

E X E Y

   

Cov X Y



,



. (Grimmett dan Stirzaker 2001)

Bukti pada Lampiran 1

Simpangan Baku dan Ragam Peubah Acak Diskret

Misalkan X adalah peubah acak diskret dengan himpunan semua kemungkinan nilai X adalah A. Jika p_X

 

x adalah fungsi massa peluang dari X

dan E X

 

 adalah nilai harapan dari X, _X dan Var X

 

masing-masing adalah simpangan baku (standard daviation) dan ragam (variance) dari X dan didefinisikan sebagai:





2

X E X

 _  _ 

 

dan

 





2





2

 

X x A

Var X E X  X  p x



 

 _  _



 .

(21)

5 Suku Bunga

Bunga dapat dianggap sebagai imbalan yang dibayar oleh satu orang atau organisasi (peminjam) untuk penggunaan aset yang disebut sebagai modal, milik orang lain atau organisasi (McCutcheon & Scott 1986).

Anuitas dan Future Value

Anuitas adalah pembayaran dalam jumlah tertentu, yang dilakukan setiap selang waktu dan lama tertentu, secara berkelanjutan (Futami 1993).

Berdasarkan waktu pembayaran, anuitas dibedakan atas:

a. Anuitas awal adalah anuitas yang pembayarannya dilakukan pada awal periode, misal jika periodenya tahun, artinya pembayaran dilakukan pada awal tahun, dan seterusnya.

b. Anuitas akhir adalah anuitas yang pembayarannya dilakukan pada akhir periode, misal jika periodenya tahun, artinya pembayaran dilakukan pada akhir tahun, dan seterusnya.

Future Value adalah nilai uang di masa yang akan datang dari uang yang

diterima atau dibayarkan pada masa sekarang dengan memperhitungkan tingkat bunga setiap periode selama jangka waktu tertentu.

Anuitas awal yang dibayarkan selama n tahun sebesar 1 satuan, maka nilai akumulasi anuitas tersebut n tahun kemudian disebut nilai akhir atau future value

dinotasikan dengan |

n s .

FUTURE VALUE

SUATU ANUITAS

Anuitas bukan sesuatu yang baru dalam kehidupan ekonomi saat ini, dengan mudah dapat ditemui contoh-contoh anuitas di antaranya orang tua yang membelikan motor untuk anaknya secara kredit, tetangga yang membeli rumah secara kredit, atau orang tua yang mempersiapkan tabungan pendidikan untuk anak-anaknya, semuanya merupakan contoh kongkrit dari anuitas. Anuitas dari

annuity dapat didefinisikan sebagai rangkaian pembayaran dalam jumlah tertentu

yang dilakukan secara berkala pada jangka waktu tertentu. Kata annuity asalnya berarti pembayaran annual (tahunan), akan tetapi seiring dengan berjalannya waktu kata anuitas juga mencakup pembayaran yang dilakukan pada interval waktu yang lain juga, seperti pembayaran bulanan, tiga bulanan, dan seterusnya. Pembayaran dapat dilakukan pada awal atau pada akhir periode, dengan jumlah tetap atau bervariasi. Jika dibayarkan pada awal periode disebut anuitas awal dan jika dibayarkan pada akhir periode disebut anuitas pasti. Nilai akumulasi dari anuitas tersebut setelah beberapa tahun kemudian disebut nilai akhir atau future value.

(22)

6

atau deret geometri. Kemudian dikaji pula FV suatu anuitas yang pembayarannya mengikuti bentuk deret aritmatika atau deret geometri dengan suku bunga acak. Pada Bab ini akan mengkaji ulang tentang future value anuitas awal yang pembayarannya bervariasi mengikuti bentuk deret aritmatika dan deret geometri dengan tingkat suku bunga tetap dan suku bunga acak yang dibayarkan selama k

tahun. Anuitas dengan suku bunga tetap terdapat berbagai macam variasi pembayaran di antaranya anuitas awal dengan pembayaran sebesar 1 satuan, anuitas awal yang meningkat sebesar 1 satuan, anuitas awal sebesar 1, 2 ,2 ,k2, anuitas awal yang menurun, serta anuitas awal yang pembayarannya bervariasi mengikuti bentuk deret aritmatika dan deret geometri. Selanjutnya, anuitas dengan tingkat suku bunga acak terdapat anuitas awal yang pembayarannya bervarisi mengikuti bentuk deret aritmatika dan deret geometri.

Anuitas dengan Suku Bunga Tetap

Notasi dasar yang digunakan dalam teori anuitas adalah sebagai berikut:

j : Tingkat bunga tahunan dan tetap selama periode k tahun.

v : Faktor diskon tahunan dengan v 



1 j



1.

d : Tingkat diskon tahunan dengan d  1 v.

Selanjutnya akan dibahas mengenai future value atau nilai akhir dari anuitas awal dengan berbagai macam bentuk pembayaran.

Anuitas Awal Sebesar 1 Satuan Selama k Tahun

Jika anuitas awal sebesar 1 satuan dibayarkan selama k tahun, maka future

value anuitas awal tersebut dinotasikan oleh

|

k j

s dan diberikan oleh rumus



 



1





| 1 1 1

k k

k j

s   j   j     j



1



1

.

k

j d

 

 (1)

Bukti:



 































1 |

1 2

| | |

1 1 1

1 1 1 1

1 1 1

1 1

k k

k j

k k

k j

k k j

s j j j

v s j j j

v s j

d s j



 

      

       

   

  





|

1 1

.

k

k j

j s

d

 



Selain persamaan (1), s_{k j}_| juga dapat dinyatakan secara rekursif sebagai









| 1 1 1| .

k j k j

(23)

7 Bukti:



 





 















1 2 | 1 2 1|

1 1 1 1

1 1 1 ,

k k

k j

k k

k j

s j j j j

s j j j

                    sehingga



 





 





 













1 2 | 1 2

1 1 1 1

1 1 1 1 1

k k

k j

k k

s j j j j

j j j j



 

        









| 1 1 1| .

k j k j

s   j s _

Anuitas Awal Sebesar 1, 2, ,k Selama k Tahun

Jika besarnya pembayaran anuitas awal meningkat masing-masing 1, 2, ,k

yang dibayarkan selama k tahun, maka future value anuitas awal tersebut dinotasikan dengan

 

Is _{k j}_| dan diberikan oleh rumus

 









1





| 1 2 1 1

k k

k j

Is   j   j   k  j

| . k j s k d 

 (3)

Bukti:

 













 

















 



 







 

1 | 1 2 | 1 | | |

1 2 1 1

1 2 1 1 1

1 1 1 1

k k k j k k k j k k k j k j k j

Is j j k j

v Is j j k j k

v Is j j j k

d Is s k

                              

 

| | . k j k j s k Is d  

Persamaan berikut merupakan formula rekursif untuk

 

|

k j

Is yaitu

 

Is _{k j}_|  



1 j





k

 

Is _k__1|_j



. (4) Bukti:

 



















 















1 2 | 1 2 1|

1 2 1 1 1 1

1 2 1 1 1 ,

k k

k j

k k

k j

Is j j k j k j

Is j j k j

                      sehingga

 





















 















1 2 | 1 2

1 2 1 1 1 1

1 1 2 1 1 1

k k

k j

k k

Is j j k j k j

j j j k j k



 

         

         

 

_|



1





 

_1|



.

k j k j

(24)

8

Anuitas Awal Sebesar 1, 2 ,2 ,k2 Selama k_Tahun

Future value dari anuitas awal dengan pembayaran meningkat

masing-masing 1, 2 ,2 ,k2 dinotasikan dengan

 

2 |

k j

I s dan diberikan oleh rumus

 

2





2





1 2





| 1 2 1 1

k k

k j

I s   j   j   k  j

 

2

| | 2 . k j k j

Is s k d

 

 (5)

Bukti:

 













 











 



 



















 















 











1

2 2 2

|

1 2 2

2 2 2

| 1 2 2 2 | 1 2 | 1 2

1 2 1 1

1 2 1 1 1

1 1 3 1 5 1 2 1 1

2 1 4 1 2 1

1 1 1 1

k k

k j

k k

k j

k k k

k j

k k

k j

k k k

I s j j k j

v I s j j k j k

v I s j j j k j k

d I s j j k j

j j j j k

                                             _         _

 













2 1 2 2 |

| 2 1 2 1 1

k k

k j k j

d I s  _  j  j   k  j _s k

 

2

 

| | 2

| 2 . k j k j k j

Is s k I s

d

  

Selain persamaan (5),

 

2 |

k j

I s juga dapat dinyatakan secara rekursif sebagai

 

2







2

 

2



| 1 1| .

k j k j

I s j k I s



   (6)

Bukti:

 











 







 











 



1 2 2

2 2 2

|

1 2 2

2 2

1|

1 2 1 1 1 1

1 2 1 1 1 ,

k k

k j

k k

k j

I s j j k j k j

I s j j k j

                      sehingga

 











 









 











 



1 2 2

2 2 2

|

1 ₂ 2 2 ₂

1 2 1 1 1 1

1 1 2 1 1 1

k k

k j

k k

I s j j k j k j

j j j k j k



 

         

         

 

2







2

 

2



| 1 1| .

k j k j

I s j k I s

   

Persamaan berikut diperoleh dari persamaan (5) dan (3) yang mengatur hubungan antara

 

2

|

k j

I s dan s_{k j}_| .

 

2







| 2



2

2 |

1 2 2

.

k j k j

v s k k k I s

d

   

 (7)

(25)

9 Selanjutnya dari beberapa persamaan yang diperoleh berlaku hubungan berikut

 

Is k1|j 

 

Is k j| sk j| , (8)

 

2

 

2

 

| | 1| | 2 k j k j.

k j k j

I s I s Is s

    (9)

Bukti persamaan (8) dan (9)

Untuk membuktikan persamaan (8) gunakan persamaan (4) sehingga:

 







 



 



 



 

| 1|

| 1

1

k j k j

k j

Is j k Is

Is

Is k

j v Is k



  

 



 

substitusi persamaan (3), sehingga didapat:

 





|

1| |

|

1 k j

k j

k j

s k

Is d k

d s k

s k k d



 

  _ _

 



   

 

Is k1|j 

 

Is k j| sk j| .

Untuk membuktikan persamaan (9) gunakan persamaan (6) sehingga:

 







 



 





 

2 2 2

| 1|

2 |

2 2

1|

2 2

| 1

1

k j k j

k j

I s j k I s

I s

I s k

j v I s k



  

 



 

substitusi persamaan (5), sehingga didapat:

 





 

2 | |

2 2

1|

2 |

| 2 2

| | 2

1 2

2

k j k j k j

k j k j

Is s k

I s d k

d

Is s k

Is s k k

d



   

 

  

 

 

 

    

 

2

 

2

 

| |

1| | 2 k j k j.

k j k j

I s I s Is s

   

Anuitas Awal yang Menurun

Future value dari anuitas awal dengan pembayaran menurun masing-masing

, 1, , 1

n n n k  yang dibayarkan selama k tahun dinotasikan dengan

 

Ds _{n k j}_{, |}

(26)

10

 



 





1







, | 1 1 1 1 1

k k

n k j

Ds n  j  n  j     n k  j

 

| 1| .

k j k j

n s Is _

  (10)

Bukti:

 



 











 















 





 



 









 



 















 



 

1 , | 1 2 , | 1 2 , | 1 2 , |

1 1 1 1 1

1 1 1 2 1 1

1 1 1 1 1 1

1 1 1 1 1

k k

n k j

k k

n k j

k k k

n k j

k k k

n k j

Ds n j n j n k j

v Ds n j n j n k j n k

v Ds n j j j j n k

d Ds n j j j j n k

Ds                                                _       _  





















1| , | 1| 1 1

1 1 1

k

k j n k j

k

k j

n j n s k

d

n j s k

d d              

substitusi persamaan (1) dan (3), sehingga didapat:

 

Ds _{n k j}_{, |} n s_{k j}_| 

 

Is _k__1|_j.

Formula rekursif dari

 

, |

n k j

Ds diberikan sebagai berikut:

 

Ds _{n k j}_{, |}  



1 j

  



Ds _{n k}_, __1|_j 



n k 1 .



(11) Bukti:

 



 











 

















1 , | 1 2 , 1|

1 1 1 1 1

1 1 1 2 1 ,

k k

n k j

k k

n k j

Ds n j n j n k j

                        maka

 



 













 













 



1 , | 1 2

1 1 1 1 1

1 1 1 1 2 1 1

k k

n k j

k k

Ds n j n j n k j

j n j n j n k j n k



 

         

 

  _             _

 

Ds _{n k j}_{, |}  



1 j

  



Ds _{n k}_, __1|_j



n k 1 .



Dari beberapa persamaan tersebut, diperoleh persamaan yang mengatur hubungan antara

 

, |

n k j

Ds ,

 

Is _{k j}_| dan s_{k j}_| sebagai berikut:

 

Ds n k j, | 



n1



sk j| 

 

Is k j| . (12) Bukti:

Dari persamaan (10) dan (8) maka:

 





 

|

, | 1|

| | |

k j

n k j k j

k j k j k j

Ds n s Is

n s Is s

n s s Is

  

  

  

(27)

11 Anuitas Awal dengan Pembayaran dalam Bentuk Deret Aritmatika

Anuitas awal dengan pembayaran bervariasi mengikuti bentuk deret aritmatika, misalkan pembayaran pertama adalah p satuan dan kemudian pembayaran berikutnya meningkat q satuan per periode, sehingga pembayaran tersebut membentuk urutan



p p, q p, 2 ,q ,p



k1



q



dengan p harus positif tetapi q dapat berupa positif atau negatif, dan p



k1



q0 untuk menghindari pembayaran negatif, maka nilai akhir anuitas tersebut akan dinotasikan dengan

 

 , 

|

p q a k j

s dan didefinisikan oleh

 

 , 



 





1









| 1 1 1 1

p q k k

a k j

s  p  j  p q  j    p k q  j

| ( ) 1| .

k j k j

p s q Is _

  (13)

Bukti:

 



 













 























  

 





















 

















, 1

|

, 1 2

|

, 1 2

|

, 1 2

|

1 1 1 1

1 1 2 1 1

1 1 1 1 1 1

1 1 1 1

p q k k

a k j

p q k k

a k j

p q k k k

a k j

p q k k k

a k j

s p j p q j p k q j

v s p j p q j p k q j p k q

v s p j q j q j q j p k q

d s p j q j j j



 

         

            

            

 

   _       _





 





 

















, 1||

|

1||

1

1 1

1 1 1

k

p q k j

a k j

k

k j

p q k

p j p q s q k

s

d

p j q s k

d d



  

    



   

 

substitusi persamaan (4) dan (6), sehingga didapat:

 

 , 

 

|

| 1| .

p q

a k j k j k j

s  p s q Is _

Formula lain dari

 

 ,  |

p q a _{k j}

s ditunjukkan oleh persamaan berikut

 

 , 





| |

| ( ) .

p q

a k j k j k j

s  p q s q Is (14)

Bukti:

Dari persamaan (13) dan (8) maka

 





,

| 1|

|

| | |

( ) ( )

( )

p q

a k j k j k j

k j k j k j

s p s q Is

p s q Is s p s q s q Is

  

  

  

 

 , 





| |

| ( ) .

p q

a k j k j k j

(28)

12

Anuitas Awal dengan Pembayaran dalam Bentuk Deret Geometri Anuitas awal dengan pembayaran bervariasi mengikuti bentuk deret geometri, misalkan pembayaran pertama adalah p dan kemudian pembayaran berikutnya meningkat sehingga membentuk deret geometri dengan q



q 1 j



rasio per periode, yaitu



2 1



, , , , k

p pq pq pq  dengan p dan q harus positif untuk menghindari pembayaran negatif, maka nilai akumulasi anuitas tersebut akan dinotasikan dengan

 

 , 

|

p q g _{k j}

s dan didefinisikan oleh

 

















, 1 ₂ 2 ₁

| 1 1 1 1

p q k k k _k

g _{k j}

s  p  j  p q  j  p q  j  p q   j



1



(1 ) .

1

k _k

j q p j

j q

   

  (15)

Bukti pada Lampiran 2 sub 2.2

Anuitas dengan Suku Bunga Acak

Andaikan tingkat suku bunga tahunan pada tahun ke-k adalah peubah acak .

k

i Diasumsikan juga untuk masing-masing k, memiliki E i

 

_k  j dan

 

2

k

Var i s serta i i1, ,2 ,in adalah peubah acak independen. Berdasarkan asumsi

ini maka



1 _k

 

1



E i   j 

dan





2





2 ₂





1 k 1 1

E_ i _  j s   f m, di mana (16) 2 2

2 .

f  j j s

Bukti pada Lampiran 3 sub 3.1 Sehingga diperoleh









2





2

1 1 1

.

k k k

Var i E i E i

m 

 

  _  _ 

 

Selanjutnya didefinisikan sebagai solusi 1

1

f r

j

  

 , (17)

dengan mensubstitusi persamaan (16) ke persamaan (17) maka didapat 2

. 1

s

r j

j

 

(29)

13 Anuitas dengan Pembayaran dalam Bentuk Deret Aritmatika

Untuk anuitas awal dengan pembayaran c c₁, ₂, ,c_k yang dibayarkan selama k tahun, maka nilai akumulasi atau future value anuitas tersebut dinotasikan dengan C_k. Dalam kasus pembayaran yang berbeda-beda mengikuti bentuk deret aritmatika di mana c_k   p



k 1



q untuk k 1, 2,3, ,n maka

future value dari suatu anuitas dengan pembayaran tersebut diberikan secara

rekursif:



1



1



1



k k k

C  i _C_  p k q _, untuk k1, 2,3, ,n (18) Bukti:

Pada tahun pertama maka C₁c₁



1i₁



pada tahun ke-2 maka C₂C₁



1i₂



c₂



1i₂

 

 1 i₂



C₁c₂



pada tahun ke-3 maka C₃ C₂



1i₃



c₃



1i₃

 

 1 i₃



C₂c₃



pada tahun ke-k maka C_k C_k_₁



1i_k



c_k



1i_k

 

 1 i_k



C_k_₁c_k



,

sehingga C_k  



1 i_k



_C_k_₁



p



k1



q



_, untuk k1, 2,3, ,n Selanjutnya, karenai_k peubah acak independen maka didapat persamaan nilai harapan E C

 

_k _k secara rekursif untuk k 2,3, ,n_{sebagai berikut:}

 

















1 1

k k k

k k

E C E i C p k q

E i E C p k q



 

  _    _

 

  _    _









1 1

k k p k q

  _ _    _, (19)

sehingga ₁  p



1 j



 p.

Lema berikut ini berasal dari persamaan (19) dan (13) Lema 1

Jika C_k menunjukkan nilai akumulasi atau future value dari suatu anuitas awal dengan pembayaran tahunan bervariasi dalam bentuk deret aritmatika, masing-masing: p p q p,  , 2 ,q ,p 



k 1



q, dan apabila suku bunga tahunan selama tahun ke-k adalah peubah acak i_k sedemikian sehingga E



1i_k



 1 j dan





2

1 _k ,

Var i s serta i i1, ,2 ,in adalah peubah acak independen, maka:

   

 , 

| .

p q k E Ck sa _{k j}

   (20)

Bukti:

Dari persamaan (19)









1 1

k k p k q

  _ _    _, didapat





1

2 2

p

p p q

 

  



(30)

14

































3 2

3

4 3 2

4

1 2

2

2 3

2 1

k k k

k

p p q p q

p p q p q p q

p p q p q p k q

   

    

      

    

      

        

substitusi  1 j dan persamaan (13), maka:



 





1









1 k 1 k 1 1

k p j p q j p k q j

 

         

 

 , 

| .

p q k sa k j

 

Selanjutnya, karenai_k peubah acak independen maka didapat persamaan rekursif momen kedua

 

2

k k

E C m untuk k2,3, ,n_{sebagai berikut:}

 





















2 2

1

2

2 ₂

1 1

1 2 1 1

k k k

E C E i C p k q

E i E C p k q C p k q



 

 

 _     _

       













2

1 2 1 1 1

k k k

m m m _  p k q  _  p k q 

 , (21)

sehingga 2

1

m  p m.

Untuk menghitung momen kedua diperlukan Lema berikut. Lema 2

Berdasarkan asumsi pada Lema 1 didapat





















2 2

2 1

1 2

1 2 1

1

2 2 1 .

k k

k

k k

k

m p m p q m p k q m

p q m  p q m  p k q m



 

       

 

 _        _ (22)

Jika M_1._k  p m2 k



p q



2mk1 



p 



k 1



q



2m (23) dan M_2._k 



p q m



k1₁



p2q m



k2₂ 



p 



k 1



q m



_k_₁, (24)

maka mk M1.k2M2.k. (25)

Dengan menggunakan persamaan (23) dan 1 f m didapat

 

2 2 2

1.k k f| 2 k 1|f k 1|f

M p s p q Is _ q I s



   . (26)

Bukti pada Lampiran 3 sub 3.2 Lema 3





2



 

2

 

2

1.k k f| 2 k f| k f| .

(31)

15









 



 



































































1 2 2

1

2. 2 ₁ ₂

1

1 2

1 1 2 1 1

1 1 1

1 2 1

1 1 1

1 2 2 1

.

1 1 1

k k

k

k _k _k

k

k k

p q f j p q f j

p k q f j

d p q q

M

d _{p q} _f _p _q _f

p k q f j

p q f p q f

q

d _k _p _k _q _f

         _ _ _{ } _ _ _    _{ } _{ } _ _    __ __   _ _ _ _ _ _ _ _  __ _   __ _{ } _ _ _       _ _ _ _ _ _             (28)



 



















  



 













 

| | 2 2 | 2 2 | | 1 1 1 . 2 k k r k k r k k f

k f k f

p q d p q q j s

q d p q q j Is

M

d _{p q} _{d p q} _{qv s}

q d p q qv Is q d I s

 _ _ _ _    _ _ _ _     _ _       _ _ _ _      (29)



 

















 





 



 















  

| 2 2

2 | |

| |

1 2

1

2 1 1 .

2 1 2 1

k f

k _{k f} _{k f}

k k

k r k r

q p d p q v qv s

m q d p q v qv Is dq v I s d

p q d p q q j s q d p q q j Is

 _ _ _{ }       _      _                (30)









 



 

2

2 | | |

2

2 | |

2 2

2

2 1 .

k k j k j k j

k j k j

q p q k

p q q

p q s s s

d d d

q

Is kd Is k

d    _   _          _{  }    _   (31)

Bukti pada Lampiran 3 sub 3.6 Teorema 2

   

 , 

|

p q

k a k j

E C  s dan Var C

 

_k m_k _k2. Bukti:

(32)

16

Corollary 1

Jika C_k menunjukkan nilai akhir atau future value dari suatu anuitas awal dengan pembayaran sebesar 1 satuan selama k tahun dan jika tingkat suku bunga tahunan selama tahun ke-k adalah peubah acak i_k sedemikian sehingga E



1i_k



 1 j

dan Var



1i_k



s2 serta i i₁, ,₂ ,i_n adalah peubah acak independen, maka: a. C_k  



1 i_k



C_k_₁1



, untuk k 2,3, ,n

b. E C

 

_k s_{k j}_| ,

c.









1

| |

2 1 2

,

k

k r k f

k

j s j s

m

j



  



d.

 

















1

| | 2 | |

2 1 2 1 2 1

.

k

k r k f k j k j

k

j s j s j s j s

Var C

j



     



Bukti pada Lampiran 3 sub 3.7 Corollary 2

JikaC_kmenunjukkan nilai akhir atau future value dari suatu anuitas awal dengan pembayaran masing-masing sebesar 1, 2, ,k selama k tahun dan jika tingkat suku bunga tahunan selama tahun ke-k adalah peubah acak i_k sedemikian sehingga E



1i_k



 1 j dan Var



1i_k



s2 serta i i₁, ,₂ ,i_n adalah peubah acak independen, maka:

a. C_k  



1 i_k



C_k_₁k



, untuk k 2,3, ,n

b.

   

| ,

k _{k j}

E C  Is

c. _1.

 

2 | ,

k _{k f}

M  I s

d.



   

 





 

2 2

| | _|

2. 2

1 1 1

,

k

k r k f _{k f}

k

j Is j Is j j I s

M

j



    



e.



  



 





 

2 ₂

| | _|

2

2 1 2 1 2

,

k

k r k f _{k f}

k

j Is j Is j j I s

m

j



    



f.

 













2 ₂

| | |

2

2 1 k ( )_{k r} 2 1 ( )_{k f} 2 ( )_{k f}

k

j Is j Is j j I s Var C

j



    



 



 

2

2 | |

2 2 1

.

k j k j

Is kd Is k

d

  



Bukti pada Lampiran 3 sub 3.8 Corollary 3

(33)

17 sehingga E



1i_k



 1 jdan Var



1i_k



s2 serta i i₁, ,₂ ,i_n adalah peubah acak independen, maka:

a. C_k  



1 i_k



_C_k_₁



n k 1



_, untuk k 2,3, ,n

b. E C

   

k  Ds n k j_{, |} ,

c. _1.





2 _|



 

_|

 

2

|

1 2 1 ,

k k j k j k j

M  n s  n Is  I s

d.





  





 

1

, | , |

2. 2

1 1 k _{n k r} 1 1 _{n k f}

k

jn j Ds j jn j Ds

M

j



     





 



 

 

2



| _|

2

1 1

,

k f _{k f}

j j n Is I s

j

  



e.



�