PENENTUAN MEDAN GRAVITASI EINSTEIN DALAM RUANG MINKOWSKI MENGGUNAKAN SIMBOL
CHRISTOFFEL JENIS I DAN II
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MELLY FRIZHA 080801032
DEPARTEMEN FISIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PENENTUAN MEDAN GRAVITASI EINSTEIN DALAM RUANG MINKOWSKI MENGGUNAKAN SIMBOL
SCHRISTOFFEL JENIS I DAN II
ABSTRAK
DETERMINATION OF EINSTEIN’S GRAVITATIONAL FIELD IN MINKOWSKI SPACE USING CHRISTOFFEL SYMBOL OF THE
TYPE I AND II
ABSTRACT
Theoretical studies have been conducted concerning the determination of Einstein's gravitational field in Minkowski space through the study on the phenomenon of bending of starlight around the sun. This assessment showed that Einstein's gravitational field manifestation of the curvature of space-time in this space-time 4 dimensional Minkowski which have Minkowski’s metric. Calculation of the gravitational field Eintein done by formulating it into the formulation of the Christoffel symbol of the type I and II . The results, showing a link between the gravitational field of the space-time which can mathematically explain the concept of physical phenomena on the deflection of starlight around the sun.
Halaman
Bab 2 Tinjauan Pustaka 2.1 Teori Relativitas Einstein ... 6
2.1.1 Teori Relativitas Khusus ... 6
2.1.1.1 Transformasi Lorentz ... 7
2.1.1.2 Kerangka Acuan Inersial ... 10
2.1.2 Teori Relativitas Umum ... 11
2.1.2.1 Prinsip Ekuivalensi ... 12
2.1.2.2 Prinsip Kovariansi Umum ... 12
2.1.2.3 Kelengkungan Ruang-Waktu ... 13
2.2 Analisis Tensor ... 16
2.2.1 Transformasi Koordinat ... 17
2.2.2 Koordinat Kurvalinier ... 19
2.2.2.1 Koordinat Kurvalinier Ortogonal ... 19
2.2.2.2 Vektor Satuan dan Faktor Skala dalam Sistem Koordinat Kurvalinier ... 19
2.2.2.3 Koordinat Kurvalinier Umum ... 20
2.2.3 Kaidah Penjumlahan ... 22
2.2.4 Klasifikasi Tensor Berdasarkan Hukum Transformasi ... 22
2.2.4.1 Vektor Kontravarian ... 22
2.2.4.2 Vektor Kovarian ... 23
2.2.4.3 Invarian ... 23
2.2.4.4 Tensor Campuran ... 24
2.2.5 Operasi-Operasi Dasar Tensor ... 25
2.2.6 Tensor Metrik ... 27
2.2.7 Tensor Konjugat ... 29
2.2.8 Differensiasi Tensor ... 29
2.2.9 Geodesik ... 31
2.3 Medan Gravitasi Einstein ... 32
Bab 3 Hasil dan Pembahasan 3.1 Pembelokan Cahaya Bintang di Sekitar Matahari Berdasarkan Teori Relativitas Umum Einstein ... 34
3.2 Ruang-Waktu Minkowski 4 Dimensi ... 36
3.2.1 Geometri Ruang Datar ... 37
3.2.2 Geometri Ruang Lengkung ... 39
3.3 Medan Gravitasi Eintein dalam Ruang-Waktu Minkowski 4 dimensi ... 41
Bab 4 Kesimpulan dan Saran 4.1 Kesimpulan ... 52
4.2 Saran ... 53
Daftar Pustaka ... 54
Lampiran A ... 56
Lampiran B ... 59
Halaman
Gambar 2.1 Kerangka acuan inersial dari S dan S’ ... . 8
Gambar 2.2 Ruang 1 dimensi (a) yang datar (b) yang lengkung ... 13
Gambar 2.3 Ruang 2 dimensi (a) yang datar (b) yang lengkung ... 14
Gambar 2.4 Ruang Euklidean dan komponen-komponen geometrinya ... . 14
Gambar 2.5 Ruang non-Euklidean dan komponen-komponen geometrinya ... 14
Gambar 2.6 (a) Dalam ruang datar C/D = π (b) Dalam ruang lengkung C/D > π atau < π ... 15
Gambar 2.7 Tampilan ruang-waktu yang melengkung oleh benda ber- massa ... 15
Gambar 2.8 Kurva-kurva dan garis koordinat ... . 17
Gambar 2.9 Sistem koordinat kurvalinier umum bola ... 20
Gambar 2.10 Jarak antara dua titik A dan B ditinjau dalam ruang ber- dimensi α ... 27
Gambar 3.1 Prinsip ekuivalensi Einstein (a) bola dipercepat dengan percepatan gravitasi (b) bola dipercepat dengan percepatan inersial ... 34
Gambar 3.2 Prinsip yang berlaku pada partikel cahaya atau foton ... 35
Gambar 3.3 Akibat melengkungnya ruang dan waktu di sekitar matahari ... 36
Gambar 3.4 Ruang datar 2 dimensi yang mewakili gambaran permukaan bumi ... 37
Gambar 3.5 Penggambaran pelengkungan yang terjadi sebagai fungsi waktu dan peninjauannya pada jarak antara titik A dan B dalam ruang lengkung ... 39
Gambar 3.6 Sistem koordinat untuk pembelokan cahaya bintang oleh matahari ... 41
Gambar 3.7 Permukaan dari bola sebagai contoh dari ruang yang meleng- kung dan transformasi koordinatnya ... 42
Gambar A.1 Kerucut cahaya yang berkorespondensi dengan ruang dan waktu 56 Gambar A.2 Diagram Ruang-Waktu ... 58
Simbol-simbol yang digunakan dalam skripsi ini dan fungsinya :
F = Gaya
G = Konstanta Gravitasi = Vektor posisi
m = Massa
c = Kecepatan cahaya
v = Keceptan pada kerangka acuan inersial g = Percepatan gravitasi
a = Percepatan inersial
l = Panjang
= Tensor metrik
= Tensor resiprokal/konjugat
= Kuadrat elemen jarak antara 2 titik = Delta kronecker
= Faktor Skala atau panjang dari suatu vektor = Ruang berdimensi sebarang
= Vektor kovarian rank 1 = Vektor kontravarian rank 1
= Vektor campuran dengan vektor kovarian dan kontravarian masing-masing berank 1
DAFTAR ISTILAH
Dimensi : Jumlah minimal koordinat yang dibutuhkan untuk menentukan titik yang ada di dalam suatu ruang
Ekuivalensi : Kesetaraan
Foton : Partikel elementer pembawa radiasi elektromagnetik tak bermassa dan berkecepatan cahaya
Geometri : Ilmu ukur yang mempelajari hubungan dalam suatu ruang
Geodesik : Jarak terpendek dalam ruang waktu lengkung
Invarian : Besaran yang tidak berubah meski telah mengalami transformasi
Isotropik : Keseragaman dalam semua orientasi Koordinat Kurvalinier : Koordinat suatu ruang lengkung
Kerangka Acuan Inersial : Kerangka yang diam atau bergerak dengan kecepatan tetap
Massa Massif : Massa yang sangat besar
Ortogonal : Tegak lurus
Ruang Euklidean : Ruang datar atau ruang dengan koordinat kartesius Ruang Non-Euklidean : Ruang Lengkung
PENENTUAN MEDAN GRAVITASI EINSTEIN DALAM RUANG MINKOWSKI MENGGUNAKAN SIMBOL
SCHRISTOFFEL JENIS I DAN II
ABSTRAK
DETERMINATION OF EINSTEIN’S GRAVITATIONAL FIELD IN MINKOWSKI SPACE USING CHRISTOFFEL SYMBOL OF THE
TYPE I AND II
ABSTRACT
Theoretical studies have been conducted concerning the determination of Einstein's gravitational field in Minkowski space through the study on the phenomenon of bending of starlight around the sun. This assessment showed that Einstein's gravitational field manifestation of the curvature of space-time in this space-time 4 dimensional Minkowski which have Minkowski’s metric. Calculation of the gravitational field Eintein done by formulating it into the formulation of the Christoffel symbol of the type I and II . The results, showing a link between the gravitational field of the space-time which can mathematically explain the concept of physical phenomena on the deflection of starlight around the sun.
BAB 1
PENDAHULUAN
Perkembangan fisika teoritik melalui Teori Relativitas Umum (TRU) yang dikemukakan oleh Albert Einstein sudah sangat pesat dan cukup baik dalam mendeskripsikan ataupun memprediksi fenomena-fenomena yang terjadi di jagad raya. Salah satu fenomena yang berhasil diprediksi adalah terjadinya pembelokan cahaya bintang di sekitar matahari.
1.1 Latar Belakang Masalah
Sejauh ini, berbagai kajian teoritis mengenai medan gravitasi Einstein pada TRU telah banyak dilakukan dan dipublikasikan. Salah satu kajian menyebutkan, medan gravitasi yang dikemukan pertama sekali oleh Newton didefenisikan sebagai hasil gaya tarik-menarik dua benda bermassa terhadap kuadrat jarak antara keduanya. Dalam perkembangan selanjutnya diketahui bahwa medan gravitasi Newton tidak sepenuhnya dapat menjelaskan semua fenomena yang terjadi di jagad raya. Sebab seperti cahaya, tidak semua benda memiliki massa di jagad raya ini. Karenanya Einstein mengemukakan idenya tentang medan gravitasi melalui TRU dibuktikan dengan kebenaran keberadaan fenomena pembelokan cahaya bintang di sekitar matahari dengan besar sudut pembelokan yang dapat diperhitungkan. Dalam kajian lainnya dinyatakan, ruang dan waktu bersifat saling bergantung dan membentuk satu kesatuan ruang-waktu 4 dimensi (Ruang-Waktu Minkowski). Dan medan gravitasi Einstein hadir sebagai konsekuensi kelengkungan ruang-waktu 4 dimensi tersebut karena adanya distribusi massa dalam ruang waktu tersebut. Untuk itu, persamaan medannya dapat ditentukan baik dalam keadaan vakum maupun dengan kehadiran materi. Kajian-kajian tersebut secara luas telah menjelaskan medan gravitasi Einstein serta kaitannya terhadap peristiwa pembelokan cahaya bintang di sekitar matahari. Namun demikian, belum ada kajian yang membahas secara khusus masalah medan gravitasi Einstein yang diperhitungkan secara matematis untuk menjelaskan fenomena fisis yang ditinjau tersebut.
Jika dalam teori gravitasi Newton, gaya gravitasinya dinyatakan melalui hukum gaya gravitasi maka dalam TRU yang secara geometri adalah teori tentang geometri ruang-waktu lengkung, medan gravitasinya dinyatakan melalui komponen-komponen tensor metrik dari kuadrat jarak ds2. Dalam skripsi ini, medan gravitasi Einstein ditinjau dalam ruang-waktu Minkowski sehingga metrik yang digunakan
adalah metrik Minkowski . Pada dasarnya, medan
dengan α, β, γ, masing-masing memiliki nilai 1, 2, 3, 4. Hasil perhitungan menunjukkan harga dan yang b ervariasi p ad a sembarang α, β, γ, d an sebagai bentuk medan gravitasi Einsteinnya. Hasilnya, fenomena pembelokan cahaya bintang di sekitar matahari tersebut dapat dijelaskan secara matematis dan secara jelas pula memperlihatkan kaitan antara ruang-waktu dengan medan gravitasi Einstein.
1.2 Batasan Masalah
Ruang lingkup penelitaian ini akan dibatasi pada:
1. Penjelasan Teori Relativitas Umum tentang peristiwa pembelokan cahaya bintang di sekitar matahari.
2. Medan gravitasi Einstein ditinjau dalam ruang-waktu Minkowski 4 dimensi. 3. Formulasi medan gravitasi Einstein dengan simbol Christoffel jenis I dan II.
1.3 Tujuan Penelitian
Adapun tujuan dari penelitian ini adalah:
1. Untuk memahami konsep Teori Relativitas Umum dalam menjelaskan peristiwa pembelokan cahaya bintang di sekitar matahari
2. Untuk meninjau medan gravitasi Einstein pada ruang-waktu Minkowski 4 dimensi.
3. Untuk memformulasikan medan gravitasi Einstein menggunakan simbol Christoffel jenis I dan II.
1.4 Manfaat Penelitian
di sekitar matahari dan memberikan informasi mengenai fenomena tersebut yang berguna dalam proses pembelajaran Teori Relativitas Umum.
1.5 Metodologi Penelitian
Metode kajian pustaka dipilih dalam penelitian ini dengan menggunakan beberapa literatur dari berbagai sumber pustaka terkait. Kegiatan studi penelitian ini diuraikan secara lebih rinci di bawah ini:
1. Studi Literatur
Merupakan tahap pengumpulan literatur mengenai: teori relativitas umum, ruang-waktu Minkowski, analisis tensor, medan gravitasi Einstein.
2. Pengkajian Literatur
Merupakan tahap penyesuaian dengan permasalahan yang akan dibahas dalam penelitian sehingga didapat informasi yang diinginkan.
3. Pengolahan Informasi
Merupakan tahap untuk menganalisa informasi sehingga didapatkan informasi yang dapat digunakan untuk menyelsaikan permasalahan dalam penelitian.
4. Merangkum Kesimpulan
Merupakan jawaban dari setiap permasalahan yang akhirnya menghadirkan suatu fakta ilmiah mengenai fenomena yang ditinjau.
5. Penulisan Laporan
1.6 Sistematika Penulisan
Adapun sistematika dalam penulisan Skripsi ini mencakup beberapa bab dan subbab seperti dijelaskan di bawah ini:
BAB I : Pendahuluan
Bab ini terdiri atas latar belakang penelitian, batasan masalah dalam penelitian, tujuan dan manfaat penelitian serta metodologi pelaksanaan penelitian dan sistematika penulisan laporan penelitian.
BAB II : Tinjauan Pustaka
Bab ini berisi dasar-dasar teori yang terkait kajian dan analisa dalam penelitian, yakni teori relativitas umum Einstein, ruang Minkowski, analisa tensor dan medan gravitasi Einstein.
BAB III : Hasil dan Pembahasan
Bab ini mencakup hasil penelitian berupa penjelasan fenomena pembelokan cahaya bintang di sekitar matahari berdasarkan teori relativitas umum, pendefenisian ruang-waktu Minkowski 4 dimensi serta rumusan perhitungan medan gravitasi Einstein.
BAB IV : Kesimpulan dan Saran
BAB 2
TINJAUAN PUSTAKA
2.1 Teori Relativitas Einstein
Relativitas merupakan subjek yang penting yang berkaitan dengan pengukuran (pengamatan) tentang di mana dan kapan suatu kejadian terjadi dan bagaimana kejadian tersebut dianalisa atau diukur menurut suatu kerangka acuan yang bergerak relatif terhadap kerangka yang lain. Topik tentang teori relativitas dibagi ke dalam dua bagian, yakni Teori Relativitas Khusus (Special Theory of Relativity) dan Teori Relativitas Umum (General Theory of Relativity).
Dalam teori relativitas khusus, subjek yang menjadi fokus adalah kerangka acuan yang inersial, yaitu kerangka yang padanya hukum gerak Newton berlaku. Sedangkan teori relativitas umum berkaitan dengan situasi yang lebih rumit dimana kerangka acuannya mengalami percepatan gravitasi. Kedua teori tersebut dibuat untuk menjelaskan bahwa gelombang elektromagnetik tidak sesuai dengan teori relativitas klasik yang didasari konsep Galileo Galilei dan didefenisikan kembali oleh Sir Isasc Newton melalui teori relativitas geraknya.
2.1.1 Teori Relativitas Khusus (TRK)
1. Postulat Relativitas: Hukum-hukum fisika berlaku sama untuk setiap pengamat di dalam kerangka acuan yang inersial.
2. Postulat Kelajuan Cahaya: Kelajuan cahaya dinyatakan dengan c yang bernilai tetap pada semua kerangka acuan.
Hadirnya kedua postulat tersebut memunculkan teori-teori baru. Seperti pada postulat pertamanya dikatakan bahwa jika hukum-hukum itu dibedakan, maka perbedaan tersebut dapat membedakan satu kerangka acuan inersial dari kerangka lainnnya. Disamping itu, yang tidak kalah baru adalah teori tentang ramalan mengenai laju radiasi elektromagnetik yang diturunkan dari persamaan Maxwell. Menurut analisis ini, cahaya dan semua gelombang elektromagnetik lain berjalan dalam ruang hampa dengan laju konstan yang sekarang didefenisikan secara eksak sebesar 299.792.458 m/s atau biasa dituliskan dengan 3 x 108 m/s. Hal ini akan kita temuka n dalam ruang hampa yang memiliki peranan penting dalam teori relativitas Einstein.
Kehadiran kedua postulat tersebut juga sukses dalam memperluas cakupan hukum-hukum gerak oleh Galileo yang terbatas di mekanika ke hukum-hukum elektromagnetik dan optik. Hasil dari memperkenalkan teori relativitas khusus ini, diperkenalkannya transformasi koordinat baru yang dinamakan Transformasi Lorentz yang sesuai untuk laju tinggi.
2.1.1.1 Transformasi Lorentz
memberikan hasil yang sama seperti transformasi Galileo apabila laju relatif antara dan adalah rendah. (Krane, Kenneth S., 2006)
z
Gambar 2.1 Kerangka acuan inersial dari S dan S’
Transformasi yang memenuhi semua persyaratan ini dikenal dengan transformasi Lorentz dan seperti halnya transformasi Galileo, ia mengaitkan koordinat suatu peristiwa sebagaimana diamati dari kerangka dengan koordinat peristiwa yang sama yang diamati dari kerangka acuan yang sedang bergerak dengan kecepatan terhadap . Dengan menganggap bahwa gerak relatifnya adalah sepanjang arah positif. Bentuk transformasi Lorentz ini adalah sebagai berikut:
(2.1)
Persamaan (2.1) adalah transformasi koordinat Lorentz yang merupakan generalisasi
dari transformasi Galileo terdahulu . Untuk
koordinat ruang maupun waktu dari suatu peristiwa dalam suatu kerangka acuan bergantung pada koordinat waktunya dalam kerangka acuan lainnya. Sekarang ruang dan waktu telah menjadi saling jalin menjalin. Kita tidak dapat lagi mengatakan bahwa panjang dan waktu mempunyai arti mutlak yang tidak tergantung kerangka acuannya.
Bentuk-bentuk transformasi Lorentz pada (2.1) dapat digunakan untuk menurunkan generalisasi relativitas sebagai efek penggunaan transformasi ini. Diantaranya:
Pemuluran Waktu Relativistik yang mana waktu bergerak lebih lambat dari penanda waktu yang berada dalam keadaan diam.
Kontraksi Panjang Lorentz,
Transformasi Kecepatan,
2.1.1.2 Kerangka Acuan Inersial
Dengan adanya peta (atlas), setiap peristiwa mempunyai label berupa 4 bilangan real, misalnya atau . Arti fisis dari atlas adalah suatu kerangka acuan dengan sistem koordinat tertentu. Kerangka acuan terdiri atas partikel-partikel berlabel yang dilengkapi dengan penanda waktu. Sebuah kerangka acuan dicirikan dengan gerakan tertentu dari partikel-partikel penyusunnya, sedangkan cara pemberian label menunjukkan sistem koordinat yang digunakan dalam kerangka acuan itu. Jadi, kerangka acuan adalah suatu sarana untuk memberikan label pada setiap peristiwa. Salah satu label menunjukkan saat terjadinya peristiwa, dan dalam mekanika klasik Newtonian, label itu bersifat mutlak.
Cara penentuan saat terjadinya peristiwa adalah dengan menyediakan penanda waktu yang sudah disinkronkan dan kemudian disebar ke dalam ruang. Saat dari suatu peristiwa ditunjukkan dengan penanda waktu yang berada di tempat peristiwa itu terjadi. Penunjukkan waktu bersifat mutlak, artinya tidak dipengaruhi oleh gerakan waktu ketika dibawa oleh partikel penyusun kerangka acuan. Karena saat dari peristiwa-peristiwa dalam ruang-waktu bersifat mutlak, maka ruang-waktu dapat dibagi menjadi sub ruang 3 dimensi, dimana setiap subruang (ruang spatial) terdiri atas peristiwa-peristiwa yang terjadi pada saat yang sama (simultan). Peristiwa dalam ruang spatial cukup diberi label berupa 3 bilangan real dan memberikan posisi dari peristiwa itu dalam ruang spatial. Mekanika klasik Newtonian menyatakan bahwa hanya ada satu cara pembagian ruang-waktu menjadi subruang yang simultan dan subruang berdimensi 3 itu berstruktur Euklidean.
Kita dapat menggunakan atlas yang lain dalam manifold ruang-waktu, misalnya menghasilkan label untuk peristiwa yang dinyatakan sebagai atau . Karena hanya ada satu cara pembagian ruang-waktu, maka itu berarti
Hubungan antara dengan mempunyai dua kemungkinan, yaitu
yang berarti kita berpindah kerangka acuan, atau
yang berarti kita hanya berganti sistem koordinat.
Jika dapat ditemukan suatu transformasi sehingga dalam ruang spatial
kerangka acuan itu, kurva lintasan partikel bebas berupa garis lurus dan kecepatannya konstan, maka kerangka acuan itu disebut sebagai kerangka acuan yang inersial. (Arief Hermanto, 2003)
2.1.2 Teori Relativitas Umum Einstein
2.1.2.1 Prinsip Ekuivalensi
Ketika Newton merumuskan hukum gerak dan hukum gravitasinya, ia mendefenisikan massa inersial dan massa gravitasi. Massa inersial diukur berdasarkan ukuran kelembaman suatu benda terhadap gaya dorong atau gaya tarik yang bekerja, sedangkan massa gravitasi diukur berdasarkan pengaruh gaya gravitasi pada benda tersebut. Para eksperimentalis sejak zaman Newton hingga pertengahan abad ke-20 telah berusaha membuktikan kesetaraan antara kedua jenis massa tersebut. Salah satu percobaan yang paling terkenal adalah percoban Eotvos yang membuktikan bahwa kedua massa tersebut setara. Berdasarkan bukti eksperimen tersebut, akhirnya Einstein menyimpulkan dalam postulatnya yang terkenal dengan nama Prinsip Ekuivalensi Massa bahwa,”Gaya gravitasi dan gaya inersial yang bekerja pada 1 benda adalah sama dan tidak terbedakan (indistinguisable) satu sama lain”. Konsekuensinya adalah bahwa tidak ada lagi kerangka acuan inersial.
2.1.2.2 Prinsip Kovariansi Umum
Akibat prinsip ekuivalensi massa yang menyebabkan tidak adanya kerangka acuan inersial, maka prinsip relativitas khusus menyatakan bahwa hukum-hukum fisika berlaku sama pada kerangka acuan inersial tidaklah berlaku umum. Oleh karena itu, Einstein merumuskan postulat keduanya yang terkenal dengan nama Prinsip Kovariansi Umum yang menyatakan bahwa,”Semua hukum-hukum fisika berlaku
sama pada semua kerangka acuan tanpa kecuali”. Konsekuensinya adalah setiap
2.1.2.3 Kelengkungan Ruang-Waktu
Dari teori relativitas khusus, baik waktu atau ruang adalah bergerak relatif terhadap gerak pengamat dengan interval panjang dan waktu diukur oleh seorang pengamat secara umum tidak sama dengan interval panjang dan waktu yang diukur oleh pengamat yang berbeda. Karena panjang dan waktu relatif dan keduanya bergantung pada gerak relatif pada lintasan yang sama maka perlu untuk menyatakan kembali bahwa ruang berdimensi 3 dan 1 dimensi waktu tidak terpisah, dan lebih dari itu juga keduanya merupakan komponen yang setara dari suatu ruang-waktu 4 dimensi yang tunggal. Untuk menggambarkannya memang sulit tapi kita masih dapat merepresentasikannya secara matematis dengan menggunakan pertimbangan persamaan yang sesuai.
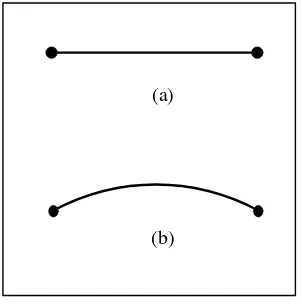
Beberapa contoh penggambaran kelengkungan ruang-waktu ditunjukkan pada gambar 2.2 yang mengilustrasikan ruang datar berimensi 1 yang berupa garis lurus. Untuk melengkungkannya, harus dibengkokkan pada arah yang lain. Tapi, kelengkungan yang ditunjukkan dalam 1 dimensi tidak cukup dan memerlukan 2 dimensi untuk mengilustrasikannya lebih lanjut. Gambar 2.3 menyajikan suatu ruang 2 dimensi dan ilustrasi bagaimana ruang itu dilihat jika dibengkokkan.
(a)
(b)
(a) (b)
Gambar 2.3 Ruang 2 dimensi (a) yang datar (b) yang lengkung
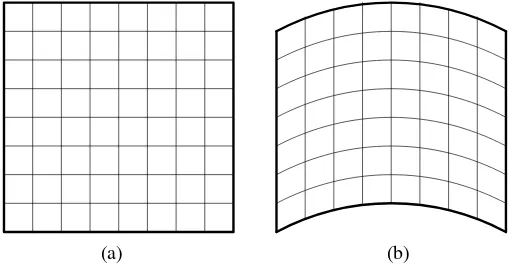
Geometri dari sistem koordinat ruang datar adalah geometri Euklidean yang aturan penggunaanya diilustrasikan pada 2.4 dengan suatu garis lurus yang menjadi jarak terpendek antara dua titik dan total sudut segitiga dalam ruang datar adalah 180o, serta garis-garis sejajar yang tidak akan saling berpotongan. Untuk geometri lengkung yang dikenal dengan geometri non-Euklidean diberikan oleh 2.5, dimana aturan geometri euklidean tidak bisa digunakan, sehingga jarak terpendek antara dua titiknya merupakan busur lingkaran besarnya dengan jumlah sudut segitiga dalam ruang ini lebih dari 180o dan garis-garis sejajarnya dapat saling berpotongan.
A B
B
A
Gambar 2.4 Ruang Euklid dan Gambar 2.5 Ruang non-Euklid dan komponen-komponen geometrinya komponen-komponen geometrinya
kurang dari (Gambar 2.6.b). Sebagaimana yang akan dibahas berikutnya, kelengkungan ruang-waktu ditentukan oleh massa terdekat atau disekitar massa massifnya, dengan kelengkungan yang dapat bernilai cukup besar untuk memberikan efek yang tampak (2.7).
Gambar 2.6 (a) Dalam ruang datar (b) Dalam ruang lengkung
atau .
Gambar 2.7 Tampilan ruang-waktu yang melengkung oleh benda bermassa Sumber: Nggieng (2007)
Banyak prediksi akan peristiwa yang terjadi yang telah berhasil dibuktikan dan dikemukakan oleh teori relativitas umum yang tentunya berbeda dari fisika klasik. Prediksinya juga telah dikonfirmasikan dalam semua percobaan dan pengamatan fisika. Walaupun teori ini bukan satu-satunya teori tentang relativistik gravitasi, ia merupakan teori paling sederhana dan konsisten dengan data-data eksperimen. Salah satu prediksinya adalah peristiwa terbeloknya cahaya matahari di sekitar matahari. Teori relativitas umum memprakirakan bahwa titik-titik kerucut cahaya (bintang) yang berada di dekat matahari akan terbelokkan menuju matahari karena pengaruh massa matahari. Karenanya cahaya yang datang dari bintang-bintang jauh dan lewat dekat matahari akan mengalami defleksi yang menyebabkan bintang-bintang tersebut tampak berbeda di posisi yang berbeda bagi pengamat di bumi. Karena bumi bergerak dengan mengorbit pada matahari maka bintang-bintang yang berbeda akan berada di belakang matahari dan cahayanya terdefleksi sehingga posisinya berubah relatif terhadap bintang lain. (Kenneth S. Krane, 1983)
2.2 Analisis Tensor
Aljabar tensor adalah suatu disiplin matematik yang sangat penting peranannya dalam fisika karena hukum fisis tidak akan bergantung pada sistem koordinat yang digunakan untuk memberikan tafsiran yang tepat pada hukum tersebut. Jika di dalam sebuah sistem koordinat terdapat suatu persamaan tensor maka bentuk daripada persamaan tersebut akan tetap sama (kovarian) di dalam semua sistem koordinat lain. Sifat tersebut menyebabkan tensor sangat banyak sekali digunakan di dalam fisika. Khususnya dalam teori relativitas umum, maka semua perumusan fisis selalu dinyatakan dengan persamaan tensor seperti yang akan dibahas.
2.2.1 Transformasi Koordinat
Misalkan koordinat-koordinat tegak lurus (x, y, z) dari sebarang titik dinyatakan sebagai fungsi-fungsi sehingga
Andaikan bahwa bentuk di atas dapat dipecahkan untuk dalam , yakni
Fungsi-fungsi dalam (2.5) dan (2.6) dianggap tunggal dan memiliki turunan-turunan yang kontiniu sehingga kaitan dengan adalah tunggal.
Diketahui sebuah titik P dengan koordinat-koordinat tegak lurus maka dari (2.5) kita dapat mengasosiasikan suatu himpunan koordinat-koordinat
yang tunggal yang disebut koordinat-koordinat kurvilinier dari P. Himpunan persamaan (2.5) dan (2.6) mendefenisikan suatu transformasi koordinat.
x
y
z
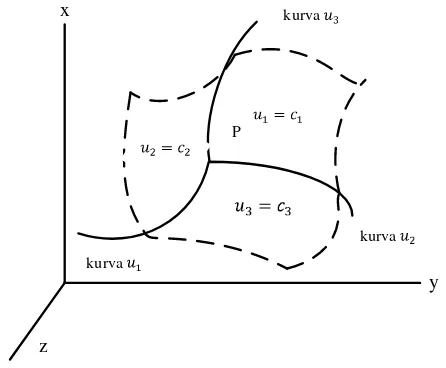
Gambar 2.8 Kurva-kurva dan garis koordinat
Selanjutnya, akan didefenisikan transformasi koordinat menyangkut sistem koordinat lain dengan dimensi yang lebih tinggi. Untuk itu perlu diketahui terlebih dahulu mengetahui ruang dengan sebarang dimensi dimana kita akan membahas sifat-sifat transformasi daripada ruang tersebut.
P
kurva
kurva
Sebuah ruang berdimensi n, dimana n adalah sembarang bilangan bulat positif, adalah merupakan himpunan daripada susunan yang teratur,
dan yang memenuhi sifat-sifat daripada sebuah ruang vektor. Komponen sebuah vektor dalam ruang berdimensi n tersebut akan dinyatakan dengan indeks tertentu. Suatu kurva di dalam sebuah ruang berdimensi n adalah himpunan dari titik-titik x yang memenuhi n buah persamaan, yaitu , dimana t adalah parameter dan
. Jika dianggap sebagai subruang dari (n < N) maka
ditunjukkan oleh dimana menyatakan n buah
parameter dan .
Kemudian diberikan sistem koordinat mencakup ruang tersebut, yaitu yang membentuk sistem koordinat di . Setiap
menyatakan titik pada ruang . Misalkan ada transformasi dari suatu sistem koordinat ke siatem yang lain maka bentuk perubahan koordinatnya dinyatakan sbb:
. . . . . . . . .
Dengan demikian, diferensial untuk dapat ditulis sebagai berikut:
Atau dapat juga disederhanakan menjadi
dimana
2.2.2 Koordinat Kurvalinier
2.2.2.1 Koordinat Kurvalinier Ortogonal
Permukaan dimana adalah konstanta, disebut
permukaan-permukaan koordinat, dan setiap pasangan permukaan-permukaan ini berpotongan melalui kurva-kurva yang disebut kurva-kurva atau garis-garis koordinat (gambar 2.8). Bila permukaan-permukaan koordinat ini berpotongan tegak lurus, maka sistem koordinatnya disebut ortogonal. Dengan menggunakan hubungan transformasi (2.5) dan (2.6), dimisalkan atau sebagai vektor posisi dari titik P. Maka berdasarkan persamaan tersebut dapat bentuk
vektornya .
2.2.2.2 Vektor Satuan dan Faktor Skala dalam Sistem Koordinat Kurvalinier
Dengan demikian,
dimana
adalah panjang vektor-vektor singgung yang bersangkutan atau disebut juga sebagai faktor skala.
Uraian di atas memberikan bentuk pernyataan untuk sistem koordinat ortogonal yang ditinjau dimana berlaku syarat:
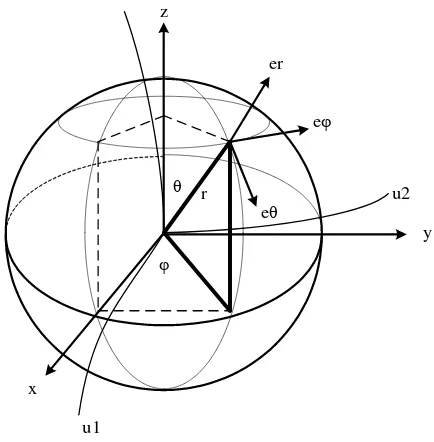
yang ketiga vektor satuan ini membentuk himpunan vektor satuan koordinat kurvalinier (gambar 2.9). Dalam hal seperti ini penggunaan sistem koordinat kurvalinier yang sesuai seperti koordinat bola ternyata mengalihkan persoalan menjadi sederhana untuk ditangani. (Hans J. Wospakrik, 1972)
2.2.2.3 Koordinat Kurvalinier Umum
z
y
x
u1
u2 er
eφ
eθ
θ
φ
r
Dari kita peroleh
Maka diferensial dari panjang busur ditentukan dari Untuk sistem ortogonal,
Untuk sistem-sistem kurvalinier yang tak ortogonal maka bentuk tidak akan memiliki bentuk yang sederhana seperti sebelumnya. Tapi secara umum dapat dituliskan sebagai berikut:
dimana komponen pada persamaan merepresentasikan koefisien-koefisien yang muncul dalam perhitungan . Bentuk dapat juga disederhanakan menjadi
Dalam bentuk matriks dapat dituliskan dengan
2.2.3 Kaidah Penjumlahan
Dalam menuliskan suatu pernyataan seperti kita dapat mempergunakan notasi singkat
atau notasi yang lebih singkat lagi , dimana menyetujui suatu kaidah (convention)
bahwa setiap sebuah indeks (indeks atas atau bawah) diulangi dalam suatu suku tertentu maka ini berarti kita menjumlahkan terhadap indeks tersebut dari 1 sampai n kecuali bila ada pernyataan lain. Inilah yang disebut kaidah penjumlahan.
2.2.4 Klasifikasi Tensor Berdasarkan Hukum Transformasi
Skalar dan vektor dapat dikatakan sebagai kasus khusus dari tensor. Karena tensor adalah objek geometri yang memerlukan uraian lebih dari satu faktor seperti skalar atau tiga faktor seperti pada vektor. Secara umum tensor termasuk didalamnya skalar dan vektor dibedakan berdasarkan penempatan indeksnya. Namun demikian, tensor juga dapat dibedakan berdasarkan hukum transformasi yang dimilikinya.
2.2.4.1 Vektor Kontravarian
Fungsi dalam sistem koordinat disebut vektor kontravarian jika pada suatu transformasi koordinat , sehingga fungsi akan ditransformasikan menjadi
disebut komponen vektor kontravarian atau tensor kontravarian rank satu.
2.2.4.2 Vektor Kovarian
Fungsi dalam sistem koordinat disebut vektor kovarian jika pada suatu transformasi koordinat , sehingga fungsi akan ditransformasikan menjadi
dimana merupakan fungsi dalam sistem koordinat
disebut komponen vektor kovarian atau tensor kovarian rank satu atau order satu.
2.2.4.3 Invarian
2.2.4.4 Tensor Campuran
Dalam konsep tensor, suatu tensor campuran adalah tensor yang bukan jenis kovarian kuat maupun kontravarian kuat. Fungsi dalam sistem koordinat
disebut tensor campuran yang memiliki komponen kontravarian rank satu dan komponen kovarian rank satu. Jika pada suatu transformasi koordinat , maka fungsi ditransformasikan menjadi
dimana merupakan fungsi dalam sistem koordinat . Diperoleh
yang menyatakan komponen tensor campuran.
Dengan menggunakan defenisi dari tensor campuran di atas akan ditunjukkan bahwa juga merupakan suatu tensor campuran. Sekarang perhatikan persamaan transformasi berikut
2.2.4.5 Tensor Simetri dan Antisimetri
Misalkan sebarang tensor kontravarian, berlaku
1. Jika maka disebut simetri terhadap pertukaran indeks dan .
2. Jika maka disebut antisimetri terhadap
pertukaran indeks dan .
Sekarang perhatikan, jika adalah suatu tensor simetri dan adalah suatu tensor antisimetri, maka . Setiap tensor selalu dapat dinyatakan sebagai penjumlahan tensor simetri dengan tensor antisimetri.
2.2.5 Operasi-Operasi Dasar Tensor
Semua sifat-sifat yang berlaku pada vektor, akan berlaku pula pada tensor. Hal itu dikarenakan operator-operator yang berlaku dan digunakan pada tensor merupakan bentuk generalisasi dari operator-operator yang berlaku pada vektor. Berikut ini akan dijelaskan operasi-operasi dasar yang berlaku pada tensor.
Penjumlahan
Penjumlahan dari dua tensor atau lebih memiliki rank dan jenis yang sama (sebagai contoh: Misalkan tensor A dan B banyaknya indeks kontravarian dan indeks kovarian adalah sama) akan menghasilkan tensor yang memiliki rank dan jenis yang sama pula. Misalkan dan merupakan tensor dalam sistem koordinat , maka
(2.21)
Pengurangan
(2.22)
merupakan tensor juga.
Perkalian (Outer Multiplication)
Hasil kali dua tensor adalah tensor dimana ranknya merupakan jumlah dari rank tensor-tensor tersebut. Komponen tensor ini disebut outer product. Sebagai contoh,
(2.23)
adalah outer product dari dan . Tetapi tidak semua bentuk tensor dapat dinyatakan sebagai hasil kali dari dua tensor yang ranknya lebih sederhana.
Konstraksi
Misalkan adalah suatu tensor campuran yang memiliki rank lima, dengan kontravarian rank dua dan kovarian rank tiga. Jika salah satu indeks kovarian samadengan salah satu indeks kontravarian, maka rank tensor tersebut akan berkurang sebanyak dua. Artinya, bentuk merupakan tensor yang memiliki rank tiga. Proses demikian lebih dikenal sebagai konstraksi tensor.
Perkalian Dalam (Inner Multiplication)
Misalkan dan merupakan tensor dalam sistem koordinat , maka
(2.24)
2.2.6 Tensor Metrik
A ⇒
B ⇒
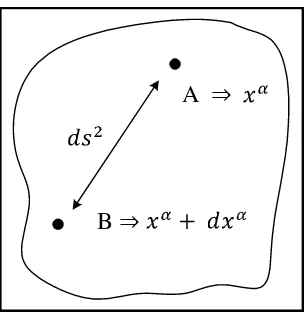
Gambar 2.10 Jarak antara dua titik A dan B ditinjau dalam ruang berdimensi α
Pada bagian ini jika A dan B adalah dua titik dalam suatu ruang berdimensi n masing-masing dengan vektor kedudukan dengan titik , maka jarak di antara kedua titik tersebut dinyatakan oleh persamaan
(2.25)
dimana Susunan besaran-besaran dapat disusun menjadi
(2.26)
Tensor dinamai tensor metrik untuk ruang tersebut. Ruang dengan metrik , di mana
(2.27)
dikenal dengan sebutan ruang Riemann. Tensor dapat dianggap sebagai sebuah tensor simetri, karena:
Karena
(
Maka
Yakni bahwa adalah sebuah tensor simetri. Jika , di mana t adalah sebuah parameter, maka
atau
Yang menyatakan jarak antara dua titik di dalam ruang Riemann tersebut. Sebuah kurva (t) dinamai kurva nol (null curve), jika
di dalam sebuah ruang non-Euklidean maka jarak antara dua titik boleh sama dengan 0, walaupun kedua titik tersebut tidak berimpit. Misalnya dalam teori relativitas khusus, setiap elemen jarak akan dinyatakan oleh persamaan
(2.29)
(2.30)
Jika:
Kurva Timelike
Kurva Spacelike
Kurva null
(Lampiran A).
2.2.7 Tensor Konjugat
Misalkan merupakan tensor metrik dan dinotasikan sebagai determinan dengan elemen-elemen dari sebagai berikut
(2.31)
maka adalah kontravarian tensor simetri rank dua yang disebut konjugat atau
reciprocal tensor dari .
2.2.8 Differensiasi Tensor
Proses differensiasi tensor adalah suatu generalisasi proses differensial yang biasa dikenal sebagai differensial fungsi. Pada analisis tensor dikenal dua jenis differensiasi yang biasa digunakan, yaitu
1. Differensiasi Kovarian 2. Differensiasi Intrinsik
Selanjutnya akan dijabarkan differensiasi kovarian yang terkait dengan pembahasan masalah selanjutnya. Untuk itu maka tinjau persamaan transformasi.
Kita telah perlihatkan bahwa bukanlah suatu tensor dan untuk membentuk tensor dari turunan parsial tersebut maka didefenisikan simbol-simbol Christoffel berikut:
1. Simbol Christoffel yang pertama, yang biasanya dinyatakan dengan notasi yang didefenisikan menurut persamaan
(2.32)
2. Simbol Christoffel yang kedua, yang biasanya didefenisikan menurut persamaan dan dinyatakan dengan notasi di mana adalah tensor metrik untuk ruang yang bersangkutan (ruang Riemann). Jadi
(2.33)
Adapun hukum transformasi untuk Simbol Christoffel diatas adalah sebagai berikut: Tinjau suatu geodesik,
untuk kedua sistem koordinat dalam ruang Riemann. Sekarang ditentukan hubungan antara dengan
Selanjutnya, persamaan di atas dikalikan dengan dan dijumlahkan harga yang sama,
Hasil di atas dibandingkan dengan bentuk geodesiknya, tampak bahwa
Ini merupakan hukum transformasi untuk . bukan merupakan komponen tensor, sehingga memungkinkan harga bernilai nol pada suatu sistem koordinat tapi bukan pada semua sistem koordinat.
2.2.9 Geodesik
Pada bagian ini akan dibahas generalisasi pengertian jarak terpendek di antara dua titik dalam suatu ruang Riemann. Andaikan kurva menguhubungkan titik A dan B dengan koordinat A dan B masing-masing diberikan oleh dan
. Maka persamaan geodesik diberikan oleh
penjumlahan pada indeks-indeks , dimana s adalah panjang busur dan adalah simbol Christoffel dari jenis kedua. Untuk kasus bagaimana persamaan geodesik untuk koordinat kartesius di ruang Euklidean. Jika koefisien jaraknya konstan maka turunannya nol, dan simbol Christoffelnya juga nol. Akibatnya, persamaan geodesiknya berbentuk
2.3 Medan Gravitasi Einstein
Disini akan ditentukan hukum suatu gerak, yang tidak tergantung pada sistem koordinat yang digunakan, yang menggambarkan medan gravitasi suatu partikel tunggal. Dalam teori relativitas khusus, elemen garis untuk koordinat ruang-waktunya adalah diberikan oleh
Dalam ruang (x, y, z, t), adalah konstanta dan ruangnya adalah Euklidean, maka . Untuk partikel yang berada di bawah pengaruh gravitasi tensor Riccinya dihilangkan. Karena , suatu ruang 4 dimensi menghasilkan
persamaan menyertakan dan turunannya. Karena , dimana , , dan untuk j = 1, 2, 3, 4, kesepuluh persamaan utama akan direduksi menjadi 6 persamaan.
Kita andaikan elemen garis (dalam kaitan dengan Schwarzchild) berubah bentuk menjadi
sehingga ruangnya menjadi non-Euklidean. Dari persamaan tersebut dapat kita susun , , ,
dan
, , , ,
Sekarang , dan karena untuk , kita
peroleh
Jika i, j, k adalah berbeda, maka . Kita juga lihat bahwa
Ketiga persamaan tersebut digunakan untuk mendapat harga-harga berikut: , , , , , , , . Dan semua yang lain dihilangkan. Selanjutnya, harga-harga tersebut digunakan untuk hukum gravitasi Einstein yang dirumuskan dalam tensor Ricci yang diberikan sebagai berikut:
Sedemikian sehingga,
BAB 3
HASIL DAN PEMBAHASAN
3.1 Pembelokan Cahaya Bintang di Sekitar Matahari Berdasarkan Teori Relativitas Umum Einstein
Fenomena pembelokan cahaya bintang di sekitar matahari adalah suatu fenomena fisis semacam ilusi yang terjadi saat melengkungnya struktur ruang angkasa akibat benda bermassa. Berawal di tahun 1915, Einstein menjelaskan dinamika massa yang dipengaruhi gravitasi. Gaya gravitasi selalu dianggap sebagai gaya tarik menarik yang besarnya sebanding dengan dan bersifat long range atau tidak ada benda yang tidak mengalami gaya tersebut. Dan gaya ini termasuk medan lemah karena harganya sebanding dengan konstanta G. Lebih lanjut, defenisi medan atau gaya gravitasi ini dikembangkan dan ditunjukkan oleh analisa prinsip ekuivalensi yang secara singkat menyatakan bahwa harga massa inersial adalah sama harganya dengan massa gravitasi. Hal ini digambarkan sebagai berikut:
a
(a)
g (b)
Pada gambar 3.1 massa inersia diperoleh dalam ruang bebas gravitasi dengan benda mengalami gaya F sehingga mengalami percepatan a (F = minersia . a). Sedangkan massa gravitasi muncul saat roket dalam keadaan diam dimana ada medan gravitasi yang berarti juga ada percepatan gravitasi g (F = mgravitasi . g).
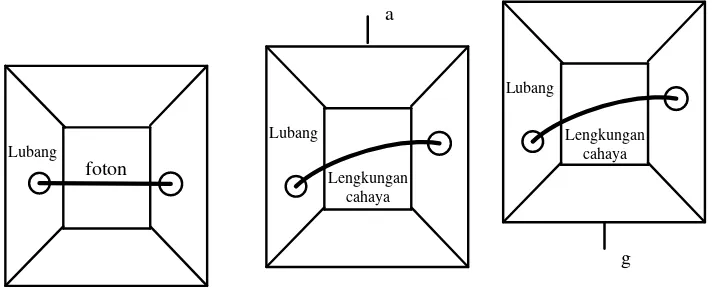
Hasil tersebut kemudian dijadikan sebagai dasar prediksi pada fenomena pembelokan cahaya bintang di sekitar matahari dengan menggunakan prinsip yang sama seperti yang diuraikan di atas dengan objek yang berbeda yakni foton. Dapat dijelaskan bahwa saat tidak ada gaya yang mempengaruhi foton atau tidak ada medan gravitasi di sekitarnya, maka foton akan bergerak dalam lintasan lurus. Oleh karena penerapan prinsip ekuivalensi, gerak foton berubah menjadi melengkung.
foton
Gambar 3.2 Prinsip yang berlaku pada partikel cahaya atau foton. Jika tidak ada gaya, lintasan cahayanya berupa garis lurus. Jika lift mengalami percepatan sebesar , dari prinsip ekuivalensi foton akan melalui lintasan foton melengkung.
berasal dari rasi bintang Hyades yang lewat di dekat permukaan matahari dibelokkan dari arah rambatannya semula dengan sudut pembelokan berkisar 1,28 detik busur. Namun hasil ini berubah berdasarkan hasil pengamatan selanjutnya untuk sudut pembelokan dengan rata-rata 1,89 detik busur dan ini mendekati hasil prediksi Einstein secara matematis, yakni 1,75 detik busur.
Matahari
Gambar 3.3 Akibat melengkungnya ruang dan waktu disekitar matahari maka lintasan cahaya pun mengikuti lengkungan sebesar sudut defleksi . Bintang yang berada di belakang matahari akan tampak saat terjadi gerhana matahari.
Dan dapat disimpulkan bahwa,”Akibat melengkungnya ruang-waktu di sekitar matahari maka lintasan cahaya mengikuti lengkungan tersebut. Dan bintang yang berada di belakang matahari akan terlihat ketika terjadi gerhana matahari”.
3.2 Ruang-Waktu Minkowski 4-dimensi
3.2.1 Geometri Ruang Datar
Untuk mendefinisikan ruang-waktu Minkowski 4 dimensi dan metrik yang dimilikinya, terlebih dahulu kita tinjau ruang datar 2 dimensi yang mewakili permukaan bumi seperti berikut ini
B
A C
Gambar 3.4 Ruang datar 2 dimensi yang mewakili gambaran permukaan bumi
Dari gambar tersebut, karena ruang datar maka posisi A dan C yang ditinjau dinyatakan oleh koordinat kartesius,
sehingga dapat dituliskan,
Sedangkan AB ditentukan dengan menggunakan teorema Phytagoras,
Jika jarak antara A dan B dalam ruang selisihnya sangat kecil, dapat dinyatakan dengan
Karena untuk ruang datar berdimensi n dengan n sembarang berlaku kuadrat jarak metrik sama dengan jumlah kuadrat diferensial koordinat kartesiusnya. Sehingga untuk ruang berdimensi 3 yang dinyatakan dengan koordinat akan memiliki bentuk kuadrat jarak metrik sebagai berikut,
(3.1)
Berikutnya ditentukan harga untuk ruang 4 dimensi dengan menerapkan teori relativitas khusus untuk mendefinisikan koordinat-koordinatnya. Sebagai konsekuensi dari teori tersebut terhadap waktu adalah dasar pegangan kita untuk secara analisis menuliskan koordinat yang kita inginkan dengan . Kita kembali pada gambar 3.4 dengan menyatakan bahwa titik A dan C berada dalam ruang-waktu 4 dimensi dimana A berada di dan C berada di dekatnya . Dengan mengingat bahwa kuadrat jarak untuk 3 dimensi mengikuti teorema Phytagoras, . Bila suatu titik cahaya dipancarkan dari A pada saat dan mencapai titik C saat maka selang waktu yang dibutuhkan dari A ke C,
dan c didefinisikan sebagai
(3.2)
dengan mensubsitusikan harga ke persamaan (3.1), diperoleh
Persamaan (3.3) didefinisikan sebagai kuadrat jarak antara 2 titik yang ditinjau dalam ruang-waktu Minkowski 4 dimensi atau metrik ruang-waktu Minkowski. Jika sebelumnya dikatakan bahwa ruang Minkowski adalah ruang datar yang berarti memiliki geodesik berupa garis lurus dan komponen-komponen dalam nya semuanya berharga positif. Tapi pada persamaan (3.3) kuadrat jaraknya tidak sepenuhnya positif sebab terkait ruang-waktu Minkowski 4 dimensi harga dapat bernilai positif, negatif dan bahkan nol.
3.2.2 Geometri Ruang Lengkung
Sejalan dengan uraian (3.2.1), suatu ruang lengkung merupakan ruang dengan geodesik berupa garis lengkung. Untuk memudahkan memahaminya kita dapat membayangkan permukaan bumi dan dalam merumuskannya kita ambil kembali titik A dan C serta meninjaunya pada lintasan yang berbeda.
A M B
Gambar 3.5 Penggambaran pelengkungan yang terjadi sebagai fungsi waktu dan peninjauannya pada jarak antara titik A dan B dalam ruang lengkung.
Dari gambar 3.5, garis lurus garis lengkung , yang berarti definisi kuadrat jarak antara kedua jenis geodesik berbeda.
dimana
Dengan demikian,
(3.4)
Untuk mendefinisikan geometri pada ruang dengan dimensi lebih lanjut kita harus mendefinisikan bentuk metriknya. Bentuknya merupakan perluasan dari teorema Phytagoras dalam ruang 3 dimensi yang mengandung semua kemungkinan hasil kali ketiga koordinat dan .
Persamaan dinamakan dengan ruang Riemann yang memiliki metrik dalam ruang lengkung. Cara yang sama digunakan untuk merumuskan kembali bentuk ruang Riemann 4-dimensi dengan koordinat dan t.
(3.5)
dalam pembahasan dapat dianggap semu jika harga yang diberikan adalah nol (2.27).
dengan
(3.6)
Pada akhirnya, ruang Riemann semu dapat juga dianggap sebagai ruang Minkowski.
3.3 Medan Gravitasi Einstein dalam Ruang Waktu Minkowski 4 Dimensi
r
θ cahaya bintangSudut Defleksi Bintang semu
Bintang nyata Pengamat di
bumi
Matahari
Gambar 3.6 Sistem koordinat untuk pembelokan cahaya bintang oleh matahari
Sekarang persamaan dipilih sebagai bentuk geometri ruang-waktu Minkowski 4 dimensi dalam menentukan medan gravitasinya, yaitu
.
Gambar 3.7 Permukaan dari bola sebagai contoh dari ruang yang melengkung dan transformasi koordinatnya
Berdasarkan gambar (3.6) dan (3.7) kita dapat nyatakan persamaan tersebut dalam bentuk koordinat polar .
Solusinya komponen-komponen tensor metrik nya dengan sembarang fungsi tanpa mengganggu simetri bola. Pernyataan untuk kemudian dapat ditulis dengan
dengan dan λ hanya sebagai fungsi . Kita dapat membaca nilai dari persamaan (3.8) berdasarkan bentuk umum pada persamaan (3.5).
Adapun ekuivalen valensinya diberikan oleh:
Tensor metrik yang diperoleh pada persamaan (3.9) dapat dinyatakan dengan matriks.
kemudian harga masing-masing tensor metrik pada persamaan (3.8) dan (3.9) disubsitusikan ke dalam bentuk matriksnya (3.11).
dan diperoleh determinan matriknya sebesar
Determinan matriks tersebut selanjutnya digunakan untuk menentukan tensor konjugat dari tensor metrik nya. Jika diberikan persamaan (2.31) sebagai berikut,
(3.13)
Dengan menggunakan harga komponen-komponen tensor metrik dan tensor konjugat pada persamaan (3.9) dan (3.13), maka kita dapat menghitung solusi akhir permasalahan yang dinyatakan dalam bentuk simbol Christoffel jenis I dan II (2.32) dan (2.33) , yakni
(Simbol Christoffel Jenis I)
(Simbol Christoffel Jenis II)
Sebelumnya, perlu kita rumuskan nilai-nilai untuk dan ,
dengan kombinasi yang mungkin diuraikan sebagai berikut:
Dengan demikian total keseluruhan kombinasi yang mungkin adalah .
Sekarang akan dirumuskan persamaan-persamaan simbol Christoffel jenis I dan II untuk menyederhanakan perhitungan.
1. Simbol Christoffel jenis I: Jika
Jika Jika Jika
2. Simbol Christoffel jenis II:
Selanjutnya kita dapat menentukan harga-harga dan yang mungkin mempergunakan kombinasi yang diuraikan sebelumnya, disubstitusikan ke persamaan (3.14) dan (3.15).
Untuk Solusi Simbol Christoffel jenis I:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
34.
35.
36.
37.
38.
39.
40.
Untuk Solusi Simbol Christoffel Jenis II:
1.
2.
3.
4.
5.
6.
7.
8.
9.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
medan gravitasi tersebut di dalamnya, maka lintasan tempuh benda akan mengalami perubahan lintasan dan posisi dari keadaan semula.
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan hasil dan pembahasan yang telah diuraikan pada bab 3 sebelumnya, dapat diambil beberapa kesimpulan:
1. Teori relativitas umum melalui prinsip ekuivalensinya menyatakan bahwa terjadinya pembelokan cahaya bintang di sekitar matahari disebabkan oleh adanya efek gravitasi yang timbul karena keberadaan matahari yang memiliki massa massif yang melengkungkan ruang dan waktu yang dilalui oleh cahaya bintang yang melintas di sekitar matahari tersebut.
2. Medan gravitasi Einstein dapat ditentukan dalam ruang-waktu Minkowski 4 dimensi dengan menggunakan metrik Minkowski dengan sistem koordinat
.
3. Simbol Christoffel jenis I dan II diaplikasikan dalam menentukan medan gravitasi Einstein dalam ruang-waktu Minkowski 4 dimensi dan dengan formulasinya diketahui 64 total komponen simbol Christoffel yang terbentuk. Hasilnya 24 buah komponen yang menunjukkan nilai yang menyatakan harga-harga medan gravitasi Einstein dan sisanya diabaikan.
4.2 SARAN
DAFTAR PUSTAKA
Alonso, M and Finn E. J. 1992. Physics. USA: Addison-Wesley.
Anugraha, R. 2005. Pengantar Teori Relativitas dan Kosmologi. Yogyakarta: Gajah Mada University Press: Yogyakarta.
Arfken, G. B. dan Weber, H. J. 1995. Mathematical Methods for Physicists. Fourth Edition. San Diego: Academic Press.
Bergmann, P. G. 1961. Introduction to Theory of Relativity. New York: Prentice- Hall. Boas, M. L. 1983. Mathematical Methods in Physical Scienses. 2nd Edition. New
York: John Wiley & Sons.
Cresser, J. D. 2003. The Special Theory of Relativity. Lecture Notes. Sydney: Macquire University.
Dirac, P. A. M. 2008. Teori Relativitas Umum. Terjemahan Miftahul Hadi. USA: Florida State University.
Halliday, D. dan Resnick, R. 20011. Dasar-Dasar Fisika Versi Diperluas. Jilid I. Tangerang: Binarupa Aksara.
Hendri D.S. 2011. Teori relativitas Umum Einstein dan Aplikasinya pada Pembelokan
Cahaya Bintang di Sekitar Massa Massif. Skripsi. Medan: Universitas
Sumatera Utara.
Hermanto, Arief. 2003. Sebuah Diskusi tentang Hukum Newton Pertama dan Kedua. Jurnal Fisika Indonesia. 7(21). Hal. 35-42.
Izkar Hadiya. 2010. Fenomena Bintang Tampak Berkelip dan Kaitannya dengan
Posisinya di Jagat Raya Menurut Teori Relativitas Einstein. Medan:
Universitas Sumatera Utara.
Krane, Kenneth S. 1983. Modern Physics. USA: John Wiley & Sons.
Lass, Harry. 1950. Vector and Tensor Analysis. Tokyo: McGraw-Hill Kogakusha. Longair, M. S. 1987. Theoretical Concepts in Physics. Great Britain: Cambridge
University Press.
Mills, Robert. 1994. Space Time and Quanta: an Introduction to Contemporary Physics. USA: W. H. Freeman and Company.
Sharivop, R. A. 2004. Quick Introduction to Tensor Analysis. Rusia: Bashkir State University.
Spiegel, Murray R. 1991. Analisis Vektor dan Suatu Pengantar Analisis tensor. Terjemahan Hans J. Wospakrik. Jakarta : Erlangga.
Weinberg, Steven. 1972. Gravitation and Cosmology: Principles and Aplications of The General Theory of Relativity. USA: John Wiley & Sons.
Wospakrik, Hans J. 1978. Berkenalan dengan Teori Kerelatifan Umum Einstein & Biografi Albert Einstein. Bandung: ITB.
Wospakrik, Hans J. 1972. Dasar-Dasar Matematika untuk Fisika. Bandung: ITB. Young, Hugh D. and Freedman, Roger A. 2003. Fisika Universitas. Jilid 2. Edisi
Kesepuluh. Jakarta: Erlangga.
Zen, Freddy P. 2009. Unifikasi Interaksi di Alam Semesta: dari Einstein sampai Superstring. Jurnal Pengajaran Fisika. 1(3). Hal. 59-75.
LAMPIRAN A
Diagram Ruang-Waktu
Sebuah peristiwa adalah sesuatu yang terjadi di suatu titik tertentu dalam ruang dan pada suatu saat yang tertentu pula. Karena itu kita dapat menentukannya dengan empat bilangan koordinat. Koordinat ini dipilih sembarang, misalnya dengan menggunakan 3 koordinat ruang dan 1 koordinat waktu. Dan dalam relativitas, tidak ada perbedaan nyata antara koordinat ruang dan waktu. Membayangkan empat koordinat dari sebuah peristiwa dengan menentukan posisinya dalam ruang 4 dimensi yang disebut ruang-waktu akan sangat membantu yang digambarkan dengan diagram ruang-waktu.
Bila sebuah batu dilempar ke kolam yang berisi air, akan timbul gelombang yang menyebar ke sekelilingnya. Jika gelombang yang menyebar itu kita ganti dengan gelombang cahaya, dan kita mempunyai model 3 dimensi yang terdiri dari permukaan 2 dimensi ruang dan 1 dimensi waktu, maka cahaya yang menyebar dari suatu peristiwa akan membentuk kerucut 3 dimensi dalam ruang-waktu 4 dimensi.
Dalam geometri Euklidean, kita menggunakan teorema Phytagoras untuk mengukur
jarak . Dalam mekanika Newton, teorema Phytagoras
adalah invarian terhadap kerangka acuan tetapi tidak dalam teori relativitas Einstein. Penyelidikan oleh Minkowski memperbolehkan kita untuk menggunakan interval ruang-waktu dalam pengukuran jarak pada geometri Non-Euklidean dari teori relativitas. Dengan menggunakan interval ruang-waktu tersebut kita dapat mengklasifikasikan dua peristiwa yang terpisah dalam tiga cara, yaitu
1. Jika , peristiwanya disebut Timelike-separation. Dalam hal ini, ada satu pengamat inersial yang mengalami peristiwa kedua-duanya. Dan peristiwa tersebut terjadi di atas garis dunia (world line) dari pengamat dimana pengamatnya bergerak dengan kecepatan kurang dari kecepatan cahaya c. Untuk peristiwa dengan
Timelike-separation, separasi dalam ruangnya kurang dari separasi waktunya,
2. Jika , peristiwanya dikatakan Lightlike-separation (null). Dalam hal ini, peristiwa dari suatu sinar yang bersumber dari suatu cahaya berada di atas
worldline. Separasi dalam ruang dan separasi waktunya adalah sama.
Timelike
Gambar A.2 Diagram Ruang-Waktu
Dalam teori relativitas khusus, lintasan dari partikel-partikel materialnya dibatasi pada
Timelike-Worldlines, lintasan foton dibatasi Likelight-Worldlines dan Spacelike-Worldlines berada di luar batas keduanya. Spacelike-Worldlines berkorespondensi pada lintasan yang bergerak lebih cepat dari kecepatan cahaya c atau mundur dalam waktu. Seperti pada gambar diagram ruang-waktu, titik O merepresentasikan kehadiran beberapa pengamat. Pengamat dimasa depan berada di suatu tempat diantara dua peristiwa Lightlike-worldlines dengan sedangkan pengamat dimasa lalu berada di . Jika kita menambahkan 1 dimensi berupa sumbu yang tegak lurus sumbu x dan t, Lightlike-worldlines akan membentuk dua kerucut yang bertemu pada titik asal. Ini disebut dengan kerucut cahaya.