SIMULASI ALGORITMA RIVEST SHAMIR ADLEMAN (RSA) PADA
SHORT MESSAGE SERVICE (SMS) DENGAN PENGUJIAN
BILANGAN PRIMA MENGGUNAKAN LUCAS
LEHMER PRIMALITY TEST
SKRIPSI
IRFAN ANTONI SIREGAR
081401048
PROGRAM STUDI S1 ILMU KOMPUTER
DEPARTEMEN ILMU KOMPUTER
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA
SIMULASI ALGORITMA RIVEST SHAMIR ADLEMAN (RSA) PADA SHORT MESSAGE SERVICE (SMS) DENGAN PENGUJIAN
BILANGAN PRIMA MENGGUNAKAN LUCAS LEHMER PRIMALITY TEST
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Komputer
IRFAN ANTONI SIREGAR 081401048
PROGRAM STUDI S1 ILMU KOMPUTER DEPARTEMEN ILMU KOMPUTER
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : SIMULASI ALGORITMA RIVEST SHAMIR
ADLEMAN (RSA) PADA SHORT MESSAGE
SERVICE (SMS) DENGAN PENGUJIAN
BILANGAN PRIMA MENGGUNAKAN LUCAS LEHMER PRIMALITY TEST
Kategori : SKRIPSI
Nama : IRFAN ANTONI SIREGAR
Nomor Induk Mahasiswa : 081401048
Program Studi : S1 ILMU KOMPUTER
Departemen : ILMU KOMPUTER
Fakultas : ILMU KOMPUTER DAN TEKNOLOGI
INFORMASI (FASILKOM-TI) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juli 2012
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Amer Sharif, S.Si, M.Kom M. Andri B., ST., M.Comp.Sc.,MEM
NIP. - NIP. 197510082008011001
Diketahui/Disetujui oleh
Program Studi S1 Ilmu Komputer Ketua,
PERNYATAAN
SIMULASI ALGORITMA RIVEST SHAMIR ADLEMAN (RSA) PADA SHORT MESSAGE SERVICE (SMS) DENGAN PENGUJIAN
BILANGAN PRIMA MENGGUNAKAN LUCAS LEHMER PRIMALITY TEST
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juli 2012
PENGHARGAAN
Alhamdulillahirabbil’alamin, penulis mengucapkan puji syukur yang tiada hentinya kehadirat Allah SWT atas limpahan rahmat dan karunia-Nya serta segala nikmat iman, islam, pikiran dan pemahaman terhadap ilmu pengetahuan sehingga penulis dapat menyelesaikan skripsi ini dengan baik. Shalawat dan salam penulis ucapkan kepada Rasulullah Muhammad SAW beserta para sahabat dan keluarganya yang telah menjadi tauladan bagi penulis dalam menjalani kehidupan.
Pada kesempatan kali ini penulis ingin mengucapkan terima kasih kepada semua pihak yang telah membantu penulis selama pengerjaan skripsi ini, antara lain kepada :
1. Bapak Dr. Poltak Sihombing, M.Kom selaku Ketua Departemen Ilmu Komputer, Fakultas Ilmu komputer dan Teknologi Informasi, Universitas Sumatera Utara.
2. Bapak Mohammad Andri Budiman, S.T, M.Comp.Sc, MEM selaku pembimbing I atas bimbingan dan nasehatnya kepada penulis dalam menyelesaikan skripsi ini. Serta Bapak Amer Sharif, S.Si, M.Kom selaku pembimbing II atas bimbingan, nasehat dan motivasi kepada penulis selama penulisan skripsi ini..
3. Ibu Dian Rachmawati, S.Si, M.Kom selaku dosen penguji I dan Ibu Maya Silvi Lydia, B.Sc., M.Sc selaku dosen penguji II atas masukan dan nasehatnya kepada penulis dalam menyelesaikan skripsi ini.
4. Dekan dan Pembantu Dekan Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara.
5. Seluruh dosen-dosen Departemen Ilmu Komputer, Fakultas Ilmu Komputer dan Teknologi Informasi, Universitas Sumatera Utara yang telah membimbing dan mencurahkan ilmunya selama masa perkuliahan.
6. Seluruh pegawai administrasi Departemen Ilmu Komputer, Fakultas Ilmu Komputer dan Teknologi Informasi, Universitas Sumatera Utara yang telah membantu penulis dalam pengurusan administrasi selama perkuliahan, seminar dan sidang meja hijau.
8. Adinda Delisma Siregar, Syahrial Efendi Siregar dan Asril Ilyas Siregar atas segala dukungan, doa dan keceriaan yang diberikan kepada penulis untuk dapat menyelesaikan skripsi ini.
9. Jamilah Daulay, atas kesetiaan, semangat, doa, dukungan, dan motivasi yang diberikan kepada penulis.
10. Reycho Surahman Sinaga, Ahmad Ihsan, Ficky Vernandes Isman, Ahmad Royhan Putra, Tengku Surya Pramana, Eko Verdianto, Gustaf Prameswara, Siska Anggraini, Bilqis, Sadifa Asrofa, Brigson Haradonal Barus, Yeni Susanti, Angga Ricardo, Heni Mulyana, Bang Joko Irwansyah, Bang Fahreza Akbar dan Bang Suharsono atas dukungan, kebersamaan dan motivasi yang diberikan kepada penulis.
11. Keluarga besar S1 Ilmu Komputer, khususnya angkatan 2008 yang telah banyak memberi dukungan, masukan dan kerjasama yang baik.
12. Teman-teman kost Pak Galung, Bang Ardinal, Bang Bembeng, Bang Taufik, Bang Faisal, Bang Iman, Bang Kabul, Muhammad Syukur, Harmoko Hariwijaya, Birman Simatupang, Abdul Mustaqim, Amir Panjaitan, Zainuddin Siregar, Anton dan Yono.
13. Semua pihak yang terlibat langsung ataupun tidak langsung dalam membantu penyelesaian skripsi ini yang tidak dapat penulis ucapkan satu persatu.
Penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan, karena kesempurnaan hanyalah milik Allah semata. Oleh karena itu penulis menerima kritik dan saran dari semua pihak yang bersifat membangun dan menyempurnakan skripsi ini. Penulis berharap semoga skripsi ini bermanfaat bagi penulis sendiri pada khususnya dan pembaca pada umumnya.
Medan, Juli 2012
ABSTRAK
Salah satu fasilitas teknologi paling populer yang ada saat ini yang menyediakan layanan pertukaran informasi adalah Short Message Service (SMS). Perlu dilakukan pengamanan terhadap isi pesan SMS dengan menggunakan kriptografi, salah satu diantaranya adalah algoritma kunci public Rivest-Shamir-Adleman (RSA) ini. Algoritma RSA menggunakan bilangan prima untuk mengenkripsi isi pesan. Bilangan prima dibangkitkan dengan menggunakan metode bilangan mersenne. Dalam penelitian ini, pengecekan terhadap keprimaan suatu bilangan menggunakan Lucas Lehmer Primality Test. Sistem yang dihasilkan dapat menjaga melakukan enkripsi dan dekripsi terhadap pesan SMS menggunakan algoritma RSA.
SIMULATION OF RIVEST SHAMIR ADLEMAN (RSA) ALGORITHM IN SHORT MESSAGE SERVICE (SMS) WITH PRIME NUMBERS
TESTING USING LUCAS LEHMER PRIMALITY TEST
ABSTRACT
One of the most popular technology facilities that exist today that provide information exchange services are Short Message Service (SMS). It is necessary to secure the content of the message by means of cryptography, one of which is the public key algorithm Rivest-Shamir-Adleman (RSA), the. RSA uses primes algorithm to encrypt the message. The prime number used are generated using the mersenne method. The primality of the prime number obtained from the mersenne method is later checked using Lucas Lehmer primality test. The resulting system are able to encrypt and decrypt message using the RSA algorithm.
2.5 Lucas Lehmer Primality Test 23
Bab 3 Analisis dan Perancangan Sistem 3.1 Analisis 24
3.2.3.1 Flowchart Pembangkitan Pasangan Kunci RSA 52 3.2.3.2 Flowchart Proses Enkripsi Algoritma RSA 53 Bab 5 Kesimpulan dan Saran 5.1 Kesimpulan 76
5.2 Saran 76
Daftar Pustaka 77
DAFTAR TABEL
Contoh Pesan SMS Submit dalam Format PDU SCA dari PDU Pengiriman
Contoh Pesan SMS Deliver dalam Format PDU SCA dari PDU Penerimaan
Nomor SMS Center Operator Seluler Di Indonesia PDU-Type dari PDU Penerimaan
Originator Address (OA) Data Coding Scheme (DCS)
Nilai Service Center Time Stamp (SCTS) User Data pada PDU Penerimaan
Blok-Blok mi Dienkripsi Menjadi Blok-Blok ci Blok-Blok ci Didekripsi Menjadi Blok-Blok mi Konversi Karakter Plaintext ke Kode ASCII Desimal Proses Enkripsi dengan Algoritma RSA
Proses Pengubahan ke Bentuk Biner 16 Bit Hasil Pengubahan Biner 8 Bit ke Karakter ASCII
Konversi Hasil Dekompresi ke Desimal ASCII dan Biner 8 Bit Hasil Konversi Biner 16 Bit ke Ciphertext Berupa Desimal ASCII
Proses Dekripsi dengan algoritma RSA Konversi dari Hasil Dekripsi ke Plaintext
DAFTAR GAMBAR
Proses Pengiriman SMS antar sesama teknologi jaringan
Proses Pengiriman SMS antar teknologi jaringan yang berbeda
Proses Enkripsi dan Dekripsi sederhana Skema Kriptografi Kunci Simetri Skema Kriptografi Kunci Asimetri Pertukaran Kunci Diffie-Hellman
Skema Global Proses Enkripsi dan EncodingPDU Skema Global Proses DecodingPDU dan Dekripsi Rancangan pengiriman SMS
Rancangan penerimaan SMS
ABSTRAK
Salah satu fasilitas teknologi paling populer yang ada saat ini yang menyediakan layanan pertukaran informasi adalah Short Message Service (SMS). Perlu dilakukan pengamanan terhadap isi pesan SMS dengan menggunakan kriptografi, salah satu diantaranya adalah algoritma kunci public Rivest-Shamir-Adleman (RSA) ini. Algoritma RSA menggunakan bilangan prima untuk mengenkripsi isi pesan. Bilangan prima dibangkitkan dengan menggunakan metode bilangan mersenne. Dalam penelitian ini, pengecekan terhadap keprimaan suatu bilangan menggunakan Lucas Lehmer Primality Test. Sistem yang dihasilkan dapat menjaga melakukan enkripsi dan dekripsi terhadap pesan SMS menggunakan algoritma RSA.
SIMULATION OF RIVEST SHAMIR ADLEMAN (RSA) ALGORITHM IN SHORT MESSAGE SERVICE (SMS) WITH PRIME NUMBERS
TESTING USING LUCAS LEHMER PRIMALITY TEST
ABSTRACT
One of the most popular technology facilities that exist today that provide information exchange services are Short Message Service (SMS). It is necessary to secure the content of the message by means of cryptography, one of which is the public key algorithm Rivest-Shamir-Adleman (RSA), the. RSA uses primes algorithm to encrypt the message. The prime number used are generated using the mersenne method. The primality of the prime number obtained from the mersenne method is later checked using Lucas Lehmer primality test. The resulting system are able to encrypt and decrypt message using the RSA algorithm.
BAB 1
PENDAHULUAN
1.1 Latar Belakang Masalah
Pada saat ini komunikasi secara langsung antara orang dengan orang lainnya semakin sedikit. Ini disebabkan oleh kesibukan yang memenuhi seluruh kehidupan masyarakat. Oleh karena itu handphone yang merupakan salah satu alat komunikasi yang cepat dan dapat digunakan dimana saja menjadi andalan. Handphone dapat digunakan untuk berbicara antara satu orang dengan orang lain serta dapat berkomunikasi dengan saling mengirim pesan singkat dengan fasilitas Short Message Service (SMS). SMS merupakan sebuah fasilitas digital sederhana yang mengizinkan handphone untuk menerima dan atau mengirim pesan teks.
Namun dari berbagai fasilitas itu terdapat hal penting yang harus diperhatikan yaitu masalah keamanan pada handphone itu sendiri. Masalah keamanan ini sering kali kurang mendapat perhatian dari para pemilik dan pengelola sistem informasi. Seringkali masalah keamanan berada di urutan kedua, atau bahkan di urutan terakhir dalam daftar hal-hal yang dianggap penting. Apabila menggangu performansi dari sistem, seringkali keamanan dikurangi atau ditiadakan. Sehingga sering terjadi penyadapan informasi baik saat berbicara menggunakan handphone maupun pada saat mengirim pesan SMS.
data-data yang tidak terlalu penting, sehingga apabila publik mengetahui data-data tersebut, pemilik data tidak terlalu dirugikan. Tetapi apabila pemilik data adalah pihak militer atau pemerintah, keamanan dalam pertukaran informasi menjadi sangat penting karena data yang mereka kirim kebanyakan adalah data rahasia yang tidak boleh diketahui oleh publik.
Kriptografi adalah salah satu teknik yang digunakan untuk meningkatkan aspek keamanan suatu informasi. Kriptografi merupakan kajian ilmu dan seni untuk menjaga suatu pesan atau informasi agar data tersebut aman. Kriptografi mendukung kebutuhan dua aspek keamanan informasi yaitu secrecy (perlindungan terhadap kerahasiaan data informasi) dan authentication (perlindungan terhadap pemalsuan dan pengubahan informasi yang tidak diinginkan).
Salah satu metode dalam kriptografi yang dapat digunakan untuk menjamin keamanan data adalah dengan metode RSA. Algoritma ini pertama kali dipublikasikan di tahun 1977 oleh Ron Rivest, Adi Shamir, dan Leonard Adleman dari Massachusetts Institute of Technology (MIT). Nama RSA sendiri adalah singkatan dari nama belakang mereka bertiga.
Oleh karena itu penulis tertarik untuk membuat penelitian tentang bagaimana melindungi data pada SMS agar tidak dapat diketahui orang lain. Untuk itulah penulis mengambil judul “Simulasi Algoritma Rivest-Shamir-Adleman (RSA) Pada Short Message Service (SMS) Dengan Pengujian Bilangan Prima Menggunakan Lucas Lehmer Primality Test”.
1.2 Rumusan Masalah
1.3 Batasan Masalah
Batasan masalah dalam skripisi ini adalah sebagai berikut:
1. Penelitian ini hanya membahas implementasi algoritma RSA dengan pengujian bilangan prima menggunakan Lucas Lehmer Primality Test dan tidak membandingkannya dengan algoritma lain.
2. Bilangan prima yang digunakan dalam algoritma RSA adalah bilangan prima mersenne dan bilangan prima yang menghasilkan bilangan mersenne.
3. Program yang digunakan untuk membangun aplikasi dalam penelitian adalah teknologi Java Micro Edition.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah sebagai berikut:
1. Mengetahui proses pengenkripsian dan pendekripsian data SMS dengan menggunakan algoritma RSA.
2. Menghasilkan aplikasi yang dapat mengamankan isi SMS dengan mengimplementasikan algoritma kriptografi RSA.
1.5 Manfaat Penelitian
Manfaat penelitian ini adalah untuk memproteksi isi pesan jika terjadi penyadapan. Dengan adanya proses pengkodean terhadap isi pesan SMS maka hal ini dapat memproteksi isi pesan SMS ketika terjadi penyadapan.
1.6 Metode Penelitian
Tahapan penelitian yang dilakukan adalah sebagai berikut:
Pada tahap ini penulis melakukan pembelajaran pada sumber-sumber referensi yang berkaitan dengan penelitian. Sumber referensi dapat diperoleh melalui buku, artikel, jurnal, makalah, maupun dari internet.
2. Perancangan Sistem
Tahap ini merupakan perancangan antar muka dan perancangan sistem dengan mengunakan algoritma RSA pada isi pesan SMS.
3. Implementasi Sistem
Pada tahap ini dilakukan pengimplementasian sistem algoritma RSA pada SMS ke dalam bahasa pemrograman Java Micro Edition (Java ME).
4. Pengujian Sistem
Pada tahap ini dilakukan pengujian terhadap aplikasi yang telah dibangun apakah aplikasi dapat berjalan sesuai dengan teori dan tujuan dari penelitian .
5. Pembuatan Laporan
Pembuatan laporan bertujuan untuk dijadikan sebagai dokumentasi hasil penelitian dalam bentuk skripsi.
1.7 Sistematika Penulisan
BAB 1 : PENDAHULUAN
Bab ini menjelaskan mengenai latar belakang pemilihan judul skripsi “Implementasi Algoritma Rivest-Shamir-Adleman (RSA) Pada Short Message Service (SMS) Dengan Pengujian Bilangan Prima Menggunakan Lucas Lehmer Primality Test”, perumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian, metodologi, dan sistematika penulisan.
BAB 2 : TINJAUAN PUSTAKA
Bab ini membahas teori-teori yang berkaitan dengan Short Message Service (SMS), kriptografi, algoritma Rivest-Shamir-Adleman (RSA) dan metode Lucas Lehmer Primality Test.
BAB 3 : ANALISIS DAN PERANCANGAN SISTEM
Bab ini menjelaskan tentang analisis kebutuhan perangkat lunak dan perancangan aplikasi Short Message Service (SMS) menggunakan algoritma Rivest-Shamir-Adleman (RSA).
BAB 4 : IMPLEMENTASI PROGRAM
Bab ini membahas tentang implementasi dari perangkat lunak dan mengulas analisis hasil pengujian yang telah dilakukan terhadap aplikasi Short Message Service (SMS).
BAB 5 : PENUTUP
BAB 2
TINJAUAN PUSTAKA
2.1 Short Message Service (SMS)
Short Message Service (SMS) adalah salah satu tipe Instant Messaging (IM) yang memungkinkan user untuk bertukar pesan singkat kapanpun, walaupun user sedang melakukan panggilan data atau suara. Kata “short” yang berarti singkat pada SMS merujuk pada ukuran maksimal dari suatu pesan teks yaitu 160 karakter pada alfabet latin. Untuk alfabet lainnya, misalnya alfabet atau kanji China, ukuran maksimum SMS-nya adalah 70 karakter [11].
2.1.1 Sejarah SMS
2.1.2 Arsitektur SMS
SMS dimaksudkan untuk menjadi alat pertukaran informasi antara dua mobile. Elemen-elemen utama pada arsitektur SMS terdiri dari Short Message Entity (SME), Short Message Service Center (SMSC) dan Email Gateway.
2.1.2.1 Short Message Entity (SME)
Short Message Entity (SME) adalah elemen yang dapat mengirim atau menerima pesan singkat. SME dapat berupa software aplikasi pada mobile handset, dapat juga berupa server yang terkoneksi dengan SMSC secara langsung atau melaui gateway.
2.1.2.2 Short Message Service Center (SMSC)
Short Message Service Center (SMSC) memegang peran kunci pada arsitektur SMS. SMSC adalah kombinasi perangkat lunak dan perangkat keras yang bertanggung jawab memperkuat, menyimpan dan meneruskan pesan pendek antar SME dan piranti bergerak (mobile phone). Secara fisik SMSC dapat berwujud sebuah PC biasa yang mempunyai interkonektivitas dengan jaringan GMS.
2.1.2.3 Email Gateway
2.1.3 Cara Kerja SMS
Ketika pengirim mengirim SMS, maka pesan terlebih dahulu dikirim ke Mobile Switching Center (MSC) melalui jaringan seluler yang tersedia meliputi tower Base Transceiver Station (BTS), diteruskan ke Base Station Controller (BSC), kemudian sampai ke MSC. Dari MSC, SMS diteruskan ke SMSC untuk disimpan. SMSC akan memeriksa melalui Home Location Register (HLR) untuk mengetahui apakah handpone tujuan sedang aktif. Jika handpone tujuan aktif maka pesan disampaikan MSC melalui jaringan yang sedang menghandle penerima (BSC dan BTS). Jika handpone sedang tidak aktif maka pesan akan disimpan di SMSC, menunggu pemberitahuan MSC bahwa handpone sudah aktif kembali dan seterusnya SMS dikirim dengan batas maksimum waktu tunggu yaitu validity period dari pesan SMS itu sendiri.
Dengan teknologi GSM/GPRS, operator jaringan telepon dapat dengan mudahnya melakukan pertukaran pesan dari jaringan yang berbeda. Pemetaan sinyal dilakukan di antara dua jaringan telepon. dalam pemetaan dua jaringan ini, SMSC dari pembuat SME mengolah HLR jaringan tujuan untuk mendapatkan informasi mengenai penerima dan mengirimnya langsung. Dalam contoh ini, SMSC penerima pesan tidak berpengaruh. Ilustrasi contoh tersebut pada gambar 2.1
Gambar 2.1 Proses Pengiriman SMS antar sesama teknologi jaringan
telepon dengan menggunakan protokol pertukaran. Seperti yang di ilustrasikan pada gambar 2.2
Gambar 2.2 Proses Pengiriman SMS antar teknologi jaringan yang berbeda
Dalam pengiriman antara dua teknologi jaringan yang berbeda terdapat beberapa tahap. Pertama, pesan dibuat dan dikirim oleh SME ke SMSC pengirim. Selanjutnya SMSC pengirim meneruskan pesan melalui SMSC penerima dan SMSC penerima mengirimkan pesan ke SME penerima. Jika status report diminta oleh pengirim pesan, maka SMSC penerima membuat status report dan mengirimkanya ke SME pengirim.
2.1.4 Sistem Kerja SMS
Semua SMS yang dikirim atau diterima sebenarnya telah mengalami pengolahan sebelumnya. Kumpulan pesan yang berupa teks telah mengalami proses yang cukup rumit, tidak semudah ketika mengetik dan mengirim SMS tersebut. Seperti halnya teks yang kita ketikkan dirubah ke dalam format PDU (Protocol Data Unit ) dimana pada tahap ini teks diolah sedemikian rupa sehingga akhirnya dapat diterima dan di baca oleh penerima.
2.1.5 Protocol Data Unit (PDU)
dengan SMS yang diterima dari SMS Center. Maksud dari bilangan heksa desimal adalah bilangan yang terdiri atas 0, 1, 2 , 3, 4, 5 ,6 ,7 ,8 ,9 ,A ,B ,C ,D ,E ,F.
Data di PDU mempunyai format data oktet yaitu format data 8 bit. Adapun karakter yang dipakai mempunyai format data 7 bit (septet). Untuk menterjemahkan karakter menjadi data PDU supaya bisa dimengerti, maka dilakukan proses konversi yaitu dari data 7 bit (format septet) ke data 8 bit (format oktet).
2.2 Kriptografi
Kriptografi dapat diartikan sebagai ilmu atau seni untuk menjaga keamanan pesan. Ketika suatu pesan dikirim dari suatu tempat ke tempat lain, isi pesan tersebut mungkin dapat disadap oleh pihak lain yang tidak berhak untuk mengetahui isi pesan tersebut. Untuk menjaga pesan, maka pesan tersebut dapat diubah menjadi suatu kode yang tidak dapat dimengerti oleh pihak lain.
2.2.1 Definisi Kriptografi
Kriptografi berasal dari bahasa Yunani, crypto dan graphia. Crypto berarti secret (rahasia) dan graphia berarti writing (tulisan). Menurut terminologinya kriptografi adalah ilmu dan seni untuk menjaga keamanan pesan ketika dikirim dari suatu tempat ke tempat yang lain [1]. Selain definisi tersebut, terdapat pula definisi yang menjelaskan bahwa kriptografi adalah ilmu yang mempelajari teknik-teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan, integritas data, serta otentikasi [6].
dikembalikan lagi menjadi informasi awal (plaintext) melalui proses dekripsi. Proses kriptografi secara umum dapat dilihat pada Gambar 2.3.
.
Gambar 2.3 Proses Enkripsi dan Dekripsi sederhana
2.2.2 Sejarah Kriptografi
Kriptografi mempunyai sejarah yang sangat menarik dan panjang sejalan dengan sejarah kehidupan manusia. Kriptografi sudah digunakan 4000 tahun yang lalu yang diperkenalkan oleh orang-orang Mesir untuk mengirim pesan ke pasukan militer yang berada di lapangan dan supaya pesan tersebut tidak terbaca oleh pihak musuh walaupun kurir pembawa pesan tersebut tertangkap oleh musuh [10].
Informasi lengkap mengenai sejarah kriptografi dapat ditemukan di dalam buku David Kahn yang berjudul The Codebreakers. Buku yang tebalnya 1000 halaman ini menulis secara rinci sejarah kriptografi mulai dari penggunaan kriptografi oleh bangsa Mesir 4000 tahun yang lalu (berupa hieroglyph yang tidak standard pada piramid) hingga penggunaan kriptografi pada abad ke-20.
2.2.3 Tujuan Kriptografi
Secara umum tujuan kriptografi diciptakan adalah untuk merahasiakan suatu pesan agar tidak bisa dibaca oleh pihak yang tidak absah. Berpedoman dari tujuan umum tersebut, terdapat empat tujuan mendasar kriptografi digunakan dalam bidang keamanan informasi, yaitu:
1. Confidentiality (Kerahasiaan), yaitu layanan yang digunakan untuk menjaga isi informasi dari siapapun kecuali yang memiliki otoritas atau kunci rahasia untuk membuka/mengupas informasi yang telah disandi. Biasanya dilakukan dengan cara membuat suatu algoritma matematis yang mampu mengubah data hingga menjadi sulit untuk dibaca dan dipahami.
2. Data Integrity (Integritas Data), yaitu layanan yang mampu mengenali atau mendeteksi adanya manipulasi (penghapusan, pengubahan atau penambahan) data yang tidak sah (oleh pihak lain).
3. Authentication (Otentikasi), yaitu layanan yang berhubungan dengan identifikasi/ pengenalan, baik secara kesatuan sistem maupun informasi itu sendiri. Dua pihak yang saling berkomunikasi harus saling memperkenalkan diri. Informasi yang dikirimkan melalui kanal harus diotentikasi keaslian, isi datanya, waktu pengiriman, dan lain-lain.
4. Non-repudiation (Nirpenyangkalan), yaitu layanan yang dapat mencegah terjadinya penyangkalan aksi terhadap pengiriman atau terciptanya suatu informasi oleh yang mengirimkan/membuat.
2.2.4 Komponen Cipher
Merupakan hal yang sangat penting dalam kriptografi, merupakan pengamanan data yang dikirimkan agar terjaga kerahasiaannya. Pesan asli disebut plaintext, yang diubah menjadi kode-kode yang tidak dimengerti. Enkripsi bisa diartikan dengan cipher atau kode. Sama halnya dengan kita tidak mengerti akan sebuah kata maka kita akan melihatnya di dalam kamus atau daftar istilah. Beda halnya dengan enkripsi, untuk mengubah teks-asli ke bentuk teks-kode kita menggunakan algoritma yang dapat mengkodekan data yang kita inginkan.
2. Dekripsi.
Merupakan kebalikan dari enkripsi. Pesan yang telah dienkripsi dikembalikan ke bentuk asalnya (teks-asli), disebut dengan dekripsi pesan. Algoritma yang digunakan untuk dekripsi tertentu berbeda dengan algoritma yang digunakan untuk dekripsi.
3. Kunci.
Yang dimaksud di sini adalah kunci yang dipakai untuk melakukan enkripsi dan dekripsi. Kunci terbagi menjadi dua bagian, kunci rahasia (private key) dan kunci umum (public key).
Algoritma kriptografi dibagi menjadi dua bagian berdasarkan kunci yang dipakai: 1. Algoritma Kunci Simetri (menggunakan satu kunci untuk enkripsi dan dekripsinya),
2. Algoritma Kunci Asimetri (menggunakan kunci yang berbeda untuk enkripsi dan dekripsi),
2.2.4.1 Algoritma Kunci Simetri
Contoh algoritma kunci simetris yang terkenal adalah DES (Data Encryption Standard) dan RC-4.
Gambar 2.4 Skema Kriptografi Kunci Simetri
Dua kategori yang termasuk pada algoritma simetris ini adalah algoritma block cipher dan stream cipher. Algoritma block cipher adalah algoritma yang masukan dan keluarannya berupa satu block, dan setiap blocknya terdiri dari banyak bit. Beberapa mode operasi enkripsi block cipher diantaranya Data Encryption Standard ( DES ), Advanced Encrytion Standard (AES), dan Blowfish.
Sedangkan stream cipher ( cipher aliran ) adalah cipher yang berasal dari hasil XOR antara bit plaintext dengan setiap bit kuncinya. Stream cipher sangat rawan terhadap attack pembalikan bit. Beberapa model algoritma stream cipher antara lain adalah algoritma One Time Pad ( OTP ), algoritma Rivest Code 4 (RC 4), algoritma IDEA, algoritma Blowfish, dan algoritma RC2.
2.2.4.2 Algoritma Kunci Asimetri
enkrispsi. Karena sifat salah satu kuncinya publik maka kriptografi kunci asimetri sering disebut juga kriptografi algoritma kunci publik.
Distribusi kunci pada kritografi kunci asimetri sangat mudah, karena kunci enkrispsi bersifat publik maka distribusi kunci dapat dilakukan di jalur mana saja bahkan jalur yang ingin diamankan sekalipun.
Gambar 2.5 Skema Kriptografi Kunci Asimetri
Kriptografi ini bukan tanpa celah, karena kunci enkripsinya yang bersifat publik maka kriptografi ini relatif lemah terhadap serangan cryptanalist terutama serangan chosen-plaintext. Selain itu, kriptografi ini memiliki kelemahan lain dalam hal kecepatan. Kriptografi asimetri 1000 kali lebih lamban dibandingkan kriptografi simetri. Adapun keunggulan dari kriptografi kunci asimetri selain distribusi kunci yang sangat mudah adalah manajemen kunci yang tidak rumit karena tiap komunikan hanya butuh sepasang kunci (enkripsi dan dekripsi), sehingga dapat dituliskan untuk n komunikan yang berkomunikasi hanya dibutuhkan n pasang kunci.
2.2.5 Jenis-Jenis Serangan Terhadap Kriptografi
Serangan terhadap sistem kriptografi dapat dikelompokkan dengan beberapa cara. Berdasarkan keterlibatan penyerang dalam komunikasi, serangan dapat dibagi atas dua macam, yaitu serangan aktif dan serangan pasif.
1. Serangan aktif
Pada jenis serangan ini, penyerang mengintervensi komunikasi dan ikut mempengaruhi sistem untuk keuntungan dirinya. Misalnya penyerang mengubah aliran pesan seperti menghapus sebagian ciphertext, mengubah ciphertext, menyisipkan potongan ciphertext palsu, me-replay pesan lama, mengubah informasi yang tersimpan, dan sebagainya.
2. Serangan pasif
Pada jenis serangan ini, penyerang tidak terlibat dalam komunikasi antara pengirim dan penerima, namun penyerang menyadap semua pertukaran pesan antara kedua entitas tersebut. Tujuannya adalah untuk mendapatkan sebanyak mungkin informasi yang digunakan untuk kriptanalisis. Beberapa metode penyadapan data antara lain:
a) Wiretapping; penyadap mencegat data yang ditransmisikan pada saluran komunikasi dengan menggunakan sambungan perangkat keras.
b) Electromagnetic eavesdropping: penyadap mencegat data yang ditransmisikan melalui saluran wireless, misalnya radio dan microwave.
c) Acoustic eavesdropping: menangkap gelombang suara yang dihasilkan oleh suara manusia.
Berdasarkan banyaknya informasi yang diketahui oleh kriptanalis, dikelompokkan menjadi 5 jenis:
1. Ciphertext-only attack
semuanya dienkripsi dengan algoritma yang sama. Tugas kriptanalis adalah menemukan plaintext sebanyak mungkin dari ciphertext tersebut atau menemukan kunci yang digunakan untuk mendekripsi.
2. Known-plaintext attack
Ini adalah jenis serangan dimana kriptanalis memiliki pasangan plaintext dan ciphertext yang berkoresponden. Plaintext mungkin diperoleh dengan mempelajari karakteristik pesan. Beberapa pesan yang formatnya terstruktur membuka peluang kepada kriptanalis untuk menerka plaintext dari ciphertext yang bersesuaian.
3. Chosen-plaintext attack
Serangan jenis ini lebih hebat dari pada known-plaintext attack, karena kriptanalis dapat memilih plaintext yang dimilikinya untuk dienkripsikan, yaitu plaintext yang lebih mengarahkan penemuan kunci.
4. Chosen-ciphertext attack
Ini adalah jenis serangan dimana kriptanalis memilih ciphertext untuk didekripsikan dan memiliki akses ke plaintext hasil dekripsi (misalnya terhadap mesin elektronik yang melakukan dekripsi secara otomatis). Jenis serangan ini bisaanya dipakai pada sistem kriptografi.
5. Chosen-text attack
Ini adalah jenis serangan yang merupakan kombinasi chosen-plaintext dan chosen-ciphertext attack.
Berdasarkan teknik yang digunakan dalam menemukan kunci, dibagi atas:
1. Exhaustive attack atau brute force attack
Ini adalah serangan untuk mengungkap plaintext atau kunci dengan mencoba semua kemungkinan kunci. Diasumsikan kriptanalis mengetahui algoritma kriptografi yang digunakan oleh pengirim pesan. Selain itu kriptanalis memiliki sejumlah ciphertext dan/ atau plaintext yang bersesuaian.
Pada jenis serangan ini, kriptanalis tidak mencoba-coba semua kemungkinan kunci tetapi menganalisis kelemahan algoritma kriptografi untuk mengurangi kemungkinan kunci yang tidak mungkin ada. Diasumsikan kriptanalis mengetahui algoritma kriptografi yang digunakan oleh pengirim pesan. Analisis dapat menggunakan pendekatan matematik dan statistik dalam rangka menemukan kunci. Secara statistik misalnya dengan menggunakan analisis frekuensi, sedangkan secara matematik dengan memecahkan persamaan-persamaan matematika (yang diperoleh dari defenisi suatu algoritma kriptografi) yang mengandung peubah-peubah yang merepresentasikan plaintext atau kunci.
2.3 Algoritma Diffie-Hellman
Sampai akhir tahun 1975, hanya ada algoritma kunci simetris. Karena kriptografi simetris menggunakan kunci yang sama untuk enkripsi dan dekripsi, maka hal ini mengimplikasikan dua pihak yang berkomunikasi saling mempercayai. Satu masalah kritis di dalam kriptografi kunci simetris adalah cara mendistribusikan kunci karena dianggap tidak aman. Masalah ini dipecahkan oleh Whitfield Diffie dan Martin Hellman dengan mengusulkan kriptografi nirsimetris (asymmetris cryptosystem) yang memungkinkan pengguna berkomunikasi secara aman tanpa perlu berbagi kunci rahasia. Algoritma Diffie-Hellman atau dinamakan juga protokol Diffie-Hellman berguna untuk mempertukarkan kunci sesi (kunci rahasia untuk komunikasi dengan kriptografi simetris) antara dua orang atau lebih. Dan algoritma ini menjadi awal mula munculnya algoritma kriptografi RSA [10].
2.3.1 Pertukaran Kunci
Langkah-langkah dalam pertukaran kunci adalah sebagai berikut:
1. Irfan membangkitkan bilangant bulat acak dengan besar x dan mengirim hasil perhitungan X = gx mod n kepada Antoni.
2. Antoni membangkitkan bilangant bulat acak dengan besar x dan mengirim hasil perhitungan Y = gy mod n kepada Irfan.
3. Irfan menghitung K = Yx mod n 4. Antoni menghitung K’ = Xy mod n
Jika perhitungan dilakukan dengan benar, maka K akan bernilai sama dengan K’ yang berarti kunci simetris sudah berhasil diterima oleh kedua belah pihak. Baik K dan K’ sama dengan gxy mod n. Regar yang menyadap pembicaraan antara Irfan dan Antoni tidak dapat menghitung K. Dia hanya memiliki informasi n, g, X dan Y, tetapi dia tidak mempunyai informasi nilai x dan y. Untuk mengetahui nilai x atau y, dia perlu melakukan perhitungan logaritma diskrit yang sangat sulit dikerjakan.
Gambar berikut 2.6 memperlihatkan diagram algoritma pertukaran kunci Diffie-Hellman.
Gambar 2.6 Pertukaran Kunci Diffie-Hellman
Misalkan Irfan dan Antoni menyepakati n = 97 dan g = 5 (g < n). Irfan dan Antoni melakukan pertukaran kunci simetri sebagai berikut:
1. Irfan memilih x = 36 dan menghitung Bangkitkan x
Hitung X = gx mod n
Hitung K = Yx mod n
Bangkitkan y
Hitung Y = gy mod n
X = gx mod n = 536 mod 97 = 50 Irfan mengirimkan X kepada Antoni. 2. Antoni memilih y = 58 dan menghitung
Y = gy mod n = 558 mod 97 = 44 Antoni mengirimkan X kepada Irfan. 3. Irfan menghitung kunci simetris K,
K = Yx mod n = 4436 mod 97 = 75 4. Antoni menghitung kunci simetris K’,
K’ = Xy mod n = 5058 mod 97 = 75
Jadi, Irfan dan Antoni sudah mempunyai kunci sesi yang sama, yaitu K = 75. Kunci siap digunakan untuk melakukan komunikasi dengan kriptografi simetris.
2.4 Algoritma RivestShamirAdleman (RSA)
RSA merupakan salah satu algoritma yang paling maju dalam bidang kriptografi. RSA masih digunakan secara luas dalam berbagai bidang kriptografi dan dipercaya dapat mengamankan kerahasiaan data dengan menggunakan kunci yang cukup panjang. Akan tetapi besarnya bilangan yang digunakan mengakibatkan lambatnya operasi yang melibatkan algoritma RSA ini [7].
2.4.1 Sejarah RSA
RSA adalah salah satu contoh kriptografi yang menerapkan konsep public key. Algoritma ini pertama kali dipublikasikan di tahun 1977 oleh Ron Rivest, Adi Shamir, dan Leonard Adleman dari Massachusetts Institute of Technology (MIT). Nama RSA sendiri adalah singkatan dari nama belakang mereka bertiga [7].
pada tahun 1997 karena merupakan proyek rahasia. Walau begitu algoritma yang dikembangkan Rivest, Shamir, dan Adleman tidak berhubungan dengan pekerjaan Cocks.
Algoritma RSA dipatenkan oleh Massachusetts Institute of Technology pada ta Semenjak Algoritma RSA dipublikasikan sebagai aplikasi paten, regulasi di sebagian besar negara-negara lain tidak memungkinkan penggunaan paten.
2.4.2 Algoritma RSA dalam Proses Enkripsi dan Dekripsi
Pada algoritma RSA terdapat 3 langkah utama yaitu key generation (pembangkitan kunci), enkripsi, dan dekripsi.
Kunci pada RSA mencakup dua buah kunci, yaitu public key dan private key. Public key digunakan untuk melakukan enkripsi, dan dapat diketahui oleh orang lain. Sedangkan private key tetap dirahasiakan dan digunakan untuk melakukan dekripsi. Pembangkitan kunci atau key generation dari RSA adalah sebagai berikut :
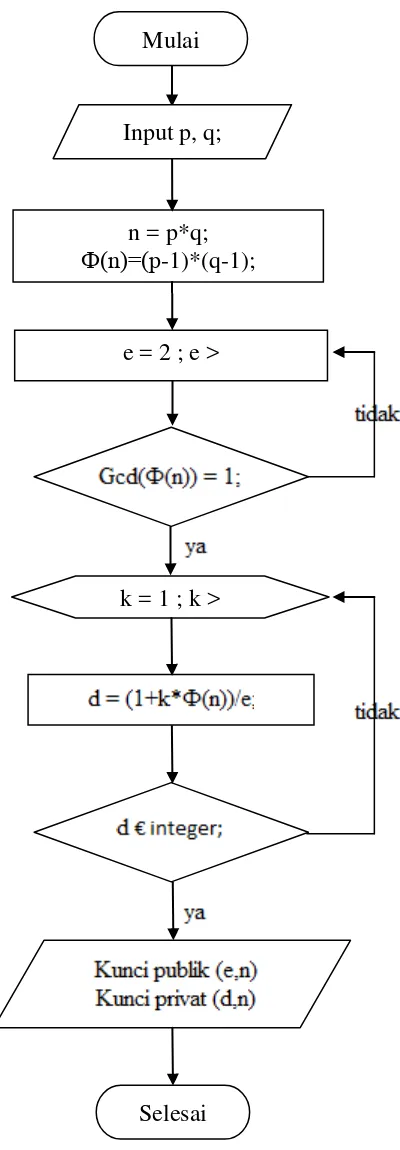
1. Pilih dua buah bilangan prima sembarang p dan q. Jaga kerahasiaan p dan q ini.
2. Hitung n = p * q. Besaran n ini tidak perlu dirahasiakan.
3. Hitung Ф(n) = (p-1) * (q-1). Sekali Ф(n)telah dihitung, p dan q dapat dihapus untuk mencegah diketahuinya oleh pihak lain.
4. Pilih sebuah bilangan bulat untuk kunci publik, sebut namanya e, yang relatif prima terhadap Ф(n)(relatif prima berarti GCD(e, Ф(n)) = 1 dengan syarat e ≠ (p-1), e ≠ (q-1), dan e < n.
5. Kunci publik (Public Key) = (n,e).
6. Hitung kunci privat (d) dengan kekongruenan e*d ≡1 (mod Ф(n)).
(1+k*Ф(n))/e sehingga nilai-nilai k dapat diselesaikan sampai didapat sebuah nilai k dan d adalah anggota bilangan bulat.
Proses enkripsi dapat dilakukan dengan :
Sedangkan proses dekripsi dilakukan dengan :
Dengan mencoba nilai k = 1, 2, 3, ..., diperoleh nilai d yang bulat. Nilai itu yang akan dipakai sebagai kunci pribadi untuk dekripsi pesan.
Dalam implementasi sebenarnya, nilai p dan q diharapkan sangat besar sekali (misalnya 100 digit) agar pekerjaan memfaktorkan n menjadi faktor primanya menjadi sangat sukar, sehingga lebih susah untuk ditembus.
2.4.3 Keamanan dan Kecepatan RSA
Kekuatan algoritma RSA terletak pada tingkat kesulitan dalam memfaktorkan bilangan menjadi faktor primanya, dalam hal ini memfaktorkan n menjadi p dan q. Masing-masing p dan q besarnya dapat mencapai 100 sampai 200 digit dan bahkan lebih. Sekali n berhasil difaktorkan, maka menghitung nilai m adalah perkara mudah. Selanjutnya, walau nilai e diumumkan, perhitungan kunci d tidaklah mudah pula karena nilai m yang tidak diketahui [10].
RSA memiliki modulus 512-bit dengan kecepatan 64 kilobit per detik. Saat ini chip sedang direncanakan akan mendekati 1 megabit per detik menggunakan modulus 512-bit. Dalam perangkat keras, kecepatan RSA sekitar 1000 kali lebih lambat dibandingkan dengan DES. Sedangkan dalam perangkat lunak, kecepatan DES adalah sekitar 100 kali lebih cepat dari kecepatan RSA [13].
Ci = mie mod n
2.5 Lucas Lehmer Primality Test
Di dalam kriptografi, bilangan prima memiliki peranan yang sangat penting. Beberapa algoritma kriptografi, seperti RSA, menggantungkan kekuatannya pada sulitnya faktorisasi bilangan besar. Oleh karena itu, penggunaan bilangan prima yang besar menjadi sangat penting. Sebenarnya ada banyak cara untuk mengetahui suatu bilangan itu prima atau bukan, dan salah satu yang bisa digunakan adalah Lucas-Lehmer primality test.
Metode ini pertama kali ditemukan oleh dua orang ilmuan yaitu Francois Edouard Lucas Anatole berkebangsaan Perancis dan Derrick Henry Lehmer berkebangsaan Amerika Serikat.
Lucas Lehmer Primality Test bekerja dengan memanfaatkan bilangan Mersenne. Rumus bilangan Mersenne yaitu Mp = 2p – 1. Rumus ini ditemukan oleh Marin Mersenne seorang berkebangsaan Perancis yang hidup antara tahun 1588-1648. Untuk memperoleh bilangan Mersenne (Mp) adalah prima, maka p juga haruslah sebuah bilangan prima. Akan tetapi Mp belum tentu prima meskipun p adalah prima. Bilangan Mersenne biasanya digunakan untuk mencari bilangan prima yang sangat besar [7].
Berikut ini merupakan langkah-langkah untuk mengetahui keprimaan suatu bilangan dengan Lucas-Lehmer primality test.
1. Masukkan bilangan Mersenne Mp = 2p – 1 dimana p ≥ 3
2. Hitung Sj = S2j-1 – 2 mod Mp dengan S1 = 4 untuk j = 2,3,…,n-1
BAB 3
ANALISIS DAN PERANCANGAN SISTEM
3.1 Analisis
Sebelum merancang sebuah sistem, perlu dilakukan analisis terlebih dahulu. Analisis sistem adalah proses menentukan kebutuhan sistem, apa yang harus dilakukan sistem untuk memenuhi kebutuhan klien (user). Tahapan analisis sistem merupakan tahapan yang sangat penting karena kesalahan di dalam tahapan ini akan menyebabkan kesalahan pada tahapan selanjutnya. Sistem yang dirancang akan lebih baik dan memudahkan pengembang sistem dalam perbaikan apabila pada kemudian hari ditemukan kesalahan atau kekurangan [11].
3.1.1 Analisis Permasalahan
Enkripsi merupakan proses dimana informasi atau data yang akan dikirim diubah menjadi bentuk yang hampir tidak dikenali sebagai informasi awalnya dengan menggunakan algoritma tertentu. Sedangkan dekripsi merupakan kebalikan dari enkripsi yaitu mengubah kembali bentuk tersamar tersebut menjadi informasi awal.
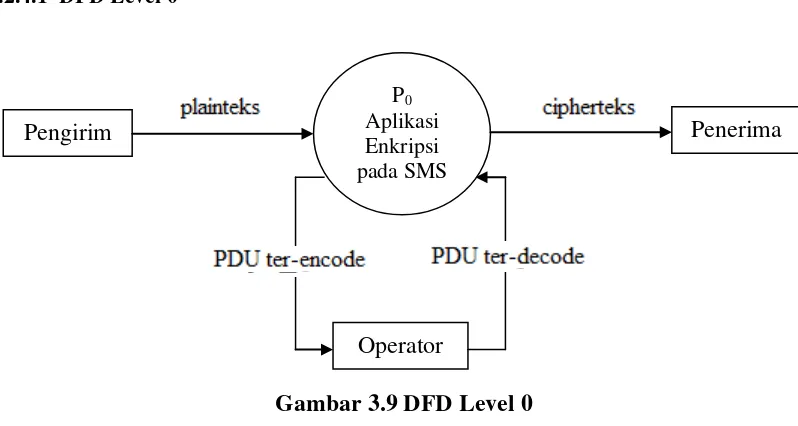
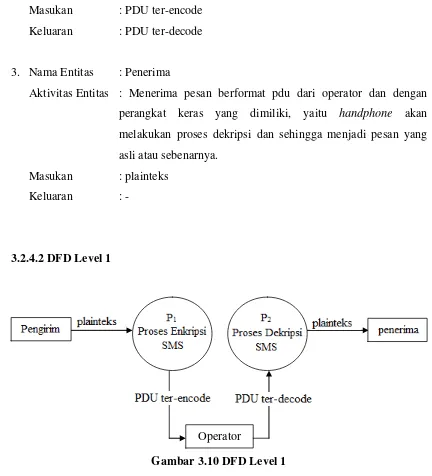
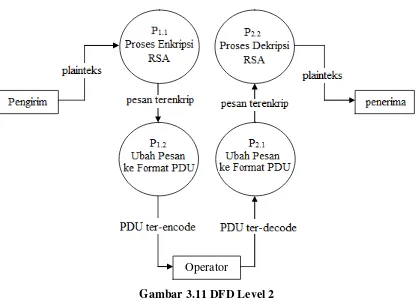
Aplikasi enkripsi dan dekripsi SMS ini dibuat dan dirancang dengan menggunakan metode pendekatan atas-bawah (Top-Down Aprroach) sehingga perancangan akan dimulai dari bentuk yang paling global, yaitu diagram konteks, kemudian akan diturunkan bertahap menjadi bentuk yang lebih rinci.
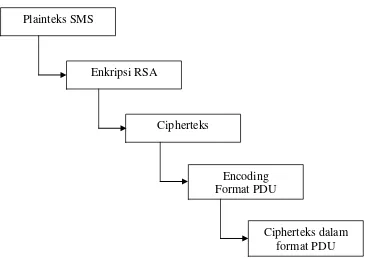
format PDU (Protocol Data Unit), dan penerimaan SMS yang di dalamnya terdapat proses decoding PDU, dekripsi dengan algoritma RSA. Skema global dari proses-proses tersebut dapat dilihat pada gambar 3.1 dan 3.2.
Gambar 3.1 Skema Global Proses Enkripsi dan EncodingPDU Plainteks SMS
Enkripsi RSA
Cipherteks
Encoding Format PDU
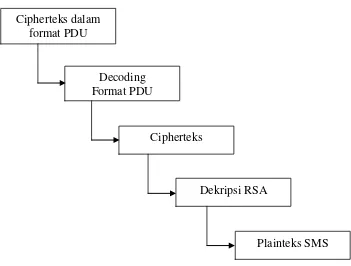
Gambar 3.2 Skema Global Proses DecodingPDU dan Dekripsi
3.1.2 Analisis Protocol Data Unit (PDU)
Dalam proses pengiriman atau penerimaan SMS, data yang dikirim maupun diterima oleh stasiun bergerak menggunakan salah satu dari 2 mode yang ada, yaitu mode teks atau mode PDU. Dalam mode PDU, pesan yang dikirim berupa informasi dalam bentuk data dengan beberapa bagian-bagian informasi. Hal ini akan memberikan kemudahan jika dalam pengiriman akan dilakukan kompresi data, atau akan dibentuk sistem penyandian data dari karakter dalam bentuk untaian bit-bitbiner.
PDU tidak hanya berisi pesan teks saja, tetapi terdapat beberapa meta informasi yang lainnya, seperti nomor pengirim, nomor SMS Center, waktu pengiriman dan sebagainya. Semua informasi yang terdapat dalam PDU, dituliskan dalam bentuk pasangan-pasangan bilangan heksadesimal. Jenis PDU SMS yang akan digunakan adalah PDU Pengiriman (SMS Submit) dan PDU Penerimaan (SMS Deliver ).
Cipherteks dalam format PDU
Decoding Format PDU
Cipherteks
Dekripsi RSA
3.1.2.1PDU Pengiriman (SMS Submit)
PDU pengiriman (SMS Submit) adalah pesan yang dikirim dari ponsel ke terminal yang kemudian dikirimkan ke SMSC. Pesan yang akan dikirimkan oleh terminal masih berbentuk teks, sedangkan dalam pengiriman ke SMSC harus dalam bentuk PDU. Oleh karena itu sebelum dikirim, terminal atau ponsel akan melakukan perubahan format teks menjadi format PDU, proses ini disebut dengan encodec. Adapun skema dari format PDU pengiriman adalah sebagai berikut.
Tabel 3.1 Skema Format PDU Pengiriman
SCA PDU-Type MR DA PID DCS VP UDL UD
Sebagai contoh bila kita mengirim pesan ke nomor 6285691511707 dengan isi pesan adalah “Info Jadwal” dengan validitas waktu selama 5 hari, 10 jam, 60 menit. Maka format PDU-nya adalah seperti pada tabel 3.2 berikut.
Tabel 3.2 Contoh Pesan SMS Submit dalam Format PDU Pesan
Asli
Irfan<spasi>08
PDU 0011000D81265896511107F70000AB8B0BOB49B939EC6C170
Berikut ini merupakan penjelasan masing-masing dari format PDU Pengiriman di atas :
1. SCA (Service Center Address)
Tabel 3.3 SCA dari PDU Pengiriman
Octet Keterangan Nilai
Len Panjang informasi SMSC 00
Type of Number
81 H = format lokal
91 H = format internasional
<none>
BCD Digits Nomor SMSC. Jika panjangnya ganjil, maka pada akhir karakter ditambahkan 0F H
<none>
2. Tipe PDU (PDU-Type)
Nilai default dari PDU untuk SMS Submit adalah 11 H. Pada tabel 3.2, nilai PDU-nya adalah 11 H.
Tabel 3.4 PDU-Type dari PDU Pengiriman
Bit 7 6 5 4 3 2 1 0
Nama RP UDHI SRI VPF VPF RD MTI MTI
Nilai 0 0 0 1 0 0 0 1
Keterangan :
(a) RP (Report Path) adalah parameter yang menunjukkan bahwa ada alur jawaban.
(b) UDHI (User Data Header Indicator), bit ini bernilai 1 jika data pengirim dimulai dengan suatu judul atau tema.
(d) VPF (Validity Period Format), format dari batas waktu pengiriman jika pesan gagal diterima.
00 : Jika pesan tidak sampai di SMSC.
10 : Format relatif (satu octet).
01 : Formatenhanced (tujuh octet).
11 : Format absolut (tujuh octet).
(e) RD (Reject Duplicates), parameter yang menandakan ya atau tidaknya Service Center akan menerima suatu pengiriman pesan SMS untuk suatu pesan yang masih disimpan dalam ServiceCenter tersebut. RD mempunyai MR dan DA yang sama sebagai pesan dan dikirimkan dari OA yang sama. (f) MTI (Message Type Indicator), bit ini bernilai 0 untuk menunjukkan bahwa
PDU ini adalah suatu SMS Deliver.
3. MR (Message Reference)
MR (Message Reference) adalah acuan dari pengaturan SMSC. Nilai yang diberikan adalah “00” dan pengaturan SMS dilakukan sendiri oleh ponsel tujuan. Pada tabel 3.2, nilai MR-nya adalah 00 H.
4. DA (Destination Address)
Tabel 3.5 Destination Address (DA)
Octet Keterangan Nilai
Len Panjang nomor tujuan 0D
Type of Number
Type of address dari SMSC
81 H = format lokal 91 H = format internasional
81
Destination Number
Nomor destination address. Jika panjangnya ganjil, maka pada akhir karakter ditambahkan 0F H
0D81265896511107F7
5. PID (Protocol Identifier)
PID adalah tipe atau format dari cara pengiriman pesan, yang biasanya diatur dari ponsel pengirim. Misalnya tipe Standard Text, Fax, E-mail, Telex, X400 dan lain-lain. Nilai default dari PID adalah 00 (Standard Text). Pada tabel 3.2, nilai PID adalah 00 H, sehingga pesan yang diterima berupa teks standar.
6. DCS (Data Coding Scheme)
7. VP (Validity Period)
VP berisi informasi jangka waktu validitas pesan SMS yang disimpan di SMSC apabila pesan tersebut gagal diterima oleh ponsel penerima. Pada tabel 3.2, nilai VP-nya adalah AB8B0B H.
Tabel 3.6 Nilai Validitas Periode
Waktu VP Nilai Validitas Periode 5 menit - 720 menit (12 jam) (Waktu VP / 5) – 1
12.5 jam - 24 jam 143 + ((Waktu VP – 12) * 2)
2 - 30 Hari 166 + Waktu VP
Lebih dari 4 minggu 192 + Waktu VP
Pada contoh di atas, waktu nya adalah 5 hari, 10 jam, 60 menit. Maka nilai VP-nya adalah :
Hari : 166 + 5 = 171 d = AB H,
Jam : 143 + (( 10 - 12 ) * 2) = 139 d = 8B H,
Menit : (60 / 5) - 1 = 11 d = 0B
Jadi hasil VP-nya adalah AB8B0B H.
8. UDL (User Data Length)
9. UD (User Data)
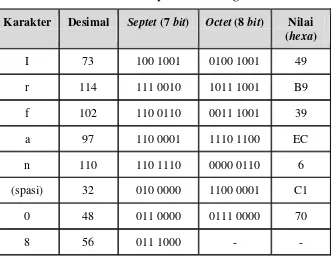
Berisi informasi data utama yang dibawa. Pesan “Info Jadwal” yang dikodekan menjadi 7 bit default alphabet (septet ) harus di-encode-kan menjadi 8 bit (octet ) untuk SMS-Deliver. Pada tabel 3.2, nilai UD-nya adalah “49B939EC6C170”. Tabel 3.7 di bawah ini menunjukkan cara pengkodean dengan menggunakan bantuan tabel defaultalphabet 7 bit. Pada tiap octet jika jumlah bit kurang dari 8, maka diambil bit paling kanan pada septet selanjutnya dan ditambahkan pada bagian kiri septet sebelumnya.
Tabel 3.7 User Data pada PDU Pengiriman
Karakter Desimal Septet (7 bit) Octet (8 bit) Nilai (hexa)
I 73 100 1001 0100 1001 49
r 114 111 0010 1011 1001 B9
f 102 110 0110 0011 1001 39
a 97 110 0001 1110 1100 EC
n 110 110 1110 0000 0110 6
(spasi) 32 010 0000 1100 0001 C1
0 48 011 0000 0111 0000 70
8 56 011 1000 - -
3.1.2.2PDU Penerimaan (SMS Deliver)
Tabel 3.8 Skema Format PDU Penerimaan
SCA PDU -Type OA PID DCS SCTS UDL UD
Contoh : Kita menerima pesan dari 6285695316565 dengan isi pesan SMS “Poli Paru” pada tanggal 20 Oktober 2011 pukul 10:45:21 WIB. Maka format PDU adalah pada tabel 3.9 :
Tabel 3.9 Contoh Pesan SMS Deliver dalam Format PDU Pesan Asli Irfan 08 (Irfan<spasi>08)
PDU 2681050000F0040D81265896356165F50000110102015 412820949B939EC6C170
Berikut merupakan penjelasan masing-masing dari format PDU.
Penerimaan di atas :
1. SCA (Service Center Address)
SCA berisi informasi SMS center. SCA memiliki tiga komponen utama, yaitu len, type of number dan ServiceCenter Number, seperti pada tabel 3.10 berikut. Pada tabel 3.9, nilai SCA-nya adalah 2681050000F0.
Tabel 3.10 SCA dari PDU Penerimaan
Octet Keterangan Nilai
Len Panjang informasi SMSC
dalam octet 26
Type of Number Type of address dari SMSC 81 H = format lokal
91 H = format internasional
85
Service Center Number
Nomor SMSC dari operator pengirim. Jika panjangnya ganjil, maka pada akhir karakter ditambahkan 0F H
Tabel 3.11 Nomor SMS Center Operator Seluler Di Indonesia No. Operator Selular Nomor SMS Center Kode PDU
1. Telkomsel 081100000 /
62811000000
06818011000000/ 07912618010000F0
2. Satelindo 0816124 / 62816125 0581806121F4 / 079126181642
3. Excelcom 0818445009 /
6281445009
06818081440590 / 079126184885400F9
4. Indosat-M3 0855000000 /
62855000000
06818055000000 / 07912658050000F0
6. 3 089644000001 /
6289644000001
0681806944000010 / 0791269846040000F1
Contoh: untuk nomor SMS Center Indosat-M3 (IM3) dapat ditulis dengan dua cara sebagai berikut:
Cara I: 0855000000 diubah menjadi:
a. 06 ada 6 pasang b. 81 1 pasang
c. 80-55-00-00-00 5 pasang
Digabung menjadi : 06818055000000
Cara II: 62855000000 diubah menjadi:
a. 07 ada 7 pasang b. 91 1 pasang
c. 26-58-05-00-00-F0 6 pasang
Contoh: untuk nomor ponsel yang dituju adalah 6285275677333 dapat ditulis dengan dua cara sebagai berikut :
Cara I: 085275677333 diubah menjadi :
a. 0C ada 12 angka b. 81
c. 80-25-57-76-37-33
Digabung menjadi : 0C81802557763733
Cara II: 6285275677333 diubah menjadi:
a. 0D ada 13 angka b. 91
c. 26-58-72-65-77-33-F3
Digabung menjadi : 0D91265872657733F3
2. Tipe PDU (PDU Type)
Berisi informasi jenis dari PDU tersebut. Nilai default dari PDU untuk SMS Deliver adalah 04 H dan nilai PDU-type pada tabel 3.9 adalah 04 H.
Tabel 3.12 PDU-Type dari PDU Penerimaan
Bit 7 6 5 4 3 2 1 0
Nama RP UDHI SRI <none> <none> MMS MTI MTI
Nilai 0 0 0 0 0 1 0 0
Keterangan :
(b) UDHI (User Data Header Indicator), bit ini bernilai 1 jika SMS menggunakan judul.
(c) SRI (Status Report Indication), bit ini bernilai 1 jika suatu status laporan akan dikembalikan.
(d) MMS (More Message to Send), bit ini bernilai 1 jika ada pesan lebih yang dikirim.
(e) MTI (Message Type Indicator), bit ini bernilai 0 untuk menunjukkan bahwa PDU ini adalah SMS Deliver.
3. OA (Originator Address)
Berisi informasi nomor pengirim. OA memiliki tiga komponen utama, yaitu len (panjangnya nomor pengirim), type of number (format dari nomor pengirim) dan originator number (nomor pengirim). Nilai OA pada tabel 3.9 adalah 0D81265896356165F5.
Tabel 3.13 Originator Address (OA)
Octet Keterangan Nilai
Len Panjang nomor
Orginator Address 0D
Type of Number
Format dari nomor pengirim
81 H = format lokal 91H = format internasional
81
Orginator Number
Nomor pengirim dari operator pengirim. Jika panjangnya ganjil, maka pada akhir karakter ditambahkan 0F H
4. PID (Protocol Identifier)
PID adalah tipe atau format dari cara pengiriman pesan, yang biasanya diatur dari ponsel pengirim. Misalnya tipe Standard Text, Fax, E-mail, Telex, X400 dan lain-lain. Nilai default dari PID adalah 00 (Standard Text). Pada tabel 3.9, nilai PID adalah 00 H.
5. DCS (Data Coding Scheme)
DCS berisi informasi skema pengkodean data yang digunakan. Nilai default-nya adalah 00 H, dengan menggunakan character coding default 7 bit dan message class 0. Pada beberapa handphone, message class 0 dengan encoding 7 bit adalah berupa flash SMS. Sedangkan encoding 16 bit Unicode (ucs2), message yang didahului “0001” dengan class 0 adalah berupa blinking flash SMS. Pada tabel 3.9, nilai DCS adalah 00 H. DCS juga menentukan message class seperti tabel di bawah ini.
Tabel 3.14 Data Coding Scheme (DCS) Nilai
(hexa)
Character
coding Message Class
00 Default (7 bit) No class
F0 Default (7 bit) Class 0 (immediate display) F1 Default (7 bit) Class 1 (mobile
equipment-specific)
F2 Default (7 bit) Class 2 (SIM specific message ) F3 Default (7 bit) Class 3 (terminate
equipment-specific)
F4 8 – bit Class 0 (immediate display)
F5 8 – bit Class 1 (mobile
equipment-specific)
F6 8 – bit Class 2 (SIM specific message) F7 8 – bit Class 3 (terminate
6. SCTS (Service Center Time Stamp)
Berisi informasi waktu dari penerimaan pesan oleh SMSC penerima. Pada tabel 3.9, nilai SCTS-nya adalah 11010201541282 yang berarti :
Tabel 3.15 Nilai Service Center Time Stamp (SCTS) Tahun 11 menjadi 2011
Bulan 01 menjadi 10, Oktober Tanggal 02 menjadi 20
Jam 01 menjadi 10 Menit 54 menjadi 45 Detik 12 menjadi 21 Zona
Waktu
82 menjadi 28, dimana 1 unit = 15 menit. (15*28) / 60 = 7, menjadi GMT+7 = WIB.
7. UDL (User Data Length)
UDL berisi informasi mengenai panjang data yang diterima dalam bentuk teks standar. Pada tabel 3.9, nilai UDL-nya adalah 09 H, yang berarti pesan yang diterima adalah sebanyak 9 karakter.
8. UD (User Data)
Tabel 3.16 User Data pada PDU Penerimaan Nilai
(hexa) Octet (8 bit) Septet (7 bit) Desimal Karakter
49 0100 1001 100 1001 73 I
B9 1011 1001 111 0010 114 r
39 0011 1001 110 0110 102 f
EC 1110 1100 110 0001 97 a
6 0000 0110 110 1110 110 n
C1 1100 0001 010 0000 32 (spasi)
70 0111 0000 011 0000 48 0
- - 011 1000 56 8
3.1.3 Analisis Lucas Lehmer Primality Test
Di dalam kriptografi, bilangan prima memiliki peranan yang sangat penting. Beberapa algoritma kriptografi, seperti RSA, menggantungkan kekuatannya pada sulitnya faktorisasi bilangan besar. Oleh karena itu, penggunaan bilangan prima yang besar menjadi sangat penting. Ada banyak cara untuk mengetahui suatu bilangan itu prima atau bukan, dan salah satu yang bisa digunakan adalah Lucas-Lehmer primality Test.
Lucas Lehmer Primality Test bekerja dengan memanfaatkan bilangan Mersenne. Rumus bilangan Mersenne yaitu:
Keterangan:
M = Bilangan Mersenne P = Bilangan Prima
Untuk memperoleh bilangan Mersenne (Mp) adalah bilangan prima, maka p yang dimasukkan juga haruslah sebuah bilangan prima dan p harus lebih besar sama dengan tiga. Akan tetapi Mp belum tentu bilangan prima meskipun p adalah bilangan prima. Bilangan Mersenne biasanya digunakan untuk mencari bilangan prima yang sangat besar.
Berikut ini merupakan langkah-langkah untuk mengetahui keprimaan suatu bilangan dengan Lucas-Lehmer primality test.
1. Masukkan bilangan Mersenne Mp = 2p – 1 dimana p ≥ 3
2. Hitung Sj = S2j-1 – 2 mod Mp dengan S1 = 4 untuk j = 2,3,…,n-1
3. Jika Sp-1 = 0 mod Mp maka dapat disimpulkan bahwa Mp bilangan prima dan jika Mp≠ 0 maka Mp adalah bilangan komposit.
Contoh 1 :
Kita cari bilangan Mersenne dengan memasukkan p = 3 Maka M3 = 23 – 1
= 8 – 1 = 7
Dengan S1 = 4 maka
S2 = S22-1 – 2 mod M3 = 42 – 2 mod 7 = 16 – 2 mod 7
= 14 mod 7 = 0
Kita dapat Sp-1 atau S3-1 atau S4 = 0 maka M3 = 7 adalah bilangan prima.
Contoh 2 :
= 32 – 1 = 31 Dengan S1 = 4 maka
S2 = S22-1 – 2 mod M5 = 42 – 2 mod 31 = 16 – 2 mod 31
= 14 mod 31 = 14
S3 = S23-1 – 2 mod M5 = 142 – 2 mod 31 = 196 – 2 mod 31
= 194 mod 31 = 8
S4 = S24-1 – 2 mod M5 = 82 – 2 mod 31 = 64 – 2 mod 31
= 62 mod 31 = 0
Kita dapat Sp-1 atau S5-1 atau S4 = 0 maka M5 = 31 adalah bilangan prima.
Contoh 3 :
Kita cari bilangan Mersenne dengan memasukkan p = 11 Maka M11 = 211 – 1
= 2048 – 1 = 2047 Dengan S1 = 4 maka
= 16 – 2 mod 2047 = 14 mod 2047 = 14
S3 = S23-1 – 2 mod M11 = 142 – 2 mod 2047 = 196 – 2 mod 2047
= 194 mod 2047 = 194
S4 = S24-1 – 2 mod M11 = 1942 – 2 mod 2047 = 37676 – 2 mod 2047
= 37674 mod 2047 = 788
S5 = S25-1 – 2 mod M11 = 7882 – 2 mod 2047 = 620944 – 2 mod 2047
= 620942 mod 2047 = 701
S6 = S26-1 – 2 mod M11 = 7012 – 2 mod 2047 = 491401 – 2 mod 2047
= 491399 mod 2047 = 119
S7 = S27-1 – 2 mod M11 = 1192 – 2 mod 2047 = 14161 – 2 mod 2047
S8 = S28-1 – 2 mod M11 = 18772 – 2 mod 2047 = 3523129 – 2 mod 2047
= 3523127 mod 2047 = 240
S9 = S29-1 – 2 mod M11 = 2402 – 2 mod 2047 = 57600 – 2 mod 2047
= 57598 mod 2047 = 282
S10 = S210-1 – 2 mod M11 = 2822 – 2 mod 2047 = 79524 – 2 mod 2047
= 79522 mod 2047 = 1736
Kita dapat Sp-1 atau S11-1 atau S10 ≠ 0 maka M11 = 2047 adalah bukan bilangan prima (23 x 89 = 2047). Dan terbukti bahwa tidak semua Mp adalah bilangan prima meskipun p adalah bilangan prima.
Bilangan prima yang dimasukkan ke dalam algoritma RSA adalah bilangan prima yang dapat menghasilkan bilangan mersenne, sehingga tidak semua bilangan prima dapat dimasukkan atau dibangkitkan dalam aplikasi.
3.1.4 Analisis Algoritma RSA
menjadi faktor-faktor prima. Pemfaktoran bertujuan untuk mendapatkan kunci privat. Jika bilangan tersebut tidak dapat difaktorkan, maka keamanan algoritma RSA tarsebut terjamin. Penjelasan metode RSA selengkapnya adalah sebagai berikut:
1. Pembangkitan Kunci RSA
a. Dapatkan 2 buah bilangan prima p dan q.
Bilangan prima p dan q ini harus dirahasiakan. Besar kecilnya bilangan prima ini menentukan tingkat keamanan data, semakin besar bilangan semakin banyak faktorialnya yang mengakibatkan semakin sulit data untuk dapat dipecahkan dalam waktu singkat. Pengujian suatu bilangan prima dilakukan dengan metode Lucas Lehmer Primality Test.
Misal, diperoleh nilai: p =31
q =7
b. Dapatkan nilai n, dimana n= p*q, dan n bersifat tidak rahasia n = 31 * 7 = 217
c. Dapatkan nilai Ф(n), dimana Ф(n)=( p-1)*(q-1), dan m bersifat rahasia Ф(n) = (31 - 1)*(7 - 1)
= 30 * 6 = 180
d. Pilih sebuah bilangan bulat kecil e yang coprime terhadap Ф(n), dimana e merupakan kunci publik untuk proses enkripsi dan e tidak rahasia.
function Euclid(a, b)
Input: Two integers a and b with a ≥ b ≥ 0 Output: gcd(a, b)
if b = 0: return a
return Euclid(b, a mod b) Sumber : Dasgupta, 2006
e = 2 => gcd(e, 180) = 2 (no) e = 3 => gcd(e, 180) = 3 (no) e = 4 => gcd(e, 180) = 4 (no) e = 5 => gcd(e, 180) = 5 (no) e = 6 => gcd(e, 180) = 6 (no) e = 7 => gcd(e, 180) = 1 (yes!)
e. Hitung kunci dekripsi, d, dengan kekongruenan e*d ≡1 (mod Ф(n))
Cari nilai d, dengan syarat (d*e)% Ф(n) ≡ 1 % Ф(n). Kita dapat menuliskan kembali pernyataan tersebut dengan d = (1+k* Ф(n))/e sehingga nilai-nilai k dapat diselesaikan sampai didapat sebuah nilai yang integer seperti berikut:
k = 0 => d = 1 / 7 = 0,14 (no) k = 1 => d = 181 / 7 = 25,86 (no) k = 2 => d = 361 / 7 = 51,57 (no) k = 3 => d = 481 /7 = 68,71 (no) k = 4 => d = 721 /7 = 103 (yes!)
Maka akan didapatkan:
Kunci Publik n = 217 e = 7
Kunci Rahasia n = 217
2. Enkripsi
a. Ambil kunci publik penerima pesan, e, dan n. Kemudian masukkan pesan yang ingin dienkripsi (plaintext).
Contoh:
Plaintext: Irfan 08
Kode ASCII dalam desimal:
I = 73 r = 114 f = 102 a = 97 n = 110 <spasi> = 32 0 = 48 8 = 56
Agar nantinya lebih mudah dalam proses dekripsi, yaitu dalam memisahkan kode ASCII desimal kedalam untuk mengembalikan kedalam
Digabungkan menjadi : m = 7311410297110324856
b. Plaintext dinyatakan dengan blok-blok m1, m2, …, mi sedemikian sehingga setiap blok merepresentasikan nilai di dalam selang [0, n-1].
Kode ASCII dalam desimal dari plaintext di atas dipecah menjadi blok-blok m. Nilai-nilai m haruslah masih dalam selang [0, 133-1]. Misalkan dibagi menjadi 2 angka dalam 1 blok. Maka blok-blok yang terbentuk adalah :
m1=73 m4=02 m7=03 m10=06
m2=11 m5=97 m8=24
m3=41 m6=11 m9=85
c. Setiap blok mi dienkripsi menjadi blok ci dengan rumus ci = mie mod n.
function modexp(x, y,N)
Input: Two n-bit integers x and N, an integer exponent y Output: xy mod N
if y = 0: return 1
z = modexp(x, y/2 , N) if y is even:
return z2 mod N else:
return x * z2 mod N Sumber : Dasgupta, 2006
Dengan kunci publik e = 7 dan n = 217, maka blok-blok m diatas dapat dienkripsi menjadi blok-blok c sebagai berikut:
Tabel 3.17 Blok-Blok mi Dienkripsi Menjadi Blok-Blok ci i mi e n ci = mie mod n
1 73 7 217 199
2 11 7 217 137
3 41 7 217 20
4 02 7 217 128
5 97 7 217 202
6 11 7 217 137
7 03 7 217 17
8 24 7 217 03
9 85 7 217 29
10 06 7 217 06
3. Dekripsi
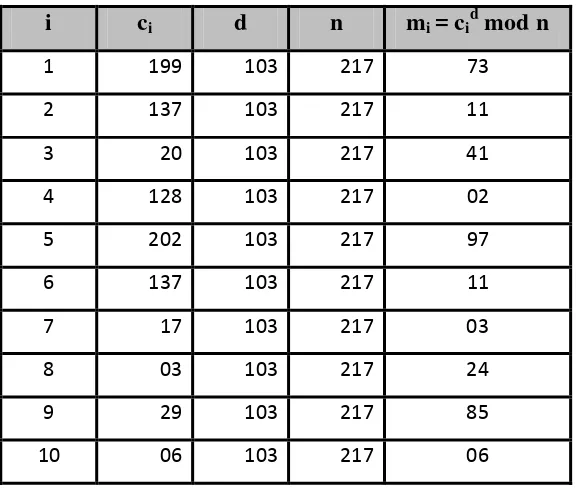
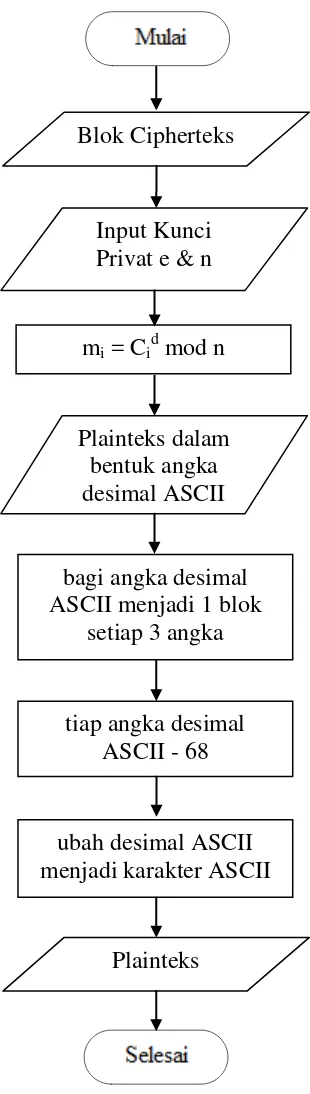
Setiap blok ciphertext ci didekripsikan kembali menjadi blok mi dengan rumus: mi = cid mod n
Dengan kunci privat, d = 103 dan n =217, maka dapat dilakukan proses dekripsi sebagai berikut:
Tabel 3.18 Blok-Blok ci Didekripsi Menjadi Blok-Blok mi i ci d n mi = cid mod n
1 199 103 217 73
2 137 103 217 11
3 20 103 217 41
4 128 103 217 02
5 202 103 217 97
6 137 103 217 11
7 17 103 217 03
8 03 103 217 24
9 29 103 217 85
10 06 103 217 06
Maka dihasilkan kembali: m = 73114102971103248506
Dengan melakukan langkah di atas, dapat dilihat bahwa pesan/data telah sama dengan data asli sebelum enkripsi yaitu bila diubah ke dalam karakter ASCII dapat dibaca sebagai berikut:
3.2 Perancangan Sistem
Perancangan sistem merupakan suatu tahapan yang sangat penting dalam pembangunan sistem perangkat lunak. Tahapan ini menentukan langkah selanjutnya yang akan dilakukan pada tahap implementasi. Tahapan ini memberikan gambaran dasar dari sistem yang dibangun [11].
3.2.1 Pesan Enkripsi
Aplikasi akan mengenkripsi pesan terlebih dahulu sebelum dikirim dengan menggunakan algoritma RSA untuk menjaga keamanan pesan tersebut. Kemudian dari hasil enkripsi tersebut, pesan diencoding kedalam format PDU.
Gambar 3.3 Rancangan pengiriman SMS
Pesan yang diterima dalam bentuk PDU akan terlebih dahulu didekoding untuk mendapatkan bentuk enkripsi yang sebenarnya. Kemudian setelah didapatkan bentuk enkripsinya, pesan kemudian didekripsi untuk mendapatkan plainteks agar pesan dapat dibaca.
Gambar 3.4 Rancangan penerimaan SMS Pesan
Enkripsi Pesan
Encoding Pesan
Pesan Dikirim
Pesan Masuk
Decoding Pesan
Enkripsi Pesan
3.2.2 Rancangan Pengiriman dan Penerimaan
Gambar 3.5 menunjukkan perancangan pengiriman dan penerimaan SMS
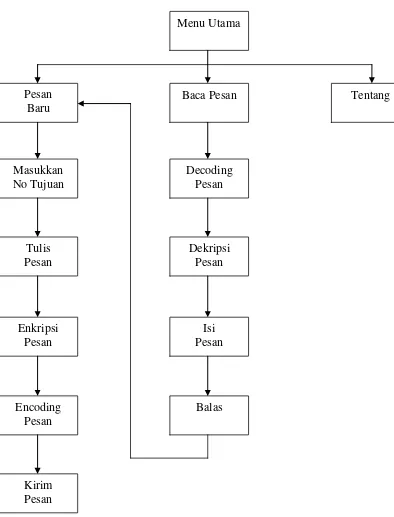
Gambar 3.5 Rancangan pengiriman dan penerimaan SMS Menu Utama
Baca Pesan Pesan
Baru
Tentang
Decoding Pesan Masukkan
No Tujuan
Tulis Pesan
Dekripsi Pesan
Enkripsi Pesan
Isi Pesan
Encoding Pesan
Balas
3.2.3 Perancangan Flowchart
Flowchart merupakan gambar atau bagan yang memperlihatkan urutan dan hubingan antar proses beserta pernyataannya. Gambaran ini dinyatakan dengan symbol dan setiap symbol menggambarkan proses tertentu. Sedangkan antara proses digambarkan dengan garis penghubung. Dengan menggunakan flowchart akan memudahkan kita untuk melakukan pengecekan bagian-bagian yang terlupakan dalam analisis masalah. Di samping itu flowchart juga berguna sebagai fasilitas untuk berkomunikasi antara pemrograman yang bekerja dalam tim suatu proyek [9].
Ada dua macam flowchart yang menggambarkan proses, yaitu Flowchart Sistem dan Flowchart Program.
1. Flowchart Sistem
Flowchart Sistem yaitu bagan dengan symbol-simbol tertentu yang menggambarkan urutan prosedur dan proses suatu file dalam suatu media menjadi file di dalam media lain dalam suatu sistem pengolahan data.
2. Flowchart Program
3.2.3.1 Flowchart Pembangkitan Pasangan Kunci RSA
Gambar 3.6 Flowchart Pembangkitan Pasangan Kunci RSA n = p*q;
Ф(n)=(p-1)*(q-1);
e = 2 ; e > Mulai
k = 1 ; k >
3.2.3.2 Flowchart Proses Enkripsi Algoritma RSA
Gambar 3.7 Flowchart Proses Enkripsi Algoritma RSA Input
Plainteks
ubah plaintext menjadi angka desimal ASCII
tiap angka desimal ASCII + 68
bagi angka desimal ASCII menjadi 1 blok
setiap 3 angka
Ci = mie mod n