IMPLEMENTASI MASSEY-OMURA CRYPTOSYSTEM DAN
LEHMANN PRIME GENERATOR UNTUK KEAMANAN
EMAIL PADA MOZILLA THUNDERBIRD
SKRIPSI
TENGKU SURYA PRAMANA
081401010
PROGRAM STUDI S1 ILMU KOMPUTER
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI
UNIVERSITAS SUMATERA UTARA
IMPLEMENTASI MASSEY-OMURA CRYPTOSYSTEM DAN LEHMANN PRIME GENERATOR UNTUK KEAMANAN EMAIL
PADA MOZILLA THUNDERBIRD
SKRIPSI
Diajukan untuk melengkapi tugas akhir dan memenuhi syarat memperoleh ijazah Sarjana Ilmu Komputer
TENGKU SURYA PRAMANA 081401010
PROGRAM STUDI S1 ILMU KOMPUTER
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : IMPLEMENTASI MASSEY-OMURA
CRYPTOSYSTEM DAN LEHMANN PRIME GENERATOR UNTUK KEAMANAN EMAIL PADA MOZILLA THUNDERBIRD
Kategori : SKRIPSI
Nama : TENGKU SURYA PRAMANA
Nomor Induk Mahasiswa : 081401010
Program Studi : SARJANA (S1) ILMU KOMPUTER
Fakultas : ILMU KOMPUTER DAN TEKNOLOGI
INFORMASI (FASILKOM-TI) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, 22 Oktober 2013
Komisi Pembimbing
Pembimbing 2 Pembimbing 1
Dian Rachmawaty, S.Si, M.Kom. Prof. Dr. Opim Salim Sitompul, M.Sc. NIP.198307232009122004 NIP.196108171987011001
Diketahui/Disetujui oleh
Program Studi S1 IlmuKomputer Ketua,
PERNYATAAN
IMPLEMENTASI MASSEY-OMURA CRYPTOSYSTEM DAN LEHMANN PRIME GENERATOR UNTUK KEAMANAN EMAIL
PADA MOZILLA THUNDERBIRD
SKRIPSI
Penulis mengakui bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa ringkasan dan kutipan yang masing-masing disebutkan sumbernya.
Medan, 22 Oktober 2013
PENGHARGAAN
Alhamdulillah. Puji dan syukur penulis ucapkan kepada Allah SWT atas limpahan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini sebagai syarat untuk memperoleh gelar Sarjana Komputer, Program Studi Ilmu Komputer Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara. Kemudian Shalawat dan salam penulis ucapkan kepada Rasulullah Muhammad SAW.
Pada pengerjaan skripsi dengan judul Implementasi Massey-Omura Cryptosystem dan Lehmann Prime Generator untuk Keamanan Email pada Mozilla Thunderbird, penulis menyadari bahwa banyak campur tangan pihak yang turut membantu dan memotivasi dalam pengerjaannya. Dalam kesempatan ini, penulis mengucapkan terima kasih kepada:
1. Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H, MSc(CTM). Sp.A(K), selaku Rektor Universitas Sumatera Utara.
2. Bapak Prof. Dr. Muhammad Zarlis, M.Sc., selaku Dekan Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara.
3. Bapak Dr. Poltak Sihombing, M.Kom, selaku Ketua Program Studi Ilmu Komputer Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara.
4. Ibu Maya Silvi Lydia, B.Sc., M.Sc selaku Sekretaris Program Studi S1 Ilmu Komputer Fakultas Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara.
5. Bapak Prof. Dr. Opim Salim Sitompul, M.Sc dan Ibu Dian Rachmawati S.Si, M.Kom selaku pembimbing yang telah banyak meluangkan waktunya dalam memberikan masukan-masukan kepada penulis.
6. Bapak Syahriol Sitorus, S.Si, MIT dan Bapak Ade Candra, ST, M.Kom sebagai dosen penguji yang telah memberikan saran dan kritikan yang sangat berguna bagi penulis.
7. Bapak M. Andri Budiman, ST, MCompSc, MEM selaku dosen kriptografi yang telah memberikan masukan-masukan kepada penulis.
8. Seluruh dosen serta pegawai di Program Studi S1 Ilmu Komputer Departemen Ilmu Komputer Fakultas Ilmu Komputer dan Teknologi Informasi USU.
9. Ayahanda tercinta Tengku Syuklan, SE dan Ibunda tercinta Sulasih, adik saya Tengku Alfan Sury, Tengku Mahfuza Aini dan Tengku Lailan Khairuni yang selalu memberikan doa, motivasi dan dukungannya baik materi maupun spiritual serta semangat yang diberikan selama kuliah dan menyelesaikan skripsi ini.
11. Teman-teman seperjuangan angkatan 2008 program studi S1 Ilmu Komputer USU, terkhusus kepada: Eko Verdianto, S.Kom, Ahmad Royhan Putra Siregar, Zainuddin Siregar, S.Kom, Gustaf Prameswara, S.Kom, Ficky Vernandes Isman, S.Kom, Irfan Antoni Siregar, S.Kom, Mirnawati, S.Kom, Anny Maghfirah, S.Kom, Heny Mulyana, S.Kom, Siska Anggraini, S.Kom dan Nurul Akhmaliyah.
12. Teman-teman yang telah memberikan semangat dan motivasi, terkhusus kepada: Nur Yusuf Ritonga , M.Syafii, S.Pd, Magdalena Sinaga dan Wilda Putri Rezekia Siregar.
Penulis menyadari bahwa skripsi ini masih jauh dari sempurna. Oleh karena itu, penulis menerima kritik dan saran dari semua pihak yang bersifat membangun dan menyempurnakan skripsi ini. Penulis berharap semoga skripsi ini bermanfaat bagi penulis sendiri pada khususnya dan pembaca pada umumnya.
Medan, 22 Oktober 2013
ABSTRAK
E-mail merupakan salah satu media untuk pengiriman informasi. Namun, pengiriman e-mail tanpa teknik enkripsi dapat menyebabkan pencurian informasi yang terdapat pada e-mail seperti pembacaan isi e-mail, penyadapan isi e-mail atau merubah isi e-mail oleh orang yang tidak berkepentingan. Skripsi ini mengkaji pengamanan terhadap informasi yang dikirim melalui e-mail dengan membangun sebuah add on pada Mozilla Thunderbird yang merupakan salah satu e-mail client. Add on ini menggunakan Massey-Omura cryptosystem untuk mengenkripsi dan mendekripsi pesan yang akan dikirim melalui e-mail. Dalam pengimplementasiannya, kriptografi Massey-Omura menggunakan metode Three Pass Protocol untuk menghindari pertukaran kunci antara pengirim e-mail dan penerima e-mail. Implementasi juga melibatkan pembangkitan bilangan prima dengan Lehmann Prime Generator. Hasil pengujian menunjukkan bahwa add on yang dibangun dapat diterapkan dengan metode Three Pass Protocol dan telah memenuhi aspek confidentiality dan data integrity yang merupakan aspek keamanan kriptografi. Implementasi dilakukan pada Mozilla Thunderbird 17.0 dengan bahasa pemrograman javascript, XUL dan CSS.
IMPLEMENTATION OF MASSEY-OMURA CRYPTOSYSTEM AND LEHMANN PRIME GENERATOR FOR EMAIL SECURITY
ON MOZILLA THUNDERBIRD
ABSTRACT
E-mail is a media for sending information. However, sending e-mail without encryption techniques can cause theft of information contained in the e-mail such as reading the e-mail contents, tapping the e-mail contents or change the email contents by unauthorized persons. This paper examines the security of information that sent via e-mail by building an add on in Mozilla Thunderbird which is one of the e-mail client. This add on use Massey-Omura cryptosystem to encrypt and decrypt the messages to be sent via e-mail. In its implementation, Massey-Omura cryptography use Three Pass Protocol method to avoid the keys exchange between the e-mail sender and receiver. The implementation also involves the generation of prime numbers with Lehmann Prime Generator. The result show that the add on which is bulit can be applied with Three Pass Protocol Method and already comply confidentiality and data integrity aspects which is the security aspects of cryptography. Implementation is done on Mozilla Thunderbird 17.0 with javascript, XUL and CSS programming language.
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak vi
1.1 Latar Belakang Masalah 1
1.2 Rumusan Masalah 3
1.3 Batasan Masalah 3
1.4 Tujuan Penelitian 3
1.5 Manfaat Penelitian 3
1.6 Metode Penelitian 4
1.7 Sistematika Penulisan 5
Bab 2 Tinjauan Pustaka 7
2.1 Keamanan Data 7
2.2 Kriptografi 8
2.2.1 Pengertian Kriptografi 8
2.2.2 Tujuan Kriptografi 9
2.2.3 Jenis Kriptografi 10
2.3 Three Pass Protocol 13
2.4 Algoritma Massey-Omura 14
2.5 Lehmann Prime Generator 16
2.6 Mozilla Thunderbird dan Add On pada Mozilla Thunderbird 18
Bab 3 Analisis dan Perancangan 20
3.1 Analisis Sistem 20
3.1.1 Analisis Masalah 20
3.1.2 Analisis Persyaratan (Requirement Analysis) 21 3.1.3 Pemodelan Persyaratan Sistem dengan Use Case 22
3.1.4 Analisis Proses Sistem 28
3.1.5 Pseudocode dan Flowchart 30
3.2 Perancangan Sistem 41
3.2.1 Perancangan Antarmuka 41
3.2.2 Perancangan Struktur Direktori Add On 42
Bab 4 Implementasi dan Pengujian 44
4.1 Implementasi Sistem 44
4.1.1 Tahapan Algoritma Massey-Omura dan Three Pass Protocol 44 dengan menggunakan Lehmann Prime Generator.
4.1.2 Spesifikasi Kebutuhan Perangkat Lunak 48
4.1.3 Tampilan Sistem 49
4.2 Pengujian Sistem 54
4.2.1 Data Hasil Pengujian 54
Bab 5 Kesimpulan dan Saran 61
5.1 Kesimpulan 61
5.2 Saran 61
Daftar Pustaka 63
DAFTAR TABEL
Tabel Nama Tabel Halaman
3.1 3.2 3.3 3.4 4.1 4.2 4.3
Spesifikasi Use Case Enkripsi Spesifikasi Use Case Send Spesifikasi Use Case Dekripsi Komponen pada Toolbar
Hasil Pengujian Aspek Confidentiality Hasil Pengujian Aspek Data Integrity Waktu Enkripsi dan Dekripsi
DAFTAR GAMBAR
Gambar Nama Gambar Halaman
2.1
Proses Enkripsi dan Dekripsi Kriptografi Simetri Proses Enkripsi dan Dekripsi Kriptografi Asimetri Skema Three Pass Protocol
Tampilan Mozilla Thunderbird
Diagram Ishikawa untuk Analisis Permasalahan Sistem Contoh Sebuah Use Case Diagram
Activity Diagram Enkripsi Activity Diagram Send Activity Diagram Dekripsi Sequence Diagram Enkripsi Sequence Diagram Send Sequence Diagram Dekripsi
Pseudocode Algoritma Enkripsi Massey-Omura Pseudocode Algoritma Dekripsi Massey-Omura Pseudocode dan Kompleksitas Algoritma LPG Flowchart Proses Three Pass Protocol
Flowchart Proses Enkripsi I Flowchart Proses Enkripsi II Flowchart Proses Dekripsi I Flowchart Proses Dekripsi II
Flowchart Proses Pembangkitan Bilangan Prima Letak Icon Add On pada Toolbar Mozilla Thunderbird Struktur Direktori untuk Add On yang Dikembangkan
Pemasangan Add On dengan Menggunakan Add-Ons Manager Icon Enkripsi pada Toolbar Mozilla Thunderbird
Icon Dekripsi pada Toolbar Mozilla Thunderbird Pesan sebelum dienkripsi oleh Pengirim
Pesan setelah dienkripsi oleh Pengirim Enkripsi Pesan oleh Penerima
Hasil Dekripsi Pesan oleh Pengirim Hasil Dekripsi Pesan oleh Penerima
ABSTRAK
E-mail merupakan salah satu media untuk pengiriman informasi. Namun, pengiriman e-mail tanpa teknik enkripsi dapat menyebabkan pencurian informasi yang terdapat pada e-mail seperti pembacaan isi e-mail, penyadapan isi e-mail atau merubah isi e-mail oleh orang yang tidak berkepentingan. Skripsi ini mengkaji pengamanan terhadap informasi yang dikirim melalui e-mail dengan membangun sebuah add on pada Mozilla Thunderbird yang merupakan salah satu e-mail client. Add on ini menggunakan Massey-Omura cryptosystem untuk mengenkripsi dan mendekripsi pesan yang akan dikirim melalui e-mail. Dalam pengimplementasiannya, kriptografi Massey-Omura menggunakan metode Three Pass Protocol untuk menghindari pertukaran kunci antara pengirim e-mail dan penerima e-mail. Implementasi juga melibatkan pembangkitan bilangan prima dengan Lehmann Prime Generator. Hasil pengujian menunjukkan bahwa add on yang dibangun dapat diterapkan dengan metode Three Pass Protocol dan telah memenuhi aspek confidentiality dan data integrity yang merupakan aspek keamanan kriptografi. Implementasi dilakukan pada Mozilla Thunderbird 17.0 dengan bahasa pemrograman javascript, XUL dan CSS.
IMPLEMENTATION OF MASSEY-OMURA CRYPTOSYSTEM AND LEHMANN PRIME GENERATOR FOR EMAIL SECURITY
ON MOZILLA THUNDERBIRD
ABSTRACT
E-mail is a media for sending information. However, sending e-mail without encryption techniques can cause theft of information contained in the e-mail such as reading the e-mail contents, tapping the e-mail contents or change the email contents by unauthorized persons. This paper examines the security of information that sent via e-mail by building an add on in Mozilla Thunderbird which is one of the e-mail client. This add on use Massey-Omura cryptosystem to encrypt and decrypt the messages to be sent via e-mail. In its implementation, Massey-Omura cryptography use Three Pass Protocol method to avoid the keys exchange between the e-mail sender and receiver. The implementation also involves the generation of prime numbers with Lehmann Prime Generator. The result show that the add on which is bulit can be applied with Three Pass Protocol Method and already comply confidentiality and data integrity aspects which is the security aspects of cryptography. Implementation is done on Mozilla Thunderbird 17.0 with javascript, XUL and CSS programming language.
BAB 1
PENDAHULUAN
1.1Latar Belakang Masalah
Dewasa ini penggunaan teknologi Internet di dunia sudah berkembang pesat. Semua kalangan telah menikmati Internet. Bahkan, perkembangan teknologi Internet tersebut semakin memudahkan penggunanya dalam berkomunikasi melalui bermacam-macam media maupun aplikasi. Salah satu aplikasi Internet yang banyak digunakan adalah pengiriman pesan secara elektronik, yang disebut e-mail. E-mail digunakan sejak awal terbentuknya Internet pada tahun 1969 dan e-mail merupakan aplikasi yang ada pada saat awal terbentuknya Internet. Penggunaan e-mail juga sudah semakin pesat, e-mail digunakan untuk mengirimkan suatu informasi yang cepat dan efisien (Kurniawan, 2004).
Seiring berjalannya waktu, e-mail menjadi sebuah aplikasi yang sering digunakan untuk mengirim pesan. Namun, ada beberapa ancaman yang tidak diketahui oleh pengguna saat menggunakan e-mail seperti penyadapan isi e-mail, merubah isi e-mail oleh orang yang tidak berkepentingan dan menjadikan e-mail itu tidak asli lagi. Keamanan menjadi suatu aspek yang sangat penting dalam pengiriman e-mail untuk mencegah atau jatuhnya data kepada pihak-pihak lain yang tidak berkepentingan sehingga adanya kemungkinan kebocoran atau penyalahgunaan data dapat dihindari (Rambe, 2010).
dengan aspek keamanan suatu sistem informasi, antara lain seperti kerahasiaan (confidentiality), integritas data (data integrity), otentikasi (authentication), dan pembuktian yang tak tersangkal (non-repudiation). Keempat aspek tersebut merupakan tujuan fundamental dari suatu sistem kriptografi (Munir, 2006).
Massey-Omura Cryptosystem merupakan algoritma kriptografi yang dalam pengimplementasiannya menggunakan three pass protocol. Three Pass Protocol merupakan suatu kerangka kerja yang memungkinkan satu pihak bisa dengan aman mengirim pesan ke pihak kedua tanpa perlu bertukar atau mendistribusikan kunci enkripsi. Dengan kata lain, pengirim dan penerima harus bertukar pesan yang telah dienkripsi dan mendekripsi ciphertext tersebut dengan kunci yang mereka miliki masing-masing untuk bisa menghasilkan plain teks (Winton, 2007).
Sebelumnya telah dilakukan penelitian oleh Rambe (2010) untuk mengamankan e-mail dengan menggunakan algoritma RSA. Hal ini terbukti bisa membuat e-mail lebih aman. Namun, karena menggunakan single encryption, keamanan e-mail tersebut tidak selamanya bisa aman oleh serangan kriptanalis. Kemudian, pernah dilakukan penelitian oleh Elveny (2011) untuk mengamankan e-mail dengan menggunakan algoritma Elgamal. Namun, penggunaannya hanya berbasis desktop. Selain itu, telah dilakukan penelitian oleh Barus (2012) untuk mengamankan e-mail dengan menggunakan algoritma XOR, dimana algoritma ini adalah salah satu algoritma kriptografi sederhana yang proses enkripsi dan dekripsinya menggunakan kunci tunggal dan operasi bit XOR.
1.2Rumusan Masalah
Berdasarkan uraian pada latar belakang masalah, maka masalah yang akan dibahas pada tugas akhir ini adalah adanya ancaman yang tidak diketahui oleh pengguna saat proses pengiriman e-mail seperti penyadapan isi e-mail atau merubah isi e-mail oleh orang yang tidak berkepentingan.
1.3Batasan Masalah
Untuk memfokuskan pengerjaan tugas akhir ini, penulis akan membatasi masalah, yaitu sebagai berikut:
1. Pembahasan hanya pada pengimplementasian dan proses kerja enkripsi dan dekripsi pada e-mail.
2. File yang akan dienkripsi dan didekripsi adalah teks yang dituliskan pada body e-mail, bukan attachment.
3. Penelitian ini hanya membahas keamanan data berdasarkan aspek keamanan kriptografi yaitu confidentiality dan data integrity.
1.4Tujuan Penelitian
Tujuan penelitian ini adalah untuk mengamankan teks yang akan dikirim melalui e-mail dari orang-orang yang ingin membaca informasi yang terdapat pada teks tersebut.
1.5Manfaat Penelitian
1.6Metode Penelitian
Metodologi penelitian yang akan digunakan adalah: a. Studi Literatur
Mempelajari literatur tentang teori dasar mengenai kriptografi, jenis-jenis kriptografi, memahami tentang algoritma Massey-Omura, Lehmann Prime Generator, Three Pass Protocol, proses enkripsi dan dekripsi pada algoritma Massey-Omura dan semua teori yang berkaitan baik dari beberapa buku, makalah, jurnal, maupun penelitian terdahulu.
b. Analisis dan Perancangan Sistem
Melakukan perancangan desain dalam bentuk struktur program, flowchart, dan antar muka sistem untuk memudahkan proses implementasi pada tahap selanjutnya.
c. Implementasi Sistem
Pada tahap ini dilakukan pembuatan add-on sesuai dengan analisis dan perancangan yang sudah didefinisikan sebelumnya.
d. Pengujian Sistem
Pengujian dilakukan terhadap keberhasilan proses kriptografi pada sistem, mencakup apakah implementasi telah sesuai dengan teori, apakah pesan hasil dekripsi sesuai dengan plainteks semula, dan keberhasilan sistem dalam menjaga keamanan e-mail.
e. Dokumentasi Sistem
1.7Sistematika Penulisan
Sistematika penulisan laporan penelitian ini dibagi menjadi 5 bab, yaitu sebagai berikut:
BAB 1 PENDAHULUAN
Berisikan penjelasan tentang konsep dasar penyusunan tugas akhir, yaitu mengenai latar belakang pemilihan judul, rumusan masalah, batasan masalah, tujuan penelitian, manfaat penelitian, metode penelitian, dan sistematika penulisan.
BAB 2 TINJAUAN TEORETIS
Bab ini akan membahas dasar teori yang menunjang penulisan tugas akhir, berkaitan mengenai kriptografi, Massey-Omura cryptosystem, Three Pass Protocol, Lehmann Prime Generator
(LPG), serta email client Mozilla Thuderbird.
BAB 3 ANALISIS DAN PERANCANGAN SISTEM
Bab ini akan menjabarkan tentang analisis kebutuhan untuk menghasilkan suatu rancang bangun yang nantinya akan diimplementasikan. Analisis dan perancangan meliputi kebutuhan sistem, pemodelan sistem hingga perancangan antar muka.
BAB 4 IMPLEMENTASI DAN PENGUJIAN
BAB 5 KESIMPULAN DAN SARAN
BAB 2
TINJAUAN PUSTAKA
2.1 Keamanan Data
Keamanan merupakan salah satu aspek yang sangat penting dari sebuah sistem informasi. Masalah keamanan sering kurang mendapat perhatian dari para perancang dan pengelola sistem informasi. Masalah keamanan sering berada diurutan setelah tampilan, atau bahkan diurutan terakhir dalam daftar hal-hal yang dianggap penting (Wahana, 2003).
Keamanan adalah keadaan bebas dari bahaya. Istilah ini dapat digunakan dengan hubungan kepada kejahatan, dan segala bentuk kecelakaan. Keamanan merupakan topik yang luas termasuk keamanan nasional terhadap serangan teroris, keamanan komputer terhadap hacker, keamanan rumah terhadap maling dan penyelusup lainnya, keamanan finansial terhadap kehancuran ekonomi dan banyak situasi berhubungan lainnya. Host / komputer yang terhubung ke network, mempunyai ancaman keamanan lebih besar dari pada host yang tidak terhubung kemana-mana. Dengan mengendalikan network security, risiko tersebut dapat dikurangi.
2.2 Kriptografi
Kriptografi merupakan salah satu ilmu pengkodean pesan yang digunakan untuk meningkatkan keamanan dalam pengiriman pesan atau komunikasi data. Kriptografi saat ini telah menjadi salah satu syarat penting dalam keamanan teknologi informasi dalam pengiriman pesan penting dan rahasia. Pengiriman pesan penting dan rahasia sangat rentan terhadap serangan yang dilakukan oleh pihak ketiga, seperti penyadapan, pemutusan komunikasi, pengubahan pesan yang dikirim, dan hal-hal yang merugikan lainnya (Anggraini, 2012).
2.2.1 Pengertian Kriptografi
Kriptografi berasal dari dua kata dalam bahasa Yunani, yaitu “cryptós” yang berarti rahasia, dan “gráphein” yang berarti tulisan. Menurut terminologinya kriptografi adalah ilmu dan seni untuk menjaga keamanan pesan ketika pesan dikirim dari suatu tempat ke tempat yang lain.
Secara umum, istilah yang sering digunakan di dalam kriptografi adalah (Munir, 2006):
1. Pesan
Pesan adalah data atau informasi yang dapat dibaca dan dimengerti maknanya. Pesan sering juga disebut plainteks (plaintext) atau pesan jelas (cleartext). Plainteks merupakan suatu pesan bermakna yang akan diproses menggunakan algoritma kriptografi.
2. Cipherteks
Cipherteks (ciphertext) atau disebut juga kriptogram (cryptogram) merupakan pesan yang telah tersandi. Pesan dalam bentuk cipherteks tidak dapat dibaca karena berisi karakter-karakter yang tidak memiliki makna setelah melalui proses enkripsi.
3. Enkripsi
4. Dekripsi
Dekripsi merupakan proses mengembalikan cipherteks menjadi plainteks semula atau disebut deciphering. Dekripsi dilakukan ketika pesan telah sampai kepada pihak yang dituju.
5. Kunci
Kunci adalah parameter yang digunakan untuk transformasi enkripsi dan dekripsi. Kunci biasanya berupa string atau deretan bilangan. Keamanan suatu algoritma kriptografi biasanya bergantung kepada kerahasiaan penyebaran kunci.
6. Kriptosistem
Kriptosistem (Cryptosystem) adalah perangkat keras atau implementasi perangkat lunak kriptografi yang diperlukan dalam mentransformasi sebuah pesan asli menjadi ciphertext dan juga sebaliknya.
2.2.2 Tujuan Kriptografi
Kriptografi bertujuan untuk memberi layanan keamanan sebagai berikut (Munir, 2006):
1. Confidentiality
Confidentiality merupakan tujuan sistem kriptografi dalam memberikan kerahasiaan pesan dan menyimpan data dengan menyembunyikan informasi lewat teknik-teknik enkripsi.
2. Data Integrity
Data integrity merupakan tujuan sistem kriptografi dalam memberikan
jaminan bahwa pesan tidak akan mengalami perubahan selama proses pengiriman. Integritas data merupakan layanan yang bertujuan untuk mencegah terjadinya pengubahan informasi oleh pihak-pihak yang tidak berwenang.
3. Non-repudiation
4. Authentication
Authentication merupakan tujuan sistem kriptografi dalam mengidentifikasikan
keaslian suatu pesan dan memberikan jaminan keotentikannya, dan menguji identitas seseorang apabila ia akan memasuki sebuah sistem. Penerima pesan dapat memastikan keaslian pengirimnya.
2.2.3 Jenis Kriptografi
Menurut (Munir, 2006) terdapat dua jenis algoritma kriptografi berdasarkan jenis kunci yang digunakan, yaitu :
1. Algoritma Kriptografi Simetri (Konvensional) 2. Algoritma Kriptografi Asimetri (Kunci Publik)
1. Kriptografi Simetri
Konsep dasar dari kriptografi kunci simetri adalah kunci yang digunakan untuk enkripsi merupakan kunci yang sama dengan kunci untuk dekripsi. Istilah lain untuk kriptografi kunci simetri adalah kriptografi kunci privat (private-key cryptography), kriptografi kunci rahasia (secret-key cryptography), atau kriptografi konvensional (conventional cryptography). Proses enkripsi dan dekripsi pada kriptografi simetri dapat dilihat pada gambar 2.1.
Gambar 2.1 Proses Enkripsi dan Dekripsi Kriptografi Simetri
Contoh algoritma kunci simetris yang terkenal adalah DES (Data Encryption Standard) dan RC-4. Dua kategori yang termasuk pada algoritma simetris ini adalah algoritma block cipher dan stream cipher.
Algoritma Enkripsi
Algoritma Dekripsi Kunci Kunci
Plaintext Ciphertext
a. Block Cipher
Algoritma block cipher adalah algoritma yang masukan dan keluarannya berupa satu block, dan setiap blocknya terdiri dari banyak bit. Beberapa mode operasi enkripsi block cipher:
1. Data Enkripsi Standard ( DES ) 2. AES ( Advanced Encrytion Standard ) 3. Blowfish
b. Stream Cipher
Stream cipher ( Cipher aliran ) adalah cipher yang berasal dari hasil XOR antara bit plaintext dengan setiap bit kuncinya. Stream cipher sangat rawan terhadap attack pembalikan bit. Beberapa model algoritma stream cipher antara lain :
1. One Time Pad ( OTP ) 2. Rivest Code 4 (RC 4)
Kelebihan kriptografi simetri adalah:
a. Proses enkripsi dan dekripsi kriptografi simetri membutuhkan waktu yang singkat.
b. Ukuran kunci simetri relatif pendek.
c. Otentikasi pengiriman pesan langsung diketahui dari cipherteks yang diterima, karena kunci hanya diketahui oleh penerima dan pengirim saja.
Kekurangan kriptografi simetri adalah:
a. Kunci simetri harus dikirim melalui saluran komunikasi yang aman dan kedua entitas yang berkomunikasi harus menjaga kerahasiaan kunci.
b. Kunci harus sering diubah, setiap kali melaksanakan komunikasi.
2. Kriptografi Asimetri
Pengirim akan mengenkripsi pesan dengan menggunakan kunci publik, sedangkan penerima mendekripsikan pesan menggunakan kunci privat. Algoritma yang memakai kunci publik diantaranya adalah:
a. Digital Signature Algorithm (DSA). b. RSA
c. Diffie-Hellman ( DH )
Proses enkripsi dan dekripsi pada kriptografi asimetri dapat dlihat pada gambar 2.2.
Gambar 2.2 Proses Enkripsi dan Dekripsi Kriptografi Asimetri
Kelebihan kriptografi asimetri adalah:
a. Hanya kunci privat yang perlu dijaga kerahasiaannya oleh setiap entitas yang berkomunikasi.
b. Pasangan kunci privat dan kunci publik tidak perlu diubah dalam jangka waktu yang sangat lama.
c. Dapat digunakan dalam pengamanan pengiriman kunci simetri.
d. Beberapa algoritma kunci publik dapat digunakan untuk memberi tanda tangan digital pada pesan.
Kelemahan kriptografi asimetri adalah:
a. Proses enkripsi dan dekripsi umumnya lebih lambat dari algoritma simetri, karena menggunakan bilangan yang besar dan operasi bilangan yang besar. b. Ukuran cipherteks lebih besar dari pada plainteks.
c. Ukuran kunci relatif lebih besar dari pada ukuran kunci simetri. Algoritma
Enkripsi
Algoritma Dekripsi
Kunci Publik Kunci Privat
Plaintext Ciphertext
2.3 Three Pass Protocol
Dalam kriptografi, three pass protocol merupakan protokol yang memungkinkan satu pihak bisa dengan aman mengirim pesan ke pihak kedua tanpa perlu bertukar atau mendistribusikan kunci enkripsi. Protokol ini pertama kali dikembangkan oleh Adi Shamir, seorang ahli kriptografi berkebangsaan Israel pada tahun 1980. Protokol yang dikembangkannya dikenal dengan nama Shamir No-Key Exchange Protocol. Protokol ini kemudian dimodifikasi oleh James Massey dan Jim K. Omura yang disebut sebagai algoritma Massey-Omura (keduanya adalah pakar teori informasi berkebangsaan Amerika Serikat) pada tahun 1982. Konsep dasar three pass protocol adalah bahwa setiap pihak memiliki kunci pribadi dan kedua pihak menggunakan kunci masing-masing secara mandiri (Degraf, et al. 2007). Three pass protocol bekerja sebagai berikut :
a. Pengirim memilih kunci enkripsi eA. Pengirim mengenkripsi pesan m dengan kunci dan mengirimkan pesan terenkripsi ke penerima.
b. Penerima memilih kunci enkripsi eB. Penerima mengenkripsi pesan C1(eA,m)
dengan kunci dan mengirim pesan terenkripsi C2(eB, C1(eA,m)) ke pengirim.
c. Pengirim mendekripsi pesan C2(eB, C1(eA,m)) dengan menggunakan dA dan
mengirim lagi pesan C3(eB,m) yang mana pesan ini dienkripsi oleh kunci
penerima. Pengirim mengirim pesan tersebut ke penerima. Dan kemudian penerima mendekripsi pesan tersebut dengan dB untuk bisa menghasilkan. Skema dari proses Three Pass Protocol dapat dilihat pada gambar 2.3.
Gambar 2.3 Skema Three Pass Protocol (Isman, 2012) m
C3(eB,m)
C2(eB, C1(eA,m))
2.4 Algoritma Massey-Omura
Algoritma Massey-Omura adalah algoritma kriptografi modern yang menggunakan sistem kriptografi asimetri (kunci privat). Algoritma Massey-Omura diusulkan oleh James Massey dan Jim K. Omura pada tahun 1982 ini, melakukan pemfaktoran bilangan yang sangat besar untuk mendapatkan kunci privat. Oleh karena alasan tersebut, Massey-Omura dianggap aman. Selain itu, Massey-Omura adalah salah satu algoritma yang pengimplementasiannya menggunakan three pass protocol (Winton, 2007).
Secara umum, besaran yang digunakan dalam algoritma Massey-Omura adalah:
1. p adalah bilangan prima (tidak rahasia)
2. eA, eB (kunci enkripsi) (rahasia)
3. dA ≡eA−1(mod p−1) (kunci dekripsi sender) (rahasia) 4. dB ≡ eB−1(mod p−1) (kunci dekripsi receiver) (rahasia)
5. m (plainteks) (rahasia)
6. C1, C2, C3 (cipherteks) (tidak rahasia)
Berikut adalah proses enkripsi dekripsi dengan menggunakan algoritma Massey-Omura (Winton, 2007) :
1. Bilangan prima yang diambil harus lebih besar dari plainteks ( p > m). 2. Ambil eA :
• 2 < eA < p – 1 • GCD ( eA , p-1 ) = 1 3. Hitung dA ≡ eA-1 (mod p-1) 4. Hitung C1 = meA mod p
5. Kirim C1 ke penerima
6. Penerima menerima C1
9. Hitung C2 =C1eB mod p
10. Kirim C2 ke pengirim
11. Pengirim menerima C2
12. Hitung C3 = C2dA mod p
13. Kirim C3 ke penerima
14. Penerima menerima C3 15. Hitung m = C3dB mod p
Sebagai contoh, A ingin mengirimkan pesan “USU” kepada B dengan p = 101. A menggunakan eA = 89 dan B menggunakan eB = 67. Dengan begitu, maka proses yang akan terjadi adalah sbb :
A : U (85) S (83) U (85)
Kunci enkripsi (eA) : 89 89 89
Kunci dekripsi (dA) : 9 9 9
C1 : 64(@) 89(Y) 64(@), dikirim ke B
B : @ (64) Y (89) @ (64)
Kunci enkripsi (eB) : 67 67 67
Kunci dekripsi (dB) : 3 3 3
C2 : 4(EOT) 27(ESC) 4(EOT), dikirim ke A
A : EOT (4) ESC (27) EOT (4)
Kunci enkripsi (eA) : 89 89 89
Kunci dekripsi (dA) : 9 9 9
C3 : 49(1) 90(Z) 49(1), dikirim ke B
B : 1 (49) Z (90) 1 (49)
Kunci enkripsi (eB) : 67 67 67
Kunci dekripsi (dB) : 3 3 3
2.5 Lehmann Prime Generator
Pada algoritma Massey-Omura, penentuan bilangan prima menjadi faktor penting untuk proses enkripsi dan dekripsi. Bilangan prima yang digunakan juga bisa lebih dari dua atau tiga digit. Penulis menggunakan algoritma Lehmann sebagai pembangkit bilangan prima karena apabila bilangan prima p bernilai 1 atau -1 berpeluang prima sebesar 50% yang apabila langkah ini diulang dan lolos sebanyak t kali maka akan menghasilkan sebuah bilangan prima p yang mempunyai kesalahan tidak lebih dari 1/2t (Mahmudi, 2010).
Ada beberapa syarat untuk membangkitkan bilangan prima dengan menggunakan Lehmann Prime Generator, antara lain :
a. ambil a secara acak sehingga 1 < a < p – 1. b. Hitung L = ��
��≡ �
�−1
2 (mod p).
c. Bila L ≡ 1 (mod p) dan L ≡ -1 (mod p) maka pasti p bukan bilangan prima. d. Bila L ≡ 1 (mod p) atau L ≡ -1 (mod p) maka kemungkinan besar ( > 50 %) p adalah prima.
e. Bila syarat d telah terpenuhi maka dilakukan pengujian ulang sebanyak digit bilangan prima yang diambil. Jika pada pengujian terakhir L ≡ 1 (mod p) atau L ≡ -1 (mod p), makan bilangan tersebut pasti prima.
Contoh 1 : penulis ingin mengetahui apakah 15 adalah bilangan prima a = 2
L ≡ 215−12
≡ 27
≡ 128 (mod 15)≡ 8
Contoh 2 : penulis ingin mengetahui apakah 11 adalah bilangan prima a = 3
L ≡ 311−12
≡ 35
≡ 243 (mod 11)≡ 1
Karena jumlah digit bilangan yang diambil ada dua. Maka dilakukan pengujian sebanyak dua kali.
a = 2 L ≡ 211−12
≡ 25
≡ 32 (mod 11) ≡ -1
Setelah dilakukan pengujian sebanyak dua kali dan dihasilkan nilai 1 dan -1. Maka, sesuai ketentuan di atas dapat ditarik kesimpulan bahwa 11 adalah bilangan prima.
Contoh 3 : penulis ingin membuktikan apakah 101 adalah bilangan prima a = 2
L ≡ 2101−12
≡ 250
≡ 1125899906842624 (mod 101)≡ -1
a = 3 L ≡ 3101−12
≡ 350
≡ 717897987691852588770249 (mod 101)≡ -1
a = 4 L ≡ 4101−12
≡ 450
Setelah dilakukan pengujian sebanyak tiga kali sesuai dengan jumlah digit pada bilangan tersebut dan dihasilkan nilai -1, -1 dan 1. Maka, sesuai ketentuan di atas dapat ditarik kesimpulan bahwa 101 adalah bilangan prima.
2.6 Mozilla Thunderbird dan Add On pada Mozilla Thunderbird
Mozilla thunderbird merupakan salah satu produk Mozilla Foundation, yang pertama kali dirilis pada tanggal 7 Desember 2004. Perangkat ini merupakan aplikasi mail client atau (MUA - Mail User Agent) yang bersifat free, open source dan multi-platform. Perangkat ini dikembangkan dengan menggunakan bahasa pemrograman C++, XUL, Javascript dan CSS. Tampilan Mozilla Thunderbird dapat dilihat pada gambar 2.4.
Gambar 2.4 Tampilan Mozilla Thunderbird
BAB 3
ANALISIS DAN PERANCANGAN SISTEM
3.1Analisis Sistem
Dalam perancangan sebuah sistem diperlukan analisis untuk menentukan kebutuhan sistem. Dengan adanya analisis sistem, sistem yang dirancang diharapkan akan lebih baik dan memudahkan dalam pengembangan sistem selanjutnya. Tujuan dari analisis sistem ini sendiri adalah untuk membantu pemodelan rancang bangun sistem yang nantinya akan diimplementasikan dalam bentuk nyata.
3.1.1 Analisis Masalah
Untuk mengidentifikasi masalah digunakan diagram Ishikawa (fishbone diagram). Diagram Ishikawa adalah sebuah alat grafis yang digunakan untuk mengidentifikasi, mengeksplorasi dan menggambarkan suatu masalah, sebab dan akibat dari masalah itu. Diagram ini juga sering disebut sebagai diagram sebab-akibat atau diagram tulang ikan. Identifikasi terhadap permasalahan akan membantu analisis persyaratan sistem yang nantinya akan dikembangkan.
Masalah utama yang mendapat perhatian adalah kenyamanan dan keamanan dalam implementasi three pass protocol. Selanjutnya masalah ini diuraikan ke dalam beberapa kategori yaitu, pengguna e-mail (people), implementasi kriptografi (method), perangkat pendukung (material) dan teknik pengimplementasian (procedure).
bila pesan ini dicuri oleh orang yang tidak bertanggung jawab kemungkinan akan merugikan pengguna. Untuk kategori implementasi kriptografi, penyebab masalah yang mungkin muncul adalah pembangkitan bilangan prima dan proses enkripsi dekripsi dengan algoritma Massey-Omura. Untuk kategori perangkat pendukung, penyebab masalah yang mungkin muncul adalah media untuk pengimplementasian kriptografi serta koneksi internet yang tidak stabil sehingga mempengaruhi waktu pengiriman pesan. Sedangkan untuk kategori teknik pengimplementasian, penyebab masalah adalah penggunaan add on pada Mozilla Thunderbird untuk proses enkripsi dan dekripsi teks yang akan dikirim melalui e-mail. Seluruh kategori dan sebab akibat yang disebutkan kemudian dimuat dalam sebuah diagram Ishikawa seperti pada gambar 3.1.
Gambar 3.1 Diagram Ishikawa untuk Analisis Permasalahan Sistem
3.1.2 Analisis Persyaratan (Requirement Analysis)
Analisis persyaratan sebuah sistem dikelompokkan ke dalam dua bagian besar yaitu : 1) Analisis Persyaratan Fungsional
2) Analisis Persyaratan Non-Fungsional
Persyaratan non-fungsional adalah persyaratan apa yang harus dilakukan sistem. Seringkali berupa batasan atau sesuatu yang menjadi perhatian stakeholder sebuah sistem. Persyaratan non fungsional meliputi performa, mudah untuk dipelajari dan digunakan, hemat biaya, dokumentasi, manajemen kualitas, dan kontrol.
a) Performa
Add on yang dibangun harus dapat mengenkripsi pesan dengan menggunakan algoritma Massey-Omura dan Lehmann Prime Generator. Dan dapat mendekripsi kembali pesan tersebut.
b) Mudah digunakan (User friendly)
Add on yang dibangun harus sederhana agar mudah digunakan oleh pengguna (user). Add on yang dimaksud adalah Add on yang memiliki interface yang menarik dan memiliki cara penggunaan yang mudah dalam pengoperasiannya.
c) Hemat biaya
Add on yang dibangun tidak memerlukan perangkat tambahan ataupun perangkat pendukung lainnya yang dapat mengeluarkan biaya.
d) Kontrol
Add On yang dibangun memiliki kontrol untuk bisa digunakan dalam setiap versi Mozilla Thunderbird.
3.1.3 Pemodelan Sistem
Pemodelan sistem dilakukan untuk memperoleh gambaran yang lebih jelas tentang objek apa saja yang akan berinteraksi dengan sistem serta hal-hal apa saja yang harus dilakukan oleh sebuah sistem sehingga sistem dapat berfungsi sesuai dengan baik sesuai dengan fungsionalitasnya.
Sesuai dengan analisis kebutuhan sistem, beberapa hal yang nantinya harus dilakukan sistem adalah :
1. Melakukan enkripsi dan dekripsi pesan teks yang terdapat pada e-mail dengan algoritma Massey-Omura
2. Melakukan enkripsi dan dekripsi pesan teks yang terdapat pada e-mail dengan menerapkan Three Pass Protocol.
3. Membangkitkan bilangan prima dengan algoritma Lehmann Prime Generator.
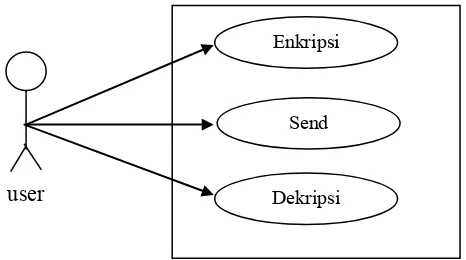
Berdasarkan informasi kebutuhan sistem dan aktor yang berperan, diagram use case pada gambar 3.2 dirancang sebagai pemodelan persyaratan sistem.
Gambar 3.2 Use Case Diagram Sistem Yang Akan Dikembangkan
Pada diagram tersebut tampak bahwa seorang pengguna melakukan proses enkripsi pada pesan sebelum pesan tersebut dikirim. Pengguna perlu mengetahui secara persis proses apa saja yang terjadi pada setiap tahap. Dengan demikian harus melakukan tahap-tahap tersebut dengan bantuan arahan dari sistem. Enkripsi dan dekripsi dipilih oleh pengguna setiap tahap, namun pilihan pengguna ini tetap akan dievaluasi oleh sistem, apakah urutan proses yang dipilih oleh pengguna sesuai dengan Three Pass Protocol. Untuk proses Send terjadi setiap selesai proses enkripsi dan dekripsi, kecuali Dekripsi II. Hal ini dikarenakan pada tahapan Three Pass Protocol setelah pesan didekripsi oleh penerima pesan, pesan itu tidak dikirimkan kembali kepada pengirim karena pesan hasil dekripsi itu merupakan pesan asli.
Spesifikasi untuk use case enkripsi dapat dilihat pada tabel 3.1.
user
Enkripsi
Tabel 3.1 Spesifikasi Use Case Enkripsi
Name Enkripsi
Actors User
Trigger User telah menginputkan plainteks yang akan dienkripsi
Preconditions Pesan yang akan diproses berada pada body e-mail Mozilla Thunderbird
Post Conditions User dapat melihat cipherteks hasil proses enkripsi
Success Scenario 1. User telah menginputkan plainteks yang akan dienkripsi.
2. User mengakses tombol enkripsi.
3. Sistem mengecek pesan yang terdapat pada body e-mail.
4. Jika tidak terdapat pesan pada bodye-mail maka user
menginputkan kembali pesan yang akan dikirim
5. Jika terdapat pesan, maka sistem akan memanggil pembangkit
kunci.
6. Sistem akan melakukan proses enkripsi terhadap plainteks yang
diinputkan dan menampilkan cipherteksnya.
7. User dapat melihat cipherteks hasil proses enkripsi.
Alternative Flows -
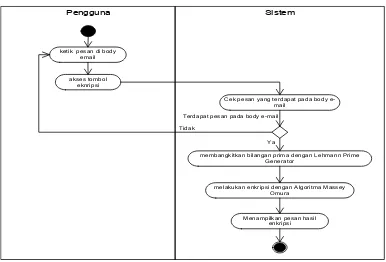
Activity diagram untuk use case enkripsi dapat dilihat pada gambar 3.3.
Pengguna Sistem
ketik pesan di body email
akses tombol eknripsi
melakukan enkripsi dengan Algoritma Massey Omura
Menampilkan pesan hasil enkripsi
membangkitkan bilangan prima dengan Lehmann Prime Generator
Cek pesan yang terdapat pada body e-mail
Terdapat pesan pada body e-mail
Terdapat dua kali proses enkripsi pada Three Pass Protocol, yang pertama dilakukan oleh pengirim pesan dan yang kedua dilakukan oleh penerima pesan. Proses yang terjadi pada saat enkipsi yang pertama tidak jauh berbeda dengan proses enkripsi yang kedua. Perbedaannya hanya pada kunci enkripsinya eA dan eB. Dimana eA merupakan kunci enkripsi pengirim pesan dan eB merupakan kunci enkripsi penerima pesan. Kemudian cipherteks hasil enkripsi pertama akan menjadi plainteks pada enkripsi kedua setelah pesan dikirim oleh pengirim ke penerima.
Untuk melakukan proses enkripsi baik pengirim maupun penerima cukup mengakses tombol enkripsi. Kemudian sistem akan membangkitkan bilangan prima dengan Lehmann Prime Generator. Bilangan prima tersebut juga akan menjadi penentu kunci enkripsi. Setelah bilangan prima dibangkitkan, selanjutnya sistem akan mengenkripsi pesan yang sudah diketikkan di body e-mail dengan algoritma Massey-Omura yang kemudian hasil enkripsinya dapat dilihat di body e-mail dimana pesan diketikkan sebelumnya.
Spesifikasi untuk use case send dapat dilihat pada tabel 3.2.
Tabel 3.2 Spesifikasi Use Case Send
Name Send
Actors User
Trigger
-Preconditions User telah menginputkan pesan di body e-mail
Post Conditions
-Success Scenario 1. User telah menginputkan pesan yang akan dikirim.
2. User mengakses tombol send.
3. Sistem mengirim pesan ke alamat e-mail yang dituju
Alternative Flows -
Sistem Pengguna
input pesan yang akan dikirim
akses tombol send
kirim pesan
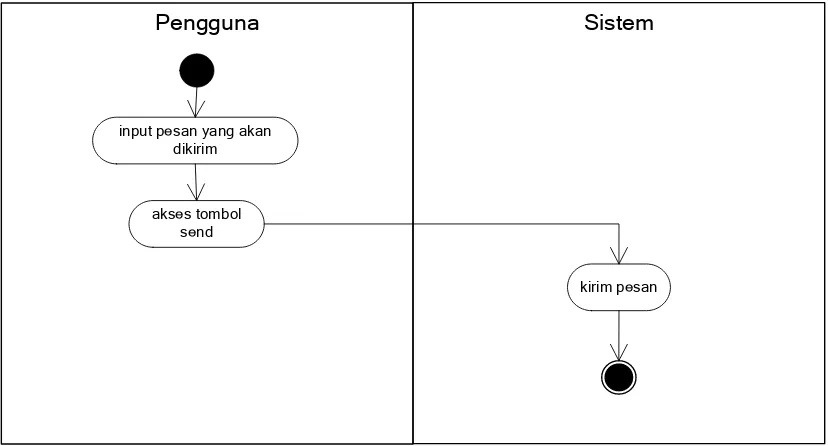
Gambar 3.4 Activity Diagram Send
Karena media yang digunakan adalah e-mail, proses pengiriman data atau pesan menjadi bagian yang penting. Baik pengirim maupun penerima akan melakukan proses send untuk mengirim pesan satu sama lain. Dalam proses Three Pass Protocol terdapat 3 kali proses send. Dari pengirim ke penerima, penerima ke pengirim dan pengirim ke penerima.
Untuk melakukan pengiriman pesan, baik pengirim maupun penerima cukup mengakses tombol send. Kemudian sistem akan mengirimkan pesan yang telah tertulis di body e-mail ke alamat e-mail yang dituju..
Spesifikasi untuk use case dekripsi dapat dilihat pada tabel 3.3.
Tabel 3.3 Spesifikasi Use Case Dekripsi
Name Dekripsi
Actors User
Trigger User telah menginputkan cipherteks yang akan didekripsi
Preconditions User mengakses tomboldekripsi
Post Conditions User dapat melihat plainteks hasil proses dekripsi
2. User mengakses tombol dekripsi.
3. Sistem mengecek pesan yang terdapat pada body e-mail.
4. Jika tidak terdapat pesan pada bodye-mail maka user
menginputkan kembali pesan yang akan dikirim
5. Jika terdapat pesan, maka sistem akan memanggil kembali kunci
yang tersimpan.
6. Sistem akan melakukan proses dekripsi terhadap cipherteks yang
diinputkan dan menampilkan plainteksnya.
7. User dapat melihat plainteks hasil proses dekripsi.
Alternative Flows -
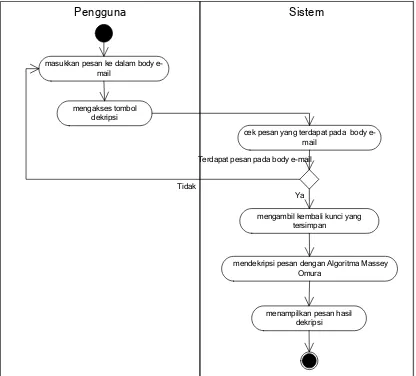
Activity diagram untuk use case dekripsi dapat dilihat pada gambar 3.5.
Sistem Pengguna
masukkan pesan ke dalam body e-mail
mengakses tombol dekripsi
mendekripsi pesan dengan Algoritma Massey Omura
menampilkan pesan hasil dekripsi
mengambil kembali kunci yang tersimpan
cek pesan yang terdapat pada body e-mail
Terdapat pesan pada body e-mail
Ya Tidak
Sama halnya pada proses enkripsi, terdapat dua kali proses dekripsi pada Three Pass Protocol, yang pertama dilakukan oleh pengirim pesan dan yang kedua
dilakukan oleh penerima pesan. Proses yang terjadi pada saat dekipsi yang pertama tidak jauh berbeda dengan proses dekripsi yang kedua. Perbedaannya hanya pada kunci dekripsinya dA dan dB. Dimana dA merupakan kunci dekripsi pengirim pesan dan dB merupakan kunci dekripsi penerima pesan.
Untuk melakukan proses dekripsi baik pengirim maupun penerima cukup mengakses tombol dekripsi. Kemudian sistem akan mengambil kembali kunci yang tersimpan. Kemudian sistem akan mendekripsi pesan yang ada di body e-mail dengan algoritma Massey-Omura yang kemudian hasil dekripsinya dapat dilihat di body e-mail dimana pesan diketikkan sebelumnya
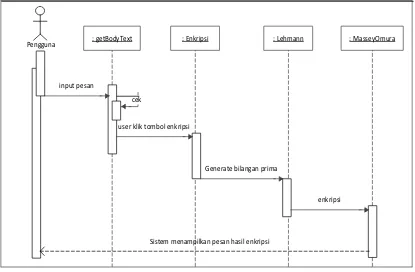
Sequence diagram untuk proses enkripsi dapat dilihat pada gambar 3.6.
: getBodyText : Enkripsi : Lehmann : MasseyOmura
Generate bilangan prima input pesan
user klik tombol enkripsi
enkripsi
Sistem menampilkan pesan hasil enkripsi Pengguna
cek
Gambar 3.6 Sequence Diagram Enkripsi
tersebut dengan algoritma Massey-Omura. Pesan hasil enkripsi (ciphertext) otomatis dituliskan kembali ke dalam body e-mail.
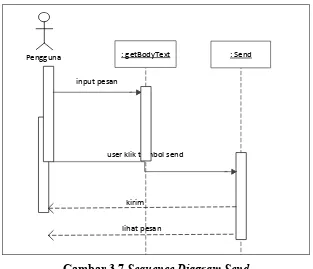
Hasil dari enkripsi pada proses yang pertama diatas akan dikirim. Sequence diagram pengirimannya dapat dilihat pada gambar 3.7.
: Send
input pesan
user klik tombol send
lihat pesan : getBodyText Pengguna
kirim
Gambar 3.7 Sequence Diagram Send
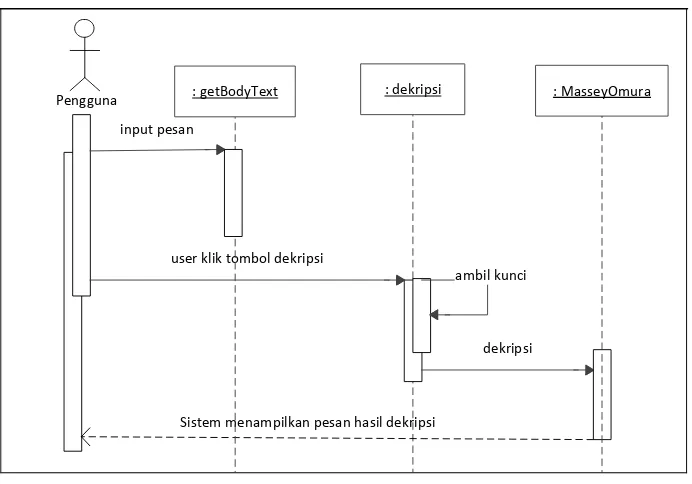
: dekripsi
dekripsi input pesan
user klik tombol dekripsi
ambil kunci
Sistem menampilkan pesan hasil dekripsi
: MasseyOmura : getBodyText
Pengguna
Gambar 3.8 Sequence Diagram Dekripsi
Pada gambar 3.8 dapat dilihat bahwa pengguna harus mengakses tombol dekripsi untuk mendekripsi pesan yang terdapat di body e-mail. Setelah pengguna mengakses tombol dekripsi, maka sistem terlebih dahulu akan mengambil kunci yang telah disimpan untuk digunakan dalam proses dekripsi. Kemudian pesan hasil dekripsi akan ditampilkan di body e-mail.
3.1.4 Pseudocode dan Flowchart
Pseudocode merupakan urutan langkah-langkah yang mendeskripsikan dari algoritma-algoritma yang mempunyai struktur sederhana dengan tujuan untuk memudahkan manusia dalam memahami prinsip-prinsip algoritma. Flowchart adalah bagan yang memperlihatkan urutan dan hubungan antar proses beserta pernyataannya. Dengan adanya flowchart pengguna dapat lebih mudah memahami bagaimana sistem bekerja.
1) Pseudocode Proses Enkripsi
Gambar 3.9 Pseudocode Algoritma Enkripsi Massey-Omura
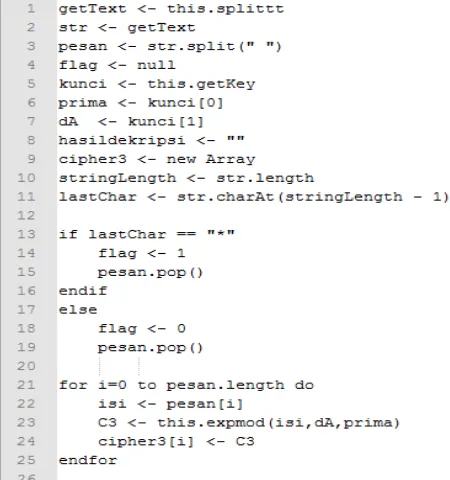
2) Pseudocode Proses Dekripsi
Urutan proses enkripsi yang dilakukan untuk mengenkripsi pesan dituliskan sebagai pseudocode seperti pada gambar 3.10.
Gambar 3.10 Pseudocode Algoritma Dekripsi Massey-Omura
eksponensial dari tiap-tiap bilangan. Namun, jika tidak terdapat tanda asterix (*) maka sistem akan menghitung modulo eksponensial dari bilangan-bilangan yang terdapat di body e-mail dan mengembalikan kode ASCII dari nilai desimal yang dihasilkan.
3) Pseudocode Pembangkit Bilangan Prima
Urutan proses pembangkitan bilangan prima yang dilakukan dituliskan sebagai pseudocode seperti pada gambar 3.11.
Gambar 3.11 Pseudocode dan Kompleksitas Algoritma LPG
tidak sama dengan nol. Kemudian dilakukan penghitungan Legendre sebanyak jumlah digit bilangan tersebut untuk memastikan bahwa bilangan tersebut pasti prima.
4) Flowchart Proses Algoritma Massey-Omura pada Three Pass Protocol
Pada algoritma Massey-Omura yang proses pengimplementasiannya menggunakan three pass protocol, terjadi dua kali enkripsi yang dilakukan oleh pengirim dan penerima pesan. Dimana pihak pertama melakukan proses enkripsi pertama (E1) akan menghasilkan cipherteks yang menjadi plainteks untuk pihak
kedua dan setelah itu pihak kedua mengenkripsi lagi (E2) menghasilkan
Mulai
Plainteks (P)
Chiperteks (C2)
Cipherteks (C1)
Enkripsi I (eA)
Enkripsi II (eB)
Plainteks (P) Chiperteks
(C3)
Dekripsi I (dA)
Dekripsi II (dB)
Selesai
5) Flowchart Enkripsi
Proses enkripsi merupakan proses mengubah pesan asli ke cipherteks sehingga tidak dimengerti. Terdapat dua kali proses enkripsi pada algoritma Massey-Omura. Proses yang terjadi pada enkripsi akan dijelaskan pada Gambar 3.13.
Mulai
Plainteks (P)
Cipherteks (C1)
Selesai
Generate bilangan prima (p)
Ambil eA 2 < eA < p - 1
dA eA-1 (mod p-1)
C1 meA (mod p)
Keterangan :
eA : Kunci enkripsi sender p : Bilangan prima m : Plainteks
dA : Kunci dekripsi sender
Mulai
Cipherteks (C1)
Cipherteks (C2)
Selesai Ambil eB 2 < eB < p - 1
dB eB-1 (mod p-1)
C2 C1eB (mod p )
Keterangan :
eB : Kunci enkripsi receiver p : Bilangan prima
m : Plainteks
dB : Kunci dekripsi receiver
6) Flowchart Dekripsi
Proses dekripsi merupakan proses mengembalikan ciphertext ke plaintext (pesan asli). Terdapat dua kali proses dekripsi pada algoritma Massey-Omura. Dimana pesan asli akan diperoleh setelah proses dekripsi ke-2. Proses yang terjadi pada dekripsikan dijelaskan pada gambar 3.15.
Mulai
Cipherteks (C2)
Cipherteks (C3)
Selesai C3 C2dA (mod p )
Mulai
Cipherteks (C3)
Plainteks (P)
Selesai C4 C3dB (mod p )
Gambar 3.16 Flowchart Proses Dekripsi II
7) Flowchart Proses Pembangkitan Bilangan Prima dengan Menggunakan Lehmann Prime Generator
Mulai
Plainteks (P)
Selesai Bilangan prima
L = 1 atau L ≡ -1 tidak
Pencarian L sebanyak jumlah
digit p L ≡ a (p-1)/2 mod p
ya
ya tidak
Generate bilangan prima p
Generate bilangan acak a, (1<a<p)
Gambar 3.17 Flowchart Proses Pembangkitan Bilangan Prima Keterangan :
L : Legendre
3.2 Perancangan Sistem
Berdasarkan hasil analisis proses yang berlangsung dalam sistem diperoleh gambaran fungsionalitas yang nantinya diterapkan pada sistem. Berdasarkan gambaran ini, dilakukan perancangan antarmuka pengguna dan perancangan struktur direktori pada berkas .xpi, dimana rancangan ini nantinya akan diimplementasikan menggunakan bahasa pemrograman.
3.2.1 Perancangan Antar Muka
Add On yang dirancangan nantinya akan diwakilkan sebagai dua buah icon yang ditempatkan pada toolbar jendela Write New Message pada aplikasi Mozilla Thunderbird. Letak icon Add On yang dirancang pada tool bar Mozilla Thunderbird dapat dilihat pada gambar 3.18.
Tabel 3.4 Komponen pada Toolbar No. Nama Komponen Keterangan
1 Menubar Mozilla Thunderbird Merupakan sebuah Menu bar yang terdapat pada Mozilla Thunderbird, didalamnya terdapat menu-menu untuk memudahkan pengguna dalam menggunakan e-mail client Mozilla Thunderbird.
2 Toolbar Mozilla Thunderbird Merupakan sebuah tools yang terdapat pada Mozilla Thunderbird, didalamnya terdapat icon-icon untuk memudahkan pengguna dalam menggunakan e-mail client Mozilla Thunderbird.
3 Icon Enkripsi Icon untuk proses enkripsi pesan yang terdapat pada body e-mail.
4 Icon Dekripsi Icon untuk proses dekripsipesan yang terdapat pada body e-mail.
5 E-mail Address Box Merupakan area untuk penulisan e-mail address pengirim dan penerima e-mail.
6 Subject Merupakan area utuk penulisan subjek dari e-mail yang akan dikirim.
7 Body E-mail Merupakan tempat penulisan pesan yang akan dikirim.
3.2.2 Perancangan Struktur Direktori Add On
2.
Gambar 3.19 Struktur Direktori untuk Add On yang Dikembangkan
Struktur direktori tersebut terdiri atas sebuah direktori yang diberi nama Add On yang sedang dirancang dan sebuah sub-direktori yang diberi nama “chrome”. Selain itu direktori utama juga berisikan dua berkas masing-masing “chrome.manifest” dan “install.rdf”. Ini merupakan standar umum untuk struktur direktori aplikasi Add On pada Mozilla Thunderbird. Di dalam sub direktori terdapat beberapa dokumen yang terdiri atas dokumen berekstensi “*.xul” yaitu dokumen overlay yang menjelaskan bahwa Add On akan melakukan fungsinya pada jendela tertentu dalam Mozilla Thunderbird. Sedangkan dokumen berekstensi “*.css” berguna untuk mengatur posisi dan ukuran icon pada jendela Mozilla Thunderbird. Berkas yang menjelaskan behavior (fungsionalitas) Add On adalah berkas berekstensi “*.js”, berkas ini berisikan program yang ditulis dengan bahasa pemrograman javascript. Secara lengkap dokumen-dokumen ini dapat ditemukan pada bagian lampiran skripsi ini.
masseyomura.xpi
chrome.manifest install.rdf
chrome button.css
MasseyOmura.js icon.png button.xul
BAB 4
IMPLEMENTASI DAN PENGUJIAN
4.1 Implementasi Sistem
Setelah dilakukan analisis dan perancangan, proses berikutnya adalah implementasi desain logik yang telah dibuat pada tahap sebelumnya.
4.1.1 Tahapan Algoritma Massey-Omura dan Three Pass Protocol dengan menggunakan Lehmann Prime Generator
Algoritma Massey-Omura adalah algoritma kriptografi modern yang menggunakan sistem kriptografi asimetri (kunci privat). Algoritma Massey-Omura diusulkan oleh James Massey dan Jim K. Omura pada tahun 1982 ini, melakukan pemfaktoran bilangan yang sangat besar untuk mendapatkan kunci privat. Oleh karena alasan tersebut, Massey-Omura dianggap aman. Selain itu, Massey-Omura adalah salah satu algoritma yang pengimplementasiannya menggunakan three pass protocol (Winton, 2007).
Dalam kriptografi, three pass protocol merupakan kerangka kerja yang memungkinkan satu pihak bisa dengan aman mengirim pesan ke pihak kedua tanpa perlu bertukar atau mendistribusikan kunci enkripsi. Konsep dasar three pass protocol adalah bahwa setiap pihak memiliki kunci pribadi dan kedua pihak menggunakan kunci masing-masing secara mandiri (Degraf, et al. 2007). Three pass protocol bekerja sebagai berikut :
a. Pengirim memilih kunci enkripsi eA. Pengirim mengenkripsi pesan m dengan kunci dan mengirimkan pesan terenkripsi ke penerima.
c. Pengirim mendekripsi pesan C2(eB, C1(eA,m)) dengan menggunakan dA dan
mengirim lagi pesan C3(eB,m) yang mana pesan ini dienkripsi oleh kunci
penerima. Pengirim mengirim pesan tersebut ke penerima. Dan kemudian penerima mendekripsi pesan tersebut dengan dB untuk bisa menghasilkan C4(Plainteks).
Pada algoritma Massey-Omura ini, dibutuhkan bilangan prima untuk proses enkripsi dan dekripsi. Bilangan prima yang digunakan juga bisa lebih dari dua atau tiga digit.Oleh sebab itu, digunakan Lehmann Prime Generator untuk membangkitkan bilangan prima secara acak sehingga penulis tidak perlu menetapkan atau mencari bilangan prima secara manual. Penulis menggunakan algoritma Lehmann sebagai pembangkit bilangan prima karena apabila bilangan prima p bernilai 1 atau -1 berpeluang prima sebesar 50% yang apabila langkah ini diulang dan lolos sebanyak t kali maka akan menghasilkan sebuah bilangan prima p yang mempunyai kesalahan tidak lebih dari 1/2t (Mahmudi, 2010). Dimana t adalah jumlah digit bilangan prima yang diuji. Maka tingkat kesalahan yang dapat dilakukan semakin kecil daripada menggunakan algoritma pembangkit bilangan prima yang sering digunakan seperti Fermat. Pembangkit bilangan prima Lehmann juga efesien untuk mencari nilai yang sangat besar.
Sebagai contoh, A ingin mengirimkan pesan “ILKOM” kepada B. A menggunakan eA = 89 dan B menggunakan eB = 67. Dengan begitu, maka proses yang akan terjadi adalah sbb :
1. Pilih bilangan prima p dengan menggunakan Lehmann Prime Generator.
Pengecekan bilangan prima yang dibangkitkan adalah dengan menggunakan Lehmann Prime Generator. Misalnya :
Bangkitkan bilangan prima 101, dan dilakukan pengecekan apakah bilangan ini merupakan bilangan prima atau bukan dengan cara sebagai berikut :
a. pilih sebuah bilangan a dimana 1< a < 101.
b. misalkan nilai random yang terpilih untuk nilai a adalah 2.
≡ 2 (101-1)/2
mod 101 ≡ 250
mod 101
≡ 1125899906842624 mod 101 ≡ -1
d. Dikarenakan 101 memiliki 3 digit, yaitu 1, 0 dan 1, maka pembuktian nilai 101 merupakan prima adalah dicari sebanyak 3 kali. Maka pilih kembali nilai a. misal a = 3, maka
≡ 717897987691852588770249 mod 101 ≡ -1
a = 4, maka
≡ 126765060022822401496703205376 mod 101 ≡ 1 Maka benar bahwa 101 merupakan bilangan prima.
2. Enkripsi pesan dengan menggunakan algoritma Massey-Omura. Karakter “I” dalam ASCII bernilai 73,
Karakter “L” dalam ASCII bernilai 76, Karakter “K” dalam ASCII bernilai 75, Karakter “O” dalam ASCII bernilai 79, Karakter “M” dalam ASCII bernilai 77,
Kemudian diketahui bahwa untuk mencari cipherteks maka kita menggunakan rumus:
C1 = meA mod p
Dimana eA telah ditentukan sebelumnya bernilai 89 dan p bernilai 101, sehingga : C1= meA mod p = 7389 mod 101 = 59
C1= meA mod p = 7589 mod 101 = 11
C1= meA mod p = 7989 mod 101 = 19
C1= meA mod p = 7789 mod 101 = 47
Plainteks “Ilkom” setelah dienkripsi dengan Massey-Omura menjadi “59 77 11 19 47”. Cipherteks ini kemudian dikirim ke B.
3. Penerapan Three Pass Protocol untuk mendapatkan plainteks.
Setelah B meneriman pesan dari A yang merupakan cipherteks, B tidak dapat langsung mendekripsi pesan tersebut untuk mendapatkan plainteksnya. Tetapi, B harus mengenkripsi cipherteks tersebut dengan rumus :
C2= C1eB mod p
Dimana eB bernilai 67 dan p bernilai 101, sehingga : C2 =C1eB mod p = 5967 mod 101 = 86
C2= C1eB mod p = 7767 mod 101 = 96
C2 =C1eB mod p = 1167 mod 101 = 12
C2 =C1eB mod p = 1967 mod 101 = 68
C2 =C1eB mod p = 4767 mod 101 = 23
Cipherteks “59 2 17 10 26” setelah dienkripsi lagi oleh B menjadi “86 96 12 68 23”. Cipherteks ini kemudian dikirim ke A. Kemudian A mendekripsi cipherteks tersebut dengan rumus :
C3 = C2dA mod p
Dimana dA ≡ eA-1 (mod p-1), sehingga : C3 = C2dA mod p = 869 mod 101 = 46
C3 =C2dA mod p = 969 mod 101 = 13
C3 =C2dA mod p = 129 mod 101 = 18
C3 =C2dA mod p = 689 mod 101 = 92
Cipherteks “86 26 14 91 83” setelah dienkripsi lagi oleh A menjadi “46 13 18 92 96”.
Cipherteks ini kemudian dikirim ke B. Kemudian B mendekripsi cipherteks tersebut dengan rumus :
m = C3dB mod p
Dimana dB ≡ eB-1 (mod p-1), sehingga : C4 = C3dB mod p = 463 mod 101 = 73
C4 = C3dB mod p = 133 mod 101 = 76
C4 = C3dB mod p = 183 mod 101 = 75
C4 = C3dB mod p = 923 mod 101 = 79
C4 = C3dB mod p = 963 mod 101 = 77
Nilai 73 dalam kode ASCII adalah karakter I Nilai 76 dalam kode ASCII adalah karakter L Nilai 75 dalam kode ASCII adalah karakter K Nilai 79 dalam kode ASCII adalah karakter O Nilai 77 dalam kode ASCII adalah karakter M
Setelah B mendekripsi pesan tersebut, maka diketahuilah bahwa pesan yang dikirim oleh A adalah “ILKOM”.
4.1.2 Spesifikasi Kebutuhan Perangkat Lunak
4.1.3 Tampilan Sistem
Berikut adalah tampilan dari sistem yang dibangun :
1) Antarmuka Add-Ons Manager pada Pemasangan Add On Kemanan E-mail
Setelah diimplementasi dalam bentuk package dengan ekstensi archive document “*.xpi”, Add On dipasangkan pada Perangkat Mozilla Thuderbird menggunakan fasilitas Add-Ons Manager.
Gambar 4.1 Pemasangan Add On dengan Menggunakan Add-Ons Manager
Pada gambar 4.1 terlihat bahwa add on Massey-Omura cryptosystem telah berhasil terpasang di e-mail client Mozilla Thunderbird dan add on ini tidak bersifat permanen, disable add on untuk tidak memakai add on ini di Mozilla Thunderbird dan remove untuk menghapus add on dari Mozilla Thunderbird.
2) Antarmuka Jendela Write Setelah Pemasangan Add On Kemanan E-mail
Gambar 4.2 Icon Enkripsi pada Toolbar Mozilla Thunderbird
Icon dekripsi digunakan untuk mendekripsi pesan. Sama seperti icon enkripsi, icon dekripsi akan otomatis muncul di toolbar apabila add on telah terpasang. Namun apabila add on telah terpasang, icon dekripsi masih belum muncul di toolbar, pengguna bisa menambahkan icon secara manual dengan menu View >> Toolbars >> Customize. Lalu drag icon ke toolbar.
3) Antarmuka Proses Enkripsi dan Dekripsi Pesan Sesuai dengan Three Pass Protocol
Proses pertama adalah pesan dimasukkan oleh pengirim pada jendela write, kemudian pengguna menekan buton “enkripsi” pada toolbar. Perangkat Add On kemudian membangkitkan bilangan prima dengan Lehmann Prime Generator dan membangkitkan kunci dengan algoritma Massey-Omura untuk melakukan enkripsi pesan. Kunci ini disimpan untuk keperluan dekripsi pada tahap selanjutnya.
Gambar 4.4 Pesan sebelum dienkripsi oleh Pengirim
Gambar 4.5 Pesan setelah dienkripsi oleh Pengirim
Pesan hasil enkripsi ini kemudian dikirimkan kepada penerima. Kemudian penerima membangkitkan kunci dengan algoritma Massey-Omura, kunci ini kemudian digunakan untuk proses enkripsi. Seperti pada proses sebelumnya kunci ini disimpan untuk keperluan dekripsi pada tahap berikutnya.
Pesan hasil enkripsi sebanyak dua kali ini dikirim kembali ke pengirim untuk selanjutnya dilakukan dekripsi dengan kunci yang telah disimpan oleh perangkat add on milik pengirim.
Gambar 4.7 Hasil Dekripsi Pesan oleh Pengirim
Kemudian pesan ini kembali dikirimkan kepada penerima untuk selanjutnya didekripsi oleh penerima sesuai dengan kunci miliknya sehingga diperoleh pesan asli.
Pada gambar 4.8 terlihat bahwa pesan telah berhasil didekripsi. Pesan hasil dekripsi tersebut sama dengan pesan sebelum dienkripsi. Hal ini menunjukkan bahwa proses enkripsi dan dekripsi dengan menggunakan algoritma Massey-Omura untuk mengamankan e-mail di Mozilla Thunderbird berjalan dengan baik.
4.2 Pengujian Sistem
Pada tahap ini dilakukan pengujian terhadap perangkat lunak yang telah diimplementasikan dalam bentuk Add On. Adapun beberapa hal yang menjadi sasaran pengujian perangkat lunak Add On keamanan E-mail ini adalah :
1. Menguji apakah aspek confidentiality dalam kriptografi telah terpenuhi dengan memastikan bahwa pesan hasil enkripsi tidak dapat dibaca oleh orang lain. 2. Menguji apakah aspek data integrity dalam kriptografi telah terpenuhi dengan
memastikan bahwa pesan sebelum dienkripsi dan setelah didekripsi adalah sama.
3. Mengukur waktu yang diperlukan untuk mengeksekusi proses enkripsi dan dekripsi.
4.2.1 Data Hasil Pengujian
Untuk mengetahui hasil pengujian aspek confidentiality dapat dilihat pada tabel 4.1.
Tabel 4.1 Hasil Pengujian Aspek Confidentiality
Pesan Enkripsi I Enkripsi II
USU 2043418 121084 2043418 6133261
* 858623 4331136 858623 *
081401010
500444 2598040 1670051 4337624
500444 1670051 500444 1670051
500444 4687829 *
815502 1941853 465300 881822
815502 465300 815502 465300
815502 *
Ilmu Komputer
2556051 5115522 2988582
5219197 2976866 495622 1478401
2988582 755033 5219197 1636821
3488046 3044722 5348281 *
4575877 4728561 5014609
2742486 3539275 396028
2469616 5014609 3129839
2055179 *
Fakultas Ilmu Komputer
dan Teknologi Informasi
255781 416055 564535 772950
666318 892019 416055 63124
277981 128321 666318 98538
772950 277981 656981 225042
98538 922376 772950 892019
609682 354969 277981 570168
416055 864483 277981 551491
609682 564535 864483 225042
666318 225042 275043 573367
277981 128321 864483 42016
225042 354969 98538 416055
63124 573367 950611 *
458858 117281 864926 171348
272402 267518 117281 307201
460050 75058 272402 596435
171348 460050 21878 416968
596435 279881 171348 267518
941669 460099 460050 853035
117281 304492 460050 663727
941669 864926 304492 416968
272402 416968 660192 610966
460050 75058 304492 30582
416968 460099 596435 117281
307201 610966 *
Implementasi Massey
Omura Cryptosystem
dan Lehmann Prime
Generator untuk
Keamanan E-Mail pada
Mozilla Thunderbird
1633623 2916815 1898716
1492768 2909374 2916815
2909374 834175 416648 3229294
1563826 3031084 2548027
1746361 3229294 1563826
1563826 2909374 1807477
2548027 372239 2916815 1134715
3205256 3229294 2548027
2654313 3205256 1807477
1898716 416648 3123964 1563826
1807477 1563826 416648 2909374
2916815 2548027 2613157
3229294 834175 2548027 1151882
2909374 1144934 2916815
3229294 834175 834175 2548027
3203993 3205256 3031084
2916815 2909374 2548027
2405542 2909374 834175 2909374
3205256 3229294 416648 3123964
3205256 2548027 1134715 834175
416648 1134715 2769103 2548027
1349219 2909374 3229294
2916815 3229294 834175 3229294
834175 2548027 661724 857977
1746361 3229294 3031084
1492768 2548027 1898716
1520444 1500076 1967088
1825298 504929 1500076 504929
726957 1275724 2083221
1216059 211232 1090562
2421961 2083221 1216059
1216059 504929 1370045
1090562 2628284 1500076
3311915 1800807 2083221
1090562 1241870 1800807
1370045 1967088 1275724
1468093 1216059 1370045
1216059 1275724 504929
1500076 1090562 2925239
2083221 726957 1090562
1627044 504929 227709 1500076
2083221 726957 726957 1090562
831081 1800807 211232 1500076
504929 1090562 2571236 504929
726957 504929 1800807 2083221
1275724 1468093 1800807
1090562 3311915 726957
1275724 3311915 3099562
1090562 2818300 504929
2083221 1500076 2083221
726957 2083221 726957 1090562
3229294 2613157 3229294
2548027 1746361 3123964
3193390 3031084 1492768
1492768 3229294 2548027
1941173 1144934 1134715 834175
2613157 2909374 3205256
1575859 3031084 3205256
2613157 3432553 *
2083221 211232 1825298
1090562 1967088 2083221
2925239 2083221 1090562
2421961 1468093 2134742
211232 1825298 1825298
2083221 1090562 1601848
227709 3311915 726957 2925239
504929 1800807 996896 211232
1800807 2925239 *
Berdasarkan tabel 4.1, dapat dilihat bahwa setelah dilakukan enkripsi I jumlah karakter terlihat bertambah. Karakter terakhir tersebut bukan merupakan penambahan karakter yang tidak diinginkan, melainkan bilangan prima yang akan dikirim ke penerima pesan. Kemudian terdapat tanda asterix (*) pada pesan hasil enkripsi yang digunakan sebagai penanda untuk melakukan proses selanjutnya. Selain itu, pesan yang telah dienkripsi dengan algoritma Massey-Omura tersebut telah berubah menjadi deretan angka-angka dan tidak dapat diketahui pesan aslinya. Hal ini menunjukkan bahwa aspek confidentiality dalam kriptografi telah terpenuhi.
Untuk mengetahui hasil pengujian aspek data integrity dapat dilihat pada tabel 4.2.
Tabel 4.2 Hasil Pengujian Aspek Data Integrity
Pesan Enkripsi I Enkripsi II Dekripsi I Dekripsi II
USU 2043418 121084
2043418 6133261 *
858623 4331136
500444 4687829 *
3044722 5348281 * 2055179 * 4988059
307201 610966 *