PERBANDINGAN WAKTU EKSEKUSI ALGORITMA
DSATUR
DAN ALGORITMA PEWARNAAN HEURISTIK
TABU
SEARCH
PADA PEWARNAAN GRAF
TESIS
JUNIDAR
117038020
PROGRAM STUDI S2 TEKNIK INFORMATIKA
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
PERBANDINGAN WAKTU EKSEKUSI ALGORITMA
DSATUR
DAN ALGORITMA PEWARNAAN HEURISTIK
TABU
SEARCH
PADA PEWARNAAN GRAF
TESIS
Diajukan untuk melengkapi tugas dan memenuhi syarat memperoleh ijazah Magister Teknik Informatika
JUNIDAR 117038020
PROGRAM STUDI S2 TEKNIK INFORMATIKA
FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI INFORMASI UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : Perbandingan Waktu Eksekusi Algoritma
Dsatur dan Algoritma Pewarnaan Heuristik Tabu Search Pada Pewarnaan Graf
Kategori : Tesis
Nama : JUNIDAR
Nomor Induk Mahasiswa : 117038020
Program Studi : Magister (S2) Teknik Informatika
Fakultas : Ilmu Komputer dan Teknologi Informasi Universitas Sumatera Utara
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dr. Erna Budhiarti Nababan, M. IT Prof. Dr. Herman Mawengkang
Diketahui/disetujui oleh
Program Studi S2 Teknik Informatika Ketua,
PERNYATAAN
PERBANDINGAN WAKTU EKSEKUSI ALGORITMA
DSATUR
DAN ALGORITMA PEWARNAAN HEURISTIK
TABU
SEARCH
PADA PEWARNAAN GRAF
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing telah disebutkan sumbernya.
Medan, 28 Agustus 2013
JUNIDAR
PERNYATAAN PERSETUJUAN PUBLIKASI
KARYA ILMIAH UNTUK KEPENTINGAN
AKADEMIS
Sebagai sivitas akademika Universitas Sumatera Utara, saya yang bertanda tangan di bawah ini:
Nama : JUNIDAR
NIM : 117038020
Program Studi : Magister (S2) Teknik Informatika Jenis Karya Ilmiah : TESIS
Demi pengembangan ilmu pengetahuan, menyetujui untuk memberikan kepada Universitas Sumatera Utara Hak Bebas Royalti Non-Eksklusif (Non-Exclusive Royalty free Right) atas Tesis saya yang berjudul:
PERBANDINGAN WAKTU EKSEKUSI ALGORITMA
DSATUR
DAN ALGORITMA PEWARNAAN HEURISTIK
TABU
SEARCH
PADA PEWARNAAN GRAF
Beserta perangkat yang ada (jika diperlukan). Dengan Hak Bebas Royalti Non-Eksklusif ini, Universitas Sumatera Utara berhak menyimpan, mengalih media, memformat, mengelola dalam bentuk data base, merawat dan mempublikasikan tesis saya tanpa meminta izin dari saya selama tetap mencantumkan nama saya sebagai penulis dan sebagai pemegang dan atau sebagai pemilik hak cipta.
Demikian pernyataan ini dibuat dengan sebenarnya.
Medan, 28 Agustus 2013
Telah diuji pada
Tanggal : 28 Agustus 2013
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Herman Mawengkang Anggota : 1. Dr. Erna Budhiarti Nababan, M.IT
RIWAYAT HIDUP
DATA PRIBADI
Nama Lengkap Berikut Gelar : Junidar, S.Si
Tempat dan Tanggal Lahir : Banda Aceh, 10 Juni 1978
Alamat Rumah : Jl. T. Hamzah No. 53 Kuta Alam, B. Aceh
Telepon/Faks/HP : +6281360136719
e-mail : [email protected]
Instansi Tempat Bekerja : FMIPA UNSYIAH
Alamat Kantor : Darussalam - Banda Aceh
Telepon/Faks/HP : +626517551819
DATA PENDIDIKAN
SD : SD Negeri No. 4 Banda Aceh Tamat : 1990
SMP : SMP Negeri 4 Banda Aceh Tamat : 1993
SMA : SMA Negeri 2 Banda Aceh Tamat : 1996
Strata-1 : FMIPA MATEMATIKA UNSYIAH Tamat : 2001
KATA PENGANTAR
Assalamu’alaikum Wr. Wb.
Pertama-tama penulis panjatkan syukur Alhamdulillah kepada Allah SWT, berkat rahmat dan kemurahanNya penulis dapat menyelesaikan tesis ini dengan judul Perbandingan Waktu Eksekusi Algoritma Dsatur dan Algoritma Pewarnaan Heuristik Tabu Search Pada Pewarnaan Graf.
Laporan tesis ini disusun dan diajukan untuk memenuhi persyaratan dalam memperoleh gelar magister pada Program Pascasarjana FasilKom TI Universitas Sumatera Utara.
Dalam penyelesaian tesis beserta penyusunan laporannya dapat berjalan dengan lancar, tidak lepas dari dukungan berbagai pihak. Oleh karena itu, penulis mengucapkan banyak terima kasih kepada:
Allah SWT yang senantiasa memberikan kemudahan dan kekuatan kepada penulis dalam memahami dan mengamalkan ilmu-ilmu yang didapatkan selama ini.
Bapak Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc (CTM), Sp. A(K) selaku Rektor Universitas Sumatera Utara, atas kesempatan yang diberikan kepada penulis untuk mengikuti dan menyelesaikan pendidikan Program Magister.
Bapak Prof. Dr. Muhammad Zarlis, selaku Dekan FasilKom TI Universitas Sumatera Utara, atas kesempatan yang diberikan kepada penulis untuk mengikuti dan menyelesaikan pendidikan Program Magister pada Program Pascasarjana FasilKom TI Universitas Sumatera Utara..
Bapak Prof. Dr. Muhammad Zarlis selaku Ketua Program Studi Magister Teknik Informatika dengan penuh perhatian telah memberikan saran, kritik, dorongan, bimbingan dan motivasi kepada penulis.
Bapak Prof. Dr. Herman Mawengkang selaku pembimbing utama yang dengan penuh kesabaran menuntun dan membimbing penulis hingga selesainya penelitian ini.
Ibu Dr. Erna Budhiarti Nababan, M. IT selaku pembimbing anggota yang dengan penuh perhatian telah memberikan saran, kritik, dorongan, bimbingan dan motivasi kepada penulis.
Seluruh dosen serta civitas akademika pada Program Studi Magister Teknik Informatika Program Pascasarjana FasilKom TI Universitas Sumatera Utara, yang telah memberikan bekal ilmu dan pengetahuan selama penulis mengikuti kuliah di Universitas Sumatera Utara.
Orangtua tercinta, ayahanda M. Yusdar Sufi dan ibunda Cut Nasrumiati serta seluruh keluarga yang senantiasa mendoakan dan memberikan dorongan kepada penulis.
Suami dan anak tercinta, Zikril Hakim dan Shaznin Kamilia Hakim yang selalu mendoakan, memberikan semangat dengan kasih sayang, sabar dan bantuan selama penulis mengikuti pendidikan. Budi baik ini tidak dapat dibalas, hanya diserahkan kepada Allah SWT. Sekali lagi terimakasih.
Rekan mahasiswa se-angkatan penulis program studi magister (S2) Teknik Informatika Komputer FasilKom TI Universitas Sumatera Utara yang telah banyak membantu penulis selama mengikuti perkuliahan.
Dekan FMIPA Unsyiah, Bapak Dr. Hizir Sofyan yang telah memberikan izin, bantuan moril dan kesempatan kepada penulis untuk mengikuti pendidikan lanjutan pada program Pascasarjana FasillKom TI Universitas Sumatera Utara
Bapak Nasrullah Ridwan, S.T yang telah banyak memberikan motivasi, bantuan dan dorongan kepada penulis selama perkuliahan serta dalam menyelesaikan tesis ini.
Semua pihak yang tidak dapat disebutkan satu-persatu, yang telah berperan serta dalam penelitian tesis ini dan dalam pembuatan laporan tesis ini.
Akhir kata penulis berharap semoga tesis beserta laporannya ini membawa manfaat dan faedah bagi pembaca dan pihak-pihak yang berkepentingan, serta buat penulis sendiri sebagai dharma bakti penulis kepada almamater.
Wassalamualaikum.Wr.Wb.
Medan, 28 Agustus 2013 Penulis
ABSTRAK
Pewarnaan graf G adalah proses pemberian warna pada verteks - verteks di G, satu warna untuk setiap verteks, sehingga verteks - verteks yang bersisian mempunyai warna yang berbeda. Jika ada kemungkinan untuk menemukan pewarnaan yang tepat dari graf G, dengan menggunakan x warna, maka G
dikatakan x-colorable. Bilangan kromatik dari graf G adalah bilangan bulat terkecil x dimana G adalah x-colorable, di notasikan dengan � � . Terdapat beberapa metode heuristik yang dapat digunakan untuk menyelesaikan permasalahan pewarnaan graf. Yaitu algoritma dsatur dan algoritma pewarnaan heuristik tabu search.
COMPARISON OF EXECUTION TIME DSATUR ALGORITHMS AND TABU SEARCH COLORING HEURISTIC ALGORITHMS ON
GRAPH COLORING
ABSTRACT
A coloring of graph G is assignment of colors to the vertices of G, one color to each vertex, so that adjacent vertices are assigned distinct colors. If x colors are used, then the coloring is referred to as an x-coloring. If it is possible to find a proper coloring of a graph G, using x colors, G is said to be x-colorable. The chromatic number of a graph G is the smallest integer x for which G is x -colorable, and is denoted by � � . There are many heuristic methods that can be used to solve graph coloring problem. One of the algorithm can be implemented is tabu seach algorithm.
DAFTAR ISI
Halaman
HALAMAN JUDUL i
PENGESAHAN ii
PERNYATAAN ORISINALITAS iii
PERSETUJUAN PUBLIKASI iv
PANITIA PENGUJI v
RIWAYAT HIDUP vi
KATA PENGANTAR vii
ABSTRAK x
ABSTRACT ix
DAFTAR ISI xii
DAFTAR TABEL xiv
DAFTAR GAMBAR xv
BAB 1 PENDAHULUAN 1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Batasan Masalah 2
1.4 Tujuan Penelitian 3
1.5 Manfaat Penelitian 3
BAB 2 TINJAUAN PUSTAKA 2.1 Pengertian Graf 4
2.1.1 Keterhubungan Graf 6
2.1.1 Subgraf dan Graf Bipartit 6
2.2 Pewarnaan Graf 8
2.3 Metode Heuristik 10
2.3.2 Algoritma Dsatur (Derajat Warna Heuristik) 12
2.3.3 Algoritma Pewarnaan Heuristik Tabu Search 14
2.4 Riset Terkait 19
2.5 Kontribusi Riset 19
BAB 3 METODOLOGI PENELITIAN 3.1 Data Yang Digunakan 21
3.2 Pewarnaan Graf 22
3.2.1 Pewarnaan Graf Dengan Algoritma Dsatur 22
3.2.2 Pewarnaan Graf Dengan Algoritma Pewarnaan Heuristik Tabu Search 23
BAB 4 HASIL DAN PEMBAHASAN 4.1 Hasil 29
4.1.1 Tampilan Input Program 29
4.1.2 Tampilan Output Program 31
4.2 Pembahasan 32
BAB 5 PENUTUP 5.1 Kesimpulan 35
5.2 Saran 35
DAFTAR TABEL
Halaman
Tabel 3.1. Graf benchmark DIMACS 22
Tabel 3.2. Hasil rata-rata paling minimum yang diperoleh dari eksekusi algoritma pewarnaan heuristik tabu search pada graf myciel3
25
Tabel 3.3. Hasil yang diperoleh dari eksekusi algoritma pewarnaan heuristik tabu search graf queen8
28 Tabel 4.1. Rata-rata running time dari algoritma dsatur 32 Tabel 4.2. Rata-rata running time dari algoritma pewarnaan heuristik
tabu search untuk graf dengan order p 50
32 Tabel 4.3. Rata-rata running time dari algoritma pewarnaan heuristik
tabu search untuk graf dengan order 50 < < 100
DAFTAR GAMBAR
Halaman
2.1 Graf G 4
2.2 Graf Tidak Sederhana 5
2.3 Graf dengan derajat minimal dan maksimal 5
2.4 Sikel 6
2.5 Dua subgragf (G1 dan G2) dari suatu graf G 7
2.6 Graf G-v 7
2.7 Graf G-e 7
2.8 Graf bipartit 8
2.9 Graf lengkap 8
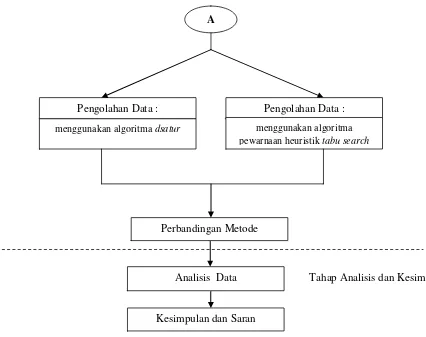
3.1 Diagram Metodologi Penelitian 21
3.2 Grafik rata-rata nilai fungsi objektif, Z, dari algoritma heuristik tabu search yang diaplikasikan pada graf myciel3
untuk menentukan nilai parameter tabu untuk maxit 120, 140 dan 150
24
3.3 Grafik rata-rata nilai fungsi objektif, Z, dari algoritma heuristik tabu search yang diaplikasikan pada graf queen8
untuk menentukan nilai parameter tabu untuk maxit 160, 180 dan 200
ABSTRAK
Pewarnaan graf G adalah proses pemberian warna pada verteks - verteks di G, satu warna untuk setiap verteks, sehingga verteks - verteks yang bersisian mempunyai warna yang berbeda. Jika ada kemungkinan untuk menemukan pewarnaan yang tepat dari graf G, dengan menggunakan x warna, maka G
dikatakan x-colorable. Bilangan kromatik dari graf G adalah bilangan bulat terkecil x dimana G adalah x-colorable, di notasikan dengan � � . Terdapat beberapa metode heuristik yang dapat digunakan untuk menyelesaikan permasalahan pewarnaan graf. Yaitu algoritma dsatur dan algoritma pewarnaan heuristik tabu search.
COMPARISON OF EXECUTION TIME DSATUR ALGORITHMS AND TABU SEARCH COLORING HEURISTIC ALGORITHMS ON
GRAPH COLORING
ABSTRACT
A coloring of graph G is assignment of colors to the vertices of G, one color to each vertex, so that adjacent vertices are assigned distinct colors. If x colors are used, then the coloring is referred to as an x-coloring. If it is possible to find a proper coloring of a graph G, using x colors, G is said to be x-colorable. The chromatic number of a graph G is the smallest integer x for which G is x -colorable, and is denoted by � � . There are many heuristic methods that can be used to solve graph coloring problem. One of the algorithm can be implemented is tabu seach algorithm.
BAB 1
PENDAHULUAN
1.1. Latar Belakang
Banyak peristiwa nyata dalam kehidupan sehari-hari dapat disajikan secara baik dan menarik dalam bentuk suatu graf. Diantaranya jaringan listrik, komunikasi, peta jalan, struktur organisasi, penyusunan jadwal, penjadwalan job shop dan pewarnaan peta dan tempat penyimpanan.
Pengertian graf secara umum adalah diagram yang terdiri dari titik-titik yang disebut dengan verteks dan ruas-ruas garis yang menghubungkan verteks disebut dengan sisi (Martono, 1990).
Permasalahan pewarnaan graf adalah memberikan warna pada verteks-verteks sedemikian sehingga dua verteks-verteks yang dihubungkan mempunyai warna yang berbeda. Sedangkan jumlah warna minimal yang dibutuhkan untuk mewarnakan graf disebut dengan bilangan kromatik (Narsingh, 1986).
Masalah pewarnaan graf merupakan masalah yang termasuk kedalam kelompok NP-complete ( Non-deterministic Polynomial) yaitu masalah yang sulit ditemukan solusinya (Gross & Yellen, 1999). Salah satu cara untuk menyelesaikan masalah NP-complete adalah dengan menggunakan metode heuristik.
Metode heuristik tidak memiliki algoritma pencarian solusi optimum yang pasti tetapi memiliki kaidah yang dapat mengeksplorasi ruang pencarian solusi optimum atau mendekati. Ciri algoritma heuristik adalah selalu menemukan solusi yang baik tetapi tidak harus yang terbaik, serta cepat dan mudah untuk diimplementasikan.
beberapa verteks saja. Sementara untuk verteks yang lebih banyak, metode heuristik lebih variatif karena metode heuristik menggunakan metode pendekatan dan melakukan penyelesaian terarah. Beberapa metode heuristik yang pernah digunakan untuk menyelesaikan pewarnaan graf adalah dengan algoritma dan algoritma pewarnaan heuristik tabu search.
Dari beberapa metode heuristik untuk menyelesaikan masalah pewarnaan graf, maka terjadi perbandingan untuk menentukan metode mana yang terbaik yang digunakan untuk menentukan warna minimum.
Malaguti (2010) menyatakan bahwa dari sekian banyaknya algoritma yang ada untuk menyelesaikan permasalahan pewarnaan graf, algoritma tabu search
merupakan salah satu pilihan yang tepat. Algoritma tabu search adalah salah satu metode heuristik untuk penyelesaian permasalahan optimasi (Glover, 1995)
Chambers (1998) menerapkan pendekatan algoritma tabu search yang dinamis, yang dapat disesuaikan dengan kondisi-kondisi pencarian yang berubah-ubah terutama pada masalah pewarnaan graf.
1.2. Perumusan Masalah
Adanya hasil pencarian bilangan kromatik pada pewarnaan graf yang tidak optimal sehingga memerlukan waktu yang lebih lama. Untuk menyelesaikan permasalahan ini akan dilakukan penyelesaian bilangan kromatik pada pewarnaan graf dengan menggunakan algoritma dsatur (atau disebut juga derajat warna heuristik) dan algoritma pewarnaan heuristik tabu search, kemudian dilakukan analisis perbandingan dengan kedua algoritma tersebut, untuk mengetahui rata-rata waktu eksekusi dalam menyelesaikan bilangan kromatik pada permasalahan pewarnaan graf.
1.3. Batasan Masalah
Batasan masalah dalam tesis ini adalah sebagai berikut :
2. Graf yang digunakan adalah graf yang tak berarah.
3. Banyaknya verteks atau order (p) yang digunakan 10 100 .
1.4. Tujuan Penelitian
Tujuan dari penulisan ini adalah menganalisis waktu eksekusi dari dua metode heuristik yaitu algoritma dsatur dan algoritma pewarnaan heuristik tabu search
yang digunakan untuk menyelesaikan bilangan kromatik pada masalah pewarnaan graf.
1.5. Manfaat Penelitian
Manfaat dari penelitian ini adalah :
1. Memberikan analisis perbandingan waktu eksekusi dari dua metode heuristik yang digunakan yaitu algoritma dsatur dan algoritma pewarnaan heuristik tabu search untuk menyelesaikan bilangan kromatik pada pewarnaan graf.
2. Memberikan solusi pewarnaan graf yang optimum kepada penerima informasi
BAB 2
TINJAUAN PUSTAKA
2.1. Pengertian Graf
Suatu graf Gadalah suatu pasangan himpunan (V(G),E(G)), dimana V(G) = { v1,
v2,…..vn } adalah himpunan tak kosong berhingga yang terdiri dari titik-titik
disebut verteks dan suatu himpunan E(G) = { e1, e2,…..en } dengan garis-garis yang
menghubungkan verteks-verteks disebut sisi (Chartrand dan Oellerman, 1993). Penulisan yang tepat untuk menyatakan sisi adalah e=(v1v2) atau e=(v2v1).
Jika e=(v1v2) adalah suatu sisi dari graf G, maka dikatakan v1 dan v2 bersisian
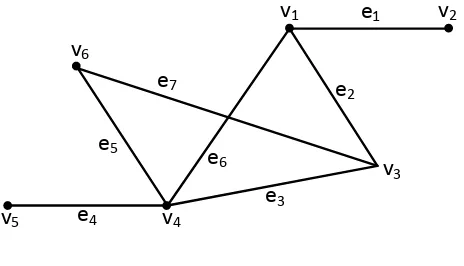
(adjacent). G :
e7
v6
v1 e1 v2
e5
e4
v5 v4
e3
e6 v
3
e2
Gambar 2.1. Graf G
Pada gambar 2.1, G adalah graf dengan :
V(G) = { v1, v2,v3,v4,v5,v6, } dan E(G) = { e1,e2,e3,e4,e5,e6,e7,}, dimana e1 = (v1v2), e2
= (v1v3), e3 = (v3v4), e4 = (v4v5), e5 = (v4v6), e6 = (v1v4), dan e7 = (v3v7).
Suatu gelang ( loop) pada suatu graf G adalah suatu sisi yang verteks awalnya sama dengan verteks akhir yaitu e=(v1v1).
Dua verteks yang dihubungkan lebih dari satu sisi maka disebut sisi paralel.
G:
v
2e
3e
2v
1e
1v
3e
6e
4e
5Gambar 2.2 Graf Tidak Sederhana
Graf G pada gambar 2.2, sisi e4 dan e5 merupakan sisi paralel dan sisi e3 merupakan gelang.
Banyaknya verteks dari suatu graf G disebut ordo (orde) dengan notasi p dan banyaknya sisi dari suatu graf G disebut ukuran (size) dengan notasi q. Suatu graf G dengan ordo p dan ukuran q dinotasikan (p,q) graf.
Suatu graf G, jika v V(G), derajat dari v dinotasikan dengan d(v) yaitu banyaknya sisi yang bertemu di v (Narsingh, 1986).
Derajat terkecil dari suatu verteks-verteks di G disebut derajat minimal dengan notasi (G) dan derajat terbesar dari suatu verteks-verteks di G disebut derajat maksimaldengan notasi Δ G .
Suatu verteks yang berderajat 0 disebut verteks isolasi dan suatu verteks yang derajat 1 disebut verteks ujung (pendant) serta suatu verteks yang memuat gelang dianggap verteks yang berderajat 2 (Fletcher, 1991).
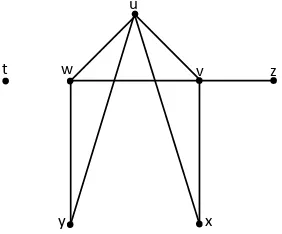
G:
t w
u
v z
x y
Graf G pada gambar 2.3, d(u) = 4, d(v) = 4, d(w) = 3, d(x) = 2, d(y) = 2, d(z) = 1 dan d(t) = 0 maka Δ(G) = 4 dan (G) = 0.
2.1.1. Keterhubungan graf
Suatu jalan (walk) dalam suatu graf G adalah barisan berganti-ganti W : v0, e1, v1, e2, v2, …, vn-1, en, vn (n ≥0) dari verteks-verteks dan sisi-sisi yang
diawali dan diakhiri dengan verteks-verteks, sehingga ei = vi-1 vi untuk I = 1, 2, …, n. Karena jalan W diawali dengan v0 dan diakhiri dengan vn, dinyatakan
sebagai suatu jalan v0– vn (a v0– vn walk) (Harary, 1994).
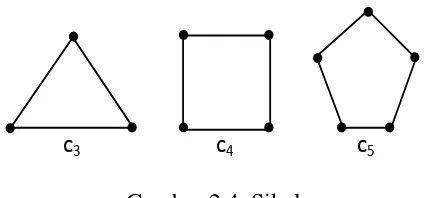
Suatu sikel (cycle) adalaj suatu jalan v0, e1, e2, …, vn-1, en, vndimana n≥3,
v0=vn dan n verteks v0,v1…, vn tanpa pengulangan, dinotasikan Cn. suatu sikel
disebut genap jika panjangnya genap. Suatu sikel disebut ganjil jika panjangnya ganjil.
Graf pada gambar 2.4, memuat C3, C4 dan C5.
c3 c4 c5
Gambar 2.4. Sikel
Suatu graf G sendiri adalah terhubung (connected) jika u terhubungkan ke v untuk setiap pasangan u,v dari verteks-verteks di G.Suatu graf G yang tidak terhubung dikatakan terputus(disconnected).
2.1.2. Subgraf dan graf bipartit
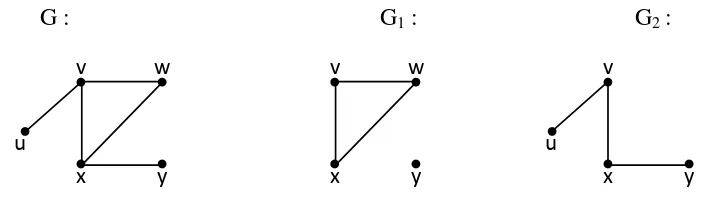
Graf G1 disebut subgraf dari G jika V1 adalah himpunan bagian dari V(G) dan E1
adalah himpunan bagian dari E(G) dari G1 sendiri merupakan suatu graf.
G : G1 : G2 :
v w
x y
v w
x y
v
x y
u u
Gambar 2.5. Dua subgragf (G1 dan G2) dari suatu graf G
Jika v suatu verteks di G, maka G-v adalah suatu subgraf G yang dihasilkan dengan menghilangkan v dan semua sisi yang bersisian di v.
Gambar 2.6 merupakan suatu graf G dengan graf G-v.
G : G-v :
x u
z
y
v
w
x u
z
y w
Gambar 2.6. Graf G-v
Jika e suatu sisi di G, maka G-e adalah suatu subgraf G yang dihasilkan dengan menghilangkan suatu sisi e di G (Liu, 1995).
Gambar 2.7 merupakan suatu graf G dengan G-e.
G : G-e
e
Gambar 2.7. Graf G-e
Suatu bagian G disebut graf bipartit jika V(G) dapat dipartisi menjadi dua himpunan bagian V1 dan V2 sedemikian sehingga V(G) = V1 V2 yaitu setiap sisi
Graf G gambar 2.8(a) adalah graf bipartit karena V(G) dapat dipartisi menjadi dua himpunan bagian V1 = {v1,v6} dan V2 = {v2, v3, v4, v5} dimana setiap sisi di G
terhubungkan dengan verteks di V1 dan V2. Setelah digambar ulang, jelas G
adalah graf bipartit, seperti pda gambar 2.8(b). G :
v1 v2
v5 v6
v3
v4
v1 v6
v2 v5
v4 v3
Gambar 2.8. Graf bipartit
Suatu graf tidak trivial G adalah bipartit jika dan hanya jika G tidak memuat sikel ganjil.
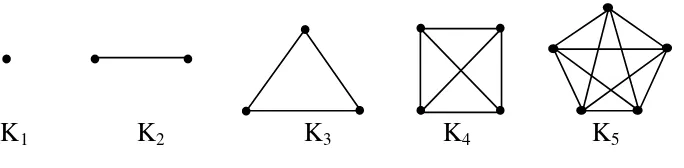
Suatu graf G disebut graf lengkap jika setiap pasang verteksnya bersisian. Graf lengkap dengan ordo p dinotasikan dengan Kp.
Graf pada gambar 2.9 adalah Kp untuk setiap p = 1, 2, 3, 4, 5.
K
3K
4K
5K
2K
1Gambar 2.9. Graf lengkap
2.2. Pewarnaan Graf
Suatu pewarnaan dari graf G adalah proses pemberian warna-warna pada verteks - verteks di G, satu warna untuk setiap verteks (Gross & Yellen, 1999). Seharusnya, setiap perwarnaan G, menggunakan x warna, partisi himpunan V(G) verteks ke dalam himpunan x, disebut sebagai kelas warna, sehingga setiap verteks dari kelas
warna tertentu akan mendapatkan warna yang sama (West, 2001). Jika x warna yang digunakan untuk mewarnai (coloring), pewarnaan ini disebut sebagai x-coloring G. Pada masalah pewarnaan graf klasik adalah bahwa kelas warna harus menjadi himpunan independen dan jenis pewarnaan ini disebut sebagai pewarnaan yang tepat, yaitu, pewarnaan yang tepat dari G adalah pemberian warna pada verteks - verteks sedemikian sehingga tidak ada dua verteks yang bersisian (adjacent) di G mempunyai warna yang sama (Wallis, 2000). Jika ada kemungkinan untuk menemukan pewarnaan yang tepat dari graf G, dengan menggunakan x warna, maka G dikatakan x-colorable. Suatu graf adalah x-colorable jika dan hanya jika graf nya adalah x-partite. Khususnya, graf 2-colorable adalah graf yang sama dengan graf bipartit (Clark & Holton, 1991). Bilangan kromatik, � � , dari graf G adalah bilangan bulat terkecil x dimana G
adalah x-colorable (West, 2001). Ini sama dengan, � � adalah bilangan bulat terkecil x dimana G adalah graf x-partit. Suatu graf G dengan bilangan kromatik x
disebut sebagai x-kromatik dan G dikatakan akan � � -colorable, seperi pewarnaan yang optimal disebut � � -coloring G (Chatrand & Oellermann, 1993).
Untuk pewarnaan derajat maksimum dengan syarat bahwa untuk setiap kelas warna �, ∆ � , dimana ℕ0. Suatu x-coloring dari graf G memenuhi persyaratan disebut sebagai ∆ ,� -coloring di G, yaitu ∆ ,�
-coloring graf G adalah d-admissible pewarnaan di G yang berkaitan dengan parameter ∆. Suatu graf ∆ ,� -colorable jika ∆ ,� -coloring dari graf yang ada. Bilangan bulat positif terkecil x yang ada ∆ ,� -coloring di G (Untuk beberapa nilai tetap ℕ0) disebut ∆ -chromatic number G, dinotasikan dengan �Δ � , dan seperti pewarnaan yang optimal disebut �Δ-coloring G. Akhirnya, suatu graf G dengan ∆ -chromatic number x disebut sebagai ∆ ,�
2.3. Metode Heuristik
Metode Heuristik adalah teknik yang dirancang untuk memecahkan masalah yang mengabaikan apakah solusi dapat dibuktikan benar, tapi yang biasanya menghasilkan solusi yang baik atau memecahkan masalah yang lebih sederhana yang mengandung atau memotong dengan pemecahan masalah yang lebih kompleks. Metode Heuristik ini bertujuan untuk mendapatkan performa komputasi atau penyederhanaan konseptual, berpotensi pada biaya keakuratan atau presisi. Metode heuristik ada dua jenis yakni metode heuristik sederhana dan metaheuristik.
Metaheuristik pada sebenarnya adalah metode pendekatan yang didasarkan pada metode heuristik. Sehingga tidak heran bahwa metode heuristik sering kali diintegrasikan di dalam metode metaheuristik.
Perbedaan utama dari metode heuristik dan metaheuristik adalah : metode heuristik bersifat problem dependent sedangkan metode metaheuristik bersifat problem independent.
Problem dependent artinya bergantung pada permasalahan, jadi metode heuristik itu hanya bisa dipakai untuk jenis permasalahan terntentu. Misalnya, metode nearest neighborhood (NN) termasuk metode heuristik. Metode hanya bisa dipakai pada permasalahan yang mengenal konsep neighborhood (tetangga), misalnya pada pewarnaan graf, Traveling Salesman Problem maupaun Vehicle Routing Problems. Sedangkan problem independent berarti tidak bergantung pada jenis permasalahan. Jadi penerapan metode metaheuristik tidak bergantung pada jenis permasalahan, alias bisa dipakai untuk berbagai jenis permasalahan. Contoh dari metode metaheuristik adalah algoritma genetik (GA), particle swam optimization (PSO), Ant Colony Optimization (ACO).
2.3.1. Tabu Search
dipaksakan oleh kebudayaan social sebagai suatu tindakan pencegahan atau sesuatu yang dilarang karena berbahaya. Bahaya yang harus dihindari dalam tabu search adalah penjadwalan yang tidak layak, dan terjebak tanpa ada jalan keluar. Dalam konteks lebih luas, larangan perlindungan dapat diganti jika terjadi tuntutan yang mendadak(Glover, 1995).
Tabu search adalah sebuah metode optimasi yang berbasis pada local search. Proses pencarian bergerak dari satu solusi ke solusi berikutnya, dengan cara memilih solusi terbaik neighbourhood sekarang (current) yang tidak tergolong solusi terlarang (tabu). Ide dasar dari algoritma tabu search adalah mencegah proses pencarian dari local search agar tidak melakukan pencarian ulang pada ruang solusi yang sudah pernah ditelusuri, dengan memanfaatkan suatu struktur memori yang mencatat sebagian jejak proses pencarian yang telah dilakukan.
Struktur memori fundamental dalam tabu search dinamakan tabu list. Tabu list menyimpan atribut dari sebagian move (transisi solusi) yang telah diterapkan pada iterasi-iterasi sebelumnya. Tabu search menggunakan tabu list
untuk menolak solusi-solusi yang memenuhi atribut tertentu guna mencegah proses pencarian mengalami cycling pada daerah solusi yang sama, dan menuntun proses pencarian menelusuri daerah solusi yang belum dikunjungi. Tanpa mengunakan strategi ini, local search yang sudah menemukan solusi optimum lokal dapat terjebak pada daerah solusi optimum local tersebut pada iterasi-iterasi berikutnya. List ini mengikuti aturan LIFO dan biasanya sangat pendek (panjangnya biasanya sebesar O( N ), dimana N adalah jumlah total dari operasi). Setiap saat ada langkah itu akan ditempatkan dalam tabu list.
Perekaman solusi secara lengkap dalam sebuah forbidden list dan pengecekan apakah sebuah kandidat solusi tercatat dalam list tersebut merupakan cara yang mahal, baik dari sisi kebutuhan memori maupun kebutuhan waktu komputasi. Jadi, tabu list hanya menyimpan langkah transisi (move) yang merupakan lawan satu kebalikan dari langkah yang telah digunakan dalam iterasi sebelumnya untuk bergerak dari satu solusi ke solusi berikutnya. Dengan kata lain
yang lama.
Pada tiap iterasi, dipilih solusi baru yang merupakan solusi terbaik dalam
neighbourhood dan tidak tergolong sebagai tabu. Kualitas solusi baru ini tidak harus lebih baik dari kualitas solusi sekarang. Apabila solusi baru ini memiliki nilai fungsi objektif lebih baik dibandingkan solusi terbaik yang telah dicapai sebelumnya, maka solusi baru ini dicatat sebagai solusi terbaik yang baru.
Sebagai tambahan dari tabu list, dikenal adanya kriteria aspirasi, yaitu suatu Penanganan khusus terhadap move yang dinilai dapat menghasilkan solusi yang dinilai dapat menghasilkan solusi yang baik namun move tersebut berstatus tabu. Dalam hal ini, jika move tersebut memenuhi criteria aspirasi yang telah ditetapkan sebelumnya, maka move tersebut dapat digunakan utnuk membentuk solusi berikutnya (status tabunya dibatalkan).
2.3.2. Algoritma Dsatur (Derajat Warna Heuristik)
Algoritma 1 dsatur (Derajat warna heuristik)
input : Suatu graf G dengan order dan suatu nilai d yang mana bilangan
kromatik harus ditentukan.
output : batas atas x pada ∆ ,� -coloring G
1: L ← � � � =∆(�)
2: Pilih v ϵ L dan misalkan � ← �1 ∪ �
3: � ←1
4: untuk semua i= 2,..., n do
5: Tentukan � � ∀ = 1,…, ,� � , = 1,…,�
6 � ← � � � , = 1,…,� dan � � � � ∀� � , = 1,…,�
7: if � > 1 then
8: Tentukan G' sedmikian sehingga � �′ =� � �1∪ �2∪ … ∪ ��
9: v ← suatu verteks di T sehingga �′ � �′ � ∀� ϵ T
10: else � = 1
11: v ← hanya verteks di T
12: end if
13: � ← � ∪ � dimana jumlah warna terkecil sehingga ∆ � ∪ �
14: if j > x maka
15: x = j
16: end if
17: end for
18: return x, = �1,…,��
Algoritma 1 dimulai dari langkah 1, dengan mendaftarkan semua vaerteks-verteks dengan derajat maksimum pada suatu list L, diikuti langkah 2 dengan mewarnai salah satu verteks di L menggunakan warna 1. Parameter x (pada langkah 13 dan 15) terus melacak jumlah warna yang akan digunakan. Pada saat
loop spanning langkah 4 hingga 17, setiap n-1 verteks lainnya, akan diwarnai pada gilirannya. Hal ini dapat dicapai dengan terlebih dahulu menentukan derajat warna pada semua verteks-verteks yang belum diwarnai pada langkah 5. Semua verteks-verteks yang belum diwarnai dengan derajat warna maksimum didaftarkan di list T, pada langkah 6. Jika list T memuat hanya satu verteks (langkah 10 dan 11), verteks ini akan diwarnai berikutnya, jika verteks dari T
dipilih, menurut pada langkah 7 - 9 algoritma. Pilih suatu verteks dari T, subgraf
semua verteks-verteks di T, kemudian dipilih diberikann warna selanjutnya, menurut langkah 9. Jika mengikat masih terjadi, setiap verteks dapat dipilih. Akhirnya, pilihlah verteks v yang diperoleh dengan kemungkinan jumlah warna terkecil, yang dialokasikan pada langkah 13, dan parameter x, diperbaharui pada langkah 15 jika perlu.
2.3.3. Algoritma Pewarnaan Heuristik Tabu Search
Hertz dan De Werra (1987) mengimplementasikan teknik tabu search untuk mendapatkan pewarnaan yang tepat pada suatu graf. Ide mereka akan diadaptasi dan di implementasikan pada konteks pewarnaan dalam algoritma pewarnaan heuristik tabu search (Nieuwoudt, 2007). Algoritma pewarnaan heuristik tabu search diberikan dalam pseudo-code berikut, yang kita sebut sebagai algoritma 2, yaitu :
Algoritma 2 Pewarnaan heuristik tabu search
input : Suatu graf G dengan order n dan suatu nilai d yang mana untuk
menentukanΔ( )-chromatic number, tabu tenure, t, size dari
candidate list, ℓ, dan jumlah maksimum dari iterasi, maxit.
output : Batas atas � Δ pada � Δ(�) sama artinya Δ ,� Δ-coloringG.
1: x ←(Δ � + 1)/( + 1)
2: � Δ ← -1
3: STOP ← false
4: while not STOP do
5: itcounter ← 0; EMPTY ← false
6: Generate random initial coloring = �1,…,��
7: ← ��1 �∆ �
8: �(0)←0
9: � � ← � −1 ∀�= 1,…,∆(�)
10: while( > and itcounter < �� and not EMPTY) do
11: count ← 1; NOMORE ← false
12: while count <ℓ+ 1 � � not NOMORE do
13: Pilih suatu verteks � � dengan � � = ∆ � untuk sebarang i
dengan kelas warna terbesar di induksi derajat maksimum
14: pilih suatu warna ≠ untuk sebarang jdengan kelas warna terbesar
15: �′← � � ,�′← � ∪ � ,�′← � ∀ = 1,…,�, ≠ ,
16: = �1′,…,��′
17: if �, � � �� �, � then
18: ← ∪
19: count←count + 1
20: end if
21: if jika semua kemungkinan pada langkah 13 dan 14 telah
dipertimbangkan then
22: NOMORE ← true
23: end if
24: end while
25: if =∅then
26: EMPTY ← true
27: else
28: ′ ← suatu kandidat di L sedemikan sehingga ′ ∀
29: if ′ � then
30: � ← ′ −1
31: end if
32: � ← � ∪ �, , where � � di s dan � �′ di ′
33: if � > then
34: Hapus entri terlama di T
35: end if
36: ← ′ ; ← ′
37: itcount ← itcount + 1
38: end if
39: end while
40: if then
41: � Δ ← �
42: ←
43: x ← x - 1
44: else
45: STOP ←true
46: end if
47: end while
48: return � Δ, = �1,…,�� Δ
sebagai warna-warna. Dimulai dari suatu initial random x-coloring G yang paling mungkin, dari suatuΔ ,� −coloring yang invalid. Strategi ini kemudian berulang menurunkan x dan mencoba mencari Δ ,� -coloring yang valid pada suatu graf G menggunakan bilangan terkecil sebagai warna, sehingga diperoleh. Dengan demikian batas atas x pada Δ −chromatic number direduksi sampai algoritma menemukan Δ ,� -coloring tidak valid untuk batas atas terkecil.
Jika himpunan verteks dipartisi menjadi suatu bilangan tetap c dari himpunan bagian (kelas warna), menghasilkan suatu pewarnaan dengan kelas warna = (�1,…,��), tujuannya adalah untuk meminimalkan kelas warna
terbesar yang diinduksi derajat maksimum, yaitu untuk minimize = max1 �Δ � . Jelas, bahwa , untuk nilai d yang telah ditentukan,
dimana Δ −chromatic number dari graf G, harus ditentukan, Δ ,� -coloring
yang valid telah diperoleh. Oleh karena itu, ini adalah yang pertama dari tiga
stopping kriteria yang diterapkan pada algoritma. Stopping kriteria kedua adalah ketika algoritma melakukan sebelum ditentukan jumlah maksimum dari iterasi,
maxit, dimana tidak ada solusi (coloring), s, dimana diperoleh, sehinggaΔ ,� −coloring G tidak valid diperoleh. Stopping kriteria yang terakhir adalah ketika tidak ada candidate solution yang dibangkitkan (generated).
Pada penerapan tabu search , oleh Hertz dan De Werra (1987) untuk pewarnaan graf yang tepat, setiap candidate solution dibangkitkan dengan cara memilih current solution, s, sebarang verteks v, dengan derajat tak nol dalam hal ini kelas warna khusus diinduksi subgraf, dan kemudian recoloring v dengan warna yang berbeda, dipilih secara acak dari warna - warna lain yang digunakan di s. Agar menjadi benar, sifat deterministik asli dari teknik tabu seach. Setiap
candidate solution, s*, pada algoritma 2 di bangkitkan dengan memilih dari
current solution, s, suatu kelas warna i, dimana kelas warna diinduksi derajat maksimum untuk s. Verteks v kemudian diwarnakan kemudian diwarnakan dengan warna yang berbeda, j, dari warna - warna lain yang digunakan di s,
untuk s, semua verteks - verteks v dalam kelas warna dengan kelas warna diinduksi derajat sama dengan kelas warna terbesar diinduksi derajat maksimum dan semua kelas warna dengan kelas warna terkecil diinduksi derajat maksimum digunakan sebagai warna baru untuk v, sampai total dari candidate solutionℓ
dibangkitkan dan disimpan di candidate list. Jika semua kemungkinan candidate solution dapat dibangkitkan, seperti dijelaskan diatas, dan jumlah candidate solution adalah lebih kecil dari pada ℓ, maka proses pembangkitan candidate solution diatas diulang untuk suatu verteks u dengan kelas warna diinduksi derajat sama dengan kelas warna terbesar kedua diinduksi derajat maksimum, dimana u
juga dalam kelas warna dengan kelas warna diinduksi derajat maksimum sama dengan kelas warna terbesar diinduksi derajat maksimum untuk s. Akhirnya, jika diinginkan, prosedur diatas dapat diulang sekali lagi dimana warna j dengan memilih verteks v yang akan diwarnai, jika sekarang suatu warna dengan kelas warna terkecil kedua diinduksi derajat maksimum untuk s. Jika kekardinalan dari
candidate list, adalah masih terkecil daripada ℓ, maka pembangkit dari candidate solution berakhir. Dari candidate list (jika ini tidak kosong), candidate solution,
′, dengan nilai fungsi objektif terkecil yang dipilih, yang dapat atau tidak dapat
sesuai untuk nilai fungsi objektif terkecil, maka didapat current solution s,
sebagai solusi selanjutnya untuk bergerak (move). Ini sangat kontras dengan tabu search proper coloring algorithm oleh Hertz dan De Werra (1987) dimana,
candidate solution, ′,dipilih secara acak diantara candidate solution dengan nilai maksimum untuk ( ′), jika suatu hubungan terjadi selama eksekusi pada
Δ ,� −coloring heuristic, satu dengan jumlah terkecil dari kelas warna dengan suatu kelas warna diinduksi derajat maksimum lebih besar dari d maka dipilih.
Bilamana suatu verteks v di kelas warna � pada current solution, s,
bergerak ke kelas warna � pada solusi selanjutnya, ′,diantara (v,i) menjadi tabu dan dimasukkan ke dalam tabu list, T. Kemudian, verteks v tidak dapat dikembalikan ke kelas warna � untuk menentukan jumlah iterasi dari algoritma diatas. Jika size dari tabu list T sesudah disisipkan diantara (v,i) kedalam T,
didefinisikan sebagai berikut : Jika suatu tabu diantara (v,i) dimasukkan kedalam solusi yang berdekatan, , current solution, s, dan nilai fungsi objektif, ( ), solusi yang berdekatan lebih besar atau sama dengan nilai fungsi aspirasi,
� , nilai fungsi objektif dari current solution, s, maka status tabu dari (v,i)
ditolak, dan solusi yang berdekatan dimasukkan ke kandidat list. Pada awalnya kriteria aspirasi, �(�), untuk setiap nilai z, ditetapkan sebagai � −1.Kemudian, jika suatu solusi ′memenuhi ( ′) � yang dipilih dari candidate list,� ditetapkan sebagai ′ -1
Berikut rincian bagaimana aspek diatas diimplementasikan pada algoritma, Langkah 1 algoritma, suatu batas atas x pada �Δ � graf G, diberikan sebagai derajat d. Jika Δ ,� −coloring G layak untuk batas atas ini maka tercapai, sehingga Δ ,� −coloring layak disimpan ( langkah 41 dan 42 pada algoritma) dan batas atas x pada �Δ � dikurangi dengan 1, pada langkah 43. Iterasi langkah 4-47, dieksekusi menggunakan nilai terbaru dari x. Iterasi ini berlanjut sampai
Δ ,� −coloring tidak layak, diperoleh, dimana kasus variabel boolean STOP pada langkah 45, maka ditetapkan benar. Pada point ini ditetapkan batas atas χΔ (langkah 41) pada �Δ � didapat dari algoritma diatas yaitu �+ 1, dimana x
adalah batas atas pertama yang mana Δ ,� −coloring yang valid, diperoleh. Kemungkinan algoritma diatas tidak menghasilkan suatu
Δ ,� −coloring G yang layak, untuk batas atas pertama pada �Δ � menggunakan x = (Δ � + 1)/( + 1) warna. Batas atas χΔ pada �Δ � ditetapkan tak layak dengan nilai−1 pada langkah 2. Jika pada akhir eksekusi algoritma, nilai χΔ diberikan −1 , ini jelas bahwa algoritma tidak dapat menetukan solusi yang layak untuk masalah Δ ,� −coloring.
Untuk suatu nilai x dengan batas atas di χΔ, pewarnaan awal pada verteks - verteks didapat pada langkah 6 algoritma, dimana nilai fungsi objectif untuk pewarnaan ditentukan pada langkah 7. Pencarian untuk suatu Δ ,� −coloring
yang layak di G di jalankan pada langkah 10 - 39. Suatu candidate list dari sizeℓ
dari candidate list asal saja bahwa candidate list tidak kosong (langkah 27), dan kriteria aspirasi di perbaharui pada langkah 30, jika perlu. Akhirnya, tabu list di perbaharui pada langkah (32 - 35). Jika candidate list kosong (langkah 25) maka variabel boolean EMPTY pada langkah 26 ditetapkan benar dan pencarian untuk suatu Δ ,� −coloring G yang layak, berakhir.
2.4. Riset Terkait
A Hertz et, al. (1987) dalam jurnalnya menyatakan dimana teknik tabu search
digunakan untuk menuju nilai minimum fungsi. Suatu tabu list yang gerakannya diperbaharui selama iterasi untuk menghindari perputaran dan terjebak dalam minimum lokal. Teknik tersebut disesuaikan dengan masalah pewarnaan graf.
Chams et, al. (1987) dalam jurnalnya bereksperimen dengan mengkombinasikan dua algoritma yaitu algoritma dsatur dan algoritma RLF (Recursive Largest First) yang digunakan dalam dua tahap pada graf yang sama.
Raphael Dorne et, al. (1998) dalam jurnalnya menyatakan dimana tabu search disajikan untuk tiga masalah pewarnaan, yaitu pewarnaan graf, t -pewarnaan dan himpunan t-pewarnaan. Algoritma tabu search disini mengintegrasikan fitur penting seperti solusi regenerasi dan tabu tenure dinamis.
Galinier et, al. (2008) dalam jurnalnya mengadaptasi metode AMA (Adapted Memory Algorithm) untuk masalah pewarnaan graf yang dinamakan metode AMACOL. Kemudian hasil pewarnaan graf yang didapat dengan metode AMACOL dibandingkan dengan algoritma GLS (Genetic Local Search).
Jan Olav Hajduk (2010) dalam tesisnya membahas dan menganalisa tabu tenure pada algoritma tabu search untuk masalah pewarnaan graf.
2.5. Kontribusi Riset
BAB 3
METODOLOGI PENELITIAN
Pada bab ini akan dibahas tentang data yang digunakan, metodologi penelitian serta langkah-langkah yang dilakukan dalam menentukan bilangan kromatik pada pewarnaan graf dengan membandingkan waktu eksekusi algoritma dsatur dan algoritma pewarnaan heuristik tabu search serta penerapannya dengan menggunakan sampel data.
Untuk membandingkan waktu eksekusi algoritma dan algoritma pewarnaan heuristik tabu search pada masalah pewarnaan graf adalah sebagai berikut :
Identifikasi Permasalahan
Penetapan Tujuan Penelitian
Studi Literatur :
- Pewarnaan Graf - Metode Heuristik - Tabu Search
Tahap Identifikasi Awal
Pengumpulan Data :
Graf benchmark DIMACS
Tahap Pengumpulan dan Pengolahan Data
Gambar 3.1. Diagram Metodologi Penelitian
3.1. Data Yang Digunakan
Data yang digunakan dalam tesis ini adalah diambil dari DIMACS website. Banyaknya masalah benchmark untuk masalah pewarnaan graf dapat diidentifikasi. Graf benchmark ini dapat diperoleh dari DIMACS website. Tetapi, bilangan kromatik tidak diketahui untuk semua graf yang ada di graf benchmark. Dalam pemilihan graf, dari graf benchmark DIMACS untuk membandingkan waktu eksekusi algoritma dsatur dan algoritma pewarnaan heuristik tabu search , hanya graf yang diketahui bilangan kromatik yang dipilih. Graf ini terdiri dari tiga kelompok, yaitu:
Pengolahan Data :
menggunakan algoritma dsatur
Pengolahan Data :
menggunakan algoritma pewarnaan heuristik tabu search
Perbandingan Metode
Analisis Data
Kesimpulan dan Saran
Tahap Analisis dan Kesimpulan
1. Graf Queen. Graf queen yang dipilih dicantumkan pada tabel 3.1 sebagai queen i_i, dengan menggunakan nama yang sama seperti yang terdapat pada DIMACSwebsite.
2. Graf Mycielski. Graf Mycielski yang dipilih, dicantumkan pada tabel 3.1 sebagai mycieli, yaitu menggunakan nama seperti yang terdapat pada
DIMACS website.
3. Graf book. Graf ini terdiri dari david (dari Dicken's David Copperfield), huck (dari Twain's Huckleberry Finn) dan jean (dari Hugo's Les Miserables).
Tabel 3.1 graf benchmark DIMACS
Graf Order Size χ
queen5_5 25 320 5
queen6_6 36 580 7
queen7_7 49 952 7
queen8_8 64 96 9
myciel3 11 20 4
myciel4 23 71 5
myciel5 47 236 6
myciel6 95 755 7
huck 74 602 11
jean 80 508 10
david 87 812 11
3.2. Pewarnaan Graf
3.2.1.Pewarnaan Graf dengan Algoritma Dsatur
Untuk pengujian algoritma dsatur akan disesuaikan dengan menentukan : 1. ∆ −bilangan kromatik untuk nilai d yang diberikan
3.2.2. Pewarnaan Graf dengan Algoritma Pewarnaan Heuristik Tabu Search
Untuk pengujian algoritma pewarnaan heuristik tabu search :
1. Graf uji di bagi menjadi dua yaitu untuk graf dengan order p 50 dan 50 < < 100 .
2. Kemudian untuk pengujian algoritma pewarnaan heuristik tabu search kita akan menentukan serangkaian input nilai terbaik untuk parameter t (tabu tenure), ℓ (size dari candidate list) dan maxit ( jumlah maksimum iterasi).
Untuk itu akan dipilih salah satu graf dari graf dimacs yaitu myciel3 ( p = 11) yang digunakan untuk menentukan rangkaian nilai untuk parameter t, ℓ dan maxit untuk graf dengan order p 50 . Untuk graf dengan order p 50 nilai parameter t bervariasi antara 6, 7, 8, 9, 10, 11, 12, 13, 14 dan 15. Nilai parameter
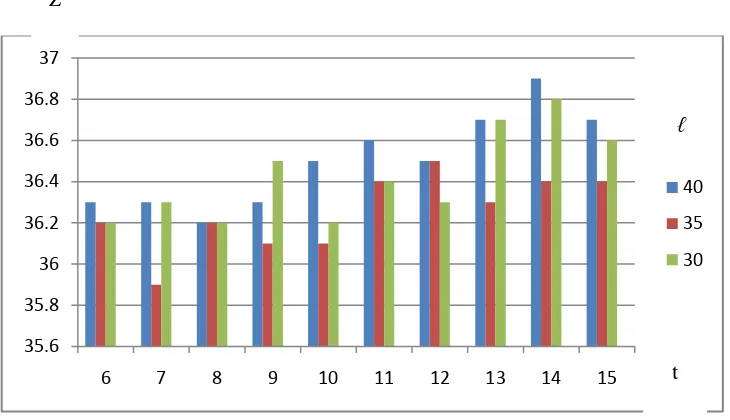
[image:41.595.114.479.501.711.2]ℓ bervariasi antara 30, 35, 40, 45 dan 50. Nilai parameter maxit bervariasi antara 120, 130, 140 dan 150. Untuk setiap rangkaian nilai parameter algoritma pewarnaan heuristik tabu search akan dieksekusi pada graf myciel3 sebanyak 15 kali runs. Setelah itu akan ditentukan rangkaian nilai parameternya dengan memilih hasil minimum dari rata - rata nilai fungsi objektif, dapat dilihat pada gambar 3.2 yang terdiri dari grafik - grafik.
(a). maxit = 120
35.6 35.8 36 36.2 36.4 36.6 36.8 37
6 7 8 9 10 11 12 13 14 15
40
35
30
t
Z
(b). maxit = 140
[image:42.595.114.476.124.360.2] [image:42.595.113.478.131.623.2](c). maxit = 150
Gambar 3.2 Grafik rata-rata nilai fungsi objektif Z, dari algoritma pewarnaan heuristik tabu search yang diaplikasikan pada graf myciel3 untuk menentukan rangkaian nilai parameter tabu dengan maxit 120, 140 dan 150.
35.4 35.6 35.8 36 36.2 36.4 36.6
6 7 8 9 10 11 12 13 14 15
40
35
30
35.6 35.8 36 36.2 36.4 36.6 36.8 37
6 7 8 9 10 11 12 13 14 15
40
35
30
t
Z
Z
t
ℓ
Dari grafik pada gambar 3.2 dapat dilihat bahwa nilai fungsi objektif minimum untuk maxit = 120 adalah 35.9, maxit = 140 adalah 35.7 dan maxit = 150 adalah 36. Untuk menentukan rangkaian nilai parameter, kita ambil empat yang paling minimum dari grafik pada gambar 3.2. Setelah itu kita eksekusikan lagi algoritma pewarnaan heuristik tabu search sebanyak 15 kali runs pada graf
myciel3. Hasil rata - rata minimum dari running time nya dapat dilihat pada tabel 3.2.
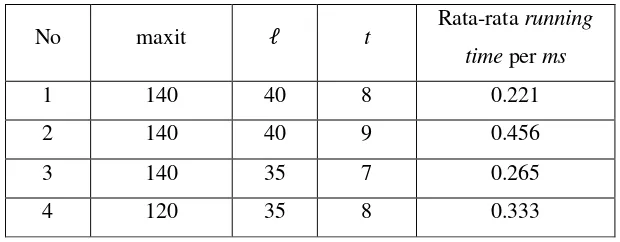
Tabel 3.2 Hasil rata-rata paling minimum yang diperoleh dari eksekusi algoritma pewarnaan heuristik tabu search pada graf myciel3
No maxit ℓ t Rata-rata running
time per ms
1 140 40 8 0.221
2 140 40 9 0.456
3 140 35 7 0.265
4 120 35 8 0.333
Dari tabel 3.2 rata - rata running time tercepat terdapat pada rangkaian nilai parameter yaitu ( 140, 40, 8). Sehingga rangkaian nilai parameter (maxit, ℓ, t) = ( 140, 40, 8) yang dipilih untuk diimplementasikan pada algoritma pewarnaan heuristik tabu search yang akan diterapkan pada graf uji dengan order p 50 .
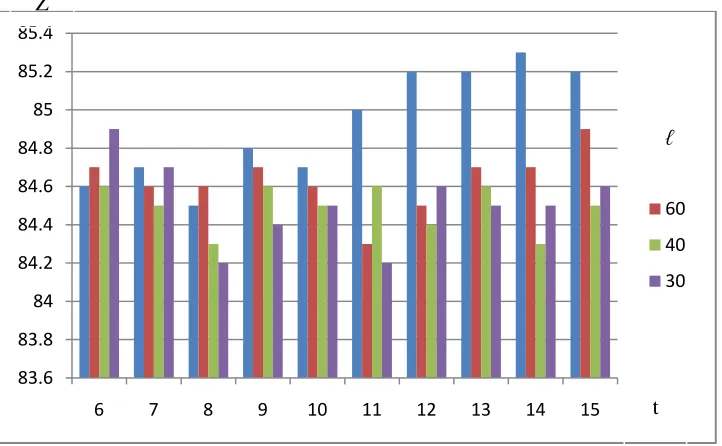
Selanjutnya kita juga akan menentukan, rangkaian nilai parameter untuk graf dengan order yaitu 50 < < 100. Untuk itu akan dipilih salah satu graf dari graf dimacs yaitu graf queen8 (p = 64) yang digunakan untuk menentukan rangkaian nilai untuk parameter maxit, ℓ, t, dan maxit. Untuk graf dengan order
p > 50, nilai parameter t bervariasi antara 6, 7, 8, 9, 10,11, 12, 13, 14 dan 15. Nilai parameter ℓ bervariasi antara 30, 40, 50 dan 60. Nilai parameter maxit bervariasi antara 160, 180 dan 200. Untuk setiap rangkaian nilai parameter algoritma pewarnaan heuristik tabu search akan dieksekusi pada graf queen8
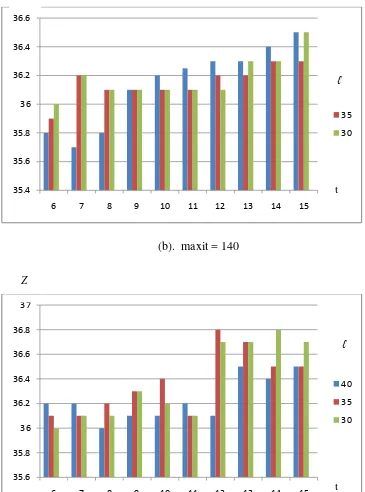
[image:43.595.146.456.308.429.2]dengan memilih hasil minimum dari rata - rata nilai fungsi objektif. Dapat dilihat pada gambar 3.3 yang terdiri dari grafik - grafik.
(a). Maxit = 160
(b). maxit = 180
84 84.5 85 85.5 86 86.5 87
6 7 8 9 10 11 12 13 14 15
100
60
40
30
82 82.5 83 83.5 84 84.5 85 85.5 86
6 7 8 9 10 11 12 13 14 15
100
60
40
30
t Z
Z
t
ℓ
(c). maxit = 200
Gambar 3.3. Grafik rata-rata nilai fungsi objektif, Z, dari algoritma pewarnaan heuristik tabu search yang diaplikasikan pada graf queen8 untuk menentukan rangkaian nilai parameter tabu untuk maxit 160, 180 dan 200.
Dari grafik pada gambar 3.3 dapat dilihat bahwa nilai fungsi objektif minimum untuk maxit = 160 adalah 84.5, maxit = 180 adalah 82.5 dan maxit = 200 adalah 84.2. Untuk menentukan rangkaian nilai parameter, kita ambil empat yang paling minimum dari grafik pada gambar 3.3. Setelah itu kita eksekusikan lagi algoritma pewarnaan heuristik tabu search sebanyak 15 kali runs pada graf
queen8. Hasil rata - rata dari running time nya dapat dilihat pada tabel 3.3.
83.6 83.8 84 84.2 84.4 84.6 84.8 85 85.2 85.4
6 7 8 9 10 11 12 13 14 15
100
60
40
30
t Z
[image:45.595.117.478.157.380.2]Tabel 3.3 Hasil yang diperoleh dari eksekusi algoritma pewarnaan heuristik tabu search pada graf queen8
No maxit ℓ t Rata-rata running
time per ms
1 180 40 7 920
2 180 40 8 901
3 180 40 9 953
4 180 40 10 938
Dari tabel 3.3 rata - rata running time tercepat terdapat pada rangkaian nilai parameter yaitu ( 180, 40, 8). Sehingga rangkaian nilai parameter (maxit, ℓ,
t) = ( 180, 40, 8) yang dipilih untuk dieksekusikan pada algoritma pewarnaan
BAB 4
HASIL DAN PEMBAHASAN
4.1. Hasil
Pada masalah ini ada dua metode heuristik yang akan di implementasikan dan dibandingkan performansi algoritmanya yaitu algoritma dsatur dan algoritma perwarnaan heuristik tabu search. Dua algoritma tersebut dimplemetasikan ke dalam sebuah program komputer dengan menggunakan bahasa pemrograman C dan di eksekusi pada Sony Series Intel Core i5 dan linux ubuntu 13.04 sebagai sistem operasi.
Tujuan penulis mengimplementasikan algoritma adalah sebagai alat bantu untuk menyelesaikan bilangan kromatik pada pewarnaan graf. Hasil yang akan dicapai adalah verteks - verteks yang bersisian tidak mempunyai warna yang sama, dimana dengan menggunakan jumlah warna yang minimum.
4.1.1. Tampilan Input Program
[image:47.595.111.516.525.706.2]Graf uji yang digunakan adalah graf yang diperoleh dari DIMACS website.Berikut adalah tampilan menggunakan bahasa pemrograman C :
4.1.2. Tampilan Output Program
Gambar 4.4 Tampilan output hasil pewarnaan graf dengan algoritma dsatur
[image:49.595.115.499.462.661.2]4.2. PEMBAHASAN
[image:50.595.129.506.208.417.2]Hasil algoritma dsatur yang di uji pada graf benchmark DIMACS website terdapat pada tabel berikut :
Tabel 4.1 Rata-rata running time dari algoritma dsatur
NO Graf Order Size χ
Rata-rata
running time (ms)
1 queen5_5 25 320 5 0.51
2 queen6_6 36 580 7 1.61
3 queen7_7 49 952 7 4.35
4 queen8_8 64 96 9 9.66
5 myciel3 11 20 4 0.02
6 myciel4 23 71 5 0.22
7 myciel5 47 236 6 1.97
8 myciel6 95 755 7 21.37
9 huck 74 602 11 8.21
10 jean 80 508 10 8.87
11 david 87 812 11 16.57
[image:50.595.128.506.495.628.2]
Tabel 4.2 Rata -rata running time algoritma pewarnaan heuristik tabu search untuk graf dengan order p 50
NO Graf Order Size χ
Time :
dsatur
Rata-rata
running time (ms)
1 queen5_5 25 320 5 0.51 60.96
2 queen6_6 36 580 7 1.61 88.77
3 queen7_7 49 952 7 4.35 127.31
4 myciel3 11 20 4 0.02 0.78
5 myciel4 23 71 5 0.22 5.25
6 myciel5 47 236 6 1.97 91.38
Pada tabel 4.2 ditampilkan rata-rata running time dari algoritma pewarnaan heuristik tabu search pada graf benchmark DIMACS dengan order tidak lebih dari 50, kemudian dibandingkan dengan rata-rata running time
Tabel 4.3 running time dari algoritma pewarnaan heuristik tabu search
untuk graf dengan order 50 < < 100
NO Graf Order Size χ
Time :
dsatur
Rata-rata
running time (ms)
1 queen8 64 96 9 9.66 136.52
2 myciel6 95 755 7 21.37 124
3 huck 74 602 11 8.21 149.25
4 jean 80 508 10 8.87 112.56
5 david 87 812 11 16.57 156
Pada tabel 4.3 ditampilkan rata-rata running time dari algoritma pewarnaan heuristik tabu search pada graf benchmark DIMACS dengan order (p) lebih dari 50. Semua data yang ada pada tabel 4.3 menggunakan nilai parameter tabu yang telah ditentukan yaitu maxit = 180, ℓ = 40 dan t = 8.
Perbandingan hasil yang diperoleh dari tabel 4.2 dan 4.3 kita tampilkan ke dalam bentuk grafik trendline seperti berikut :
Gambar 4.6 Perbandingan running time algoritma Dsatur dan algoritma phts
0 20 40 60 80 100 120 140 160
1 2 3 4 5 6 7 8 9 10 11
dsatur
phts
ms
[image:51.595.114.477.471.695.2]Berdasarkan grafik trendline yang ditampilkan, maka algoritma yang pertama yaitu dsatur merupakan algoritma greedy dengan waktu eksekusi yang sangat singkat dibandingkan dengan algoritma pewarnaan heuristik tabu search, yang telah diuji pada 11 graf, dengan rata-rata waktu eksekusi kurang dari 22 ms.
Algoritma yang kedua adalah algoritma pewarnaan heuristik tabu search
BAB V PENUTUP
5.1.Kesimpulan
Dalam penelitian ini setelah peneliti mengkaji dan membandingkan dengan mengaplikasikan dua algoritma pada graf benchmark DIMACS, dimana graf dengan banyaknya verteks atau order (p) yaitu 11 95 ternyata algoritma pewarnaan dsatur memiliki rata-rata waktu eksekusi yang sangat singkat dibandingkan dengan algoritma pewarnaan heuristik tabu search. Dan hasil pewarnaan graf yang didapat pada penelitian ini merupakan solusi optimum dari kedua metode heuristik yaitu algoritma dsatur dan algoritma pewarnaan heuristik
tabu search yaitu minimal jumlah warna yang diperlukan untuk mewarnakan suatu graf sehingga verteks-verteks yang bersisian mempunyai warna yang berbeda.
5.2.Saran
DAFTAR PUSTAKA
Balakrishnan, V. K.1995. Theory and Problem of Combinatorics, Mc. Graw Hill
Bollobăs, B. 1998. Modern Graph theory, Graduate Text in Mathematics Series, Springer - Verlag, New York.
Cham, M, A. Hertz & D. de Wera. 1987. Some experiments with simulated annealing for coloring graphs. European Journal of Operational Research, 32(2):260-266.
Chartrand, Gary & Ortrud R. Oellerman. 1993. Applied And Algorithmic Graph Theory, Mc Graw Hill.
Chiarandini, M. Bibliography on Graph Coloring, [online], Available from :
http://www.imada.sdu.dk/ ˜marco/gcp/ (accesss : Mar 1st
, 2013)
Deo, Narsingh. 1986. Graph Theory with Aplications to Engineering andComputer Science. New Delhi: Prentice Hall of India.
Dorne, Raphael & Jin-Kao Hao. 1998. Tabu search for graph coloring, T-Coloring and set T-T-Colorings. Meta-Heuristics, pages 33-47. Kluwer Academic Publishers, Boston.
Brelaz, D. 1979. New Methods to Color The Vertices of A Graph, Communications of the Association for Computing Machinery.
Fletcher, Peter. 1991. Foundationt of Discrete Mathematics, PWS-KENT, Boston Harary, Frank. 1994. Graph Theory, Third Edition, Addison-Wesley, New York. Hertz, A & D. de Werra. 1987. Using tabu search techniques for graph coloring.
Computing39 : 345-351
Galinier, P, A. Hertz & N. Zufferey. 2008. An adaptive memory algorithm for the k-coloring problem. Discrete Applied Mathematics 156(2):267-279.
Glover, Fred. 1995. Tabu Search Fundamentals and Uses. Colorado. University of Colorado.
Glover, F. & Laguna, M. 1997. Tabu Search. Kluwer, Norwell, MA.
Hajduk, J.O. 2010. An Analysis of Tabu search for the Graph Coloring Problem. Thesis. Utrecht University.
Jaziri, Wassim. 2008. Local Search Techniques Focus on Tabu search. Thesis.. University of Sfax Tunisia.
Johnson, DS & Trick, MA, DIMACS Series in Discrete Mathematics and Theoretical Computer science, [online], Available from : http:/dimacs.rutgers.edu/Volumes/Vol126.html (access : 5th Mar 2013)
Lipschutz, Seymour & Lars Lipson, Mars. 2002. Matematika Diskrit Mid 2.
Jakarta: Salemba Teknika.
Liu, C. L. 1995. Dasar-Dasar Matematika Diskret, Edisi Kedua, Gramedia Pustaka Utama, Jakarta.
Martono, Totong. 1990. Teori Graf dan Aplikasinya, PAUD IPB, Bogor. Munro, John, 1993, Discrete Mathematics for Computing, Chapman and Hall. M. Syslo, Maciej, dan Deo, Narsingh. 1983. Discrete Optimization Algorithms.
United States of Amerika: Prentice-Hall.
Munir, Rinaldi. 2005. Matematika Diskrit Edisi 3. Bandung: InformatikaBandung.
Malaguti, Enrico, 2010. Tabu search for the graph coloring problem (extended). Italy. University of Bologna.
Nieuwoudt, Isabelle. 2007. On the Maximum Degree Chromatic Number of a Graph, Dissertation Ph.D. Stellenbosch University.
Porumbel, D.C, Hao, J.K. & Kuntz, P. 2007. Reinforced Tabu search for Graph Coloring, Journal of Combinatorial Optimization.
Slamet, Sumantri dan Hendrik Makaliwe. 1991. Matematika Kombinatorik, Elex Media Komputindo, Jakarta.
Wallis, WD. 2000. A Beginner's Guide to Graph Theory, Birkhäuser Boston, New York.
LAMPIRAN 1
Data Input
c FILE: myciel3.col
c SOURCE: Michael Trick ([email protected])
c DESCRIPTION: Graph based on Mycielski transformation. c Triangle free (clique number 2) but increasing c coloring number
p edge 11 20 e 1 2
c FILE: myciel4.col
c SOURCE: Michael Trick ([email protected])
c DESCRIPTION: Graph based on Mycielski transformation. c Triangle free (clique number 2) but increasing c coloring number
p edge 23 71 e 1 2
c FILE: myciel5.col
c SOURCE: Michael Trick ([email protected])
c DESCRIPTION: Graph based on Mycielski transformation. c Triangle free (clique number 2) but increasing c coloring number
p edge 47 236 e 1 2
LAMPIRAN 2
Data Output
Myciel3.res
CLRS 4 FROM TABU[0] cpu = 2000.00 microsecs pid = 5983
1 2 3 2 4 1 2 1 2 1 3
Myciel4.res
CLRS 5 FROM TABU[0] cpu = 4000.00 microsecs pid = 5920
1 2 3 2 4 1 2 1 2 1 3 1 2 3 2 5 1 2 1 2
1 3 4
Myciel5.res
CLRS 6 FROM TABU[0] cpu = 2300 microsecs pid = 5993
1 2 3 2 4 1 2 1 2 1 3 1 2 3 2 4 1 2 1 2
1 3 5 1 2 5 2 4 1 2 1 2 1 4 1 2 6 2 4 1