Lampiran 1. Solusi Fungsi Green
1 function G = greenfunction(k, v, n, a, b) 2 % k adalah fungsi difusi
3 % v adalah fungsi adveksi
4 % n adalah jumlah diskritisasi sepanjang domain (a,b) 5 h = (b-a)/n;
6 x = linspace(a, b, n+1); 7 muval(1) = 0.0;
8 for j = 2: n+1
9 increment_m = (v(x(j))/k(x(j)) + v(x(j-1))/k(x(j-1)))*0.5*h; 10 muval(j) = muval(j-1) + increment_m;
11 end
12 mu(1:n+1) = exp(-muval(1:n+1)); 13 kval(1)=0.0;
14 for j=2:n+1
15 increment_k = ( mu(j)/k(x(j))+ mu(j-1)/k(x(j-1)))*(0.5)*h; 16 kval(j) = kval(j-1) + increment_k;
17 end 18
19 %fungsi Green untuk kondisi batas Neumann-Neumann 20 for j=1:n+1
21 for i=1:n+1
22 c = (-mu(n+1)/v(n+1) - (kval(n+1) - kval(j))) /... 23 (mu(n+1)/v(n+1) - 1/v(1) + kval(n+1));
24 if (x(i)<x(j))
25 phi(i,j) = (c/mu(i))*(1/v(1) - kval(i));
26 else
27 phi(i,j) = ((1+c)/mu(i))*(mu(n+1)/v(n+1) +...
28 (kval(n+1)-kval(i)));
29 end
30 end
31 end 32 %
33 plot(x,G(:,2500)) %Grafik fungsi Green 34 xlabel({'$x$'},'interpreter','latex') 35 %
Lampiran 2. Solusi Numerik Persamaan Diferensial Semilinear
1 function u = semilinear(f, dif, n, a, b)
2 % f adalah fungsi semilinear dan dif adalah turunan dari fungsi semilinear
3 h = (b-a)/n;
4 x = linspace(a, b, n+1); 5 for i= 1:n+1
6 k(i) = 1/(1-0.99*(x(i)ˆ2)*sin(50*pi*x(i))); 7 v(i) = 10;
8 end
9 muval(1) = 0.0; 10 for j = 2: n+1
11 increment_m = (v(j)/k(j) + v(j-1)/k(j-1))*0.5*h; 12 muval(j) = muval(j-1) + increment_m;
13 end
14 mu(1:n+1) = exp(-muval(1:n+1)); 15 kval(1) = 0.0;
16 for j=2:n+1
17 increment_k = (mu(j)/k(j)+ mu(j-1)/k(j-1))*(0.5)*h; 18 kval(j) = kval(j-1) + increment_k;
19 end 20
21 % G(i,j) adalah fungsi Green untuk kondisi batas Dirichlet-Dirichlet
22 for j=1:n+1 23 for i=1:n+1
24 c = -(kval(n+1)-kval(j))/kval(n+1); 25 if (x(i)<x(j))
26 G(i,j) = -(c/mu(i))*kval(i);
27 else
28 G(i,j) = (1 + c)/mu(i)*(kval(n+1) - kval(i));
29 end
30 end
31 end 32
33 %DG(i,j) adalah turunan fungsi Green terhadap x 34 for j = 1: n+1
35 for i = 1:n+1
38 DG(i,j) = - c*mu(i)/k(i);
39 else
40 DG(i,j) = - (1 + c)*mu(i)/k(i);
41 end
42 end
43 end 44
45 u = zeros(n+1,1);
46 % BC : u(0) = 1 dan u(1) = 0 47 for i= 1:n+1
48 u(i) = 1 - x(i); 49 end
50 Niter = 15; %Iterasi Newton 51 id = eye(n+1);
52 ja = zeros(n+1); 53 g = zeros(n+1,1); 54 for N = 1:Niter
55 g(1) = u(1)-1 ;
56 ja(1,:) = zeros(1,n+1); 57 ff(1:n+1) = f(u(1:n+1))*h;
58 ff(1) = ff(1)*0.5;
59 ff(n+1) = ff(n+1)*0.5; 60 for j = 2:n
61 g(j) = u(j) - ff*G(:,j) - k(1)*DG(1,j); 62 ja(j,:) = dif(u(j))*G(:,j)*h;
63 ja(j,1) = ja(j,1)*0.5;
64 ja(j,n+1) = ja(j,n+1)*0.5;
65 end
66 g(n+1) = u(n+1);
67 ja(n+1,:) = zeros(1,n+1);
68 jac = id - ja;
69 u = u - jac\g
70 end 71 %
72 plot(x ,u, 'r');
73 xlabel({'$x$'},'interpreter','latex') 74 %
Lampiran 3. Solusi Fungsi Green dengan Menggunakan Algoritma MCMC
1 function phi = greenmcmc(bc, xi, a, b, nx, k, v, ht, nt) 2 % bangkitkan koordinat
3 hx = (b-a)/nx;
4 x = linspace(a, b, nx+1); 5 %
6 % bangkitkan matriks diskritisasi operator diferensial. 7 A = zeros(nx +1);
8 kinterface = 0.5*(k(x(1:nx)) + k(x(2:nx+1))); 9 kinterface = kinterface/hx;
10 vinterface = 0.5*(v(x(1:nx)) + v(x(2:nx+1))); 11 for i = 2:nx
12 A(i,i) = kinterface(i-1)+ kinterface(i)+ vinterface(i); 13 end
14 for i = 1:nx
15 A(i,i+1) = -kinterface(i);
16 A(i+1,i) = A(i,i+1)- vinterface(i); 17 end
18 A = 0.5*ht*A; 19 AA = -A;
20 for i = 2:nx
21 A(i,i) = A(i,i) + hx; 22 AA(i,i) = hx + AA(i,i); 23 end
24 % left boundary condition 25 if (bc(1) == 1)
26 A(1,1) = 1; A(1,2) = 0;
27 AA(1,1) = -1; AA(1,2) = 0; 28
29 elseif (bc(1) == 2)
30 A(1,1) = 0.5*hx + 0.5 * ht * (kinterface(1) + ( vinterface(1)- v(x(1))));
31 AA(1,1) = - A(1,1) + hx; 32
33 elseif (bc(1) == 3)
34 A(1,1) = 0.5*hx + 0.5* ht *(kinterface(1) + vinterface (1));
35 AA(1,1) = -A(1,1) + hx;
36 end
38 % right boundary condition 39 if (bc(2) == 1)
40 A(nx+1,nx+1) = 1; A(nx+1,nx) = 0; 41 AA(nx+1,nx+1) = -1; AA(nx+1,nx) = 0; 42 elseif (bc(2) == 2)
43 A(nx+1,nx+1) = 0.5*hx + 0.5* ht* (kinterface(nx)+ v(x(nx +1)));
44 AA(nx+1,nx+1) = - A(nx+1,nx+1) + hx; 45
46 elseif (bc(2) ==3)
47 A(nx+1, nx+1) = 0.5*hx + 0.5* ht* kinterface(nx); 48 AA(nx+1,nx+1) = -A(nx+1,nx+1) + hx;
49 end
50
51 A = sparse(A); 52 %
53 % MCMC dengan Metropolis-Hasting 54 if (bc(1) == 1)
55 f(1,1) = 0.0; 56 else
57 f(1,1) = randn(1,1)*sqrt(hx*ht); 58 end
59 f(2:nx,1) = randn(nx-1,1)*sqrt(2*hx*ht); 60 if (bc(2) == 1)
61 f(nx+1,1) = 0.0; 62 else
63 f(nx+1,1) = randn(1,1)*sqrt(hx*ht); 64 end
65 Ux(:,1) = A \ f; 66 for l = 2:nt 67 %white noise 68 if (bc(1) == 1)
69 f(1,1) = 0.0;
70 else
71 f(1,1) = randn(1,1)*sqrt(hx*ht) ;
72 end
73 f(2:nx,1) = randn(nx-1,1)*sqrt(2*hx*ht); 74 if (bc(2) == 1)
75 f(nx+1,1) = 0.0;
76 else
77 f(nx+1,1) = randn(1,1)*sqrt(hx*ht);
79 f = f + AA*Ux(:,l-1);
80 u = A \ f;
81 R = u(xi) - Ux(xi,l-1); 82 alpha = exp(min(0,R)); 83 if (rand<alpha)
84 Ux(:,l) = u; % accept
85 else
86 Ux(:,l) = Ux(:,l-1); % reject, jadi pakai yang sebelumnya .
87 end
88 end
89 % Hitung rata-rata
90 phi = sum(Ux,2)/nt; %ini fungsi Greenya. 91 size(phi)
92 hold on
93 plot(x, phi,'r ');
94 xlabel({'$x$'},'interpreter','latex') 95 %
Andrieu C., Freitas De N., A. D. a. J. M. 2003. An Introduction to MCMC for Machine Learning. Kluwer Academic Publisher. Manufactured in the Netherlands, pages 4–43.
Boyce, W. and DiPrima, R. 2008.Elementary Differential Equations and Boundary Value Problems. Wiley.
Chang, J. 1999. Brownian Motions.
Chapra, S. 2008. Surface Water-Quality Modeling. Waveland Press.
Chapra, S. and Canale, R. 2010. Numerical Methods for Engineers. McGraw-Hill Higher Education.
Davar, K. 2001. Five Lectures on Brownian Sheet: Summer Internship Program Univer-sity of Wiscousin-Madison.
Duffy, D. 2001. Green’s Functions with Applications. Applied Mathematics. CRC Press. Edwin, L. 2006. Introduction to Green’s Functions: Lecture notes.
Evans, L. C. 1998. Partial Differential Equations, volume 19 of Graduate Studies in Mathematics. American Mathematical Society, Providence, Rhode Island.
Ferziger, J. and Peric, M. 2001. Computational Methods for Fluid Dynamics. Springer Berlin Heidelberg.
Haberman, R. 1998. Elementary Applied Partial Differential Equations: with Fourier Series and Boundary Value Problems. Prentice Hall International (UK).
Logan, J. D. 2004. Applied Partial Differential Equations, 2nd. Springer. Parnell, W. J. 2013. Green’s Functions, Integral Equations and Applications.
Pinchover, Y. and Rubinstein, J. 2005. An Introduction to Partial Differential Equations. University Press Camridge, Camridge.
Varberg, D., Purcell, E., and Rigdon, S. 2000. Calculus. Prentice Hall. Walsh, B. 2004. Markov Chain Monte Carlo and Gibbs Sampling.
FUNGSI GREEN
3.1 Fungsi Green dengan Pendekatan Metode Numerik
Dalam penerapan persamaan diferensial secara fisik, ada beberapa permasalahan yang
masih bisa dicari penyelesaian analitiknya sehingga bisa ditemukan fungsi eksplisit
yang memenuhi permasalahan yang akan dicari. Tetapi dalam permasalahan yang
le-bih kompleks seringkali didapati kesulitan sehingga tidak mungkin lagi untuk mencari
solusi analitiknya sedemikian sehingga dalam masalah ini yang perlu dilakukan
ada-lah mencari pendekatan solusinya secara numerik. Selain itu, seiring berkembangnya
penggunaan komputer pendekatan solusi secara numerik dirasakan lebih praktis
diban-dingkan dengan mencari solusi permasalahan dengan metode analitik.
Pendekatan solusi secara numerik dapat dilakukan dengan mendiskritisasi pada
titik - titik disepanjang batas domain. Sehingga solusi yang diperoleh hanyalah pada
titik - titik yang dicari pendekatan numeriknya.
Gambar 3.1.Diskritisasi
Dari ilustrasi pada gambar diatas, diskritisasi dilakukan pada domain dengan
batas interval(a, b)yang dibagi menjadin sub interval yang sama panjang. Panjang
setiap n sub interval dapat diekspresikan sebagai ∆x = b−a
n sehingga titik - titik
yang didiskritisasi menjadi{xi =a+i∆x, i= 1,2,3, ..., n}.
Ketika suatu permasalahan sudah tidak bisa lagi dicari penyelesaian analitiknya,
maka satu - satunya cara yang dapat dilakukan adalah mencari pendekatan solusinya
pada titik - titik tertentu sehingga dapat diperoleh grafik pendekatan dari solusi
kesalahan atau disebut juga dengan galat. Maka untuk meminimalkan kesalahan
terse-but dapat dilakukan dengan memperkecil sub interval sehingga∆xmenuju nol.
Pada Lemma 2.1 telah diberikan solusi fungsi Green dari suatu operator
diferen-sial adalah
G(x;ξ) =
1 µ(x)
G(0;ξ)−c
Z x
0
µ(t) k(t)dt
, jikax≤ξ
1 µ(x)
µ(ℓ)G(ℓ;ξ) + (1 +c)
Z ℓ
x µ(t) k(t)dt
, jikax > ξ
Dari persamaan diatas terdapat beberapa integrasi yang harus dilakukan untuk mencari
solusi fungsi Green secara eksplisit. Pada kenyataannya, tidak semua persamaan
ma-tematika yang dapat dicari anti derivatifnya. Sehingga untuk mengatasi permasalahan
tersebut dapat dilakukan dengan mencari pendekatan dari integral atau disebut juga
dengan integrasi numerik.
Untuk mencari pendekatan numerik dari solusi fungsi Green, langkah pertama
yang harus dilakukan adalah mencari integrasi numerik dari µ(x). Integrasi numerik
yang dilakukakan adalah menggunakan aturan trapezoidal (Trapezoidal Rule) yaitu dengan mendiskritisasi variabel spasial x menjadin buah partisi yang sama panjang
dan memandang masing - masing sub interval sebagai luasntrapesium di bawah kurva
(Varbeget al.2000) .
Jikaµ(x)didiskritisasi menjadin titik disepanjang interval domain(0, ℓ)maka
untukxi, i= 0,1,2,3, ..., n,
µ(xi) = exp
−
Z xi
x0
v(s) k(s) ds
.
µ(xi)dengan menggunakan aturan trapezoidal adalah
Dari integrasi di atas diperoleh pendekatan dariµ(xi)≈µiadalah
µi = exp (−yi).
Setelah diperoleh pendekatan dariµ(xi), selanjutnya adalah mencari integrasi numerik
dari
Dengan menggunakan aturan trapezoidal seperti sebelumnya, maka
Z x
solusi fungsi Green pada Lemma 2.1 dapat ditulis seperti berikut
Gi,j =
1
µi (G0,j−c gi), i≤j
1
µi (µnGn,j + (1 +c)(gn−gi)), i > j
(3.1)
dengan
µi = exp(−yi),
dan
c= G0,j−µnGn,j −(gn−gj)
gn .
Jika suatu operator diferensial eliptik diikuti dengan kondisi batas pada
domain-nya, maka solusi eksplisit fungsi Green yang terdapat pada Lemma 2.2 sampai Lemma
2.6 dapat didiskritisasi sehingga diperoleh solusi fungsi Green secara numerik.
3.2 Pendekatan Numerik Fungsi Green dengan Algoritma MCMC
Markov Chain Monte Carlo (MCMC) adalah sebuah rangkaian metode untuk
men-ciptakan barisan sampel random yang berasal dari distribusi peluang dengan
meng-gunakan rantai Markov yang sesuai dengan distribusi tertentu yang diinginkan.
Salah satu algoritma MCMC yang digunakan dalam penelitian ini adalah
al-goritma Metropolis-Hasting yaitu dengan menggunakan mekanisme penerimaan dan
penolakan (accept/reject) untuk membangkitkan barisan sampel dari suatu distribusi tertentu .
White dan Stuart (2009) dalam artikelnya menyebutkan bahwa jika suatu
distri-busi peluang dan algoritma fungsi ruang sampel dikonstruksi dengan benar, maka rata
- rata dari fungsi ruang sampel konvergen dengan fungsi Green tertentu . Pada artikel
derivativeterhadap ukuran Gaussian atau distribusi normalπ0 sebagai berikut
dπ dπ0 ∝
exp(Θ(φ)).
Notasi∝diatas menyatakan sifat proposional atau sebanding.
Untuk memperoleh fungsi Green dari suatu operator diferensial eliptikL
bersa-maan dengan kondisi batas pada domain, maka operator kovarian dari ukuran Gaussian
πadalahC =−L−1. Diketahui bahwaπ ∼ N(φ,C)dimanaφ=−Cδ(x−ξ)atau
Lφ=δ(x−ξ).
Ukuranπ adalah invarian terhadap SPDE (Stochastic Partial Differential Equa-tion) berikut
∂φ
∂t +Lφ+δ(x−ξ) = √
2∂
2w
∂x∂t. (3.2)
Persamaan diatas disebut Persamaan Diferensial Parsial Stokastik karena
dida-lamnya terdapat proses stokastik yaituWiener Processatau juga dikenal dengan gerak Brownian (Brownian motion) yang merupakan fungsi terhadapxdan terhadapt.
Fungsi Green bisa diperoleh dengan mendiskritisasi persamaan diferensial
sto-kastik diatas. Akan tetapi fungsi Delta Dirac akan membuat permasalahan menjadi
lebih rumit. Oleh karena itu, dengan menghilangkan fungsi Delta Dirac, persamaan
(3.2) dapat ditulis menjadi
∂φ
∂t +Lφ= √
2∂
2w
∂x∂t, (x, t)∈(0, ℓ)×(0,∞) (3.3)
yang merupakan invarian terhadapπ0, dimana
L= ∂ ∂x
−k(x) ∂
∂x +v(x)
Selanjutnya persamaan (3.3) dapat didiskritisasi menjadimsub interval padax
bentuk integral dan mendekati solusi persamaan pada sejumlahcontrol volume (CV) berhingga.
Dengan mengambilCVi = (xi−1 2, xi+
1
2)×(tn−1, tn),i= 1,2,3, ..., m−1dimana
panjang masing - masinggridadalah xi+1 2 −xi−
1
2 = ∆xdantn−tn−1 = ∆t maka
integral dari persamaan (3.3) disepanjangCViadalah
Z x
Dengan mengintegrasikan turunan φ terhadap waktu dan mengintegrasikan operator
diferensial terhadap variabelxmaka diperoleh
Z x
Selanjutnya dilakukan beberapa pendekatan numerik pada persamaan di atas. Pertama,
pendekatan menggunakan aturan titik tengah (mid point rule) pada integrasi terhadap variabel x yaitu dengan melakukan pendekatan menggunakan luas persegi panjang
yang melalui titik tengah kurva pada setiapcontrol volumes. Sehingga diperoleh
Z x
Kedua, melakukan pendekatan menggunakan aturan trapezoidal terhadap waktu pada
Z tn
Selanjutnya dengan menggunakan pendekatan turunan, maka turunan pertama φ
ter-hadapxpada fungsi difusi di atas dapat ditulis sebagai berikut
Kemudian dengan melakukan pendekatan upwindmaka φ pada fungsi adveksi diap-roksimasi menjadi
Sehingga pendekatanφpada fungsi adveksi dapat ditulis menjadi
Ka-rena turunan dari gerakBrownianterhadap waktu adalah
dimanaη(x)adalah suatuwhite noiseyang berdistribusi normal denganN(0,1). Se-hingga diperoleh
Hal yang sama juga berlaku untuk turunan dari Brownian motion terhadapx. Sehingga
diperoleh
White noise yang dinotasikan denganε merupakan generalisasi dari proses stokastik
dengan sekumpulan bilangan acak yang berfluktuasi, dimana ε berdistribusi normal
denganN(0,1).
Andaikan bahwa pendekatan φ(xi, tn) ≈ Φn
i untuk i = 1,2,3..., m−1 dapat
ditulis ke dalam sistem persamaan aljabar berikut
(Φn
−ki−
hanakan ke dalam bentuk perkalian matriks berukuran(m+ 1)×(m+ 1)yaitu
F =√2 ∆x∆t
dimana entri - entri bukan nol yang terdapat pada matriks diatas adalah
Ai,i−1 = −
Dari persamaan matriks di atas maka dapat diperoleh solusi Φn
Karena diskritisasi SPDE diatas tidak mengikuti fungsi Delta Dirac maka fungsi
Green dapat diperoleh dengan menggunakan algoritma Metropolis-Hasting MCMC
yaitu dengan menerima atau menolakΦn
i yang telah didapatkan sebelumnya .
Langkah - langkah dari algoritma Metropolis-Hasting adalah
1. Aturn = 0.
2. Bangkitkan bilangan acakεyang berdistribusi normalN(0,1). Sehingga dengan
menggunakan persamaan (3.5) diperoleh vektorΦ0
i yang invarian terhadapπ0.
3. Ulangi iterasin= 1,2,3, ..., M.
• Bangkitkan bilangan acak ε sehingga diperoleh calon Φ∗
i dari distribusi
proposalπ0.
• MisalkanΦ∗
j =φ(ξ, t). Hitung
α= expmin(0, R)
dimanaR= Φ∗ j −Φ
n−1
j .
• Bangkitkan sampel randomv ∼ U(0,1).
• Jikav < α, makaΦ∗
i diterima, sehinggaΦni = Φ∗i
dan jika sebaliknya makaΦn
i = Φn−i 1diterima sebagai anggota sampel dari
distribusi targetπ.
Selanjutnya dengan menggunakan iterasi Monte Carlo, maka diperoleh fungsi
Green
G(xi;ξj) = 1 M
M
X
n=0
Φni. (3.6)
3.2.1 Kondisi Batas Dirichlet
Andaikan terdapat kondisi batasDirichletpada persamaan (3.2) yaitu
MakaΦn
0 = 0danΦnm = 0. Sehingga entri matriks yang terdapat pada
persama-an (3.5) untuk batas kiri domain adalah
A0,0 =B0,0 = 1, A0,1 =B0,0 = 0,
dan entri matriks pada batas kanan domain adalah
Am,m =Bm,m= 1, , Am,m−1 =Bm,m = 0.
3.2.2 Kondisi BatasNeumann
Andaikan terdapat kondisi batas Neumann pada persamaan (3.2) yaitu
k(0)φ′(0, t) = 0.
Makaφ(0, t)dapat diperoleh menggunakan pendekatan integral dari SPDE pada batas
sebelah kiri. Diketahui bahwaCV0 = (x0, x1
2)×(tn−1, tn)dimana panjanggridadalah
x1
2 − x0 =
∆x
2 dan tn −tn−1 = ∆t. Sehingga pendekatan integral dari SPDE di sepanjangCV0 adalah sebagai berikut
Z tn
tn−1
Z x1 2
x0
∂φ ∂t +
∂ ∂x
−k(x)∂φ
∂x +v(x)φ
dxdt=
Z tn
tn−1
Z x1 2
x0
√ 2∂
2w
∂x∂t dxdt.
(3.7)
Pertama, dilakukan integrasi dari turunanφterhadap waktu dengan menggunakan
atur-an titik kiri (left end rule) pada variabel spasialxyaitu
Z x1 2
x0
Z tn
tn−1
∂φ
∂t dtdx= (φ(x0, tn) +φ(x0, tn−1)) ∆x
2 . (3.8)
maka diperoleh
. Sehingga integrasi dari operator diferensial dapat disederhanakan seperti berikut
Z tn
Dengan melakukan itegrasi terhadap t menggunakan aturan trapezoidal maka
persa-maan diatas dapat ditulis menjadi
Turunanφpada fungsi difusi dapat didekati menggunakan pendekatanφpada turunan
pertama terhadapxseperti berikut
dan dengan melakukan pendekatan upwindterhadap φ pada fungsi adveksi sehingga menjadi
φ(x1
2, tn)≈φ(x0, tn), φ(x 1
2, tn−1)≈φ(x0, tn−1). (3.11)
Selanjutnya adalah melakukan integrasi pada turunan dari gerakBrownianterhadapx
dantyaitu
Sehingga pendekatan φ(x0, tn) ≈ Φn0 pada CV0 dapat dituliskan dalam persamaan
aljabar sebagai berikut
(Φn
Persamaan diatas dapat diatur ulang menjadi seperti berikut
∆x
Sehingga entri matriks yang terdapat pada persamaan (3.5) untuk batas kiri domain
adalah
Jika padax=ℓterdapat kondisi batasNeumannyaitu
−k(ℓ)φ′(ℓ) = 0,
maka pendekatanφ(ℓ, t)dapat diperoleh menggunakan pendekatan integral dari SPDE
pada sebelah kanan. DiketahuiCVm = (xm−1
2, xm)×(tn−1, tn)dimana panjang grid
adalahxm−xm−1
2 =
∆
di sepanjangCVmadalah sebagai berikut
Pertama, lakukan integrasi dari turunanφterhadap waktu dengan menggunakan aturan
titik kanan (right end rule) pada variabel spasialxyaitu
Z tn
Selanjutnya dengan melakukan integrasi operator diferensial terhadap x disepanjang
CVnmaka diperoleh
Z tn
Sehingga integrasi dari operator diferensial dapat disederhanakan seperti berikut
Z tn
Dengan melakukan itegrasi menggunakan aturan trapezoidal terhadap t maka
persa-maan di atas dapat ditulis menjadi
turunan pertama terhadapxseperti berikut
dengan melakukan pendekatanupwindterhadapφpada fungsi adveksi menjadi
φ(xm−12, tn)≈φ(xm−1, tn) φ(xm− 1
2, tn−1)≈φ(xm−1, tn−1). (3.14)
Selanjutnya adalah melakukan integrasi disepanjangCVmpada turunan dari gerak Bro-wnianterhadapxdantyaitu
Z tn
Sehingga pendekatanφ(xm, tn)≈φn
mpadaCVmdapat ditulisakan dalam
persa-maan aljabar sebagai berikut
(φnm−φ
Persamaan diatas dapat diatur ulang sehingga menjadi
− km−
adalah
Am,m−1 =
km−1 2
∆x +vm−12
!
∆t
2 , Am,m =
∆x 2 +
km−1 2
∆x +vm
!
∆t 2 ,
dan
Bm,m−1 =−
km−1 2
∆x +vm−12
!
∆t
2 , Bm,m =
∆x 2 −
km−1 2
∆x +vm
!
∆t 2 .
3.2.3 Kondisi BatasRobin
Andaikan terdapat kondisi batasRobinpada persamaan (3.2) yaitu
−k(0)φ′(0, t) +v(0)φ(0, t) = 0,
makaφ(0, t)dapat diperoleh dengan menggunakan langkah - langkah pendekatan
in-tegral dari SPDE disepanjang CV0 seperti yang telah dijabarkan pada subbab 2.6.2.
Perbedaan yang terdapat pada kondisi Robinhanyalah pada pendekatan integrasi ter-hadap operator diferensial.
Karenax0 = 0dan−k(0)φ′(0, t) +v(0)φ(0, t) = 0maka hasil integrasi operator
diferensial terhadapx0 adalah
−k(x)∂φ
∂x +v(x)φ
x0
= 0.
Sehingga integrasi dari operator diferensial dapat disederhanakan menjadi seperti
ber-ikut
Z tn
tn−1
−k(x1 2)φ
′(x
1
2, t) +v(x 1 2)φ(x
1 2, t) dt.
ma-ka persamaan diatas dapat ditulis menjadi
Selanjutnya turunan φ pada fungsi difusi didekati menggunakan pendekatan φ
pada turunan pertama terhadap x seperti yang terdapat pada persamaan (3.10) dan
melakukan pendekatan upwind terhadap φ pada fungsi adveksi yang terdapat pada (3.11).
Sehingga pendekatanφ(x0, tn) ≈ Φn0 danφ(x1, tn) ≈ Φn0 padaCV0 dapat
ditu-liskan dalam persamaan aljabar berikut
(Φn0 −Φn−0 1)∆x
Persamaan diatas dapat diatur kembali menjadi seperti berikut
∆x
Sehingga entri matriks yang terdapat pada persamaan (3.5) untuk batas kiri domain
dan
B0,0 =
∆x 2 −
k1 2 ∆t
2 ∆x −v12
∆t
2 , B0,1 = k1
2 ∆t
2 ∆x.
Jika padax=ℓterdapat kondisi batasRobinyaitu
−k(ℓ)φ(ℓ) +v(ℓ)(φ(ℓ) = 0,
makaφ(ℓ)dapat diperoleh dengan menggunakan langkah - langkah pendekatan
inte-gral dari SPDE disepanjangCVm seperti yang telah dijabarkan pada subbab 2.6.2.
Karenaxm = ℓ dan −k(ℓ)φ(ℓ) +v(ℓ)φ(ℓ) = 0, maka hasil integrasi operator
diferensial terhadapx0 adalah
−k(x)∂φ
∂x +v(x)φ
xm = 0.
Sehingga integrasi dari operator diferensial dapat disederhanakan menjadi seperti
ber-ikut
Z tn
tn−1
k(xm−1 2)φ
′(x
m−12, t)−v(xm− 1
2)φ(xm− 1 2, t) dt.
Kemudian dengan melakukan integrasi terhadap t menggunakan aturan trapezoidal
maka persamaan diatas dapat ditulis menjadi
k(xm−1 2)φ
′(x m−1
2, tn)−v(xm− 1
2)φ(xm− 1 2, tn)
∆t
2 +
k(xm−1 2)φ
′(x m−1
2, tn−1)−v(xm− 1
2)φ(xm− 1 2, tn−1)
∆t
2 .
Selanjutnya turunanφpada fungsi difusi dapat didekati menggunakan
pendekat-an φ pada turunan pertama terhadap x seperti yang terdapat pada persamaan (3.13)
Sehingga pendekatan φ(xm, tn) ≈ Φn
m dan φ(xm−1, xn) ≈ Φnm−1 pada CVm dapat dituliskan dalam persamaan aljabar berikut
(Φn
Persamaan di atas dapat diatur kembali menjadi
− km−
Sehingga diperoleh entri matriks yang terdapat pada persamaan (3.5) untuk batas
kan-an domain adalah
Am,m−1 =−
3.3 Solusi Numerik Permasalahan Nilai Batas Orde Dua Semilinear
Pada Lemma 2.7 telah diketahui bahwa solusi permasalahan nilai batas orde dua
semilinear adalah
u(ξ) =
Z ℓ
0
G(x;ξ)f(u(x))dx+B.C,
dimana B.C. adalah kondisi batas yang bergantung padaξ yang fungsinya dapat
dipe-roleh dari lemma - lemma sebelumnya sesuai dengan tipe kondisi batas suatu
integrasi secara ekplisit tidak akan bisa dilakukan sehingga diperlukan integrasi
nume-rik untuk memperoleh pendekatan solusinya.
Dengan menggunakan aturan trapezoidal, persamaanu(ξj)dapat ditulis menjadi
u(ξj) = n
X
i=1
Z xi
xi−1
G(x;ξj)f(u(x)) dx+B.C
= n
X
i=1
G(xi−1;ξj)f(u(xi−1)) +G(xj;ξj)f(u(xi))
∆x
2 +B.C(ξj) +Error,
dimanai, j = 0,1,2,3, ..., n.
Andaikanu(ξj) ≈uj,G(xi;ξj)≈ Gi,j,f(u(xi)) ≈f(ui)dan B.C(ξj) ≈B.Cj.
Maka diskritisasiuj dapat ditulis sebagai sistem persamaan aljabar nonlinear berikut
uj =G0,jf(u0) + 2G1,jf(u1) + 2G2,jf(u2) +. . .
+ 2Gn−1,jf(un−1) +Gn,jf(un)
∆x
2 +B.Cj
=G0,jf(u0) + 2
n−1
X
i=1
Gi,jf(ui) +Gn,jf(un)∆x
2 +B.Cj.
(3.15)
Karena persamaan diatas merupakan sistem persamaan nonlinear simultan dengan n
buahunknown, makaudapat diketahui solusinya dengan mendefinisikan suatu fungsi
H :Rn →Rnsedemikian sehinggaHj(u) =0,
dimanau = (u0, u1, u2, ..., un).
kiri, maka diperoleh
H0(u) = u0−
∆x
2 G0,0f(u0) + ∆x n−1
X
i=1
Gi,0f(ui) +
∆x
2 Gn,0f(un)
−B.C0 = 0,
H1(u) = u1−
∆x
2 G0,1f(u0) + ∆x n−1
X
i=1
Gi,1f(ui) +
∆x
2 Gn,1f(un)
−B.C1 = 0,
H2(u) = u2−
∆x
2 G0,2f(u0) + ∆x n−1
X
i=1
Gi,2f(ui) +
∆x
2 Gn,2f(un)
−B.C2 = 0.
. . .
. . .
. . .
Hn(u) = un−∆x
2 G0,nf(u0) + ∆x n−1
X
i=1
Gi,nf(ui) + ∆x
2 Gn,nf(un)
−B.Cn= 0.
(3.16)
Ada beberapa metode yang dapat dilakukan untuk mencari pendekatan solusiui
dari suatu sistem persamaan nonlinear. Diantaranya metode yang paling baik yang
sering digunakan untuk mencari pendekatan solusi adalah metode iterasi Newton.
Metode iterasi Newton pada sistem persamaan nonlinear didasari oleh ekspansi
deret Taylor pada turunan pertama dimana persamaan (3.16) dapat ditulis menjadi
Hi(u)≈Hi(uk) + ∂H0
∂u0
(u0−u0k) +
∂H1
∂u1
(u1−u1k) +...+
∂Hn
∂un(un−unk) = 0,
dimana uk = (u0k, u1k, u2k, ..., unk) adalah titik - titik untuk perkiraan awal (initial
yaitu
Maka pendekatan solusiuadalah
Sehingga persamaan matriks diatas dapat ditulis
uk+1 =uk−[J(uk)]−1H(u
k), (3.17)
dengan JacobianJ(n,n) = [∂Hn/∂un].
Dari persamaan (3.16) diperoleh matriks Jacobian adalah
Selanjutnya dengan menkonversikan metode iterasi newton diatas ke dalam
HASIL DAN PEMBAHASAN
4.1 Solusi Fungsi Green dari Suatu Operator Diferensial Eliptik
Berikut ini diberikan beberapa persoalan untuk mencari fungsi Green secara teoritis
dari suatu operator diferensial eliptik dan operator kondisi batas dengan menggunakan
konsep yang terdapat pada Lemma - Lemma di BAB 2.
4.1.1 Kondisi Batas Dirichlet-Dirichlet
Pada persoalan rambatan panas yang dimodelkan sebagai persamaan panas ste-ady statepada satu dimensi dengan kondisi batasDirichlet-Dirichletyaitu kondisi di-mana solusi dikedua ujung sistem diketahui nilainya. Persamaannya dapat ditulis
Lu=−u′′(x), x∈(0,1)
u(0) = 1danu(1) = 0.
Suatu sistem dikatakansteady statejika sistem berada dalam keadaan setimbang atau tidak berubah seiring waktu yang artinya tidak ada kalor yang keluar atau masuk. u
melambangkan sebagai temperatur dari sistem disepanjang lokasi domain. Tanda
mi-nus menyatakan bahwa suhu hanya akan naik apabila gradien suhu turun. u(0) dan
u(1)menyatakan temperatur di kedua ujung sistem tersebut. Tetapi dalam hal mencari
fungsi Green, temperatur dikedua ujung sistem diasumsikan sama dengan nol.
Berda-sarkan bentuk umum operator diferensialLyang dibahas pada penelitian ini maka dari
persamaan diatas dapat diketahui bahwak(x) = 1, v(x) = 0,danµ(t) = 1.
Dengan menggunakan formula c pada Lemma 2.2, maka diperoleh
c=−
Z ℓ
ξ µ(t) k(t)dt
Z ℓ
0
µ(t) k(t)dt
=−
Z 1
ξ 1 dt
Z 1
0
1 dt
=− (1−ξ)
1 =ξ−1.
yaitu
Sehingga diperoleh fungsi Green dari persamaan panassteady statedi atas adalah
G(x, ξ) =
Selanjutnya, jika pada sistem dipengaruhi oleh konduktivitas termal yaitu
ke-mampuan suatu medium dalam menghantarkan panas dilambangkan dengank(x)
se-perti yang terdapat pada persamaan berikut.
cpada Lemma 2.2 diperoleh
c=−
Jikacdisubtitusikan ke persamaan fungsi Green pada Lemma 2.2 maka akan
Sehingga diperoleh fungsi Green untuk persamaan panas di atas adalah
4.1.2 Kondisi BatasNeumann-Dirichlet
Pada persoalan berikut ini adalah persamaan panassteady statedengan kondisi
Neumann-Dirichletyaitu kondisi dimana turunan solusi pada titik awal dan solusi pada batas kanan domain yang diketahui.
Fungsi Green pada persoalan ini dapat dicari menggunakan Lemma 2.4, dengan
men-subtitusikank(x), v(x)danµ(t)pada formulaG(0, ξ)diperoleh
G(0, ξ) = −
Z 1
0
1 dt
−1 = 1−ξ.
JikaG(0, ξ)disubtitusikan pada formula fungsi Green pada Lemma 2.4, yaitu
G(x, ξ) =
maka diperoleh fungsi Green untuk kondisi diatas adalah
4.1.3 Kondisi BatasRobin-Dirichlet
Misalkan dalam suatu ruangan terdapat sumber lampu yang menghantarkan
pa-nas. Panas yang dihasilkan oleh lampu akan berdifusi secara acak melalui medium
udara dengan konduktivitas termal k(x). Selain itu di dalam ruangan tersebut juga
terdapat proses adveksiv(x) dari kipas angin yang memberikan pengaruh kecepatan
aliran udara didalam ruangan sehingga panas yang dihasilkan lampu akan lebih cepat
tersebar memenuhi ruangan. Permasalahan ini dapat dituliskan dalam bentuk
persa-maan diferensial satu dimensi dengan kondisi batas berikut
Dengan mensubtitusikank(x), v(x), danµ(x)ke formula fungsi Green pada Lemma
2.3 yaitu
Sehingga solusi fungsi Green untuk permasalahan di atas adalah
G(x, ξ) =
4.1.4 Kondisi BatasNeumann-Neumann
advek-si dengan kondiadvek-si batasNeumann-Neumannyang artinya informasi yang diketahui ada pada turunan dari solusi pada kedua ujung sistem yang dituliskan dalam persamaan
diferensial berikut
Maka dapat diperolehcpada Lemma 2.6 adalah
c=
Dengan mensubtitusikan c, k(x), v(x), dan µ(x) ke formula Green pada Lemma 2.6,
yaitu
G(x, ξ) =
(1 +x) + 1 (1 +x)
1 6 +
2 3(1 +ξ)2
jika x≤ξ
4 3 +
4 3(1 +ξ)2
1 +x
8 +
1 2(1 +x)
, jika x > ξ.
4.2 Solusi Fungsi Green Secara Numerik
Ketika metode teoritis tidak bisa lagi diandalkan dalam mencari solusi dari
sua-tu permasalahan, maka metode numerik dapat dipakai unsua-tuk mendapatkan pendekatan
solusi. Integrasi numerik pada formula fungsi Green dapat digunakan untuk
mempe-roleh solusi fungsi Green dari suatu operator diferensial dengan operator kondisi batas
tertentu. Selain itu juga terdapat alternatif lain untuk memperoleh pendekatan fungsi
Green yaitu dengan menggunakan algoritma MCMC.
4.2.1 Menggunakan Integrasi Numerik
Penyelesaian persoalan berikut ini menggunakan persamaan numerik fungsi Green
yang terdapat pada (3.1), dimana persoalan matematika yang lebih kompleks dapat
diselesaikan secara numerik dan akan diperoleh pendekatan solusi yang dapat
digam-barkan grafik penyelesaiannya.
Sebelum membahas penyelesaian fungsi Green secara numerik, berikut ini
ada-lah contoh permasaada-lahan yang dapat diketahui solusi analitik dari fungsi Green
kemu-dian akan dilakukan pendekatan numerik untuk mengetahui konvergensi solusi
nume-rik dengan solusi analitiknya.
Pada subab 3.1.4 telah dibahas penyelesaian analitik fungsi Green dengan
kon-disi batas Neumann- Neumann yang dapat diperoleh fungsi eksplisitnya. Selanjut-nya untuk memperoleh penyelesaian numerik, dapat menggunakan solusi fungsi Green
berikut,
Gi,j =
c µi
1 v0 −
gi
i≤j
1 +c µi
µn
vn +gn−gi
i > j,
dengan
c= −µn
vn −(gn−gj) µn
vn − 1 v0
+gn ,
dimanai, j = 0,1,2,3, ..., n.
Dengan menggunakan program MATLAB yang terdapat pada lampiran 1, maka
diperoleh grafik penyelesaian fungsi Green secara numerik.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0.92
0.94 0.96 0.98 1 1.02 1.04
x
analitik ∆x=1 4
∆x=1 8
∆x= 1 16
∆x= 1 32
∆x= 1 64
Gambar 4.1. Perbandingan solusi analitik dan solusi numerik untuk beberapa∆x.
Pada Gambar 4.1diberikan grafik fungsi Green yang diperoleh secara analitik
dan juga numerik. Dari ilustrasi yang diberikan pada gambar tersebut, dapat
fungsi Green secara numerik akan semakin mendekati solusi analitiknya.
Diberikan suatu persamaan diferensial dengan kondisi batasDirichlet-Dirichlet
berikut yaitu
Lu=−k(x)u′+v(x)u′, x∈(0,1)
u(0) = 1, danu(1) = 0,
dengank(x) = 1
1−0.99x2 sin(50πx) danv(x) = 10.
Dalam kasus ini, penyelesaian secara analitik tidak bisa lagi dilakukan karena
integrasiµ(x)tidak dapat diperoleh fungsi eksplisitnya. Oleh karena itu, penyelesaian
fungsi Green hanya dapat dilakukan dengan menggunakan pendekatan numerik.
De-ngan menggunakan penyelesaian fungsi Green yang terdapat pada Lemma 2.2, dapat
ditulis ke dalam solusi numerik fungsi Green yaitu
Gij, =
− c
µigi, jikai≤j
1 +c
µi (gn−gi), jikai > j,
(4.1)
dengan
c=−(gn−gj) Bn
dimanai, j = 0,1,2,3, ..., n.
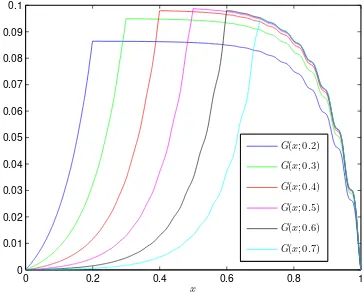
Dengan mengimplementasikan persamaan (4.1) ke dalam program MATLAB
yang terdapat pada lampiran 1, maka diperoleh pendekatan fungsi Green untuk
0 0.2 0.4 0.6 0.8 1 0
0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
x
G(x; 0.2)
G(x; 0.3)
G(x; 0.4)
G(x; 0.5)
G(x; 0.6)
G(x; 0.7)
Gambar 4.2. Pendekatan Fungsi Green
4.2.2 Menggunakan Algoritma MCMC
Berikut ini adalah contoh permasalahan numerik dari fungsi Green yang
dipero-leh dengan mengkonstruksi algoritma Metropolis-Hasting MCMC. Pada contoh
beri-kut ini menggunakan operator diferensial eliptik yang terdapat pada bagian 3.1.4
de-ngan kondisi batasDirichlet - Dirichletyaitu
L= (−(1 +x)2 u′+ (1 +x)u)′, x∈(0,1),
u(0) = 0, danu(1) = 0.
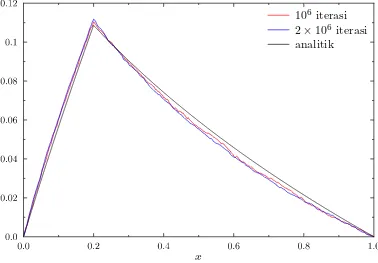
Dimanak(x) = (1 +x)2 dan v(x) = 1 +x. Dengan bantuan program
MAT-LAB yang terdapat pada lampiran 3, maka solusi fungsi Green dari operator diferensial
diatas ditunjukkan oleh Gambar 4.3 denganξ = 0.2.
x
106 iterasi
2×106 iterasi analitik
Gambar 4.3. Fungsi Green dengan Pendekatan MCMC
106 dan 2×106 dengan selang waktu ∆t = 1 dan diskritisasi domain adalah∆x =
2×10−3. Pada gambar tersebut juga diberikan grafik analitik yang menunjukkan bahwa
jika iterasi semakin besar maka fungsi Green yang dikonstruksi menggunakan
algorit-ma MCMC akan sealgorit-makin dekat dengan solusi analitiknya.
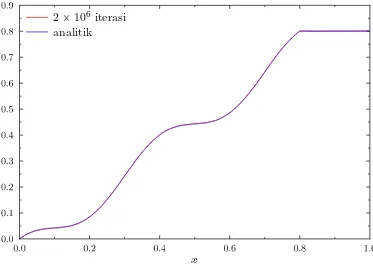
Berikut ini adalah kasus persamaan panas dengan kondisi batasDirichlet-Neumann
yaitu
Lu=
− 1
1−0.9 sin(5πx)u ′
′
x∈(0,1)
u(0) = 0, danu′(1) = 0.
Dimana k(x) = 1
1−0.9 sin(5π x) dan v(x) = 0. Gambar 4.4 adalah solusi fungsi
Green dari operator diferensial di atas dengan menggunakan algoritma MCMC yang
terlampir pada lampiran 3 dengan iterasi sebanyak 2×106. Diskritisasi terhadap x
diketahui dengan jelas bahwa pendekatan fungsi Green dengan iterasi 2×106 sudah
mendekati solusi analitiknya.
x
2×106 iterasi analitik
Gambar 4.4. Fungsi Green dengan Pendekatan MCMC
4.3 Solusi Permasalahan Nilai Batas Semilinear
Andaikan terdapat suatu persamaan panas nonhomogen seperti berikut
−u′′ =eu, x∈(0,1)
u(0) = 1danu(1) = 0.
Dimana k(x) = 1, v(x) = 0, danf(u) = eu. Solusi fungsi green pada persamaan
panassteady statetelah diperoleh pada bagian 3.1.1 yaitu
G(x, ξ) =
x(1−ξ), x≤ξ
Dengan mensubitusikan kondisi batas u(0) = 1 dan u(1) = 0 pada solusi u yang
terdapat pada Lemma 2.8, maka solusiudapat disederhanakan menjadi seperti berikut
u(ξ) =
Z 1
0
G(x;ξ)f(u) dx+G′(0;ξ).
Selanjutnya G′(0, ξ) dapat diperoleh dari turunan pertama fungsi Green terhadap x
yaitu
G′(x;ξ) =
1−ξ, x≤ξ
−ξ, x > ξ,
maka diperolehG′(0;ξ) = 1−ξ. Sehingga
u(ξ) =
Z 1
0
G(x;ξ)f(u) dx+ 1−ξ.
Berdasarkan solusi numerik u yang telah dijabarkan pada subbab 2.5, maka u dapat
ditulis ke dalam sistem persamaan aljabar nonlinear berikut
u0 = 1,
uj =G0,jeu0 + 2
n−1
X
i=1
Gi,jeui+Gn,jeun∆x
2 + 1−ξj,
un= 0,
dimanaj = 1,2,3..., n−1.
Selanjutnya dengan mentranformasikan persamaan aljabar diatas pada sebuah fungsi
H :Rn→Rnsedemikian sehingga
Hj(u) =0.
H0(u) = u0−1,
Hj(u) = uj−∆x
2 G0,je
u0 + ∆x
n−1
X
i=1
Gi,jeui+ ∆x 2 Gn,je
un
−1 +ξj = 0,
Hn(u) = un.
Sehinggau dapat diperoleh dengan menggunakan formula iterasi Newton yang
terdapat pada persamaan (3.17) pada subbab 2.7 dengan matriks jacobian adalah
Jn,n=
1 0 0 · · · 0
−∆x G0,1eu0/2 1−∆xG1,1eu1 −∆x G2,1eu2 · · · −∆x Gn,1eun/2
−∆x G0,2eu0/2 −∆x G1,2eu1 1−∆x G2,2eu2 · · · −∆x Gn,2eun/2
..
. ... . .. ...
0 0 0 · · · 1
dengan menggunakan program MATLAB yang terlampir pada lampiran 2, maka dapat
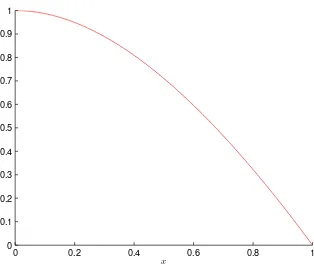
digambarkan grafik pendekatan solusiudengan∆x = 5×10−3 seperti pada Gambar
4.5.
Selanjutnya solusi persamaan nilai batas semilinear berikut
−k(x)u′−v(x)u′ =eu, x∈(0,1)
u(0) = 1, danu(1) = 0,
dengank(x) = 1
1−0.99x2 sin(50πx) danv(x) = 10.
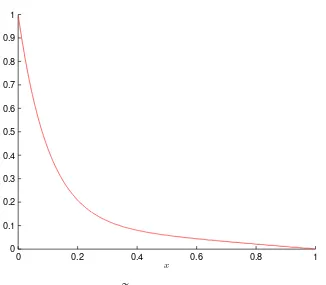
Pada bagian 3.2.1 telah diperoleh pedekatan numerik fungsi Green dari operator
diferensial eliptik diatas yang diperoleh dalam bentuk grafik yang terdapat pada
0 0.2 0.4 0.6 0.8 1 0
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
x
Gambar 4.5. Solusi dariu′′ =eu dengan pendekatan numerik
yang terdapat pada Lemma 2.8 dapat disederhanakan seperti berikut
u(ξ) =
Z 1
0
G(x;ξ)f(u) dx+G′(0;ξ).
Andaikan pendekatan dari turunan fungsi Green adalahG′(x;ξ)≈DG
i,jdimanai, j = 0,1,2,3, . . . , ndan diketahui bahwa kondisi batas fungsi Green adalahG(0;ξ) = 0
danG(ℓ;ξ) = 0maka pendekatan numerik dari turunan fungsi Green adalah sebagai
berikut
DGi,j =
−cµi
ki, jikai≤j
−(1 +c)µi
Sehingga solusiudapat ditulis kedalam sistem persamaan aljabar nonlinear berikut
u0 = 1,
uj =G0,jeu0 + 2
n−1
X
i=1
Gi,jeui +Gn,jeun∆x
2 +DG0,j,
un= 0,
denganj = 1,2,3, . . . , n−1.
Selanjutnya dengan mentransformasikan persamaan aljabar diatas pada suatu
fungsi yang didefenisikan sebagai H : Rn → Rn sedemikian sehingga Hj(u) = 0
dan menggunakan metode iterasi Newton seperti yang telah dijabarkan pada, maka
grafik pendekatan solusi u dengan diskritisasi ∆x = 2× 10−3 adalah seperti pada
Gambar 4.6
0 0.2 0.4 0.6 0.8 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
x
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Selain menggunakan integrasi numerik pada fungsi Green, algoritmaMetropolis-Hasting
MCMC juga dapat digunakan sebagai alternatif untuk memperoleh pendekatan fungsi
Green dari suatu operator diferensial eliptik L dengan kondisi batas Dirichlet, Neu-manndanRobin.
Jika diketahui fungsi Green dari suatu operator diferensial eliptik baik secara
analitik maupun secara numerik, maka pendekatan solusi dari suatu permasalahan
nilai batas semilinear dapat diperoleh menggunakan metode iterasi Newton dengan
mentransformasikan integrasi dari fungsi Green dan fungsi semilinear ke dalam sistem
persamaan aljabar nonlinear.
5.2 Saran
Pada penelitian ini penulis menggunakan pendekatan fungsi Green pada operator
di-ferensial yang bersifat eliptik. Penulis berharap ada ketertarikan dari pembaca untuk
mengembangkan penelitian ini dengan mencoba pendekatan fungsi Green pada
opera-tor diferensial yang bersifat hiperbolik dan parabolik dengan menggunakan algoritma
TINJAUAN PUSTAKA
Sebelum membahas definisi dari fungsi Green, penulis akan menjelaskan persamaan
diferensial semilinear yang berkaitan dengan penelitian ini dan hubungannya dengan
penyelesaian permasalahan dengan menggunakan fungsi Green.
2.1 Persamaan Diferensial Semilinear
Menurut Evans (2010), suatu persamaan diferensial nonlinear dikatakan semilinear
jika suku dengan orde tertinggi dari fungsiunknownuhanya bergantung pada variabel
xtidak pada uataupun turunannya. Secara umum persamaannya dapat ditulis dalam
bentuk berikut,
a0(x)
dnu dxn +an
dn−1
u dxn−1,
dn−2
u dxn−2, ...,
du dx, u, x
= 0.
Sebagai contohu′′
(x) +u′
(x) +u2
= 0, dimana suku yang membuat persamaan
diferensial orde dua ini menjadi nonlinear adalahu2
. Karena nonlinear tidak terletak
pada suku dengan orde tertinggi dari persamaan tersebut, maka persamaan diferensial
ini bersifat semilinear. Contoh lainnya adalah persamaan diferensial parsial dariutt−
ux + sinu = 0, dikatakan semilinear karena terdapat fungsi unknownuyang terikat
pada fungsi sinus yang nonlinear.
2.2 Fungsi Green dan Hubungannya dengan Fungsi Delta Dirac
Fungsi Delta Dirac diperkenalkan oleh seorang fisikawan Inggris Paul Dirac pada
me-kanika kuantum Dirac. Pada abad ke 19, para ilmuwan matematika dan fisika mulai
menggunakan fungsi Delta Dirac walaupun sebenarnya fungsi ini tidak dapat
digam-barkan secara nyata. Tetapi dalam aplikasinya, fungsi Delta Dirac dianggap sebagai
limit barisan dari fungsi yang memiliki lonjakan tinggi pada titik asalnya. Oleh karena
itu, fungsi Delta Dirac yang dinotasikan dengan δ(x−ξ) dapat dinyatakan sebagai
Dirac mendefinisikan fungsi Delta sebagai fungsi yang bernilai besar sekali di
ξ dan bernilai nol diluar ξ. Definisi dari fungsi Delta Dirac pada ruang dimensi satu
dapat dituliskan secara matematis sebagai berikut.
δ(x−ξ) =
0, jikax6=ξ
∞, jikax=ξ
dengan memenuhi sifat
1. Z ∞
−∞
δ(x−ξ) dx= 1,
2. Z ∞
−∞
f(x)δ(x−ξ) dξ=f(ξ).
Keseluruhan konsep dari fungsi Green erat kaitannya dengan fungsi Delta
Di-rac dalam pendefinisian fungsinya. Andaikan jika terdapat suatu operator diferensial
orde n dinotasikan dengan L pada ruang satu dimensi yang mengatur fungsi u dan
bersamaan dengan operator kondisi batas B, maka fungsi Green G(x;ξ) dapat
dide-finisikan sebagai suatu fungsi yang diatur oleh operator diferensial L dengan fungsi
nonhomogennya adalah fungsi Delta Dirac dan fungsi homogennya adalah operator
kondisi batas pada domain.
2.3 Fungsi Green untuk Operator Diferensial Eliptik pada Satu Dimensi
Secara umum suatu persamaan diferensial eliptik orde dua pada ruang satu dimensi
dapat ditulis dalam bentuk berikut,
− d dx
a(x)du dx
+b(x)du
dx +c(x)u=f(x).
Persamaan diferensial eliptik dapat ditemukan di berbagai aplikasi dan
pemode-lan fisika diantaranya yaitu pada potensial bidang gravitasi dan elektrostatik. Selain itu
diaplikasikan juga pada kepadatan peluang suaturandom-walk, aliran panas stasioner
operator kondisi batas homogen yang dinotasikan denganLdanByaitu
Maka operator diferensialLedikatakan sebagaiadjointdari operator diferensialLjika
memenuhi sifat
leh dengan melakukan integrasi pada bagian sebelah kanan yaitu
Z b
Dengan menggunakan intergrasi parsial disepanjang(a, b)pada bagian sebelah kanan,
diperoleh
Selanjutnya integrasi pada persamaan diatas juga dapat ditulis seperti berikut
Z b
Dengan melakukan integrasi parsial sekali lagi pada suku pertama maka persamaan
diatas dapat ditulis menjadi
−k(x)du
Dengan mengasumsikan Bau = Bbu = 0 dan mengatur adjoint dari kondisi batas
Sehingga diperoleh
Z b
a
uLwdx= Z b
a w
d dx
−k(x)du dx
−v(x)du dx
dx=
Z b
a
wLeudx,
dimanaadjointoperator diferensialLeadalah
e L = d
dx
−k(x) d dx
−v(x) d dx.
Turunan - turunan yang terdapat pada operator diferensial diatas adalah turunan
terhadap variabel spasialx. k(x)adalah fungsi yang bergantung pada turunan kedua
uyang menggambarkan sebagai difusi dan v(x)adalah fungsi yang bergantung pada
turunan pertamauyang menggambarkan sebagai adveksi.
Adveksi dihasilkan oleh aliran yang bersifat searah dan tidak mengubah zat yang
dipindahkan. Sedangkan difusi mengacu pada pergerakan massa zat akibat gerakan
pencampuran air. Dalam permasalahan fisika model adveksi dan difusi dapat
dicon-tohkan pada gerakan pasang surut air yang menyebabkan air bergerak searah keluar
dari muara sungai. Apabila pemodelan fokus kepada efek pencemaran bakteri dari
lu-apan air hujan jangka pendek, maka karakteristik dari perpindahannya sebagai
meka-nisme adveksi. Dalam skala waktu yang lebih lama, pergerakan pasang surut air akan
menggerakkan air bolak - balik yang membentuk siklus dapat dikategorikan sebagai
mekanisme difusi (Chapra, 2008).
Selain itu pemodelan difusi dan adveksi juga banyak dipakai dalam ilmu
biolo-gi. Difusi digambarkan sebagai pergerakan acak partikel - partikel zat kimia yang
me-nyebabkannya untuk bergerak dari konsentrasi tinggi ke konsentrasi rendah. Adveksi
digambarkan sebagaik transportasi partikel zat kimia yang bergerak dalam medium
tertentu, misalnya udara, air, darah, dan lain- lain. Salah satu contoh permasalahan
biologi yang menggunakan adveksi dan difusi adalah memodelkan kepadatan
popu-lasi zooplankton pada sebuah danau. Pergerakan zooplankton secara vertikal adalah
bermigrasi ke permukaan air adalah adveksi ( Logan, 2004).
Jika terdapat suatu operator diferensial orde duaLbersamaan operator batasB0
danBℓ pada ruang satu dimensi(0, ℓ), maka fungsi Green terkait memenuhi
LG(x;ξ) =δ(x−ξ), x∈(0, ℓ)
B0 = 0,Bℓ = 0.
Berikut ini diberikan Lemma penyelesaian fungsi Green dari operator diferensial
eliptik orde dua yang telah disebutkan diatas.
Lemma 2.1. Andaikan terdapat dua fungsik : (0, ℓ)→R+
danv : (0, ℓ)→Rdengan operator diferensialLyang didefinisikan sebagai
Lu=−k(x)u′
+v(x)u ′ .
Maka fungsi Greennya adalah
Bukti. Berdasarkan definisi fungsi Green pada satu dimensi, maka fungsi Green yang
memenuhi operator diferensial diatas adalah
−k(x)G′
(x;ξ) +v(x)G(x;ξ) ′
=δ(x−ξ), x∈(0, ℓ) (2.3)
dimanaδ(x−ξ) = 0ketikax∈(0, ξ)danx∈(ξ, ℓ). Turunan - turunan yang terdapat
pada fungsi Green di atas adalah turunan terhadap variabelx. Selanjutnya integrasikan
persamaan diatas terhadapxsehingga diperoleh
−k(x)G′
(x;ξ) +v(x)G(x;ξ) = c, x≤ξ (2.4)
−k(x)G′
(x;ξ) +v(x)G(x;ξ) =d, x > ξ. (2.5)
Kemudian kalikan kedua sisi persamaan diatas dengan− 1
k(x)dan faktor integrasiµ(x) sehingga menjadi
µ(x)G′
(x;ξ)− v(x)
k(x)µ(x)G(x;ξ) =−c µ(x)
k(x), x≤ξ
µ(x)G′
(x;ξ)− v(x)
k(x)µ(x)G(x;ξ) = −d µ(x)
k(x), x > ξ
(2.6)
dengan
µ(x) =exp− Z x
0
v(s) k(s)ds
.
Maka sisi sebelah kiri dari persamaan (2.6) dapat dianggap sebagai derivatif dariµ(x)G(x, ξ),
yaitu
d dx
µ(x)G(x;ξ)=−cµ(x)
k(x), x≤ξ (2.7)
d dx
µ(x)G(x;ξ)=−dµ(x)
k(x), x > ξ. (2.8)
Kemudian integrasikan kedua sisi persamaan (2.7) terhadap t dengan batas(0, x)
se-hingga didapatkan
µ(x)G(x;ξ)−µ(0)G(0;ξ) = −c Z x
0
Dengan memindahkan bagian kedua di ruas kiri persamaan ke ruas kanan dan
menga-likan hasilnya denganµ−1
(x), diperoleh
Di sini telah digunakan fakta bahwa µ(0) = 1. Dengan melakukan hal yang serupa
terhadap (2.8), yakni integrasi dengan batas(x, ℓ), maka diperoleh
G(x;ξ) = 1
Selanjutnya dengan menggunakan sifat integral dari fungsi delta Dirac, diperoleh
Z ℓ
Karena bagian sebelah kiri persamaan di atas adalah
−k(ℓ)G′
(ℓ;ξ) +v(ℓ)G(ℓ;ξ)−−k(0)G′
(0;ξ) +v(0)G(0;ξ),
dan dengan menggunakan (2.4) dan (2.5), maka didapatkan hubungan
d= 1 +c. (2.11)
dengan mensubtitusikand pada persamaan (2.9) maka diperoleh persamaan (2.1)
se-bagai fungsi Green dari operator diferensial diatas.
Selanjutnyacdapat diketahui dengan menggunakan kekontinuan dari fungsi
Gre-en ketikax=ξ, yaitu
kanan maka didapatkan
maka dapat diperolehcyang telah disebutkan pada Lemma 2.1.
Pada pembuktian Lemma diatas telah diperoleh solusi fungsi Green untuk
ope-rator diferensial eliptikL. Sehingga turunan dari fungsi Green terhadapxyang
dino-tasikan denganG′
(x;ξ)adalah
Turunan suku kedua persamaan fungsi Green untukx≤ξadalah
MakaG′
(x;ξ)dapat disederhanakan menjadi
G′
Berikut ini diberikan beberapa Lemma yang menggunakan operator diferensial
pada Lemma 2.1 dengan mengkombinasikan operator kondisi batas Dirichlet,
Neu-mann dan Robinpada masing - masing domain.
Lemma 2.2. Andaikan terdapat suatu operator diferensial dan operator kondisi batas
Maka fungsi Greennya adalah
G(x;ξ) =
dimanaµ(t)seperti yang tertera di Lemma 2.1 dan
c=−
Bukti. Diketahui bahwa kondisi batas pada permasalahan diatas adalah G(0;ξ) = 0
danG(ℓ;ξ) = 0, maka persamaan (2.1) pada Lemma 2.1 dapat disederhanakan
Lemma 2.3. Andaikan terdapat suatu operator diferensial dan operator kondisi batas
Maka fungsi Greennya adalah
G(x;ξ) =
Bukti. Diketahui dari kondisi batas
−k(0)G′
(0;ξ) +v(0)G(0;ξ) = 0 dan G(ℓ;ξ) = 0.
Jika x = 0, maka persamaan (2.2) untuk x ≤ ξ pada Lemma 2.1 menjadi c = 0.
Sehingga persamaan (2.1) menjadi
G(x;ξ) =
Karenac= 0, makacpada Lemma 2.1 menjadi
0 =
Sehingga dapat diperoleh
G(0;ξ) = Z ℓ
ξ µ(t) k(t)dt.
Dengan mensubtitusikanG(0;ξ)ke persamaan (2.19), maka diperoleh (2.18) sebagai
Lemma 2.4. Andaikan terdapat suatu operator diferensial dan operator kondisi batas
Maka fungsi Greennya adalah
G(x;ξ) =
denganµ(t)seperti yang telah disebutkan pada Lemma 2.1 dan
G(0;ξ) =−
Bukti. Diketahui dari kondisi batas fungsi Green adalah
−k(0)G′
(0;ξ) = 0 dan G(ℓ;ξ) = 0.
Jikax= 0maka persamaan (2.2) untukx≤ξpada Lemma 2.1 menjadi
v(0)G(0;ξ) =c.
Sehingga jikacdanG(ℓ;ξ) disubtitusikan pada persamaan (2.1) maka diperoleh
per-samaan (2.21) sebagai solusi fungsi Green pada permasalahan diatas. Selanjutnya
de-ngan mensubtitusikancpada Lemma 2.1 diperoleh
v(0)G(0;ξ) =
Dengan mengubah persamaan diatas dan mengelompokkan G(0;ξ) ke sebelah kiri,
Lemma 2.5. Andaikan terdapat suatu operator diferensial dan operator kondisi batas
Maka fungsi Greennya adalah
G(x;ξ) =
Bukti. Diketahui dari kondisi batas fungsi Green adalah
−k(0)G′
(0;ξ) = 0 dan −k(ℓ)G′
(ℓ;ξ) +v(ℓ)G(ℓ;ξ) = 0.
Jikax= 0, maka persamaan (2.2) untukx≤ξpada Lemma 2.1 menjadi
v(0)G(0;ξ) =c.
Jikax=ℓmaka persamaan (2.2) untukx > ξpada Lemma 2.1 menjadi
−k(ℓ)G′
(ℓ;ξ) +v(ℓ)G(ℓ;ξ) = d= 0.
Karena pada (2.11) diketahui bahwa d = c+ 1 = 0makac = −1. Sehingga untuk
x≤ξpada persamaan (2.1) dapat disederhanakan menjadi
Untukx > ξ pada persamaan (2.1) dapat disederhanakan menjadi
G(x;ξ) = 1
µ(x)µ(ℓ)G(ℓ;ξ) (2.25)
Selanjutnya dengan mensubtitusikancpada Lemma 2.1 diperoleh
−1 =
Dengan mengubah persamaan diatas dan mengelompokkanµ(ℓ)G(ℓ;ξ)ke sebelah kiri
persamaan, maka didapatkan
µ(ℓ)G(ℓ;ξ) = − 1
Sehingga jikaµ(ℓ)G(ℓ;ξ)disubtitusikan pada (2.25) maka diperoleh persamaan (2.24)
sebagai solusi fungsi Green untuk permasalahan di atas.
Lemma 2.6. Andaikan terdapat suatu operator diferensial dan operator kondisi batas
Maka fungsi Greennya adalah
G(x;ξ) =
dimanaµ(t)seperti yang telah disebutan pada Lemma 2.1 dan
dengan syaratv(0)6= 0danv(ℓ)6= 0.
Bukti. Diketahui dari kondisi batas fungsi Green adalah
−k(0)G′
(0;ξ) = 0 dan −k(ℓ)G′
(ℓ;ξ) = 0.
Jikax= 0maka persamaan (2.2) untukx≤ξpada Lemma 2.1 menjadi
v(0)G(0;ξ) =c.
Jikax=ℓmaka persamaan (2.2) untukx > ξpada Lemma 2.1 menjadi
v(ℓ)G(ℓ;ξ) =d= 1 +c.
Dari persamaan diatas maka diperoleh
G(0;ξ) = c
v(0) dan G(ℓ;ξ) =
(1 +c) v(ℓ) .
Selanjutnya dengan mensubtitusikanG(0;ξ)untukx≤ ξpada persamaan (2.1) dapat
disederhanakan menjadi
G(x;ξ) = 1 µ(x)
c v(0) −c
Z x
0
µ(t) k(t)dt
= c
µ(x) 1
v(0) − Z x
0
µ(t) k(t)dt
,
dan mensubtitusikanG(ℓ;ξ)untukx > ξpada persamaan (2.1) dapat disederhanakan
menjadi
G(x;ξ) = 1 µ(x)
µ(ℓ)(1 +c)
v(ℓ) + (1 +c) Z ℓ
x µ(t) k(t)dt
= (1 +c) µ(x)
µ(ℓ) v(ℓ) +
Z ℓ
x µ(t) k(t)dt
.
Sehingga diperoleh persamaan (2.27) sebagai solusi fungsi Green dari permasalahan
Lemma 2.1, diperoleh
c= c
v(0) −µ(l)
(1 +c) v(ℓ) −
Z ℓ
ξ µ(t) k(t) dt Z ℓ
0
µ(t) k(t) dt
.
Dengan mengubah persamaan diatas dan mengelompokancke sebelah kiri, maka akan
diperolehcseperti yang telah disebutkan pada (2.28).
2.4 Solusi Permasalahan Nilai Batas Orde Dua Semilinear
Ada beberapa metode yang dapat digunakan untuk mencari solusi dari suatu
perma-salahan nilai batas yang nonhomogen, salah satu diantaranya adalah dengan mencari
fungsi Green dari permasalahan tersebut.
Jika terdapat suatu permasalahan dengan kondisi batas yang homogen, maka
so-lusinya dapat direpresentasikan sebagai kombinasi linear dari fungsi Green dan fungsi
nonhomogennya . Adapun jika suatu permasalahan diferensial orde dua dengan
kondi-si batas yang nonhomogen, maka solukondi-sinya tidak hanya dipengaruhi oleh integral dari
fungsi Green dan fungsi nonhomogennya, tetapi juga dipengaruhi oleh kondisi batas
dari fungsi Green tersebut.
Lemma berikut ini membahas solusi dari suatu persamaan diferensial jika fungsi
Green dari persamaan diferensial tersebut diketahui.
Lemma 2.7. Andaikan terdapat suatu persamaan diferensial orde dua semilinear pada
dimensi satu yang dirumuskan sebagai mencariu:R→Ryang memenuhi
e
Lu(x) = −(k(x)u′ (x))′
−v(x)u′
(x) = f(u(x)), x∈(0, ℓ). (2.29)
Makauadalah
u(ξ) = Z ℓ
0
dimana
Bukti. Dengan menggunakan persamaan diferensial pada (2.29), diketahui bahwa
G(x;ξ)f(u(x)) =G(x;ξ)Leu(x) = G(x;ξ)
Dengan mengintegrasikan persamaan diatas pada(0, ℓ)dan memandang integral pada
ruas kanan menjadi pengurangan dari integral
Z ℓ
Kemudian dengan mengaplikasikan integrasi parsial pada suku pertama di ruas kanan,
diperoleh
Dengan melakukan integrasi parsial sekali lagi terhadap integral diruas kiri, akan
di-peroleh
persa-maan (2.34)
Dengan menggabungkan persamaan (2.35), (2.36), dan (2.37) maka diperoleh
Z ℓ
Karena integral pada ruas kiri dapat ditulis sebagai fungsi delta Dirac dan dengan
menggunakan sifat dari fungsi delta Dirac, diperoleh
Z ℓ
Sehingga diperoleh (2.30) sebagai solusi dariu.
Jika persamaan diferensial diatas diberikan kondisi batas tertentu seperti
Dirich-let, Neumann, danRobin, maka penyelesaiannya akan dipengaruhi oleh kondisi batas
yang diberikan. Seperti yang terdapat pada Lemma - Lemma berikut ini.
Lemma 2.8. Andaikan terdapat masalah nilai batas semilinear pada ruang satu
di-mensi yang memenuhi
Maka solusiuadalah
u(ξ) = Z ℓ
0
G(x;ξ)f(u(x)) dx−k(ℓ)G′
(ℓ;ξ)uℓ+k(0)G′
(0;ξ)u0, (2.40)
dimanaG(x;ξ)adalah fungsi Green yang diatur oleh
LG=δ(x−ξ), x, ξ ∈(0, ℓ)
G(0;ξ) = 0 danG(ℓ;ξ) = 0.
(2.41)
Bukti. Diketahui dari kondisi batas pada fungsi Green bahwaG(0;ξ) = 0danG(ℓ;ξ) =
0. Sehingga diperoleh
G(x;ξ)k(x)du dx
x=ℓ
x=0 = 0
dan v(x)G(x;ξ)u(x)x
=ℓ
x=0 = 0
. (2.42)
Demikian pula, dengan menggunakan kondisi batas yang diberikan untuk u, maka
solusiuyang disebutkan pada Lemma 2.7 dapat disederhanakan menjadi
u(ξ) = Z ℓ
0
G(x;ξ)f(u(x)) dx−k(ℓ)dG(ℓ;ξ)
dx uℓ+k(0)
dG(0;ξ)
dx u0 (2.43)
Lemma 2.9. Andaikan terdapat masalah nilai batas semilinear pada ruang satu
di-mensi yang memenuhi
e
Lu=f(u(x)), x∈(0, ℓ)
−(k(0)u′
(0)) =g0, dan u(ℓ) =uℓ
(2.44)
Maka solusiuadalah
u(ξ) = Z ℓ
0
G(x;ξ)f(u(ξ)) dx+G(0;ξ)g0−k(ℓ)G
′
(ℓ;ξ)uℓ (2.45)
dimanaG(x, ξ)adalah fungsi Green yang diatur oleh
LG=δ(x−ξ), x, ξ∈(0, ℓ)
−k(0)G′
(0;ξ) +v(0)G(0;ξ) = 0 danG(ℓ;ξ) = 0
Bukti. Diketahui dari kondisi batas fungsi Green adalah G(ℓ;ξ) = 0. Sehingga B.C
yang terdapat pada Lemma 2.7 dapat disederhanakan
G(x;ξ)k(x)du dx
x=ℓ
x=0 =−G(0;ξ)k(0)u
′
(0), (2.47)
dan
v(x)G(x;ξ)u(x)x
=ℓ
x=0 =
−v(0)G(0;ξ)u(0). (2.48)
Kemudian
−k(x)dG(x;ξ) dx u(x)
x=ℓ
x=0 =
−k(ℓ)G′
(ℓ;ξ)u(ℓ) +k(0)G′
(0;ξ)u(0). (2.49)
Karena kondisi batas yang diberikan padaG(x;ξ)ketikax= 0adalah
−k(0)G′
(0;ξ) +v(0)G(0;ξ) = 0.
Maka dengan menggabungkan persamaan (2.48) dan suku kedua pada ruas kanan
per-samaan (2.49), diperoleh
−−k(0)G′
(0;ξ) +v(0)G(0;ξ)u(0) = 0.
Selanjutnya, dengan menggunakan kondisi batas padaumaka persamaan (2.47)
men-jadi
−G(0;ξ)k(0)u′
(0) = G(0;ξ)u0,
dan suku pertama ruas kanan persamaan (2.49) menjadi
−k(ℓ)G′
(ℓ;ξ)u(ℓ) =−k(ℓ)G′
(ℓ;ξ)uℓ.
Sehingga persamaanupada lemma 2.7 dapat disederhanakan menjadi (2.45).
di-mensi yang memenuhi
e
Lu=f(u(x)), x∈(0, ℓ)
−k(0)u′
(0)−v(0)u(0) =g0, dan u(ℓ) =uℓ.
(2.50)
Maka solusiuadalah
u(ξ) = Z ℓ
0
G(x;ξ)f(u(x)) dx+G(0;ξ)g0−k(ℓ)G
′
(ℓ;ξ)uℓ. (2.51)
dimanaG(x;ξ)adalah fungsi Green yang diatur oleh
Lu=δ(x−ξ), x, ξ∈(0, ℓ)
k(0)G′
(0;ξ) = 0 danG(ℓ;ξ) = 0.
(2.52)
Bukti. Diketahui dari kondisi batas fungsi Greenk(0)G′
(0, ξ) = 0. Sehingga
−k(x)dG(x;ξ) dx u(x)
x=ℓ
x=0 =
−k(ℓ)dG(ℓ;ξ)
dx u(ℓ), (2.53)
dan jikaξ=ℓ, makaG(ℓ;ξ) = 0. Sehingga
G(x;ξ)k(x)du dx x
=ℓ
x=0 =−G(0;ξ)k(0)u
′
(0). (2.54)
dan
v(ξ)G(x;ξ)u(ξ)x
=ℓ
x=0 =−v(0)G(0;ξ)u(0). (2.55)
Dengan menggabungkan persamaan (2.54) dan (2.55), dan menggunakan kondisi batas
padaumaka dapat disederhanakan
G(0;ξ)−k(0)u′
(0)−v(0)u(0)=G(0;ξ)g0, (2.56)
dan persamaan (2.53) menjadi
−k(ℓ)G′
(ℓ;ξ)u(ℓ) =−k(ℓ)G′
(ℓ;ξ)uℓ. (2.57)
dapat disederhanakan menjadi (2.51).
Lemma 2.11. Andaikan terdapat masalah nilai batas semilinear pada ruang satu
di-mensi yang memenuhi
e
Lu=f(u(x)), x∈(0, ℓ)
−k(0)u′
(0)−v(0)u(0) =g0, dan −k(ℓ)u
′
(ℓ) =gℓ.
(2.58)
Maka solusiuadalah
u(ξ) = Z ℓ
0
G(x;ξ)f(u(ξ)) dx+G(0;ξ)g0−G(ℓ;ξ)gℓ. (2.59)
dimanaG(x;ξ)adalah fungsi Green yang diatur oleh
LG=δ(x−ξ), x, ξ∈(0, ℓ)
−k(0)G′
(0;ξ) = 0 dan −k(ℓ)G′
(ℓ;ξ) +v(ℓ)G(ℓ;ξ) = 0.
(2.60)
Bukti. Diketahui bahwa kondisi batas fungsi Green adalah −k(0)G′
(0) = 0, maka
B.C pada Lemma 2.7 dapat disederhanakan menjadi
−k(x)dG(x;ξ) dx u(x)
x=ℓ
x=0 =
−k(ℓ)G′
(ℓ;ξ)u(ℓ). (2.61)
Selanjutnya B.C lainnya adalah
G(x;ξ)k(x)du dx x
=ℓ
x=0 =G(ℓ;ξ)k(ℓ)u
′
(ℓ)−G(0;ξ)k(0)u′
(0). (2.62)
dan
v(x)G(x;ξ)u(x)x
=ℓ
x=0 =v(ℓ)G(ℓ;ξ)u(ℓ)−v(0)G(0;ξ)u(0). (2.63)
Karena kondisi batasG(x, ξ)ketikax=ℓadalah
−k(ℓ)G′
(ℓ;ξ) +v(ℓ)G(ℓ;ξ) = 0.
persama-an (2.63), maka diperoleh
−k(ℓ)G′
(ℓ;ξ) +v(ℓ)G(ℓ;ξ)u(ℓ) = 0.
Selanjutnya dengan menggabungkan pesamaan (2.62) dan (2.63) dan menggunakan
kondisi batas padau, maka diperoleh
−G(0;ξ)−k(0)u′
(0)−v(0)u(0)−G(ℓ;ξ)k(ℓ)u′
(ℓ) = G(0;ξ)g0−G(ℓ;ξ)gℓ.
(2.64)
Sehingga persamaanupada Lemma 2.7 dapat disederhanakan menjadi (2.59).
Lemma 2.12. Andaikan terdapat masalah nilai batas semilinear pada ruang satu
di-mensi yang memenuhi
e
Lu=f(u(x)), x∈(0, ℓ)
−k(0)u′
(0)−v(0)u(0) =g0, dan −k(ℓ)u
′
(ℓ)−v(ℓ)u(ℓ) =gℓ.
(2.65)
Maka solusiuadalah
u(ξ) = Z ℓ
0
G(x;ξ)f(u(ξ)) dξ+G(0;ξ)g0−G(ℓ;ξ)gℓ. (2.66)
dimanaG(x;ξ)adalah fungsi Green yang diatur oleh
LG=δ(x−ξ), x, ξ∈(0, ℓ)
−k(0)G′
(0;ξ) = 0 dan −k(ℓ)G′
(ℓ;ξ) = 0.
(2.67)
Bukti. Diketahui bahwa kondisi batas fungsi Green adalah −k(0)G′
(0;ξ) = 0 dan
−k(ℓ)G′
(ℓ;ξ)sehingga B.C pada Lemma 2.7 dapat disederhanakan menjadi
−k(ξ)dG(x, ξ) dξ u(ξ)
ξ=ℓ ξ=0 = 0.
B.C lainnya adalah
G(x;ξ)k(x)du dx
x=ℓ
x=0 =G(ℓ;ξ)k(ℓ)u
′
(ℓ)−G(0;ξ)k(0)u′
dan
v(x)G(x;ξ)u(x)x
=ℓ
x=0 =v(ℓ)G(ℓ;ξ)u(ℓ)−v(0)G(0;ξ)u(0).
(2.69)
Selanjutnya dengan menggabungkan ruas kanan persamaan (2.68) dan (2.69) dan
me-nerapkan kondisi batas padau, maka diperoleh
G(0;ξ)−k(0)u′
(0)−v(0)u(0)−G(ℓ;ξ)−k(ℓ)u′
(ℓ)−v(ℓ)u(ℓ)
=G(0;ξ)g0−G(ℓ;ξ)gℓ.