PENYELESAIAN STACKER CRANE PROBLEM DENGAN
ALGORITME LARGEARCS DAN SMALLARCS
HARDONO
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
HARDONO. Penyelesaian Stacker Crane Problem dengan Algoritme Largearcs dan Smallarcs. Dibimbing oleh FARIDA HANUM dan TONI BAKHTIAR.
Rural Postman Problem (RPP) merupakan permasalahan dalam pencarian rute terpendek dengan biaya minimum dan hanya sebagian sisi atau sisi berarah diperlukan saja yang harus dilewati. Salah satu jenis RPP ialah Stacker Crane Problem (SCP), yaitu RPP pada graf campuran yang harus melewati setiap sisi berarah. SCP dapat diselesaikan menggunakan dua macam algoritme heuristik, yaitu algoritme Largearcs dan algoritme Smallarcs yang dalam langkah-langkah penyelesaian juga memerlukan beberapa algoritme lain. Penentuan path terpendek diselesaikan dengan algoritme Dijkstra, penentuan minimum bipartite matching diselesaikan dengan metode Hungaria, penentuan minimum spanning tree diselesaikan dengan algoritme Prim, dan sirkuit Euler ditentukan dengan algoritme van Aardenne-Ehrenfest & de-Bruijn dan algoritme Fleury. Untuk menyelesaikan masalah SCP perlu dipilih sirkuit Euler terpendek dari dua algoritme heuristik yang digunakan. Contoh aplikasi SCP dalam karya ilmiah ini adalah penentuan rute pengiriman katering dengan jarak minimum.
ABSTRACT
HARDONO. The Solution of Stacker Crane Problem using Largearcs and Smallarcs Algorithm. Supervised by FARIDA HANUM and TONI BAKHTIAR.
In graph theory, the Rural Postman Problem (RPP) aims to determine the shortest route with minimum cost, in which only certain edges or arcs are necessarily traversed. One type of RPP is Stacker Crane Problem (SCP) which deals with a mixed graph but only arcs are necessarily traversed. SCP can be solved by using two heuristic algorithms, i.e. Largearcs and Smallarcs algorithms, which include other algorithms in their steps, such as: Dijkstra algorithm to determine shortest route, Hungaria method to determine minimum bipartite matching, Prim algorithm to determine minimum spanning tree, and van Aardenne-Ehrenfest & de-Bruijn algorithm and Fleury algorithm to determine Euler circuits. The shortest Euler circuit resulted from two heuristic algorithms can be used to find a solution of SCP. The application of SCP is illustrated in establishing the minimum distance route of catering delivery.
PENYELESAIAN STACKER CRANE PROBLEM DENGAN
ALGORITME LARGEARCS DAN SMALLARCS
HARDONO
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi : Penyelesaian
Stacker Crane Problem dengan Algoritme
Largearcs dan Smallarcs
Nama
: Hardono
NIM
: G54080026
Menyetujui
Tanggal Lulus:
Pembimbing I,
Dra. Farida Hanum, M.Si.
NIP: 19651019 199103 2 002
Pembimbing II,
Dr. Toni Bakhtiar, M.Sc.
NIP: 19720627 199702 1 002
Mengetahui:
Ketua Departemen,
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah swt atas berkat, rahmat dan kasih sayang-Nya sehingga penulis mampu menyelesaikan karya ilmiah ini. Berbagai kendala dialami oleh penulis sehingga banyak sekali orang yang membantu dan berkontribusi dalam pembuatan karya ilmiah ini. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih kepada:
1. keluarga tercinta: Alm. Bapak dan Alm. Ibu yang pasti selalu mendoakanku, kakakku Mas Ismail dan Mbak Woro (terima kasih atas doa, dukungan, kesabaran, kasih sayang, dan motivasinya), Mbak Resti, Mas Taufan, Mbak Mulyati (terima kasih atas doa, semangat, motivasi dan dukungannya), Fenny Risnita (terima kasih atas kasih sayang, dan doanya),
2. Dra. Farida Hanum, M.Si. selaku dosen pembimbing I yang telah meluangkan waktu dan pikiran dalam membimbing, memberi motivasi, semangat dan doa,
3. Dr. Toni Bakhtiar, M.Sc. selaku dosen pembimbing II yang telah memberikan ilmu, kritik dan saran, motivasi serta doanya,
4. Drs. Siswandi, M.Si. selaku dosen penguji yang telah memberikan ilmu, saran dan doanya,
5. semua dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan, 6. staf Departemen Matematika: Bapak Yono, Ibu Susi, Ibu Ade, Alm. Bapak Bono, Bapak
Deni, Mas Hery, Ibu Yanti atas semangat dan doanya,
7. teman-teman satu bimbingan: Nurul, Maya, Ana dan Ali Vikri yang selalu saling mengingatkan dan memberi motivasi dalam penyusunan skripsi ini,
8. teman-teman mahasiswa Matematika angkatan 45: Herlan, Arbi, Beni, Izzudin, Haryanto, Hendri, Ari, Ridwan, Isna, Santi, Laisanopaci, Regita, Primastuti, Putri, Yunda, Fitryah, Finata, Dewi, Prama, Chastro, Fuka, Ade, Tiwi, Fikri, Irwan, Dimas, Ito, Rianiko, Nova, Dini, Heru, Bram, Kunedi, Khafidz, Irma dan teman-teman lainnya atas doa, dukungan semangatnya serta kebersamaannya selama 3 tahun,
9. kakak-kakak Matematika angkatan 43, dan 44 yang menjadi cermin untuk menjadi pribadi yang lebih baik,
10. adik-adik Matematika angkatan 46 dan 47 yang terus mendukung agar berkembang, 11. Gumatika brilian yang menunjukkan sebuah hal yang baru,
12. semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.
Bogor, Januari 2013
RIWAYAT HIDUP
Penulis dilahirkan di Tangerang pada tanggal 11 Mei 1990 dari bapak Lasimun Hadi Atmodjo (Alm) dan ibu Sri Retno Wati (Alm). Penulis merupakan putra bungsu dari tiga bersaudara.
Pada tahun 1996 penulis lulus dari TK Tunas Rimba, tahun 2002 penulis lulus dari SD Negeri Kembangan Selatan 01 Pagi, tahun 2005 penulis lulus dari SMP Negeri 105 Jakarta Barat, tahun 2008 penulis lulus dari SMA Negeri 57 Jakarta Barat. Penulis diterima sebagai mahasiswa Institut Pertanian Bogor pada tahun 2008 melalui jalur Undangan Seleksi Masuk IPB (USMI), Tingkat Persiapan Bersama. Pada tahun 2009, penulis memilih mayor Matematika pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Analisis Numerik (S1) pada semester ganjil dan semester pendek tahun akademik 2011-2012 dan 2012-2013. Tahun 2009-2010 dan 2011-2012 penulis mendapatkan beasiswa BBM (Bantuan Belajar Mahasiswa) dari Institut Pertanian Bogor.
DAFTAR ISI
Halaman
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... x
DAFTAR LAMPIRAN ... x
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan Penulisan ... 1
II LANDASAN TEORI 2.1 Graf dan Digraf ... 1
2.2 Graf Euler ... 7
2.3 Penentuan Path Terpendek dengan Algoritme Dijktra ... 8
2.4 Penentuan Minimum Bipartite Matching dengan Metode Hungaria ... 9
2.5 Penentuan Minimum Spanning Tree dengan Algoritme Prim ... 10
2.6 Penentuan Sirkuit Euler dengan Algoritme van Aardenne-Ehfrenfest - de Bruijn ... 11
2.7 Penentuan Sirkuit Euler dengan Algoritme Fleury ... 12
III PENYELESAIAN STACKER CRANE PROBLEM 3.1 Algoritme Preprocess ... 13
3.2 Algoritme Largearcs ... 14
3.3 Algoritme Smallarcs ... 16
IV APLIKASI MASALAH 4.1 Penyelesaian SCP dengan Algoritme Largearcs ... 20
4.2 Penyelesaian SCP dengan Algoritme Smallarcs ... 23
V SIMPULAN DAN SARAN 5.1 Simpulan ... 25
5.2 Saran ... 25
DAFTAR PUSTAKA ... 26
LAMPIRAN ... 27
DAFTAR TABEL
Halaman
1 Penentuan path terpendek dimulai dari verteks 0= 1 ... 9
2 Tabel biaya yang berhubungan dengan model penugasan ... 10
3 Penjelasan setiap verteks pada graf kasus katering di Jakarta Pusat ... 20
4 Penentuan path terpendek dimulai dari verteks 0= 1 ... 31
5 Penentuan path terpendek dimulai dari verteks 0= 2 ... 31
6 Penentuan path terpendek dimulai dari verteks 0= 3 ... 32
7 Penentuan path terpendek dimulai dari verteks 0= ... 32
8 Penentuan path terpendek dimulai dari verteks 0= 1 ... 33
9 Penentuan path terpendek dimulai dari verteks 0= 2 ... 33
10 Penentuan path terpendek dimulai dari verteks 0= 3 ... 33
11 Penentuan path terpendek dimulai dari verteks 0= 4 ... 34
12 Penentuan path terpendek dimulai dari verteks 0= 5 ... 34
13 Penentuan path terpendek dimulai dari verteks 0= 6 ... 34
14 Penentuan path terpendek dimulai dari verteks 0= 7 ... 35
15 Penentuan path terpendek dimulai dari verteks 0= 8 ... 35
16 Bobot ( ) setiap sisi , , dengan , ∈ ( ) ... 37
DAFTAR GAMBAR
Halaman 1 Graf ... 22 Digraf ... 2
3 Graf berbobot ... 2
4 Graf campuran ... 2
5 Graf 3 ... 3
6 Subgraf dari 3 ... 3
7 Spanning subgraph dari 3 ... 3
8 Multigraf ... 3
9 Multidigraf ... 3
10 Digraf balans ... 4
11 Graf lengkap ... 5
12 Graf terhubung ... 5
13 Graf tak terhubung ... 5
14 Komponen ke-1 dari graf pada Gambar 13 ... 5
15 Komponen ke-2 dari graf pada Gambar 13 ... 5
16 Graf yang terdapat bridge ... 6
17 Tree ... 6
18 Graf 7 ... 6
19 Spanning tree dari 7 ... 6
20 Arborescence ... 6
21 Graf 8 ... 6
22 Spanning arborescence dari 8 ... 6
23 Graf bipartite ... 7
24 Graf dengan matching ... 7
25 Graf dengan matching perfect ... 7
26 Graf Euler ... 8
27 Graf berbobot dan tidak berarah ... 9
28 Graf contoh algoritme Prim ... 11
29 Minimum spanning tree dari graf pada Gambar 28 ... 11
30 Graf untuk contoh algoritme van Aardenne-Ehrenfest - de Bruijn ... 11
31 Spanning arborescence dari digraf 11 ... 11
32 Pelabelan pada algoritme van Aardenne-Ehrenfest - de Bruijn ... 11
33 Graf Euler untuk contoh algoritme Fleury ... 12
34 Iterasi pertama: inisialisasi 0 ... 12
35 Iterasi kedua: sisi {1,6} dihapus ... 12
36 Iterasi ketiga: sisi {6,2} dihapus ... 12
37 Graf terakhir dari algoritme Fleury ... 12
38 Graf 13 untuk ilustrasi algoritme preprocess ... 13
39 Graf ∗ yang diperoleh dari Langkah 1 algoritme preprocess ... 14
40 Graf ′ yang memenuhi syarat 1 dan 2 ... 14
41 Skema penyelesaian SCP dengan algoritme Largearcs ... 15
42 Skema penyelesaian SCP dengan algoritme Smallarcs ... 17
43 Skema penyelesaian SCP ... 18
44 Peta Katering Eco Raosdi Jakarta Pusat ... 19
45 Graf kasus Katering Eco Raos di Jakarta Pusat dengan arah pendistribusian katering ... 20
46 Subgraf ... 20
47 Graf bipartite ... 21
48 Graf ... 21
49 Komponen 1 dan 2 ... 21
50 Graf ... 21
51 Graf ... 22
52 Graf ... 22
53 Spanning arborescence digraf ... 22
54 Graf yang sudah dilabeli ... 22
55 Graf kasus Katering Eco Raos di Jakarta Pusat dengan algoritme Largearcs ... 23
56 Subgraf ... 23
57 Graf ... 23
58 Minimum spanning tree padagraf ... 23
59 Graf lengkap ... 23
60 Matching perfect minimum dari graf ... 24
61 Graf ... 24
62 Graf ... 24
63 Graf ... 24
64 Spanning arborescence digraf ... 25
65 Graf yang sudah dilabeli ... 25
66 Graf kasus Katering Eco Raos di Jakarta Pusat dengan algoritme Smallarcs ... 25
67 Graf ∗= , ∪ ... 30
68 Graf Kasus Katering Eco Raos di Jakarta Pusat ... 31
69 Graf lengkap ... 36
DAFTAR LAMPIRAN
Halaman 1 Penentuan Minimum Bipartite Matching dengan metode Hungaria ... 282 Langkah penentuan minimum spanning tree dengan algoritme Prim ... 28
3 Langkah solusi sirkuit Euler dengan menggunakan algoritme Fleury ... 29
4 Penentuan path terpendek dengan menggunakan algoritme Dijkstra ... 30
5 Penentuan path terpendek pada kasus Katering menggunakan algoritme Dijkstra ... 31
6 Penentuan Minimum Bipartite Matching dengan metode Hungaria ... 34
7 Penentuan path terpendek 1 dan 2 ... 34
8 Penentuan path terpendek dan ... 35
9 Langkah penentuan minimum spanning tree dengan algoritme Prim ... 35
10 Penentuan Matching yang perfect dengan bobot minimum ... 36
11 Penentuan solusi sirkuit Euler dengan menggunakan algoritme Fleury ... 37
I PENDAHULUAN
1.1 Latar Belakang
Teori graf merupakan topik yang banyak mendapat perhatian saat ini karena teori graf dapat diaplikasikan di berbagai bidang. Pada penerapannya, dapat dihubungkan dengan berbagai bidang ilmu dan juga kehidupan sehari-hari seperti masalah transportasi yang bertujuan menentukan jarak atau biaya optimal.
Salah satu teori graf yang dikembangkan untuk menyelesaikan masalah transportasi adalah Rural Postman Problem (RPP) yang merupakan kasus khusus dari Chinese Postman Problem (CPP). Eiselt et al. (1995a) menyatakan bahwa CPP bertujuan mencari jarak minimum dalam suatu lintasan dengan kondisi setiap jalur harus dilewati paling tidak satu kali. Jika diharuskan melewati jalur yang telah ditentukan, maka permasalahannya menjadi RPP (Eiselt et al. 1995b). RPP pertama kali diperkenalkan oleh Orloff pada tahun 1974. Dalam jurnalnya (Orloff 1974), disebutkan bahwa RPP merupakan formulasi masalah untuk menentukan biaya minimum yang melintasi setiap jalur yang diperlukan pada suatu lintasan. RPP dengan graf berarah biasanya digunakan untuk lintasan yang memiliki jalur satu arah saja, sedangkan jalur yang memiliki dua arah menggunakan RPP dengan graf tidak berarah. Jika kedua jalur,
baik yang satu arah atau pun dua arah, bisa dilayani secara bersamaan, maka dapat digunakan RPP dengan graf campuran. Contoh aplikasi RPP sangat banyak, di antaranya penentuan rute terpendek penyapuan jalan, pengiriman surat atau barang dengan rute terpendek atau biaya minimumnya, penentuan rute bus sekolah, penentuan rute pengiriman bahan bakar, rute pengiriman katering, dsb. Ada beberapa tema yang dibahas dalam RPP, yaitu undirected
RPP, directed RPP, Stacker Crane Problem
(SCP), dan Capacitated Arc Routing Problem
(CARP).
Pada karya ilmiah ini akan dibahas penyelesaian Stacker Crane Problem
menggunakan dua macam algoritme heuristik, yaitu Largearcs dan Smallarcs yang bersumber dari Eiselt et al. (1995b).
1.2 Tujuan Penulisan
Tujuan dari karya ilmiah ini adalah: 1. menyelesaikan masalah SCP dengan dua
macam algoritme heuristik, yaitu algoritme Largearcs dan algoritme
Smallarcs,
2. mengaplikasikan masalah SCP ke dalam masalah penentuan rute pengiriman katering.
II LANDASAN TEORI
Dalam bab ini akan dibahas beberapa landasan teori yang berkaitan dengan bahasan karya ilmiah ini.
2.1 Graf dan Digraf
Teori graf merupakan salah satu dari beberapa bidang matematika yang diketahui dengan pasti awal perkembangannya. Teori ini pertama kali dikenal sejak Euler (1736) mengemukakan penelitiannya tentang masalah jembatan Königsberg. Dua abad kemudian (1936), untuk pertama kalinya dibuat buku tentang teori graf yang ditulis oleh Denes König. Dalam periode yang sangat singkat, teori graf kini mengalami perkembangan yang sangat pesat.
(Chartrand & Oellermann 1993)
Definisi 1 (Graf)
Suatu graf adalah pasangan terurut
, dengan adalah himpunan berhingga dan takkosong dari elemen-elemen graf yang disebut verteks (node, simpul) dan adalah himpunan pasangan yang menghubungkan dua elemen subhimpunan dari yang biasa disebut sisi (edge, line). dapat dituliskan dan = , setiap sisi , pada dapat dinotasikan dengan atau . Banyaknya verteks dari graf disebut order
dari dan banyaknya sisi dari graf disebut
size dari graf .
:
e13
e14
e3 e4
e5 e6 e9 e10 e12 e11 e7 e2 e1 e8 v1 v8 v3 v2
v5 v6
v7
v4
v9
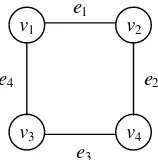
Gambar 1 Graf. Pada Gambar 1 diperlihatkan bahwa
= 1, 2, 3, 4, 5, 6, 7, 8, 9 dan
E = {e1, e2, e3, e4, e5, e6, e7, e8, e9, e10, e11, e12,
e13, e14}
Definsi 2 (Graf berarah/digraf)
Digraf atau graf berarah (directed graph) adalah pasangan terurut , dengan adalah himpunan takkosong yang hingga, dan
adalah himpunan pasangan terurut yang menghubungkan elemen-elemen di . Elemen-elemen dari disebut sisi berarah (arc). Notasi sisi berarah secara umum ialah
, , yaitu sisi berarah dari verteks ke verteks .
(Chartrand & Zhang 2009) : e2 e5 e6 e4 e3 e1 v1 v4 v2 v5 v3
Gambar 2 Digraf.
Pada Gambar 2 terdapat contoh sisi berarah, yaitu 1, 3 , 2, 1 , 3, 2 ,
3, 5 , 4, 2 , 4, 5 .
Definisi 3 (Adjacent dan incident)
Misalkan dan verteks pada graf .
Verteks dikatakan tetangga (adjacent) dari jika ada sisi yang menghubungkan verteks dan , yaitu = . Himpunan semua
tetangga dari verteks dinotasikan dengan . Jika = adalah sisi pada graf maka dikatakan incident dengan verteks dan .
(Chartrand & Zhang 2009) Ilustrasi adjacent dan incident
diperlihatkan pada Gambar 1. Verteks 9
adjacent dengan verteks 7 dan verteks 8, tetapi verteks 9 tidak adjacent dengan verteks 5 dan verteks 6. Verteks 9incident dengan sisi 13 dan sisi 14, tetapi verteks 6 tidak incident dengan sisi 1 dan sisi 2. Definisi 4 (Graf berbobot)
Suatu graf = , dikatakan berbobot jika terdapat sebuah fungsi ∶ → (dengan adalah himpunan bilangan real) yang disebut bobot. Setiap bobot dengan ∈ dinotasikan dengan .
(Foulds 1992) 1 :
5 v1 4 2 6 v3 v4 v2
Gambar 3 Graf berbobot.
Graf 1 pada Gambar 3 merupakan contoh graf berbobot dengan bobot sebagai berikut:
sisi 1 2 memiliki bobot ( 1 2) = 5, sisi 1 4 memiliki bobot 1 4 = 4, dan seterusnya.
Definisi 5 (Graf campuran)
Graf campuran G = (V, A ∪ E) merupakan graf yang setidaknya memiliki satu sisi berarah dan satu sisi tidak berarah. merupakan himpunan sisi-sisi berarah pada dan merupakan himpunan sisi-sisi tidak berarah pada .
(Balakrishnan 1997) 2 :
v1
v2 v3
Definisi 6 (Subgraf)
Graf = ( , ) adalah subgraf dari
= , jika ( ) dan
( ).
(Chartrand & Oellermann 1993) 3 :
e1
v1
v2 v3
v4 v5
e3
e4
e6
e5
e2
Gambar 5 Graf 3.
:
e2
e4
e3 e1
v1
v4
v2 v3
Gambar 6 Subgraf dari 3. Definisi 7 (Spanning subgraph)
Suatu subgraf dikatakan spanning subgraph dari graf jika semua verteks pada graf terdapat pada subgraf .
(Vasudev 2006) 1∶
e1 v1
v2 v3
v4 v5
e4 e5
e2
Gambar 7 Spanning subgraph dari 3.
Definisi 8 (Multigraf dan multidigraf) Suatu graf (digraf) dikatakan multigraf (multidigraf) bila graf (digraf) tersebut memiliki lebih dari satu sisi (sisi berarah) yang incident dengan satu pasang verteks.
(Foulds 1992) Ilustrasi multigraf dapat dilihat pada gambar berikut:
v2
v3 v4
v1
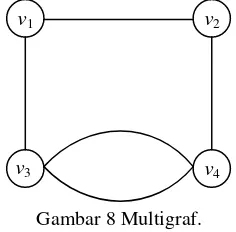
Gambar 8 Multigraf.
Gambar 8 merupakan contoh multigraf karena verteks 3 dan 4 dihubungkan oleh lebih dari satu sisi. Ilustrasi multidigraf bisa dilihat pada Gambar 9 berikut.
v
2v
3v
4v
1Gambar 9 Multidigraf. Definisi 9 (Derajat/degree)
Derajat suatu verteks adalah banyaknya sisi yang incident pada verteks, dan dinotasikan dengan degG( ) atau deg atau
( ).
(Vasudev 2006) Pada Gambar 8 diperlihatkan bahwa
( 1) = 2, ( 2) = 2, 3 = 4 = 3. Definisi 10 (Graf genap)
Suatu graf dikatakan graf genap, jika setiap verteksnya berderajat genap.
Definisi 11 (Derajat masuk/indegree) Pada graf berarah, indegree suatu verteks , yang dinotasikan dengan −( ), adalah banyaknya sisi berarah yang berakhir di verteks .
(Vasudev 2006) Pada Gambar 9 diperlihatkan derajat masuk tiap verteksnya, yaitu −( 1) =
−(
2) = −( 3) =1, −( 4) = 2. Definisi 12 (Derajat keluar/outdegree)
Pada graf berarah, outdegree suatu verteks , yang dinotasikan dengan +( ), adalah banyaknya sisi berarah yang dimulai dari verteks .
(Vasudev 2006) Pada Gambar 9 diperlihatkan derajat keluar tiap verteksnya, yaitu +( 1) =
+(
2) = +( 4) =1, +( 3) = 2. Definisi 13 (Balans)
Suatu digraf dikatakan balans jika setiap verteks pada digraf tersebut memiliki � = 0, dengan � adalah selisih dari derajat masuk dengan derajat keluar dari verteks .
(Diestel 1997)
v4
v1
v3
v2
Gambar 10 Digraf balans.
Digraf pada Gambar 10 merupakan digraf balans karena setiap verteks memiliki
�
= 0
.Definisi 14 (Underlying graph)
Jika suatu graf didapat dengan cara menghapus semua arah dari sisi berarah pada digraf, maka graf tersebut adalah underlying graph dari digraf.
(Vasudev 2006) Ilustrasi underlying graph bisa dilihat dari Gambar 3 dan Gambar 10. Graf pada Gambar 3 merupakan underlying graph dari digraf pada Gambar 10.
Definisi 15 (Jalan/walk)
Suatu walk W pada graf adalah barisan bergantian antara verteks dan sisi yang
dimulai dan diakhiri oleh verteks. Walk yang dimulai dari 0 dan berakhir di disebut
walk 0− dan walk memunyai panjang karena melalui sisi (tidak harus berbeda).
Walk yang sisi-sisinya memiliki orientasi arah disebut directed walk atau walk berarah.
(Chartrand & Oellermann 1993) Ilustrasi walk dapat dilihat pada Gambar 1, yaitu W = v1 e1 v2 e4 v4 e6 v6 e10 v5. Ilustrasi walk
berarah dapat dilihat pada Gambar 2, yaitu
= 1 2 3 5 5.
Definisi 16 (Walk tertutup)
Suatu walk pada graf dikatakan tertutup (closed) jika verteks awal dan verteks akhir pada walk tersebut adalah sama.
(Foulds 1992) Ilustrasi walk tertutup dapat dilihat pada Gambar 1, yaitu WT = v1e8 v7e11 v5e7 v3e2 v1
merupakan walk tertutup karena verteksnya dimulai dan diakhiri dengan verteks yang sama.
Definisi 17 (Jalur/path)
Path adalah walk dengan tidak ada verteks yang diulang.
(Chartrand & Oellermann 1993) Ilustrasi path dapat dilihat pada Gambar 1, yaitu �= 1 2 3 7 5 10 6 merupakan path karena tidak ada verteks yang diulang. Definisi 18 (Cycle)
Cycle adalah walk tertutup, yang memuat sedikitnya tiga verteks, dan semua verteks pada walk tersebut berbeda.
(Foulds 1992) Ilustrasi cycle dapat dilihat pada Gambar 1. CE = v7 e12 v8 e13 v9 e14 v7 merupakan cycle
karena tidak ada verteks yang diulang dan verteksnya dimulai di 7 dan berakhir di 7. Definisi 19 (Lintasan/trail)
Trail adalah walk dengan tidak ada sisi yang diulang.
(Chartrand & Oellermann 1993) Ilustrasi trail dapat dilihat pada Gambar 1, yaitu = v3 e3 v4 e6 v6 e10 v5 e7 v3 e2 v1
merupakan trail karena tidak ada sisi pada yang diulang.
Definisi 20 (Circuit)
Circuit adalah trail yang tertutup.
Ilustrasi circuit dapat dilihat pada Gambar 1, yaitu = v6e9v8 e12 v7 e14 v9 e13 v8 e5 v2 e4
v4 e6 v6 merupakan circuit karena tidak ada sisi
pada yang diulang dan merupakan walk
tertutup.
Definisi 21 (Graf lengkap)
Graf lengkap adalah graf dengan verteks sehingga terdapat tepat satu sisi yang menghubungkan tiap pasang verteks.
(Balakrishnan 1997) 4:
v1 v2
v4
v3
Gambar 11 Graf lengkap. Definisi 22 (Terhubung/connected)
Suatu graf = , dikatakan terhubung (connected) jika untuk setiap pasang verteks dan di , maka dihubungkan dengan .
Jika terdapat pasangan verteks − di sehingga tidak ada path − , maka graf tersebut dikatakan tak terhubung (disconnected).
(Chartrand & Oellermann 1993) 5 :
v1
v2 v3
v4 v5
v6
Gambar 12 Graf terhubung.
v1
v2 v3
v4 v5
v6
Gambar 13 Graf tak terhubung. Definisi 23 (Komponen graf)
Suatu subgraf terhubung yang tidak termuat pada subgraf lainnya yang juga terhubung disebut komponen graf. Banyaknya komponen dari graf dituliskan sebagai
.
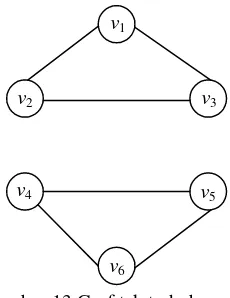
(Balakrishnan 1997) Graf pada Gambar 13 terdiri atas dua komponen, yaitu 1 dan 2 sebagai berikut:
1 :
v1
v2 v3
Gambar 14 Komponen ke-1 dari graf pada Gambar 13.
2:
v4 v5
v6
Gambar 15 Komponen ke-2 dari graf pada Gambar 13.
Definisi 24(Bridge)
Pada graf suatu sisi yang terhubung disebut bridge jika sisi tidak terletak pada suatu cycle di sehingga pada saat sisi tersebut dihilangkan menyebabkan graf menjadi tak terhubung.
6 :
e4
e5
e2
v1
v3
v2
e3
e7
e6
v5
v6
v4
e1
Gambar 16 Graf yang terdapat bridge. Pada Gambar 16, sisi 2 merupakan
bridge, karena jika sisi 2 dihapus, maka graf 6 menjadi tak terhubung.
Definisi 25 (Tree)
Suatu graf yang bersifat connected dan tidak memunyai cycle disebut tree.
(Chartrand & Zhang 2009)
v1
v4
v3
v2
Gambar 17 Tree.
Definisi 26 ( Spanning Tree)
Suatu spanning tree adalah subgraf yang merupakan tree.
(Vasudev 2006)
v1
v4
v3 v2
v5
Gambar 18 Graf 7.
v1
v4
v3
v2
v5
Gambar 19 Spanning tree dari 7.
Definisi 27 (Arborescence)
Suatu tree yang memiliki verteks yang
indegree-nya bernilai 0 (nol), sementara verteks-verteks lainnya memiliki indegree 1 (satu) disebut arborescence.
(Balakrishnan 1997)
Verteks yang indigree-nya bernilai 0 (nol) pada arborescence disebut akar arborescence.
v1
v4
v3
v2
Gambar 20 Arborescence.
Tree pada Gambar20 adalah arborescence
dengan verteks 3 sebagai akar arborescence. Definisi 28 (Spanning arborescence)
Spanning tree yang bersifat arborescence
disebut spanning arborescence.
(Vasudev 2006)
v
1v
4v
3v
2v
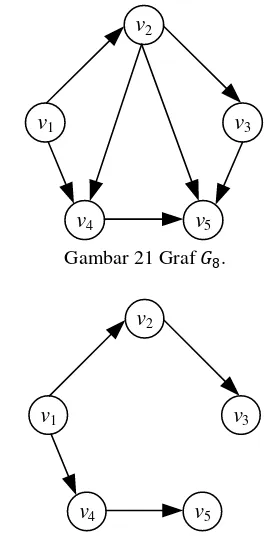
5Gambar 21 Graf 8.
v
1v
4v
3v
2v
5Gambar 22 Spanning arborescence dari 8.
Tree pada Gambar 22 merupakan
Definisi 29 (Graf bipartite)
Graf dikatakan bipartite jika dapat dipartisi menjadi dua subhimpunan takkosong
1 dan 2 sehingga setiap sisi di menghubungkan suatu verteks di 1 dengan verteks di 2.
(Chartrand & Oellermann 1993) 9:
v1 v3 v5
v2
v4
V1
V2
Gambar 23 Graf bipartite.
Graf 9 pada Gambar 23 merupakan graf
bipartite dengan 1= 1, 3, 5 dan 2= 2, 4 .
Definisi 30 (Graf r-regular)
Sebuah graf merupakan graf -regular, atau graf regular berderajat , jika setiap verteks pada graf memiliki derajat .
(Chartrand & Oellermann 1993) Graf 4pada Gambar 11, merupakan graf regular berderajat 3 karena setiap verteks memiliki derajat 3.
Definisi 31 (Matching)
Matching pada sebuah graf merupakan subgraf 1-regular, yaitu berupa himpunan sisi-sisi yang tidak adjacent.
(Chartrand & Oellermann 1993)
e5
e1
e2
e4
e3
v1
v3 v4
v2
v5
Gambar 24 Graf dengan matching. = { 1, 4} adalah salah satu matching pada graf di Gambar 24.
Definisi 32 (Matching yang perfect)
Graf ber-order yang mempunyai
matching berkardinalitas /2, maka matching
tersebut dikatakan matching yang perfect. (Chartrand & Oellermann 1993)
e1
e2
e3
e4
v1
v3 v4
v2
Gambar 25 Graf dengan matching perfect.
Graf pada Gambar 25 ber-order 4 dan 1= { 1, 3} merupakan matching berkardinalitas 2, sehingga 1 adalah
matching yang perfect.
Definisi 33 (Matching berbobot minimum)
Matching berbobot minimum merupakan
matching dengan jumlah bobot pada sisinya adalah minimum.
(Chartrand & Oellermann 1993) Ilustrasi matching yang perfect dapat dilihat pada graf Gambar 3, yaitu 2= 1, 2 , 3, 4 dengan bobot 7, 3= 1, 4 , 2, 3 dengan bobot 10. Jadi, 2 adalah matching yang perfect dengan bobot minimum.
2.2 Graf Euler
Leonhard Euler (1707-1783) lahir di Swiss. Ia dipandang sebagai salah satu matematikawan terbesar sepanjang masa. Euler menyumbangkan berbagai penemuan penting di berbagai bidang antara lain kalkulus dan teori graf.
Graf Euler merupakan salah satu penemuan Euler yang terkenal di bidang teori graf. Berikut ini akan dijelaskan beberapa definisi yang berkaitan dengan graf Euler yang dipakai dalam karya ilmiah ini.
Definisi 34 (Lintasan Euler)
Lintasan Euler adalah lintasan yang melewati semua sisi pada graf 3 tepat satu kali. Karena setiap sisi hanya boleh dilewati satu kali, maka lintasan Euler sering juga disebut trail Euler.
(Vasudev 2006) Pada Gambar 5 lintasan Euler dari graf 3 salah satunya ialah EL= v2 e3 v3 e2 v1 e1 v2 e4
v4 e6 v5 e5 v3.
Definisi 35 (Sirkuit Euler)
Sirkuit Euler adalah lintasan Euler yang tertutup.
Ilustrasi sirkuit Euler bisa dilihat pada Gambar 26. Sirkuit Euler yang diperoleh salah satunya ialah = v1 e1 v3 e4 v5 e3 v4 e2
v3 e5 v2 e6 v1.
e3
e2
e1
e6
e5 e4
v1 v4
v3
v2 v5
Gambar 26 Graf Euler. Definisi 36 (Graf Euler)
Graf yang memiliki sirkuit Euler disebut graf Euler.
(Vasudev 2006) Ilustrasi graf Euler bisa dilihat pada Gambar 26. Graf pada Gambar 26 merupakan graf Euler, karena graf tersebut memiliki sirkuit Euler.
Selanjutnya akan diberikan teorema-teorema yang digunakan sebagai dasar pengerjaan karya ilmiah ini.
Teorema 1
Suatu graf merupakan graf Euler jika dan hanya jika setiap verteks pada graf tersebut berderajat genap.
(Chartrand & Oellermann 1993) Teorema 2
Suatu digraf terhubung yang takkosong adalah digraf Euler jika dan hanya jika d+(vi) = d–(vi) untuk setiap verteks pada digraf balans.
(Chartrand & Oellermann 1993) 2.3 Penentuan Path Terpendek dengan
Algoritme Dijkstra
Algoritme Dijkstra dapat digunakan untuk mencari path terpendek atau jarak terpendek pada graf atau digraf atau graf campuran yang
tidak berbobot maupun yang berbobot pada graf ber-order . Misalkan diberikan graf berbobot = ( , ) dengan himpunan
= {1,2,3,…. } dan bobot pada tiap verteksnya taknegatif. Pada setiap langkah dalam algoritme didefinisikan sebuah variabel PARENT(v) yang menyatakan verteks yang mendahului verteks v pada path terpendek − yang telah diperoleh. Variabel PARENT(v) diperbaharui jika ditemukan path
− yang lebih pendek. Misalkan adalah himpunan semua verteks dari yang jaraknya dengan 0 sudah diketahui.
Langkah–langkah pada algoritme Dijkstra untuk menentukan jarak dari 0 ke setiap verteks di sebagai berikut:
Langkah 1. Inisialisasikan sebuah verteks awal 0 dengan jarak 0 = 0,
( ←0), ←{ 0}, ′← −{ 0}, dan jarak verteks lainnya bernilai ∞ untuk semua ∈ −{ 0}, PARENT ← 0; jika = 1, maka proses dihentikan; lainnya, proses dilanjutkan.
Langkah 2. Untuk setiap ∈ ′ sehingga , ∈ , diperiksa: jika
+ , maka proses
dilanjutkan; lainnya, ← + , dan PARENT ← .
Langkah 3. Ditentukan m = min{l(v)| v
∈ ′}. Jika ∈ ′ dipilih sebagai verteks dengan = , maka adalah jarak antara 0 dengan , dan +1← .
Langkah 4. Pembaharuan dan ′, yaitu ← ∪ +1 , dan ′← ′− +1 .
Langkah 5. ← + 1. Jika = −1, maka berhenti. Jika tidak, kembali ke Langkah 2.
(Chartrand
Oellermann 1993) Contoh Penggunaan Algoritme Dijkstra10 :
7
6 7
6
8
9
4
7
9
3
6
7 5
10 4
5
1
3 4
8 7
6
2
Gambar 27 Graf berbobot dantidak berarah. Akan ditentukan jarak terpendek dari satu
verteks ke verteks lainnya. Misalkan verteks awalnya adalah verteks 0= 1, maka dengan algoritme Dijkstra (penghitungan lebih
lengkap dapat dilihat pada Tabel 1) akan diperoleh path terpendek dari verteks 1 menuju verteks lainnya.
Tabel 1 Penentuan path terpendek dimulai dari verteks 0= 1
Iterasi l(1) l(2) l(3) l(4) l(5) l(6) l(7) l(8) Penambahan
S
0 0 (∞,–) (∞,–) (∞,–) (∞,–) (∞,–) (∞,–) (∞,–) 1
1 (9,1) (7,1) (5,1) (7,1) (∞,–) (∞,–) (∞,–) 4
2 (9,1) (7,1) – (7,1) (13,4) (14,4) (∞,–) 3
3 (9,1) – – (7,1) (13,4) (14,4) (17,3) 5
4 (9,1) – – – (13,4) (13,5) (17,3) 2
5 – – – – (13,4) (13,5) (16,2) 6
6 – – – – – (13,5) (16,2) 7
7 – – – – – – (16,2) 8
Dari Tabel 1, dapat diketahui beberapa path
terpendek dari verteks 0= 1 ke verteks lainnya. Contohnya path terpendek dari verteks 0= 1 menuju verteks 6, yaitu path terpendek �1= 1−4−6 dengan jarak 13, untuk path terpendek dari verteks 0= 1 menuju verteks 8 ialah �2= 1−2−8 dengan jarak 16.
2.4 Penentuan Minimum Bipartite
Matching dengan Metode Hungaria
Misalkan ada karyawan dan pekerjaan. Notasi = 1,2,…,
menunjukkan karyawan ke- dan notasi
= 1,2,…, menunjukkan pekerjaan ke- . Jika banyaknya karyawan sama dengan banyaknya pekerjaan, maka dengan mempertimbangkan aspek tertentu seperti pengoptimalan profit (keuntungan) yang didapat dari penempatan karyawan terhadap pekerjaan dikenal dengan masalah penugasan optimal. Masalah penugasan
(assignment problem) adalah suatu masalah mengenai pengaturan objek untuk melaksanakan tugas, dengan tujuan meminimalkan biaya, waktu, jarak, dan sebagainya ataupun memaksimalkan keuntungan yang salah satu penyelesaiannya menggunakan metode Hungaria.
Misalkan graf bipartite, sehingga himpunan karyawan dianggap sebagai 1 dan himpunan pekerjaan sebagai 2. Misalkan adalah biaya yang diperlukan ketika karyawan
ditugaskan untuk menyelesaikan pekerjaan . Untuk mencari solusi dari masalah penugasan optimal yang dinyatakan sebagai graf bipartite
Tabel 2 Tabel biaya yang berhubungan dengan model penugasan
Kar
y
awa
n
Pekerjaan
1 2
1 11 12 1
2 21 22 2
1 2
Metode ini dimulai dengan mengurangi setiap elemen pada baris dengan nilai minimum baris tersebut, kemudian setiap elemen kolom dari tabel yang dihasilkan dikurangi dengan nilai minimum kolom tersebut. Tabel biaya yang dihasilkan akan memuat paling sedikit satu nol pada setiap baris dan kolom. Semua elemen tabel yang dihasilkan bernilai taknegatif. Dengan elemen-elemen nol ini akan ditentukan suatu penugasan yang fisibel (yaitu pada matriks yang dihasilkan tersebut dapat dipilih tepat 1 nol pada setiap baris dan 1 nol pada setiap kolom). Jika itu mungkin maka penugasan itu optimal, karena elemen-elemen biaya adalah taknegatif dan nilai minimum fungsi tujuan lebih kecil daripada nol sehingga suatu penugasan dengan biaya nol adalah optimum.
Jika penugasan yang fisibel pada elemen-elemen nol tidak diperoleh, maka aturan lebih lanjut diperlukan untuk menemukan penugasan yang fisibel. Aturan tersebut diberikan sebagai berikut:
1 Sejumlah minimum garis yang melalui beberapa baris dan kolom digambarkan sedemikian sehingga menutup semua elemen nol. (Sejumlah minimum garis yang dibutuhkan adalah sama dengan jumlah maksimum pekerja yang dapat ditugaskan dengan menggunakan elemen nol).
2. Pilih elemen minimum yang tidak tertutupi garis, elemen ini dikurangi dengan setiap baris elemen yang tidak tertutupi garis dan ditambahkan ke setiap elemen yang berada di titik potong antara dua garis. Jika solusi optimum tidak ditemukan dalam langkah di atas, prosedur penggambaran garis tersebut harus diulangi sampai satu penugasan yang fisibel diperoleh.
Untuk menyelesaikan masalah penugasan dengan tujuan memaksimumkan, masalah diubah ke masalah meminimumkan sebelum diaplikasikan ke metode Hungaria, yaitu dengan cara mengalikan semua elemen dari matriks penugasan dengan −1.
(Ravindran et al. 1987).
Contoh Penggunaan Metode Hungaria Diberikan tabel biaya sebagai berikut:
1 2 3
1 3 6 8
2 6 4 3
3 1 5 4
Dengan metode Hungaria (Lampiran 1) didapatkan Minimum Bipartite Matching pada tabel berikut.
1 2 3
1
0 3
2
5 0
3
1 1
Tabel terakhir memberikan biaya minimum yang ditunjukkan dengan elemen nol yang diberi kotak, yaitu elemen (1,2), (2,3), (3,1) sehingga diperoleh minimum dari
bipartite matching, yaitu himpunan sisi {{1,2}, {2,3}, {3,1}} dengan total biayanya adalah 6 + 3 + 1 = 10.
2.5 Penentuan Minimum Spanning Tree
dengan Algoritme Prim
Minimum spanning tree adalah spanning tree T yang memiliki bobot atau nilai minimum. Salah satu cara untuk menentukan
minimum spanning tree dari suatu graf/digraf adalah dengan menggunakan algoritme Prim.
Algoritme Prim membentuk minimum spanning tree dengan langkah per langkah. Pada setiap langkah diambil sisi graf yang memiliki bobot minimum namun yang terhubung dengan spanning tree T yang telah terbentuk.
Misalkan diberikan graf dengan banyaknya verteks adalah , maka:
Langkah 1. Ambil sisi dari graf yang berbobot minimum, masukkan ke dalam T.
Langkah 2. Pilih sisi , di graf yang memiliki bobot minimum dan adjacent
dengan sisi di T. Jika , tidak membentuk
cycle, maka , ditambahkan ke dalam T
dan lanjut ke langkah 3. Sebaliknya, jika penambahan sisi , membentuk cycle, maka sisi tersebut tidak dipilih dan kembali ke langkah kedua.
0
0
Langkah 3. Proses berhenti jika T
memiliki −1 sisi.
(Balakrishnan 1997) Contoh Penggunaan Algoritme Prim
Diberikan graf berbobot tak berarah sebagai berikut: 2 4 3 1 6 8 5 1 3 5 2 4
Gambar 28 Graf contoh algoritme Prim. Dengan algoritme Prim (Lampiran 2) didapatkan minimum spanning tree dengan bobot minimum seperti pada gambar berikut:
2 1 2 5 1 4 3 3 5
Gambar 29 Minimum spanning tree dari graf pada Gambar 28.
2.6 Penentuan Sirkuit Euler dengan Algoritme van Aardenne-Ehrenfest - de Bruijn
Misalkan = , adalah digraf yang balans.
Langkah 1. Bentuk sebuah spanning arborescence dari digraf balans yang berakar di .
Langkah 2. Sisi berarah yang keluar dari tiap-tiap verteks diurutkan dan dilabeli, dan sisi berarah yang terakhir dilabeli adalah sisi berarah pada spanning arborescence.
Langkah 3. Tentukan sirkuit Euler dengan melintasi tiap-tiap sisi berarah yang telah dilabeli, mulai dari label yang terkecil sampai dengan label terbesar. Proses berhenti jika tiap sisi berarah yang dilabeli telah dilewati.
(Eiselt et al. 1995a)
Contoh Penggunaan Algoritme van Aardenne-Ehrenfest - de Bruijn
Misalkan diberikan digraf balans sebagai berikut:
11 :
3 3
1 3
2
2 4 3
2 4 2 4 5 6 1 3
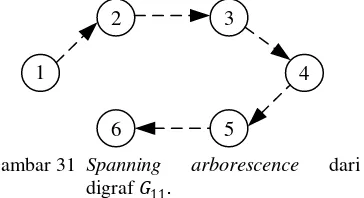
Gambar 30 Graf untuk contoh algoritme van Aardenne-Ehrenfest - de Bruijn. Langkah pertama yang akan ditentukan adalah penentuan spanning arborescence dari digraf balans tersebut, misalkan diambil spanning arborescence yang berawal di verteks 1 adalah sebagai berikut:
2 4 5 6 1 3
Gambar 31 Spanning arborescence dari digraf 11.
Semua sisi berarah diurutkan dan dilabeli, dengan label terakhir (terbesar) adalah label untuk sisi berarah pada spanning arborescence. L1 L1 L2 L2 L2
L1 L1 L1
L1 L2 2 4 5 6 1 3
2.7 Penentuan Sirkuit Euler dengan Algoritme Fleury
Misalkan = , adalah graf
terhubung yang semua verteksnya berderajat genap.
Langkah 1. Inisialisasikan i = 0. Dimulai dari verteks 0 dan didefinisikan trail 0: 0.
Langkah 2. Misalkan Ti= v0 e1 v1 e2 v2
e3 ... ei vi sebagai trail dari 0 ke pada iterasi ke- , lalu dipilih sebuah sisi +1 yang menghubungkan dengan +1 yang bukan merupakan bridge dari himpunan sisi
= − 1, 2,… . Jika +1 adalah
bridge pada subgraf yang didapat dari setelah menghapus sisi yang dimiliki Ei dari
, dan tidak ada pilihan lain yang bisa diambil, maka sisi tersebut dimasukkan ke dalam trail = 0 1 1 2 2 3… +1. Jika tidak ada sisi lagi yang bisa dipilih maka proses berhenti.
Langkah 3. Kemudian diganti menjadi
+ 1, lalu kembali ke Langkah 2.
Trail yang terbentuk dari urutan sisi yang diambil merupakan sirkuit Euler pada graf .
(Balakrishnan 1997) Contoh Penggunaan Algoritme Fleury
Misalkan diberikan graf seperti pada Gambar 33. 12: 3 3 1 3 2
2 4 3
2 4 2 4 5 6 1 3
Gambar 33 Graf Euler untuk contoh algoritme Fleury.
Untuk mencari sirkuit Euler pada graf tersebut dengan algoritme Fleury, dilakukan prosedur sebagai berikut:
1. dipilih sembarang verteks, misalkan verteks 1, yang dilabeli sebagai 0,
3
v0
3
1 3
2
2 4 3
2 4 2 4 5 6 1 3
Gambar 34 Iterasi pertama: inisialisasi 0.
2. dipilih sisi yang incident dengan 0 dan bukan merupakan bridge pada graf. Misalkan sisi {1,6} dipilih, lalu sisi tersebut dihapus dan didefinisikan verteks 6 sebagai verteks 1, sehingga graf menjadi seperti pada Gambar 35.
v1
v0
3
1 3
2
2 4 3
2 4 2 4 5 6 1 3
Gambar 35 Iterasi kedua: sisi {1,6} dihapus. 3. dipilih sisi {6,2} yang bukan bridge pada
subgraf , sehingga graf menjadi seperti pada Gambar 36.
v2
v1 v0
1 3
2
2 4 3
2 4 2 4 5 6 1 3
Gambar 36 Iterasi ketiga: sisi {6,2} dihapus. Iterasi selanjutnya diberikan secara lengkap pada Lampiran 3. Setelah semua sisi dihapus, sehingga dihasilkan graf seperti pada Gambar 37, maka sirkuit Euler sudah bisa ditemukan.
v10
v9 v8
v7 v6 v5 v4 v3 v2 v1 v0 2 4 5 6 1 3
Gambar 37 Graf terakhir dari algoritme Fleury.
III PENYELESAIAN STACKER CRANE PROBLEM
Rural Postman Problem (RPP) merupakan permasalahan dalam pencarian rute terpendek dengan biaya minimum dan hanya sebagian sisi atau sisi berarah yang diperlukan saja yang harus dilewati. Misalkan diberikan graf
campuran = , ∪ dengan
himpunan sisi berarah dan himpunan sisi tidak berarah pada graf . Misalkan merupakan himpunan sisi berarah yang harus dilewati minimal satu kali (required arc) pada , yaitu ⊆ ∪ . Selanjutnya, diberikan bobot/nilai untuk setiap sisi berarah , dan sisi tidak berarah { , } yang dinotasikan dengan .
RPP memiliki banyak jenis yaitu URPP (Undirected RPP)/RPP yang tidak berarah, DRPP (Directed RPP)/RPP yang berarah, SCP (Stacker Crane Problem)/RPP dengan graf campuran, dan CARP (Capacitated Arc Routing Problem)/RPP dengan graf berkapasitas. Pada karya ilmiah ini, hanya dibahas kasus SCP (Stacker Crane Problem) saja, yaitu RPP dengan himpunan sisi berarah yang harus dilewati minimal satu kali
= .
Stacker Crane Problem (SCP) dapat dinyatakan sebagai permasalahan dalam pencarian rute dengan biaya atau jarak minimum dan diharuskan melewati ruas jalan yang telah ditentukan paling tidak satu kali. Arah sisi berarah dari dapat dilihat sebagai pergerakan yang harus dilakukan oleh sebuah crane dengan arah yang telah ditentukan, masing-masing tepat satu kali. Permasalahan tersebut juga dapat dinyatakan sebagai masalah menemukan sirkuit Euler yang merepresentasikan rute terpendek yang melewati sisi yang telah ditentukan tepat satu kali pada suatu graf Euler.
Frederickson et al. (1978) mengajukan dua metode heuristik untuk menyelesaikan SCP dengan ketentuan graf campuran =
, ∪ memenuhi syarat berikut:
Syarat 1. Setiap verteks adalah incident
dengan setidaknya satu sisi berarah di A. Syarat 2. Fungsi bobot pada sisi ,
yaitu , memenuhi pertidaksamaan segitiga,
yaitu + , ∀ , , ∈ .
Apabila graf tidak memenuhi kedua syarat tersebut, algoritme Preprocess akan mengubahnya menjadi graf yang memenuhi kedua syarat Frederickson tersebut.
3.1 Algoritme Preprocess
Input : Graf campuran = , ∪ dan fungsi bobot .
Output : Graf campuran ′ = ′, ′∪
memenuhi syarat 1 dan fungsi bobot ′ memenuhi syarat 2. 1. Jika bukan endpoint (verteks awal atau
verteks akhir dari sisi berarah) pada graf , maka verteks dan sisi berarah
, ditambahkan pada graf dengan bobot 0. Untuk semua dalam , sisi
, ditambahkan pada graf dengan bobot .
2. Pada ditambahkan semua verteks yang merupakan endpoint dari sisi berarah dan ditentukan path terpendek antara setiap pasang verteks dan , sisi ,
ditambahkan pada , dan ditetapkan dari bobot path terpendek yang diperoleh.
Contoh algoritme Preprocess
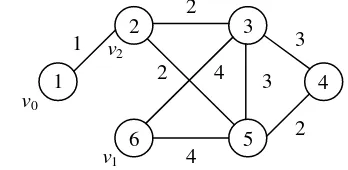
Misalkan diberikan graf campuran 13= , ∪ seperti pada Gambar 38. Graf tersebut tidak memenuhi syarat 1 dan 2 karena terdapat verteks 3 yang bukan merupakan endpoint dari sisi berarah manapun dan fungsi bobot tidak memenuhi pertidaksamaan segitiga, karena 32 31+
12. 13∶
2
4
8
v
1v
3v
2Gambar 38 Graf 13 untuk ilustrasi algoritme
preprocess.
Langkah 1. Pada graf 13 terdapat verteks 3 yang bukan merupakan endpoint dari sisi berarah manapun. Sisi berarah
∗ :
8 4
0 2
4
8
v1
v3
v2
vf
Gambar 39 Graf ∗ yang diperoleh dari Langkah 1 algoritme preprocess.
Langkah 2. Verteks v1, v2, v3, vf merupakan
endpoint dari suatu sisi berarah. Dengan algoritme Dijkstra didapat bobot terpendek antarverteks pada graf ∗ (detail penghitungan dapat dilihat di Lampiran 4). Path terpendek antara verteks dan 2, yaitu �3= −
1− 2 dengan bobot 2= 6 sehingga bobot sisi , 2 diganti dengan bobot 2= 6 dan
path tependek antara verteks 3 dan 2, yaitu �4= 3− 1− 2 dengan bobot 32= 6 sehingga bobot sisi 3, 2 diganti dengan bobot 32= 6. Graf ′ yang memenuhi syarat 1 dan 2 tersebut adalah:
′ ∶
6 4
0 2
4 6
v1
v3
v2
vf
Gambar 40 Graf ′ yang memenuhi syarat 1 dan 2.
Frederickson et al. (1978) mengajukan dua metode heuristik untuk menyelesaikan penentuan rute terpendek pada graf campuran
= , ∪ yang memenuhi syarat 1 dan 2. Kedua metode heuristik tersebut, yaitu
Largearcs dan Smallarcs. 3.2 Algoritme Largearcs
Misalkan diberikan graf campuran
= , ∪ , dengan = himpunan sisi berarah yang harus dilewati minimal satu kali dan bobot setiap sisi , atau sisi berarah
, adalah . Langkah-langkah algoritme
Largearcs adalah sebagai berikut:
Langkah 1. Subgraf = , yang dibentuk dari graf dengan menghilangkan
E. Himpunan verteks-awal dari sisi berarah di dinotasikan dengan 1 dan himpunan verteks-akhir dari sisi berarah di dinyatakan dengan 2.
Langkah 2. Dibentuk graf bipartite = 1∪ 2, ′ dengan ′ = {{vi,vj}| vi ∈
V1, vj ∈V2 dan {(vi,vj) A}.
Langkah 3. Minimumbipartitematching
ditentukan dari graf . Selanjutnya graf
= ( , ∪ ) dibentuk dengan
himpunan sisi berarah dari dan himpunan matching berbobot minimum yang diarahkan dari 2 ke 1.
Langkah 4. Komponen-komponen pada ditentukan dan dinotasikan dengan 1,…, . Jika = 1, maka ∪ dijadikan sebagai hasil output dan proses selesai. Jika tidak, maka dibentuk graf lengkap yang tidak berarah = ,
dengan himpunan verteks = 1,…, dan bobot atau nilai tiap sisi yang menghubungkan dan ialah
= min∈ , ∈ � , 1 dengan � , merupakan panjang path
terpendek dari verteks pada komponen dengan verteks j pada komponen .
Langkah 5. Misalkan himpunan sisi tidak berarah pada yang terletak pada
path terpendek yang berpadanan dengan sisi-sisi minimum spanning tree pada . Graf
= , ∪ ∪ dibentuk dengan
menentukan minimum spanning tree pada . Langkah 6. Graf = ( , ∪ ∪
) dibentuk dengan ∗ ialah himpunan sisi berarah yang diperoleh dengan menambahkan dua sisi yang arahnya berlawanan untuk sisi dari spanning tree
terpendek.
Langkah 7. Ditentukan sirkuit Euler pada dan dijadikan sebagai solusi dari SCP.
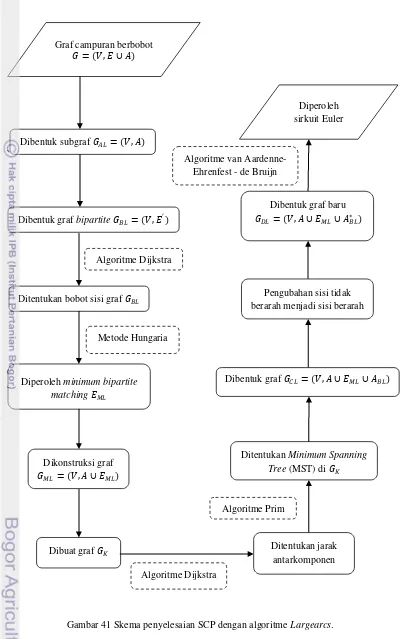
(Eiselt et al. 1995b) Pada Gambar 41 diberikan skema tahapan penyelesaian SCP dengan algoritme
`
Gambar 41 Skema penyelesaian SCP dengan algoritme Largearcs. Graf campuran berbobot
= , ∪
Ditentukan bobot sisi graf
Dibentuk graf bipartite = ( , ′)
Dibentuk subgraf = ,
Diperoleh minimum bipartite matching
Dikonstruksi graf
= ( , ∪ )
Dibuat graf
Algoritme Dijkstra
Metode Hungaria
Algoritme van Aardenne-Ehrenfest - de Bruijn
Algoritme Dijkstra
Algoritme Prim
Dibentuk graf = , ∪ ∪
Ditentukan Minimum Spanning Tree (MST) di
Pengubahan sisi tidak berarah menjadi sisi berarah
Diperoleh sirkuit Euler
Dibentuk graf baru
= , ∪ ∪ ∗
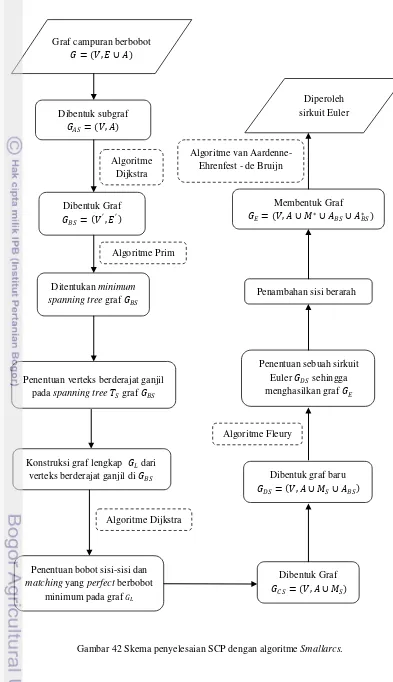
3.3 Algoritme Smallarcs
Misalkan diberikan graf campuran
= , ∪ , dengan = himpunan sisi berarah yang harus dilewati minimal satu kali dan bobot setiap sisi , atau sisi berarah
, adalah . Langkah-langkah algoritme
Smallarcs adalah sebagai berikut:
Langkah 1. Dibentuk subgraf = , dari graf dengan menghilangkan E.
Langkah 2. Graf diubah menjadi graf tidak berarah = ′, ′ dengan ′ ialah himpunan verteks yang mewakili sisi berarah ,ℎ pada subgraf . Untuk setiap verteks dan , ′ , ditentukan sebagai minimum dari , , ,ℎ , ℎ, , dan ℎ,ℎ . Jarak antarverteks
, dari ditentukan dengan
′ , . Antara verteks dan dihubungkan dengan sisi yang bobotnya ialah jarak terpendek ′ , .
Langkah 3. Minimum spanning tree
ditentukan dari graf dengan algoritme Prim.
Langkah 4. Diidentifikasi verteks berderajat ganjil pada spanning tree dari graf . Selanjutnya dibentuk graf lengkap dari verteks berderajat ganjil tersebut dengan jarak antarverteks-nya merupakan jarak terpendek yang diperoleh dari Langkah 1.
Langkah 5. Matching yang perfect dan berbobot minimum, yaitu , ditentukan dari graf .
Langkah 6. Setiap verteks dan diubah kembali menjadi sisi berarah seperti pada , sisi spanning tree graf dan
matching yang perfect berbobot minimum graf diganti dengan path terpendek yang
diperoleh dari Langkah 1, sehingga menghasilkan graf = , ∪ dengan
= ∪ .
Langkah 7. Jika dan ℎ pada berderajat ganjil, maka ditambahkan sisi
,ℎ dan diarahkan dari ℎ ke . Graf yang dihasilkan diberi nama = , ∪ ∪
dengan himpunan sisi berarah ,ℎ
yang diperoleh dari penambahan sisi dari verteks berderajat ganjil pada dan diarahkan dari ℎ ke .
Langkah 8. Sirkuit Euler ditentukan pada dengan mengabaikan arah dari sisi berarah pada verteks berderajat genap. Arah sirkuit Euler dibalikkan jika terdapat sisi berarah pada verteks berderajat genap yang dilintasi dengan arah yang salah yang bobotnya melebihi dari setengah total bobot sisi berarah pada verteks berderajat genap dari graf .
Langkah 9. Dibentuk graf = , ∪ ∗∪ ∪ ∗ dengan ∗ adalah himpunan sisi spanning tree graf dan
matching yang perfect berbobot minimum graf yang telah ditetapkan arahnya dari sirkuit Euler dan ∗ ialah himpunan sisi berarah yang diperoleh dengan menambahkan dua sisi berarah ,ℎ pada sisi berarah dari verteks berderajat genap ,ℎ yang dilintasi dengan arah sirkuit Euler yang salah.
Langkah 10. Sirkuit Euler ditentukan pada dan dijadikan sebagai solusi dari SCP.
(Eiselt et al. 1995b) Pada Gambar 42 diberikan skema tahapan penyelesaian SCP dengan algoritme Smallarcs
Gambar 42 Skema penyelesaian SCP dengan algoritme Smallarcs. Graf campuran berbobot
= , ∪
Dibentuk subgraf
= ,
Dibentuk Graf
= ′, ′
Algoritme Prim
Ditentukan minimum spanning tree graf
Penentuan verteks berderajat ganjil pada spanning tree graf
Konstruksi graf lengkap dari verteks berderajat ganjil di
Algoritme Dijkstra
Penentuan bobot sisi-sisi dan
matching yang perfect berbobot minimum pada graf
Dibentuk Graf
= ( , ∪ )
Dibentuk graf baru
= , ∪ ∪
Algoritme Fleury
Penentuan sebuah sirkuit Euler sehingga menghasilkan graf Penambahan sisi berarah
Membentuk Graf
= , ∪ ∗∪ ∪ ∗
Diperoleh sirkuit Euler
Algoritme Dijkstra
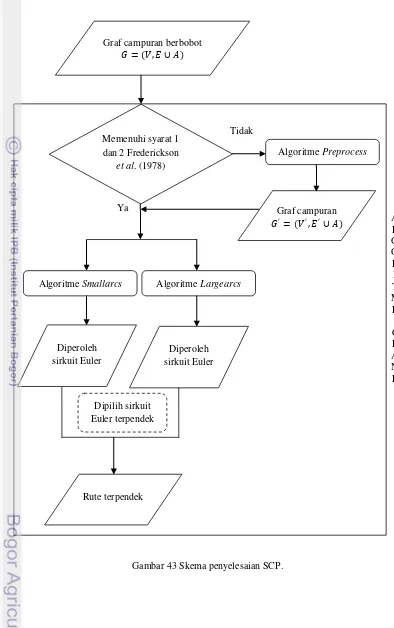
Gambar 43 Skema penyelesaian SCP.
A L G O R I T M E C R A N E Ya
Algoritme Smallarcs
Tidak
Algoritme Largearcs
Graf campuran berbobot
= , ∪
Memenuhi syarat 1 dan 2 Frederickson
et al. (1978)
Algoritme Preprocess
Diperoleh sirkuit Euler
Graf campuran ′ = ′, ′∪
Diperoleh sirkuit Euler
IV APLIKASI MASALAH
Katering adalah salah satu jasa/pelayanan untuk memenuhi pesanan makanan dari pihak yang membutuhkan makanan dalam jumlah besar untuk acara yang diadakannya. Terdapat banyak katering yang tersebar di Jakarta, misalnya Katering Eco Raos yang berlokasi di Jakarta Pusat. Katering Eco Raos adalah perusahaan katering dengan empat dapur yang masing-masing bertugas untuk menyiapkan makanan untuk satu pelanggan yang menggunakan jasanya (Gambar 44), namun hanya memiliki satu kendaraan untuk mengantarkan makanan dari dapur Katering Eco Raos ke pelanggan. Kendaraan tersebut berada di Dapur 1 yang diasumsikan memiliki
tempat penyimpanan kendaraan. Agar proses pengantaran makanan berjalan lancar dan optimal, maka pihak Katering Eco Raos harus menentukan rute atau jalan terbaik untuk proses pengantaran makanan. Pada karya ilmiah ini akan dibahas penentuan rute pengantaran makanan dari dapur-dapur Katering Eco Raos ke pelanggan yang menggunakan katering tersebut. Lokasi dapur Katering Eco Raos dan pelanggan yang menggunakan katering serta jarak tempuhnya dinyatakan dengan graf pada Gambar 45. Verteks 1, 4, 5, dan 8 menyatakan dapur Katering Eco Raos, dan lokasi pelanggan katering ialah verteks lainnya.
Gambar 44 Peta Katering Eco Raosdi Jakarta Pusat. (www.googlemaps.co.id). Keterangan :
: Lokasi dapur Katering Eco Raos di Jakarta Pusat : Lokasi pelanggan katering
Asumsi yang digunakan dalam penentuan rute tersebut adalah sebagai berikut:
1. Semua jalur pendistribusian makanan harus dilewati tanpa kecuali.
2. Jalur pilihan boleh dilewati atau tidak. 3. Pendistribusian makanan dimulai pada
Dapur 1 di pertigaan jalan Sutan Syahrir dan berakhir di tempat yang sama.
4. Mobil mengambil makanan dari dapur Katering Eco Raos untuk diantarkan ke pelanggan.
5. Waktu pengiriman makanan tidak diperhitungkan.
Pada Gambar 45, bobot pada setiap sisi
{ , } atau sisi berarah ( , ) merupakan jarak dari verteks ke verteks . Jarak diperoleh dari perkiraan dengan satuan kilometer. Model di atas dapat dibuat menjadi graf sebagai berikut:
2
6 7
3 8
1
� :
7
6 7
6
8
9
4
7
9
3
6
7 5
10 4
5
1
3 4
8 7
6
2
Gambar 45 Graf kasus Katering Eco Raos di Jakarta Pusat dengan arah pendistribusian katering. Ket : Arah distribusi katering yang harus dilewati
Jalur pilihan
Tabel 3 Penjelasan setiap verteks pada graf kasus katering di Jakarta Pusat
Verteks Keterangan
1 Tempat awal dan akhir mobil pengantar makanan dari dapur Katering Eco Raos.
2 Pertigaan jalan Sutan Syahrir, jalan Teuku Umar, dan jalan RP Soeroso.
3 Perempatan jalan Teuku Umar, jalan HOS Cokroaminoto, jalan Cut Mutia dan jalan Cut Nyakdien.
4 Dapur Katering Eco Raos di perlimaan jalan Wahid Hasyim, jalan Kebon Kacang, jalan Jaksa, jalan Cut Nyak Dien, dan jalan Lombok. 5 Dapur Katering Eco Raos di
pertigaan jalan Kebon Kacang, jalan Kampung Bali, dan jalan Jaksa.
6 Pertigaan jalan Kampung Bali, jalan Jaksa dan jalan Kebon Sirih.
7 Perempatan jalan Wahid Hasyim, jalan Kebon Sirih, jalan Jaksa, dan jalan Cikini Raya.
8 Dapur Katering Eco Raos di pertigaan jalan Cikini Raya, jalan Cut Mutia, dan jalan RP Soeroso.
Dalam bahasan berikut, graf campuran � = , ∪ memenuhi syarat 1 dan 2, sehingga algoritme Preprocess tidak digunakan. Ada dua metode heuristik yang digunakan, yaitu Largearcs dan Smallarcs. 4.1 Penyelesaian SCP dengan Algoritme
Largearcs
Langkah 1. Subgraf = ( , ) dari graf � adalah sebagai berikut:
∶
9
10 9
7
5
1
3 4
8 7
6
[image:30.595.326.497.463.616.2]2
Gambar 46 Subgraf .
∶
6 10 12
8
16 6 7
4 7
7
13 13
1 2
3
4
5 6
7 8
V2
[image:31.595.91.508.33.819.2]V1
Gambar 47 Graf bipartite . Langkah 3. Dengan metode Hungaria didapat solusi matching berbobot minimum
pada , yaitu = 1,3 , 8,2 , 4,6 , 5,7 (Lampiran 6). Selanjutnya graf
= ( , ∪ ) dibentuk dari graf
dengan menambahkan sisi dari matching
dan arahnya dari 2 ke 1. :
4
5 6
7 8
7 6
9
1 2
3 8
9 7
7
10
Gambar 48 Graf .
Langkah 4. Pada terdapat 2 komponen yaitu 1 dan 2.
1 ∶
1 2
3 8
9
7
7
10
2∶ 4
5 6
7
8
7 6
9
Gambar 49 Komponen 1 dan 2. Karena pada terdapat 2 komponen, maka dibentuklah graf lengkap = ,
dengan banyaknya verteks sesuai dengan banyaknya komponen pada , yaitu 2. Bobot setiap verteks dapat dicari dengan cara mencari path terpendek yang menghubungkan komponen 1 dan 2 dari tiap-tiap verteksnya. Dengan menggunakan algoritme Dijkstra (Lampiran 7), didapat panjang path
terpendek antarkomponen adalah: ∶
K1 K2
4
Gambar 50 Graf .
Jarak terpendek antara 1 dan 2 diperoleh dari panjang path terpendek, yaitu path (8,7). Langkah 5. Graf merupakan minimum spanning tree, agar terhubung maka ditentukan , yaitu himpunan sisi tidak berarah pada yang berpadanan dengan yang menghubungkan 1 dan 2. Pada kasus ini dipilih path (8,7), karena path tersebut pada berpadanan dengan minimum spanning tree sehingga graf =
( , ∪ ∪ ) dengan = 8,7
[image:31.595.322.490.125.346.2]∶
1 2
3 8
9
7
7
10
4
5 6
7
8
7 6
[image:32.595.95.290.44.784.2]9 4
Gambar 51 Graf .
Langkah 6. Graf = ( , ∪ ∪
∗ ) dibentuk dan dua sisi ditambahkan dengan arah yang berlawanan untuk setiap sisi dari minimumspanning tree , sehingga sisi
= 8,7 menjadi sisi berarah =
8,7 , 7,8 . ∶
1 2
3 8
9 7
7
10
4
5 6
7 8
7 6
9
4 4
Gambar 52 Graf .
Langkah 7. Penentuan sirkuit Euler pada Gambar 52 dilakukan dengan algoritme van Aardenne-Ehrenfest - de Bruijn.
Spanning arborescence dari graf berawal dari verteks 5 adalah sebagai berikut:
9
7 8
9 10 7
4
4
5 6
7
1 2
[image:32.595.330.506.154.373.2]3 8
Gambar 53 Spanning arborescence digraf .
Hasil dari pelabelan dengan algoritme van Aardenne-Ehrenfest - de Bruijn untuk graf
dapat dilihat pada Gambar 54. ∶
L
1L
1L
1L
1L
1L
1L
1L
1L
2L
24
5 6
7
1 2
[image:32.595.325.492.433.671.2]3 8
Gambar 54 Graf yang sudah dilabeli. Dari Gambar 54 dapat diperoleh sirkuit Euler yang dimulai dari verteks 1, yaitu
1−2−8−7−5−6−4−7−8−3−1
Aplikasi algoritme Largearcs pada kasus Katering Eco Raos di Jakarta Pusat sebagai berikut: ∶ 4 7 6 7 6 8 9 4 7 9 3 6 7 5 10 4 5 1 3 4 8 7 6 2
Gambar 55 Graf kasus Katering Eco Raos di Jakarta Pusat dengan algoritme
Largearcs.
Ket : Arah distribusi katering yang harus dilewati Jalur pilihan
Jalur distribusi katering 4.2 Penyelesaian SCP dengan Algoritme
Smallarcs
Langkah 1. Subgraf = ( , ) dari graf � adalah sebagai berikut:
∶ 9 10 9 7 5 1 3 4 8 7 6 2
Gambar 56 Subgraf .
Langkah 2. Selanjutnya graf = ′, ′ dibuat dari himpunan sisi berarah
yang diubah menjadi verteks , sehingga diperoleh hasil sebagai berikut:
sisi berarah (5,6) menjadi verteks 1 sisi berarah (4,7) menjadi verteks 2 sisi berarah (8,3) menjadi verteks 3 sisi berarah (1,2) menjadi verteks 4
Penentuan path terpendek (Lampiran 8) untuk setiap verteks dan diperoleh hasil sebagai berikut:
1, 2 = 3
1, 3 = 7
1, 4 = 7
2, 3 = 4
2, 4 = 5
3, 4 = 6
: 3 4 7 7 5 6
n1 n2
n4
[image:33.595.97.517.87.814.2]n3
Gambar 57 Graf .
Langkah 3. Minimum spanning tree graf ditentukan dengan menggunakan algoritme Prim (Lampiran 9), sehingga didapat minimum spanning tree TS= {{n1,n2},
{n2,n3}, {n2,n4}}sebagai berikut:
:
5 4
3
n3
n1 n2
[image:33.595.321.510.90.334.2]n4
Gambar 58 Minimum spanning tree padagraf .
Langkah 4. Verteks berderajat ganjil pada
minimum spanning tree dari graf adalah
{ 1, 2, 3, 4}. Graf lengkap dibentuk dengan himpunan verteksnya adalah verteks berderajat ganjil pada minimum spanning tree
dari graf . ∶
n1 n2
n4
n3
Langkah 5. Terdapat 4 verteks pada , maka matching yang perfect berisi 2 sisi. Dari Lampiran 10, diperoleh sisi matching yang
perfect dan berbobot minimum ialah sisi 1, 2 , dan { 3, 4} dengan total bobot 9, sehingga diperoleh = 1, 2 , 3, 4
sebagai berikut: ∶ 6 n