POTENSI PEMANFAATAN KELUARAN MODEL NWP UNTUK
PREDIKSI CUACA JANGKA PENDEK (STUDI KASUS: PONTIANAK,
PEKANBARU, SEMARANG, SURABAYA, DAN PALU)
ANDI SYAHID MUTTAQIN
DEPARTEMEN GEOFISIKA DAN METEOROLOGI
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
ANDI SYAHID MUTTAQIN. Potensi Pemanfaatan Keluaran Model NWP untuk Prediksi Cuaca Jangka Pendek (Studi Kasus: Pontianak, Pekanbaru, Semarang, Surabaya, dan Palu). Dibimbing oleh AHMAD BEY dan RAHMAT HIDAYAT.
Numerical Weather Prediction (NWP) adalah sebuah model prediksi cuaca harian menggunakan beberapa persamaan dinamika atmosfer berupa persamaan matematik yang dilakukan oleh super-computer. Keakuratan hasil model ini meningkat secara signifikan sejak pertama kali dibangun sekitar empat puluh tahun lalu. Kebutuhan mendasar untuk prediksi cuaca jangka pendek di Indonesia mendorong kita untuk memanfaatkan hasil keluaran model NWP untuk digabungkan dengan skema prediksi cuaca yang sudah biasa dilakukan. NWP menyediakan tuntunan mendasar untuk melakukan prediksi cuaca untuk beberapa jam yang akan datang. Sayangnya, resolusi spasial NWP masih terlalu kasar untuk menggambarkan kondisi lokal seperti di Indonesia. Teknik Model Output Statistics (MOS) digunakan untuk mengurangi nilai error dan meningkatkan akurasi dari keluaran model NWP. Tujuan penelitian ini adalah menentukan kombinasi terbaik dari prediktor di atmosfer untuk model curah hujan harian, kelembaban relatif, suhu maksimum, dan suhu minimum di lima wilayah kajian, yaitu Pontianak, Pekanbaru, Semarang, Surabaya, dan Palu yang mewakili tiga wilayah tipe hujan di Indonesia, untuk musim hujan dan musim kemarau. Tujuan lain dalam penelitian ini adalah untuk mengidentifikasi wilayah kajian yang memiliki data keluaran model NWP yang membangkitkan data observasi. Pola keluaran model NWP dibandingkan dengan data observasi untuk menganalisis konsistensi serta menerapkan faktor koreksi jika dianggap penting. Hasil kajian dalam penelitian ini menyimpulkan bahwa kelembaban di lapisan dekat permukaan (rh0), kelembaban pada lapisan pertengahan troposfer (rh8), serta kecepatan vertikal pada pertengahan troposfer (vv7 dan vv5) adalah variabel yang relevan untuk model curah hujan harian di semua wilayah kajian dan semua musim. Potensi pemanfaatan model NWP terbesar adalah untuk Kota Palu. Di wilayah kajian Palu, suhu lapisan permukaan (T0) dan suhu titik embun pada lapisan permukaan (DP0) adalah variabel yang relevan untuk model kelembaban relatif; kelembaban pada lapisan permukaan (rh0) adalah variabel yang relevan untuk model suhu maksimum; sedangkan suhu titik embun pada lapisan permukaan (DP0) adalah variabel yang relevan untuk model suhu minimum. Kedekatan keluaran model NWP terhadap data observasi diduga dengan menggunakan indikator nilai error, yaitu: Root Mean Square Error (RMSE) dan Mean Absolute Error (MAE).
ABSTRACT
ANDI SYAHID MUTTAQIN. Utilization of NWP Model Outputs for Short-Range Weather Forecast (Case study: Pontianak, Pekanbaru, Semarang, Surabaya, and Palu). Supervised by AHMAD BEY and RAHMAT HIDAYAT.
Numerical weather prediction (NWP) is an operational daily weather forecasting using mathematical equations by super-computer. The skill of NWP has improved significantly since it was first generated fourty years ago. The urgent needs for daily weather forecasting in Indonesia has led to the utilization of NWP model outputs to be incorporated into the forecasting scheme. NWP provides the basic guidance for weather forecasting beyond the first few hours. Unfortunately, spatial resolution of NWP model is still too rough to describe local conditions. Model output statistics (MOS) technique may be used to reduce error and increase accuracy of NWP model ouputs. The objective of this study includes the selection of the best combination of atmospheric predictors for daily precipitation, relative humidity, maximum temperature, and minimum temperature in five locations, namely, Pontianak, Pekanbaru, Semarang, Surabaya, and Palu which characterized three dominant rainfall regions in Indonesia, for the wet and dry seasons. The subsequent objective is to identify locations where NWP model outputs resemble observational data. Model outputs patterns are compared with observational data to analyze consistency, and whenever necessary some forms of correction factor is applied. The results indicate that humidity at the surface (at z=2m) and at mid-tropospheric levels (rh0 and rh8), and pressure vertical velocity at mid-tropospheric levels (vv7 and vv5) are the relevant variables for daily precipitation in all of the locations and all seasons analyzed. The most potential location to utilize NWP model is Palu. In Palu, surface air temperature (T0) and surface dew point temperature (DP0) are the relevant variables for relative humidity; humidity at the surface (rh0) is the relevant variable for maximum temperature; while surface dew point temperature (DP0) is the relevant variable for minimum temperature. Closeness of model outputs with observational data is inferred using error indicators, namely, Root Mean Square Error (RMSE) and Mean Absolute Error (MAE).
POTENSI PEMANFAATAN KELUARAN MODEL NWP UNTUK
PREDIKSI CUACA JANGKA PENDEK (STUDI KASUS: PONTIANAK,
PEKANBARU, SEMARANG, SURABAYA, DAN PALU)
ANDI SYAHID MUTTAQIN
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Mayor Meteorologi Terapan
Departemen Geofisika dan Meteorologi
DEPARTEMEN GEOFISIKA DAN METEOROLOGI
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi : Potensi Pemanfaatan Keluaran Model NWP untuk Prediksi Cuaca
Jangka Pendek (Studi Kasus: Pontianak, Pekanbaru, Semarang,
Surabaya, dan Palu)
Nama
: Andi Syahid Muttaqin
NIM
: G24070010
Disetujui
Pembimbing I
Prof. Dr. Ir. Ahmad Bey
NIP. 19510823 197603 1 002
Pembimbing II
Dr. Rahmat Hidayat, S.Si., M.Sc.
NIP. 19740301 200003 1 001
Diketahui
Ketua Departemen Geofisika dan Meteorologi
Dr. Ir. Rini Hidayati, MS.
NIP. 19600305 198703 2 002
KATA PENGANTAR
Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2011 ini ialah potensi pemanfaatan model prediksi cuaca, dengan judul “Potensi Pemanfaatan Keluaran Model NWP untuk Prediksi Cuaca Jangka Pendek (Studi Kasus: Pontianak, Pekanbaru, Semarang, Surabaya, dan Palu)”.
Terima kasih yang sebesar-besarnya kepada semua pihak yang telah turut peran serta dalam penyusunan karya ilmiah ini, terutama kepada:
1. Bapak Prof. Dr. Ir. Ahmad Bey dan Bapak Dr. Rahmat Hidayat, S.Si., M.Sc., selaku dosen pembimbing.
2. Bapak Prof. Ir. Handoko, M.Sc., Ph.D. dan Bapak Ir. Bregas Budianto Ass. Dpl. selaku dosen penguji yang telah memberi masukan untuk menyempurnakan tulisan ini.
3. Keluarga Besar Departemen Geofisika dan Meteorologi IPB, staff dan seluruh dosen, sahabat GFM 44, 43, 45, dan 46. Terima kasih atas segala bentuk dukungan, semangat, dan doa yang selalu kalian berikan.
4. Keluarga yang penulis sangat sayangi, terima kasih atas segala dukungan, doa, cinta, dan kasih sayang yang telah diberikan selama ini.
5. Rysda Nurharmelya, terima kasih atas segala bantuan, doa, dan dukungannya.
Semoga semua bantuan yang diberikan kepada penulis, mendapatkan balasan dari Allah SWT, dan semoga karya ilmiah ini dapat bermanfaat bagi semua pihak yang membutuhkan.
Bogor, Juli 2011
RIWAYAT HIDUP
Penulis dilahirkan di Kab. Purwakarta, Prop. Jawa Barat, pada 25 April 1989 dari ayahanda Ade Subadio dan ibunda Juju Juniah. Penulis merupakan putera pertama dari dua bersaudara.
Tahun 2007 penulis lulus dari SMA Negeri 1 Cisarua Kabupaten Bandung dan SMA Plus Yayasan Darmaloka Propinsi Jawa Barat, secara bersamaan. Kemudian pada tahun tersebut, penulis diterima sebagai mahasiswa pada Program Studi Meteorologi Terapan, Departemen Geofisika dan Meteorologi, Fakultas Matematika dan Ilmu Pengetahuan Alam IPB sebagai Program Studi Mayor, melalui Undangan Seleksi Masuk IPB. Pada tahun kedua di IPB, penulis memilih Program Studi Sistem Informasi dari Departemen Ilmu Komputer sebagai Program Studi Minor.
DAFTAR ISI
Halaman
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... x
DAFTAR LAMPIRAN ... xi
I. PENDAHULUAN ... 1
1.1. Latar Belakang ... 1
1.2. Tujuan ... 1
II. TINJAUAN PUSTAKA ... 1
2.1. Klasifikasi Tipe Prediksi Cuaca ... 1
2.2. Model Numerical Weather Prediction (NWP) ... 2
2.2.1. Persamaan Model NWP ... 2
2.2.2. Kualitas Hasil Prediksi ... 3
2.2.3. Tipe Model NWP ... 4
2.3. Model Output Statistics (MOS) ... 4
2.3.1. Penentuan Peubah Prediktor ... 4
2.3.2. Diagnostik Multikolinearitas ... 4
2.3.3. Analisis Faktor ... 5
2.3.4. Meningkatkan Kinerja Model ... 5
2.4. Karakteristik Curah Hujan di Indonesia ... 5
2.4.1. Tiga Pola Curah Hujan di Indonesia ... 5
2.4.2. Penentuan Musim Hujan dan Musim Kemarau Tahun 2008 di Lima Wilayah Kajian ... 6
III. METODOLOGI ... 6
3.1. Waktu dan Tempat Penelitian ... 6
3.2. Data dan Peralatan ... 6
3.3. Metode Penelitian ... 6
3.3.1. Melihat Kinerja Model NWP ... 6
3.3.2. Mereduksi Data Kajian... 6
3.3.3. Post-processing Keluaran Model NWP dengan Teknik Model Output Statistics (MOS) ... 6
IV. HASIL DAN PEMBAHASAN ... 9
4.1. Numerical Weather Prediction (NWP) ... 9
4.2. Kinerja Model NWP yang Digunakan ... 9
4.3. Reduksi Data Kajian ... 11
4.4. Model Output Statistics (MOS) ... 11
4.5. Potensi Pemanfaatan Keluaran Model NWP di Lima Wilayah Kajian ... 11
V. SIMPULAN DAN SARAN ... 20
5.1. Simpulan ... 20
5.2. Saran ... 21
DAFTAR PUSTAKA ... 21
DAFTAR TABEL
Halaman
1 Perbandingan metode analitik dan numerik ... 2
2 Nama dan koordinat wilayah kajian ... 6
3 Variabel NWP dalam beberapa level tekanan ... 7
4 Bulan perwakilan MH dan MK untuk masing-masing wilayah kajian tahun 2008 ... 11
5 Kontribusi (%) prediktor terhadap variasi hujan harian menggunakan model downscaling untuk musim hujan dan kemarau (Cavazos 2002). ... 11
6 Peubah penjelas yang berpengaruh terhadap CH (Sutikno 2008) ... 11
7 Parameter model NWP yang berkorelasi besar terhadap Curah Hujan (Ristanti 2009) ... 11
8 Variabel model NWP yang terbukti berkorelasi besar dengan CH berdasarkan penelitian Sutikno (2008) ... 12
9 Parameter model NWP yang terbukti berkorelasi besar dengan CH berdasarkan penelitian Ristanti (2009) ... 12
10 Parameter Model NWP yang berkorelasi besar dengan CH Model ... 12
11 Persamaan regresi linear berganda dan nilai R2 model CH (CH^) ... 13
12 Faktor koreksi model CH untuk masing-masing wilayah kajian ... 17
13 Regresi model RH dan Suhu Kota Palu ... 18
DAFTAR GAMBAR
Halaman
1 Grid model NWP global ... 2
2 Koordinat spherical ... 3
3 Perkembangan skill prediksi yang semakin membaik di Amerika Utara ... 3
4 Tiga wilayah tipe hujan di Indonesia ... 5
5 Diagram alir metodologi penelitian ... 8
6 Pola suhu rata-rata diurnal bulan Februari tahun 2008 untuk lima wilayah kajian ... 9
7 Pola RH rata-rata diurnal bulan Februari tahun 2008 untuk lima wilayah kajian ... 10
8 Plot nilai CH Model dan CH observasi untuk masing-masing wilayah kajian Tahun 2008 .... 14
9 Plot nilai CH^ dan CH observasi untuk masing-masing wilayah kajian Tahun 2008 ... 15
10 Plot nilai CH* dan CH observasi untuk masing-masing wilayah kajian Tahun 2008 ... 16
DAFTAR LAMPIRAN
Halaman 1 Nilai koefisien korelasi antara CH model terhadap rh0, vv8, rh8, vv7, vv5, u7, dan z2
Kota Pontianak pada Musim Kemarau tahun 2008 ... 24
2 Nilai koefisien korelasi antara CH model terhadap rh0, vv7, dan vv5 Kota Pontianak pada Musim Hujan tahun 2008 ... 24
3 Nilai koefisien korelasi antara CH model terhadap rh0, DP0, vv8, rh8, u7, u5, vv7, vv5, dan rh7 Kota Pekanbaru pada Musim Kemarau tahun 2008 ... 24
4 Nilai koefisien korelasi antara CH model terhadap z7, rh0, vv7, dan vv5 Kota Pekanbaru pada Musim Hujan tahun 2008 ... 24
5 Nilai koefisien korelasi antara CH model terhadap z7, rh0, DP0, rh8, dan rh7 Kota Semarang pada Musim Kemarau tahun 2008 ... 24
6 Nilai koefisien korelasi antara CH model terhadap rh0, vv7, vv5, dan rh7 Kota Semarang pada Musim Hujan tahun 2008 ... 25
7 Nilai koefisien korelasi antara CH model terhadap rh0, DP0, rh8, dan rh7 Kota Surabaya pada Musim Kemarau tahun 2008 ... 25
8 Nilai koefisien korelasi antara CH model terhadap rh0, rh8, vv7, vv5, dan DP0 Kota Surabaya pada Musim Hujan tahun 2008 ... 25
9 Nilai koefisien korelasi antara CH model terhadap rh0, rh8, vv7, vv5 dan rh7 Kota Palu pada Musim Kemarau tahun 2008 ... 25
10 Nilai koefisien korelasi antara CH model terhadap rh7, vv5, rh0, rh8, vv7, dan DP0 Kota Palu pada Musim Hujan tahun 2008 ... 25
11 Nilai koefisien korelasi antara RH model NWP terhadap T0 dan Dp0 Kota Palu pada Musim Kemarau tahun 2008 ... 25
12 Nilai koefisien korelasi antara RH model NWP terhadap T0 dan Dp0 Kota Palu pada Musim Hujan tahun 2008 ... 26
13 Nilai koefisien korelasi antara Tmax model NWP terhadap rh0 dan Dp0 Kota Palu pada Musim Kemarau tahun 2008 ... 26
14 Nilai koefisien korelasi antara Tmax model NWP terhadap rh0 dan DP0 Kota Palu pada Musim Hujan tahun 2008 ... 26
15 Nilai koefisien korelasi antara Tmin model NWP terhadap rh0 dan DP0 Kota Palu pada Musim Kemarau tahun 2008 ... 26
16 Nilai koefisien korelasi antara Tmin model NWP terhadap rh0 dan DP0 Kota Palu pada Musim Hujan tahun 2008 ... 26
17 Nilai Variance Inflation Factor (VIF) prediktor CH model Kota Pontianak pada Musim Kemarau tahun 2008 ... 26
18 Nilai Variance Inflation Factor (VIF) prediktor CH model Kota Pontianak pada Musim Hujan tahun 2008 ... 26
19 Nilai Variance Inflation Factor (VIF) prediktor CH Model Kota Pekanbaru pada Musim Kemarau tahun 2008 ... 27
20 Nilai Variance Inflation Factor (VIF) prediktor CH model Kota Pekanbaru pada Musim Hujan tahun 2008 ... 27
Halaman
22 Nilai Variance Inflation Factor (VIF) prediktor CH Model Kota Semarang pada Musim
Hujan tahun 2008 ... 27
23 Nilai Variance Inflation Factor (VIF) prediktor CH Model Kota Surabaya pada Musim Kemarau tahun 2008 ... 27
24 Nilai Variance Inflation Factor (VIF) prediktor CH Model Kota Surabaya pada Musim Hujan tahun 2008 ... 27
25 Nilai Variance Inflation Factor (VIF) prediktor CH model Kota Palu pada Musim Kemarau tahun 2008 ... 27
26 Nilai Variance Inflation Factor (VIF) prediktor CH model Kota Palu pada Musim Hujan tahun 2008 ... 28
27 Nilai Variance Inflation Factor (VIF) prediktor RH model Kota Palu pada Musim Kemarau tahun 2008 ... 28
28 Nilai Variance Inflation Factor (VIF) prediktor RH model Kota Palu pada Musim Hujan tahun 2008 ... 28
29 Analisis Faktor model CH Kota Pontianak pada Musim Kemarau tahun 2008 ... 28
30 Analisis faktor model CH Kota Pontianak pada Musim Hujan tahun 2008 ... 30
31 Analisis faktor model CH Kota Pekanbaru pada Musim Kemarau tahun 2008... 30
32 Analisis faktor model CH Kota Pekanbaru pada Musim Hujan tahun 2008 ... 31
33 Analisis faktor model CH Kota Semarang pada Musim Kemarau tahun 2008 ... 31
34 Analisis faktor model CH Kota Semarang pada Musim Hujan tahun 2008 ... 32
35 Analisis faktor model CH Kota Surabaya pada Musim Kemarau tahun 2008... 32
36 Analisis faktor model CH Kota Surabaya pada Musim Hujan tahun 2008 ... 33
37 Analisis faktor model CH Kota Palu pada Musim Kemarau tahun 2008 ... 34
38 Analisis faktor model CH Kota Palu pada Musim Hujan tahun 2008 ... 34
39 Analisis regresi RH model Kota Palu pada Musim Kemarau tahun 2008 ... 35
40 Analisis regresi RH model Kota Palu pada Musim Hujan tahun 2008 ... 35
41 Analisis regresi Tmax model Kota Palu pada Musim Kemarau tahun 2008 ... 36
42 Analisis regresi Tmax Model Kota Palu pada Musim Hujan tahun 2008 ... 36
I. PENDAHULUAN
1.1. Latar Belakang
Prediksi cuaca dilakukan dengan tujuan untuk menyelamatkan kehidupan, pertanian, objek-objek penting, serta untuk memberi tahu kita apa yang sedang terjadi bahkan apa yang akan terjadi di lingkungan atmosfer kita. Mengetahui kondisi apa yang akan terjadi di atmosfer untuk waktu yang akan datang merupakan hal yang sangat penting bagi manusia (Ahrens 2009). Sebagai contoh, prediksi curah hujan lebat akan memberikan gambaran yang baik bagi perencanaan penanggulangan banjir. Selain itu, prediksi cuaca akan sangat membantu pengaturan jadwal transportasi udara (penerbangan) sehingga kecelakaan penerbangan akibat cuaca buruk dapat dihindari. Bahkan, beberapa acara olah raga tertentu (luar ruangan) akan merasakan dampak dari cuaca buruk jika sebelumnya hal terebut tidak diprediksi dengan baik.
Sebelum teknologi berkembang pesat seperti sekarang ini, manusia sudah memiliki kemampuan dalam memprediksi kondisi cuaca yang akan terjadi. Salah satunya dengan memperhatikan gejala alam atau tingkah laku binatang melalui teknik perkiraan sederhana. Seiring perkembangan teknologi dan ilmu pengetahuan, perkembangan teknik prediksi cuaca pun semakin berkembang baik. Berawal dari penemuan mesin penghitung sederhana, komputer generasi pertama, hingga super -computer seperti sekarang ini, mampu memberikan kontribusi yang besar dalam bidang analisis dan prediksi cuaca.
Prediksi cuaca sekarang ini umumnya sudah terkomputerisasi, dimana komputer dapat menghitung interaksi non-linear yang sangat rumit antara angin, suhu, dan kelembaban pada ribuan lokasi dan ketinggian di seluruh dunia. Komputer mampu memplotkan, menganalisis data, dan melakukan prediksi kondisi cuaca yang akan terjadi dengan menggunakan persamaan gerak atmosfer secara matematik atau dikenal dengan Numerical Weather Prediction yang biasa disebut sebagai NWP (Stull 2000).
Model NWP adalah sekumpulan kode komputer yang merepresentasikan persamaan-persamaan atmosfer secara numerik, digunakan untuk memprediksi kondisi atau status atmosfer yang akan datang dengan menggunakan kemampuan komputer yang tinggi. Prediksi atau ramalan cuaca dirumuskan dengan menyelesaikan persamaan pergerakan atmosfer. Persamaan-persamaan
tersebut meliputi persamaan diferensial parsial non-linear dan time-dependent dari angin, temperatur, kelembaban dan tekanan (BMG 2006).
Model NWP dibangun berdasarkan persamaan gerak atmosfer berskala global dan regional serta belum memperhatikan kondisi lokal. Pemanfaatan data keluaran model NWP harus disertai dengan proses analisis statistik sebagai tahapan post-processing agar dapat mendekati kondisi sebenarnya dengan hasil pengukuran langsung (observasi) di lapangan. Kebutuhan mendasar untuk prediksi cuaca jangka pendek di Indonesia, mendorong kita untuk mampu membangun model NWP yang merepresentasikan dengan baik semua kondisi atmosfer di sekitar Indonesia. Sementara itu, kita pun harus mampu memanfaatkan hasil keluaran model NWP yang telah dilakukan oleh negara lain untuk digabungkan dengan skema prediksi cuaca yang sudah biasa dilakukan di Indonesia.
1.2. Tujuan
Tujuan penelitian ini adalah:
1. Menganalisis kinerja model NWP yang digunakan.
2. Membuat analisis statistik sebagai upaya pemanfaatan data keluaran model NWP untuk potensi prediksi cuaca jangka pendek di lima wilayah kajian (Pontianak, Pekanbaru, Semarang, Surabaya, dan Palu).
3. Menentukan wilayah kajian yang berpotensi tinggi untuk memanfaatkan keluaran model NWP.
II. TINJAUAN PUSTAKA
Pada dasarnya, prediksi cuaca menunjukkan bagaimana kondisi atmosfer saat ini akan berubah untuk beberapa waktu yang akan datang. Konsekuensinya adalah jika kita akan membuat suatu prediksi cuaca untuk waktu yang akan datang, kondisi cuaca saat ini (pada skala yang cukup luas) harus diketahui dengan baik.
2.1. Klasifikasi Tipe Prediksi Cuaca Pengelompokkan tipe prediksi cuaca didasarkan pada sejauh mana jangka waktu prediksi cuaca tersebut dibuat, baik beberapa jam maupun beberapa hari yang akan datang. Ahrens (2009) mengelompokkan tipe prediksi ke dalam empat kategori, yaitu:
untuk beberapa jam yang akan datang, biasanya tidak lebih dari 6 jam),
2. prediksi cuaca jangka pendek (prediksi cuaca untuk 12 jam hingga beberapa hari yang akan datang),
3. prediksi cuaca jangka menengah (prediksi cuaca untuk 3 hingga 8,5 hari yang akan datang), dan
4. prediksi cuaca jangka panjang (prediksi cuaca untuk lebih dari 8,5 hari yang akan datang, namun keakuratan hasil akan sangat buruk untuk prediksi suhu dan curah hujan untuk prediksi lebih dari 16 hari).
2.2. Model Numerical Weather Prediction (NWP)
Model dapat diartikan sebagai penyederhanaan suatu sistem. Sedangkan sistem adalah gambaran suatu proses atau beberapa proses (beberapa subsistem) yang teratur. Model hanya menggambarkan beberapa aspek dari suatu sistem dan tidak harus mencerminkan seluruh proses yang terjadi dalam sistem tersebut. Berdasarkan tujuannya, model dapat dibagi menjadi tiga macam (Handoko 1994), yaitu: pemahaman proses, prediksi, serta keperluan manajemen.
Model NWP adalah sekumpulan kode komputer yang merepresentasikan secara numerik persamaan-persamaan atmosfer, digunakan untuk memprediksi kondisi atau status atmosfer yang akan datang dengan menggunakan kemampuan komputer yang sangat tinggi (BMG 2006).
Stull (2000) menjelaskan bahwa prediksi cuaca dilakukan dengan terlebih dahulu menyelesaikan beberapa persamaan gerak atmosfer seperti persamaan momentum, kontinuitas masa, dan konservasi kelembaban. Namun, sangat sulit untuk menyelesaikan persamaan-persamaan tersebut secara analitik dikarenakan sistem atmosfer yang sangat kompleks. Sehingga, untuk menyelesaikan permasalahan seperti ini perlu menggunakan tiga alternatif:
1. Menentukan solusi analitik sederhana sebagai upaya pendekatan,
2. Membangun model fisik sederhana, 3. Menentukan solusi numerik sebagai
upaya pendekatan seluruh persamaan atmosfer.
Model NWP yang dibangun sekarang ini menggunakan metode alternatif yang ketiga (solusi numerik). Pendekatan yang digunakan adalah metode elemen terbatas ( finite-difference) pada lokasi yang diskrit yang biasa disebut sebagai grid (Gambar 1).
Gambar 1 Grid model NWP global (Sumber: en.wikipedia.org)
Solusi persamaan gerak atmosfer dapat dicari dengan menggunakan metode numerik. Metode numerik merupakan suatu teknik meramu permasalahan matematika sedemikian rupa sehingga dapat diselesaikan dengan operasi aritmatik. Tujuan dari metode numerik adalah memperoleh metode terbaik yang efisien dan akurat (Dukkipati 2010). Perbandingan antara metode analitik dan numerik ditunjukkan pada Tabel 1.
Tabel 1 Perbandingan metode analitik dan numerik
Metode analitik Metode numerik
1 Menggunakan aturan kalkulus
Menggunakan aritmatika 2 Hasil berupa
suatu fungsi/relasi Hasil berupa angka 3
Nilai perhitungan adalah nilai sejati
(exact)
Nilai perhitungan adalah hampiran (terdapat error) 4
Tidak selalu mudah memproses solusi
Solusi selalu dapat diperoleh dengan bantuan komputer
Model numerik merupkan model yang menggambarkan bentuk-bentuk hubungan kuantitatif berdasarkan persamaan-persamaan matematik. Dalam pemodelan numerik, fenomena atmosfer skala global memiliki kaitan erat dengan sirkulasi atmosfer skala yang lebih kecil. Kondisi ini telah banyak dibuktikan oleh keandalan Model Atmospheric Global Circulation Model (AGCM) dalam melakukan forcing kepada sirkulasi atmosfer berskala regional maupun lokal (Swarinoto 2001 dalam Swarinoto 2009).
2.2.1. Persamaan Model NWP
a. Persamaan Momentum dalam Koordinat Berotasi:
Jika kita mengasumsikan bahwa hanya gaya-gaya nyata yang bekerja di atmosfer adalah gaya gradien tekanan (PGF), gravitasi, dan friksi, maka bentuk persamaan momentum adalah:
r
p g F
U Dt
U
D
1 2
dimana Fr menunjukkan gaya friksi, dan gaya sentrifugal telah digabungkan dengan gravitasi yang kemudian disebut sebagai gravitas g.
Untuk tujuan analisis teoritis dan prediksi numerik, penting sekali untuk mengembangkan persamaan momentum vektorial ke dalam komponen skalar. Akan sangat baik sekali jika persamaan tersebut dikembangkan dalam kordinat spherical (
,
,z), dimana adalah bujur,
adalah lintang, dan zadalah jarak vertikal di atas permukaan bumi (Gambar 2).Gambar 2 Koordinat spherical
Sehingga, persamaan gerak dalam kordinat spherical adalah:
rx F w v x p a uw a uv Dt Du cos 2 sin 2 1 tan ry F u y p a vw a u Dt Dv sin 2 1 tan 2 rz F u g z p a v u Dt Dw
2 cos
1 2 2
b. Persamaan Kontinuitas (Metode Eulerian):
0 U t c. Hukum I Termodinamika:
J Dt D p Dt D
cv
Persamaan-persamaan pergerakan atmosfer (persamaan primitif) juga dirinci oleh Riegel (1992) sebagai berikut:
a. Persamaan pergerakan relatif:
F g p V dt
dV
1 2
b. Persamaan kontinuitas:
0 V dt d
c. Hukum I Termodinamika:
dt q dt d p dt dT
cv
d. Persamaan Status:
RT p
2.2.2. Kualitas Hasil Prediksi
Prediksi cuaca menitikberatkan pada kondisi nilai awal (initial value problem). Sehingga, untuk melakukan prediksi cuaca harus diawali dengan observasi kondisi cuaca sebenarnya yang biasa dilakukan di stasiun meteorologi. Sehingga, model numerik akan memberikan hasil yang kurang baik jika menggunakan nilai observasi yang kurang baik (jarak antar stasiun yang jauh, sedikitnya observasi udara atas, adanya nilai error dalam observasi, dan fenomena lokal).
Keakuratan hasil model NWP telah meningkat secara signifikan sejak pertama kali dibangun sekitar empat puluh tahun lalu. Indikator yang digunakan untuk melihat peningkatan keakuratan salah satunya adalah skor S1 (Gambar 3).
Gambar 3 Perkembangan skill prediksi yang semakin membaik di Amerika Utara
(Sumber: Kalnay (2003))
) , max( ) , max( . 100 1 y y x x y y x x V F V F V F V F S dimana: j i F j i F x
F , 1,
(gradien prediksi timur-barat)
1 ,
,
Fy Fi j Fij (gradien prediksi utara-selatan)
j i j i
x V V
V , 1,
(gradien verivikasi timur-barat)
1 ,
,
Vy Vi j Vi j (gradien verifikasi utara-selatan)
Peningkatan akurasi (skill) prediksi NWP dikarenakan empat faktor (Kalnay 2003):
1. Peningkatan kekuatan super-computer sehingga menghasilkan resolusi numerik yang lebih baik,
2. Perbaikan representasi dari proses fisik skala kecil (awan, hujan, kelembaban, momentum, turbulensi) dalam model, 3. Penggunaan metode yang lebih akurat
untuk asimilasi data, dan
4. Peningkatan ketersediaan data, khususnya data satelit dan pesawat di atas lautan dan di Belahan Bumi Selatan (BBS).
2.2.3. Tipe Model NWP
Terdapat dua tipe dasar dari model NWP, yaitu model barotropik dan baroklinik. Kedua tipe model tersebut menyediakan konsep fisik mendasar dan biasanya termasuk ke dalam kategori (Riegel 1992):
a. model kesetimbangan, berdasarkan persamaan vortisitas dan persamaan kesetimbangan,
b. model persamaan primitif, berdasarkan sistem, biasanya memasukkan konsep persamaan hidrostatik.
Setiap pusat prediksi cuaca, akan memiliki model numerik yang berbeda sehingga untuk lokasi dan waktu yang sama memungkin hasil prediksi yang berbeda. Dalam skala internasional, penelitian utama mengenai NWP umumnya dilakukan di negara-negara maju seperti European Center for Medium Range Weather Forecasts (ECMWF), National Center for Environmental Prediction (NCEP), weather services of UK (Inggris), Perancis, Jerman, Scandinavian, Kanada, Jepang, dan Australia.
2.3. Model Output Statistics (MOS)
MOS merupakan model yang
menghubungkan peubah prediktan y
(observasi stasiun cuaca) dan peubah prediktor x (parameter NWP) yang biasa dibangun dalam suatu persamaan regresi linear berganda. Di samping itu, peubah prediktor dapat juga berupa parameter geografi seperti lintang, bujur, dan waktu (BMG 2006).
2.3.1. Penentuan Peubah Prediktor Proses pemilihan prediktor merupakan salah satu bagian terpenting dalam MOS. Setiap lokasi yang berbeda kemungkinan juga akan berbeda pula peubah prediktor yang berpengaruh terhadap peubah prediktan. Terdapat dua pendekatan yang digunakan dalam penentuan prediktor, yaitu: pendekatan secara statistik dan pertimbangan ilmiah/keahlian (scientific judgment) (Tapp & McNamara 1989).
Pada penelitian Sutikno (2008) di Karawang, Subang, dan Indramayu, peubah penjelas (prediktor) yang berpengaruh terhadap curah hujan adalah kelembaban spesifik, komponen angin zonal, dan ketinggian geopotensial terutama pada musim kemarau. Sedangkan, pada musim hujan, peubah penjelas (prediktor) yang berpengaruh terhadap curah hujan adalah precipitable water, komponen angin zonal, dan kelembaban spesifik.
2.3.2. Diagnostik Multikolinearitas (Kekolinearan Ganda)
Suatu persamaan regresi linear berganda tidak akan bisa diandalkan jika peubah-peubah penjelas (prediktor) saling berkorelasi tinggi. Hal ini mengakibatkan koefisien regresi dugaannya cenderung bervariasi sangat besar dari sampel satu ke sampel lainnya, sehingga tidak diperoleh informasi yang tepat mengenai koefisien regresi yang sebenarnya (populasi). Hal tersebut biasa disebut sebagai multikolinearitas atau kekolinearan ganda (Widiharih 2001).
Suatu metode formal untuk mendeteksi adanya kekolinearan ganda yang banyak digunakan adalah faktor inflasi ragam (Variance Inflation Factors = VIF). Faktor ini mengukur seberapa besar ragam koefisien regresi dugaan membesar dibandingkan seandainya peubah-peubah bebasnya tidak berkorelasi linear. Faktor inflasi ragam (FIR) bagi dugaan koefisien regresi ke-k dinotasikan (FIR)k dan didefinisikan sebagai:
(FIR)k = (1-Rk 2
)-1
lainnya dalam model. Nilai FIR terbesar di antara semua peubah bebas X digunakan sebagai indikator tingkat keparahan kekolinearan ganda (Widiharih 2001). Dalam penelitian ini, nilai FIR terbesar yang lebih besar dari 4 digunakan sebagai indikasi adanya kekolinearan ganda.
2.3.3. Analisis Faktor
Costello dan Osborne (2005) menyatakan bahwa analisis faktor (factor analysis) lebih baik daripada Principal Component Analysis (PCA). PCA hanya merupakan sebuah metode reduksi data. Sedangkan, analisis faktor adalah analisis lebih lanjut dari PCA. Analisis faktor merupakan transformasi ortogonal matriks faktor loading yang didapatkan dari PCA. Tujuan dari rotasi adalah untuk menyederhanakan dan mengklarifikasi struktur data. Hasil dari transformasi ini adalah sebaran nilai faktor loading yang sudah dirotasi yang memisahkan antara nilai korelasi kecil dengan nilai korelasi yang besar. Metode rotasi yang umum digunakan adalah rotasi Varimax (Haan 1979).
2.3.4. Meningkatkan Kinerja Model Kelengkapan data observasi (suhu, kelembaban dan curah hujan) sebagai prediktan sangat mempengaruhi performance model. Berdasarkan hasil validasi model MOS yang dilakukan oleh BMG (2006), performance antar stasiun sangat beragam dan pada stasiun tertentu hasilnya kurang memuaskan. Kinerja (performance) model dapat ditingkatkan dengan melakukan beberapa cara, yaitu (BMG 2006):
1. tidak dilakukan reduksi dimensi data NWP,
2. data dibagi berdasarkan musim hujan dan kemarau (komposit), dan
3. berdasarkan identifikasi sisaan model, di beberapa stasiun menunjukkan pola dependensi antar waktu, sehingga sisaan model akan dimodelkan dengan menggunakan analisis deret waktu.
2.4. Karakteristik Curah Hujan di Indonesia
2.4.1. Tiga Pola Curah Hujan di Indonesia
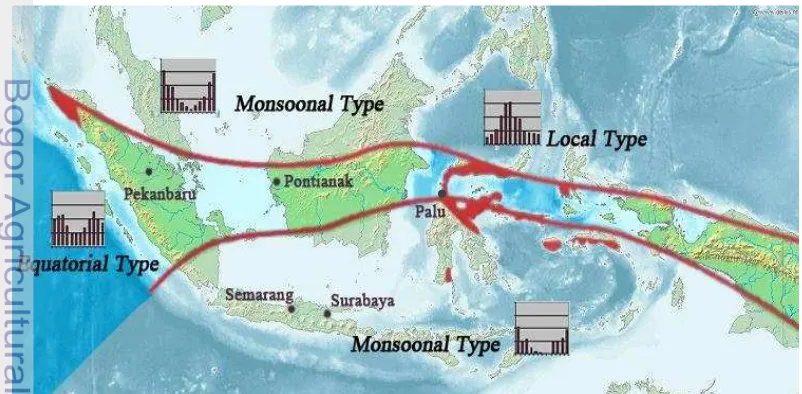
Pola hujan di Indonesia secara klimatologis dapat dibagi menjadi tiga wilayah (Boer 2002, Aldrian & Susanto 2003, Tjasyono 2004) yaitu pola Monsunal, Ekuatorial, dan Lokal (Gambar 3). Pola Monsunal dicirikan oleh bentuk pola hujan yang bersifat unimodal (satu puncak musim hujan). Secara umum musim kemarau berlangsung dari bulan April sampai bulan September dan musim hujan dari bulan Oktober sampai bulan Maret. Pola ekuatorial dicirikan oleh pola hujan dengan bentuk bimodal (dua puncak hujan) yang biasanya terjadi sekitar bulan Maret dan Oktober yaitu pada saat matahari berada di atas ekuator. Pola lokal dicirikan oleh bentuk pola hujan unimodal (satu puncak hujan) tapi bentuknya berlawanan dengan pola hujan pada tipe monsun.
Lima wilayah yang dikaji dalam penelitian ini mengacu pada tiga wilayah tipe hujan di Indonesia. Wilayah dengan tipe hujan Ekuatorial diwakili oleh Kota Pontianak dan Pekanbaru, wilayah tipe hujan Monsunal diwakili oleh Kota Semarang dan Surabaya, sedangkan wilayah tipe hujan Lokal diwakili oleh Kota Palu (Gambar 3).
2.4.2. Penentuan Musim Hujan dan Musim Kemarau Tahun 2008 di Lima Wilayah Kajian
Penentuan Musim Hujan (MH) dan Musim Kemarau (MK) di suatu wilayah ditentukan setelah mengetahui kapan terjadinya awal musim hujan (AMH) dan awal musim kemarau (AMK). Menentukan AMH menggunakan data total hujan dasarian. Satu tahun kalender dibagi ke dalam 36 dasarian. Dasarian pertama mencatat total hujan dari tanggal 1 hingga tanggal 10 bulan yang bersangkutan. Dasarian kedua mencatat total hujan dari tanggal 11 hingga 20 pada bulan yang bersangkutan. Selanjutnya dasarian ketiga mencatat mencatat total hujan dari tanggal 21 hingga akhir bulan (BMG 2008).
Menentukan AMH dari seri data total hujan dasarian di masing-masing lokasi yang bersangkutan dengan acuan 50 mm/dasarian yang diikuti oleh minimal dua dasarian berturut-turut. Jika AMH dan AMK sudah dapat ditentukan, maka dapat dilakukan penentuan Panjang Musim Hujan (PMH). PMH berakhir saat total hujan dasarian telah mencapai kurang dari 50 mm/dasarian yang diikuti oleh minimal dua dasarian berurutan. (BMG 2008).
III. METODOLOGI
3.1. Waktu dan Tempat Penelitian
Penelitian ini dilaksanakan pada bulan Februari sampai dengan Juli tahun 2011, bertempat di Laboratorium Meteorologi dan Pencemeran Atmosfer, Departemen Geofisika dan Meteorologi, FMIPA-IPB.
3.2. Data dan Peralatan
Data yang digunakan dalam penelitian ini berupa:
1. Data observasi harian curah hujan (CH), suhu maksimum (Tmax), suhu minimum (Tmin) dan kelembaban relatif (RH) kota Pontianak, Pekanbaru, Semarang, Surabaya, dan Palu untuk periode data 1 Januari 2008 – 31 Desember 2008 (BMKG
–banyumilih.blogspot.com).
2. Data keluaran model Numerical Weather Prediction (NWP), produk The National Weather Services (NWS), National Centers for Environmental Prediction (NCEP), dengan waktu analisis dan prediksi 3 (tiga) jam, untuk periode data 1 Januari 2008 – 31 Desember 2008, yang diunduh dari website NOAA:
http://ready.arl.noaa.gov/READYamet.php
untuk lima wilayah kajian berdasarkan tiga wilayah tipe hujan di Indonesia yang ditampilkan pada Tabel 2.
Tabel 2 Nama dan koordinat wilayah kajian No. Stamet oBujur oLintang
1 Supadio,
Pontianak 109,40 -0,15
2 Simpangtiga,
Pekanbaru 101,45 0,46
3 Ahmadyani,
Semarang 110,38 -6,98
4 Juanda,
Surabaya 112,76 -7,36
5 Mutiara,
Palu 119,73 -0,68
Parameter-parameter keluaran NWP yang digunakan dalam penelitian ini merujuk pada penelitian Tereza Cavazos dan Bruce Hewitson (2002) yang berjudul “Relative Performance of Empirical Predictors of Daily Precipitation” tanpa menyertakan variabel kelembaban spesifik (q) yang dimuat dalam Tabel 3. Analisis data dalam studi ini menggunakan perangkat lunak Minitab 15 dan Microsoft Office 2007.
3.3. Metode Penelitian
3.3.1. Melihat Kinerja Model NWP Menentukan suhu dan kelembaban relatif (RH) sebagai variabel yang digunakan untuk melihat pola diurnal, serta menentukan bulan tertentu yang digunakan untuk melihat pola diurnal tersebut. Kemudian, membandingkan pola diurnal antar mandatory layer (1000, 850, 700, dan 500 hPa) dan juga membandingkan pola tersebut antar wilayah kajian.
3.3.2. Mereduksi Data Kajian
Menentukan bulan yang mewakili musim hujan (MH) dan musim kemarau (MK) untuk masing-masing wilayah kajian. Proses ini diawali dengan penentuan panjang musim hujan (PMH) dan panjang musim kemarau (PMK) tahun 2008 untuk masing-masing wilayah kajian.
3.3.3. Post-processing Keluaran Model NWP dengan Teknik Model Output Statistics (MOS)
(Universal Time Coordinate). Sedangkan, untuk prediktan Tmin menggunakan waktu pengamatan pada jam 18.00 UTC (BMG 2006).
2. Menguji parameter-parameter keluaran model NWP hasil penelitian Cavazos T (2002), Sutikno (2008), dan Ristanti D (2009) yang berkorelasi tinggi dengan curah hujan, Tmax, Tmin, dan RH.
3. Melakukan diagnostik multikolinearitas dengan cara formal (Variance Inflation Factor, VIF). Indikator adanya multikolinearitas dapat ditinjau dari nilai VIF terbesar yang lebih dari 4 (VIF terbesar > 4).
4. Melakukan Analisis Faktor (Factor Analysis) untuk menghilangkan masalah multikolinearitas jika ada.
5. Membangun regresi linear berganda dari faktor yang terbentuk. Regresi linear berganda yang terbentuk adalah sebagai berikut:
nk Ekj Xik Xk sk n
j j i
yˆ 0 1 1 /
dimana, yˆi
adalah
nilai dugaan modelke-i, j dan k merupkan jumlah faktor dan jumlah peubah prediktor, Ekj merupakan matriks hasil perkalian antara
1/2 λ * 1 D L
R , dan sk merupakan ragam peubah prediktor.
6. Plot nilai y dan yˆ serta hitung nilai RMSE (Root Mean Square Error) dan MAE (Mean Absolute Error).
a. RMSE =
n y y n
i i i
1 2 ˆ
b. MAE =
n
i yi yi
n 1 ˆ
1
dimana, yˆi adalah nilai dugaan (ramalan) ke-i, yi merupakan nilai observasi ke-i, dan n merupakan banyaknya observasi. 7. Menentukan faktor koreksi untuk
mendekatkan nilai ramalan dengan nilai observasi.
Tabel 3 Variabel NWP dalam beberapa level tekanan
Sirkulasi Kelembaban Ketebalan
Permukaan:
Tekanan Permukaan Laut (slp)
Komponen angin zonal dan meridional (u0, v0) Suhu (T0)
Suhu Titik Embun (DP0)
RH (rh0) 500 – 1000 hPa (th1)
850-hPa:
Ketinggian Geopotensial (z8)
Komponen angin zonal dan meridional (u8, v8) Komponen angin vertikal (vv8)
RH (rh8)
500 – 850 hPa (th8) 700-hPa:
Ketinggian Geopotensial (z7)
Komponen angin zonal dan meridional (u7, v7) Komponen angin vertikal (vv7)
RH (rh7)
500-hPa:
Ketinggian Geopotensial (z5)
Komponen angin zonal dan meridional (u5, v5) Komponen angin vertikal (vv5)
RH (rh5)
200-hPa:
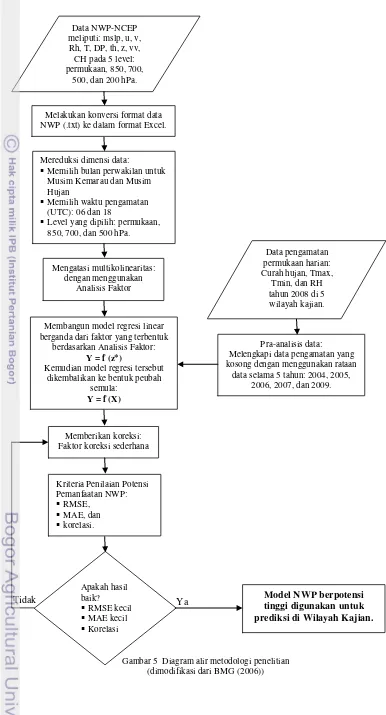
Gambar 5 Diagram alir metodologi penelitian (dimodifikasi dari BMG (2006))
Data pengamatan permukaan harian: Curah hujan, Tmax,
Tmin, dan RH tahun 2008 di 5
wilayah kajian.
Ya Tidak
Data NWP-NCEP meliputi: mslp, u, v, Rh, T, DP, th, z, vv, CH pada 5 level: permukaan, 850, 700,
500, dan 200 hPa.
Melakukan konversi format data NWP (.txt) ke dalam format Excel.
Pra-analisis data: Melengkapi data pengamatan yang kosong dengan menggunakan rataan
data selama 5 tahun: 2004, 2005, 2006, 2007, dan 2009. Mereduksi dimensi data:
Memilih bulan perwakilan untuk Musim Kemarau dan Musim Hujan
Memilih waktu pengamatan (UTC): 06 dan 18
Level yang dipilih: permukaan, 850, 700, dan 500 hPa.
Membangun model regresi linear berganda dari faktor yang terbentuk
berdasarkan Analisis Faktor: Y = f (z*)
Kemudian model regresi tersebut dikembalikan ke bentuk peubah
semula: Y = f (X)
Mengatasi multikolinearitas: dengan menggunakan
Analisis Faktor
Memberikan koreksi: Faktor koreksi sederhana
Kriteria Penilaian Potensi Pemanfaatan NWP: RMSE,
MAE, dan korelasi.
Apakah hasil baik? RMSE kecil MAE kecil Korelasi
besar
IV. HASIL DAN PEMBAHASAN
4.1 Numerical Weather Prediction (NWP) Atmosfer sebagai suatu sistem mungkin terlihat sangat rumit karena banyak proses dan komponen yang terlibat di dalamnya, namun sistem tersebut tetap merupakan suatu keteraturan. Terdapat dua jenis model atmosfer, yaitu model statistik dan model dinamik. Model statistik menghitung kondisi atmosfer berdasarkan perilaku dari data-data sebelumnya (sejarah). Sedangkan, model dinamik menggunakan sejumlah persamaan fisika untuk menggambarkan keadaan dan proses-proses dalam atmosfer yang diselesaikan dalam grid ruang dan waktu. Model-model seperti ini dapat menggambarkan dinamika atmosfer, tetapi bergantung pada penyederhanaan, kondisi awal (initial value problem) dan asimilasi data untuk mengatasi sistem atmosfer yang bersifat chaotic. Seluruh proses yang terjadi dalam suatu sistem atmosfer tidak selalu digambarkan dengan baik oleh suatu model, sehingga dalam pemanfaatannya perlu dilakukan interpretasi ulang dan memperhatikan faktor-faktor regional yang dapat mempengaruhi dinamika cuaca.
Model NWP yang digunakan dalam penelitian ini merupakan model Global Data Assimilation System (GDAS) produk The National Weather Service's (NWS), National Centers for Environmental Prediction (NCEP) milik Amerika Serikat (USA). GDAS dijalankan empat kali dalam sehari yaitu pada pukul 00, 06, 12 dan 18 UTC. Keluaran dari model ini digunakan untuk waktu analisis dan prediksi 3, 6 dan 9 jam. GDAS1 merupakan model skala global dengan waktu prediksi tiap 3 jam dengan ukuran grid satu derajat lintang-bujur.
4.2 Kinerja Model NWP yang Digunakan Kinerja model NWP yang digunakan dalam penelitian ini dilihat dengan adanya peninjauan terhadap pola diurnal dari berbagai variabel yang mampu mencirikan kondisi atmosfer yang selalu mengalami perubahan (dinamika) selama satu siklus harian (diurnal). Perubahan variabel yang terjadi kemudian dianalisis dengan mempertimbangkan pola yang sesuai dengan kondisi yang logis yang seharusnya terjadi, misalnya kapan waktu terjadinya suhu udara maksimum atau minimum, dan kelembaban maksimum atau minimum.
Variabel yang akan ditinjau adalah variabel yang memiliki dinamika yang cukup
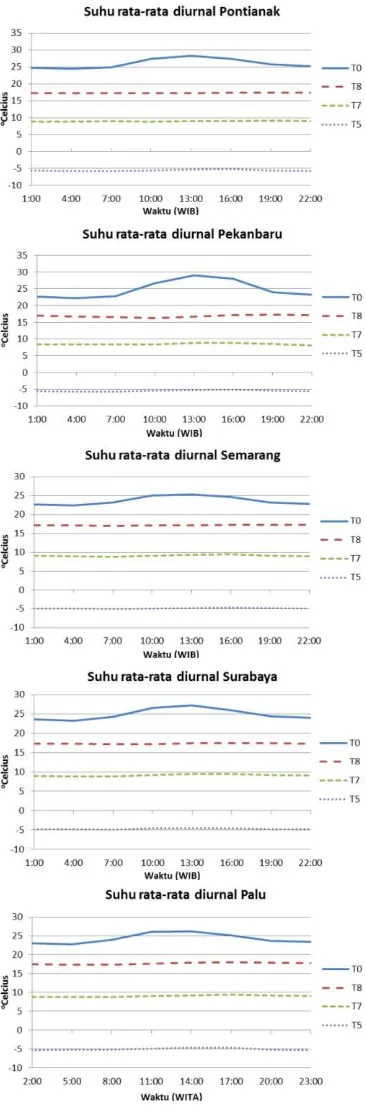
signifikan dalam satu siklus harian, yaitu suhu udara dan kelembaban udara. Berikut ini (Gambar 6) merupakan gambaran pola suhu rata-rata diurnal bulan Februari tahun 2008 di seluruh wilayah kajian serta perbandingannya antar mandatory layer (lapisan).
Ahrens (2009) menjelaskan bahwa suhu maksimum terjadi pada waktu yang bervariasi. Jika setelah tengah hari kondisi langit cerah tak berawan, suhu maksimum kemungkinan terjadi antara pukul 15.00 hingga 17.00. Sedangkan, jika setelah tengah hari kondisi langit berawan, suhu maksimum biasanya terjadi satu atau dua jam lebih awal. Hal ini digambarkan dengan cukup baik oleh model NWP (GDAS1), seperti yang ditunjukkan pada Gambar 6. Secara keseluruhan, nilai suhu maksimum pada lapisan 1000 hPa (T0) di lima wilayah kajian terjadi pada pukul 13.00 WS dan suhu minimum terjadi pada pukul 04.00 WS. Sedangkan, pada mandatory layer 850 (T8), 700 (T7), dan 500 hPa (T5) menunjukkan pola suhu rata-rata diurnal yang konstan terhadap waktu. Hal ini memperlihatkan adanya pengaruh karakteristik permukaan bumi (surface forcing) terhadap pola diurnal suhu dekat permukaan. Suhu udara dekat permukaan dipengaruhi oleh gradien suhu dan perpindahan panas dari permukaan.
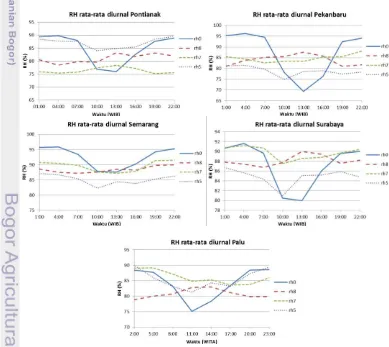
Parameter selanjutnya, kelembaban relatif (RH), merupakan parameter yang biasa
digunakan untuk menggambarkan kelembaban (moisture) di atmosfer. Besaran nilai RH (dinyatakan dalam persen) tidak mengindikasikan jumlah aktual uap air di udara, melainkan menggambarkan seberapa dekat udara untuk menjadi jenuh. Kelembaban relatif merupakan rasio antara jumlah uap air di udara dengan jumlah maksimum uap air yang dibutuhkan untuk menjenuhkan udara tersebut pada suhu dan tekanan yang sama (Ahrens 2009). Dengan kata lain, kelembaban relatif merupakan rasio kandungan uap air suatu parsel udara terhadap kapasitas udara tersebut dalam menampung jumlah uap air maksimum.
Pola diurnal RH rata-rata bulan Februari tahun 2008 untuk masing-masing wilayah kajian memiliki pola yang berkebalikan dengan suhu diurnal. Secara umum, RH pada lapisan 1000 hPa (rh0) bernilai minimum pada kisaran waktu siang hari, di mana nilai minimum tersebut terjadi pada pukul 13.00 WS, kecuali untuk wilayah kajian Palu terjadi pada pukul 11.00 WS (Gambar 7).
Hal ini menunjukkan bahwa keluaran model NWP untuk variabel RH memiliki pola yang sesuai dengan kondisi seharusnya. Informasi lain yang bisa didapatkan dari grafik tersebut adalah adanya perbedaan pola kelembaban antar lapisan. Pola diurnal rh0 sama dengan pola RH 500 hPa (rh5) yang memiliki nilai minimum saat siang hari. Pola diurnal rh8 secara umum berkebalikan dengan pola rh0 di mana pola rh8 memiliki nilai maksimum saat siang hari. Sedangkan, pola diurnal rh7 tidak memiliki pola yang seragam untuk semua wilayah kajian.
4.3 Reduksi Data Kajian
BMG (2006) dalam Laporan Proyek Pengembangan Meteorologi dan Geofisika, menjelaskan bahwa salah satu cara untuk meningkatkan kinerja model adalah membagi data atau mengelompokkan data menjadi beberapa kelompok musim. Kelompok musim yang digunakan adalah musim hujan (MH) dan musim kemarau (MK).
Selanjutnya, pada penelitian ini musim hujan dan kemarau akan diwakili oleh masing-masing satu bulan untuk mempermudah analisis. Tabel 4 berikut ini menunjukkan bulan yang mewakili MH dan MK untuk masing-masing wilayah kajian.
Tabel 4 Bulan perwakilan MH dan MK untuk masing-masing wilayah kajian tahun 2008
Kota
Bulan yang mewakili
Musim Hujan Musim Kemarau Pontianak Oktober Februari Pekanbaru November Juli
Semarang Februari Juli Surabaya Januari Juli Palu Agustus Februari
4.4 Model Output Statistics (MOS)
Pemanfaatan keluaran model NWP dioptimalkan dengan melakukan post processing. Beberapa metode yang seringkali digunakan untuk post-processing NWP adalah model output statistics (MOS), perfect prognosis (PP), dan Kalman filtering. Penelitian ini menggunakan MOS yang biasa digunakan untuk meramal parameter cuaca permukaan dari model NWP. Neilley (2004) menjelaskan bahwa MOS mempunyai dua fungsi utama, yaitu: (1) teknik MOS menghasilkan ramalan cuaca kuantitatif, (2) MOS mereduksi rataan sisaan (error) dari
ramalan raw model NWP dengan memperkecil bias dan pengkoreksian model secara statistik.
4.5 Potensi Pemanfaatan Keluaran Model NWP di Lima Wilayah Kajian
Hal pertama yang dilakukan dalam upaya pemanfaatan keluaran NWP adalah dengan analisis korelasi antara CH keluaran model NWP dengan parameter keluaran NWP lainnya. Penelitian ini memanfaatkan hasil penelitian sebelumnya yang telah melakukan kajian yang serupa. Penelitian yang digunakan sebagai acuan adalah Cavazos T. (2002), Sutikno (2008), dan Ristanti D. (2009). Ketiga penelitian tersebut menunjukkan beberapa variabel yang berkorelasi nyata dan berpengaruh terhadap CH yang ditunjukkan pada Tabel 5, 6, dan 7.
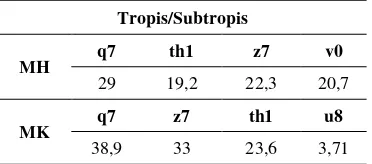
Tabel 5 Kontribusi (%) prediktor terhadap variasi hujan harian menggunakan model downscaling untuk musim hujan dan kemarau (Cavazos 2002).
Tropis/Subtropis
MH
q7 th1 z7 v0
29 19,2 22,3 20,7
MK q7 z7 th1 u8 38,9 33 23,6 3,71 Sumber: Tereza Cavazos (2002)
Tabel 6 Peubah penjelas yang berpengaruh terhadap CH (Sutikno 2008)
Musim
Kemarau Hujan
Kelembaban spesifik Preicipitable water Komp. angin zonal Komp. angin zonal Ketinggian geopot. Kelembaban
spesifik Sumber: Sutikno (2008)
Tabel 7 Parameter model NWP yang ber-korelasi besar terhadap Curah Hujan (Ristanti 2009)
Kota Bulan
DJF MAM JJA SON
Kota Bulan
DJF MAM JJA SON
Padang Rh0 Vv8 Vv7 Vv5 Rh0 Vv8 Rh8 Vv7 Vv5 Rh0 Vv8 Vv7 Vv5
Setelah melakukan pengujian (uji korelasi) terhadap variabel yang telah dikemukakan di atas, diketahui bahwa tidak semua variabel yang telah disebutkan tersebut berkorelasi tinggi (> 0,5 atau < -0,5) dengan CH untuk lima wilayah kajian dalam penelitian ini.
Berdasarkan penelitian yang telah dilakukan oleh Cavazos T dan Bruce Hewitson (2002), variabel yang terbukti berkorelasi tinggi adalah untuk variabel ketinggian geopotensial level 700 hPa (z7) untuk Pekanbaru Musim Hujan dan Semarang Musim Kemarau. Sedangkan, berdasarkan penelitian Sutikno (2008) dan Ristanti (2009) dapat dilihat pada Tabel 8 dan 9.
Tabel 8 Variabel model NWP yang terbukti berkorelasi besar dengan CH berdasarkan penelitian Sutikno (2008) Wilayah Kajian Musim Kemarau (MK) Hujan (MH) Pontianak u7, z2 - Pekanbaru u7, u5 -
Semarang z7 -
Surabaya - -
Palu - -
Tabel 9 Parameter model NWP yang terbukti berkorelasi besar dengan CH berdasarkan penelitian Ristanti (2009) Wilayah Kajian Musim Kemarau Musim Hujan
Pontianak RH0, vv8, vv7, vv5 RH0, vv8, vv7, vv5 Pekanbaru RH0, vv8, RH8, vv7, vv5 RH0, vv8, vv7, vv5 Semarang RH0, DP0, vv8, RH8, vv7, vv5 RH0, T0, RH8, vv8, vv7, vv5 Surabaya RH0, DP0, vv8, RH8, vv7, vv5 RH0, T0, RH8, vv8, vv7, vv5 Palu RH0, vv8, RH8, vv7, vv5 vv8, RH7, vv5
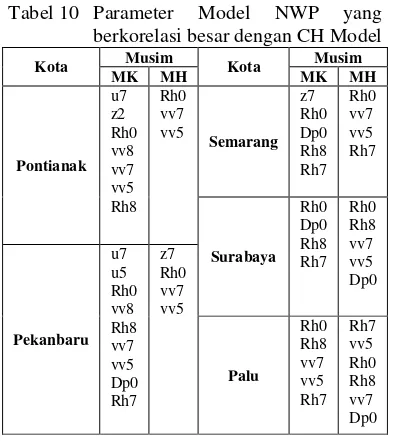
Proses pengujian yang dilakukan sebagai pelengkap meliputi uji variabel silang (cross variable testing) dan uji variabel yang terlewatkan (missing variable testing) sehingga mampu menunjukkan beberapa variabel yang berkorelasi besar dengan curah hujan untuk lima wilayah kajian dalam penelitian ini (Tabel 10).
Tabel 10 Parameter Model NWP yang berkorelasi besar dengan CH Model
Kota Musim Kota Musim
MK MH MK MH
Pontianak u7 z2 Rh0 vv8 vv7 vv5 Rh8 Rh0 vv7 vv5 Semarang z7 Rh0 Dp0 Rh8 Rh7 Rh0 vv7 vv5 Rh7 Surabaya Rh0 Dp0 Rh8 Rh7 Rh0 Rh8 vv7 vv5 Dp0 Pekanbaru u7 u5 Rh0 vv8 Rh8 vv7 vv5 Dp0 Rh7 z7 Rh0 vv7 vv5 Palu Rh0 Rh8 vv7 vv5 Rh7 Rh7 vv5 Rh0 Rh8 vv7 Dp0
Variabel yang selalu menjadi prediktor untuk kelima wilayah kajian adalah Rh0. Varaiabel lain yang sering muncul sebagai prediktor CH model adalah vv7, vv5, dan Rh8. Hal ini menunjukkan bahwa dalam
proses pendugaan CH model
mempertimbangkan nilai kelembaban relatif pada lapisan 1000 dan 850 hPa serta kecepatan angin vertikal pada lapisan 700 dan 500 hPa. Kondisi seperti ini dimungkinkan karena lapisan 700 hingga 500 hPa adalah lapisan terbentuknya awan. Jika masih ada kecepatan vertikal pada lapisan tersebut, maka masih ada massa udara yang mengembang dan bergerak naik ke atas sehingga menghasilkan awan-awan yang berkembang vertikal yaitu awan yang dihasilkan oleh kantung udara hangat dan lembab yang masih mampu naik sampai ketinggian yang cukup tinggi (awan berpotensi hujan) setelah melewati aras kondensasi (pada umumnya ± 850 hPa) yang ditunjukkan oleh variabel Rh8 yang sering muncul sebagai prediktor di lima wilayah kajian. Secara umum, prediktor yang memiliki korelasi tinggi dengan CH adalah Rh0, Dp0, vv8, Rh8, vv7, Rh7, u7, z7, vv5, u5, dan z2.
Tabel 11 Persamaan regresi linear berganda dan nilai R2 model CH (CH^)
Kota Musim Persamaan Regresi R2 (%)
Pontianak MK
CH^ = - 0,052 + 0,701 vv8 + 0,090 rh8 – 3,701
vv5 – 0,880 u7 82
MH CH^ = - 52,2 + 0,665 rh0 - 1,31 vv7 - 1,80 vv5 83
Pekanbaru
MK CH^ = - 31,812 + 0,411 rh0 – 0,612 vv8 – 0,296
u7 – 0,208 u5 – 0,943 vv5 + 0,018 rh7 78
MH CH^ = - 44 + 0,07 z7 + 0,318 rh0 - 0,364 vv7 -
1,74 vv5 80
Semarang
MK CH^ = - 238,648 + 0,711 z7 + 0,078 rh0 + 0,111
rh8 + 0,045 rh7 65
MH CH^ = - 182 + 0,956 rh0 - 2,42 vv7 - 1,04 vv5 + 1,16 rh7 87
Surabaya
MK CH^ = - 13,674 + 0,161 rh0 + 0,022 rh8 + 0,015
rh7 58
MH CH^ = - 48,3 + 0,762 rh0 - 0,171 rh8 + 0,286
vv7 - 2,66 vv5 + 0,06 DP0 88
Palu
MK CH^ = - 33,104 + 0,442 rh0 + 0,038 rh8 vv7 – 1,445 vv5 – 0,012 rh7 – 0,625 89 MH CH^ = - 108,898 + 0,024 rh7 – 1,060 vv5 + 0,913
rh0 – 0,987 vv7 + 1,779 DP0 88
yang tinggi diantara peubah-peubah bebas, mengakibatkan pendugaan dengan metode kuadrat terkecil tidak dapat diandalkan. Pendeteksian multikolinearitas dapat dilakukan dengan cara formal yaitu dengan meninjau nilai dari Variance Inflation Factor (VIF). Penelitian ini menggunakan metode formal (VIF) dengan tujuan meminimalisir adanya multikolinearitas sehingga persamaan regresi yang dibangun bisa diandalkan.
Langkah selanjutnya adalah mem-bangun regresi linear berganda. Metode Factor Analysis digunakan untuk menghilangkan masalah multikolinearitas. Nilai score rotated factor loading (z*) yang dipilih kemudian diregresikan sehingga mendapatkan persamaan regresi serta nilai koefisien determinasi (R2) yang ditunjukkan oleh Tabel 11.
Model regresi yang paling baik adalah model regresi untuk kota Palu (Tabel 10). Hal ini ditunjukkan oleh koefisien determinasi (R2) yang relatif lebih tinggi dibandingkan
dengan nilai R2 untuk wilayah kajian lain. Musim kemarau untuk wilayah kajian Palu (Palu-MK) memiliki koefisisen determiniasi 89% sedangkan musim hujan (Palu-MH) memiliki nilai R2 sebesar 88%. Kota Palu memiliki nilai R2 yang sama baiknya untuk kedua musim.
Gambar 8 Plot Nilai CH Model dan CH observasi untuk masing-masing wilayah kajian Tahun 2008
Prediksi NWP untuk CH harian diakui masih kurang baik untuk diterapkan di lima wilayah kajian. Hal ini dapat dilihat dari perbedaan pola grafik CH model dengan CH observasi (Gambar 8). Pada beberapa lokasi, plot grafik menunjukan pola yang hampir serupa, sedangkan untuk beberapa lokasi lain menunjukkan pola yang berbeda. Hal ini disebabkan karena terdapat beberapa faktor yang berpengaruh terhadap curah hujan yang tidak tergambarkan dengan baik oleh model NWP.
Berdasarkan analisis grafik pada Gambar 8, potensi pemanfaatan model NWP di
beberapa wilayah kajian tergantung pada musim. Pola model NWP yang lebih mendekati observasi secara umum terjadi pada musim kemarau untuk seluruh wilayah kajian. Sedangkan, untuk Kota Palu, baik MK mapun MH memiliki pola yang hampir serupa antara keluaran NWP dengan observai.
Gambar 9 Plot Nilai CH^ dan CH observasi untuk masing-masing wilayah kajian Tahun 2008
Perlu dicari suatu upaya untuk meminimalkan nilai error antara CH^ dengan CH observasi. Upaya tersebut dapat dilakukan dengan mencari faktor koreksi. Faktor koreksi yang dimaksud dalam penelitian ini adalah suatu nilai yang digunakan untuk mengkoreksi
faktor koreksi digunakan nilai Root Mean Square Error (RMSE) dan Mean Absolute Error (MAE). Berikut ini merupakan grafik
yang menunjukkan bahwa CH^ yang sudah diberi faktor koreksi sehingga menjadi CH* (Gambar 10).
Sebelum diberikan faktor koreksi, nilai error (RMSE dan MAE) antara model dengan observasi, secara umum lebih besar pada musim hujan (MH) untuk semua wilayah kajian. Hal ini mengindikasikan bahwa proses sub-grid cell untuk menduga presipitasi seperti proses konveksi tidak digambarkan dengan baik oleh model. Nilai error yang cukup besar mungkin juga berhubungan dengan ketersediaan data observasi yang digunakan untuk analisis.
Secara konseptual, pengguanaan faktor koreksi seharusnya akan mengurangi nilai error. Konsep tersebut dibuktikan pada Tabel 12. Pengurangan nilai RMSE dan MAE terbesar terjadi pada wilayah kajian Surabaya musim kemarau (Surabaya-MK). Hal ini terjadi karena nilai CH observasi harian untuk bulan Juli 2008 di Surabaya bernilai nol, sehingga nilai faktor koreksi yang diberikan sekecil-kecilnya (mendekati nol) menghasilkan pola yang sangat dekat antara model dan observasi. Secara umum, dapat dikatakan bahwa penggunaan faktor koreksi sangat berpengaruh besar (efektif) diterapkan untuk musim kemarau di seluruh wilayah kajian seperti yang ditunjukkan pada Tabel 12.
Parameter cuaca yang biasa diprediksi secara harian selain curah hujan (CH) adalah suhu maksimum (Tmax), suhu minimum (Tmin), kelembaban relatif rata-rata (RH).
Selanjutnya akan dicari faktor koreksi dalam upaya prediksi paramater Tmax, Tmin, dan RH. Langkah pencarian faktor koreksi untuk suhu dan kelembaban sama dengan langkah yang digunakan untuk curah hujan.
Kajian lebih difokuskan pada wilayah kajian Palu dikarenakan wilayah Palu dapat dikatakan berpotensi lebih tinggi dalam memanfaatkan keluaran NWP dibandingkan dengan wilayah kajian lain. Hal ini dapat dilihat dari koefisien determinasi dari persamaan regresi CH untuk Kota Palu lebih besar dibandingakan dengan wilayah kajian lain. Di samping itu, pengurangan nilai error Kota Palu pun bisa dikatakan lebih baik dibandingakan dengan wilayah kajian lain (Tabel 12).
Penentuan persamaan regresi model suhu dan kelembaban diwali dengan proses pengujian korelasi antara suhu dan kelembaban dengan variabel hasil model NWP lain yang diasumsikan berpengaruh. Penelitian ini memanfaatkan hasil penelitian yang telah dilakukan oleh Ristanti D. (2009). Berdasarkan penelitiannya, Ristanti (2009) menjelaskan bahwa model kelembaban dipengaruhi oleh suhu permukaan (T0) dan suhu titik embun permukaan (DP0). Setelah dilakukan uji korelasi, ternyata kedua parameter tersebut memiliki korelasi yang besar (> 0,5 atau < -0,5) dengan kelembaban.
Tabel 12 Faktor koreksi model CH untuk masing-masing wilayah kajian
No Wilayah kajian
Faktor koreksi (CH^) (%)
RMSE dan MAE Pengurangan error
Sebelum sesudah RMSE (%) MAE (%)
1
Pontianak-MK 35 RMSE 10,9 5,8 46,5 50,1 MAE 7,2 3,6
Pontianak-MH 125 RMSE 23,7 23,1 2,5 -5,4 MAE 15,2 15,9
2
Pekanbaru-MK 25 RMSE 6,8 3,9 43,2 60,8 MAE 5,6 2,2
Pekanbaru-MH 75 RMSE 20,6 20,5 0,6 10,1 MAE 12,5 11,3
3
Semarang-MK 30 RMSE 2,0 0,7 64,7 65,4 MAE 1,4 0,5
Semarang-MH 38 RMSE 29,2 24,9 14,4 20,5 MAE 23,6 18,8
4
Surabaya-MK 1 RMSE 0,7 0,007 99,0 99,0 MAE 0,5 0,005
Surabaya-MH 50 RMSE 11,9 9,5 20,4 24,8 MAE 7,9 5,9
5
Palu-MK 5 RMSE 12,3 1,7 86,5 89,8 MAE 8,3 0,8
Tabel 13 Regresi model RH dan Suhu Kota Palu
Model Musim Prediktan Konstanta
Regresi Prediktor
Koefisien Regresi Prediktor R
2 (%)
RH
MK RH^ 102 T0 -4,92 99,8
Dp0 4,74
MH RH^ 99,6 Dp0 T0 -4,894,84 99,8
Tmax MK Tmax^ 37,5 Rh0 -0,143 85,0
MH Tmax^ 37,2 Rh0 -0,142 73,8
Tmin MH Tmin^ 7,95 Dp0 0,698 80,1
Model suhu dipengaruhi oleh kelembaban relatif pada level permukaan (rh0) dan suhu titik embun permukaan (DP0). Berdasarkan uji korelasi, yang memiliki korelasi besar dengan suhu maksimum adalah rh0, sedangkan untuk suhu minimum adalah DP0. Model suhu minimum hanya dilakukan untuk musim hujan (Palu-MH). Hal ini disebabkan karena tidak terdapatnya variabel yang berkorelasi besar dengan suhu minimum untuk Palu-MK. Sehingga persamaan regresi linear berganda hanya untuk model kelembaban saja. Model suhu kini menjadi persamaan regresi linear sederhana dengan satu peubah prediktor. Nilai koefisien determinasi (R2) dari persamaan regresi linear berganda untuk model RH dan suhu dapat dilihat pada Tabel 13.
Pengaruh prediktor masing-masing model dapat dilihat dari model regresi seperti tertera pada Tabel 13. Berdasarkan model regresi pada Tabel 13, variabel yang berkorelasi dengan RH adalah suhu permukaan (T0) dan suhu titik embun permukaan (DP0). Pada model RH^ ini, T0 memiliki hubungan negatif. Hal ini menunjukkan bahwa setiap kenaikan nilai T0 akan menyebabkan penurunan kelembaban. Sedangakan, DP0 memiliki hubungan positif dengan kelembaban yang menunjukkan bahwa setiap kenaikan nilai DP0 menyebabkan kenaikan
nilai kelembaban pula. Hubungan fungsional seperti ini sesuai dengan konsep dan fakta (Gambar 6 dan Gambar 7) yang menyatakan bahwa suhu dan kelembaban memiliki hubungan yang terbalik (korelasi negatif).
Sedangkan, pada model suhu maksimum (Tmax^), prediktor yang menyusun persamaan tersebut hanyalah rh0 serta memiliki hubungan negatif. Pada model suhu minimum, DP0 memiliki hubungan postif. Hal ini menunjukkan bahwa kenaikan nilai DP0 (keluaran model) menyebabkan nilai suhu minimum (observasi) meningkat.
Gambar 11 Plot Nilai model (^) dan observasi untuk RH, Tmax, dan Tmin (kiri) serta perbandingannya dengan hasil koreksi (kanan) di Kota Palu Tahun 2008
Walaupun hasil model RH, Tmax, dan Tmin sudah dapat dikatakan baik, namun nilai faktor koreksi tetap perlu dicari untuk meminimalisir error dan meningkatkan akurasi prediksi model. Pola model yang sangat menyerupai observasi terjadi pada model RH musim hujan (Gambar 11) .
Analisis potensi pemanfaatan model NWP tidak cukup hanya berdasarkan analisis pola grafik. Perlu disertai adanya analisis terhadap nilai error (RMSE dan MAE). Nilai RMSE dan MAE akan memberikan gambaran yang lebih jelas mengenai sejauh mana model mampu menduga nilai observasi serta mampu menjadi acuan dalam pemberian faktor koreksi. Persentase pengurangan nilai RMSE
dan MAE didasarkan pada selisih nilai error sebelum dan sesudah pemberian faktor koreksi. Pemberian faktor koreksi sangat efektif untuk model suhu maksimum (Tmax) baik musim kemarau maupun musim hujan di Kota Palu tahun 2008 dengan pengurangan nilai RMSE dan MAE mencapai rata-rata 60%.
Tabel 14 Faktor koreksi model RH dan suhu kota Palu
No Model Faktor Koreksi (%) RMSE & MAE % pengurangan error sebelum sesudah RMSE MAE
1 RH-MK 88 RMSE 12,337 6,539 47,0 53,0 MAE 10,858 5,108
2 RH-MH 95 RMSE 5,594 3,632 35,1 35,7 MAE 4,561 2,934
3 Tmax-MK 133 RMSE 7,039 2,865 59,3 68,3 MAE 6,766 2,147
4 Tmax-MH 114,7 RMSE 5,385 2,091 61,2 65,2 MAE 5,154 1,795
5 Tmin-MH 98,8 RMSE 0,585 0,506 13,5 20,0 MAE 0,449 0,359
Nilai faktor koreksi model RH, Tmax dan Tmin masing-masing musim disajikan dalam Tabel 14. Secara umum, hasil penelitian ini menunjukkan bahwa faktor koreksi lebih terlihat pengaruhnya terhadap model suhu maksimum (musim hujan dan musim kemarau) serta model CH musim kemarau dibandingkan dengan model lainnya. Hal ini dapat terlihat dari penurunan nilai RMSE dan MAE yang jauh lebih besar dibandingkan dengan model lainnya. Namun, penilaian potensi pemanfatan model tidak hanya dilihat dari efektifitas faktor koreksi, melainkan juga dilihat dari koefisien determinasi, nilai RMSE dan MAE sebelum faktor koreksi dan pola grafik yang terbentuk.
Model NWP tidak memasukkan faktor lokal dalam perhitungannya sehingga hasil prediksinya biasanya kurang tepat dari keadaan sebenarnya di lapangan. Oleh karena itu, dapat dikatakan bahwa faktor koreksi tersebut merupakan pengganti dari faktor-faktor lokal yang tidak dimasukkan dalam model NWP.
V. SIMPULAN DAN SARAN
5.1. Simpulan
Fokus kajian dalam penelitian ini adalah meninjau variabel-variabel di atmosfer yang paling berpengaruh terhadap curah hujan, kelembaban, suhu maksimum, dan suhu minimum sebagai parameter cuaca yang biasa diprediksi dalam jangka pendek. Selain itu, kajian ini bertujuan menentukan wilayah kajian yang paling berpotensi untuk memanfaatkan keluaran model NWP. Penilaian potensi pemanfaatan dilihat dari beberapa hal, yaitu: (1) pola garfik antara data
observasi dan keluaran model, (2) nilai koefisien determinasi model hasil regresi (3) nilai error antara observasi dan model, serta (4) persentase pengurangan nilai error (efektifitas faktor koreksi).
Kelembaban (rh0 dan rh8) serta kecepatan angin vertikal (vv7 dan vv5) merupakan variabel yang paling relevan terhadap curah hujan harian. Parameter kelembaban dipengaruhi oleh suhu udara (T0) dan suhu titik embun (DP0). Selain itu, parameter suhu maksimum dipengaruhi oleh kelembaban (rh0), sedangkan suhu minimum dipengaruhi oleh suhu titik embun (DP0). Persamaan regresi model NWP untuk curah hujan harian menghasilkan error yang cukup besar untuk musim hujan, hal ini mengindikasikan bahwa proses-proses yang berpengaruh terhadap curah hujan pada skala yang lebih kecil dari grid model (resolusi lebih tinggi), tidak digambarkan dengan baik oleh model NWP. Sedangkan, model kelembaban dan suhu menghasilkan error yang sama kecilnya untuk musim hujan maupun kemarau. Hal ini disebabkan karena prediktor yang berpengaruh terhadap curah hujan lebih banyak (kompleks) dibandingkan dengan suhu dan kelembaban.
5.2. Saran
Pemodelan curah hujan umumnya masih belum memuaskan, untuk itu perlu dilakukan penelitian lebih lanjut untuk memperoleh hasil yang lebih baik dengan menambah periode waktu analisis dan menggunakan metode analisis yang lebih baik. Memperbanyak wilayah kajian adalah keputusan yang baik de