FUNGSI QUASI-LIKELIHOOD UNTUK PENAKSIRAN
PARAMETER DALAM DISTRIBUSI PARETO
TESIS
Oleh
AGUS BUDIANTO 087021076/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
2010
FUNGSI QUASI-LIKELIHOOD UNTUK PENAKSIRAN
PARAMETER DALAM DISTRIBUSI PARETO
TESIS
Diajukan Sebagai Salah Satu Syarat
Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
AGUS BUDIANTO 087021076/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2010
Judul Tesis : FUNGSI QUASI-LIKELIHOOD UNTUK PENAKSIRAN PARAMETER DALAM DISTRIBUSI PARETO
Nama Mahasiswa : Agus Budianto Nomor Pokok : 087021076 Program Studi : Matematika
Menyetujui, Komisi Pembimbing
(Dr. Sutarman, M.Sc.) (Prof.Dr. Opim Salim S M.Sc)
Ketua Anggota
Ketua Program Studi, Dekan
(Prof. Dr. Herman Mawengkang) (Prof. Dr. Eddy Marlianto, M.Sc)
Tanggal lulus: 17 Mei 2010
Telah diuji pada
Tanggal 17 Mei 2010
PANITIA PENGUJI TESIS
Ketua : Dr. Sutarman, M.Sc
Anggota : 1. Prof. Dr. Opim Salim S, M.Sc 2. Prof. Dr. Herman Mawengkang 3. Drs. Open Darnius, M.Sc
ABSTRAK
Fungsi quasi-likelihood yang digunakan untuk penaksiran berkaitan antara mean dan varians dari pengamatan-pengamatan sampel. Metode penaksiran likelihood dikon-sentrasikan pada hal dimana observasi adalah independen, tetapi perluasan dapat dibuat termasuk korelasi diantara titik-titik data. Pada tesis ini, penaksiran Bayesian untuk distribusi Pareto yang bertujuan untuk meninjau kemungkinan penggunaan fungsi quasi-likelihood dalam pendekatan Bayesian. Suatu metode baru yang dina-makan penaksiran Quasi-Likelihood. Metode ini mengurangi penaksiran Bayesian biasa, jika distribusi itu adalah suatu anggota dari keluarga eksponensial. Digu-nakan penaksiran quasi-likelihood maksimum dari parameter-parameter tak dikenal dari distribusi Pareto. Prinsip Pareto yang dikenal sebagai 20-80 peraturan dapat juga berkenaan dengan efisiensi Pareto. Prinsip Pareto yang berkaitan dengan pe-naksiran banyak diaplikasikan dalam berbagai bidang, seperti: ekonomi, sosial, sains dan geofisika.
Kata kunci : Quasi-likelihood, model linier, metode estimasi bayes, distribusi pareto
ABSTRACT
Quasi-likelihood can be used for estimation a relation between the mean and variance of the observations sample. Likelihood estimation method concentrated on cases where the observation are independent, but extensions can be made to include correlations between the data points. In this thesis, Bayesian estimation for the Pareto distribution aims to discuss the possibility of using the quasi-likelihood function in the Bayesian approach. A new method which called ” Quasi-Likelihood Estimation”. This method has been reduced to the usual Bayesian Estimation if the distribution is a member of the exponential family. The maximum quasi-likelihood estimation used the unknown parameters. The Pareto principle known as the 80-20 rule can also refer to Pareto efficiency. The Pareto principle referred to estimation has been applied in various area, such as : economic, social, sciences and geophysica.
Keywords : Quasi-likelihood, linear model, bayesian estimation method , pareto distribution
KATA PENGANTAR
Dengan rasa rendah hati, Penulis mengucapkan Puji dan Syukur kehadirat Tuhan Yang Maha Esa atas segala kasih dan karunia yang telah dilimpahkanNya, sehingga penulis dapat menyelesaikan penulisan tesis ini.
Tesis ini disusun untuk memenuhi salah satu syarat untuk memperoleh gelar sarjana Magister Sain di program studi S2 Matematika FMIPA Universitas Sumatera Utara Medan.
Dalam penyusunan tesis ini, penulis telah banyak mendapat bimbingan dan petunjuk dari berbagai pihak. Pada kesempatan ini penulis mengucapkan terimakasih yang sebesar-besarnya kepada:
Bapak Prof. DR. Herman Mawengkang, MSc, selaku ketua Prodi Magister Matema-tika dan pembanding I yang telah memberikan bimbingan, jurnal dan arahan serta saran-saran, sehingga selesainya tesis ini.
Bapak DR. Saib Suwilo, MSc, selaku Sekretaris Prodi Magister Matematika yang telah banyak memberikan motivasi, saran dan arahan sehingga selesainya tesis ini.
Bapak DR. Sutarman, MSc, selaku Ketua Komisi Pembimbing yang telah membim-bing dengan sabar, memberikan saran dan masukan, sehingga selesainya tesis ini.
Bapak Prof. DR. Opim Salim Sitompul, MSc, selaku Anggota Komisi Pembimbing yang telah memberikan bimbingan, saran dan masukan, sehingga selesainya tesis ini.
Bapak Drs. Open Darnius, MSc, selaku Pembanding II yang telah banyak mem-berikan saran-saran dan masukan kepada Penulis, sehingga selesainya tesis ini.
Semoga tesis ini bermanfaat bagi Negara khususnya pendidikan.
Medan, 17 Mei 2010
Penulis,
Agus Budianto
RIWAYAT HIDUP
Agus Budianto dilahirkan di Deli Serdang pada tanggal 16 Agustus 1972 dan merupakan anak ke 2 dari 4 bersaudara, anak dari Ayah H Raslim dan Ibu Hj Sudarmi (alm). Menamatkan Sekolah Dasar (SD) Negeri 106164 di Deli Serdang pada tahun 1984, Sekolah Menengah Pertama (SMP) Negeri 2 Percut Sei Tuan Deli Serdang pada tahun 1987 dan Sekolah Menengah Atas (SMA) Negeri 10 Medan jurusan Fisika pada tahun 1990. Tahun 1990 memasuki Perguruan Tinggi Universitas Pembangunan Nasional Veteran (UPN) Yogyakarta dibawah naungan Dephankam RI jurusan Teknik Geologi dan memperoleh gelar Sarjana Teknik pada tahun 1997. Pada tahun 2000 transfer kejurusan Pendidikan Matematika STKIP Teladan Medan dan memperoleh gelar Sarjana Pendidikan tahun 2002. Tahun 1998 sampai dengan sekarang mengajar bidang studi Matematika SMP/SMA Bina Siswa Deli Serdang. Tahun 2002 mengajar bidang studi Matematika dan Fisika di SMA Suci Murni Medan sampai sekarang. Tahun 2003 mengajar bidang studi Matematika di SMP Negeri 2 Percut Sei Tuan
Deli Serdang sampai sekarang. Tahun 2008 mengikuti sekolah pada Program Studi S2 Magister Matematika Universitas Sumatera Utara (USU) Medan dan memperoleh gelar Magister Sain tahun 2010. Pada tahun 2009 sebagai sekretaris umum Forum Ilmiah Guru Sumatera Utara (FIGURSU) sampai dengan sekarang.
DAFTAR ISI
Halaman
ABSTRAK i
ABSTRACT ii
KATA PENGANTAR iii
RIWAYAT HIDUP v
DAFTAR ISI vi
DAFTAR TABEL viii
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Permasalahan 3
1.3 Tujuan Penelitian 4
1.4 Manfaat Penelitian 4
1.5 Metodologi Penelitian 4
BAB 2 TINJAUAN PUSTAKA 6
2.1 Fungsi Quasi-Likelihood 6
2.2 Model Linier Tergeneralisir 7
2.3 Statistika Bayes 8
BAB 3 DISTRIBUSI PARETO 10
3.1 Prinsip Pareto 10
3.2 Hubungan Distribusi Pareto dengan Distribusi yang Lain 11
3.3 Penaksiran Parameter Distribusi Pareto 12
3.4 Aplikasi Distribusi Pareto 12
BAB 4 PENAKSIRAN BAYESIAN UNTUK PARAMETER PARETO
MENG-GUNAKAN FUNGSI QUASI-LIKELIHOOD 14
4.1 Penaksiran Quasi-Bayesian 14
4.2.1 Penaksiran Quasi-Likelihood 16
4.2.2 Penaksiran Quasi-Bayesian untuk Distribusi Pareto 17
BAB 5 KESIMPULAN DAN SARAN 22
5.1 Kesimpulan 22
5.2 Saran 22
DAFTAR PUSTAKA 23
DAFTAR TABEL
Nomor Judul Halaman
4.1 Penaksiran Bayesian dan Quasi-Likelihood untuk Data Pareto untuk
k ketikaα diketahui (α = 2). (Menurut Youssef, 2009) 20
4.2 Penaksiran Bayesian dan Quasi-Likelihood untuk Data Pareto untuk
α ketikak diketahui (k = 2). (Menurut Youssef, 2009) 20 4.3 Efisiensi Penaksiran Quasi-Bayesian dari Parameterα ketika k
dike-tahui (k = 3). (Menurut Youssef, 2009) 21
4.4 Efisiensi Penaksiran Quasi-Bayesian dari Parameterk ketikaα
dike-tahui (α = 2). (Menurut Youssef, 2009) 21
ABSTRAK
Fungsi quasi-likelihood yang digunakan untuk penaksiran berkaitan antara mean dan varians dari pengamatan-pengamatan sampel. Metode penaksiran likelihood dikon-sentrasikan pada hal dimana observasi adalah independen, tetapi perluasan dapat dibuat termasuk korelasi diantara titik-titik data. Pada tesis ini, penaksiran Bayesian untuk distribusi Pareto yang bertujuan untuk meninjau kemungkinan penggunaan fungsi quasi-likelihood dalam pendekatan Bayesian. Suatu metode baru yang dina-makan penaksiran Quasi-Likelihood. Metode ini mengurangi penaksiran Bayesian biasa, jika distribusi itu adalah suatu anggota dari keluarga eksponensial. Digu-nakan penaksiran quasi-likelihood maksimum dari parameter-parameter tak dikenal dari distribusi Pareto. Prinsip Pareto yang dikenal sebagai 20-80 peraturan dapat juga berkenaan dengan efisiensi Pareto. Prinsip Pareto yang berkaitan dengan pe-naksiran banyak diaplikasikan dalam berbagai bidang, seperti: ekonomi, sosial, sains dan geofisika.
Kata kunci : Quasi-likelihood, model linier, metode estimasi bayes, distribusi pareto
ABSTRACT
Quasi-likelihood can be used for estimation a relation between the mean and variance of the observations sample. Likelihood estimation method concentrated on cases where the observation are independent, but extensions can be made to include correlations between the data points. In this thesis, Bayesian estimation for the Pareto distribution aims to discuss the possibility of using the quasi-likelihood function in the Bayesian approach. A new method which called ” Quasi-Likelihood Estimation”. This method has been reduced to the usual Bayesian Estimation if the distribution is a member of the exponential family. The maximum quasi-likelihood estimation used the unknown parameters. The Pareto principle known as the 80-20 rule can also refer to Pareto efficiency. The Pareto principle referred to estimation has been applied in various area, such as : economic, social, sciences and geophysica.
Keywords : Quasi-likelihood, linear model, bayesian estimation method , pareto distribution
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Perkembangan ilmu pengetahuan matematika dan penerapannya dalam berba-gai bidang keilmuan selalu mencari metode baru untuk memudahkan dalam mem-prediksi dan menaksir parameter-parameter dari data untuk menyelesaikan beragam permasalahan yang semakin kompleks dan rumit
Maksud utama dari banyak analisis menunjukkan bagaimana jawaban rata-rata di buat oleh beberapa covariat. Kadang-kadang tidak cukup informasi tentang data untuk menentukan suatu model data. Bagaimanapun, dimungkinkan bisa untuk menentukan beberapa dari keistimewaan data. Sebagai contoh,
i Apakah data kontinu atau diskrit.
ii Bagaimana rata-rata atau nilai tengah dibuat oleh Stimulan eksternal.
iii Bagaimana variable jawaban berubah dengan jawaban rata-rata.
iv Apakah pengamatan itu independen.
v Apakah jawaban dari distribusi tidak simetris.
Dikembangkan analisis berdasarkan pada penaksiran likelihood. Dikonsentrasikan pada hal dimana observasi adalah independen, tetapi perluasan dapat dibuat terma-suk korelasi diantara titik-titik data.
Sering penaksiran parameter mempertimbangkan suatu intuisi. Perkiraan X pasti kelihatannya pantas sebagai suatu perkiraan dari suatu populasi rata-rata µ. Berdasarkan atas S2 sebagai suatu perkiraan dari σ2 adalah X. Perkiraan untuk
suatu parameter binomial p adalah hanya suatu ukuran sampel, yang tentu adalah suatu rata-rata dan mempertimbangkan berdasarkan penalaran logika. Tetapi ada banyak situasi yang tidak semua nyata apakah perkiraan tepat dilakukan. Dalam statistika, filosofi berbeda menghasilkan metode perkiraan berbeda.
2
distribusi komponen acak di dalam model, dan menggantikannya oleh suatu asumsi tentang bagaimana perubahan varian dengan rata-rata.
Dalam statistika, perkiraan quasi-likelihood adalah satu cara yang membolehkan untuk overdispersi. Kebanyakan sering digunakan dengan model-model untuk perhi-tungan data atau kelompok data biner, data sebaliknya menggunakan model Poisson atau distribusi binomial.
Fungsi-likelihood menggambarkan suatu fungsi yang mempunyai kemiripan sifat dengan fungsi log-likelihood, kalau tidak suatu fungsi quasi-likelihood adalah bukan log-likelihood yang cocok untuk banyak distribusi probabilitas yang sebenarnya. Mo-del quasi-likelihood dapat dicocokkan menggunakan suatu perluasan algoritma tepat
digunakan untuk model linier yang umum.
Hanya suatu hubungan antara mean dan varians sebagai pengganti menen-tukan suatu distribusi probabilitas untuk data dikhususkan pada bentuk dari su-atu fungsi varians, diberikan varians sebagai susu-atu fungsi dari mean. Umumnya, fungsi ini diberikan termasuk suatu perkiraan faktor yang dikenal sebagai parame-ter overdispersi atau parameparame-ter skala yang diperkirakan dari data. Biasanya, fungsi varians adalah suatu bentuk seperti bahan perluasan parameter overdispersi pada ke-satuan hasil dalam varians-mean berhubungan dengan suatu distribusi probabilitas yang nyata seperti Binomial atau Poisson.
Fungsi quasi-likelihood bisa digunakan untuk memperkirakan dalam cara yang sama seperti fungsi likelihood yang umum. Wedderburn (1974) dan McCullagh (1983) menunjukkan bahwa perkiraan quasi-likelihood maksimum mempunyai banyak kemiri-pan sifat tertentu untuk diteliti, perkiraan quasi likelihood maksimum dari vektor β (vektor dari parameter-parameter dalam model regresi) adalah suatu normal asimp-totis dengan rata-rata β , dan kovarians asymptotic bisa berasal dari cara yang umum dari turunan kedua matriks dari fungsi quasi-likelihood. Juga, jika distribusi dasar datang dari suatu keluarga eksponensial alami dari perkiraan quasi-likelihood maksimum memaksimalkan fungsi likelihood dan demikian itu mempunyai penuh keefisienan asimptotik. Di bawah distribusi-distribusi yang lebih umum sekitar hi-langnya efisiensi, yang telah diselidiki oleh Firth (1987) dan Hill & Tsai (1988).
Metode likelihood maksimum adalah fungsi likelihood yang berukuran maksi-mum yang merupakan suatu metode statistik populer digunakan untuk mencocokkan model statistika untuk data, dan menetapkan perkiraan-perkiraan untuk parameter-parameter model.
3
Perkiraan quasi-likelihood maksimum menggambarkan satu dari kebanyakan pendekatan penting untuk perkiraan dalam semua dari kesimpulan statistik.
Diperkenalkan perkiraan-perkiraan quasi-likelihood maksimum dari parameter-parameter tidak diketahui dari distribusi Pareto dan metoda baru yaitu perkiraan quasi-Bayesian.
Sejauh dicocokkan model menggunakan likelihood maksimum dengan maksud mengira bahwa ada suatu kemungkinan model untuk data. Tujuannya menentukan suatu mekanisme generasi data sebagai contoh data terdiri dari menghitung kejadian dalam suatu proses Poisson. Agar dikemukakan seperti suatu mekanisme, dibutuhkan ilmu pengetahuan dari proses-proses fisik petunjuk untuk data, atau pengalaman
penting dengan data serupa.
Suatu metode baru dari penerapan ilmu pengetahuan matematika diperkenalkan oleh Youssef (2009), yang meneliti kemungkinan penggunaan fungsi quasi-likelihood dalam pendekatan Bayesian yang kemudian dinamakan dengan perkiraan quasi likeli-hood. Metode ini mengurangi perkiraan Bayesian biasa jika distribusi itu adalah suatu anggota dari keluarga eksponensial. Digunakan perkiraan-perkiraan quasi-likelihood maksimum dari parameter-parameter tak diketahui dari distribusi Pareto dan metode penaksiran quasi-Bayesian.
Fungsi likelihood untuk parameter distribusi Pareto berguna dalam menemukan penaksir untuk α dan menentukan dimana bernilai nol. Penaksir likelihood maksi-mum untuk α juga dapat menaksir kesalahan pengiraan statistik. Distribusi Pareto menjadi pilihan, menurut Nolan (1998), distribusi Pareto merupakan distribusi yang digambarkan dari parameterparameter stabil yang umum, sehingga berperan untuk mendiagnosa distribusi yang stabil. Selanjutnya menurut Youssef (2009), data Pareto berperan dalam penaksiran Bayesian dan quasilikelihood, sehingga dapat diketahui perbedaan antara koefisien dari variasi penaksiran Bayesian dan penaksiran quasi-Bayesian dengan perbedaan ukuran sampel dan nilai dari parameter prior dan dapat diketahui tingkat efisiensi dari penaksiran quasi-Bayesian dari parameter α ketika k diketahui dan parameter k ketika α diketahui. Hal inilah yang mendasari penulis dalam tesis ini memilih quasi-likelihood dan quasi-Bayesian untuk menaksir parame-ter dalam distribusi Pareto.
1.2 Permasalahan
4
Kesulitan dalam memprediksi dan menaksir parameter-parameter dengan cara-cara lain dari data yang ada mendorong penulis untuk membahas penggunaan metode fungsi quasi-likelihood untuk penaksiran parameter dalam distribusi Pareto dan mem-fokuskan pada estimasi Bayesian untuk parameter parameter Pareto dan efisiensi dari estimasi quasi-Bayesian.
1.3 Tujuan Penelitian
Tesis ini bertujuan untuk meninjau kemungkinan pemakaian fungsi quasi-likelihood dalam pendekatan Bayes untuk penaksiran parameter dalam distribusi Pareto.
1.4 Manfaat Penelitian
Melalui tulisan ini diharapkan agar pemakaian fungsi quasi-likelihood dalam pendekatan Bayes dapat dimanfaatkan dalam hal-hal yang berkaitan dengan pe-naksiran yang bertepatan dengan ilmu sosial, ekonomi, sains, geofisika, maupun bi-dang lainnya.
1.5 Metodologi Penelitian
Dalam proses penyusunan tesis ini ditunjukkan untuk lebih mengenal hubungan antara fungsi quasi-likelihood, metode Bayesian dan model linier yang digunakan untuk penaksiran parameter dalam distribusi Pareto.
Tesis ini membahas penaksiran Bayesian dan quasi-likelihood untuk data Pareto dan juga efisiensi dari perkiraan quasi-Bayesian dari data parameter.
Konseptualisasi proses penulisan tersebut kemudian dituangkan menjadi suatu metode penelitian dengan analisis observasi dan pengumpulan data melalui studi pus-taka yang diperlukan untuk melukiskan fenomena tersebut. Oleh karena itu metode yang digunakan dalam penelitian ini adalah Deskriptis-Analitis.
Sesuai dengan anggapan dasar dalam penulisan tesis ini bahwa deskripsi yang di-maksudkan menggambarkan metode penaksiran Bayesian menggunakan fungsi quasi-likelihood yang digunakan untuk menaksir parameter-parameter untuk data Pareto serta mengintepretasikannya dalam suatu hasil tesis, sehingga dapat dilakukan pe-narikan dan penyusunan suatu kesimpulan.
5
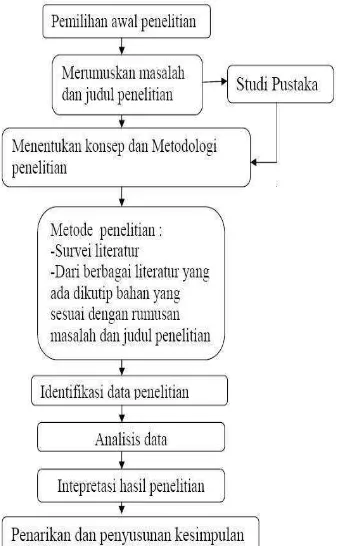
tahapan tertentu yang dibuat pada suatu alur kegiatan metode kerja penelitian yang diperlihatkan pada gambar dibawah ini :
Gambar 1.1 : Alur Kegiatan Metode Kerja Penelitian
BAB 2
TINJAUAN PUSTAKA
2.1 Fungsi Quasi-Likelihood
Menurut Wedderburn (1974), suatu likelihood didefinisikan sebagai suatu spe-sifikasi bentuk distribusi dari pengamatan-pengamatan, tetapi untuk mendefinisikan suatu fungsi quasi-likelihood dibutuhkan hanya spesifikasi suatu hubungan antara mean dan varians dari pengamatan-pengamatan sampel dan quasi-likelihood dapat kemudian digunakan untuk penaksiran. Untuk suatu log likelihood eksponensial famili satu parameter adalah sama sebagaimana quasi-likelihood dan mengikutinya bahwa menganggap suatu eksponensial famili satu parameter adalah pengandaian distribusi pendek terlemah yang dapat dibuat.
Selanjutnya McCullagh (1983), diketahui dengan baik bahwa jika fungsi likeli-hood mempunyai bentuk eksponensial famili, perkiraan likelilikeli-hood maksimum dari pa-rameter regresi dapat sering ditemukan menggunakan metode weighted least squares. Disini digunakan istilah weighted least squares dalam suatu pengertian umum agak baik : khusus perhitungan meliputi fungsi respon nonlinier dan bobot berubah-ubah dari satu iterasi ke yang berikutnya : Khusus, ketika varians dianggap konstan kuan-titas menjadi berukuran minimum adalah suatu jumlah dari sisa kuadrat, dan hasil-hasil asimptotis. Memodifikasi dan likelihood bersyarat kadang-kadang membutuhkan bentuk eksponensial. Hingga metode weighted least square boleh digunakan untuk sebagian likelihood. Untuk likelihood bersyarat dari jenis yang timbul dalam pertim-bangan dari kondisi double 2x2 atau tabel kemungkinan yang lebih besar. Pada keny-ataannya metode weighted least squares dapat digunakan untuk menemukan perki-raan likelihood maksimum merata dalam beberapa hal dimana fungsi likelihood tidak mempunyai bentuk eksponensial famili.
Selanjutnya Firth (1987), suatu metode quasi-likelihood untuk penaksiran pa-rameter dalam model regresi dimana ada beberapa anggapan berkaitan antara mean dan varian dari masing-masing pengamatan, tetapi tidak perlu suatu likelihood khusus secara lengkap, jika yang mendasari distribusi datang dari suatu eksponensial famili alami perkiraan quasi-likelihood berukuran maksimum, likelihood juga mempunyai efisiensi asymptotis yang penuh, dibawah distribusi-distribusi yang lebih umum ada beberapa kehilangan dari efisiensi. Efisiensi asymptotis dari perkiraan quasi-likelihood adalah dihitung dibawah beberapa distribusi-distribusi partikular, dan kemudian lebih
7
umum melalui suatu perkiraan untuk small departures dari eksponensial famili alami yang sesuai.
Selanjutnya McCullagh dan Nelder (1989), metode quasi-likelihood sering men-jadi kompleks dan dengan perhitungan intensif untuk mencocokkan kepasangan atau perhitungan data. Metode ini mempunyai keuntungan dari perhitungan yang relative sederhana , kecepatan dan kekuatan, sebagaimana metode-metode itu dapat digu-nakan lebih dari algoritma sesungguhnya berkembang menjadi model linier umum yang tepat.
Selanjutnya Aldrich (1997), metode likelihood maksimum sesuai untuk banyak metode perkiraan yang dikenal baik dalam statistik. Sebagai contoh, andaikan
diam-bil suatu sampel dari beberapa nomor dari tinggi orang Amerika, tetapi tidak seluruh populasi dan catatan tinggi mereka. Selanjutnya dianggap bahwa tinggi adalah dis-tribusi normal dengan beberapa mean dan varians tidak diketahui. Kemudian sampel mean adalah penaksir likelihood maksimum dari mean populasi, dan sampel varians adalah suatu perkiraan tertutup untuk penaksir likelihood maksimum dari varians populasi.
Selanjutnya Youssef (2009), meneliti penerapan penaksiran quasi-Bayesian dan quasi likelihood untuk distribusi Pareto. Pada bab IV tesis ini akan dibahas secara detail.
2.2 Model Linier Tergeneralisir
Menurut Hardin dan Hilbe (2007), dalam statistik, model linier teregeneralisasi adalah suatu generalisasi fleksibel dari paling sedikit regresi square biasa. Hubungan-nya dengan distribusi random dari ukuran variabel dari percobaan (fungsi distribusi) pada porsi sistematik (bukan random) dari percobaan (penduga linier) selanjutnya suatu fungsi dinamakan fungsi link.
8
Model linier tergeneralisasi diformulasikan oleh Nelder dan Wedderburn sebagai suatu cara menyatukan variasi model-model statistika yang lain, termasuk regresi linier, regresi logistik dan regresi Poisson, dibawah satu kerangka. Hal ini memberikan mereka untuk mengembangkan suatu algoritma umum untuk penaksiran likelihood maksimum dalam semua model ini. Perluasannya natural meliputi banyak model-model lain yang baik.
Dalam suatu model linier tergeneralisasi, masing-masing menghasilkan variabel tak bebas, Y dianggap menjadi generasi dari suatu fungsi distribusi khusus dalam eksponensial famili, suatu range yang besar dari distribusi probabilitas termasuk distribusi-distribusi normal, binomial dan poisson, diantara yang lain. Mean(µ) dari distribusi itu bergantung pada variabel bebas X, berikutnya: E(Y) = µ=g−1(Xβ)
DimanaE(Y) adalah nilai perkiraan dariY;Xβ adalah penduga linier, suatu kombi-nasi linier dari parameter tak diketahui β; g adalah fungsi link. Dalam kerangka ini, varians adalah suatu fungsi khusus V, dari mean: Var(Y) = V(µ) = V = V(g−1(Xβ)). Tepat jikaV mengikuti dari distribusi eksponensial famili, tetapi boleh
disederhanakan menjadi varians adalah suatu fungsi dari nilai prediksi.
Parameter tak diketahui β adalah perkiraan khusus dengan likelihood maksimum, quasi-likelihood maksimum, atau teknik Bayesian.
2.3 Statistika Bayes
Menurut Berger (1985), dalam teori penaksiran dan teori keputusan, suatu pe-naksir Bayes atau suatu peraturan Bayes adalah suatu pepe-naksir atau peraturan kepu-tusan bahwa ukuran minimum nilai pengharapan posterior dari suatu loss fungsi (pos-terior expected loss). Ekuivalen, ukuran maksimum pos(pos-teriornya dari suatu fungsi utilitas.
Selanjutnya menurut Lehman dan Casella (1998), andaikan suatu parameter tak diketahuiθ adalah mengetahui suatu distribusi priorπ. Memperkirakanσ =σ(x) menjadi suatu penaksir dari θ (didasarkan pada beberapa ukuranx), dan memperki-rakan L(θ, σ) menjadi suatu loss fungsi, seperti squared error. Resiko Bayes dari σ didefinisikan Eπ{L(θ, σ)}, dimana pengharapan diambil melebihi distribusi probabi-litas dari θ : fungsi resiko didefinisikan sebagai suatu fungsi dari σ. Suatu penaksir σ diketahui menjadi suatu penaksir jika ukuran minimumnya resiko Bayes diantara semua penaksir. Ekuivalen, penaksir yang mana ukuran minimum posterior expected loss E{L(θ, σ)|x} untuk masing-masing x juga ukuran minimum resiko Bayes dan
9
oleh karena itu adalah suatu penaksir Bayes.
Jika prior adalah tidak layak kemudian suatu penaksir yang posterior expected loss berukuran minimum untuk masing-masingxdinamakan suatu penaksir Bayes tergen-eralisir.
Contoh : penaksiran minimum mean square error.
Kebanyakan fungsi resiko yang lazim digunakan untuk penaksiran Bayesian adalah mean square error (MSE), juga dinamakan squared error risk. MSE didefinisikan se-bagaiMSE =E[(ˆθ(x)θ)].
Dimana pengharapan diambil melebihi distribusi joint dari θ dan x.
Menggunakan MSE sebagai resiko, perkiraan Bayes dari parameter tak diketahui
adalah mean simpel dari distribusi posterior, ˆθ(x) =E[θ|X] =R
θf(θ|x)dθ. Dikenal sebagai penaksir minimum mean square error (MMSE). Resiko Bayes dalam hal ini adalah varians posterior.
Selanjutnya menurut Walpole (2007), metode klasik dari perkiraan dipelajari be-gitu jauh semata-mata didasarkan pada informasi yang diberikan oleh sampel random. Metode ini pada dasarnya menafsirkan probabilitas sebagai frekuensi relatif. Sebagai contoh, pada kedatangan 95% interval kepercayaan untuk p, pernyataan ditafsirkan: P(−1,96 < Z < 1,96) = 0,95 untuk mean 95% dari waktu dalam percobaan yang berulang-ulang Z akan turun antara -1,96 dan 1,96. Karena Z = σ/x−µ¯√
n. Untuk suatu
sampel normal dengan varians diketahui, pernyataan probabilitas disini berarti bahwa 95% dari interval random (¯x−1,96σ/√nx¯+ 1,96σ/√n) berisi kebenaran rata-rata. Pendekatan lain untuk metode statistik perkiraan dinamakan metodologi Bayesian.
Menggunakan metodologi Bayesian dapat diperoleh distribusi posterior dari pa-rameter. Penaksiran Bayes dapat juga diperoleh menggunakan distribusi posterior ketika mendatangkan suatu fungsi loss. Misalnya, perkiraan Bayes yang terpopuler digunakan adalah dibawah squared-error loss function yang mirip dengan least squares estimates. Rata-rata dari distribusi posterior π(θ|X), menunjukkan θ∗, dinamakan
perkiraan Bayes dari θ, dibawah squared- error loss function.
BAB 3
DISTRIBUSI PARETO
Menurut Nolan (1998), distribusi Pareto adalah distribusi yang mempunyai per-aturan atau hukum yang stabil, sehingga berperan untuk mendiagnosa distribusi yang stabil.
Selanjutnya menurut Reed (2001), distribusi Pareto adalah distribusi probabi-litas yang kontinu.
Pada bab ini akan dibahas hal-hal yang berkaitan dengan distribusi Pareto an-tara lain: prinsip Pareto, hubungan distribusi Pareto dengan distribusi yang lain, penaksiran parameter dalam distribusi Pareto dan yang terakhir adalah aplikasi dis-tribusi Pareto.
3.1 Prinsip Pareto
Menurut Bunkley (2008), distribusi Pareto diistilahkan sebagaimana nama ahli ekonomi Italia Vilpredo Pareto, merupakan suatu distribusi probabilitas yang memi-liki peraturan yang kuat bertepatan dengan ilmu sosial, sains, geofisika, yang ber-hubungan dengan penaksiran dan banyak tipe-tipe yang lain dari fenomena yang tampak.
Prinsip Pareto (juga dikenal sebagai 20-80 peraturan, beberapa peraturan vital, dan prinsip dari sparsity faktor) menyatakan, banyak kejadian kira-kira 80 persen dari efek yang berasal dari 20 persen dari penyebab. Diamati bahwa 80 persen dari tanah di Itali dimiliki oleh 20 persen dari populasi. Dengan matematika, dimana sesuatu dibagi diantara suatu kumpulan peserta yang besar dengan cukup, berada di suatu nomor k diantara 50 dan 100 seperti k persen, diambil (100-k) persen dari peserta. k boleh berubah-ubah dari 50 (dalam kasus dari distribusi yang sama) mendekati 100 (ketika satu nomor kecil dari perhitungan peserta untuk hampir semua dari sumber). Tidak ada yang spesial tentang angka 80 persen dengan matematika, tetapi banyak sistem yang nyata mempunyai tempatk sekitar daerah ini dari lanjutan ketidakseimbangan dalam distribusi.
Prinsip Pareto dapat juga berkenaan dengan efisiensi Pareto, yang mana juga diperkenalkan oleh ahli ekonomi yang sama. Pareto dihasilkan kedua konsep dalam
11
hubungan dari distribusi penghasilan dan kekayaan diantara populasi.
3.2 Hubungan Distribusi Pareto dengan Distribusi yang Lain
Distribusi Pareto mempunyai beberapa hubungan dengan distribusi yang lain, antara lain:
1. Hubungannya dengan distribusi eksponensial
Distribusi Pareto dihubungkan sebagai mengikuti distribusi eksponensial. An-daikanX adalah distribusi Pareto dengan minimumχm dan indexα. Misalkan
Y = log
X χm
KemudianY adalah distribusi eksponensial dengan intensitasα, atau ekuivalen dengan nilai pengharapan 1/α:
P r(Y > y) =e−αy
Ekuivalen, jikaY adalah distribusi eksponensial dengan intensitasα, kemudian χmeY adalah distribusi Pareto dengan minimumχm dan index α
2. Hubungannya dengan distribusi kondisional
Distribusi probabilitas kondisional dari suatu variabel random distribusi Pareto, diberikan kejadian bahwa lebih besar dari atau sama dengan suatu nomor par-tikularχ1 melebihi χm adalah suatu distribusi Pareto dengan index Pareto α,
tetapi dengan minimumχ1 sebagai pengganti χm.
3. Hubungannya dengan Zipfs law
Menurut Reed (2001), distribusi pareto adalah distribusi probabilitas yang kon-tinu. Zipfs law, juga kadang-kadang dinamakan distribusi zeta, boleh dipikirkan sebagai suatu perimbangan yang berlainan dari distribusi Pareto.
12
3.3 Penaksiran Parameter Distribusi Pareto
Menurut Wedderburn (1974), fungsi likelihood untuk parameter distribusi Pareto α dan χm, diberikan suatu sampel χ= (χ1, χ2, . . . , χn) adalah Oleh karena itu, fungsi likelihood logaritmik adalah
l(α, χm) =nlnα+nαlnχm−(α+ 1) n
X
i=1
lnχi
Dapat dilihat bahwa l(α, χm) adalah bertambah secara monoton dengan χm, nilai
yang lebih besar dari χmnilai yang lebih besar dari fungsi likelihood. Karenanya,
sejak χ≥χm disimpulkan bahwa ˆχm = min i χi.
Untuk menemukan penaksir untuk α, dihitung sesuai derivatif sebagian dan menen-tukan dimana bernilai nol:
∂ℓ
Jadi penaksir likelihood maksimum untuk α adalah:
ˆ
α= P n
i(lnχi−ln ˆχm)
Kesalahan pengiraan statistik adalah:
∂ = √αˆ
n
3.4 Aplikasi Distribusi Pareto
Distribusi Pareto dapat diaplikasikan dalam berbagai bidang keilmuan yang berhubungan dengan penaksiran, antara lain:
1. Dalam bidang ekonomi.
Menurut Krugman (2006), prinsip Pareto juga digunakan untuk atribut pele-baran ketidaksamarataan ekonomi dalam ”USA to skill-biased technical change” yaitu pertumbuhan penghasilan bertambah untuk itu dengan pendidikan dan keterampilan diperlukan untuk mengambil keuntungan dari teknologi baru dan globalisasi. Bagaimanapun pemenang hadiah nobel dalam bidang ekonomi Paul Krugman dalam New York Times menghilangkan ”80-20 buah pikiran yang ke-liru” sebagaimana disebutkan ”tidak karena itu benar, tetapi karena itu menye-nangkan”. Ditegaskan bahwa manfaat dari pertumbuhan ekonomi 30 tahun terakhir sebagian besar dikonsentrasikan pada paling atas 1 persen, daripada paling atas 20 persen.
13
2. Dalam bidang software.
Menurut Gen dan Cheng (2002), pada ilmu pengetahuan komputer dan teori pengawasan keteknikan seperti untuk energi elektromekanik, prinsip Pareto da-pat digunakan untuk optimisasi usaha. Selanjutnya menurut Rooney (2002), mikrosoft juga dicatat bahwa bahan-bahan perlengkapan paling atas 20 persen dari laporan kerusakan, 80 persen dari kesalahan dan benturan akan dihilangkan. Selanjutnya menurut Slusallek (2009), pada komputer grafik prinsip Pareto di-gunakan untuk sinar jiplakan 80 persen, dari geometri sinar silang-menyilang 20 persen.
3. Dalam bidang logistik dan pengawasan kualitas produksi.
Menurut Rushton dan Croucher (2000), prinsip Pareto banyak digunakan pada pengawasan kualitas. Sebagai dasar untuk grafik Pareto, satu dari kunci alat yang digunakan pada pengawasan kualitas total dan six sigma. Prinsip Pareto berguna sebagai suatu garis dasar untuk analisis ABC dan analisis XYZ, di-gunakan dalam logistik secara luas dan usaha mendapatkan untuk maksud op-timisasi persediaan dari barang-barang, sebaik harga pemeliharaan dan per-lengkapan persediaan
4. Dalam bidang kesehatan
Menurut Weinberg (2009), pada pemeliharaan kesehatan di Amerika, ditemukan bahwa 20 persen dari pasien menggunakan 80 persen dari sumber pemeliharaan kesehatan.
5. Dalam bidang Geofisika
Menurut Nassim (2007), prinsip Pareto adalah suatu gambaran dari suatu hubun-gan ”power law”, yang mana juga terjadi pada fenomena seperti pemadaman api dan gempa bumi. Karenanya persis diatas suatu daerah magnitudo yang luas, dihasilkan perbedaan hasil yang lengkap. Prinsip Pareto juga dapat digunakan untuk menaksir nilai dari cadangan minyak dalam lahan minyak (beberapa la-han yang besar, banyak lala-han yang kecil).
BAB 4
PENAKSIRAN BAYESIAN UNTUK PARAMETER PARETO MENGGUNAKAN FUNGSI QUASI-LIKELIHOOD
Pada bahasan ini, penulis hanya meninjau penelitian yang telah dilakukan oleh Youssef (2009) yang telah meneliti penaksiran Bayesian untuk parameter Pareto menggunakan fungsi quasi-likelihood. Digunakan penaksiran quasi-likelihood maksi-mum parameter tak diketahui dari distribusi Pareto. Penaksiran Bayesian dan quasi-likelihood untuk data Pareto beberapa ukuran sampel dari parameter prior dan juga efisiensi dari penaksiran quasi-Bayesian dari parameterα ketikak diketahui dan pa-rameterk ketikaα nya diketahui.
4.1 Penaksiran Quasi-Bayesian
Dalam bagian ini, penaksiran quasi-Bayesian saat ini, dihadirkan suatu teknik penaksiran Bayesian yang baru. Didapat penerapannya tanpa penetapan fungsi quasi-likelihood dari pengamatan-pengamatan sampel, jika mengetahui hubungan antara rata-rata dan varians. Untuk membangun distribusi Pareto fungsi likelihood bisa digantikan dengan eksponensial alami dari fungsi quasi-likelihood. Metoda ini men-gurangi estimasi Bayesian yang umum, jika quasi-likelihood dan fungsi log-likelihood adalah identik.
Misalkan x1, x2, . . . , xn menjadi suatu sampel random bebas, dengan rata- rata
µ=µ(θ), dimanaθ adalah suatu vektor dari parameter dan varians var (x) =ϕV(µ), dimana V(µ) adalah beberapa fungsi varians yang diketahui dan ϕ adalah suatu penyebaran parameter yang dapat diketahui atau tidak diketahui. Quasi likelihood Q(x;µ, ϕ) dapat menjadi penetapan hubungan
dan eksponensial alami dariQ(x;µ, φ) digunakan sebagai fungsi likelihood.
Menggunakan suatu densitas prior yang sesuai g(θ, φ) distribusi posterior f∗∗(θ, φ x)
dapat menjadi konsepsi sebagai
f∗∗(θ, φ|x)α
15
raan Bayes untuk θ densitas marginal mungkin dihasilkan dari (4.1.2) oleh peng-gabungan satu atau lebih dari parameter tak diketahui, kumpulan yang lain dari perkiraan Bayes untuk parameter tak diketahui dapat diberlakukan dengan respek untuk beberapa fungsi yang hilang, menggunakan densitas marginal.
Sekarang, digunakan metode diatas untuk suatu fungsi varians sederhana. An-daikan x1, x2, . . . , xn adalah sampel acak bebas dari suatu distribusi tak diketahui
dan andaikan varian dan rata-rata diketahui menjadi sebanding dan tetap dari kese-bandinganθ = 1, sehingga
E(x|µ) = µdan Var = (x|µ) = µV(µ) (4.1.3)
Dimana V(µ) merupakan fungsi varian dari (4.1.1), dimiliki
Q(x;µ) = logµ−µdan exp[Q(x;µ)] =µxθ−µ (4.1.4)
Agar membangun suatu distribusi posterior, suatu densitas prior konjuget alami dari µadalah
g(µ) = 1 µΓν (µν)
v
e−µv, ν > 0, µ > 0 (4.1.5)
Menggunakan (4.1.4) dan (4.1.5), fungsi distribusi probabilitas posterior (p.d.f) dari µadalah
Ini, berhubungan dengan suatu pengkuadratan, loss function, penaksir quasi-Bayesian adalah rata-rata posterior untuk (4.1.6) yaitu
µ∗∗ =E(µ/x) =
Resiko Bayes dari µ∗∗ adalah
16
Penaksir Bayes yang lain adalah mode dari posterior p.d.f (2.5) yaitu
µ= θ0−1
λ (4.1.9)
Mungkin dicatat bahwa fungsi varians V(µ) = µ adalah dihubungkan dengan distribusi Poisson yang mana adalah suatu anggota dari eksponensial famili dan juga eksponensial alami dari quasi-likelihood dan fungsi likelihood adalah sama dan ini membuat hasil quasi-Bayesian identik dengan hasil Bayesian biasa.
4.2 Penaksiran Quasi-Likelihood untuk Distribusi Pareto
Dalam bagian ini, didapat penaksiran quasi-likelihood maksimum dan penaksiran Quasi-Bayesian untuk parameter tak diketahui dari distribusi pareto. Distribusi ini sangat berguna dalam fungsi quasi-likelihood untuk penaksiran parameter karenanya fungsi quasi-likelihood dan loglikelihoodnya berbeda, dan prediksi memungkinkan un-tuk dibuat perbandingan antara metode quasi-Bayesian dan penaksiran likelihood Bayesian.
4.2.1 Penaksiran Quasi-Likelihood
Anggap p.d.f dari distribusi Pareto diberikan oleh
f(y) =αkαy−(α+1), α >0, y ≥k >0 (4.2.1) Dimana V(µ) = µ2 adalah fungsi varians. Jadi untuk suatu sampel dari ukuran n,
fungsi quasi-likelihood diberikan oleh
17
Substitusi untuk µ dari (4.2.2) pada (4.2.5), fungsi quasi-likelihood (4.2.5) sebagai suatu fungsi dari α, k, menjadi
Q(y;k, α) = −α−1
Penaksiran quasi-likelihood maksimum dari α, k diperoleh mengikuti
∂Q
Persamaan diatas menjadi nol, didapatkan perkiraan quasi-likelihood dari α, ditun-jukkan oleh ˜α sebagai
˜
Berikutnya, karena k adalah suatu batas bawah pada variabel random y, Q(y, k, α) menjadikan subyek harus menjadi berukuran maksimal
˜
k ≤minyi (4.2.9)
Diperiksa nilai dari ˜k yang berukuran maksimum (4.2.6) subyek ke (4.2.9) adalah
˜
k = minyi (4.2.10)
Hingga (4.2.8) dan (4.2.10) memberikan penaksiran quasi-likelihood maksimum dari α dan k.
Perhatikan bahwa ˜k adalah penaksiran likelihood maksimum dari k, tetapi bukan ˜α,
nα
(n−2) perkiraan yang sama (4.2.8), dan (4.2.10), dapat diperoleh dari hubungan fungsi
quasi-likelihood yang diperluas dengan fungsi varians (4.2.3).
4.2.2 Penaksiran Quasi-Bayesian untuk Distribusi Pareto
Dalam sub bagian ini, metode penaksiran quasi-Bayesian diterapkan pada disitribusi Pareto. Dari (4.2.6), eksponensial alami dari fungsi quasi-likelihood untuk suatu sampel dari ukuran n pengamatan dari distribusi Pareto diberikan oleh
18
Sekarang, didapat tiga distribusi posterior dari α dan k; dimana α diketahui dank tidak diketahui, ketika k diketahui danα tidak diketahui, dan ketika keduanya α dan k tidak diketahui.
Kasus (1) : α diketahui dan k tidak diketahui
Karena α diketahui dan k tidak diketahui, suatu P.d.f prior dari k diberikan oleh (4.2.12), sebagai
f1(k) =a0b0−a0ka0−1 0< k < b0 (4.2.12)
Dimana a0, b0 adalah positif. Dari (4.2.11) dan (4.2.12) posterior P.d.f dari k adalah
f∗
yaituA1 adalah suatu fungsi gamma tidak lengkap, dan sudah diperhitungkan
menu-rut umenu-rutan angka. Mode dari (4.2.13), yang mana adalah suatu perkiraan Bayes dari k adalah
Juga, median dari (4.2.13) adalah perkiraan Bayes yang lain darik dan diberikan oleh
k∗∗
Dimana k∗∗ adalah median dari (4.2.13)
Bahkan perkiraan Bayes yang lain dari k adalah mean dari posterior p.d.f (4.2.13), yaitu
E(k/α, y) = 1 A1
kD2+1e−D3/k∂k= 0,5 (4.2.17)
Yang berhubungan dengan resiko Bayes adalah varians dari p.d.f posterior (4.2.13), yaitu
Median, mean dan varians diberikan berturut-turut oleh (4.2.16), (4.2.13) dan (4.2.18).
19
Kasus (2) : α tidak diketahui dan k diketahui
Karena k diketahui dan α tidak diketahui, dibolehkan menggunakan f(α) = ααco−1
e−d0α, α >0 sebagai suatu p.d.f prior dari α, sehingga
f2(α) =ααco−1e−d0α, α >0 (4.2.19)
Dimana c0, d0 adalah positif. Jadi, p.d.f posterior dari α adalah
f∗
k dan A2 adalah konstanta normal, diberikan oleh
A2 =
Mode dari (4.2.20), diberikan oleh
d0(α∗)3−(n+D5 +d0) (α∗)2+ (D5 +D6)α∗−D6 = 0 (4.2.22)
Juga, median dari (4.2.20) diberikan oleh
Z ε∗∗
Bahkan perkiraan Bayes yang lain dari k adalah mean posterior dan varians dari (4.2.20) adalah
Mode, median, mean dan varians berturut-turut diberikan oleh (4.1.9), (4.2.23), (4.2.24) dan (4.2.25). Dihitung perkiraan quasi-Bayesian dan koefisien dari variasi untukk ketikaα diketahui yang diberikan oleh (4.2.17) dan (4.2.18) juga sesuai hasil yang didapatkan dari perkiraan Bayesian dan hasil ini didaftar pada tabel (4.1). Tabel (4.2) ringkasan hasil dari Bayesian dan perkiraan quasi-Bayesian untukαketika k diketahui, yang diberikan oleh (4.2.24) dan (4.2.25).
Tabel, (4.3) dan (4.4) dengan berurutan memberi efisiensi dari perkiraan quasi-Bayesian dari k ketika α diketahui, dan dariα ketikak diketahui.
20
Tabel 4.1 : Penaksiran Bayesian dan Quasi-Likelihood untuk Data Pareto untuk k ketika α diketahui (α = 2). (Menurut Youssef, 2009)
Ukuran Sampel n= 10 n= 20 n= 30
Parameter Koefisien Koefisien Koefisien
Variasi Penaksiran Variasi Penaksiran Variasi Penaksiran
Prior Bayes Quasi-Bayes Bayes Quasi-Bayes Bayes Quasi-Bayes
a0 b0 dari k darik dari k darik dari k darik
1 1 0,0465 0,1640 0,0326 0,1630 0,0161 0,0912
2 2 0,0443 0,1554 0,0239 0,1549 0,0156 0,0910
0,5 3 0,0471 0,1703 0,0246 0,1640 0,0190 0,0980
0,42 3,1 0,0476 0,1709 0,0246 0,1656 0,0163 0,0981
0,6 3,1 0,0472 0,1690 0,0244 0,1652 0,0160 0,0931
1 3,2 0,0453 0,1625 0,0240 0,1632 0,0157 0,0914
2 3 0,0406 0,1516 0,0236 0,1548 0,0153 0,0872
3 3,5 0,0432 0,1394 0,0231 0,1459 0,0151 0,0834
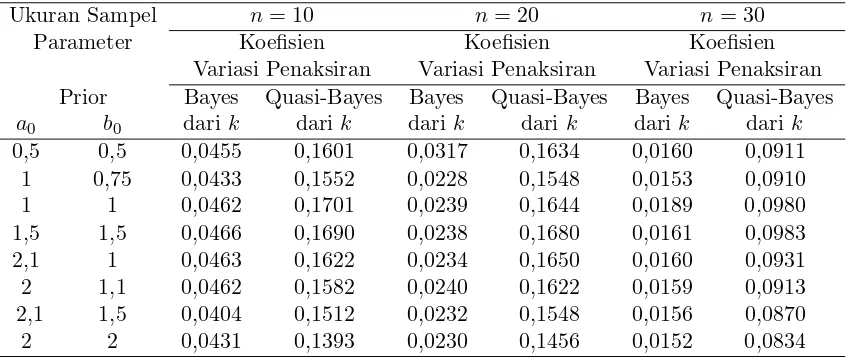
Tabel 4.2 : Penaksiran Bayesian dan Quasi-Likelihood untuk Data Pareto untuk α ketika k diketahui (k= 2). (Menurut Youssef, 2009)
Ukuran Sampel n= 10 n= 20 n= 30
Parameter Koefisien Koefisien Koefisien
Variasi Penaksiran Variasi Penaksiran Variasi Penaksiran
Prior Bayes Quasi-Bayes Bayes Quasi-Bayes Bayes Quasi-Bayes
a0 b0 dari k darik dari k darik dari k darik
0,5 0,5 0,0455 0,1601 0,0317 0,1634 0,0160 0,0911
1 0,75 0,0433 0,1552 0,0228 0,1548 0,0153 0,0910
1 1 0,0462 0,1701 0,0239 0,1644 0,0189 0,0980
1,5 1,5 0,0466 0,1690 0,0238 0,1680 0,0161 0,0983
2,1 1 0,0463 0,1622 0,0234 0,1650 0,0160 0,0931
2 1,1 0,0462 0,1582 0,0240 0,1622 0,0159 0,0913
2,1 1,5 0,0404 0,1512 0,0232 0,1548 0,0156 0,0870
2 2 0,0431 0,1393 0,0230 0,1456 0,0152 0,0834
Tabel (4.1) dan (4.2) menunjukkan bahwa perbedaan antara koefisien dari variasi penaksiran Bayesian dan penaksiran quasi-Bayesian adalah kecil, selanjutnya pengu-rangan ukuran sampel yang berbeda dan nilai dari parameter prior bertambah. Juga, koefisien variasi penaksiran quasi-Bayesian dari α adalah lebih kecil dari koefisien variasi penaksiran Bayesian dariα.
Tabel (4.3) menunjukkan penaksiran quasi-Bayesian dari parameter k mempunyai suatu efisiensi relatif rendah pada perkiraan Bayesian, juga efisiensi berkurang seba-gaimana penambahan ukuran sampel.
21
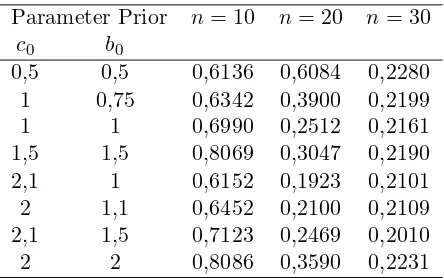
Tabel 4.3 : Efisiensi Penaksiran Quasi-Bayesian dari Parameterα ketikak diketahui (k = 3). (Menurut Youssef, 2009)
Parameter Prior n= 10 n= 20 n= 30
c0 b0
0,5 0,5 0,6136 0,6084 0,2280
1 0,75 0,6342 0,3900 0,2199
1 1 0,6990 0,2512 0,2161
1,5 1,5 0,8069 0,3047 0,2190
2,1 1 0,6152 0,1923 0,2101
2 1,1 0,6452 0,2100 0,2109
2,1 1,5 0,7123 0,2469 0,2010
2 2 0,8086 0,3590 0,2231
Tabel 4.4 : Efisiensi Penaksiran Quasi-Bayesian dari Parameterk ketikaα diketahui (α = 2). (Menurut Youssef, 2009)
Parameter Prior n= 10 n= 20 n= 30
c0 b0
1 1 0,1158 0,0620 0,0381
2 2 0,1173 0,0363 0,0371
0,5 3 0,1126 0,0365 0,0425
0,42 3,1 0,1147 0,0367 0,0312
0,6 3,1 0,1147 0,0363 0,0372
1 3,2 0,1150 0,0360 0,0380
2 3 0,1172 0,0368 0,0399
3 3,5 0,1270 0,0375 0,0415
Tabel (4.4) menunjukkan penaksiran quasi-Bayesian dari parameter α mempunyai suatu efisiensi yang tinggi bahkan untuk ukuran sampel yang kecil dan nilai yang besar dari parameter prior. Tetapi efisiensi berkurang sebagaimana ukuran sampel bertambah.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Tesis ini mendiskusikan metode fungsi quasi-likelihood untuk penaksiran param-eter dalam distribusi Pareto. Pemakaian fungsi quasi-likelihood dalam pendekatan Bayes untuk penaksiran parameter dalam distribusi Pareto dapat dimungkinkan, karena mempunyai kelebihan yaitu : hanya dibutuhkan spesifikasi suatu hubungan an-tara mean dan varians dari pengamatan-pengamatan sampel. Selanjutnya, penaksiran quasi-Bayesian dari parameter a mempunyai suatu efisiensi yang tinggi bahkan un-tuk ukuran sampel yang kecil dan nilai yang besar dari parameter prior. Kelemahan metode penaksiran quasi-Bayesian dari parameter α adalah efisiensi berkurang seba-gaimana ukuran sampel bertambah.
Penaksiran parameter menggunakan prinsip Pareto (20-80 peraturan) sudah banyak diaplikasikan dalam berbagai bidang, seperti : ekonomi, sosial, sains, dan geofisika.
5.2 Saran
Pemakaian fungsi quasi-likelihood dalam pendekatan Bayes untuk penaksiran parameter dalam distribusi Pareto sebaiknya dipakai untuk ukuran sampel yang tidak terlalu besar agar efisiensinya tinggi.
DAFTAR PUSTAKA
Aldrich, J (1997), ”R.A. Fisher and The making of maximum likelihood 1912-1922”. Statistical Science 12 (3) : pp 162-176.
Berger, J.O (1985), Statistical decision theory and Bayesian Analysis (2nd ed.), New York. ISBN O-387-96098-8.
Bunkley, N (2008), ”Joseph Juran, 103, Pioneer
in Quality Control, Dies”, NewYorkTimes,
http://www.nytimes.com/2008/03/03/business/03juran.html.
Firth, D (1987), ”On the efficiency of quasi-likelihood estimation”. Biometrika, vol 74, No.2,pp.233-245.
Gen,M.; Cheng,R (2002), Genetic Algorithms and Engineering Optimization, New York : Wiley.
Hardin, J; Hilbe, J (2007), Generalized Linear Models and Extensions (2nd ed.). College Station : Stata Press. ISBN 1597180149.
Hill, J.R and Tsai, C.L (1988) ”Calculating the efficiency of maximum quasi-likelihood estimation”,Apple Statist. 37,2,219 -230.
Krugman, P (2006), ”Graduates versus Oligarchs”.New York Times : pp. A19.
Lehman, E.L; Casella, G (1998), Theory of Point Estimation. Springer.p. 2nd ed. ISBN O-387-98502-6.
McCullagh, P (1983), ”Generalized linear models”. London:Chapman and Hall.
McCullagh, P and Nelder, J.A (1989), Generalized linear models.(Second ed.) London: Chapman and Hall. ISBN O-412-31760-5.
Nassim,T (2007), ”Black Swan and Domains of Statistics”, The American Statis-cian, Vol. 61, No. 3.
Nolan, J.P (1998), ”Parameterizations and modes of stable distributions”,Stat. Prob. Letters 38 : 187 - 195
Reed, W. J (2001), ”The Pareto, Zipf and other power laws”. Economic Letters 74 (1) : 15-19.
Rooney, P (2002), Microsofts CEO : 80-20 Rule Applies To Bugs, Not Just Features, Channel Web,http://www.crn.com/security/18821726.
Rushton, A; Oxley, J; Croucher, P (2000), The handbook of logistics and distri-bution management (2nd ed.), London: Kogan Page, ISBN 9780749433659.
Slusallek, P (2009), Ray Tracing Dynamic Scenes,
http://graphics.cs.unisb.de/new/fileadmin/cguds/courses/ws0809/ cg/slides/CG04-RT-III.pdf.
Walpole, R. E (2007), Probability & Statistics for Engineers & Scientists, eight ed, Pearson Prentice Hall, Education, Inc.
Wedderburn , R.W. M (1974), ”Quasi-likelihood function, generalized linear models, and the Gauss-Newton method”.Biometrika 61, 439-447.
Weinberg, M (2009), In health-care reform, the 20-80 solution, http://www.projo.com/opinion/contributors/content/CT wein-berg27 07-27-09 HQF0P1E v15.3f89889.html.
24
Youssef, M.S (2009), ”Bayesian Estimation for the Pareto Parameters Using Quasi-Likelihood Function”Applied Mathematical Sciences, Vol. 3, no. 11, 509-517