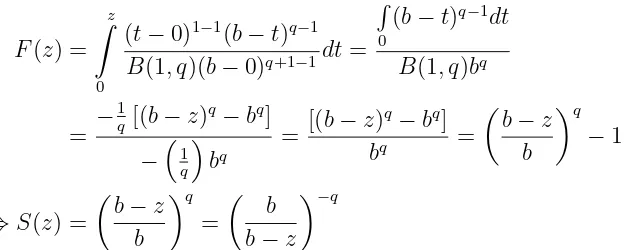PEMODELAN MEAN RESIDUAL LIFE DENGAN
ADANYA RESIKO PERSAINGAN
TESIS
Oleh AMALIA 097021082/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PEMODELAN MEAN RESIDUAL LIFE DENGAN
ADANYA RESIKO PERSAINGAN
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh AMALIA 097021082/MT
Judul Tesis : PEMODELAN MEAN RESIDUAL LIFE DENGAN ADANYA RESIKO PERSAINGAN
Nama Mahasiswa : AMALIA Nomor Pokok : 097021082
Program Studi : Magister Matematika
Menyetujui, Komisi Pembimbing
(Prof. Dr. Herman Mawengkang) (Prof. Dr. Opim Salim S, M.Sc)
Ketua Anggota
Ketua Program Studi Dekan
Telah diuji pada
Tanggal 19 Januari 2012
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Herman Mawengkang Anggota : 1. Prof. Dr. Opim Salim S, M.Sc
PERNYATAAN
PEMODELAN MEAN RESIDUAL LIFE DENGAN ADANYA RESIKO PERSAINGAN
TESIS
Saya mengakui bahwa tesis ini hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sumbernya.
Medan, 19 Januari 2012 Penulis
ABSTRAK
Penambahan konstan resiko bersaing biasanya sering meningkatkan peranan re-liability dan analisis survival. Hal ini sering disebut mengangkat, sebagai efek untuk meningkatkan fungsi tingkat hazard (HR) yang konstan. Tentu saja peruba-han bentuk ini mengubah titik balik dari fungsi hazard (HR). Namun menaiknya fungsi hazard (HR) tidak berarti menurunkan fungsi mean residual life (MRL) yang konstan. Penting untuk memeriksa perubahan bentuk fungsi mean residual life (MRL) dan dalam lokasi titik-titik balik yang dihasilkan dari fungsi hazard (HR).
ABSTRACT
The addition of a constant competing risk corresponding to an additional, usually less significant, source of failure, frequently improves the fit in reliability and sur-vival analysis. This is often termed a lift, as the effect is to increase the hazard rate (HR) function by a constant, which does not, of course, change the shape and hence the turning points of the HR function. However, lifting the HR function does not, in general, mean lowering the corresponding mean residual life (MRL) function by a constant. Hence, it is of interest to examine the changes in the shape of the MRL function, and in the locations of its turning points, resulting from a lift in the HR function.
KATA PENGANTAR
Dengan ucapan puji syukur kehadirat Tuhan Yang Maha Esa atas berkat dan karunia-Nya yang telah diberikkan kesempatan sehingga penulis dapat menye-lesaikan tesis ini dengan judul Pemodelan Mean Residual Life Dengan Adanya Resiko Persaingan.
Tesis ini merupakan salah satu persyaratan penyelesaian studi pada program studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
Pada kesempatan ini penulis menyampaikan terima kasih dan penghargaan yang sebesar-besarnya kepada:
Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara
Dr. Sutarman, M.Sc selaku Dekan Fakultas Matematika dan Ilmu Penge-tahuan Alam.
Prof. Dr. Herman Mawengkangselaku ketua Program Studi Magister Mate-matika FMIPA Universitas Sumatera Utara dan juga sebagai pembimbing pada penulisan tesis ini yang berkat dorongan dan bantuan beliau sehingga penulisan tesis ini dapat diselesaikan.
Prof. Dr. Opim Salim, S, M.Sc juga sebagai pembimbing dalam penulisan tesis ini.
Dr. Saib Suwilo, M.Sc selaku pembanding atas saran dan bantuannya untuk kesempurnaan penulisan tesis ini serta bimbingan selama perkuliahan berlang-sung.
Seluruh Staf Pengajarpada Program Studi Magister Matematika FMIPA Uni-versitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan.
Ibu Misiani, S.Siselaku Staf Administrasi Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
Seluruh sahabat dan rekan-rekan seperjuangan mahasiswa angkatan 2010 atas kebersamaan dan bantuan dalam mengatasi masalah selama perkuliahan berlangsung.
Secara khusus penulis menyampaikan rasa terima kasih kepada orang tua penulis Ayahanda tercinta (Alm.) Syamsuddin Bahasan dan Ibunda Zuraida ser-ta kepada abang dan kakak, terimakasih aser-tas dorongan dan perhatiannya yang disertai dengan doa-doanya yang tulus, sehingga penulis dapat menyelesaikan pen-didikan ini.
Semoga tesis ini dapat bermanfaat bagi pembaca, dan pihak-pihak lain yang memerlukannya. Tentunya sebagai manusia tidak pernah luput dari kekurangan sehingga tulisan ini jauh dari sempurna.
Medan, Januari 2012 Penulis,
RIWAYAT HIDUP
DAFTAR ISI
Halaman
PERNYATAAN i
ABSTRAK ii
ABSTRACT iii
KATA PENGANTAR iv
RIWAYAT HIDUP vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
BAB 1 PENDAHULUAN 1
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Tujuan Penelitian 2
1.4 Manfaat Penelitian 3
1.5 Metode Penelitian 3
BAB 2 FUNGSI MEAN RESIDUAL LIFE 4
2.1 Sifat-Sifat Peluang 4
2.1.1 Identitas dasar 4
2.1.2 Batas untuk fungsi MRL 6
2.1.3 Sifat dari MRL (formula invers) 7 2.2 Fungsi MRL untuk Distribusi Spesifik 9
2.2.1 Linier MRL 9
3.2 Perbandingan Fungsi MRL dan Mengubah Titik 13
3.3 Reliability 13
3.4 Fungsi Hazard 15
3.5 Fungsi Analisis Survival 16
3.6 Distribusi Weibull 16
3.7 Weibull Proportional Hazard Model 18 3.8 Simulasi distribusi Weibull dengan MATLAB 19
BAB 4 PEMBAHASAN 20
4.1 Perhitungan Fungsi Mean Residual Life (MRL) µ(t) dan µλ(t) 21 4.2 Perbandingan Fungsi MRL dan Mengubah Titik-Titik Baliknya 26
4.3 Resiko Bersaing 28
BAB 5 KESIMPULAN 36
DAFTAR GAMBAR
Nomor Judul Halaman
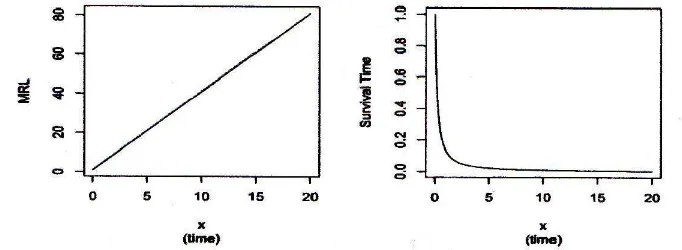
2.1 (kiri)Linier MRL untuk X dengan A = 4 (slope) dan B = 1
(intercept). (kanan) fungsi survival yang berhubungan dari X 10 2.2 (kiri) Linier MRL untukX dengan A=−0.2 (slope) danB = 1
(intercept). (kanan) fungsi survival yang berhubungan dengan X 11 2.3 (kiri) Linier MRL untuk X dengan A = 0 (slope) dan B = 1
(intercept). (kanan) fungsi survival yang berhubungan dengan X 12 3.1 Hubungan antara fungsi Hazard dan fungsi Survivor 18 4.1 Fungsi lognormal survival (panel atas) dan fungsi MRL (panel
bawah) dengan parameter α = 2 dan σ = 0.5, dan mengangkat
λ = 0 (garis padat), λ = 0.005 (garis putus-putus), λ = 0.01
ABSTRAK
Penambahan konstan resiko bersaing biasanya sering meningkatkan peranan re-liability dan analisis survival. Hal ini sering disebut mengangkat, sebagai efek untuk meningkatkan fungsi tingkat hazard (HR) yang konstan. Tentu saja peruba-han bentuk ini mengubah titik balik dari fungsi hazard (HR). Namun menaiknya fungsi hazard (HR) tidak berarti menurunkan fungsi mean residual life (MRL) yang konstan. Penting untuk memeriksa perubahan bentuk fungsi mean residual life (MRL) dan dalam lokasi titik-titik balik yang dihasilkan dari fungsi hazard (HR).
ABSTRACT
The addition of a constant competing risk corresponding to an additional, usually less significant, source of failure, frequently improves the fit in reliability and sur-vival analysis. This is often termed a lift, as the effect is to increase the hazard rate (HR) function by a constant, which does not, of course, change the shape and hence the turning points of the HR function. However, lifting the HR function does not, in general, mean lowering the corresponding mean residual life (MRL) function by a constant. Hence, it is of interest to examine the changes in the shape of the MRL function, and in the locations of its turning points, resulting from a lift in the HR function.
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Banyak aplikasi dalam aktuaria, ekonomi, teknik, dan literature medis meli-batkan penggunaan tingkat hazard (HR) dan fungsi mean residual life (MRL). Dalam matematika sifat fungsi ini mengungkapkan berbagai fitur dalam data. Hal ini juga umum untuk mengamati kekuatan eksternal, yang biasanya disebut dengan resiko bersaing. Yang mana resiko bersaing ini dapat bekerja pada sistem dan dapat mengubah dinamikanya. Perubahan tersebut dan efek dari resiko per-saingan ini menarik untuk diamati karena berbagai alasan seperti merumuskan pencegahan pemeliharaan kebijakan dalam rekayasa kehandalan atau pengaturan premi asuransi. Masalah ini akan dibahas secara detail dengan mengacu pada sejumlah distribusi reliability yang umum dan model mortalitas.
Data survival merupakan data yang mendeskripsikan waktu terhadap su-atu kejadian tertentu. Kejadian ini dapat mengacu pada kegagalan mesin atau meninggalnya seseorang. Begitupun data survival dapat juga mempresentasikan waktu hingga pasien penderita kanker yang memburuk. Fungsi survival dari vari-abel acak positifxmendefinisikan probabilitas hidup setelah waktux, yang ditulis dengan bentuk
S(x) = Pr(X > x) = 1−F(x)
F(x) adalah fungsi distribusi. Fungsi Hazard menentukan probabilitas kegagalan dalam waktu berikutnya dengan diketahui hidup hingga waktu x, yaitu :
h(x) = lim ∆x→0
Pr[x < X 6x+ ∆x|X > x] ∆x
= f(x)
2
Dimana f(x) fungsi kepadatan probabilitas (Klugman, 2004). Mean Residual Life (MRL) menghitung ekspektasi waktu hidup sisa dari suatu subjek dengan diketahui hidup hingga waktu x. Andaikan bahwa F(0) = 0 dan µ = E(x) =
Fungsi mean residual life banyak menarik perhatian karena kemudahan pema-hamannya dan pemakaiannya (Gauss dan Proschan, 1985). Lebih lanjut lagi fungsi ini mengkarakterisasi distribusi survival melalui formula inversi untuk x
kontinu denganµ <∞, fungsi survival didefinisikan melalui fungsi mean residual life :
Selanjutnya akan dihitung fungsi mean residual life (MRL)µλ(t) untuk be-berapa distribusi lifetime parametric yang menggambarkan kompleksitas µλ(t) pada kasus sederhana. Lalu akan dibahas jarak antara fungsi MRLµ(t) danµλ(t) pada titik balik dan fungsi serta hubungannya ke titik-titik yang sesuai dengan fungsi hazard (HR).
1.2 Perumusan Masalah
Dengan adanya resiko persaingan maka penting untuk memeriksa perubahan bentuk fungsi mean resisual life (MRL) dan lokasi titik-titik balik yang dihasilkan dalam fungsi hazard (HR) yang akan mengacu pada sejumlah distribusi umum dalam keandalan dan model mortalitas.
1.3 Tujuan Penelitian
3
1.4 Manfaat Penelitian
Selain untuk tambahan literatur dan pengetahuan pembaca mengenai ben-tuk model mean residual life (MRL) dengan adanya resiko persaingan, dalam bidang ekonomi penelitian ini juga bermanfaat untuk membantu pengambilan kebijakan perusahaan dan juga premi asuransi.
1.5 Metode Penelitian
1. Membuat formulasi model mean residual life (MRL)
2. Menghitung fungsi mean residual life (MRL) µ(t) danµλ(t)
3. Membandingkan fungsi mean residual life (MRL) dan mengubah titik-titik baliknya
BAB 2
FUNGSI MEAN RESIDUAL LIFE
2.1 Sifat-Sifat Peluang
2.1.1 Identitas dasar
Pertama akan ditunjukkan sebuah hubungan dasar di antara fungsi survival dan momen dari distribusi. Untuk sebuah random variabel kontinu dengan ni-lai non-negatif dan mempunyai rata-rata yang berhingga, maka µ ≡ E(X) =
R∞
dimana limit x menuju tak berhingga dari xS(x) adalah 0, karena diasumsikan rata-ratanya berhingga R∞
0 tf(t)dt <∞
dan fungsi distribusinya kontinu. Se-cara umum, fungsi distribusi hanya membutuhkan kontinu ke kanan dengan rata-rata berhingga untuk limit menuju 0. Argumen mengikuti: untuk sebuah fungsi distribusi kanan, fungsi distribusi didefinisikan sebagai S(x) = R∞
x f(t)dt ⇒
xS(x) = xR∞
densi-5
Mengaplikasikan limit untuk setiap bentuk, limx→∞0 ≤ limx→∞xR∞
x f(t)dt ≤
Momen kedua dapat juga ditulis sebagai sebuah fungsi dari fungsi survival. Mengasumsikan keberadaan dari momen ke-2, dapat ditulis
E(X2) =
Selanjutnya dengan mengasumsikan keberadaan dari momen kedua
Z ∞
0
x2f(x)dx <∞
untuk fungsi distribusi kontinu (setidaknya kontinu ke kanan), dapat ditulis
x2S(x) = x2
Dengan mengaplikasikan limit untuk setiap bentuk lim kemudian dengan menggunakan Teorema Squeeze, lim
x→∞x
2S(x) = 0.
Secara umum, jika rth momen ada untuk sebuah random variabel kontinu
X maka berlaku:
E(Xr) =r
∞
Z
6
demikian dapat ditentukan pula variansi dari fungsi survivalnya yaitu sebagai berikut:
Telah didefinisikan MRL sebagai ekspektasi dari sisa hidup sampai waktu x. Diperoleh bentuk untuk fungsi MRL dari fungsi survival dengan bentuk berikut (London , 1988):
dimana limit pertama di langkah terakhir mengarah ke 0 karena diasumsikan bahwa momen pertama ada, dan limit kedua mengarah ke 0 karena F(∞) = 1. Maka dapat dengan mudah dilihat bahwa momen pertama ekuivalen dengan fungsi MRL dengan x= 0.
2.1.2 Batas untuk fungsi MRL
Pertama diketahui bahwa m(x) + x(i)=E(X|X > x), yang mengarah ke
7
(a) m(x) ≤ (T −x)+ untuk semua x, dengan persamaan jika dan hanya jika
F(x) =F(T−) atau 1, (perlu diingatT− bahwa kita mendekati T dari kiri)
(b) m(x) ≤ µ
S(x) −x untuk semua x dengan persamaan jika dan hanya jika
F(x) = 0
S(x) untuk x < T dengan persamaan jika dan hanya jika
F(x) = 0
2.1.3 Sifat dari MRL (formula invers)
Sifat berikut adalah dasar dari pengembangan untuk teorema karakterisasi untuk fungsi MRL, yaitu (Hall dan Wallner, 1981):
(a) m(x) non negatif dan kontinu ke kanan, dan m(0) =µ >0
8
Sifat (d) diketahui sebagai Formula Invers. Dan dibuktikan sebagai berikut:
Pembuktian Formula Invers (Hall dan Wallner, 1981): Didefinisikan fungsi
k(x)≡ R∞
−S(x). Sekarang diperlihatkan x
Disimpulkan ringkasan dari sifat untuk fungsi MRL dengan sebuah hasil utama bahwa syarat perlu dan cukup yang mana sebuah fungsi adalah fungsi MRL untuk sebuah distribusi survival, dan dengan demikian merupakan karakter dari fungsi MRL.
Teorema Karakterisasi (Hall dan Wallner, 1981): Diketahui sebuah fungsi
m(x) dengan pemetaan R+ → R+ dari (a) m(x) adalah kontinu ke kanan dan adalah sebuah fungsi distribusi atasR+dengan F(0) = 0, T
9
2.2 Fungsi MRL untuk Distribusi Spesifik
2.2.1 Linier MRL
Jika fungsi MRL adalah linier, m(x) = Ax +B(A > −1, B > 0), maka dengan menggunakan formula invers, fungsi Survival menjadi berbentuk:
S(x) =
ditunjukkan bentuk asal Survival ketika A6= 0 berikut :
S(x) =
10
MRL linier denganA, B >0. Misalkan diberikanz ∈[β,+∞] dimanaz=Ax+B
dan Ax > 0. Akhirnya, karenaZ ≥β >0⇒ βz >0 fungsi survival selalu positif, maka tidak diperlukan penyesuaian untuk membuat fungsi bernilai positif.
Gambar 2.1 (kiri)Linier MRL untuk X dengan A= 4 (slope) dan B = 1 (inter-cept). (kanan) fungsi survival yang berhubungan dari X
Untuk−1 < A <0 fungsi survival adalah berasal dari distribusi beta. pdf dari sebuah distribusi beta diberikan dengan
f(z;a, b, p, q) = (z−a) linier untuk memperoleh pdf. Pdf akan mengumumkan model apa dari bentuk hasil reparameter dari rescaled beta dengan S(x) = B
Ax+B
A1+1
+ . Perlu diingat bagian positif adalah diperloleh ketika −Ax ≤ B → x ≤ −B/A, maka ketika
11 Kemudian pdf dan fungsi survival diberikan dengan,
F(z) =
adalah meneliti transformasi fungsi survival
Gambar 2.2 (kiri) Linier MRL untuk X dengan A = −0.2 (slope) dan B = 1 (intercept). (kanan) fungsi survival yang berhubungan dengan X
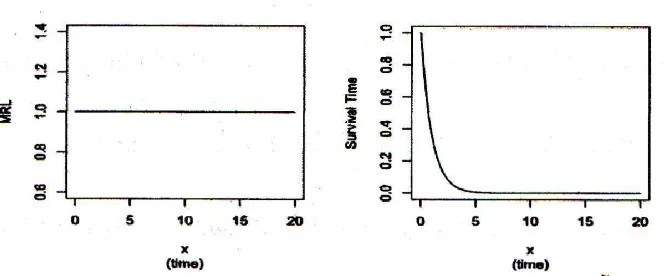
untukA = 0, fungsi survival adalah eksponensial :
S(x) =
12
Gambar 2.3 (kiri) Linier MRL untuk X dengan A = 0 (slope) dan B = 1 (intercept). (kanan) fungsi survival yang berhubungan dengan X
mengikuti distribusi yang baik (Pareto dan diskala ulang beta). Sekarang kembali ke daerah asaldari fungsi survival, dikatakan diatas bahwa untuk A≤ 0X dapat diambil nilai dari 0 damapai tak hingga, dimana untuk −1 < A < 0X berasal dari 0 untuk −B/A. Didalam contoh, daerah asal untuk fungsi survival ketika
BAB 3
MENGHITUNG MEAN RESIDUAL LIFE
3.1 Menghitung Fungsi Mean Residual Life (MRL) µ(t) dan µλ(t) Diketahui bahwa S(t) = exp{−
t
R
0
h(x)dx} dengan hλ(t) = h(t) +λ maka dapat diperoleh Sλ(t) = exp−λtS(t), dimana Sλ(t) adalah fungsi survival dari
hλ(t). Fungsi survival bersyarat yaitu S(x|t) = P[T > t +x|T > t] = S(x+t)S(t) dengan demikianµt(t) =E[Tλ−t|Tλ > t] =
R∞
t Sλ(x)dx
Sλ(t) = R∞
0 e−λxS(x|t)dxdimana
Tλ adalah fungsi variable acak Sλ(t).
Menghitung Fungsi Mean Residual Life (MRL) µ(t) dan µλ(t) untuk dis-tribusi parametric dimulai dengan disdis-tribusi eksponensial. Kemudian akan dapat ditunjukkan bagaimana gagasan resiko bersaing konstan yang muncul secara ala-mi dalam konteks aktuaria.
3.2 Perbandingan Fungsi MRL dan Mengubah Titik
Mengubah titik yang mana monotonitas dari fungsi HR ataupun peruba-han dari fungsi MRL dalam aplikasi aktuaria memungkinkan untuk memahami pola kurva mortalitas (Bebbington et al., 2007). Dalam reliability, titik-titik ini menyediakan informasi untuk menentukan kebijakan burn-in. Secara khusus ki-ta ingin mengukur jarak anki-tara titik t∗
0 dan t∗λ yang merupakan titik balik dari masing-masing fungsiµ(t) danµλ(t). Jumlah ini tentu saja tergantung pada ben-tuk fungsi MRL yang menaik (Increasing) atau menurun (Decreasing). Berbenben-tuk buthtub (BT), yang menurun dibawah titik balik, menaik di atas, dan terbalik berbentuk upside-down buthtub (UBT), yang menaik di bawah titik balik, dan penurunan di atas (Bebbington et al., 2007).
14
bilitas dari sistem yang bekerja keseluruhan pada spesifikasi waktu dan spesifikasi pekerjaan tertantu dimana fungsi reliability adalah fungsi dari waktu tugast. Jika waktu diasumsikan sebagai nilai khusus yang tetap, reliability dikatakan sebagai reliability statik. Setelah mekanisme ditolak secara riil maka reability tidak dapat dianalisis secara keseluruhan, penilaian statistik secara umum dapat digunakan untuk mengestimasi reliability dari suatu sistem. Dengan mengikuti konsep dasar dari reliability maka akan menuju ke distribusi waktu hidup dari suatu sistem.
Dinotasikan sebuah variabel acakT sebagai waktu hidup dari sistem dan F
sebagai fungsi distribusi kumulatif dari T maka F(t) = Pr{T ≤ t}. Kemudian fungsi reliabilityR(t) adalah
R(t) =P r {waktu sistem tanpa kegagalan sampai waktu t} R(t) = Pr{T > t}
R(t) = 1−Pr{T ≤t} R(t) = 1−F(t)
Diberikan reliability bersyarat dari umur t sebagai R(x|t) ≡ Pr{T > t+x|T > t} = R(t+x)R(t) jika R(t) >0. Probabilitas bersyarat dari kegagalan selama interval berikutnyaxdari umurtadalahR(x|t)≡Pr{t < T ≤t+x|T > t}= F(t+x)R(t)−F(t) = 1−R(x|t). Tingkat kegagalan atau fungsi tingkat hazard diberikan sebagai :
h(t) ≡ lim
Fungsi tingkat kegagalan mewakili karakteristik dari sistem. Jika sebuah sistem berada dalam waktu sistem yang buruk, reliability bersyarat dari umur t
adalah R(x|t) yang menurun dit,∀x≥0 dan diperolehh(t) = lim x→0 1
x[1−R(x|t)] yang menaik di t. Sebaliknya jika tingkat kegagalan menaik di t maka R(t) = expn−Rt
t +xh(u)du
o
adalah menurun di t, ∀x ≥ 0. Dengan demikian jika ter-dapat fungsi tingkat kegagalan maka kenaikan reliability bersyarat adalah setara untuk kenaikan fungsi tingkat kegagalan.
15
Mean Residual Life dari umur t adalah m(t) ≡ E[T −t|T > t] = R∞
t R(u)du
R(t) , jika
R(t)>0. Sebuah kenaikan fungsi tingkat kegagalan memiliki kondisi yang lebih kuat dari pada kenaikan dari mean residual life (Hwang, 2004).
Ahli elektronika menggunakan cara kenaikan ini untuk mengetahui bentuk bathtub kurva tingkat kegagalan. Bentuk bathtub kurva tingkat kegagalan dapat menurun sampai dua kurva tingkat kegagalan yang bebas dengan adanya model reliability resiko persaingan. Satu kurva tingkat kegagalan dihasilkan dari mo-del kegagalan ekstrinstik yang mana distribusi kegagalannya menaik dan kurva menurun tingkat kegagalan yang lainnya menunjukkan model kegagalan intrinstik.
3.4 Fungsi Hazard
Misalkan T adalah variabel random tunggal nonnegatif kontinu pada inter-val [0,∞) yang menunjukkan ketahanan hidup individu dalam suatu populasi. Jika f(t) dan F(t) masing-masing adalah fungsi densitas dan fungsi distribusi dari T, maka fungsi hazard untuk T didefinisikan sebagai berikut :
h(t) = lim ∆t→0
F(t+ ∆t)−F(t) ∆tS(t) =
F(t)
S(t) =
f(t)
S(t)
dengan S(t) = 1−F(t) fungsi survival, dan F(t)<1
Dan dalam distribusi uji hidup didefinisikan beberapa fungsi-fungsi sebagai berikut :
Fungsi survival atau fungsi reliabilitas,
S(t) = Pr(T > t) =
∞
Z
t
f(x)dx= 1−F(t)
Hubungan H(t) danS(t) atau fungsi hazard kumulatif t
16
Untuk memperoleh data ketahanan hidup yang terbaik dari suatu populasi, dilakukan pengujian terhadapnbenda pada berbagai kondisi (sensor). Sensor di-lakukan untuk memperpendek waktu atau memperkecil biaya pengujian, terutama bagi benda-benda yang cukup handal. Sensor tipe I ; pengujian akan dihentikan jika telah dicapai waktu tertentu (waktu pensensoran) dan dalam sensor tipe II, pengujian akan dihentikan setelah kegagalan atau kematian benda ke-r dimana (r < n) diperoleh. Analisis ketahanan hidup diamati dan digunakan untuk esti-masi, misalnya estimasi fungsi hazard h (Agustina, 2000).
3.5 Fungsi Analisis Survival
Analisis survival adalah suatu metode yang berhubungan dengan waktu, mulai dari time origin atau start point sampai dengan terjadinya suatu kejadian khusus atau end point. Dengan kata lain, analisis survival memerlukan data yang merupakan waktu survival dari suatu individu.
Tujuan utama dari analisis survival ini adalah untuk memodelkan dan meng-analisis data sampai terjadi suatu kejadian; yaitu data yang memiliki batas waktu usia dari suatu kejadian dimana kejadian itu disebut dengan ’failures’. Beberapa contoh antara lain: waktu sampai komponen elektronik rusak, waktu kematian, waktu untuk mempelajari suatu keahlian.
Suatu failure time dalam suatu kasus mungkin saja tak teramati baik karena rancangan percobaannya ataupun karena random censoring. Misalnya ternyata pasien masih hidup sampai akhir dari suatu percobaan klinis. Analisis survival adalah suatu istilah modern yang diberikan terhadap sekumpulan prosedur statis-tik yang mengakomodasi waktu sampai terjadi suatu kejadian dari data yang tersensor.
3.6 Distribusi Weibull
17
del dalam menganalisis realibilitas sistem yang berlainan jenis (Tableman, 2004). MisalT adalah failure time danT berdistribusi Weibull, makaT merupakan suatu variabel random positif dengan fungsi densitas diberikan sebagai berikut:
f(t;µ, α) = α
µ
t µ
α−1
exp
−
t µ
α
dimanaα >0 merupakan shape parameter danµ >0 merupakan scale parameter. Sehingga secara umum memiliki nilai ekspektasiT berikut:
E(T) =µ.r(1 + 1/α) dan fungsi distribusi kumulatifnya :
f(t;µ, α) =P(T ≤t;µ, α) = 1−exp
−
t µ
α
Karena fungsi survivornya didefinisikan sebagai S(t) = 1−F(t), sehingga diper-oleh
S(t) = exp(−(t/µ)α)
dari formula h(t) = S(t)f(t) , maka diperoleh Fungsi Hazard sebagai berikut :
f(t;µ, α) = α
µ
t µ
18
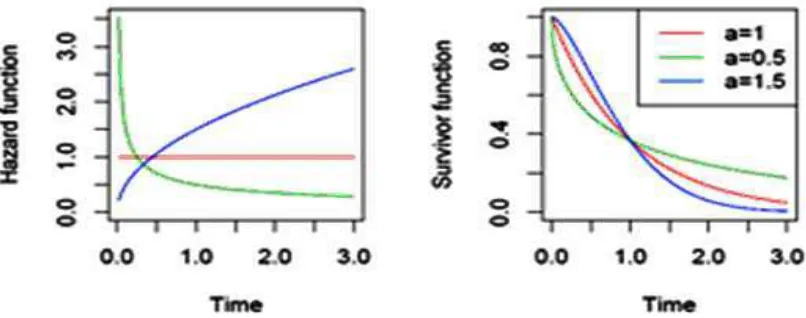
Berikut ini adalah gambaran secara grafis hubungan antara fungsi hazard dan fungsi kelangsungan :
Gambar 3.1 Hubungan antara fungsi Hazard dan fungsi Survivor
3.7 Weibull Proportional Hazard Model
Pertama dilakukan reparameterisasi dari model Weibull dengan menggu-nakan λ, dimana λ = µ−α, sehingga diperoleh : h(t) = λαtα−1 dan S(t) = exp(−λtα). Misal x→ = {x(1), x(2), ..., x(m)} adalah vector kovariat yang ada, se-hingga fungsi hazard menjadi sebagai berikut :
h(t|x) = h0(t).exp(x′β)
h(t|x) = αλαtα−1exp(x′β) =α(λ.(exp(x′β)α1)αtα−1
h(t|x) = α(˜λ)αtα−1 dimana : ˜λ=λ.(exp(x′β))1
α
atau fungsi ini biasa juga ditulis sebagai berikut :
hi(t;xi) = exp.(xT
i β).λαtα−1
Model mengasumsikan bahwa individu ke-idan ke-j dengsn kovariatxi dan
xj memiliki proportional hazard fungsi sebagai berikut :
hi(t;xi)
hj(t;xj)
= exp(x T i β) exp(xT
jβ)
= exp((xi−xj)Tβ)
19
3.8 Simulasi distribusi Weibull dengan MATLAB
Dalam MATLAB, diperlukan Statistics Toolbox untuk menjalankan baris perintah berikut. Bangkitkan data prediktor y berdistribusi Weibull dengan prediktor x, dengan baris perintah sebagai berikut:
x= 4∗rand(100,1);
A= 50∗exp(−0.5∗x);B = 2;
y=wblrnd(A, B);
Kemudian lakukan fitting pada model Cox dengan perintah berikut: [b, logL, H, stats] =coxphf it(x, y);
Tampilkan dalam grafik estimasi Cox dengan menggunakan baseline fungsi sur-vivor bersama dengan fungsi Weibull yang telah diketahui sebagai berikut:
stairs(H(:,1), exp(−H(:,2)))
xx=linspace(0,100);
line(xx,1−wblcdf(xx,50∗exp(−0.5∗mean(x)), B),′color′,′r′)
xlim([0,50])
BAB 4 PEMBAHASAN
MisalkanF(t) adalah fungsi distribusi lifetime yang dijelaskan oleh variable nonnegative acakT. Kita asumsikan bahwaF(0)−0. Fungsi survival dinotasikan dengan S(t) = 1−F(t) dan fungsi hazard (HR) dengan h(t) = f(t)/S(t) untuk
t dimana S > 0, asalkan f(t) = F′(t) ada. Fungsi mean residual life (MRL)µ(t) adalah waktu tersisa yang diharapkan untuk kegagalan (failures), mengingat sis-tem sudah bertahan untuk waktu t, maka µ(t) =E[T −t] = (1/S(t))R∞
t S(x)dx untuk t dimana S >0.
Misalkan terdapat dua fungsi Hazard, hλ(t) dan h(t) yang terkait dengan persamaan
hλ(t) =h(t) +λ (4.1) dimana λ > 0 konstan. Tentu saja mengangkat fungsi HR tidak mengubah sifat geometric dan dengan demikian jumlah titik balik pseudo tidak berubah. Meskipun fungsi HR hλ(t) hanya mengangkat dari fungsi HR h(t) yang konstan
λ > 0 , fungsi MRL µλ(t) tidak umum untuk penurunan sederhana µ(t) yang konstan. Secara khusus akan diperlihatkan bagaimana persamaan fungsi MRL
µλ(t) dan µ(t) yang terkait satu sama lain, dan bagaimana titik balik dari dua fungsi MRL tersebut (Bebbington et al., 2008).
21
4.1 Perhitungan Fungsi Mean Residual Life (MRL) µ(t) dan µλ(t) Dimulai denganS(t) = exp{−λt
0h(x)dx}dimana dari persamaan (4.1)hλ(t) =
h(t) +λ maka diberikanSλ(t) = exp−λtS(t), dimanaSλ(t) adalah fungsi survival yang berkorespondensi dengan hλ(t) . Fungsi survival bersyarat yaitu
S(x|t) =P[T > t+x|T > t] = S(x+t) dimana Tλ adalah fungsi variabel acak Sλ(t).
Dengan mengintegrasikan sisi kanan dari persamaan bagian (4.3), diperoleh :
µλ(t) = 1
Rt. Perhatikan bahwa ketika λ ↓ 0 , sebelah kanan sisi pada persamaan (4.4) konvergen ke E[Rt] = µ(t). Peran transformasi Laplace dalam menggambarkan karakteristik distribusi lifetime berbeda secara rinci dalam interprestasi dan apli-kasi yang dapat ditemukan.
Transformasi Laplace dari residual life Rt yang hanya 1−λµλ(t) dapat di-interpresentasikan dalam aplikasi aktuaria dimana jumlah ganti rugi yang terkait dengan resiko, pendapatan terkait dengan transaksi keuangan, atau premi asu-ransi jiwa seumur hidup. Sebagai contoh λ dapat disamakan dengan tingkat diskon pada pemodelan premi dan cadangan. Dengan menggunakan fungsi utility (cekung)G(t) = 1−e−x/θ, didapat bahwaE[G(Rt)] = 1−E[e−Rt/θ] dan khususnya
mengambil t = 0 diperoleh E[G(T)] = 1−E[e−Tt/θ]. Ini menghubungkan fungsi
22
Contoh 1
Fungsi survival dari distribusi eksponensial adalah S(t) = exp{−t/θ} dengan
θ >0. Fungsi Hazard adalah h(t) = 1/θ dan memoryless propertyS(x|t) =S(x)
Oleh karena itu, untuk distribusi eksponensial, mengangkat fungsi HR dengan konstan yang rendah fungsi MRL adalah constant. Ciri dari distribusi eksponen-sial ini terbukti seperti dalam teorema 1 berikut ini
Teorema 1 (Bebbington et al., 2008)
Diberikan λ > 0 dan c > 0 adalah konstan, dan anggap bahwa keputusan dari dua fungsi HRh∗(t) dan h∗(t) dan kemiripan keduanya dengan fungsi MRLµ∗(t) dan µ(t) adalah sedemikian hingga sehingga diperoleh persamaan
h∗(t) = h(t) +λdanµ∗(t) =µ(t)−c (4.5) berlaku untukt≥0. Kemudian yang mendasari fungsi survival adalah eksponen-sial dengan rata-rata Dengan membedakan persamaan terakhir, diperoleh
S′′(t)−λS′(t)− λ
cS(t) = 0 (4.7)
Sehingga persamaan differensial orde kedua yang homogen ini dengan koefisien konstan memiliki solusi umumx1 = λ+
√
λ2+4λc−1
2 dan x2 =
λ−√λ2+4λc−1 2
23
eksponensial : S(t) = exp{x2t} Dimana x2 adalah negative, dapat dituulis ulang kembali dalam bentuk S(t) = exp{−t/θ(λ, c)}, dimana constant positif θ(λ, c) seperti yang diberikan dalam parsamaan (4.6). Hal ini menyimpulkan pembuktian
dari teorema 1.
Distribusi eksponensial merupakan sarana untuk dapat menginterpresen-tasikan atau menafsirkan mengenai fungsi MRL µλ(t), melalui kesetaraan dari yang sebelumnya dengan transformasi Laplace dari residual life. Anggap se-buah variable acak E0, memiliki distribusi eksponensial dengan rata-rata θ, maka
P[Rt≤Eθ] =E[e−Rt/θ]. Oleh karena itu, transformasi Laplace adalah probabili-tas dari residual life keadaan akhir untuk penyebab yang alami, sebelum kejadian eksponensial terjadi. Dengan variable acak eksponensial yang sama E0, dimiliki bahwaE[Rt∧Eθ] =θ(1−E[e−Rt/θ]). Oleh karena itu, transformasi Laplace adalah suatu transformasi linier sederhana dari residual life yang diharapkan, yang mana dihentikan dengan sebab alamiah atau kecelakaan eksponensial (Denuit, 2001).
Contoh 2
Fungsi survival dari distribusi Lomax adalah S(t) = (1 +βt)−α, dengan λ > 0 dan β > 0. Fungsi HR adalah h(t) = αβ/(1 +βt) yang menurun langsung. Ini sangat mudah untuk melihat bahwa S(x|t) adalah distribusi Lomax S(x), dima-naβ diganti denganβ/(1 +βt). Dengan menggunakan pengamatan terakhir dan persamaan (4.3), dan juga dengan mengasumsikan λ >0 maka kejadian pertama diperoleh lengkap. Sebuah aplikasi dari aturan LHospital diberikan fungsi MRL :
µ(t) =
24
Contoh 3
Fungsi survival dari fungsi HR yang linier diberikanS(t) = exp{−λ1t−λ2t2/2}, dimana λ1 > 0 dan λ2 > 0 atau setidaknya satu dari keduanya tidak nol. Ke-sesuaian fungsi HR adalah h(t) = λ1 +λ2t. Dari sini, ketika λ2 > 0, fungsi HR menaik langsung. Pertama perlu diingat bahwa fungsi survival e−λtS(t),adalah fungsi survival asli S(t) dengan parameter λ1 digantikan oleh λ+λ1, dan fungsi survivalS(t) dapat ditulis sebagaicφ(√λ2t+λ1/√λ2, dimanaφ(u) adalah proba-bilitas fungsi kepadatan standar normal (pdf), dan c adalah konstanta. Dengan demikianSλ(t) =cφ(√λ2t+ (λ1+λ)/√λ2, dan dengan menggunakan persamaan
Dimana Φ(u) adalah fungsi distribusi standard normal. Menetapkan λ= 0 yang menghasilkan µ(t) (Bebbington et al., 2008).
Dari contoh yang diberikan diatas, digunakan persamaan (4.3) untuk menghi-tung fungsi MRL µλ(t) dan µ(t), namun ketika distribusi dinyatakan sebagai in-tegral, hal ini menuju kepada integral ganda. Oleh karena itu, perhatikan bahwa
µλ(t) =
Maka dari persamaan (4.8), dengan menggunakan aturan LHopital, diperoleh
µ(t) =
Rλ
t xf(x)dx
S(t) −t (4.9)
Persamaan di atas diperlukan untuk menghitung fungsi MRLµλ(t) danµ(t) dalam contoh berikutnya. Ini adalah distribusi gamma, yang memiliki sifat dan aplikasi di bidang ekonomi dan ilmu aktuaria.
Contoh 4
Fungsi survival gamma dengan parameter a, b > 0 diberikan dengan persamaan
sebelum-25
h(t) = abtb−1e−at/Γ(b, at). Sisi kanan dari persamaan terakhit ini dapat juga di-tulis sebagai kebalikan dari integralR∞
0 (1 +x/t)b−1e−axdx. Hal ini menunjukkan bahwa fungsi HR h(t) adalah menurun langsung saat 0 < b < 1, konstan saat
b = 1, dan menaik langsung ketika b >1. Untuk menghitung fungsi MRL µλ(t), pertama-tama kia perhatikan bahwa faktor eλxdibawah tanda integral pada sisi kanan persamaan (4.8) dapat dimasukkan ke dalam kepadatan fungsi gamma
f(x), yang menghasilkan µλ(t) = λ1 1− (1+λ/a)eλtΓ(b,(a+λ)t)bΓ(b,at)
. Dengan persamaan (4.8) dan (4.9) ini memberikanµ(t) = abΓ(b,at)−1tbe−at +ab −t (Bebbington et al., 2008).
Contoh 5
Fungsi lognormal survival adalah S(t) = 1−Φ((logt−α)/σ), dimana φ adalah fungsi distribusi standard normal dan α, σ >0. Dimulai dengan persamaan (4.9) dan kemudian menukar variable dari integrasixmenjadi exp{σx+σ2+α}, diper-oleh
µ(t) = 1−Φ((logt−α)/σ−σ)
1−Φ((logt−α)/σ) .exp{α+σ 2/2
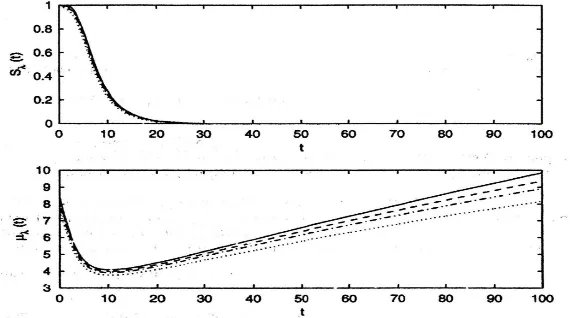
} (4.10) ketika α = 0 dan σ = 1. Namun fungsi MRL µλ(t) tidak tampak dinyatakan dalam bentuk fungsi yang diketahui tanpa menggunakan integral. Dapat dilihat fungsi ini pada Gambar 4.1 (Bebbington et al., 2008).
Gambar 4.1 Fungsi lognormal survival (panel atas) dan fungsi MRL (panel bawah) dengan parameter α = 2 dan σ = 0.5, dan mengangkat
26
4.2 Perbandingan Fungsi MRL dan Mengubah Titik-Titik Baliknya
Dengan pernyataan e−λx didalam integral tengah pada persamaan (4.8) tidak melampaui e−λx , dimiliki bahwa µλ(t) ≤ µ(t) untuk semua t ≥ 0, dan menegaskan bahwa meningkatnya fungsi Hazard (HR) menurunkan fungsi Mean Residual Life (MRL). Pemesanan HR yang lebih kuat daripada pemesanan fungsi MRL dalam arti bahwa jika sebuah fungsi HR tidak di bawah satu sama lain, maka fungsi MRL sesuai dengan bentuk fungsi HR tidak akan lebih tinggi daripa-da fungsi MRL yang berkorespondensi. Kembali kepadaripa-da mengangkat fungsi HR
hλ(t), yang lebih tinggi dengan λ >0 dari h(t), secara alami perlu untuk menge-tahui berapa banyak fungsi MRL µλ(t) yang lebih rendah dari µ(t) (Lai dan Xie, 2006).
Pertama perhatikan bahwa jikaS(x|t) tergantung pada t, maka perbedaan
µ(t)−µλ(t) =
Z ∞
0
q1(x)S(x|t).dx dengan q1(x) = 1−e−λx (4.11) juga tergantung pada t. Ini terlihat dengan mengasumsikan bahwa sisi kanan tidak tergantung padat, dan kemudian mencatat bahwa Teorema 1 menyiratkan bahwaS(x) harus eksponensial, atau dapat disebut memoryless. Oleh karena itu, kecuali dalam kasus distribusi eksponensial, jarak antara fungsi MRL µλ(t) dan
µ(t). tidak selalu sama atas t. Oleh karena itu penting untuk mengetahui jarak maksimal antara dua fungsi atau setidaknya menaksir perkiraan jarak. Dengan memiliki ekspresi eksplisit untuk kedua fungsi seperti pada contoh pada bagian 2 tentu saja sangat membantu. Secara umum, masalah ini adalah ekspresi yang lebih rumit dan berbagai ekspresi seperti persamaan (4.11) menjadi berguna. Se-hingga diperoleh juga
µ(t)−µλ(t) =
Z ∞
0
q2(x)S(x)
S(t)dx dengan q2(x) =λ.e
λte−λtµ(x) (4.12)
µ(t)−µλ(t) ==
Z ∞
0
q3(x)S(x|t).dx dengan q3(x) = λ.e−λtµ(x+t) (4.13) Persamaan (4.11)-(4.13) mengukur besarnya perbedaan µ(t)−µλ(t) dalam hal
27
fungsi monoton dari fungsi HR atau fungsi MRL diganti. Dalam aplikasi aktu-aria, satu ini memungkinkan untuk mengerti pola dari kurva mortalitas. Dalam ketidakpastian, disediakan informasi untuk menemukan kebijakan burn-in. Secara khusus ingin mengukur jarak antara titik t∗
0 dan t∗λ yang mana merupakan titik balik dari masing-masing fungsiµ(t) danµλ(t)secara berurutsn. Jumlah ini tentu saja tergantung pada bentuk fungsi MRL, yang menaik (Increasing) atau menu-run (Decreasing), berbentuk buthtub (BT), yang menumenu-run dibawah titik balik, menaik di atas, dan terbalik berbentuk upside-down buthub (UBT), yang menaik di bawah titik balik, dan penurunan di atas (Bebbington et al., 2007).
Teorema 2 (Bebbington et al., 2008)
Diberikan fungsi HRh(t) dapat dideferensiasi dan berada dalam kelas BT. Menye-babkan t1 ∈ (0,∞) yang dinotasikan sebagai titik balik/belok dari h(t). Jika
h(0)E[T] > 1, maka fungsi MRL µ(t) yang berada pada kelas UBT dan titik balik/belok t∗
0 dari µ(t) adalah dalam interval (0, t1). Jika h(0)E[T] ≤ 1, maka fungsi MRLµ(t) berada dalam kelas menurun (D).
Contoh 6
Diberikan fungsi survival adalah S(t) = (1 +βt)−θ/βe−δt2
/2, dengan δ, β, θ > 0. Fungsi HR adalah h(t) =δt+θ/(1 +βt). Karenanya, jikaβθ/δ ≤1, maka fungsi HR berada dalam kelas menaik (I), ketika βθ/δ > 1, maka fungsi HR berada dalam kelas BT, dengan titik balik
t1 =
r
θβ δ −1
!
1
β (4.14)
diasumsikan bahwa βθ/δ > 1. Kemudian dari teorema 2, diketahui bahwa jika
θE[T]>1, ketika fungsi MRL berada dalam kelas UBT dan memiliki titik belok yang unik t∗
0 pada interval (0, t1) dan jika θE[T] ≤ 1, maka fungsi MRL berada dalam kelas menaik (D). Sekarang saatnya untuk memperhitungkan fungsi MRL
28
bangkan nilai dari λ(t)>0, dimiliki bahwa
(θ+λ)
Z ∞
0
e−λx−δx2/2
(1 +βx)θ/βdx >1 (4.15)
Ketika fungsi MRLµλ(t) berada dalam kelas UBT dengan titik belokt∗
λ ∈(0, t1). Walaupun demikian, jika kondisi pada persamaan (4.15) tidak terpenuhi, maka fungsi MRL µλ(t) berada dalam kelas menaik (D). Situasi dari bagaimana titik belok t∗
λ dan t∗0 dari fungsi MRL µλ(t) dan µ(t) adalah berkaitan satu dan lain-nya dengan hasil akhir berikutlain-nya, yang akan dikemukakan dalam sebuah bentuk komperatif yang sederhana (Belzunce, 2007).
Teorema 3 (Bebbington et al., 2008)
Diberikan fungsi MRL µ(t) berada dalam kelas UBT. Kemudian, untuk setiap
λ > 0, titik belok t∗λ dari titik belok µλ(t) adalah lebih besar dari titik belok t∗0
dari fungsi MRLµ(t).
Contoh 6 menunjukkan bahwa fungsi MRLµλ(t) boleh diubah dalam bentuk variasi λ dan ini perlu untuk memahami bahwa t∗
λ dalam teorema 3 mungkin adalah 0 atau dengan kata lain, µλ(t) adalah tidak lebih panjang dari UBT tapi menaik (D). Dilihat juga dalam teorema 2 dan 3, diketahui bahwa jika fungsi HR
h(t) adalah differensiabel dan berada dalam kelas BT, dan jika kondisih(0)E[T]>
1 terpenuhi, maka untuk setiapλ >0 sedemikian hingga (h(0)+λ)E[Tλ]>1, titik belok t∗
0, t∗λ, dan t1 dari fungsi µ(t), µλ(t), dan h(t), secara berurutan memenuhi
t∗
0 < t∗λ < t1. Untuk mendapatkan formula yang eksplisit untuk titik belokt∗0 dan
t∗λ, nilai numerik dari t∗0 telah disediakan.
4.3 Resiko Bersaing
terse-29
Aturan dari resiko bersaing sering dimodelkan sebagai berikut. Unit dipa-parkan untuk (K ≥2) resiko dari kegagalan. Satu dan hanya satu-satunya klaim yang sebenarnya dari kehidupan disebut penyebab dari kegagalan (kematian). Hal ini dianggap bahwaX1, X2, . . . , Xk adalah random variabel kontinu yang bernilai positif yang menotasikan seumur hidup (waktu untuk kegagalan) untuk sebuah unit atas resiko k. Dengan kata lain, Xi disebut sebagai waktu ke-i dari unit, merupakan ketahanan acak dari sebuah unit ketika sebuah unit tersebut terkena resiko ke-i itu sendiri. Bagaimanapun semua resiko k bergerak secara simultan dan nilai sebenarnya dari ketahanan dari unit ke-i adalah random variabel posi-tif T = min{X1, X2, . . . , Xk}. Juga, diasumsikan kegagalan disebabkan kematian atau resiko yang mana benar-benar menjadi penyebabnya, menjadi diketahui. Dinotasikan sebagai δ dan didefinisikan sebagai berikut:
δ =j if T =Xj, j = 1,2, . . . , k
Selanjutnya data yang tersedia dari n independen salinan dari unit: (Ti, δi), i= 1,2, . . . , n.
Dapat dilihat hubungan antara k ketahanan didalam resiko bersaing diatur dan ketahanan dari k komponen merupakan serangkaian sistem.
Setelah data tersebut dikumpulkan, pertanyaan untuk membuat kesimpu-lan tentang mengasumsikan pengembangan modelnya. Model peluang dispesi-fikasikan sebagai fungsi survival gabungan dari X1, X2, . . . , Xk dinotasikan de-ngan:
F(x1, x2, . . . , xk) =P [X1> x1, X2> x2, . . . , Xk > xk] Fungsi Si(t), i= 1,2, . . . , k didefinisikan sebagai
Si(t) = P[T > t, δ=i], i= 1,2, . . . , k
30
dan koleksinya
{Si, i= 1,2, . . . , k}
dari fungsi insiden. Sebelumnya sudah diketahui bahwa di dalam kasus dependen,
F tidak teridentifikasi sebagai
{Si, i= 1,2, . . . , k}
Hal ini jelas secara mengkonstruksinya secara explisit sebuah fungsi survival ga-bungan,
fungsi survival gabungan F danG juga mengarah ke himpunan yang sama
{Si, i= 1,2, . . . , k} dari fungsi insiden.
Terdapat banyak studi mengenai mengidentifikasi aspek dari pembentukan parametrik. Sebagai contoh, bivariate normal teridentifikasi dan juga bivariate Makeham dan dua buah versi distribusi Pareto. Dimana solusi eksplisit untuk parameter dari kesemua distribusi tersebut berbentuk fungsi insiden.
Terdapat masalah dalam mengidentifikasi di dalam kasus dari ketahanan independent. Sebuah angka yang besar dari prosedur statistika telah menja-di alat dalam menginferensi fungsi survival gabungan F(x1, x2, . . . , xk) atau se-cara ekuivalen di dalam kasus independen, fungsi survival marginal Fi(x) dari ketahanan. Sebuah deskripsi dari proses dari estimasi, percobaan dan masalah-masalah lainnya, ketika keluarga parametrik dari Fis berada diketahui. Prose-durnya berdasarkan kepada dasar likelihood
31
Sebagai contoh, jikaFi adalah distribusi eksponensial dengan parameterλi, maka m.l.eλi adalah
ˆ
λi =
ni n
P
j=1
tj
dimanatj adalah ketahanan dari unit, j = 1,2, . . . , ndan ni adalah anggota dari unit yang gagal pada resiko ke-i. Dengan cara yang sama, dapat dihitung interval konfidensi dan uji untuk hipotesis yang lebih spesifik (David, 1978).
Non Parametrik
Akan dibahas beberapa kontribusi dari kesimpulan non parametrik menge-nai resiko bersaing yang independen. Pertama di dalam konteks dari reliability dari ketahanan laten berhubungan dengan ketahanan dari komponen yang disusun ke dalam barisan. Sehingga masuk akal untuk berbicara tentang sisa waktu hidup dari sebuah komponen yang tidak terjadi kegagalan jika sistemnya telah gagal. Untuk mengestimasiFi di dalam non parametrik, sistem seumur hidup akan di-anggap sebagai variabel tersensor. Maka standar dari Kaplan-Meier produk limit estimator dari fungsi survival akan digunakan untuk mengestimasi nilai dari Fi. Dimisalka, terdapat hanyak= 2 resiko yang bekerja di sistem ini. Pengujian un-tuk hipotsis null H0 :F1(x) =F2(x). Sekarang dimisalkan bahwa F1(x) =F0(x), dispesifikasikan untuk sebuah fungsi distribusi dan F2(x) = Fθ(x), θ > 0 bagian dari keluarga parametrik yang sama. Kemudian dihitung uji rank Locally Most Powerful (LMP) untuk H0 : θ = 0 terhadap H1 : θ > 0. Di sini statistik pe-ringkat didefinisikan dengan cara berikut: Diberikan Th1i < Th2i < . . . < Thni
adalah ketahanan dari n sistem yang independen. Diberikan Wj merupakan δ yang berhubungan ke Thii . Maka tipe dari statistiknya:
S = n
X
j=1
CjWj
men-32
Dalam model statistik. Dalam model logistik dengan:
Fθ(x) = (1 +e−(x+θ))−1
Uji peringkat LMP adalah dasar dari statistik dengan bentuk:
V =
Biasanya bentuk ekuivalen dari statistiknya dapat diekspresikan sebagai statistik peringkat linier . Di mana yang terkandung di dalam literatur:
(i) U1 =
Distribusi berhingga dari setiap adalah normal mengikuti statistik U-asimtotik. Distribusi null yang tepat ditemukan dengan menggunakan teknik Moment Gene-rating Function. Pada kenyataannya dapat dilihat bahwa U1 memiliki distribusi null yang sama dengan statistik peringkat Wilcoxon dengan (n−1) diganti dengan
n.
Analisis dari resiko bersaing terikat (Dependent)
di-33
dari (T, δ) dengan Si(t), i = 1,2. Selain dari bagian yang telah didiskusikan sebelumnya, dapat dilihat bahwa dari X dan Y yang independen tidak dapat diuji untuk basis dari data resiko bersaing. Dapat dipahami hanya pertanyaan statistik yang mengakui distribusi peluang dari (T, δ) terkait. Telah diperlihatkan pertanyaan di dalam istilah dari penyebab spesifik dari hazard rate (Kalbfleisch, 1980):
λi(t) = lim 0∆i→0
1
∆iP [t < T ≤∆i, δ= 2−i|T > t], i= 1,2, dimana telah dikonsentrasikan kedalam peluang dengan kondisi Q
i(t) = P(δ = 2−i|T = t). Pembahasan berikut dipusatkan kepada pertanyaan yang dimun-culkan dalam istilah dari Si(t), i = 1,2 secara langsung dan metodologi yang dikembangkan untuk pertanyaan tersebut.
Fungsi insiden yang empirik Sin(t) mengandung estimator yang konsisten dari fungsi insiden yang sebenarnya, dimana Sin(t) didefinisikan sebagai:
Sin(t) = 1
n
n
X
j=1
I(Tj > t, δj = 2−i), i= 1,2.
Permasalahan dari estimator Bayes dari nilai yaitu:
Sin(t) at 0< ti < t2 < . . . < tk <∞
telah dibahas. Dapat ditunjukkan bahwa estimator dari Si(tj) dengan batasan:
Si(t1)> Si(t2)> . . . > Si(tk)
dan
S1(tk) +S2(tk)≤1
dapat diperoleh distribusi Dirichlet sebelumnya untuk perbedaan:
pij =Si(tj−1)−Si(tj).
34
Telah dikembangkan teori dari fungsi respon untuk mempelajari perbedaan di antara fungsi distribusi. Model yang disarankan untuk fungsi insiden dari dua resiko adalah sebagai berikut:
Model I
S1(t) = θ
1−θS2(t),0< θ <1
Model ini memperlihatkan situasi dimana T dan δ independen. Juga ekuivalen ke keproporsionalan dari dua penyebab spesifik dari hazard rate .
Model II
S1(α1) =S2(t), t > α >0
Di dalam lingkungan gabungan, resiko pertama merupakan berpengaruh terhadap kenaikan umurt sama seperti resiko kedua yang berpengaruh terhadap αt, untuk setiap t >0 .
Model III
S1(t) = (θS(t))v;S2(t) =S(t)−(θS(t))v, v >0,0< θ <1, dimana S(t) =P[T > t] .
Di dalam kasus resiko bersaing yang dependen, maka dapat dilihat bagaima-na kedua resiko sama kuat, hal ini mebagaima-narik untuk menguji hipotesis dari bivariate simetri dengn alternatif satu sisi, misalkan:
H0 :F(x, y) =F(y, x) ∀x, y terhadap
35
Jika didefinisikan si(t) untuk i = 1,2 fungsi subdensity sesuai untuk dua fungsi insiden, maka likelihood marginal dariR1 = (R
1, . . . , Rn), urutan dari (T1, . . . , Tn) dan sesuai indikasi W1 = (W
1, W2, . . . , Wn) dapat ditulis sebagai
P[θ|R, W] =
Z n
Y
i=1
{s(ti, θ)}Wi{h(ti)−s(ti, θ)}1−Widt
dimana integralnya atast1 < t2 < . . . < tndanh(t) adalah kepadatan yang sesuai untuk H(t) =P[T ≤t] .
Telah diperlihatkan bahwa uji secara lokal yang paling kuat untukH0 :θ =
θ0 terhadap H1 :θ > θ0 sebagai berikut:
tolakH0, jikaL= n
X
j=1
Wjaj terlalu besar
disini
aj =
Z
s′(t
j, θ0)
s(tj, θ0) n
Y
i=1
S(ti, θ0)dti,
dan integral dengan batasant1 < t2 < . . . < tn. Jika bagian s1 dans2 dimodifikasi dari peluang kepadatan yang telah diketahui, maka akan diperoleh uji yang sudah diketahui untuk resiko bersaing sebagai uji LMP rank .
Telah digunakan statistik Kolmogorov-Smirnov
Dn =√n|S1n(t)−S2n(t)|
BAB 5 KESIMPULAN
DAFTAR PUSTAKA
Agustina, Fitriani dan Bambang, Avip Priyatna. 2000.Estimasi Fungsi Hazard de-ngan Menggunakan Wavelet. Jurusan Pendidikan Matematika FMIPA UPI, Bandung.
Bebbington, M., Zitikis, R. dan Lai, C. D. 2007. Modeling human mortality us-ing mixtures of bathtub shaped failure distributions. Journal of Theoretical Biology; 245:528-538.
Bebbington, M., Zitikis, R. dan Lai, C. D. 2007. Optimum burn-in time for a bathtub shaped failure distribution. Methodology and Computing in Applied Probability 2007; 9:120.
Bebbington, M., Zitikis, R. dan Lai, C. D. 2008. Reduction in Mean Residual Life in the presence of a constant Competing Risk. Institute of Information Science and Technology, Massey University, New Zealand.
Belzunce, F., Ortega, E., Ruiz J.M. 2007. On non-monotonic ageing properties from the Laplace transform, with actuarial applications. Insurance: Mathe-matics and Economics; 40:114
David, H. A. dan Moeschberger, M. L., 1978. The Theory of Competing Risk, Monograph, Griffin, London.
Denuit M. 2001. Laplace transform ordering of actuarial quantities. Insurance: Mathematics and Economics; 29:83102.
Gauss, F. dan F. Proschan. Mean Residual Life : Theory and Applications Tech-nical Report85-178, North Carolina State University and Florida State Uni-versity. Tellahasse, Florida, 1985.
Hall, W.J dan Wallner, Jon A. 1981. Mean Residual Life. Statistics Departement University of Rochester, New York U.S.A.
Hwang Jung Yoon. 2004. Spatial Stochastic Processes for Yield and Reliability Management with Application. Submitted to the Office of Graduate Studies of Texas A & M University.
Kalbfleisch, J. D. dan Prentice, R. L., 1980. Statistical Analiysis of Failure Time, Willey.
Klein, J. P., Moeschberger, L. M. 2005.Survival Analysis: Techniques for Censored and Truncated Data (Statistics for Biology and Health). Springer.
Klugman, S. A, Panjer, H. H. Willmot, G. E. 2004. Loss Models From Data to Decisions. A John Wiley & Sons, Inc, Publication.
38
Sun, Y. dan Tiwari, R. G. 1995.Analysis of Censored Data, IMS-LNMS, Hayword. Oakes, D., Dasu, T. 2003.Inference for the Proportional Mean Residual Life Model.
University of Rochester and AT & T Labs Research.