PERBANDINGAN MODEL AUTOREGRESSIVE
DAN MODEL ANALISIS PATH
UNTUK DATA SUHU MINIMUM
PONDOK BETUNG TANGERANG
TAHUN 2007
Abdurrahman Ahadiansyah
PROGRAM STUDI MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI
SYARIF HIDAYATULLAH
JAKARTA
PERBANDINGAN MODEL AUTOREGRESSIVE
DAN MODEL ANALISIS PATH
UNTUK DATA SUHU MINIMUM
PONDOK BETUNG TANGERANG
TAHUN 2007
Skripsi
Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Sarjana Sains
Fakultas Sains dan Teknologi
Universitas Islam Negeri Syarif Hidayatullah Jakarta
Oleh :
Abdurrahman Ahadiansyah
104094003016
PROGRAM STUDI MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI
SYARIF HIDAYATULLAH
JAKARTA
PENGESAHAN UJIAN
Skripsi berjudul “Perbandingan Model Autoregressive dan Model Analisis Path untuk Data Suhu Minimum Pondok Betung Tangerang” yang ditulis oleh Abdurrahman Ahadiansyah, NIM 104094003016 telah di uji dan dinyatakan lulus dalam sidang Munaqosah Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta pada hari ..., .... Skripsi ini telah diterima sebagai salah satu syarat untuk memperoleh gelar Sarjana Strata Satu (S1) Program Matematika.
Menyetujui :
Penguji 1, Penguji 2,
Nur Inayah, S.Pd, M.Si Cecep Anwar HFS, M.Si NIP. 150 326 911
Pembimbing 1, Pembimbing 2,
Hermawan Setiawan, M.Kom Nina Fitriyati, M.Kom
NIP. 250 000 505 NIP. 150 377 448
Mengetahui :
Dekan Fakultas Sains dan Teknologi, Ketua Program Studi Matematika,
Dr. Syopiansyah Jaya Putra, M.Sis Nur Inayah, S.Pd, M.Si
PERNYATAAN
DENGAN INI SAYA MENYATAKAN BAHWA SKRIPSI INI BENAR-BENAR HASIL KARYA SENDIRI YANG BELUM PERNAH DIAJUKAN SEBAGAI SKRIPSI PADA PERGURUAN TINGGI ATAU LEMBAGA MANAPUN.
Jakarta, 22 Juni 2009
Abdurrahman Ahadiansyah
ABSTRAK
Banyak metode untuk memprediksikan sesuatu hal yang akan terjadi. Misalkan memprediksi terjadinya banjir, naik turunnya nilai mata uang, dan lain-lain. Adapun metode yang digunakan antara lain Autoregressive(AR), Autoregressive Moving Average(ARMA), Autoregressive Integrated Moving Average(ARIMA) untuk meneliti tentang yang akan terjadi. Dalam penelitian ini menggunakan metode Autoregressive dan metode analisis Path. Dengan membandingkan metode Autoregressive dengan metode analisis Path terhadap data suhu minimum Pondok Betung Tahun 2007. Untuk mengetahui metode yang lebih baik melalui perbandingan nilai Mean Absolute Persentage Error (MAPE)
Hasil peramalan dan perbandingan nilai MAPE dari data suhu minimum Pondok Betung tahun 2007, metode Autoregressive lebih baik dibandingkan dengan metode analisis Path karena memiliki nilai MAPE yang lebih kecil dari metode analisis Path.
ABSTRACT
Many methods for the predicted something will happen. Suppose predict the occurrence of floods, increased depreciation of currencies, and others. used to examine what will happen later as well as predicted when the occurrence of floods, increased depreciation of currencies and others. In this research using Autoregressive methods and Path analysis methods. By comparing the method with the method Autoregressive analysis of the data path Pondok Betung minimum temperature in 2007. To find out a better method through comparison of the value of Mean Absolute Error Persentage (MAPE)
Forecasting results and comparison of data values Mape Pondok Betung minimum temperature in 2007, Autoregressive method better than the method of Path analysis for the value of smaller Mape's Path analysis method.
Key word: Autoregressive, Path Analysis and MAPE Comparison
PERSEMBAHAN
Skripsi ini aku persembahkan untuk ibuku Ety Kusumayati, ayahku Sugeng Hidayat, adik-adikku, seluruh keluarga, dan keluarga besar Prodi Matematika serta
teman-teman yang aku sayangi.
MOTTO
”Maka barang siapa mengerjakan kebaikan seberat zarrah, niscaya dia akan melihat(balasan)nya. Dan barang siapa yang mengerjakan kejahatan seberat
KATA PENGANTAR
Segala puji bagi Allah SWT yang telah memberikan karunia nikmat dan rahmat-Nya kepada kita, Shalawat serta salam semoga senantiasa tercurahkan kepada junjungan besar kita Nabi Muhammad SAW beserta para sahabatnya, tanpa mereka agama Islam yang sempurna ini tidak akan sampai kepada kita
Dengan segala kemudahan dan kelancaran yang telah diberikan oleh Allah SWT sehingga penulis dapat menyelesaikan Skripsi dengan judul
“PERBANDINGAN MODEL AUTOREGRESSIVE DAN MODEL ANALISIS
PATH UNTUK DATA SUHU MINIMUM PONDOK BETUNG TANGERANG
TAHUN 2007”. Dan penulis sangat menyadari bahwa laporan ini dapat diselesaikan karena dukungan dan bantuan dari berbagai pihak. Oleh karena itu pada kesempatan ini penulis ingin menyampaikan terima kasih kepada:
1. Dr. Syopiansyah Jaya Putra, M.Sis, Dekan Fakultas Sains dan Teknologi
2. Nur Inayah, M.Si, Ketua Program Studi Matematika dan Nina Fitiriyati, M.Kom, Sekretaris Program Studi Matematika, Pembimbing II
3. Hermawan Setiawan, M.Kom, Pembimbing I
4. Papa Sugeng dan Mama Ety, terima kasih untuk semua doa serta dorongan spiritual sehingga skripsi ini bisa terselesaikan
6. Ibu Ida, Kepala Bidang Managemen Data Badan Meteorologi dan Geofisika, dan seluruh staff Badan Meteorologi dan Geofisika
7. Untuk Mega, terima kasih untuk semua bantuannya, semoga kamu bisa memberikan aku semangat secara terus menerus
8. Untuk Ninda, Riri, Feby dan Koyah, semangatnya sudah tersampaikan, semoga kalian selalu berada dalam lindungan-Nya
9. Untuk Beny, Wawan dan Mutaqin, Nasihatnya udah dijalankan, perjuangan kita masih belum berakhir
10.Untuk semua teman seperjuangan yang masih berjuang menyusun skripsi, tetap semangat
11.Teman-teman mahasiswa matematika angkatan 2002 s/d 2007.
Semoga kita semua berada dalam lindungan-Nya dan selalu mendapatkan rahmat dan hidayah-Nya, Amin.
Jakarta, 12 Juni 2009
DAFTAR ISI
HALAMAN JUDUL ... i
PENGESAHAN UJIAN ... ii
PERNYATAAN ... iii
PERSEMBAHAN DAN MOTTO ... iv
ABSTRAK ... v
ABSTRACT ... vi
KATA PENGANTAR ... vii
DAFTAR ISI ... ix
DAFTAR TABEL ... xi
DAFTAR GAMBAR ... xii
DAFTAR LAMPIRAN ... xiii
BAB I PENDAHULUAN ... 1
1.1. Latar Belakang ... 1
1.2. Permasalahan ... 2
1.3. Pembatasan Masalah ... 2
1.4. Tujuan Penelitian ... 2
1.5. Manfaat Penelitian... 3
BAB II LANDASAN TEORI ... 4
2.1. Data Deret Waktu ... 4
2.2. Kestasioneran ... 5
2.2.2. Pengujian Stasioneritas Berdasarkan Akar-akar Unit ... 7
2.3. Fungsi Autokorelasi (ACF) ... 8
2.4. Fungsi Autokorelasi Parsial (PACF) ... 11
2.5. Model Autoregressive (AR) ... 13
2.6. Analisis Path... 16
BAB III METODOLOGI PENELITIAN 3.1 Waktu dan Tempat Penelitian ... 23
3.2 Metode Pengumpulan Data ... 23
3.3 Metode Pengolahan Data ... 23 3.4 Alur Penelitian ... 25
BAB IV HASIL DAN PEMBAHASAN ... 26
4.1. Uji Stasioner Data ... 26
4.2. Analisis Model Autoregressive... 29
4.3. Hasil Peramalan Model Autoregressive... 30
4.4. Analisis Model Path... 31
4.5. Hasil Peramalan Model Analisis Path... 36
4.3. Perbandingan Model... 38
BAB V KESIMPULAN DAN SARAN ... 40
5.1. Kesimpulan ... 40
5.2. Saran ... 41
REFERENSI ... 42
DAFTAR TABEL
[image:12.595.109.521.208.563.2]Tabel 4.1 Deskripsi Data Suhu Minimum... 26 Tabel 4.2 Hasil Pengolahan ACF dan Correlogram dari Data Suhu Minimum 27 Tabel 4.3 Hasil Uji Akar-akar Unit ... 28 Tabel 4.4 Hasil Peramalan Model Autoregressive... 30 Tabel 4.5 Hasil Peramalan Model Analisis Path... 36
DAFTAR GAMBAR
Gambar 2.1. Stasioner dalam Rata-rata Hitung... 5
Gambar 2.2. Stasioner dalam Varians ... 6
Gambar 2.3. Grafik Correlogram data yang stasioner ... 6
Gambar 2.4. Model 2 faktor ... 17
Gambar 2.5. Model 3 faktor ... 17
Gambar 2.6. Model n Faktor ... 18
Gambar 3.1. Alur Penelitian... 24
Gambar 4.1. Plot Data Suhu Minimum Tahun 2007... 25
Gambar 4.2. Plot Peramalan Suhu Minimum tahun 2008 Mengunakan Model Autoregressive... 30
Gambar 4.3. Diagram Analisis Path Order 2 ... 31
Gambar 4.4. Diagram Analisis Path Order 3 ... 32
Gambar 4.5. Diagram Analisis Path Order 4 ... 33
Gambar 4.6. Diagram Analisis Path Order 5 ... 34
Gambar 4.7. Plot Peramalan Suhu Minimum tahun 2008 dengan Mengunakan Metode Analisis Path... 37
DAFTAR LAMPIRAN
Lampiran 1. Data Suhu Minimum Daerah Pondok Betung Tahun
2007 ... 43 Lampiran 2. Langkah-langkah Membuat Model Autoregressive
dengan Menggunakan Software E-View 4.1... 44 Lampiran 3. Langkah-langkah dalam mengestimasi nilai f
Menggunakan program Amos 7. ... 47 Lampiran 4. Langkah-langkah dalam Menguji Kestasioneran Menggunakan
BAB I
PENDAHULUAN
1.1. Latar Belakang
Indonesia termasuk negara beriklim tropis sehingga di wilayah ini tidak ditemukan musim dingin tetapi memiliki tingkat curah hujan yang cukup tinggi. Hal ini dikarenakan wilayah perairan Indonesia mendapatkan sinar matahari yang kuat sepanjang tahun serta posisi matahari yang tepat melintasi khatulistiwa 2 kali dalam setahun. Sehingga Indonesia hanya memiliki 2 musim yaitu kemarau dan hujan. Musim kemarau terjadi dari bulan Mei hingga Agustus dan musim hujan dari Oktober hingga Maret.Tingkat curah hujan di Indonesia pun cukup tinggi walaupun suhu udara rata-rata di Indonesia tidak memiliki perbedaan yang mencolok antar musim, namun demikian suhu udara merupakan salah satu unsur iklim yang perlu diamati. Hal ini berkaitan dengan aplikasi suhu udara untuk berbagai keperluan antara lain mendeteksi daerah rawan banjir, prakiraan cuaca maupun iklim, mengetahui kondisi pemanasan global dan lain sebagainya.
Judul penelitian yang penulis lakukan adalah “Perbandingan Model Autoregressive dan Model Analisis Path untuk Data Suhu Minimum Pondok
Betung Tangerang Tahun 2007”.
1.2. Permasalahan
Permasalahan dapat dirumuskan sebagai berikut:
Bagaimana perbandingan nilai Mean Absolute Persentage Error (MAPE) dari model Autoregressive dan model analisis Path?
1.3. Pembatasan Masalah
Penulis membatasi masalah sebagai berikut:
1. Suhu minimum ini tidak membahas seluruh wilayah Indonesia hanya mencakup stasiun klimatologi Pondok Betung Tangerang tahun 2007.
2. Metode Autoregressive order kedua hingga order kelima. 3. Metode Analisis Path order kedua hingga order kelima.
1.4. Tujuan Penulisan
1.5. Manfaat Penelitian
Manfaat dari penelitian ini antara lain:
1. Mengetahui cara kerja metode Autoregressive. 2. Mengetahui cara kerja metode analisis Path.
BAB II
LANDASAN TEORI
2.1Data Deret Waktu
Pada dasarnya setiap nilai dari hasil pengamatan, selalu dapat dikaitkan dengan waktu pengamatannya. Hanya pada saat analisisnya, kaitan variabel waktu dengan pengamatan sering tidak dipersoalkan. Dalam hal kaitan variabel waktu dengan pengamatan diperhatikan, sehingga data dianggap sebagai fungsi atas waktu, menurut [2] data seperti ini dinamakan data deret waktu (time series).
Menurut [2], ada beberapa jenis pola data deret waktu, diantaranya: 1. Pola stasioner adalah pola yang terbentuk karena data berfluktuasi di sekitar
nilai rata-rata yang konstan
2. Pola trend adalah pola yang terbentuk karena terdapat kenaikan atau penurunan data untuk jangka waktu yang panjang
3. Pola musiman adalah suatu deret data dipengaruhi oleh faktor berskala musiman (misalnya kuartal, tahunan, bulanan, atau hari pada minggu tertentu).
4. Pola siklis adalah suatu deret data yang terjadi bilamana datanya dipengaruhi oleh fluktuasi ekonomi jangka panjang seperti yang berhubungan dengan siklus bisnis atau ekonomi.
2.2 Kestasioneran
Kestasioneran data merupakan kondisi yang diperlukan dalam analisis deret waktu karena dapat meminimalkan kekeliruan model, sehingga jika data tidak stasioner maka harus dilakukan transformasi stasioneritas melalui proses diferensi. Data yang tidak stasioner memiliki rata-rata atau varian yang tidak konstan sepanjang waktu. Dengan kata lain, secara khusus data stasioner adalah data yang tidak mengalami kenaikan dan penurunan.
Secara umum, menurut [6] kestasioneran data diklasifikasikan atas tiga bentuk, yaitu
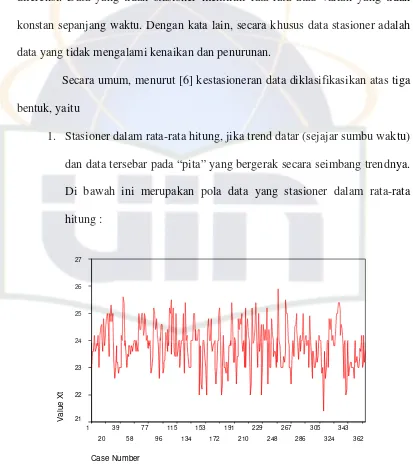
1. Stasioner dalam rata-rata hitung, jika trend datar (sejajar sumbu waktu) dan data tersebar pada “pita” yang bergerak secara seimbang trendnya. Di bawah ini merupakan pola data yang stasioner dalam rata-rata hitung :
Case Number
362 343 324 305 286 267 248 229 210 191 172 153 134 115 96 77 58 39 20 1
V
a
lu
e
X
t
27
26
25
24
23
22
[image:19.595.112.525.230.696.2]21
2. Stasioner dalam varians, jika trend datar dan data tersebar membangun pola melebar atau menyempit yang bergerak secara seimbang trendnya. Adapun bentuk polanya adalah sebagai berikut:
Gambar 2.2 Stasioner dalam Varians
3. Stasioner dalam rata-rata hitung dan varians, jika trend datar dan data tersebar membangun pola melebar sejajar sumbu waktu.
Menurut [8], untuk pengujian stasioneritas dapat dilakukan dengan beberapa metode seperti uji correlogram yang terdiri dari grafik ACF dan PACF dan uji akar-akar unit, di antaranya yaitu:
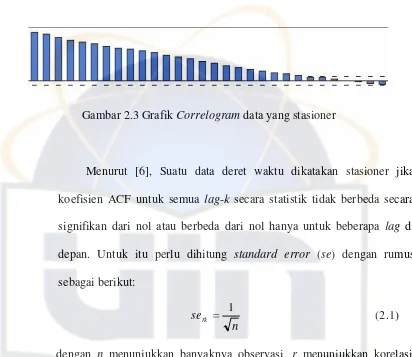
2.2.1. Pengujian Stasioneritas Berdasarkan Correlogram
berbeda, hal ini dapat dilihat dari nilai ACF pada berbagai jarak (lag) yang terdapat pada grafik correlogram.
Gambar 2.3 Grafik Correlogram data yang stasioner
Menurut [6], Suatu data deret waktu dikatakan stasioner jika koefisien ACF untuk semua lag-k secara statistik tidak berbeda secara signifikan dari nol atau berbeda dari nol hanya untuk beberapa lag di depan. Untuk itu perlu dihitung standard error (se) dengan rumus sebagai berikut:
n serk 1
(2.1)
dengan n menunjukkan banyaknya observasi, r menunjukkan korelasi dan k menunjukkan banyaknya lag.
2.2.2. Pengujian stasioner berdasarkan akar-akar unit
Sebuah tes stasioner atau non-stasioner yang menjadi sangat populer beberapa tahun belakangan adalah akar-akar unit. Stasioner dapat diperiksa dengan mencari akar unit data deret waktu, jika data deret waktu mengandung akat unit maka data tersebut tidak stasioner.
pengujian kestasioneran data deret waktu untuk menentukan apakah suatu data deret waktu mengandung akar unit atau tidak. Di dalam pengujian ini dilakukan uji hipotesa menggunakan uji-t dan uji probabilitas, yaitu :
Ho : Data memiliki akar unit atau data tidak stasioner H
1 : Data tidak memiliki akar unit atau bersifat stasioner
Dengan 5%
Jika t-statistik < t-kritis : Ho ditolak Jika t-statistik > t-kritis : Ho diterima
Adapun rumus t-statistiknya, sebagai berikut:
ˆ ˆ se t
(2.2)
dengan
se: koefisien standard error ˆ : Parameter dari
t : t-statistik
Apabila penarikan kesimpulan menggunakan probabilitas maka: jika probabilitas < daripada taraf signifikan ( ) maka Ho ditolak jika probabilitas > dari maka Ho tidak ditolak.
2.3 Fungsi Autokorelasi (ACF)
dari variabel yang sama. Konsepsi autokorelasi setara dengan korelasi Pearson untuk data bivariat. Deskripsinya adalah sebagai berikut, jika dimiliki sampel data deret waktu X
1, X2,...,Xn dan dapat dibangun pasangan nilai (X1,Xk+1),(X2,Xk+2),...,(Xk,Xn) autokorelasi lag-k, dari sampel tersebut adalah sebagai berikut :
k n t t k n t t k n t k t t k t t k X X X X X X X X X X corr r 1 2 2 2 1 1 1 2 1
, (2.3)
Dengan :
a
X : data pada variabel pertama X1 ,X2,...,Xk b
X : data pada variabel kedua Xk 1,Xk 2,...,Xn
1
X : rata-rata pada verianbel pertama
2
X : rata-rata pada variabel kedua
Pada analisis data deret waktu, diperlukan nilai n yang cukup besar untuk mend apatkan hasil yang baik. Dan dalam praktek biasanya diperlukan
50 n . Jika n x x x x n t t 1 2
1 (2.4)
n t t k n t k t t k x x x x x x r 1 2 1 (2.5)
dan perumusan autokorelasi seperti inilah yang digunakan dalam analisis data deret waktu. Karena rk merupakan fungsi dalam k, maka hubungan autokorelasi
dengan lagnya dinamakan fungsi autokorelasi (ACF), dan dinotasikan oleh
n t t k n t k t t k k x x x x x x r 1 2 1
ˆ (2.6)
dengan:
t : periode k : jarak (lag)
xt : nilai pengamatan pada periode ke-t,
t k
x : nilai pengamatan pada periode ke-(t k ) x : rata-rata sampel data.
k : fungsi autokorelasi (ACF)
Jika dimiliki sampel data deret waktu, x1 ,x2,...,xn maka yang harus
dihitung untuk mendapatkan autokorelasi sampel lag-k secara “manual” adalah :
n t t x n x 1 1 (2.7)
2. Autokovarians sampel lag-k,
k n t k t t
k x x x x
k n S 1 1 (2.8)
3. Autokorelasi sampel lag-k,
0 S Sk k
(2.9)
2.4 Fungsi Autokorelasi Parsial (PACF)
Fungsi autokorelasi parsial (PACF), yang ditulis dengan notasi
kkdidefinisikan sebagai berikut:
n n kk
P
P
*(2.10)
Dengan Pn adalah matriks autokorelasi k kdan
*
n
P adalah Pn kolom
terakhir diganti dengan :
k
2 1
1 1 1 1 1 2 1 1
22 = 2 1 2 1 2 1
dan 1 1 1 1 1 2 2 1 1 2 1 3 2 2 2 1 1 1
33 = 2 2 2 2 1 2 1 3 3 2 1 2 2 1 2 1 3 1 2 2 1 2 (2.11) . Dan seterusnya.
Nilai estimasi kk
^
dapat diperoleh dengan mengganti k menjadi rk, yaitu: 1 1 , 1 11 1 , 1 ˆ 1 ˆ ˆ k j k j k k j j k j k k kk r r r
(2.12) dengan j k k kk j k
kj ˆ 1, ˆ ˆ 1,
ˆ untuk j=1,2,...,k-1 (2.13)
Menurut [6], Jika data deret waktu berautokorelasi pada lag-k, maka selanjutnya membangun model hubungan fungsional antar pengamatan (model order-k (lag-k), ditulis AR(k), yang persamaannya
a
x
x
x
x
t 1 t1 2 t 2 ... k t k t(2.14)
Dengan at adalah nilai error yang diasumsikan berdistribusi identik independen dengan rata-rata 0, varians konstan s2dan kadalah koefisien autokorelasi pada lag ke-k. Jika dalam persamaan regresi menunjukkan bahwa variabel dependen terhadap variabel lainnya dalam waktu yang bersamaan, maka model (2.14) menunjukkan bahwa variabel dependen terhadap variabel lainnya dengan waktu yang berbeda.
1. Model Autoregressive Order Pertama (AR(1))
Model autoregresi order pertama merupakan model regresi sederhana yang melibatkan variabel dependen Xt terhadap Xt-1, Xt-1 terhadap Xt-2, dan seterusnya. Oleh karena itu, dapat ditulis model relasi Xt dan Xt-1 secara matematis sebagai berikut
Xt Xt 1 at
(2.15) Dengan
Xt = nilai pengamatan periodde ke t Xt-1 = nilai pengamatan periode ke t-1
Karena a
t independen dengan Xt-1, maka dengan menggunakan varians pada kedua sisi pada persamaan (2.15) diperoleh:
t t
t X a
X var var
var 12 1
2 0 2 1
0 a
penyelesaian untuk 0menghasilkan 2 1 2 0 1 a (2.16)
Dari persamaan (2.15), maka persamaan untuk at adalah sebagai berikut:
1
t t
t X X
a (2.17)
Sedangkan nilai estimasi dari adalah:
N t t N t t t x x x x x x 2 2 1 2 1
(2.18)
2. Model Autoregressive Order Kedua (AR(2))
Pada model Autoregressive order 2 (AR(2)), variabel Xt terikat terhadap variabel Xt-1dan Xt-2 atau dengan kata lain varibel Xt terikat dengan 2 variabel lampau sebelum Xt.
Model Autoregressivenya sebagai berikut:
x
x
x
a
t t t
t 1 1 2 2
x
x
x
a
t t 1 t 1 2 t 2(2.20) Untuk mencari nilai estimasi dari 1 dan 2 dapat ditunjukkan dalam
bentuk matriks yaitu:
x
x
x
N Y ... 4 3x
x
x
x
x
x
N N X 2 1 2 3 1 2 ... ... 2 1 2 1 2 1 1 2 1 1 2 2 ' N t t N t t t N t t t N t tx
x
x
x
x
x
X X dan N t t t N t t tx
x
x
x
Y X 3 2 3 1 ' makaY
X
X
X
'
1'
2 1
(2.21) dengan '
X = matriks transpos dari X (variabel bebas)
1
'X
X = matriks inverse dari X’X
Analisis Path adalah sebuah metode untuk menguji teori dan kesesuaian model yang akan dikembangkan menjadi sebuah persamaan struktural. Menurut [4], teknik analisis Path ini pertama kali dikembangkan oleh Sewell Wright pada tahun 1930-an. Teknik ini digunakan untuk menguji hubungan kausal yang diduga masuk akal antara satu variabel dengan variabel yang lain didalam kondisi non-eksperimental.
Adapun jenis variabel yang terdapat dalam analisis Path ini diantaranya: 1. Variabel eksogen adalah variabel yang variabilitasnya diasumsikan bahwa
nilainya ditentukan oleh sebab-sebab yang berada diluar model atau lebih dikenal dengan variabel bebas.
2. Variabel endogen adalah variabel yang terikat dalam sistem atau disebut juga variable terikat.
3. Variabel kesalahan adalah semua faktor lain yang mempengaruhi variabel endogen dan dapat dipandang sebagai gabungan semua faktor eksogen yang tidak diukur.
Berdasarkan jenis data yang diperoleh, analisis Path hanya memiliki variabel terukur yaitu variabel yang diperoleh melalui pengamatan, survey dan test.
Dalam metode analisis Path, ada beberapa tahapan dalam pembuatan sebuah model sebelum diestimasi nilai keakuratan modelnya, yaitu:
Analisis Path berbasis kepada hubungan sebab akibat, dimana perubahan sebuah variabel diasumsikan menghasilkan perubahan kepada variabel lainnya.
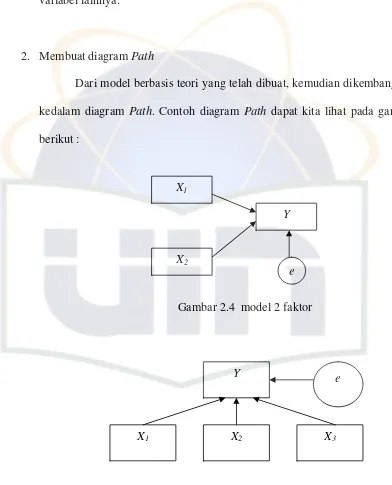
2. Membuat diagram Path
[image:31.595.110.502.176.661.2]Dari model berbasis teori yang telah dibuat, kemudian dikembangkan kedalam diagram Path. Contoh diagram Path dapat kita lihat pada gambar berikut :
Gambar 2.4 model 2 faktor
Gambar 2.5 Model 3 faktor X1
Y
e X2
X3 X2
X1
...
Gambar 2.6 Model n Faktor
Keterangan gambar:
X : variabel eksogen (independen) Y : variabel endogen (terikat) e : nilai error
? : variabel terukur ? : variabel laten
Dari diagram Path diatas tampak bahwa ada variabel independen dan variabel dependen dengan e sebagai estimasi nilai error dari model tersebut.
3. Konversi diagram Path kedalam model struktural
Tahap ini adalah menterjemahkan diagram Path kedalam model struktural yang lebih formal. Dari gambar yang ditunjukkan pada gambar 2.4 maka model persamaan strukturalnya adalah sebagai berikut:
dengan ß
1 dan ß2 adalah koefisien regresi dari model tersebut dan e adalah estimasi nilai error yang dihasilkan. Setelah itu data disubstitusi berdasarkan asumsi hubungan antar variabel.
Secara umum, untuk mencari nilai koefisien regresi dapat menggunakan metode least square dengan tujuan untuk meminimumkan Sum Square Error (SSE), dengan persamaan SSE:
N i i e SSE 1 2 (2.23)
dan persamaan least square:
n Y Y Y Y 2 1 p n n n p p X X X X X X X X X X , 2 , 1 , , 2 22 21 , 1 12 11 p 2 1 ˆ p 2 1
ˆ
Dengan melakukan penurunan rumus dalam bentuk matriks dari persamaan di atas dan mengangap nilai matriks ˆ sama dengan nol, maka diperoleh :
Y Xˆ
ˆ X'X 1X'Y
(2.24) dengan :
'
1
'X
X = matriks inverse dari X’X
4. Identifikasi model.
Menentukan derajat bebas dari model yang dibuat. Perbedaan antara banyaknya koefisien yang harus diestimasi dengan banyaknya korelasi atau kovarians inputnya disebut sebagai derajat bebas (df).
Persamaan derajat bebas dapat ditulis sebagai berikut:
df 1 2 p q p q 1 t (2.25)
dengan,
p : banyaknya variable terikat (endogen), q : banyaknya variable bebas (eksogen),
t : banyaknya koefisien yang diestimasi pada model yang diteliti.
Selanjutnya dilakukan proses evaluasi model dengan kriteria goodness of fit. dimana dalam tahapan ini ada beberapa hal yang perlu dievaluasi, diantaranya kesalahan estimasi, kesesuaian model secara keseluruhan, kesesuaian model pengukuran dan kesesuaian model struktural.
5. Interpretasi dan modifikasi model.
sedangkan kategori empiris yang memiliki hubungan yang baru bisa ditambahkan.
2.7 Uji Tingkat Ketepatan Model dengan MAPE
Salah satu metode yang digunakan untuk menguji ketepatan model data deret waktu adalah Mean Absolute Persentage Error (MAPE), yang dihitung menggunakan persamaan berikut:
^ 1
100
t t
n t
t
X X X MAPE
n (2.26)
dengan:
^
t
X : hasil peramalan pada saat t, Xt: Data aktual, dan
n : Banyaknya data yang diramalkan.
BAB III
METODOLOGI PENELITIAN
3.1 Waktu dan Tempat Penelitian
Penelitian ini dilaksanakan di kantor Balai II Badan Meteorologi dan Geofisika Pondok Betung pada bulan Agustus tahun 2008. Dengan mempertimbangkan variabel-variabel yang mempengaruhi proses terjadinya hujan yang terjadi belakangan ini. Berupa data suhu harian dari tahun 2007 di wilayah Pondok Betung.
3.2 Metode Pengumpulan Data
Pada penelitian ini data yang digunakan adalah data sekunder, yaitu data berupa transkip cuaca seperti kelembaban udara, suhu maksimum, suhu minimum, curah hujan dan kecepatan angin maksimum pada bulan Januari 2007 hingga Desember 2007 yang diperoleh dari arsip Balai II Badan Meteorologi dan Geofisika kecamatan Pondok Betung. Data diperoleh dari divisi Managemen data berupa transkrip data cuaca pada stasiun Klimatologi Pondok Betung.
3.3 Metode Pengolahan Data
Adapun tahap-tahap dalam pengolahan data : 1. Uji stasioner
Setiap data deret waktu sebelum di analisis terlebih dahulu di uji kestasioneran data jika tidak stasioner lakukan diferensi hingga data menjadi stasioner setelah itu baru dilakukan analisis.
2. Analisis model Autoregressive
Analisis ini bertujuan untuk mengestimasi nilai dari order kedua hingga order kelima
3. Peramalan dengan metode Autoregressive dari order kedua hingga kelima 4. Analisis model analisis Path
Analisis ini dilakukan estimasi untuk mengestimasi nilai dari order kedua hingga kelima
5. Peramalan dengan metode analisis Path dari order kedua hingga kelima 6. Perbandingan model dengan nilai MAPE
Hitung nilai MAPE yang didapat dari hasil prediksi kedua metode diatas sehingga dapat dibandingkan metode mana yang lebih baik.
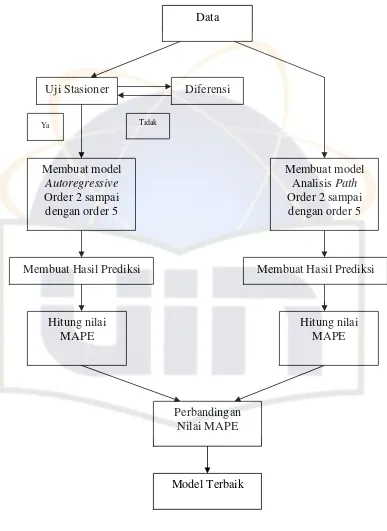
Alur pengolahan data pada penelitian ini adalah seperti Gambar 3.1.
Gambar 3.1. Alur Penelitian Data
Uji Stasioner
Membuat Hasil Prediksi
Membuat model Analisis Path Order 2 sampai dengan order 5
Perbandingan Nilai MAPE
Membuat Hasil Prediksi
Hitung nilai MAPE
Hitung nilai MAPE Membuat model
Autoregressive Order 2 sampai dengan order 5
Ya
Diferensi
Tidak
BAB IV
HASIL DAN PEMBAHASAN
4.1 Uji Stasioner Data
Sebelum melakukan pemodelan dan peramalan suhu minimum, terlebih dahulu diuji kestasioneran data. Uji stasioneritas dilakukan menggunakan uji correlogram dan uji akar unit dengan menggunakan lag sebanyak 30 hari.
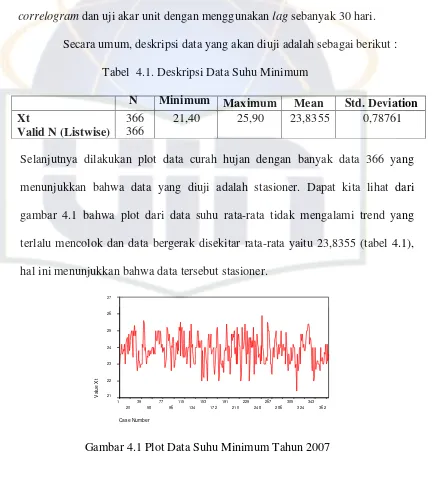
Secara umum, deskripsi data yang akan diuji adalah sebagai berikut : Tabel 4.1. Deskripsi Data Suhu Minimum
N Minimum Maximum Mean Std. Deviation
Xt
Valid N (Listwise)
366 366
21,40 25,90 23,8355 0,78761
Selanjutnya dilakukan plot data curah hujan dengan banyak data 366 yang menunjukkan bahwa data yang diuji adalah stasioner. Dapat kita lihat dari gambar 4.1 bahwa plot dari data suhu rata-rata tidak mengalami trend yang terlalu mencolok dan data bergerak disekitar rata-rata yaitu 23,8355 (tabel 4.1), hal ini menunjukkan bahwa data tersebut stasioner.
[image:39.595.111.544.266.747.2]Case Number 362 343 324 305 286 267 248 229 210 191 172 153 134 115 96 77 58 39 20 1 V a lu e X t 27 26 25 24 23 22 21
[image:39.595.195.439.550.691.2]Untuk mendukung pengamatan berdasarkan plot suhu minimum tahun 2007, maka akan dilakukan uji stasioneritas dengan menggunakan uji correlogram dan uji akar unit.
[image:40.595.112.551.238.750.2]Berikut ada hasil pengolahan ACF dan Correlogram dari data asli :
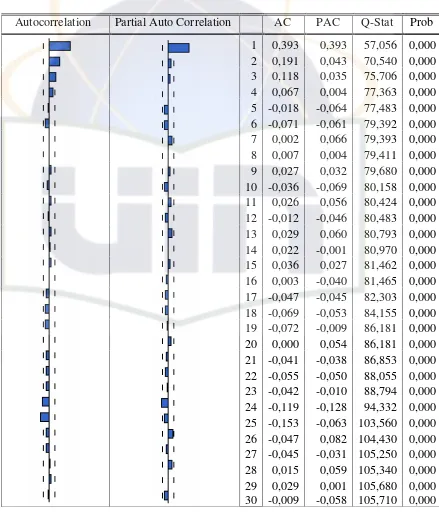
Tabel 4.2 Hasil Pengolahan ACF dan Correlogram dari Data Suhu Minimum Autocorrelation Partial Auto Correlation AC PAC Q-Stat Prob
1 0,393 0,393 57,056 0,000
2 0,191 0,043 70,540 0,000
3 0,118 0,035 75,706 0,000
4 0,067 0,004 77,363 0,000
5 -0,018 -0,064 77,483 0,000
6 -0,071 -0,061 79,392 0,000
7 0,002 0,066 79,393 0,000
8 0,007 0,004 79,411 0,000
9 0,027 0,032 79,680 0,000
10 -0,036 -0,069 80,158 0,000
11 0,026 0,056 80,424 0,000
12 -0,012 -0,046 80,483 0,000
13 0,029 0,060 80,793 0,000
14 0,022 -0,001 80,970 0,000
15 0,036 0,027 81,462 0,000
16 0,003 -0,040 81,465 0,000
17 -0,047 -0,045 82,303 0,000
18 -0,069 -0,053 84,155 0,000
19 -0,072 -0,009 86,181 0,000
20 0,000 0,054 86,181 0,000
21 -0,041 -0,038 86,853 0,000
22 -0,055 -0,050 88,055 0,000
23 -0,042 -0,010 88,794 0,000
24 -0,119 -0,128 94,332 0,000
25 -0,153 -0,063 103,560 0,000
26 -0,047 0,082 104,430 0,000
27 -0,045 -0,031 105,250 0,000
28 0,015 0,059 105,340 0,000
29 0,029 0,001 105,680 0,000
Tabel di atas menunjukkan hasil pengolahan uji correlogram, dari output tersebut diperoleh bahwa nilai koefisien ACF (Autocorrelation Function) mulai dari lag 1 (0,393) menurun secara eksponensial sampai pada lag 4 (0.067) lalu kembali naik ke arah negatif pada lag 5 (-0,018) dan seterusnya. Sehingga dapat disimpulkan bahwa data suhu minimum harian ini bersifat stasioner.
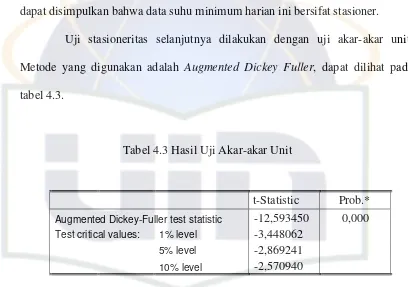
[image:41.595.109.517.271.558.2]Uji stasioneritas selanjutnya dilakukan dengan uji akar-akar unit. Metode yang digunakan adalah Augmented Dickey Fuller, dapat dilihat pada tabel 4.3.
Tabel 4.3 Hasil Uji Akar-akar Unit
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -12,593450 0,000
Test critical values: 1% level -3,448062
5% level -2,869241
10% level -2,570940
Dari hasil uji akar-akar unit di atas (tabel 4.3) dapat dilakukan uji t dan uji probabilitas, yaitu sebagai berikut:
H0 : Data memiliki akar unit atau data bersifat tidak stasioner
H1 : Data tidak memiliki akar unit atau data bersifat stasioner
Dari tabel diatas nilai t-statistic -12.59345 lebih kecil dari nilai kritis %
5 yaitu -2.869241 sehingga dapat disimpulkan bahwa H0 ditolak.
Apabila keputusan ditentukan dengan menggunakan nilai probabilitas maka nilai probabilitas tersebut dibandingkan dengan nilai .
Dari gambar 4.3 terlihat bahwa nilai probabilitas = 0.00 lebih kecil dari pada = 0.05 sehingga disimpulkan bahwa Ho ditolak.
Dari fakta yang diberikan oleh uji correlogram dan uji akar-akar unit maka dapat disimpulkan bahwa data bersifat stasioner. Untuk itu tidak perlu dilakukan pembedaan (differencing) pada data yang ada.
4.2 Analisis Model Autoregressive
Dari data suhu minimum daerah Pondok Betung tahun 2007 maka dapat dibuatkan model Autoregressive sebagai berikut:
Order kedua
Xt= 0.3767Xt-1 + 0,04311Xt-2 + at (4.1)
Order ketiga
Xt= 0,3752Xt-1 + 0,0295Xt-2+ 0,0347Xt-3+ at (4.2)
Order keempat
Xt= 0.375Xt-1 + 0,0295Xt-2+ 0,0326Xt-3+ 0,00426Xt-4+ at (4.3)
Order kelima
Untuk proses estimasi nilai dari tiap-tiap model dapat dilihat pada lampiran 2.
4.3. Hasil Peramalan Model Autoregressive
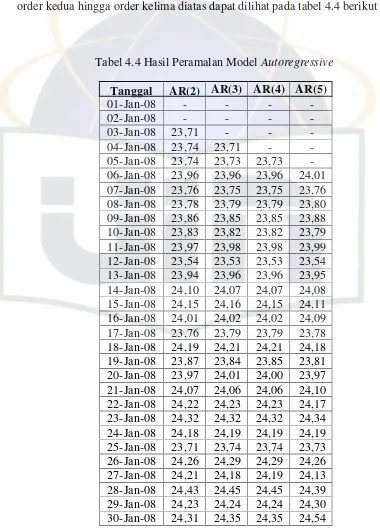
[image:43.595.113.493.228.760.2]Untuk peramalan suhu minimum tahun 2008 dari model Autoregressive order kedua hingga order kelima diatas dapat dilihat pada tabel 4.4 berikut ini:
Tabel 4.4 Hasil Peramalan Model Autoregressive
Tanggal AR(2) AR(3) AR(4) AR(5)
01-Jan-08 - - - -
02-Jan-08 - - - -
03-Jan-08 23,71 - - -
31-Jan-08 24,25 24,26 24,27 24,25
Adapun peramalan pada bulan-bulan berikutnya dapat dilihat pada lampiran 5. Sedangkan untuk plot peramalan dari tabel di atas adalah sebagai berikut:
21,5 22 22,5 23 23,5 24 24,5 25 25,5
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
[image:44.595.113.508.202.530.2]Aktual AR(2) AR(3) AR(4) AR(5)
Gambar 4.2 Plot Peramalan Suhu Minimum Tahun 2008 Mengunakan Model Autoregressive
4.4 Analisis Model Path
Dengan metode analisis Path, maka Analisis dari data suhu minimum daerah Pondok Betung tahun 2007 dapat dimodelkan sebagai diagram path sebagai berikut:
Order kedua
Gambar 4.3 Diagram Analisis Path Order 2
Dari gambar 4.3 maka persamaan model strukturalnya sebagai berikut:
Xt= 0.394Xt-1 + at (4.5)
Xt-1= 0.393Xt-2 + at (4.6)
untuk peramalan dari analisis Path order kedua hanya dilakukan pada ujung dari persamaan tersebut. Hal ini dikarenakan Xt+1terikat terhadap Xt dan tidak terikat oleh Xt-1maupun Xt-2. Sehingga, peramalan pada persamaan (4.6) diabaikan.
Order ketiga
Dengan asumsi bahwa variabel Xtterikat terhadap Xt-1. Variabel Xt-1terikat terhadap Xt-2. Variabel Xt-2 terikat terhadap Xt-3 maka diagram path order ketiga
dapat dilihat pada gambar dibawah ini: Xt
Xt-1
Xt-2 at
Gambar 4.4 Diagram Analisis Path Order 3
Dari gambar 4.4 maka persamaan model strukturalnya sebagai berikut:
Xt= 0.392Xt-1 + at (4.7)
Xt-1= 0.395Xt-2 + at-1 (4.8)
Xt-2= 0.392Xt-3 + at-3 (4.9)
untuk peramalan dari analisis Path order ketiga hanya dilakukan pada ujung dari persamaan tersebut. Hal ini dikarenakan Xt+1 terikat terhadap Xt dan tidak terikat oleh Xt-1, Xt-2maupun Xt-3 Sehingga, peramalan pada persamaan (4.8)
dan (4.9) diabaikan.
Xt
Xt-3 Xt-2 Xt-1 at
at-1
Order keempat
Dengan asumsi bahwa variabel X
tterikat terhadap Xt-1. Variabel Xt-1terikat terhadap Xt-2. Variabel Xt-2 terikat terhadap Xt-3. Variabel Xt-3terikat terhadap Xt-4
[image:47.595.112.491.203.563.2]maka diagram path order keempat dapat dilihat pada gambar dibawah ini:
Gambar 4.5 Diagram Analisis Path Order 4
Dari gambar 4.5 maka persamaan model strukturalnya adalah sebagai berikut:
Xt= 0.392Xt-1 + at (4.10)
Xt-1= 0.394Xt-2 + at-1 (4.11)
Xt
Xt-3 Xt-2 Xt-1 at
at-1
at-2
Xt-4
X
t-2= 0.395Xt-3 + at-2 (4.12)
Xt-3= 0.392Xt-4 + at-3 (4.13)
untuk peramalan dari analisis Path order ketiga hanya dilakukan hanya pada ujung dari persamaan tersebut. Hal ini dikarenakan Xt+1 terikat terhadap Xt
dan tidak terikat oleh Xt-1, Xt-2, Xt-3 maupun Xt-4 Sehingga, peramalan pada persamaan (4.11), (4.12) dan (4.13) diabaikan.
Order kelima
Dengan asumsi bahwa Variabel Xtterikat terhadap Xt-1. Variabel Xt-1terikat terhadap Xt-2. Variabel Xt-2terikat terhadap Xt-3. Variabel Xt-3terikat terhadap Xt-4.
[image:48.595.111.513.243.699.2]Variabel Xt-4 terikat terhadap Xt-5 maka diagram path order kelima dapat dilihat pada gambar dibawah ini:
Gambar 4.6. Diagram Analisis Path Order 5 Xt
Xt-3 Xt-2 Xt-1 at
at-1
at-2
Xt-4 at-3
X
t = 0.394Xt-1 + at (4.14)
Xt-1 = 0.393Xt-2 + at-1 (4.15)
Xt-2 = 0.393Xt-3 + at-2 (4.16)
Xt-3 = 0.394Xt-4 + at-3 (4.17)
Xt-4 = 0.396Xt-5 + at-4 (4.18)
untuk peramalan dari analisis Path order ketiga hanya dilakukan hanya pada ujung dari persamaan tersebut. Hal ini dikarenakan Xt+1 terikat terhadap Xt dan
tidak terikat oleh Xt-1, Xt-2, Xt-3, Xt-4 maupun Xt-5 Sehingga, peramalan pada
persamaan (4.15), (4.16), (4.17) dan (4.18) diabaikan.
Untuk proses estimasi nilai dari tiap-tiap model dapat dilihat pada lampiran 3.
4.5. Hasil Peramalan Model Analisis Path
[image:49.595.202.447.618.742.2]Untuk peramalan suhu minimum tahun 2008 dengan menggunakan metode Analisis Path diatas dapat dilihat pada tabel 4.5 berikut ini :
Tabel 4.5 Hasil Peramalan Model Analisis Path
Tanggal AP(2) AP(3) AP(4) AP(5)
01-Jan-08
02-Jan-08
03-Jan-08 23,507
04-Jan-08 23,507 23,508
05-Jan-08 23,507 23,508 23,508
07-Jan-08 23,507 23,508 23,508 23,507
08-Jan-08 23,647 23,647 23,647 23,647
09-Jan-08 23,925 23,925 23,925 23,925
10-Jan-08 23,786 23,786 23,786 23,786
11-Jan-08 24,344 24,343 24,343 24,344
12-Jan-08 22,671 22,672 22,672 22,671
13-Jan-08 24,344 24,343 24,343 24,344
14-Jan-08 24,762 24,76 24,76 24,762
15-Jan-08 24,901 24,9 24,9 24,901
16-Jan-08 24,344 24,343 24,343 24,344
17-Jan-08 23,507 23,508 23,508 23,507
18-Jan-08 25,18 25,178 25,178 25,18
19-Jan-08 23,786 23,786 23,786 23,786
20-Jan-08 24,344 24,343 24,343 24,344
21-Jan-08 24,622 24,621 24,621 24,622
22-Jan-08 25,18 25,178 25,178 25,18
23-Jan-08 25,459 25,456 25,456 25,459
24-Jan-08 24,901 24,9 24,9 24,901
25-Jan-08 23,228 23,229 23,229 23,228
26-Jan-08 25,459 25,456 25,456 25,459
27-Jan-08 25,041 25,039 25,039 25,041
28-Jan-08 25,877 25,874 25,874 25,877
29-Jan-08 25,041 25,039 25,039 25,041
30-Jan-08 25,459 25,456 25,456 25,459
31-Jan-08 25,18 25,178 25,178 25,18
21 22 23 24 25 26 27
[image:51.595.110.505.111.540.2]1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 Aktual AP(2) AP(3) AP(4) AP(5)
Gambar 4.9 Plot Peramalan Suhu Minimum Tahun 2008 dengan Mengunakan Model Analisis Path
4.5. Perbandingan Model
Perbandingan model dilakukan dengan membandingkan nilai MAPE terhadap kedua metode yang dapat kita lihat dalam tabel berikut:
Tabel 4.6 Perbandingan Kedua Metode Dengan Perbandingan Nilai MAPE MAPE
Order
Autoregressive Analisis Path
2 2,353653 3,35607127
3 2,358741 3,36012283
4 2,363872 3,36832436
5 2,357686 3,37385279
[image:51.595.195.413.561.680.2]Path. Untuk metode Autoregressive model terbaik dimiliki oleh Autoregressive order kedua karena memiliki nilai MAPE yang terkecil sebesar 2,353653 dibandingkan lainnya. Sedangkan untuk metode Analisis Path dimiliki oleh model analisis Path order kedua dengan nilai MAPE sebesar 3,35607127.
[image:52.595.110.501.274.542.2]Hal ini membuktikan bahwa metode Autoregressive lebih baik dibandingkan metode Analisis Path. Untuk grafik perbandingan kedua metode dapat dilihat pada gambar dibawah ini:
21 22 23 24 25 26 27
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
Aktual AP(2) AR(2)
BAB V
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Berdasarkan hasil dan pembahasan, maka dapat disimpulkan data suhu minimum daerah Pondok Betung tahun 2007 bersifat stasioner yaitu pergerakan nilai harian suhu minimum tidak mengalami trend naik dan trend turun yang berlebihan. Mayoritas data bergerak pada titik rata-rata yaitu 28,8355, hal ini dipertegas dengan hasil uji kestasioneran data menggunakan uji correlogram dan uji akar-akar unit.
Data suhu minimum daerah Pondok Betung tahun 2007 lebih cocok menggunakan Autoregressive order kedua dengan nilai MAPE yang terkecil sebesar 2,353653 dibandingkan metode Autoregressive order-order lainnya, hal ini juga dapat dilihat pada gambar 4.4. Untuk hasil peramalan dari tiap-tiap order untuk bulan-bulan berikutnya dapat dilihat pada lampiran 6
Data suhu minimum daerah Pondok Betung tahun 2007 juga lebih cocok menggunakan model analisis Path order kedua dengan nilai MAPE yang terkecil sebesar 3,35607127 dibandingkan metode analisis Path order-order lainnya, hal ini juga dapat dilihat pada gambar 4.9. Untuk hasil peramalan dari tiap-tiap order untuk bulan-bulan berikutnya dapat dilihat pada lampiran 6
dengan model Analisis Path. Sedangkan untuk metode Analisis Path, lebih cocok untuk regresi dan analisis trend.
5.2 Saran
Saran-saran yang penulis anjurkan untuk penelitian tinggi tentang metode analisis path adalah sebagai berikut:
1. Penelitian ini dapat dilanjutkan dengan menggunakan perbandingan autoregressive dengan order yang lebih tinggi, sehingga lebih terlihat lebih jelas perbedaan model analisis Path dengan model Autoregressive.
2. Menggunakan variabel lain yang bisa diuji seperti cuaca, kurs jual beli, harga saham dan semua variabel yang sifatnya berkala.
REFERENSI
[1] Augusty Ferdinand. Structural Equation Modeling dalam Penelitian Managemen. Universitas Diponegoro. Fakultas Ekonomi, 2002.
[2] http://www.analisis%20data%20deret%20waktu.pdf
[11 November 2008 8.36 WIB]
[3] http://www.jonathansarwono.info/sem/sem.htm
[Friday, November 28, 2008, 9:17:08 PM]
[4] Tulus Winarsunu. Statistik dalam Penelitian Psikologi dan Pendidikan. Edisi ke-Empa. UMM Press, 2007.
[5] John E Hanke dan Arthur G. Reitsch. Business Forecasting. Sixth Edition. Eastern Washington University, 1998.
[6] Shudakar, M Pandit dan Wu Shien Ming.Timeseries and System Analysis With Applications. John Wiley&sons, INC. New York Chichester Brisbane Toronto Singapure. Canada, 1983
[7] Bqockwell, P. J. Time Series And Analysis with Application. New York.1997.
Lampiran 1
:
Data Suhu Minimum Daerah Pondok Betung T
ahun 2007 31 23,2 23,8 24 22,3 24 24,2 23,2 30 24,8 24,2 23,7 24 23,2 24 24,2 24,6 23,4 24,6 24,2 29 25 24,8 23 24 22,8 24,2 24,8 24,5 23,2 24,2 23,2 28 24,7 24 24,6 24 22,2 23 24,8 23 23,4 24 25,1 23 27 25,3 24 24,4 24 22,4 23 24,4 23 24 23,4 25,4 24,2 26 24,7 23,8 25 23,6 23,8 24,2 23 24 24 23 25,4 23,6 25 25 23,6 25,2 23,4 22 23 25,2 24,4 23,4 23 25 23,7 24 23,4 23,7 23,4 25 24,4 22,4 23 22,4 22,4 23,6 25 23,4 23 24,6 23,8 23 25 24,4 22 24 25,2 23 23,6 24,4 23 22 25 23,5 23 23,4 24 24 23,6 24 23 22,6 24,4 23 21 24,8 23,8 22,8 23,6 24 25,2 24 24 23,8 23,4 23,8 23,4 20 24,4 23,8 24 25,2 24,4 25 25 24,4 24 24 23,8 23,2 19 24,2 23,4 23,8 24,8 24 24 24,6 24 25 24,9 24,2 23,2 18 23,8 23,5 24 23,5 25 24 24,8 24,6 25 23 24 24 17 24,8 23 23,7 25,5 25 23 24,4 23 25,5 24 24 22,6 16 23,6 23,6 24,2 25 24 22,4 24,8 22 23,6 24 24,8 23 15 24,2 24 24 25,2 24 23 23,4 24,6 23,2 23,8 24,4 23 14 24,6 23,8 24,8 23,8 24 24 23,4 24 23,4 24,2 24,8 23 13 25 25 25 24 23 24 22 24 23 24 23 23 12 24,2 25,6 24,4 23,6 23 23,8 24 25 23 24 24 23,2 11 23 24 24 24 23 24 24 23 23 24 24 23 10 24,2 24,2 25 24,3 23,4 24 23,2 23,1 23 25 23 22,7 9 23,8 23 25 23,3 23,8 24,8 23,2 24 23,8 24 22,6 23,8 8 23,9 23 24,4 23,2 24,2 24 24,6 25,4 24 24 23,4 24 7 23,7 23 24,4 23 24 24 25,4 24,4 29,9 23,6 23,6 22,2 6 23,6 22,8 24,4 22,8 25,4 24,8 23,8 24 23,2 24,2 21,4 22 5 24,2 23,2 25 24,6 22,8 24,4 24 24 24,1 24 23 24 4 23,6 23,2 23,6 24,6 24,4 22 23,8 23,9 23 23,3 22,8 23,8 3 24 24 24 24 25 22 24 25 24 24 24 23 2 23,6 23 24 24,1 24 23 22,5 22,4 23,6 24,4 24 23,8 Tanggal 1 23 22,6 23,6 22,6 24 23,4 23,2 22 23,4 25 24 24,4
Data Suhu Minimum Daerah Pondok Betung Tahun 2007
Lampiran 2 : Langkah-langkah membuat Model Autoregressive dengan Menggunakan Software E-View 4.1
Cara Membuat Model Autoregressive Dengan Menggunakan Software E-View 4.1
Buka lembar kerja baru, klik File- New- Workfile. Maka muncul tampilan :
Pilih undate or irregular sehingga data sesuai dengan keinginan. Di start observation tulis 1 dilanjutkan pada end observation tulis 456. lalu OK. Maka muncul tampilan :
lalu pilih Empty Group (Edit Series). makamuncul tampilan
Pada kolom OBS tuliskan nama variable (misalkan suhu kita simbolkan dengan X). lalu masukkan data mulai dari kolom angka 1 sampai baris 365..
Untuk membuat model Autoregressive klik Quick – Estimate Equation maka akan muncul tampilan dibawah ini
Untuk Autoregressive order 1 ketik X C X(-1) lalu ok Untuk order 2 ketik X C X(-1) X(-2) lalu ok
Dan seterusnya
Sedangkan untuk peramalannya klik Forecast maka akan muncul tampilan
Lampiran 3: Langkah-langkah dalam mengestimasi nilai f dengan menggunakan program Amos 7.
Cara estimasi nilai f
Sebelum melakukan estimasi kita harus memiliki save data dalam format spss Klik Amos Graphics, maka akan muncul tampilan seperti dibawah ini
Selanjutnya klik gambar maka akan muncul tampilan seperti dibawah ini:
Untuk membuat model yang diinginkan, klik untuk variabel terobservasi dan untuk variabel laten.
Contoh model dapat dilihat pada gambar dibawah ini
Selanjutnya klik kanan pada tiap-tiap variabel, pilih object properties maka akan muncul tampilan berikut
Pada kolom estimation pilih Generalized Least Squares Pada kolom Numerical klik try to fit unidentified models Lalu close
Pilih analyze klik calculate estimates maka akan muncul tampilan dibawah ini Standardized Regression Weights: (PATH - model AR(1))
Lampiran 4 : Langkah-langkah dalam menguji Kestasioneran dengan menggunakan Software E-views 4
Cara Uji Correlogram
Buka lembar kerja baru, klik File- New- Workfile. Maka muncul tampilan :
Pilih undate or irregular sehingga data sesuai dengan keinginan. Di start observation tulis 1 dilanjutkan pada end observation tulis 456. lalu OK. Maka muncul tampilan :
lalu pilih Empty Group (Edit Series). makamuncul tampilan
Pada kolom OBS tuliskan nama variable (misalkan suhu). lalu masukkan data mulai dari kolom angka 1 sampai baris 365..
Untuk mencari gambar Correlogram, pilih Quick - series statistic Lalu pilih correlogram. maka muncul tampilan :
Cara uji akar Unit
Untuk mencari gambar uji akar unit, pilih Quick… lalu..series statistic…. Lalu pilih Unit root test … maka muncul tampilan :
Pada kolom series name tuliskan nama variable sesuai dengan yang ditulis di kolom OBS di atas. Lalu klik OK. Maka muncul tampilan :
Lampiran 5 : Peramalan Dengan Metode Autoregressive
Tanggal AR(2) AR(3) AR(4) AR(5)
01-Jan-08 02-Jan-08 03-Jan-08 23,71
04-Jan-08 23,74 23,71
05-Jan-08 23,74 23,73 23,73
29-Nop-08 24,03 24,07 24,07 24,04 30-Nop-08 24,14 24,18 24,18 24,12 01-Des-08 24,08 24,08 24,09 24,02 02-Des-08 23,85 23,87 23,87 23,80 03-Des-08 23,37 23,39 23,40 23,39 04-Des-08 23,77 23,79 23,79 23,75 05-Des-08 23,90 23,86 23,86 23,82 06-Des-08 23,15 23,15 23,15 23,12 07-Des-08 23,14 23,18 23,18 23,25 08-Des-08 23,83 23,79 23,79 23,79 09-Des-08 23,83 23,77 23,77 23,71 10-Des-08 23,41 23,42 23,41 23,48 11-Des-08 23,47 23,49 23,49 23,60 12-Des-08 23,56 23,54 23,54 23,52 13-Des-08 23,57 23,55 23,55 23,52 14-Des-08 23,50 23,48 23,48 23,53 15-Des-08 23,49 23,48 23,48 23,51 16-Des-08 23,49 23,47 23,47 23,49 17-Des-08 23,34 23,32 23,32 23,33 18-Des-08 23,85 23,83 23,83 23,86 19-Des-08 23,60 23,56 23,56 23,59 20-Des-08 23,57 23,59 23,58 23,60 21-Des-08 23,65 23,63 23,64 23,72 22-Des-08 23,50 23,49 23,49 23,46 23-Des-08 23,49 23,48 23,48 23,50 24-Des-08 23,64 23,62 23,62 23,65 25-Des-08 23,77 23,74 23,74 23,75 26-Des-08 23,74 23,73 23,73 23,76 27-Des-08 23,96 23,96 23,96 24,00 28-Des-08 23,54 23,53 23,53 23,55 29-Des-08 23,56 23,59 23,59 23,59 30-Des-08 23,95 23,93 23,93 23,95 31-Des-08 23,61 23,59 23,59 23,54
Lampiran 5 : Peramalan Dengan Metode Autoregressive
Tanggal AR(2) AR(3) AR(4) AR(5)
01-Jan-08 02-Jan-08 03-Jan-08 23,71
04-Jan-08 23,74 23,71
05-Jan-08 23,74 23,73 23,73
29-Nop-08 24,03 24,07 24,07 24,04 30-Nop-08 24,14 24,18 24,18 24,12 01-Des-08 24,08 24,08 24,09 24,02 02-Des-08 23,85 23,87 23,87 23,80 03-Des-08 23,37 23,39 23,40 23,39 04-Des-08 23,77 23,79 23,79 23,75 05-Des-08 23,90 23,86 23,86 23,82 06-Des-08 23,15 23,15 23,15 23,12 07-Des-08 23,14 23,18 23,18 23,25 08-Des-08 23,83 23,79 23,79 23,79 09-Des-08 23,83 23,77 23,77 23,71 10-Des-08 23,41 23,42 23,41 23,48 11-Des-08 23,47 23,49 23,49 23,60 12-Des-08 23,56 23,54 23,54 23,52 13-Des-08 23,57 23,55 23,55 23,52 14-Des-08 23,50 23,48 23,48 23,53 15-Des-08 23,49 23,48 23,48 23,51 16-Des-08 23,49 23,47 23,47 23,49 17-Des-08 23,34 23,32 23,32 23,33 18-Des-08 23,85 23,83 23,83 23,86 19-Des-08 23,60 23,56 23,56 23,59 20-Des-08 23,57 23,59 23,58 23,60 21-Des-08 23,65 23,63 23,64 23,72 22-Des-08 23,50 23,49 23,49 23,46 23-Des-08 23,49 23,48 23,48 23,50 24-Des-08 23,64 23,62 23,62 23,65 25-Des-08 23,77 23,74 23,74 23,75 26-Des-08 23,74 23,73 23,73 23,76 27-Des-08 23,96 23,96 23,96 24,00 28-Des-08 23,54 23,53 23,53 23,55 29-Des-08 23,56 23,59 23,59 23,59 30-Des-08 23,95 23,93 23,93 23,95 31-Des-08 23,61 23,59 23,59 23,54