Vojnotehnicki glasnik Military Technical

(1)

(2)

(3)

(4)

(5)

(6)

Ј

Ј „ ”

е и . џ ,

. Мл е , - , http://orcid.org/0000-0002-3558-4312 Д г

Ј Ч

Не јш ,

e-mail: nebojsa.gacesa@mod.gov.rs, tel.: 011/3241-311, 064/80-80-118, http://orcid.org/0000-0003-3217-6513 Ђ Ч

– - . , ,

, ђ , http://orcid.org/0000-0002-0961-993X,

– - . , , ђ

, http://orcid.org/0000-0002-3558-4312,

– . , , , http://orcid.org/0000-0001-9038-0876,

– . , щ , - , я я (Hydrographic society,

St. Petersburg, Russian Federation), http://orcid.org/0000-0002-5264-6634,

– . Ismat Beg, Lahore School of Economics, Lahore, Pakistan, http://orcid.org/0000-0002-4191-1498, – . . , The University of Auckland, Department of Electrical and Computer Engineering, Auckland,

New Zealand, http://orcid.org/0000-0002-2432-3088,

– . , „ “, , http://orcid.org/0000-0002-7054-6928,

– . . , ы ы ы , ,

(Minsk State Higher Aviation College, Minsk, Republic of Belarus), http://orcid.org/0000-0002-5358-9037,

– . . , ы , ,

(Kharkiv National University of Economics, Kharkiv, Ukraine), http://orcid.org/0000-0002-0737-8714,

– . Ђ , , , http://orcid.org/0000-0002-6076-442X,

– , , , http://orcid.org/0000-0002-1766-8184,

– . Ј. , , , http://orcid.org/0000-0001-5114-2867, – . . Ј , Old Dominion University Norfolk, USA, http://orcid.org/0000-0002-8626-903X,

– . , , , http://orcid.org/0000-0001-9334-9639,

– . , - , , http://orcid.org/0000-0002-7915-9430,

– . , , , http://orcid.org/0000-0003-1893-7187,

– . . . , , , http://orcid.org/0000-0002-4834-3550,

– . , Combustion and CCS Centre, Cranfield University, Cranfield, United Kingdom, http://orcid.org/0000-0002-8377-7717,

– . . Ј , , Ч , http://orcid.org/0000-0002-1337-3821,

– . , , , http://orcid.org/0000-0002-3255-8127,

– . . Penumarthy Parvateesam Murthy, University Guru Ghasidas Vishwavidyalaya, Department of Pure and Applied Mathematics, Bilaspur (Chhattisgarh), India, http://orcid.org/0000-0003-3745-4607,

– , ,

, http://orcid.org/0000-0002-0455-7506,

– . Ј. , ,

, , http://orcid.org/0000-0002-3173-597X,

– . , , , http://orcid.org/0000-0001-8254-6688,

– . , , , http://orcid.org/0000-0001-6432-2816,

– . Ј , Transilvania University of Brasov, Romania, http://orcid.org/0000-0001-5947-7557, – . , RWTH Aachen University, Faculty for Georesourcen and Materials Engineering,

IME Process Metallurgy and Metal Recycling, Aachen, Deutschland, http://orcid.org/0000-0002-1752-5378, – . . , , , http://orcid.org/0000-0002-3325-0933,

– . Ч , ы , , я я

(Vladimir State University, Vladimir, Russian Federation), http://orcid.org/0000-0003-1830-2261,

– . , , ђ

, http://orcid.org/0000-0003-3217-6513.

: Ј Ч , Ј 19,

http://www.vtg.mod.gov.rs

http://aseestant.ceon.rs/index.php/vtg/issue/current http://scindeks.nb.rs/journaldetails.aspx?issn=0042-8469 http://elibrary.ru/title_about.asp?id=53280

http://doaj.org/toc/0310c0550a134f2ba6a53e54ab177224 e-mail: vojnotehnicki.glasnik@mod.gov.rs

: e-mail: pretplata@odbrana.mod.gov.rs; .- x: 011/3241-009; : 840-312849-56 и и е е ћ ј

Ч

В ј ех и ггл и 1. 1. 1953.

В ј ех и ггл и 1. 1. 2011.

В ј ех и игл и EBSCO Publishing-a, ,

. В ј ех и ггл и EBSCO Publishing-a.

(7)

Ы

„ “

е и . ,

Ы .

- , - , http://orcid.org/0000-0002-3558-4312

я :

- Ч

,

e-mail: nebojsa.gacesa@mod.gov.rs, .: +381 11 3241 311, +381 64 80 80 118, http://orcid.org/0000-0003-3217-6513

– - я , я ы

ы ы я, ,

http://orcid.org/0000-0002-0961-993X,

– - , ы . ,

я , http://orcid.org/0000-0002-3558-4312,

– - , ы . , я я,

http://orcid.org/0000-0001-9038-0876,

– . , щ , - , я я,

http://orcid.org/0000-0002-5264-6634,

– - Ismat Beg, Lahore School of Economics, Lahore, Pakistan, http://orcid.org/0000-0002-4191-1498, – - . , The University of Auckland, Department of Electrical and Computer Engineering, Auckland, New

Zealand, http://orcid.org/0000-0002-2432-3088,

– - я , « », , http://orcid.org/0000-0002-7054-6928,

– - , ы ы ы , ,

, http://orcid.org/0000-0002-5358-9037,

– - , ы , , ,

http://orcid.org/0000-0002-0737-8714,

– - , , Э ,

http://orcid.org/0000-0002-6076-442X,

– - . , я я ы, , http://orcid.org/0000-0002-1766-8184,

– - , . , , http://orcid.org/0000-0001-5114-2867,

– - M. , Trine University, Allen School of Eggineering and Technology, Department of Engineering Technology, Angola, Indiana, USA, http://orcid.org/0000-0002-8626-903X,

– - , , Э ,

http://orcid.org/0000-0001-9334-9639,

– - я . , « – », . , http://orcid.org/0000-0002-7915-9430, – ы - , , . , http://orcid.org/0000-0003-1893-7187,

– - . , , я , http://orcid.org/0000-0002-4834-3550,

– - M. , Combustion and CCS Centre, Cranfield University, Cranfield, UK, http://orcid.org/0000-0002-8377-7717, – - , ы . , Ч я, http://orcid.org/0000-0002-1337-3821

– - . , , ,

http://orcid.org/0000-0002-3255-8127,

– - Penumarthy Parvateesam Murthy, University Guru Ghasidas Vishwavidyalaya, Department of Pure and Applied Mathematics, Bilaspur (Chhattisgarh), India, http://orcid.org/0000-0003-3745-4607,

– ы - , я щ

«IRITEL AD» . , http://orcid.org/0000-0002-0455-7506,

– - , ы ,

, , http://orcid.org/0000-0002-3173-597X,

– - я , , я,

http://orcid.org/0000-0001-8254-6688,

– - я , , , http://orcid.org/0000-0001-6432-2816,

– - , . , ы я, http://orcid.org/0000-0001-5947-7557, – ы - . , RWTH Aachen University, Faculty for Georesourcen and Materials

Engineering, IME Process Metallurgy and Metal Recycling, Aachen, Deutschland, http://orcid.org/0000-0002-1752-5378,

– - я , . , я,

http://orcid.org/0000-0002-3325-0933,

– - Ч , ы , , я

я, http://orcid.org/0000-0003-1830-2261,

– , - ,

, http://orcid.org/0000-0003-3217-6513.

: Ј Ч , Ј 19,

http://www.vtg.mod.gov.rs

a: e-mail: pretplata@odbrana.mod.gov.rs; .- : +381 11 3241 009; № : 840-312849-56

и, и л е е ии л е я

ы я

ы - ы щ 1.1.1953 .

я я я щ 1.1.2011 .

- EBSCO – я я ы .

(8)

MINISTRY OF DEFENCE OF THE REPUBLIC OF SERBIA ODBRANA MEDIA CENTRE

Director

Col Stevica S. Karapandžin

UNIVERSITY OF DEFENCE IN BELGRADE Rector

Major General Mladen Vuruna, PhD, Professor, http://orcid.org/0000-0002-3558-4312 Head of publishing department

Dragana Marković

EDITOR OF THE MILITARY TECHNICAL COURIER Lt Col Nebojša Gaćeša MSc

e-mail: nebojsa.gacesa@mod.gov.rs, tel: +381 11 3241 311, +381 64 80 80 118, http://orcid.org/0000-0003-3217-6513 EDITORIAL BOARD

– Major General Bojan Zrnić, PhD, Professor, Ministry of Defence, Head of the Department for Defence Technologies, Material Resources Sector, Belgrade (Head of the Editorial Board), http://orcid.org/0000-0002-0961-993X – Major General Mladen Vuruna, PhD, Professor, Rector of the University of Defence, Belgrade (Deputy Head of the

Editorial Board), http://orcid.org/0000-0002-3558-4312

– Colonel Milenko Andrić, PhD, Professor, University of Defence in Belgrade, Military Academy, http://orcid.org/0000-0001-9038-0876

– Sergej A. Argunov, MSc,Hydrographic society, St. Petersburg, Russian Federation, http://orcid.org/0000-0002-5264-6634 – Professor Ismat Beg, PhD, Lahore School of Economics, Lahore, Pakistan, http://orcid.org/0000-0002-4191-1498 – Stevan M. Berber, PhD, The University of Auckland, Department of Electrical and Computer Engineering, Auckland, New

Zealand, http://orcid.org/0000-0002-2432-3088

– Professor Vladimir Chernov, DSc, Vladimir State University, Department of Management and Informatics in Technical and Economic Systems, Vladimir, Russia, http://orcid.org/0000-0003-1830-2261

– Professor Aleksandr V. Dorohov, PhD, Kharkiv National University of Economics, Kharkiv, Ukraine, http://orcid.org/0000-0002-0737-8714 – Professor Željko Đurović, PhD, University in Belgrade, Faculty of Electrical Engineering, http://orcid.org/0000-0002-6076-442X – Professor Leonid I. Gretchihin, PhD, Minsk State Higher Aviation College, Minsk, Republic of Belarus,

http://orcid.org/0000-0002-5358-9037

– Vukica M. Jovanović, PhD, Trine University, Allen School of Eggineering and Technology, Department of Engineering Technology, Angola, Indiana, USA, http://orcid.org/0000-0002-8626-903X

– Assistant Professor Sanja Lj. Korica, PhD, University Union - Nikola Tesla, Belgrade, http://orcid.org/0000-0002-7915-9430 – Scientific Advisor Ana Kostov, PhD, Institute of Mining and Metallurgy, Bor, Serbia, http://orcid.org/0000-0003-1893-7187 – Professor Branko Kovačević, PhD, University of Belgrade, Faculty of Electrical Engineering, http://orcid.org/0000-0001-9334-9639 – Associate Professor Slavoljub S. Lekić, PhD, University of Belgrade, Faculty of Agriculture, http://orcid.org/0000-0002-4834-3550 – Vasilije M. Manović, PhD, Combustion and CCS Centre, Cranfield University, Cranfield, UK, http://orcid.org/0000-0002-8377-7717 – Lt Colonel Jaromir Mares, PhD, Associate Professor, University of Defence in Brno, Czech Republic,

http://orcid.org/0000-0002-1337-3821

– Professor Gradimir V. Milovanović, PhD, Member of the Serbian Academy of Sciences and Arts, Mathematical Institute of the SASA, Belgrade, http://orcid.org/0000-0002-3255-8127

– Associate Professor Penumarthy Parvateesam Murthy, PhD, University Guru Ghasidas Vishwavidyalaya, Department of Pure and Applied Mathematics, Bilaspur (Chhattisgarh), India, http://orcid.org/0000-0003-3745-4607,

– Scientific Advisor Predrag Petrović, PhD, Executive Director for R&D and Radio Communications, Institute of telecommunications and electronics IRITEL AD, Belgrade, http://orcid.org/0000-0002-0455-7506

– Professor Slavko Pokorni, PhD, Information Technology School, Belgrade, http://orcid.org/0000-0002-3173-597X – Professor Stojan N. Radenović, PhD, University of Belgrade, Faculty of Mechanical Engineering, http://orcid.org/0000-0001-8254-6688, – Professor Andreja Samčović, PhD, University of Belgrade, Faculty of Transport, http://orcid.org/0000-0001-6432-2816, – Professor Ionel Staretu, PhD, Transilvania University of Brasov, Romania, http://orcid.org/0000-0001-5947-7557 – Scientific Advisor Srećko S. Stopić, PhD, RWTH Aachen University, Faculty for Georesources and Materials Engineering,

IME Process Metallurgy and Metal Recycling, Aachen, Germany, http://orcid.org/0000-0002-1752-5378

– Professor Miroslav Trajanović, PhD, University of Niš, Faculty of Mechanical Engineering, http://orcid.org/0000-0002-3325-0933 – Professor Sanja Vraneš, PhD, Institute "Mihajlo Pupin", Belgrade, http://orcid.org/0000-0002-7054-6928

– Professor Aleksa Zejak, PhD, University of Novi Sad, Faculty of Technical Sciences, http://orcid.org/0000-0001-5114-2867 – Nikola P. Žegarac, PhD, Serbian Academy of Inventors and Scientists, Belgrade, http://orcid.org/0000-0002-1766-8184 – Lt Colonel Nebojša Gaćeša, MSc, Editor of the Military Courier, (Secretary of the Editorial Board),

http://orcid.org/0000-0003-3217-6513.

Address: MILITARY TECHNICAL COURIER, Braće Jugovića 19, 11000 Beograd, Serbia http://www.vtg.mod.gov.rs/index-e.html

Subscription to print edition: e-mail: pretplata@odbrana.mod.gov.rs; Tel.-fax: +381 11 32 41 009; account: 840-312849-56 Manuscripts are not returned

The journal is published quarterly

The first printed issue of the Military Technical Courier appeared on 1st January 1953.

The first electronic edition of the Military Technical Courier on the Internet appeared on 1st January 2011.

(9)

Ј

Ч Ч

Sumit C. Chandok, Ми . Ј ић, ј Н. е ић

ђ - ... 331-345

Badshah-е-Rome, Muhammad Sarwar

... 346-358

Ни л . Ј ић, и јК. А ђе ић, Јеле Д. Ј ић

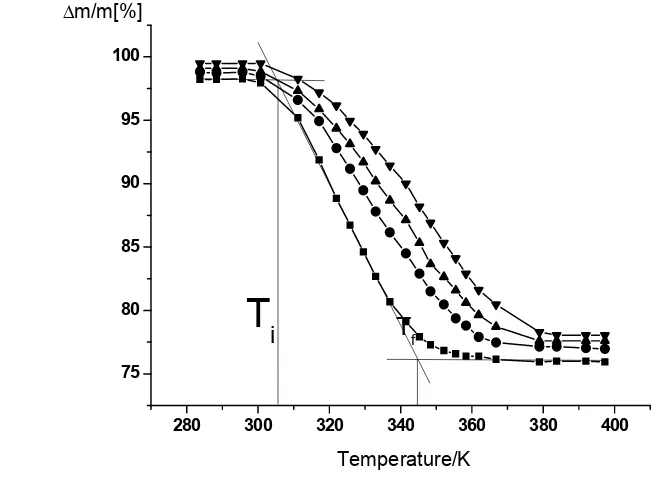
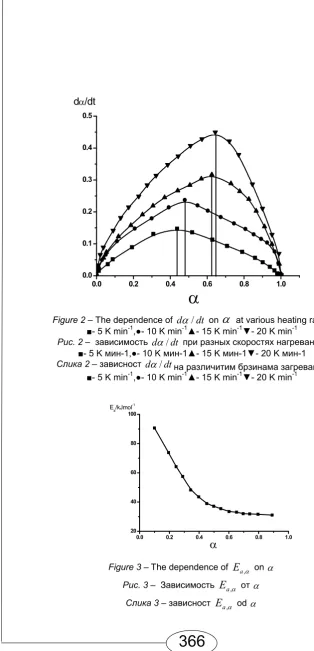
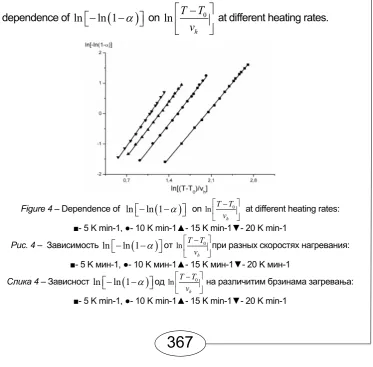
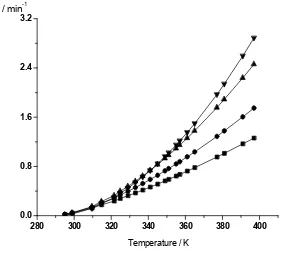
CMS-3A... 359-377

Мих ил . М

Ni22Cr10Al1Y

- - ... 378-391

Ни л . ег

... 392-420

Мил . Ш и

... 421-441

Ни л . М е, Ј г л З. А и, Д ге . е е и, Мил . ић, Деј Д. ић

:

Single Sign-On ... 442-463

Ч

Д г Д. Мл е ић

ђ ... 464-480

М М. К ић

, ,

... 481-498

Ч Ч

Деј Д. Ди ић, Мил З. Де ић

... 499-512

Не јш Д. Ђ ђе ић

... 513-529

и И. ић, И . В лић

PKI ... 530-549

л Ј. и

19. ђ ICDQM-2016 ( ).... 550-557

Њ Ј

Д г М. В ић...558-572 ... 573-589

(10)

Ы Ч Ы

и Ц. , Ми . и , я Н. е и

я ы щ я

Geraghty... 331-345

ш х-е- е, М х е

ы я

...346-358

Ни л . и , и К. А е и , ле Д. и

я ,

я CMS-3 ... 359-377

Мих ил . М

ы я Ni22Cr10Al1Y

ы я... 378-391

Ни л . ег

ы я

я ы ... 392-420

Мил л . Ш ля и

я

ы ы ы ... 421-441

Ни л . М е, Юг л З. А и, Д ге . е е и, Мил . и, Дея Д. и

я я :

Single Sign-On... 442-463

Ы

Д г , Д. Мл е и

я

... 464-480

М М. К и

я я ,

я я ... 481-498

Ы

Дея Д. Ди и , Мил З. Де и

я ы ... 499-512

Не ш Д. Д е и

я : я я... 513-529

и И. и , И . В ли

я PKI я... 530-549

Ы

л . и

19- я я я ICDQM-2016 ( ) ... 550-557

. ... 558-572

... 573-589

(11)

C O N T E N T S

ORIGINAL SCIENTIFIC PAPERS

Sumit C. Chandok, Mirko S. Jovanović, Stojan N. Radenović

Ordered b-metric spaces and Geraghty type contractive mappings ... 331-345 Badshah-е-Rome, Muhammad Sarwar

Extensions of the Banach contraction principle in multiplicative metric spaces ... 346-358 Nikola S. Jovančić, Borivoj К. Adnađević, Jelena D. Jovanović

Kinetics of the non-isothermal desorption of ethanol absorbed onto CMS-3A .. 359-377 Mihailo R. Mrdak

Structure and properties of Ni22Cr10Al1Y coatings deposited

by the vacuum plasma spray process... 378-391 Nikola P. Žegarac

Experience in developing an innovation in view of its scientific verification

and the product placement on the market... 392-420 Miloljub S. Štavljanin

Mathematical modeling and identification of the mathematical model

parameters of diesel fuel injection systems ... 421-441 Nikola S. Manev, Jugoslav Z. Achkoski, Drage T. Petreski, Milan Lj. Gocić, Dejan D. Rančić Smart field artillery information system: model development with

an emphasis on collisions in Single Sign-On authentication ... 442-463 REVIEW PAPERS

Dragan D. Mladenović

Vulnerability assessment and penetration testing in the military and IHL context ... 464-480 Marko M. Krstić

Tendency of using chemical, biological, radiological and nuclear weapons

for terrorist purposes... 481-498 PROFESSIONAL PAPERS

Dejan D. Dinčić, Milan Z. Despotović

Improved performances of the wind inlet of the Savonius rotor ... 499-512 Nebojša D. Đorđević

Usability: key characteristic of software quality... 513-529 Radomir I. Prodanović, Ivan B. Vulić

Model for PKI interoperability in Serbia... 530-549 REVIEWS

Slavko J. Pokorni

19th international conference on dependability and quality management

ICDQM-2016 (review of the proceedings)... 550-557 MODERN WEAPONS AND MILITARY EQUIPMENT

(12)

Cha

ndok, S.C. et al,

rdered

b-metric spac

e

s

and Gerag

h

ty

type contracti

v

e mapp

ings, p

p

. 331–

34

5

ORDERED B-METRIC SPACES AND

GERAGHTY TYPE CONTRACTIVE

MAPPINGS

Sumit C. Chandoka, Mirko S. Jovanovićb, Stojan N. Radenovićc

a _{Thapar University, School of Mathematics, Patiala, India,}

e-mail: sumit.chandok@thapar.edu,

ORCID iD: http://orcid.org/0000-0003-1928-2952

b_{University of Belgrade, Faculty of Electrical Engineering, Belgrade,}

Republic of Serbia, e-mail: msj@sbb.rs,

c_{University of Belgrade Faculty of Mechanical Engineering, Belgrade,}

Republic of Serbia, e-mail: radens@beotel.rs,

https://dx.doi.org/10.5937/vojtehg65-13266 FIELD: Mathematics, Subject Classification: 47H10, 54H25, 46Nxx

ARTICLE TYPE: Original Scientific Paper ARTICLE LANGUAGE: English

Abstract:

The paper shows a new approach to proving the recent fixed point results in ordered b-metric as well as ordered metric spaces, established by several authors, with much shorter and nicer proofs. An example is given to illustrate our results.

Key words: fixed point, b-metric, comparable, well order, Geraghty mapping, b-Cauchy, b-complete.

Ч

Ы

Ч Ы

(13)

VOJNOTEHNI

Č

KI GLASNIK / MILITARY

TECHNICAL

CO

URIER, 201

7., Vol. 65, Issue 2

Introduction and preliminaries

One of important generalizations of metric spaces are so-called b -metric spaces (type -metric spaces by some authors). This concept was introduced by Bakhtin in 1989 and Czerwik in 1993.

Consistent with (Bakhtin, 1989, pp.26-37) and (Czerwik, 1993, pp.5-11), the following definition and results will be needed in the sequel.

Definition 1.1. (Bakhtin, 1989), (Czerwik, 1993) Let X be a

(nonempty) set and

s



1

be a given real number. A function

) [0, :XX  

d is a b-metric if and only if, for all x,y,zX, the following conditions are satisfied:

(b₁)

d

 

x

,

y

=

0

if and only ifx= y,

(b₂)

d

   

x

,

y

=

d

y

,

x

,

(b3)

d

 

x

,

z



s



d

   

x

,

y



d

y

,

z



.

The pair



X

,

d



is called a b-etric space.

It should be noted that the class of b-metric spaces is effectively larger than that of metric spaces, since a b-metric is a metric when

s

=

1.

The following example shows that, in general, a b-metric does not necessarily need to be a metric, see also (Aghajani, et al, 2014), (Abbas, et al, 2016, pp.1413-1429), (Ansari, et al, 2016), (Ding, et al, 2016, pp.151-164), (Djukić, et al, 2011), (Huang, et al, 2015a, pp.808-815), (Huaping, et al, 2015), (Huang, et al, 2015b, pp.800-807), (Hussain, et al, 2012), (Hussain, et al, 2013), (Jleli, et al, 2012, pp.175-192), (Jovanović, et al, 2010), (Kadelburg, et al, 2015, pp.57-67), (Khamsi, Hussain, 2010, pp.3123-3129), (Parvaneh, et al, 2013), (Roshan, et al, 2015), (Roshan, et al, 2014, pp.229-245), (Zabihi, Razani, 2014).

Example 1.1.Let



X

,

d



be a metric space, and



 

x

,

y

=



d

 

x

,

y



p

,

1 >

p is a real number. Then



is a b-metric with =2p1,

s but



is not a

metric on

X

.

Otherwise, for more concepts such as b-convergence,

(14)

Cha

ndok, S.C. et al,

rdered b-metric spac e s and Gerag h ty type contracti v e mapp ings, p p . 331– 34 5

2013), (Roshan, et al, 2015), (Roshan, et al, 2014, pp.229-245), (Zabihi, Razani, 2014) and the references mentioned therein. Also, for the concepts such as partial order, comparable, well ordered, nondecreasing, increasing, dominated, dominating and other, we refer the reader to (Aghajani, et al, 2014, pp.941-960), (Abbas, et al, 2016, pp.1413-1429), (Ansari, et al, 2016).

The following three lemmas are very significant in the theory of a fixed point in the framework of metric and b-metric spaces. Also, we use these in the proof of our main results.

Lemma 1.2. (Aghajani, et al, 2014, pp.941-960, Lemma 2.1) Let



X

,

d



be a b-metric space with s1, and suppose that

 

x_n and

 

y_n

are b-convergent tox,yrespectively, then we have

 

, lim



,



lim



,



 

, .

1 2

2 d x y d x y d x y s d x y

s  n n n  n n n  (1.1)

In particular, if x= y, then we have limnd



xn,yn



=0. Moreover,

for each zX we have

 

, lim



,



lim



,



 

, .

1 z x sd z x d z x d z x d

s  n n  n n  (1.2)

Lemma 1.3. (Jovanović, et al, 2010, Lemma 3.1) Let

 

yn be a

sequence in a b-metric space



X

,

d



with s1,such that



yn yn



d



yn yn



d , _₁ 



_₁, (1.3)

for some [0,1),

s 



and each n=1,2,... Then

 

y_n is a b-Cauchy

sequence in a b-metric space



X

,

d



.

Lemma 1.4. (Radenović, et al, 2012, pp.625-645, Lemma 2.1), (Jleli, et al, 2012, pp.175-192, Lemma 2.1) Let



X

,

d



be a metric space and let

 

yn be a sequence inX such that d



yn,yn1



is nonincreasing and that



,



=

0.

lim

1



 n n

n

y

d

_(1.4)

If

 

y₂_n is not a Cauchy sequence, then there exist an



>

0

and two sequences

 

m_k and

 

n_k of positive integers such that the following four sequences tend to



when

k





:

. ) , ( , ) , ( , ) , ( , ) ,

( ₂ ₂ ₂ ₂ _₁ ₂ _₁ ₂ ₂ _₁ ₂ _₁

k n k m k n k m k n k m k n k

m y d y y d y y d y y

(15)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

Main results

Let  be the family of all nondecreasing functions

) [0, ) [0,

:   



such that _lim n

 

t =0

n



for all

t

>

0.

If

,

 



then



 

t

<

t

for all

t

>

0

and



 

0

=

0.

Our first result is the following:

Theorem 2.1. Let



X

,





be a partially ordered set and there exists a b-metric

d

onX such that



X

,

d



is a b-complete b-metric space. Suppose

1

>

s

and f :X  X is an increasing mapping with respect to



such

that there exists an element x0X with x0°fx0. Assume that

 



x fx



d



fx fy





M

 

x y



L N

 

x y

d y x sd

s , , ,

, 2 1 1

,

1 _ _ _ _

 





(2.1)

for all comparable elements x,yX,where L0,

 

  

 





















fy

fx

d

fy

y

d

fx

x

d

y

x

d

y

x

M

,

1

,

max

=

,

and

 

x

,

y

=

min



d



x

,

fx

 

,

d

x

,

fy

 

,

d

y

,

fx

 

,

d

y

,

fy





.

N

If

(1) f is continuous, or

(2) whenever

 

x_n is a nondecreasing sequence in X such that

,

X u

x_n   one has

x

_n



u

for all nN,

then f has a fixed point. Moreover, the set of fixed points of f is well ordered if and only if f has one and only one fixed point.

Proof. Suppose that x_n  x_n_₁ for all n=0,1,2,..., where

.

=

₀

1

fx

f

x

_n_ _n n In this case, we have xn xn1 for all n=0,1,2,.. Therefore, putting x= xn,y= xn1 in (2.1) we shall prove that



1 2





, 1



1

, _ _

 n n n

n d x x

s x

x

d  (2.2)

(16)

Cha

ndok, S.C. et al,











1 2



1 1 , , 2 1 1 , 1       n n n n n n x x d x x d x x sd s



 



 



_                     2 1 2 1 1 1 , 1 , , , , max n n n n n n n n x x d x x d x x d x x d





 





, , , , , , ,



.

min _₁ _₂ _₁ _₁ _₁ _₂

L d xn xn d xn xn d xn xn d xn xn

Since,











 









1



2 1 2 1 1 1 1 , < , 1 , , , , 2 1 1 , 1 < 1 _           n n n n n n n n n n n n x x d x x d x x d x x d x x d x x sd and



x_n_₁,x_n_₁



=0,

d we have sd



x_n_₁,x_n_₂









d



x_n,x_n_₁



 

<d x_n,x_n_₁



.

Hence, (2.2) follows.

Further, using (2.2), we have



2 _n, 2 _n_₁



<1



_n, _n_₁



< 1₂ d



x_n,x_n_₁



.

s fx fx d s x f x f d

As 1₂ [0,1),

s

s  therefore by using Lemma 1.4, the sequence

 

f2x_n _n₌₀ =



x₂,x₃,...



is a b-Cauchy sequence. This further implies that the sequence

 

fx

_n _n₌₀

=



x

₁

,

x

₂

,...



is a b-Cauchy sequence. Since



X

,

d



is b-Complete,

 

x_n b-converges to a point

u



X

.

(1) First, we suppose that f is continuous. Therefore, we have

,

=

)

lim

(

=

lim

=

lim

=

x

₁

fx

f

x

fu

u

_n

n n n n

n   

that is,

u

is a fixed point of f.

(2) Further, consider (2) of theorem holds. Using the assumption of



X

,

d

,





,

we have

x

_n



u

.

Now, we show that fu=u. Firstly, we have



,

 

,

 

,



.

1

1 d fx fu

x u d fu u d

s  n  n

Now, using the assumption

x

_n



u

and inequality (2.1), we have



 







M



x u



u x sd s x x d x u d fu u d

s _n n

n n n , , 1 , 2 1 1 , , 1 1

1 _ 

 

(17)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201











1 ,





,



.

, 2 1 1 ₁ u x N L u x sd s x x d n n n n      

Since M



x_n,u



0 and N



x_n,u



0 as

n





, the result follows, i.e.,

. =u fu

From Theorem 2.1, we have the following result which is an improvement from the corresponding results (Theorems 2.7 and 2.8) of (Ansari, et al, 2016).

Corollary 2.1. Let



X

,





be a partially ordered set and there exists a b-metric

d

on X such that



X

,

d



is a b-complete b-metric space. Suppose

s

>

1

and f :X  X is an increasing mapping with respect to



such that there exists an element x₀X with

x

₀



fx

₀

.

Assume that

 



x fx



d



fx fy





d

 

x y

  

M x y L N

 

x y

d y x sd , , , , , 2 1 1 , 1       



(2.3)

for all comparable elements x,yX,

where L0, :[0, ) [0,1)

s  



with

 

s tn

1





implies tn 0,

 

  

 





















fy

fx

d

fy

y

d

fx

x

d

y

x

d

y

x

M

,

1

,

max

=

,

and

 

x

,

y

=

min



d



x

,

fx

 

,

d

x

,

fy

 

,

d

y

,

fx

 

,

d

y

,

fy





.

N

If

(1)f is continuous, or

(2) whenever

 

,

X u

x

_n



u

for all nN,

thenf has a fixed point. Moreover, the set of fixed points of f is well ordered if and only if f has one and only one fixed point.

Proof. Since



 

,



<1,

s y x d

(18)

Cha

ndok, S.C. et al,

 



,





,



 

,

 

, , 2 1 1 , 1

1 N x y L y x M fy fx d fx x d y x sd

s    

  

(2.4)

where

L

₁

=

s



L

.

On the similar lines of Theorem 2.1, we have the result. On the similar lines of Theorem 2.1, we have the following result.

Theorem 2.2. Let



X

,





be a partially ordered set and suppose that there exists a b-metric

d

onX such that



X

,

d



is a b-complete b-metric space (with parameter

s

>

1

). Let f :X  X be an increasing mapping

with respect to



such that there exists an element x0X with

.

0 0

fx

x



Suppose that



fx

,

fy





d

 

x

,

y

  

M

x

,

y

L

N

 

x

,

y

,

d

s











(2.5)

for all comparable elements x,yX,

where L0, :[0, ) [0,1)

s  



with

 

s t_n 1



implies tn 0,

 

  

 





















fy

fx

d

fy

y

d

fx

x

d

y

x

d

y

x

M

,

1

,

max

=

,

and

 

x

,

y

=

min



d



x

,

fx

 

,

d

x

,

fy

 

,

d

y

,

fx

 

,

d

y

,

fy





.

N

If

(2) whenever

 

,

X u

x

_n



u

for all nN,

then f has a fixed point. Moreover, the set of fixed points of f is well ordered if and only if f has one and only one fixed point.

Proof. The condition (2.5) implies



,



1₂ M

 

x,y L₁ N

 

x,y ,

s fy fx

d     (2.6)

for all comparable elements x,yX, where ₁= 0.

s L

L The rest of the

proof is similar to Theorem 2.1.

(19)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

with them. Our approach in Theorems 2.1-2.2, as well as in Corollary 2.1 covers all the results of (Aghajani, et al, 2014, pp.941-960) without utilizing the lemma mentioned above. It is clear that our proofs are much shorter and nicer.

Also, it is not hard to see that the main results in (Abbas, et al, 2016, pp.1413-1429) have much shorter proofs by the application of our approach, that is, without using Lemma 1.2 of (Aghajani, et al, 2014, pp.941-960).

In the sequel, we consider all three results in the case where s=1,

that is,



X

,

d



is a standard metric space. Here we have to use Lemma 1.4 to obtain our results.

Theorem 2.3. Let



X

,





be a partially ordered set and suppose that there exists a metric

d

on X such that



X

,

d



is a complete metric space. Suppose f :X  X is an increasing mapping with respect to



such that there exists an element x₀ X with

x

₀



fx

₀

.

Assume that

 



x fx



d



fx fy





M

 

x y



L N

 

x y

d y x d , , , , 2 1 1 , 1      



(2.7)

for all comparable elements x,yX, where L0,

 

  

 





















fy

fx

d

fy

y

d

fx

x

d

y

x

d

y

x

M

,

1

,

max

=

,

and

 

x

,

y

=

min



d



x

,

fx

 

,

d

x

,

fy

 

,

d

y

,

fx

 

,

d

y

,

fy





.

N

If

(2) wheneve r

 

,

X u

xn   one has

x

n



u

for all nN,

then f has a fixed point. Moreover, the set of fixed points of f is well ordered if and only if f has one and only one fixed point.

(20)

Cha

ndok, S.C. et al,







,





,





,





,



, 2 1 1 , 1 1 1 2 1 1 1       _ _ _ _   n n n n n n n n n n x x N L x x M x x d x x d x x d



where







 



 



=



,



, , 1 , , , , max = , ₁ 2 1 2 1 1 1 1                 n n n n n n n n n n n

n d x x

x x d x x d x x d x x d x x M

because





<1,

, 1 , 2 1 2 1    

 n n

n n x x d x x d and



xn,xn1



=min



d



xn,xn1

 

,d xn,xn2

 

,d xn1,xn1

 

,d xn1,xn2





=0.

N

Since











1



 

1



1 1 , < , 1, > , 2 1 1 , 1       n n n n n n n n x x d x x M x x d x x d



and N



x_n,x_n_₁



(2.8)

becomes d



xn1,xn2

 

<d xn,xn1



,

i.e., d



xn,xn1



is a decreasing sequence. Therefore, there exists

r



0

such that

lim

n d



xn,xn1



=r. Assume that

r

>

0

, from (2.8), we have

0, 2 1 2 1 1 1       r r r r r

which is a contradiction. Hence limnd



xn,xn1



=0.

Now, we suppose that the sequence

 

x_n is not a Cauchy sequence in a metric space



X

,

d



.

By putting

x

=

x

_m_{ }_k

,

y

=

x

_n_{ }_k in (2.7), we obtain

   





   



,





  ,  





 ,  





 ,  



, 2 1 1 , 1 1 1 1 k n k m k n k m k n k m k m k m k n k m x x N L x x M x x d x x d x x d           (2.9) where    



x

mk

x

nk



M

,

   







   





   



   





, , 1 , , , , max = 1 1 1 1 1                k n k m k n k n k m k m k m k m x x d x x d x x d x x d and    



x

mk

x

nk



(21)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

   







   





   





   





,



.

min

=

d

x

_m_k

x

_m_k_₁

d

x

_m_k

x

_n_k_₁

d

x

_n_k

x

_m_k_₁

d

x

_n_k

x

_n_k_₁

Now, letting to the limit in (2.9), as k, and using Lemma 1.4, we get

 

0,

2 1 < 0 2 1 1 1        







L

which is a contradiction. Hence the sequence

 

x_n is a Cauchy sequence. The rest of the proof is the same as in Theorem 2.1.

Corollary 2.2. Let



X

,





be a partially ordered set and suppose there exists a metric

d

onX such that



X

,

d



is a complete metric space. Suppose f :X  X is an increasing mapping with respect to



such that there exists an element x₀ X with

x

₀



fx

₀

.

Assume that

 



x fx



d



fx fy





d

 

x y

  

M x y L N

 

x y

d y x d , , , , , 2 1 1 , 1       



(2.10)

for all comparable elementsx,yX,

where L0,



:[0,)[0,1) with



 

t

_n



1

 implies t_n 0,

 

  

 





















fy

fx

d

fy

y

d

fx

x

d

y

x

d

y

x

M

,

1

,

max

=

,

and

 

x

,

y

=

min



d



x

,

fx

 

,

d

x

,

fy

 

,

d

y

,

fx

 

,

d

y

,

fy





.

N

If

(1) f is continuous, or

(2) whenever

 

,

X u

xn   one has xnu for all nN,

then f has a fixed point. Moreover, the set of fixed points of f is well ordered if and only if f has one and only one fixed point.

Proof. Since





d

 

x

,

y



<

1,

the condition (2.10) implies that

 



,





,



 

,

 

, . 2 1 1 , 1 y x N L y x M fy fx d fx x d y x d       (2.11)

(22)

Cha

ndok, S.C. et al,

Remark 2.2. It is not hard to see that both functions



and



in all results are superfluous. But in our next result, the function



is not superfluous.

Theorem 2.4. Let



X

,





be a partially ordered set and suppose that there exists a metric

d

onX such that



X

,

d



is a complete metric space. Let f :X  X be an increasing mapping with respect to



such that the-re exists an element x0X with

x

0



fx

0

.

Suppose that



fx

,

fy





d

 

x

,

y

  

M

x

,

y

L

N

 

x

,

y

,

d









(2.12)

for all comparable elements x,yX, where

0,



L



:[0,)[0,1)with



 

t

_n



1

implies t_n 0,

 

  

 





















fy

fx

d

fy

y

d

fx

x

d

y

x

d

y

x

M

,

1

,

max

=

,

and

 

x

,

y

=

min



d



x

,

fx

 

,

d

x

,

fy

 

,

d

y

,

fx

 

,

d

y

,

fy





.

N

If

(1) f is continuous, or

(2) whenever

 

,

X u

x

_n



u

for all nN,

then f has a fixed point. Moreover, the set of fixed points of f is well ordered if and only if f has one and only one fixed point.

The following example support our theoretical result given with Corollary 2.1.

Example 2.3. Let

X

=



0,1,2



and define the partial order



on X

by



:=



       

0,0

,

1,1

,

2,2

,

0,1



.

Consider the function f :X  X given as

0 = 3 1, = 1 =

0 f f

f which is nondecreasing with respect to



. Let

0. =

0

(23)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

conditions of Corollary 2.1 for each ) 2 1 [0, ) [0,

:  



with tn 0

whenever

 

. 2 1_

 n

t



Finally, we formulate the following result (Geraghty fixed point theorem in the framework of a b-complete b-metric space):

Theorem 2.5. Let



X

,

d



be a b-complete b-metric space and let

1.

>

s

Suppose that a mapping f :X  X satisfies the condition



fx

,

fy





d

 

x

,

y

  

d

x

,

y

,

d





for all x,yX,where



:[0,)[0,1) with tn 0whenever

 

t_n 1



for each sequence t_n

 

0,.

Question. Prove or disprove Theorem 2.5.

References

Abbas, M., Chema, I.Z., & Razani, A., 2016. Existence of common fixed po-int for b-metric rational type contraction. Filomat, 30(6), pp.1413-1429.

Aghajani, A., Abbas, M., & Roshan, J.R., 2014. Common fixed point of ge-neralized weak contractive mappings in partially ordered-metric spaces. Math. Slovaca, 4, pp.941-960.

Ansari, A.H., Razani, A., & Hussain, N., 2016. Fixed and coincidence points for hybrid rational Geraghty contractive mappings in ordered b-metric spaces, to appear in. Int. J. Nonlinear Anal. Appl. Available at: http://dx.doi.org/10.22075/IJNAA.2016.453.

Bakhtin, I.A., 1989. The contraction principle in quasimetric spaces. Funct. Anal., 30, pp.26-37.

Czerwik, S., 1993. Contraction mappings in-metric spaces. Acta Math. In-form. Univ. Ostrav, 1, pp.5-11.

Djukić, D., Kadelburg, Z., & Radenović, S., 2011. Fixed points of Geraghty-type mappings in various generalized metric spaces. Abstr. Appl. Anal. Article ID 561245, 13 pages.

Huang, H., Vujaković, J., & Radenović, S., 2015a. A note on common fixed point theorems for isotone increasing mappings in ordered b-metric spaces. J. Nonlinear Sci. Appl., 8, pp.808-815.

Huang, H., Paunović, Lj., & Radenović, S., 2015b. On some new fixed point results for rational Geraghty contractive mappings in ordered b-metric spaces. J. Nonlinear Sci. Appl., 8, pp.800-807.

(24)

Cha

ndok, S.C. et al,

rdered

b-metric spac

e

s

and Gerag

h

ty

type contracti

v

e mapp

ings, p

p

. 331–

34

5

Hui-Sheng, D., Imdad, M., Radenović, S., & Vujaković, J. ,2016. On some fixed po-int results in b-metric, rectangular and b-rectangular metric spaces. Arab J. of Math. Sci,

pp.151-164. Available at: http://dx.doi.org/10.1016/j.ajmsc.2015.05.003.

Hussain, N., Đorić, D., Kadelburg, Z., & Radenović, S., 2012. Suzuki-type fixed point results in metric type spaces. Fixed Point Theory Appl., 126.

Hussain, N., Parvaneh, V., Roshan, J.R., & Kadelburg, Z., 2013. Fixed po-ints of cyclic



,,L,A,B



- contractive mappings in ordered b-metric spaces with applications. Fixed Point Theory Appl., 256.

Jleli, M., Rajić, V.Ć., Samet, B., & Vetro, C., 2012. Fixed point theorems on ordered metric spaces and applications to nonlinear elastic beam equations.

J. Fixed Point Theory Appl, pp.175-192. Available at: http://dx.doi.org/10.1007/s11784-012-0081-4.

Jovanović, M., Kadelburg, Z., & Radenović, S., 2010. Common fixed point re-sults in metric-type spaces. Fixed Point Theory Appl. Article ID 978121, 15 pages.

Kadelburg, Z., Paunović, Lj., & Radenović, S., 2015. A note on fixed point theorems for weakly T-Kannan and weakly T-Chatterjea contractions in b-metric spacesa. Gulf Journal of Mathematics, 3(3), pp.57-67.

Khamsi, M.A., & Hussain, N., 2010. KKM mappings in metric type spaces.

Nonlinear Anal., 73, pp.3123-3129.

Parvaneh, V., Roshan, J.R., & Radenović, S., 2013. Existence of tripled co-incidence points in ordered b-metric spaces and an application to a system of integral equations. Fixed Point Theory Appl., 130.

Radenović, S., Kadelburg, Z., Jandrlić, D., & Jandrlić, A., 2012. Some re-sults on weakly contractive maps. Bulletin of the Iranian Mathematical Society,

38(3), pp.625-645.

Roshan, J.R., Parvaneh, V., Shobkolaei, N., Sedghi, S., & Shatanawi, W., 2013. Common fixed points of almost generalized (



,



)_s- contractive mappings in ordered b-metric spaces. Fixed Point Theory Appl., 159.

Roshan, J.R., Parvaneh, V., Radenović, S., & Rajović, M., 2015. Some co-incidence point results for generalized





,







weakly contractions in ordered b-metric spaces. Fixed Point Theory Appl., 68.

Roshan, J.R., Parvaneh, V., & Kadelburg, Z., 2014. Common fixed point theorems for weakly isotone increasing mappings in ordered b-metric spaces.

J. Nonlinear Sci. Appl., 7, pp.229-245.

Zabihi, F., & Razani, A., 2014. Fixed point theorems for hybrid rational Geraghty contractive mappings in ordered b-metric spaces. J. Appl. Math.,

(25)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

Ч Ы Ч

Щ GERAGHTY

и Ч , Ми . , я .

a _, _, _, _я

, , . ,

я

, я, . ,

я

:

: я я я

Ы :

е е:

В я е е, л г я е ,

е ле е шие е л и ле и

е и и, е е е и и.

е ле ие х е л е ле и е и.

Кл е е л : я , - , ы ,

я ы , GERAGHTY- , - , - .

Ђ - Ч

Њ Ј

и Ч , Ми . Ј , ј .

a

, , ,

:

Ч :

Ј Ч :

е :

К ишћење г и , е е и

е и е л е и е е, ј је ил ише

, г ћии ле ши и . Н е е јеи и е ји

ил је.

К е е и: , - , , ђ ,

(26)

Cha

ndok, S.C. et al,

rdered

b-metric spac

e

s

and Gerag

h

ty

type contracti

v

e mapp

ings, p

p

. 331–

34

5

Paper received on / я ы / : 24.01.2017.

Manuscript corrections submitted on / я ы /

: 11. 03. 2017.

Paper accepted for publishing on / я ы /

:13. 03. 2017.

w.vtg.mod.gov.rs, . . . ). This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license

(http://creativecommons.org/licenses/by/3.0/rs/).

я я «Creative Commons» (http://creativecommons.org/licenses/by/3.0/rs/).

(www.vtg.mod.gov.rs, . . . ).

(27)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

EXTENSIONS OF THE BANACH

CONTRACTION PRINCIPLE IN

MULTIPLICATIVE METRIC SPACES

Badshah- -Romea, Muhammad Sarwarb

University of Malakand, Department of Mathematics, Chakdara Dir(L), Pakistan

a

e-mail: baadeshah@yahoo.com,

b

e-mail: sarwarswati@gmail.com,

https://dx.doi.org/10.5937/vojtehg65-13342 FIELD: Mathematics.

ARTICLE TYPE: Original Scientific Paper ARTICLE LANGUAGE: English

Abstract:

In this paper, we have proven several generalizations of the Banach contraction principle for multiplicative metric spaces. We have also derived the Cantor intersection theorem in the setup of multiplicative metric spa-ces. Non-trivial supporting examples are also given.

Key words: Multiplicative metric, Multiplicative open ball, Multiplicative Cauchy sequence, Multiplicative contraction.

Introduction

The study of fixed points of mappings satisfying certain contractive condi-tions has many fruitful applicacondi-tions in various branches of mathematics; hen-ce, it has extensively been investigated by many authors (Rad, et al, nd), (Radenović, et al, nd), (Mustafa, et al, 2016, pp.110-116), (Radenović, et al, 2016, pp.38-40). The Banach contraction principle has been the most versati-le and effective tool in the fixed-point theory (Banach, 1922, pp.133-181). Ge-neralization of the Banach contraction principle has been one of the most in-vestigated branches of research. Matthews (1994, pp.183-197) introduced the concept of partial metric space as a part of the study of denotational seman-tics of dataflow networks, showing that the Banach contraction mapping theo-rem can be generalized to the partial metric context for applications in pro-gram verification. Hitzler (2001) generalized the Banach contraction principle in the context of a dislocated metric space.

(28)

Rome, B., et al,

Extensions of t

he banach contraction principle in mult

iplicative metric spaces, pp. 346–358

Zeyada (2005, pp.111-114) improved the work of Hitzler in a disloca-ted quasi metric space. Shatanawia & Nashine (2012, pp.37-43) studied the Banach contraction principle for nonlinear contraction ina partial metric space. Suzuki (2008, pp.1861-1869) characterized metric completeness by the generalized Banach contraction principle. Boyd and Wong (1969, pp.458- 464) showed that the constant used in the Banach contraction principle can be replaced by an upper semi-continuous function. Hadžić and Pap (2001) extended the contraction principle to probabilistic metric. Jainet al. (2012, pp.252-258) generalized the Banach contraction principle for cone metric spaces. There have been a number of generalizations of a metric space. Some examples of such generalizations are given above. One such generalization is a multiplicative metric space, where Ӧzavsar and Cevikel (2012) introduced the notion of multiplicative contraction map-pings and derived some ﬁxed-point results for such mappings on a com-plete multiplicative metric space.

Hxiaoju, et al. (2014) established some common ﬁxed points for weak commutative mappings on a multiplicative metric space.

In the current paper, we establish an extension of the famous Banach contraction principle in multiplicative metric spaces. The Banach theorem is extended in two ways:

1. The contraction constant depends on the multiplicative distance between the points under consideration.

2. The behavior of d(x; T x) is considered instead of the comparison of d(T x, T y) and d(x, y).

The derived results carry the ﬁxed-point results of Dugundji and Gra-nas (1982) in a metric space to a multiplicative metric space. Furthermore, to complete the proof of the extension of the Banach theorem, we also de-rived the Cantors intersection theorem in multiplicative metric spaces.

De_ﬁnition 1.1. (Bashirov et al, 2008) A multiplicative metric on a nonempty set X is a mapping

d: X ×X

→

R

satisfying the following condition:

(1)

d(x, y)

≥

1 for all

x, y X

;

(2)

d(x, y)

= 1 if and only if

x = y

;

(3)

d(x, y) = d(y, x)

for all

x, y X

;

(4) d(x,

z)

≤

d(x, y). d(y, z) for all x, y, z X.

The pair (X,d) is called a multiplicative metric space.

Example 1.1. Let Rn denote the set of n-tuples of positive real numbers.

(29)

VOJNOTEHNI

Č

TECHNICAL

CO

URIER, 201

* *

* 1 2 3

1 2 3

( , ) . . ... n

n

x x

d x y

y y y y



Where x=(x1, x2, …, xn) , y=(y1, y2, …, yn) Rn and

*

. :R_R_ is defi-ned as

*

if 1 1

if 1

a a

a

a a

 



  _



Then, clearly, d* (x, y) is a multiplicative metric (Bashirov et al, 2008).

Example 1.2. Let (X,d) be a metric space, then the mapping da

deﬁned on X as follows is a multiplicative metric, ( , )

where 1.

( , )

a

d x y

a

d x y



a



The following definitions are given by Ӧzavsar and Cevikel (2012).

De_ﬁnition 1.2. Let (X,d) be a multiplicative metric space. If a∈X and

r>1, then a subset

( ) ( ; ) { : ( ; ) }

r

B a B a r  x  X d a x  r

of X is called a multiplicative open ball centered at a with the radius r.

Analogously, one can de_ﬁne a multiplicative closed ball as ( ) ( ; ) { : ( ; ) }

r

B a B a r  x  X d a x  r

De_ﬁnition 1.3. Let A be any subset of a multiplicative metric space

(X,d). A point x∈X is called a limit point of A if and only if

( ( )) { }A  B_ x  x   _{for every}



_₁_.

De_ﬁnition 1.4. Let (X,d) and (Y,ρ) be given multiplicative metric spa-ces and a∈X. A function f:

   

X d, Y,



is said to be multiplicative conti-nuous at a, if for given



1, there exists a δ >1 such that

 

,

( ( ), ( )) or equivalently ( ( ; ))

( ( ); ).

Where ( ; ) and ( ( ); )

d x a

d f x f a

f B a

B f a

B a

B f a













 





are open balls in (X,d) and (Y,ρ) respectively. The function f is said to be continuous on X if it is continuous at each point of X.

De_ﬁnition 1.5. A sequence {x_n}_{in a multiplicative metric space}_(X,d) is said to be multiplicative convergent to a point x∈X if for a given



1

(30)

positi-Rome, B., et al,

Extensions of t

he banach contraction principle in mult

iplicative metric spaces, pp. 346–358

ve integer

n

₀ such that nn₀ x_n B_( )x then the sequence { }xn is

said to bemultiplicative-convergent to a point x∈ X denoted by xn→ x(n →

∞).

De_ﬁnition 1.6. A sequence {x_n}in a multiplicative metric space (X,d)

is said to be multiplicative Cauchy sequence if for every 1 there exists a positive integer n0such that d x x( n, m) for all n, m≥n0 .

De_ﬁnition 1.7. A multiplicative metric space (X,d) is said to be com-plete if every multiplicative Cauchy sequence in X converges in X in the multiplicative sense.

De_ﬁnition