KARYA TULIS
JOURNAL REPORT
ON APPLICATION OF INTEGER PROGRAMMING
A Critique on
AN OPTIMIZATION MODEL FOR ANNUAL HARVEST
PLANNING
BY:
RAHMAWATY
DEPARTEMEN KEHUTANAN
FAKULTAS PERTANIAN
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Tuhan Yang Maha Esa, yang telah memberikan segala
rahmat dan karunia-Nya sehingga KARYA TULIS ini dapat diselesaikan. Judul yang dipilih adalah
“
AN
OPTIMIZATION MODEL FOR ANNUAL HARVEST PLANNING
”.
Tulisan ini merupakan suatu kritik
mengenai Aplikasi INTEGER PROGRAMMING DI Bidang Kehutanan, Penulisnya adalah Jenny
Karlsson, Mikael Rönnqvist, Johan Bergström dan bersumber dari Journal: Canadian Journal of
Forest Research; Aug 2004; 34, 8 pg. 1747
.
Kami menyadari bahwa karya tulis ini masih jauh dari sempurna, oleh karena itu kami
mengharapkan saran dan kritik yang bersifat membangun untuk lebih menyempurnakan karya tulis ini.
Akhir kata kami ucapkan semoga karya tulis ini dapat bermanfaat.
Medan, April 2010
DAFTAR ISI
I.
Title of the Study
1
II.
Introduction
1
A. Back ground
1
B. Objectives of the Study
3
III.
Mixed Integer Programming (MIP)
3
A. Definition
3
B. MIP Problem
4
C. Solving MIP Problem
4
D. A Review of MIP Solution Methods
6
E. Application Domains and Software
8
IV. Problem Description
8
A. Harvest Areas
8
B. Harvest teams
8
C. Wood-Processing Facilities
9
D. Roads
9
V.
Mathematical Formulation
10
VI. A Single District Case Study
11
VII. Computational Results
12
A. Test Problems
12
B. CPLEX Directly
12
C. Heuristic Solution Approach
13
VIII. Conclusion
13
IX. General Comments on the Paper
14
A. Strengths
14
B. Weakness /Limitations
14
C. Suggestion
14
A Critique on
AN OPTIMIZATION MODEL FOR ANNUAL HARVEST PLANNING
Authors: Jenny Karlsson, Mikael Rönnqvist, Johan Bergström.Journal: Canadian Journal of Forest Research; Aug 2004; 34, 8 pg. 1747. By:
Rahmawaty
I. Title of the Study
• As a researcher, the title provided by the authors has the element of simplicity, brevity, specificity and location and subject matter focused. The reader can easily determine what the study is all about and what it tries to investigate (An optimization model for annual harvest planning) and what mathematical model? A mixed integer programming (MIP). Brief title but very informative. To more make informative, it would be better if the author mention the location of the study and the MIP on the title, so the reader know the location and the mathematical model of the study.
• Just going through the title, one can easily understand that the concern of the research study is related to optimization model in forestry. The keywords used such as “annual harvest planning” clearly indicate that the subject matter is in the field of forestry.
II. Introduction
A. Background of the Study:
• According the authors, In Sweden, wood flow planning for forest companies, including harvest and transportation planning, occurs in different stages. Harvest planning includes decisions on different levels, both spatial and temporal. Prognoses are made for long-time horizons (strategic planning), in Sweden typically 100 years. The maximum harvested volumes are estimated, as well as proportions of thinning and final felling, with respect to requirements on sustainable forestry.
• This stage of harvest planning is usually called the tactical level. Time for thinning and final felling is estimated to maximize the total value. On a medium or annual level, planning is aimed to identify which areas to harvest in given months to balance supply and demand. On a shorter time horizon, plans are often made for a number of weeks only.
• Larger forest companies in Sweden have an organization whereby operations are divided into smaller regions, which may be composed of one or several districts. Plans at different levels are continuously updated on rolling planning horizons. The different levels of harvest planning are described in Figure 1.
• The problem we consider in this paper is the annual planning problem at the district level. The annual planning starts from a list or a pool of areas that correspond to 1.5-2 years of harvesting. The main decisions deal with which areas to harvest and which crew to assign. The selection of harvesting areas strongly affects the production level of different assortments, as each area has a particular assortment mix. It also affects the choice of crew, as each area has an average tree size and harvest teams have a given capacity and efficiency depending on this size.
• The output from this plan is the distribution of harvest areas over the year, assuring accessibility, as well as assuring that the monthly harvested amount corresponds to the demand of the wood-processing facilities. The result from the annual plan yields input to short-term, operational planning.
• Currently, planning for harvesting and transportation for each district, both on an annual and operative level, is carried out manually. There are usually a limited number of qualified and experienced persons that make the short-term harvest plans, and they spend a large amount of time preparing qualitative plans. Coordination between districts is limited and is only considered in particular situations during the year.
• In short-term planning, the storage level and age of the harvested timber is considered to obtain a better estimate of storage cost. To determine the harvested amount of different assortments each week, we need to determine the sequence of harvest areas during the planning period.
• There have been many studies dealing with harvesting planning on different levels. The terminology is not uniform; planning on time horizons between 1 and 70 years is sometimes mentioned as tactical planning. A medium-range, tactical harvest schedule model called OPTIMED is mentioned in Epstein et al. (1999). This model supports decisions concerning which stands to harvest, how much timber is needed to satisfy projected demands, and which roads are needed to gain access to the harvest areas for a total planning horizon of 2-5 years.
• Annual harvesting planning is found in Newham (1991), where a version of the system LOGPLAN II is described. This is a model based on linear programming (LP) that can be used to schedule timber harvesting and regeneration activities given available equipment, wood resources, planting stock, and mill demands in order to minimize cost. An annual planning problem within Swedish forestry is described in Gunnarsson et al. (2004). Here the problem is to decide where and when forest residues are to be converted into forest fuel and how the residues are to be transported and stored to satisfy demand at heating plants.
• Tactical and operational harvesting planning often includes discrete decisions about specific stands or roads, which create integer or mixed-integer problems. The presence of integer variables and the size of real-world problems often lead to heuristic methods to achieve practical solution times.
• A long-term, spatially constrained harvest-scheduling problem is studied in Yoshimoto et al.
(1994). They developed a heuristic procedure in which the problem is partitioned into a number of subproblems, which are then solved independently. Weintraub el al. (1995) describes a heuristic algorithm for solving a tactical problem for 2-3 decades, including harvesting decisions and road building.
• The solution procedure iterates between solving relaxed LP versions of the model and applying rules to fix fractional variables to integer variables. A branch-and-price algorithm is used to obtain optimal integer solutions. To achieve compatible decision made at different levels, different approaches have been used. Hierarchical methods have been developed to integrate tactical and strategic planning.
• The authors start by developing a mathematical model, which gives a mixed integer problem (MIP). To test the model, we have made a case study. The annual planning typically starts with a large number of areas, which leads to a large number of binary and continuous variables and numerous constraints. According the authors, case study problem corresponds to planning on a district level.
B. Objectives of the Study:
• The main contribution of this paper is a model describing the annual harvesting planning problem, including decisions about harvest areas, simultaneous allocation of harvest teams, and overall transportation and storage planning.
• The case study gives input to a future development of a decision support system. The remainder of this paper is organized as follows: in the following section, the annual harvesting planning problem is described. We then present the mathematical formulation of the problem. A case study is then described, followed by Computational Results. Finally, concluding remarks are made.
III. Mixed Integer Programming (MIP)
A. Definition
• Algorithms and computer-based tools for analyzing infeasible linear and nonlinear programs have been developed in recent years, but few such tools exist for infeasible mixed-integer or integer linear programs (Guieu and Chinneck, 1999). A mixed-integer programming (MIP) problem is one where some of the decision variables are constrained to have only integer values (i.e. whole numbers such as -1, 0, 1, 2, etc.) at the optimal solution. The use of integer variables greatly expands the scope of useful optimization problems that we can be define and solve (http://www.solver.com/probtype3.htm). A mixed-integer program is the minimization or maximization of a linear function subject to linear constraints. In practice linear programs can be solved efficiently for reasonable-sized problems, or even for big problems with special structure. However when some or all of the variables must be integer, corresponding to pure integer and mixed integer programming respectively, the problem becomes formally intractible (http://www.cs.sandia.gov/opt/survey/mip.html).
• According to Guieu and Chinneck (1999), Mixed-integer and integer linear programs (here collectively referred to as MILPs) are much harder to solve than ordinary linear programs (LPs) because of the inherent combinatorial nature of the solution approaches necessitated by the integer variables. Infeasible MILPs are even more difficult to analyze because they usually require numerous solutions of variations of the original model. In addition, when a branch-and-bound solution procedure finds the original model infeasible, little useful information (such as constraint sensitivity in linear programs) is initially available to guide the analysis of the infeasibility. Some form of automated assistance in analyzing infeasible MILPs is needed, especially as models grow in size in step with increases in computing power.
• In relationship to Linear Programming, given an integer program:
• There is an associated linear program called the linear relaxation (LR) formed by dropping the integrality restrictions:
¾ If (IP) is a minimization, the optimal objective value for (LR) is less than or equal to the optimal objective for (IP).
¾ If (IP) is maximization, the optimal objective value for (LR) is greater than or equal to that of (IP).
¾ If (LR) is infeasible, then so is (IP).
¾ If (LR) is optimized by integer variables, then that solution is feasible and optimal for (IP).
¾ If the objective function coefficients are integer, then for minimization, the optimal objective for (IP) is greater than or equal to the ``round up'' of the optimal objective for (LR). For maximization, the optimal objective for (IP) is less than or equal to the ``round down'' of the optimal objective for (LR).
• So solving (LR) does give some information: it gives a bound on the optimal value, and, if we are lucky, may give the optimal solution to IP. We saw, however, that rounding the solution of LR will not in general give the optimal solution of (IP). In fact, for some problems it is difficult to round and even get a feasible solution. The general methods can be easily extended to the mixed-integer case (http://www.cs.sandia.gov/opt/survey/mip.html)
B. Mixed-Integer Programming (MIP) Problems
• An important special case is a decision variable x1 that is integer with 0 <= x1 <= 1. This forces x1 to be either 0 or 1 at the solution. Variables like x1, called 0-1 or binary integer variables, can be used to model yes/no decisions, such as whether to build a plant or buy a piece of equipment. However, integer variables make an optimization problem non-convex, and therefore far more difficult to solve. Memory and solution time may rise exponentially as you add more integer variables. Even with highly sophisticated algorithms and modern supercomputers, there are models of just a few hundred integer variables that have never been solved to optimality. This is because many combinations of specific integer values for the variables must be tested, and each combination requires the solution of a "normal" linear or nonlinear optimization problem. The number of combinations can rise exponentially with the size of the problem (http://www.solver.com/probtype3.htm).
C. Solving MIP Problems
• Since MIP problems are non-convex, they must be solved by some kind of systematic and potentially exhaustive search. The "classic" method for solving these problems is called Branch and Bound (http://www.solver.com/probtype3.htm). This method begins by finding the optimal solution to the "relaxation" of the problem without the integer constraints (via standard linear or nonlinear optimization methods). If in this solution, the decision variables with integer constraints have integer values, then no further work is required. If one or more integer variables have non-integral solutions, the Branch and Bound method chooses one such variable and "branches," creating two new subproblems where the value of that variable is more tightly constrained. These subproblems are solved and the process is repeated, until a solution that satisfies all of the integer constraints is found.
1. Branch and Bound
• The most widely used method for solving integer programs is branch and bound. Subproblems are created by restricting the range of the integer variables. For binary variables, there are only two possible restrictions: setting the variable to 0, or setting the variable to 1. More generally, a variable with lower bound l and upper bound u will be divided into two problems with ranges l to q and q+1 to u respectively. Lower bounds are provided by the linear-programming relaxation to the problem: keep the objective function and all constraints, but relax the integrality restrictions to derive a linear program. If the optimal solution to a relaxed problem is (coincidentally) integral, it is an optimal solution to the subproblem, and the value can be used to terminate searches of subproblems whose lower bound is higher. See the branch and bound section of this survey for more details on how lower bounds, upper bounds, and branching interact.
http://www.cs.sandia.gov/opt/survey/mip.html
• According to Trick (1998), they have seen all parts of the branch and bound algorithm. The essence of the algorithm is as follows:
1. Solve the linear relaxation of the problem. If the solution is integer, then we are done. Otherwise create two new subproblems by branching on a fractional variable.
2. A subproblem is not active when any of the following occurs: 1. You used the subproblem to branch on,
2. All variables in the solution are integer, 3. The subproblem is infeasible,
4. You can fathom the subproblem by a bounding argument.
3. Choose an active subproblem and branch on a fractional variable. Repeat until there are no active subproblems.
2. Branch and Cut
• For branch and cut, the lower bound is again provided by the linear-programming (LP) relaxation of the integer program. The optimal solution to this linear program is at a corner of the polytope which represents the feasible region (the set of all variable settings which satisfy the constraints). If the optimal solution to the LP is not integral, this algorithm searches for a constraint which is violated by this solution, but is not violated by any optimal integer solutions. This constraint is called a cutting plane. When this constraint is added to the LP, the old optimal solution is no longer valid, and so the new optimal will be different, potentially providing a better lower bound. Cutting planes are iteratively until either an integral solution is found or it becomes impossible or too expensive to find another cutting plane. In the latter case, a tradional branch operation is performed and the search for cutting planes continues on the subproblems. http://www.cs.sandia.gov/opt/survey/mip.html
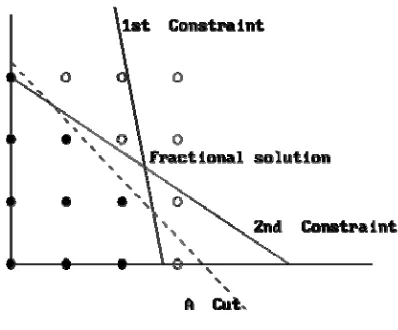
• There is an alternative to branch and bound called cutting planes which can also be used to solve integer programs. The fundamental idea behind cutting planes is to add constraints to a linear program until the optimal basic feasible solution takes on integer values. Of course, we have to be careful which constraints we add: we would not want to change the problem by adding the constraints. We will add a special type of constraint called a cut This is illustrated in Figure 2. A cut relative to a current fractional solution satisfies the following criteria:
Figure 2. A cut
• There are two ways to generate cuts. The first, called Gomory cuts, generates cuts from any linear programming tableau. This has the advantage of ``solving'' any problem but has the disadvantage that the method can be very slow. The second approach is to use the structure of the problem to generate very good cuts. The approach needs a problem-by-problem analysis, but can provide very efficient solution techniques (Trick, 1998).
3. Branch and Price
• This is essentially branch and bound combined with column generation. This method is used to solve integer programs where there are too many variables to represent the problem explicitly. Thus only the active set of variables are maintained and columns are generated as needed during the solution of the linear program. Column generation techniques are problem specific and can interact with branching decisions.
D. A Review of MILP Solution Methods
• There are two main methods of solving MILPs in practice, cutting-plane methods and branch-and-bound, plus a hybrid of the two, branch-and-cut. Cutting-plane methods work by iteratively adding constraints ("cuts") to the set LC (or BD), which reduce the size of the feasible region of the LP-relaxation such that the optimum solution of the LP-relaxation gradually approaches the optimum solution of the original MILP. In the cutting-plane method, infeasibility of the original MILP is detected when an added cut renders the current LP-relaxation infeasible. Guieu and Chinneck (1999).
• The well-known branch-and-bound method operates by creating a tree of nodes, each of which is an LP based on the original LP-relaxation with altered variable bounds. A node is expanded (child nodes are derived from it) when it has an LP-relaxation that is feasible, but for which the LP-relaxation optimum point has at least one integer variable that does not have an integral value; one such variable is chosen as the branching variable. Two child nodes are created by copying all of the constraints in the parent node and then altering the lower bound on the branching variable to create one child node and altering the upper bound on the branching variable to create the other child node (Guieu and Chinneck,1999).
integer restrictions (in which case it is also a feasible solution for the original MILP), 2) the LP-relaxation of the node is infeasible, or 3) the optimum value attained by the LP-relaxation of a node is worse than the best known MILP-feasible solution (does not occur in infeasible MILPs) (Guieu and Chinneck,1999).
Figure 3. The branch-and-bound solution of this MILP fails to terminate
• For our purposes, it is important to note that feasibility of a MILP is detected by the branch-and-bound method as soon as the first MILP-feasible node is created. However, infeasibility is only decided when the tree has been fully expanded and the LP-relaxation of every leaf node proves infeasible. Thus, it is generally much more computationally expensive to recognize infeasibility than feasibility of a MILP using branch-and-bound. Guieu and Chinneck (1999).
• In certain cases, the size of the branch-and-bound tree can become very large, possibly exceeding available memory, and in special cases growing infinitely. For example, consider the MILP in Figure 3 in which both ? and y are nonnegative integer variables. The nonnegativity constraint on y and the two parallel diagonal constraints form a pipeshaped feasible region. Because the objective is to minimize x + y, the first LP-relaxation optimum solution is at the point marked 1. Because x is not integral at that point, the branch and bound procedure creates two child nodes; one is infeasible, and the LP-relaxation of the other has an optimum solution at point 2 in Figure 3. Now x has an integral value, but y does not, leading to the creation of two more child nodes on the branch-and-bound tree. The solution process alternates between x and y as the branching variable, causing the sequence of solutions to climb the pipe, as shown in Figure 3.
• A branch-and-bound solution of the MILP in Figure 1 will never terminate. It is also easy to construct examples that will terminate, but that require an excessive number of iterations to do so. For example, imagine that the two diagonal constraints in Figure 3 are angled very slightly towards one another so that they eventually cross at a great distance from the origin. It may take a great number of iterations before infeasibility can be determined. In the same manner, if the diagonal constraints are very slightly angled away from each other, it may require a great number of iterations before the first MILP-feasible point is reached (Guieu and Chinneck,1999).
E. Application Domains and Software
• Mixed integer programs can be used to formulate just about any discrete optimization problem. They are heavily used in practice for solving problems in transportation and manufacturing: airline crew scheduling, vehicle routing, production planning, etc. Michael Trick's Operations Research Page contains pointers to many web sites on operations research in general, including math programming, specific methods, and specific problems or problem areas. The following are good journals to look at for technical papers applying integer programming: Operations Research, Mathematical Programming Series A and B,
and SIAM Journal on Optimization.
• Commercial code includes IBM's Optimization Subroutine Library OSL, CPLEX, and XPRESS-MP by Dash. The University of Karlsruhe has a list of 23 commerical solvers, with some comparison information. Compass Modeling Solutions, provides an AMPL (AT&T
Mathematical Programming Language interface to some commercial solvers. There are
other modeling languages, sometimes provided with the MIP package
(http://www.cs.sandia.gov/opt/survey/mip.html)
IV. Problem description
A. Harvest areas
• A district is divided into harvest areas. Annual planning starts with a list of areas, identified as suitable for harvest during the next 1.5-2 years. Each harvest area is unique with its own properties. It varies in size and in available volumes of assortments, and areas require between 1 and 20 days of work to harvest. The operations are either final felling or thinning.
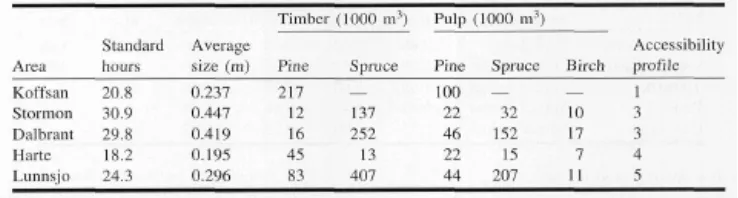
• The production time depends on the average size of the trees and the equipment of the harvest team. Each area is also connected to a particular road or road group. Table 1 gives typical data for five areas in the case study. The name of the areas, the number of standard hours to harvest the area, the average tree diameter, and quantities of the different assortments are given.
[image:11.612.132.501.554.653.2]• The accessibility profile code implies a certain annual profile of the accessibility, i.e., a certain grade of accessibility for each month. Areas with accessibility profile 5 correspond to areas with soft ground, and areas with accessibility profile 1 correspond to areas with high accessibility, possible to harvest during thawing. There is generally a shortage of areas with a good accessibility profile.
Table 1. Information used for five harvest areas.
B. Harvest teams
bucks, and piles the trees. The forwarder collects the log piles and moves them to pick-up points adjacent to the forest road. Some teams concentrate on final felling and others on thinning. Each team has a unique capacity (with respect to average tree diameter size) and efficiency rate (to estimate the specific number of standard hours needed for harvesting), depending on their equipment. Each person in the teams travels back and forth to a home base each working day. Each combination of team and harvest area corresponds to a particular cost.
C. Wood-processing facilities
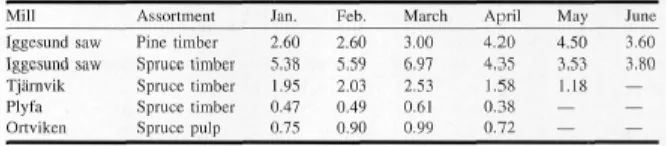
[image:12.612.133.466.303.376.2]• The demand for each mill (saw-, pulp-, or paper-mills) is given per month and assortment. Each mill has a given storage capacity that can be used for a fixed cost per cubic meter. Some mills also have terminals for storage, which are outdoor locations where the logs are stored, adjacent to the mill. The transportation cost depends on assortment and distance and is assumed proportional to the volume transported. An example of demand for the first 6 months for four mills is given in Table 2.
Table 2. An example of demand levels (x1000 m3) for four mills during
a 6-month period.
D. Roads
• Individual forest roads are aggregated into a group of forest roads and assigned a specific ID number. Some areas are connected directly to the state road network. Most areas are connected to a forest road group, which in turn is connected to the state road network. Road groups are used because single roads are regarded as too detailed. Also, there are areas that are connected to forest roads, which are connected to another forest road group before the state road network is reached. This hierarchy decides how maintenance and snow removal must be carried out.
• Accessibility of the state roads is guaranteed. During parts of the year, some roads must be avoided because of soft ground, and some forest roads need restoring to be accessible, e.g., snow removal in wintertime. The road dependence is illustrated in Fig. 4. In this example, areas 1, 2, 3, and 4 are connected to road group 1, which is connected to the state road network. Areas 5, 6, 7, and 11 are connected to road group 2, and areas 8, 9, 10, to road group 3. Road group 3 is connected to road groups 1 and 4, and road group 2 is connected to road groups 1 and 5, before reaching the state road network.
V. Mathematical Formulation
• First the defined sets used in the model are introduced.
T is the number of time periods i I is the set of harvesting areas i J is the set of mills j
K is the set of assortments k
Q is the set of all harvesting teams q
R is the set of roads r connecting the areas to state roads
RP(r) is roads adjacent to road r, i.e., roads connecting r to a higher level in the road hierarchy
R(i) is the set of roads r that connects area I to the next level of roads (or public roads) connecting the areas to state roads
I (r) is the set of areas connected to road r
• The data needed to formulate the model are given below.
• All costs are unit costs when applicable. The penalty costs are used to make sure that a near feasible solution always is attainable (see the original journal)
• The objective is to minimize the total cost.
• The first term Σiєl ΣqєQ ΣtєT CHiq ziqt represents the harvesting cost, including harvesting,
forwarding, and traveling cost. There is a specific cost for each combination of harvesting team and area.
• The second term ΣrєR ΣtєT C R
rt urt corresponds to the road-opening cost, mainly because of
the need of snow removal during the winter periods.
• The third term in the objective function ΣjєJΣkєKΣtєT C B
kt vjkt corresponds to costs associated
with purchased logs, and the next term Σiєl ΣjєJ ΣkєK ΣtєT C T
ijkt xijkt corresponds to
transportation from areas to mills. The following three terms Σiєl ΣkєK ΣtєTH F
kt l F
ikt + ΣjєJΣkєK
ΣtєT Hljk lljkt+ ΣjєJ ΣkєK ΣtєT HTjkl lTjkt represent storage cost in the forest, at terminals, and at
mills, respectively. The storage cost at the forest and terminals are due to quality deterioration of timber stored outdoors.
• Further, the eight term (ΣjєJ ΣkєK ΣtєT P s
sjkt ) represents a large cost for not satisfying the
demand. The next two term (ΣrєR ΣtєT PRrt urt + Σiєl ΣqєQΣtєT PAit (yliqt+y2iqt-1)).represent the
estimated risk for area or roads with low accessibility respectively.
• Finally, the last two term ΣiєlΣqєQΣtєT P D
y2iqt + ΣqєQΣtєT P O
q w O
qt correspond to penalty for
harvesting an area in two different (adjacent) time periods and penalty for assigning more working days to a team than the standard overtime, respectively.
• Constraints 2 mean that each harvest area can be harvested at most once. The next constraints 3 specify that total proportion of each harvest area will sum to 1, which means that if an area is harvested, it is fully harvested.
• The variable y1ikt and y2ikt are needed, since harvesting in areas can begin in one period t
and be finished in the beginning of the next time period t+1. if an area is harvested, it is always fully harvested. Each area corresponds to at most one time period of harvesting. Given this, no area is harvested in more than two adjacent time periods. The interpretation of y1ikt and y2 ikt-1 are identical, but we have included a low cost corresponding to y2ikt, to
decrease the risk of obtaining solutions where harvesting of areas are divided into two time periods.
• The constraints 4 and 5 correspond to the storage balances at harvest areas and mills, respectively. The storage at terminals is directly included in the storage balance at mills. The slack variable in eq. 5 is introduced to guarantee feasible solutions, and the penalty cost for slack assures that the demand will be satisfied (if possible). The constraints 6 restrict the total volume of purchased raw material, and constraints 7 and 8 specify the storage capacity at mills and terminals, respectively.
• Constraints 9 and 10 require at least one road connected to area i to be open if transportation of logs from i is done or if area i is harvested, respectively. These two constraints are needed, as the logs can be transported from an area i in a later time period than the area was harvested. Constraints 11 specify the precedence relation between roads. The set RP(r) is the set of roads connecting road r to the next level (or higher level, if the state road is the highest) in the road hierarchy. Constraints 12 correspond to the restriction that the crews have a limited number of working days each month to use; the use of more working days corresponds to a penalty cost. Finally, the variable restrictions are given in 13 and 14.
• The annual harvesting planning problem gives a large-scale, mixed-integer, linear problem. There are a number of binary variables corresponding to harvesting and road opening decisions and continuous variables describing storage and flow. The linear relaxation of this model gives a good estimation of the objective value of the integer problem. For each harvest area, the value of the corresponding (binary) harvest decision variable gives the proportion of the volume at that area, which is possible to use, to fulfill the demand, (constraints 3 and 4). The road network is highly aggregated, which gives that constraints 10 allow small values of urt. However, the cost corresponding to road opening is small
compared with the total cost, so these constraints do not result in a weak lower bound from the linear relaxation.
VI. A single district case study
• The case study comes from Bergsjö district in the Iggesund region. Holmen Skog is one of the largest forest owners in Sweden, with more than 106 hectares of forest. Holmen Skog is responsible for providing raw material to the Swedish wood-processing facilities included in Holmen, consisting of a group of companies where saw-, pulp- and paper-mills are included. The Iggesund region is divided into six districts. The annual harvested volume at Bergsjö district is about 250 000 m3. Holmen Skog owns the forest and also the mills. Annual harvest planning at a district aim to distribute the harvest areas during the year, ensuring that the demand at the mills is satisfied and total cost is minimized.
• The list of areas included in the case study corresponds to the pool of areas for the district. At this time, the total supply of the areas included in the list corresponds to about 1.5 years of harvesting at the district. Areas in the case study are of various sizes, with total supplies between 100 and 1000 m3 and correspond to 1-20 days of work to harvest and forward.
• There are five harvesting teams working full time in the district. The harvesting plan is made for these harvesting crews working permanently at the district, with the possibility to utilize some overtime. The extra working days correspond to overtime or contracting of a part-time, extra working team. One of the teams has two sets of machinery, and the number of possible extra working days corresponds to almost full-time schedule. In the model, it is possible to utilize an unlimited number of extra days, above the normal overtime, to a penalty cost. There are five mills in the case study with different production. Two of the mills can use a terminal for storage.
• During the rest of the year, this causes considerable costs, which increase for each week of storing. The unit cost for one time period of storing is assumed to be the cost corresponding to about 2-3 weeks of storing. The cost for planning harvesting of an area with low accessibility is assumed to be in the same range, and this is an estimation of the risk taken in that case. Some basic data and the size of the problem corresponding to the district used in the case study are summarized in Table 3. This district is typical for Holmen Skog as well as other Swedish forest companies.
VII. Computational results
• The mathematical model is implemented in the language AMPL (Fourer et al. 1993). The authors solve the MIP problem directly with the commercial software CPLEX 8.1. With a 1% tolerance from optimality, the problem is solvable directly. All computations are performed on a 2.66 GHz PC with 2 GB RAM memory.
A. Test problems
• The authors have generated five problems based on the basic case. The main purpose is to test the model and its practical usage. The second purpose is to test the performance of the heuristic solution procedure and to give some input to a future, decision support system. This is an example of sensitivity analyses that Holmen Skog has defined are of interest.
• Problem 1, the basic case. Problem 2, accessibility at all areas and roads 100%. The cost of harvesting an area or using a road with accessibility less than 100% is 0, which means road-opening decisions are not considered. The road-road-opening variables are excluded and the constraints 9, 10, and 11 are relaxed.
• Problem 3, accessibility at all areas 100%. The corresponding term in the objective is excluded.
• Problem 4, no storage cost because of quality deterioration. The corresponding two terms in the objective are excluded.
• Problem 5, no upper limit on harvesting capacity. The upper limit in constraints 12 is removed.
• Problem 6, simultaneous planning of two adjacent districts. Starting from Bergsjö case, an adjacent district is simulated and added to the basic case.
B. CPLEX directly
• The size of the six test problems and results using CPLEX directly are presented in Table 4.
• CPLEX is the implementation of fundamental branch-and-bound technique and utilizes state-of-the-art algorithms, including heuristics and a variety of branching and node selection strategies. Users can set duration limits, priorities, and tolerances on solution quality.
• In Table 4, Gap means the difference between best integer solution and best bound (from LP relaxation) divided with best bound, given as a percentage.
C. Heuristic solution approach
• This model is intended to be a component in a decision support system. This means we need to guarantee feasible solutions within a practical time limit. It is desirable to use this system for coordination of two or more districts. This corresponds to even larger problems. Therefore, we propose a heuristic solution approach. The purpose is to provide feasible solutions within a practical time limit. Linear relaxation (LP) of the problem is repeatedly solved and variables are fixed. This approach can be used if no MIP solver is available.
• According the authors, the proposed heuristic is a simple approach to mimic limited branch-and-bound in CPLEX, but where we select the branching rules is based on the actual harvesting problem. The integrality gap is small, and we get large fractional values on binary harvesting decision variables. Therefore, the branch with large fractional values of harvest variables is more likely to give a good solution.
• The heuristic will provide feasible solutions, even if backtracking is not included, if harvest decisions are considered in time order. By this we mean that integer variables are fixed to one based on the time period, e.g., variables are fixed in time period 3 before 4 or higher. Fixing a harvest variable to 1 means that we choose a fractional area to be fully harvested.
• The harvest teams are allowed to work overtime, and there is no limitation on storage or road openings. There is a surplus of areas corresponding to 1.5-2 times the demanded volumes. Therefore, starting from an LP solution, fixing fractional binary road and harvesting variables in time order provides feasible solutions.
• The maximum number of binary variables equal to 1 in a feasible solution is equal to number of areas harvested plus the number of roads opened. That gives about 300 in a regular district. That means fixing a number of binary variables to 1 in each iteration will provide a feasible solution after a limited number of LP problems.
• Computational experiments show that producing a limited branch-and-bound tree is a feasible approach to find a feasible solution within a reasonable time limit. For the basic case, repeated solutions of LP and fixing harvesting variables and corresponding roads in time order gives a feasible solution within 1.5% from optimal value of LP in 1.5 h after 43 LP problems.
• The proposed heuristic is a particular implementation of branching rules in CPLEX that cannot be done by selecting parameter settings. In each iteration, the size of the LP problem decreases, because a number of binary variables are fixed. A feasible solution is obtained after a limited number of LP problems. This approach does not require a MIP solver, as only LP problems are solved. The quality of the heuristic solution can not be guaranteed. An optimistic estimation of the optimal objective is obtained in the first step as the linear relaxation of the problem is solved.
VIII. Conclusion
• To be competitive in the market, it is important to deliver high-quality sawlogs and pulp logs. However, it is a complex task for the entrepreneurs to supply the wood-processing facilities with timber of high quality at low cost. Decision support systems based on optimization models can be important tools in this development. At present, annual harvesting plans are carried out manually.
• The developed model and the solution process are important parts of a future decision support system for annual harvesting planning.
• The contributions of this model with respect to earlier work are that this model is detailed and it integrates decisions about harvesting, scheduling of harvest crews, and storage. The model requires information that now is available from customer databases.
• The resulting mixed-integer linear problem is large, but the LP relaxation gives a lower bound close to the objective value. This problem is directly solvable using an integer solver.
IX. General Comments on the Paper
A. Strengths
• On the whole, this paper is very good, because of giving information to us about An optimization model for annual harvest planning using a mixed integer programming approach.
• The reader can easy to understand that this paper related with Optimization Model in Forestry, because this paper using a mixed integer programming approach for annual harvest planning. This method was applied in various cases was linked with forestry.
• More appropriate using a goal programming approach than other mathematical model (like: goal programming, linear programming, and dynamic programming), because there are
• This paper used a model, so this study more effective because no need go to the field to all the measurement. Using a mixed integer programming approach, model for annual harvest planning can be analyzed and assessed. The linkages with the field of forestry that need the long time to research, so this model was very helpful.
• This paper had been answering all the following questions investigated (on the objective this paper).
B. Weakness /Limitations
• The model gave the guide for us to take the decision in the forestry, although is not the end decision; at least this paper gave information and is useful as suggest for decision maker.
C. Suggestion
REFERENCES
Epstein, R., Morales, R., Seron, J., and Weintraub, A. 1999. Use of OR systems in the Chilean forestry industry. Interfaces, 29(1): 7-29.
Fourer, R., Gay, D.M., and Kernighan, B.W. 1993. AMPL - a modeling language for mathematical programming. Scientific Press, Danvers, Mass.
Guieu, O., J. W Chinneck. 1999. Analyzing Infeasible Mixed-Integer and Integer Linear Programs informs Journal on Computing. .Vol.11, Iss. 1; pg. 63, 15 pgs
Gunnarsson, H., Lundgren, J., and Rönnqvist, M. 2004. Supply chain modelling of forest fuel. Eur. J. Oper. Res. 158: 103-123.
Karlsson, J., M. Ronnqvist., and J. Bergstrom. 2004. An Optimization Model for Annual Harvest Planning. Canadian Journal of Forest Research; Agt 2004; 34, 8, pg.1747.
Michael A. Trick .1998. A Tutorial on Integer Programming. The Operations Research Faculty of GSIA. http://mat.gsia.cmu.edu/orclass/integer/integer.html
Weintraub, A., Jones, G., Meacham, M., Magendzo, A., Magendzo, A., and Malchuk, D. 1995. Heuristic procedures for solving mixed-integer harvest scheduling - transportation planning models. Can. J. For. Res. 25: 1618-1626.
www.solver.com/probtype3.htm. Optimization Problem Types - Mixed-Integer and Constraint Programming
www.cs.sandia.gov/opt/survey/mip.html. Mixed Integer Programming.