SKRIPSI
SYAUVIKA LUBIS
061401001
PROGRAM STUDI S-1 ILMU KOMPUTER
DEPARTEMEN ILMU KOMPUTER
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Komputer
SYAUVIKA LUBIS 061401001
PROGRAM STUDI S-1 ILMU KOMPUTER DEPARTEMEN ILMU KOMPUTER
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : KRIPTOGRAFI KUNCI PUBLIK ALGORITMA
ELGAMAL DENGAN METODE THE SIEVE OF ERATOSTHENES UNTUK PEMBANGKITAN BILANGAN PRIMA
Kategori : SKRIPSI
Nama : SYAUVIKA LUBIS
Nomor Induk Mahasiswa : 061401001
Program Studi : SARJANA (S1) ILMU KOMPUTER
Departemen : ILMU KOMPUTER
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan,
Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Maya Silvi Lydia, B. Sc, MSc M. Andri Budiman, S.T, M.CompSc, MEM
NIP. 197401272002122001 NIP. 197510082008011001
Diketahui/ Disetujui oleh
Departemen Ilmu Komputer FMIPA USU Ketua,
PERNYATAAN
KRIPTOGRAFI KUNCI PUBLIK ALGORITMA ELGAMAL DENGAN METODE THE SIEVE OF ERATOSTHENES
UNTUK PEMBANGKITAN BILANGAN PRIMA
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan,
PENGHARGAAN
Alhamdulillahirrabbil’alamin. Puji dan syukur penulis panjatkan kepada Allah SWT atas limpahan rahmat dan karunia-Nya sehingga penulis dapat menyelesaikan tugas akhir ini sebagai salah satu syarat untuk menyelesaikan studi pada S1 Ilmu Komputer FMIPA USU. Shalawat dan salam kepada Rasulullah Muhammad SAW.
Pada kesempatan ini penulis ingin menyampaikan terima kasih kepada pihak-pihak yang telah bersedia membantu dalam proses pembuatan tugas akhir ini hingga selesai. Dengan tulus penulis mengucapkan terima kasih kepada:
1. Bapak M. Andri Budiman, S.T, M.CompSc, MEM dan Ibu Maya Silvi Lydia, B. Sc, MSc selaku dosen pembimbing yang telah bersedia meluangkan waktu, tenaga, dan pikiran untuk penulis demi terselesaikannya tugas akhir ini.
2. Bapak Dr. Poltak Sihombing, M. Kom selaku dosen pembanding I dan Ketua Program Studi S1 Ilmu Komputer Fakultas MIPA Universitas Sumatera Utara, serta Ibu Dian Rachmawati, S. Si, M. Kom selaku dosen pembanding II dan Kepala Lab. Studio Tugas Akhir yang telah memberikan kritik dan saran untuk perbaikan skripsi ini.
3. Dekan dan Pembantu Dekan Fakultas MIPA Universitas Sumatera Utara. 4. Seluruh Dosen Program Studi S1 Ilmu Komputer Fakultas MIPA Universitas
Sumatera Utara yang telah memberikan ilmu yang bermanfaat kepada penulis selama kuliah.
5. Semua pegawai Studi S1 Ilmu Komputer.
6. Teman-teman kuliah, terutama Siti Rezeki, Faurina, Suharsono, Putri, dan Amelia yang membantu memberikan motivasi dan saran.
7. Adik-adik tersayang, Syaravina dan Sofyanda yang membantu memberikan semangat.
8. Dan yang teristimewa Ibunda Syafrida Rahmi dan Ayahanda Satria Muda
Lubis yang selalu mendukung moril dan materil, serta berdořa untuk kebaikan
diri penulis.
Akhirnya, penulis hanya dapat memanjatkan dořa, semoga Allah SWT
ABSTRAK
Pada penelitian untuk tugas akhir ini dibangun sistem kriptografi kunci publik berdasarkan algoritma ElGamal yang berguna mengamankan pesan user tanpa perlu mengalami kesulitan dalam mendistribusikan kunci karena kunci untuk dekripsi (kunci privat) berbeda dengan kunci untuk enkripsi (kunci publik) sehingga kunci enkripsi dapat didistribusikan kepada publik tanpa harus mengungkapkan kunci dekripsi, berbeda dengan kriptografi kunci simetri yang kunci dekripsi dan enkripsinya sama. Selain algoritma ElGamal, penelitian ini juga menerapkan pembangkit bilangan prima metode The Sieve of Eratosthenes pada sistem karena proses pembangkitan kunci algoritma ElGamal melibatkan bilangan prima. Dengan diterapkannya metode The Sieve of Eratosthenes pada sistem, proses pembangkitan kunci dimulai dengan input bilangan integer N untuk membangkitkan deretan bilangan prima antara 2 dan N menggunakan The Sieve of Eratosthenes, kemudian pasangan kunci publik dan kunci privat algoritma ElGamal dibangkitkan berdasarkan deretan tersebut. Sistem diwujudkan dalam bentuk sebuah aplikasi komputer yang dibangun menggunakan bahasa pemrograman Java dan NetBeans IDE. Pengujian pada aplikasi membuktikan sistem dapat menjalankan fungsi-fungsinya sesuai dengan rancangan, yaitu enkripsi pada aplikasi ini dapat mengubah plainteks ke bentuk cipherteks kemudian mengembalikannya ke bentuk plainteks semula melalui proses dekripsi, serta mampu menghasilkan pasangan kunci untuk digunakan pada proses enkripsi dan dekripsi dengan syarat kunci publik p lebih besar dari plainteks.
ELGAMAL PUBLIC KEY CRYPTOSYSTEM USING THE SIEVE OF ERATOSTHENES
TO GENERATE PRIME NUMBERS
ABSTRACT
This work is to built a public key cryptosystem based on the ElGamal algorithm which is useful for securing user messages without having difficulty in key distribution since it uses a different key for decryption (private key) and encryption (public key). Thus the encryption key can be distributed to public without having to disclose the decryption key, in contrast to symmetric key cryptography which uses the same key for encryption and decryption. Not only ElGamal algorithm, this research applies The Sieve of Eratosthenes method as a prime numbers generator on the system because the ElGamal key generation algorithm involves prime numbers. With the implementation of the Sieve of Eratosthenes method on the system, key generation process starts with an integer input N to generate a set of primes between 2 and N using the Sieve of Eratosthenes, then the public and private key pair's of ElGamal algorithm will be generated based on the set. System embodied in the form of a software is built using the Java programming language and NetBeans IDE. Tests on the software prove the system can carry out its functions in accordance with the design, that is encryption on this software can convert a plaintext into ciphertext form then convert it back to its original plaintext form through a decryption process and is able to generate key pairs for use in the process of encryption and decryption with terms the public key p is greater than the plaintext.
DAFTAR ISI
Halaman
Persetujuan ii
Pernyataan iii
Penghargaan iv
Abstrak v
Abstract vi
Daftar Isi vii
Daftar Tabel ix
Daftar Gambar x
Bab 1 Pendahuluan 1
1.1Latar Belakang Masalah 1
1.2Rumusan Masalah 2
1.3Batasan Masalah 3
1.4Tujuan Penelitian 3
1.5Manfaat Penelitian 3
1.6Metode Penelitian 4
1.7Sistematika Penulisan 4
Bab 2 Landasan Teori 6
2.1 Kriptografi 6
2.1.1 Tujuan Kriptografi 7
2.1.2 Sejarah Kriptografi 7
2.2 Kriptografi Kunci Publik 10
2.2.1 Konsep Kriptografi Kunci Publik 11
2.2.2 Aplikasi Penggunaan Kriptografi Kunci Publik 14
2.3 Algoritma ElGamal 14
2.3.1 Bilangan Prima 15
2.3.2 The Sieve of Eratosthenes 16
2.3.3 Relatif Prima 18
2.3.4 Fungsi Totient Euler 19
2.3.5Akar Primitif (Primitive Root) dari Bilangan Prima p 19
2.3.6 Perpangkatan Modulo 20
2.4 NetBeans IDE 21
Bab 3 Analisis dan Perancangan Sistem 23
3.1 Analisis Sistem 23
3.1.1 Pembangkit Bilangan Prima 24
3.1.1.1 The Sieve of Eratosthenes 25
3.1.2.2 Proses Enkripsi Algoritma ElGamal 27
3.1.2.3 Proses Dekripsi Algoritma ElGamal 27
3.2 Perancangan Aplikasi 31
3.2.1 Perancangan Antar Muka 32
3.2.2 Flowchart 35
3.2.2.1 Flowchart Pembangkit Kunci 35
3.2.2.2 Flowchart The Sieve of Eratosthenes 36
3.2.2.3 Flowchart Enkripsi 38
3.2.2.4 Flowchart Dekripsi 39
Bab 4 Implementasi dan Pengujian 40
4.1 Tampilan Antar Muka 40
4.1.1 Jendela Menu Utama 40
4.1.2 Jendela Pembangkit Kunci 41
4.1.3 Jendela Enkripsi 42
4.1.4 Jendela Dekripsi 43
4.2 Pengujian 44
Bab 5 Kesimpulan dan Saran 50
5.1 Kesimpulan 50
5.2 Saran 51
Daftar Pustaka 52
DAFTAR TABEL
Halaman 2.1 Komputasi running time pembangkit bilangan prima
metode standar pada komputer 3.2 GHz sistem operasi
Linux 17
2.2 Komputasi running time pembangkit bilangan prima metode The Sieve of Eratosthenes pada komputer 3.2
GHz sistem operasi Linux 17
2.3 Prosedur Pembangkit Bilangan Prima Metode Standar 17 2.4 Prosedur Pembangkit Bilangan Prima Metode The Sieve
of Eratosthenes 18
3.1 Tabel Bilangan Prima di antara Bilangan 1-350 28
4.1 Tabel Hasil Pengujian Aplikasi KriptoElGamal 44
DAFTAR GAMBAR
Halaman
2.1 Skema Kriptografi Nirsimetri 12
3.1 Tampilan Rancangan Jendela Menu Utama 32
3.2 Tampilan Rancangan Jendela Pebangkit Kunci 33
3.3 Tampilan Rancangan Jendela Enkripsi 34
3.4 Tampilan Rancangan Jendela Dekripsi 35
3.5 Flowchart Prosedur Pembangkit Kunci 36
3.6 Flowchart Prosedur Pembangkit Bilangan Prima The Sieve of
Eratosthenes 37
3.7 Flowchart Prosedur Enkripsi 38
3.8 Flowchart Prosedur Dekripsi 39
4.1 Jendela Menu Utama Aplikasi KriptoElGamal 41
4.2 Jendela Pembangkit Kunci Aplikasi KriptoElGamal 41
4.3 Jendela Enkripsi Aplikasi KriptoElGamal 42
4.4 Jendela Dekripsi Aplikasi KriptoElGamal 43
4.5 Tampilan Output Pembangkitan Kunci 47
4.6 Tampilan Output Enkripsi 48
ABSTRAK
Pada penelitian untuk tugas akhir ini dibangun sistem kriptografi kunci publik berdasarkan algoritma ElGamal yang berguna mengamankan pesan user tanpa perlu mengalami kesulitan dalam mendistribusikan kunci karena kunci untuk dekripsi (kunci privat) berbeda dengan kunci untuk enkripsi (kunci publik) sehingga kunci enkripsi dapat didistribusikan kepada publik tanpa harus mengungkapkan kunci dekripsi, berbeda dengan kriptografi kunci simetri yang kunci dekripsi dan enkripsinya sama. Selain algoritma ElGamal, penelitian ini juga menerapkan pembangkit bilangan prima metode The Sieve of Eratosthenes pada sistem karena proses pembangkitan kunci algoritma ElGamal melibatkan bilangan prima. Dengan diterapkannya metode The Sieve of Eratosthenes pada sistem, proses pembangkitan kunci dimulai dengan input bilangan integer N untuk membangkitkan deretan bilangan prima antara 2 dan N menggunakan The Sieve of Eratosthenes, kemudian pasangan kunci publik dan kunci privat algoritma ElGamal dibangkitkan berdasarkan deretan tersebut. Sistem diwujudkan dalam bentuk sebuah aplikasi komputer yang dibangun menggunakan bahasa pemrograman Java dan NetBeans IDE. Pengujian pada aplikasi membuktikan sistem dapat menjalankan fungsi-fungsinya sesuai dengan rancangan, yaitu enkripsi pada aplikasi ini dapat mengubah plainteks ke bentuk cipherteks kemudian mengembalikannya ke bentuk plainteks semula melalui proses dekripsi, serta mampu menghasilkan pasangan kunci untuk digunakan pada proses enkripsi dan dekripsi dengan syarat kunci publik p lebih besar dari plainteks.
ELGAMAL PUBLIC KEY CRYPTOSYSTEM USING THE SIEVE OF ERATOSTHENES
TO GENERATE PRIME NUMBERS
ABSTRACT
This work is to built a public key cryptosystem based on the ElGamal algorithm which is useful for securing user messages without having difficulty in key distribution since it uses a different key for decryption (private key) and encryption (public key). Thus the encryption key can be distributed to public without having to disclose the decryption key, in contrast to symmetric key cryptography which uses the same key for encryption and decryption. Not only ElGamal algorithm, this research applies The Sieve of Eratosthenes method as a prime numbers generator on the system because the ElGamal key generation algorithm involves prime numbers. With the implementation of the Sieve of Eratosthenes method on the system, key generation process starts with an integer input N to generate a set of primes between 2 and N using the Sieve of Eratosthenes, then the public and private key pair's of ElGamal algorithm will be generated based on the set. System embodied in the form of a software is built using the Java programming language and NetBeans IDE. Tests on the software prove the system can carry out its functions in accordance with the design, that is encryption on this software can convert a plaintext into ciphertext form then convert it back to its original plaintext form through a decryption process and is able to generate key pairs for use in the process of encryption and decryption with terms the public key p is greater than the plaintext.
BAB I
PENDAHULUAN
1.1Latar Belakang Masalah
Keamanan media penyimpanan dan komunikasi data merupakan hal yang penting, tidak hanya bagi militer dan pemerintahan, namun dalam dunia bisnis dan bagi setiap pribadi, pastinya memiliki informasi yang bersifat penting dan rahasia. Karena itulah banyak pihak yang tidak diinginkan berusaha mencuri atau melakukan manipulasi terhadap informasi rahasia tersebut. Di sinilah peran kriptografi, sebagai ilmu yang mempelajari bagaimana mengamankan informasi yang bersifat rahasia dan penting dari pihak yang tidak berwenang untuk mengetahuinya.
Kriptografi modern mengenal dua jenis algoritma, yaitu algoritma kriptografi nirsimetri dan algoritma kriptografi kunci simetri. Berbeda dengan algoritma kriptografi kunci simetri yang hanya menggunakan sebuah kunci untuk melakukan enkripsi dan dekripsi, algoritma kriptografi kunci nirsimetri memiliki dua kunci, yaitu kunci privat yang berguna untuk dekripsi yang hanya diketahui oleh penerima pesan dan kunci publik yang berguna untuk enkripsi yang diumumkan kepada publik, karena ini pula kriptografi kunci nirsimetri disebut juga kriptografi kunci publik.
Cara kerja kriptorafi kunci publik ini memberikan dua kelebihan yaitu tidak perlu mencari saluran komunikasi yang aman untuk mendistribusikan kunci publik, dan untuk berkomunikasi secara rahasia kepada banyak orang tidak memerlukan kunci rahasia sebanyak jumlah orang tersebut cukup dengan kunci publik dan kunci privat.
Deffie-Hellman. Tidak seperti kriptografi kunci simetri yang kekuatannya terletak pada panjang kuncinya, algoritma ElGamal sebagai algoritma kriptografi kunci publik memiliki kekuatan yang terletak pada sulitnya memecahkan masalah matematis logaritma diskrit.
Algoritma ElGamal menggunakan sembarang bilangan prima untuk membangkitkan pasangan kuncinya, metode The Sieve of Eratosthenes, yang merupakan algoritma sederhana untuk membangkitan bilangan prima, dapat digunakan sebagai pembangkitnya. Metode The Sieve of Eratosthenes membangkitkan bilangan prima dari satu sampai dengan bilangan maksimum yang ditentukan dengan cara mengeliminasi bilangan yang diketahui memiliki faktor bilangan prima selain dirinya sendiri. Metode ini ditemukan oleh Eratosthenes seorang matematikawan Yunani kuno.
Berdasarkan uraian di atas, penulis memilih tugas akhir dengan judul
ŖKriptografi Kunci Publik Algoritma ElGamal dengan Metode The Sieve of Eratosthenes untuk Pembangkitan Bilangan Primaŗ yang akan membahas bagaimana kinerja algoritma ElGamal dan The Sieve of Eratosthenes untuk pembangkitan bilangan prima dalam proses enkripsi dan dekripsi pesan.
1.2Rumusan Masalah
Berdasarkan latar belakang, masalah yang dibahas dalam penelitian ini, yaitu:
1. Bagaimana merancang aplikasi kriptografi kunci publik dengan algoritma ElGamal dan
1.3Batasan Masalah
Agar tidak meluasnya pembahasan, maka ruang lingkup penelitian ini dibatasi pada 1. Algoritma kriptografi kunci publik yang diterapkan adalah algoritma ElGamal. 2. Pembangkit bilangan prima digunakan metode The Sieve of Eratosthenes yang
bersifat deterministik.
3. Rancangan aplikasi ini hanya dapat mengenkripsi dan mendekripsi data berupa tulisan yang diinputkan melalui user interface yang disediakan, tidak berupa gambar atau suara.
4. Penelitian ini menggunakan bahasa pemrograman Java dan NetBeans IDE 7.0.1.
1.4Tujuan Penelitian
Tujuan penelitian ini adalah
1. Menghasilkan aplikasi kriptografi kunci publik algoritma ElGamal yang menggunakan metode The Sieve of Eratosthenes untuk pembangkitan bilangan prima.
2. Menghasilkan penelitian yang dapat menambah wawasan bagi siapapun yang tertarik dengan materi kriptografi kunci publik ElGamal dan Algoritma The Sieve of Eratosthenes.
1.5Manfaat Penelitian
1.6Metode Penelitian
Tahapan yang diambil dalam penelitian ini yaitu: 1. Studi kepustakaan.
Mempelajari literatur mengenai kriptografi kunci publik, algoritma ElGamal, metode the sieve of eratosthenes dan teori-teori pendukung lainnya.
2. Analisis dan Perancangan Sistem
Pada tahap ini dilakukan analisis kebutuhan sistem dan fungsi-funsi yang ada pada sistem, hasil analisis akan menjadi dasar untuk merancang sistem yang akan dibangun. Hasil analisis berupa Flowchart dan user interface.
3. Implementasi dan Pengujian Sistem.
Pada tahap ini sistem dibangun berdasarkan hasil rancangan pada tahap sebelumnya menjadi sebuah aplikasi. Kemudian dilakukan pengujian terhadap aplikasi untuk dapat memastikan fungsi-fungsi aplikasi telah berjalan dengan baik sesuai rancangan.
4. Dokumentasi dan Penulisan Skripsi
Pada tahap ini dilakukan penulisan skripsi sebagai dokumentasi terhadap penelitian yang telah dilakukan.
1.7Sistematika Penulisan
Sistematika penulisan tugas akhir ini terdiri dari lima bab, masing-masing bab diuraikan sebagai berikut:
BAB 1 PENDAHULUAN
BAB 2 LANDASAN TEORI
Berisi penjelasan mengenai kriptografi kunci publik, algoritma ElGamal, dan metode the sieve of eratosthenes.
BAB 3 ANALISIS DAN PERANCANGAN SISTEM
Membahas analisa dan perancangan aplikasi kriptografi kunci publik algoritma ElGamal dengan Metode The Sieve of Eratosthenes untuk pembangkit bilangan prima.
BAB 4 IMPLEMENTASI DAN PENGUJIAN
Berisi implementasi sistem berupa aplikasi yang telah dibangun berdasarkan rancangan pada tahap perancangan dan pengujian tarhadap aplikasi untuk menemukan kesalahan.
BAB 5 KESIMPULAN DAN SARAN
BAB II
LANDASAN TEORI
2.1Kriptografi
Kriptografi adalah kata yang berasal dari bahasa Yunani, yaitu Ŗcryptosŗ artinya Ŗsecretŗ (rahasia) dan Ŗgrapheinŗ yang artinya Ŗwritingŗ (tulisan). Jadi, kata kriptografi dapat diartikan sebagai Ŗsecret writingŗ atau tulisan rahasia [6].
Menurut Menezes [4] kriptografi adalah studi tentang teknik matematika yang berhubungan dengan aspek keamanan informasi seperti kerahasiaan (confidentiality), integritas data (data integrity), otentikasi entitas (entity authentication), dan otentikasi asal data (data origin authentication).
Menurut Kurniawan [3] seni dan ilmu untuk menjaga kerahasian pesan disebut
kriptografi. Kata Ŗgraphyŗ di dalam Ŗcryptographyŗ itu sendiri sudah menyiratkan sebuah seni [6].
Ahli kriptografi disebut sebagai cryptographer. Cryptanalyst merupakan orang yang melakukan cryptanalisis, yaitu seni dan ilmu untuk memcahkan ciphertext menjadi plaintext tanpa melalui cara yang seharusnya (dekripsi) [3].
Menurut Stallings [11] proses menyandikan plaintext ke bentuk ciphertext disebut enkripsi, sedangkan proses mengembalikan ciphertext ke plaintext yang semula disebut dekripsi.
Algoritma kriptografi disebut juga cipher yaitu aturan untuk enciphering dan deciphering, atau fungsi matematika yang digunakan untuk enkripsi dan dekripsi [6].
2.1.1 Tujuan Kriptografi
Tujuan kriptografi adalah mengamankan pesan, keamanan yang dimaksud adalah sebagai berikut [4] [11].
1. Kerahasiaan (confidentiality), adalah layanan yang menjaga kerahasiaan pesan, memberikan perlindungan dari pihak-pihak yang tidak berhak mengetahuinya. 2. Integritas data (data integrity), perlindungan yang menjamin pesan tetap utuh
dan asli dari upaya manipulasi data secara tidak sah seperti penghapusan, penyisipan, dan pendistribusian data lain ke dalam data asli.
3. Otentikasi (authentication), merupakan layanan untuk mengidentifikasi kebenaran pihak-pihak yang berkomunikasi (user authentication atau entity authentication) maupun mengidentifikasi kebenaran sumber pesan (data origin authentication).
4. Nirpeyangkalan (non-repudiation), sebuah layanan untuk mencegah terjadinya penyangkalan oleh pihak-pihak yang telah melakukan komunikasi, sehingga pengirim tidak dapat menyangkal pernah mengirim pesan dan penerima tidak dapat menyangkal telah menerima pesan.
2.1.2 Sejarah Kriptografi
terkesan lebih agung dan penting. Seiring waktu tulisan ini semakin lama semakin rumit dan orang-orang kehilangan minat menguraikannya [2].
Sejarah kriptografi sebagian besar merupakan sejarah kriptografi klasik, yaitu metode enkripsi yang menggunakan kertas dan pensil atau mungkin dengan bantuan alat mekanik sederhana. Secara umum algoritma kriptografi klasik dikelompokkan menjadi dua kategori, yaitu algoritma transposisi (transposition cipher) dan algoritma subtitusi (subtitution cipher). Cipher transposisi mengubah susunan huruf-huruf di dalam pesan, sedangkan cipher subtitusi mengganti setiap huruf atau kelompok huruf dengan sebuah huruf atau kelompok huruf lain. Sejarah kriptografi klasik mencatat penggunaan cipher transposisi oleh tentara Sparta di Yunani pada permulaan 400 SM [6]. Mereka menggunakan sistem kriptografi dalam bentuk sepotong papyrus atau perkamen dibungkus dengan batang kayu yang disebut Scytale cipher untuk berkirim pesan rahasia diantara pasukan militer [2]. Sedangkan algoritma substitusi yang paling awal dan paling sederhana adalah Caesar cipher [6], sekitar 50 SM, Julius Caesar, kaisar Roma, menggunakan cipher substitusi yaitu huruf-huruf alfabet disubstitusi dengan huruf-huruf yang lain pada alfabet yang sama, metode ini dikenal sebagai Caesar cipher [2].
Kriptografi umum digunakan oleh kalangan militer seperti pada Perang Dunia ke II, pemerintah Nazi Jerman membuat mesin enkripsi bernama enigma. Mesin yang menggunakan beberapa buah rotor (roda berputar) ini melakukan enkripsi dengan cara yang sangat rumit. Namun Enigma cipher ini berhasil dipecahkan oleh pihak sekutu dan keberhasilan memecahkan Enigma sering dikatakan sebgai faktor yang memperpendek perang dunia ke-2 [6].
untuk enkripsi informasi yang tidak bersifat rahasia, yaitu DES, Data Encryption Standard, merupakan mekanisme kriptografi yang paling dikenal dalam sejarah [4].
Kriptografi modern menggunkan kunci yang merupakan parameter yang digunakan untuk transformasi enkripsi dan dekripsi. Kriptografi modern terbagi atas dua jenis, yaitu :
1. Kriptografi kunci simetri, yang kunci enkripsi dan dekripsinya sama, contohya DES, IDEA,dan AES.
2. Kriptografi kunci publik, yang kunci enkripsi dan dekripsinya berbeda, contohnya RSA, DSA, dan ElGamal.
Kriptografi simetri merupakan satu-satunya jenis kriptografi yang dikenal dalam catatan sejarah hingga tahun 1976. Semua algoritma kriptografi klasik termasuk ke dalam sistem kriptografi simetri [6].
Penemuan konsep kriptografi kunci pubik merupakan hal revolusioner dalam sejarah kriptografi dipublikasikan pertama kali pada tahun 1976 oleh Whitfield Diffie dan Martin Hellman, dua orang ilmuwan dari Stanford University melalui makalah pertamanya di jurnal IEEEyang berjudul ŖNew Directions in Cryptographyŗ [4] [10] [6]. Makalah mereka membahas distribusi kunci rahasia pada saluran komunikasi publik (yang tidak aman) dengan metode pertukaran kunci Diffie-Hellman [6].
Namun sebenarnya penemu kriptografi kunci publik adalah James H. Ellis, Clifford Cocks, dan Malcolm Williamson yang berkerja untuk markas komunikasi pemerintah Inggris, GCHQ [10] pada awal tahun 1970 [6]. Mereka menemukan mekanisme pertukaran kunci, yang kemudian dikenal dengan nama algoritma pertukaran kunci Diffie- Hellman. Sayangnya algoritma mereka tersebut dirahasiakan dan tidak pernah dipublikasikan hingga tahun 1997 [6].
Akhirnya, sejak tahun 1976 berbagai algoritma enkripsi, tanda tangan digital, pertukaran kunci, dan teknik lain dikembangkan dalam bidang kriptografi kunci-publik, misalnya algoritma ElGamal untuk enkripsi dan tanda tangan digital dan algoritma DSA untuk tanda tangan digital. Pada tahun 1980 Neal Koblitz memperkenalkan eliptic-curve cryptography sebagai keluaran baru yang analog dengan algoritma kriptografi kunci-publik. Hingga saat ini kriptografi kunci-publik terus berkembang pesat seiring dengan aplikasinya yang begitu luas [6].
2.2Kriptografi Kunci-Publik
Sampai tahun 1976, hanya ada kriptografi kunci-simetri. Karena kriptografi simetri menggunakan kunci yang sama untuk enkripsi dan dekripsi, maka hal ini mengimplikasikan dua pihak yang saling berkomunikasi dan mempercayai. Kedua pihak harus menjaga kerahasiaan kunci. Satu masalah kritis di dalam sistem kriptografi kunci-simetri adalah cara mendistribusikan kunci. Oleh karena itu kunci harus dikirim melalui saluran yang benar-benar aman, umumnya jalur ini lambat dan mahal [6]. Teknik kriptografi kunci publik awalnya ditemukan untuk memecahkan permasalahan distibusi kunci dan menyediakan otentikasi [10].
Masalah ini dipecahkan oleh Diffie dan Hellman yang mengusulkan konsep kriptografi nirsimetri (asymmetric cryptography) yaitu kunci berbeda untuk enkripsi dan dekripsi. Kunci enkripsi dapat diumumkan kepada publik sehingga dapat diketahui oleh siapapun, sementara kunci untuk dekripsi hanya diketahui oleh penerima pesan (rahasia), oleh karena itulah teknik kriptografi ini disebut juga dengan kriptografi kunci publik. Hal ini memungkinkan pengguna berkomunikasi secara aman tanpa perlu berbagi kunci rahasia [6].
Keuntungan kriptografi kunci publik dibandingkan dengan kriptografi kunci simetri, antara lain :
pesan. Perhatikan bahwa saluran untuk mengirim pesan umumnya tidak aman [6].
2. Jumlah kunci dapat ditekan. Untuk berkomunikasi secara rahasia dengan banyak orang tidak perlu kunci rahasia sebanyak jumlah orang tersebut, cukup membuat dua buah kunci, yaitu kunci publik bagi para koresponden untuk mengenkripsi pesan, dan kunci privat untuk mendekripsi pesan. Berbeda dengan kriptografi kunci-simetri dimana jumlah kunci yang dibuat adalah sebanyak jumlah pihak yang berkorespondensi [6].
3. Tidak perlunya pihak-pihak yang terlibat komunikasi untuk saling mengenal sebelumnya. Siapapun dapat mengirim pesan yang dienkripsi dengan kunci publik tersebut, tetapi hanya penerima pesan yang dapat mendekripsi pesan karena hanya ia yang mengetahui kunci privatnya sendiri [10].
4. Keuntungan lainnya dari kriptografi kunci publik adalah penggunaan digital signatures yang mengizinkan pengguna untuk menandai secara digital data seperti pemesanan elektronik atau transfer uang. Teknologi inilah yang menyebabkan teknologi e-commerce dan komunitas digital mungkin untuk dilakukan [10].
2.2.1 Konsep Kriptografi Kunci-Publik
Seperti telah dijelaskan pada bagian awal, pada kriptografi kunci-publik, setiap pengguna memiliki sepasang kunci, satu kunci untuk enkripsi diumumkan kepada publik - oleh karena itu tidak rahasia Ŕ sehingga dinamakan kunci publik (public-key), disimbolkan dengan e dan satu kunci untuk dekripsi bersifat rahasia Ŕ sehingga dinamakan kunci privat (private-key), disimbolkan dengan d. Karena kunci enkripsi tidak sama dengan kunci dekripsi itulah maka kriptografi kunci publik disebut juga kriptografi nirsimetri [6].
Misalkan E adalah fungsi enkripsi dan D adalah funsi dekripsi. Misalkan (e, d) adalah pasangan kunci untuk enkripsi dan dekripsi sedemikian sehingga
untuk suatu plainteks m dan cipherteks c. Kedua persamaan ini menyiratkana bahwa dengan mengetahui e dan c, maka secara komputasi hampir tidak mungkin menemukan m. Asumsi lainnya, dengan mengetahui e, secara komputasi hampir tidak mungkin menurunkan d. � digambarkan sebagai fungsi pintu-kolong (trapdoor) satu-arah dengan d adalah informasi trapdoor yang diperlukan untuk menghitung fungsi inversinya, D, yang dalam hal ini membuat proses dekripsi dapat dilakukan [6]. Dinamakan fungsi satu arah trapdoor karena fungsi ini secara efektif benar-benar merupakam fungsi satu arah kecuali kunci trapdoor tersebut diketahui [10].
Gambar 2.1 Skema Kriptografi Nirsimetri
Kriptografi kunci publik dapat berkerja dikarenakan dua kuncinya dihubungkan secara matematis sedemikian rupa sehingga mengetahui kunci publik tidak memberikan informasi apapun tentang kunci privat-nya. Namun dengan mengetahui kunci privat, informasi yang dienkripsi dengan kunci publik dapat diketahui [10].
Sistem kriptografi kunci publik yang aman memiliki dua karakteristik sebagai berikut [6]:
1. Komputasi untuk enkripsi/dekripsi pesan mudah dilakukan.
2. Secara komputasi hampir tidak mungkin (infeasible) menurunkan kunci privat, d, bila diketahui kunci publik, e, pasangannya.
Dua karakteristik di atas dapat dianalogikan dengan dua masalah matematika berikut yang sering menjadi dasar pembangkitan sepasang kunci pada kriptografi kunci publik [6]:
�
Enkripsi
�
Dekripsi Kunci publik, e Kunci privat, d
Chiperteks, c
1. Perkalian vs pemfaktoran. Mengalikan dua buah bilangan prima, , mudah, tetapi memfaktorkan n menjadi faktor-faktor primanya lebih sulit.
Contoh : (perkalian, mudah) (pemfaktoran, sulit)
Diberikan bilangan bulat n, faktorkan n menjadi faktor primanya Contoh :
Semakin besar n, semakin sulit memfaktorkan (butuh waktu sangat lama). Algoritma yang menggunkan prinsip ini: RSA.
2. Perpangkatan vs logaritmik dikrit. Melakukan perpangkatan modulo,
, mudah, tetapi menemukan x dari lebih sulit. Semakin besar a,b, dan n semakin sulit memfaktorkan (butuh waktu yang lama).
Contoh : (perpangkatan modulo, mudah)
Carilah x dari (logaritmik diskrit, sulit) Sistem kriptografi yang dibangun berdasarkan masalah logaritma diskrit antara lain ElGamal dan DSA .
Tidak seperti kriptografi kunci-simetri yang didasarkan pada substitusi dan permutasi, kriptografi kunci-publik didasarkan pada fungsi matematika. Jika kekuatan kriptografi kunci-simetri terletak pada panjang kuncinya yang membutuhkan usaha sangat besar untuk menemukan kunci, maka kriptografi kunci-publik kekuatannya terletak pada sulitnya memcahkan masalah matematis seperti pemfaktoran dan logaritma diskrit [6].
khusus untuk mengambil surat dan membaca surat di dalamnya karena ia yang memiliki kuncinya.
2.2.2. Aplikasi Penggunaan Kriptografi Kunci Publik
Aplikasi penggunaan kriptografi kunci publik dapat diklasifikasikan ke dalam tiga kategori [11], yaitu:
1. Enkripsi, dekripsi. Enkripsi pesan dengan kunci publik penerima pesan. 2. Tanda tangan digital (Digital Signature), pengirim menandai (Ŗsign”) pesan dangan kunci privatnya. Tanda tangan dilakukan dengan menggunakan algoritma kriptografi pada pesan atau pada blok kecil data yang merupakan fungsi pesan.
3. Pertukaran kunci (key exchange), kedua belah pihak berkerja sama untuk bertukar kunci sesi. Terdapat beberapa pendekatan yang mungkin dilakukan, yaitu melibatkan kunci privat salah satu pihak atau keduanya.
2.3Algoritma ElGamal
Algoritma ElGamal dibuat oleh Taher ElGamal pada tahun 1984. Algoritma ini pada mulanya digunakan untuk digital signature, namun kemudian dimodifikasi sehingga juga bisa digunakan untuk enkripsi dan dekripsi. ElGamal digunakan didalam perangkat lunak sekuriti yang digunakan oleh GNU, program PGP, dan pada sistem sekuriti lainnya [6].
Sistem kriptografi ElGamal dibangun berdasarkan masalah logaritma diskrit. Keamanan algoritma ini terletak pada sulitnya menghitung logaritma diskrit [12]. Masalah logaritma diskrit: jika p adalah bilangan prima dan g dan y adalah sembarang bilangan bulat. Carilah x sedemikian sehingga . Melakukan perpangkatan modulo, , mudah, tetapi menemukan x dari
lebih sulit. Semakin besar a,b, dan n semakin sulit memfaktorkan (butuh waktu yang lama) [6].
Carilah x dari (logaritmik diskrit, sulit)
Berikut ini merupakan algoritma kunci publik ElGamal [4] [12]. 5. Pasangan kunci dibangkitkan oleh penerima pesan.
i. Pilih sembarang bilangan prima p.
ii. Pilih bilangan bulat acak a, syarat 2 ≤ a≤ p-1
iii. Tentukan α, dimana α primitive root modulo p, dengan ketentuan α ≠ p dan α ≠ a.Primitive root dari sebuah bilangan prima p adalah sebuah bilangan asli g yang mana orde modulo dari g (mod p) adalah p-1 [10].
iv. Hitung
v. Kunci publik (y, α, p) disebarkan dan kunci privat (a) disimpan
6. Enkripsi oleh pengirim.
i. Menerima kunci publik (y, α, p)
ii. Mempersiapkan plainteks (m), representasikan plainteks dalam rentang 0…p-1.
iii. Memilih bilangan asli acak sebagai kunci sesi b, syarat b≤ p-1 iv. Cipherteks pertama,
v. Cipherteks kedua,
vi. Cipherteks (c1, c2) dikirim kepada penerima.
7. Dekripsi oleh penerima.
i. Terima Cipherteks (c1, c2)
ii. Hitung ( )
iii. Dekripsi chiperteks menjadi plainteks, ( )
2.3.1 Bilangan Prima
prima harus lebih besar daripada 1, maka barisan bilangan prima dimulai dari 2, yaitu
2, 3, 5, 7, 11, 13, …. Seluruh bilangan prima adalah bilangan ganjil kecuali 2 yang merupakan bilangan genap [6].
Pembangkitan bilangan prima dibutuhkan untuk hampir semua algoritma kunci publik [10]. Seperti yang telah dijabarkan pada bagian sebelumnya dalam kriptografi kunci publik algoritma ElGamal menggunakan bilangan prima sebagai salah satu nilai parameternya, oleh karena itu dibutuhkan suatu metode pembangkitan bilangan prima. Beberapa algoritma-algoritma yang dapat digunakan untuk membangkitkan bilangan prima antara lain algoritma probabilistik seperti Lehman dan Rabin-Miller atau algoritma deterministik seperti Sieve of Eratosthenes. Bedanya algoritma deterministik menghasilkan bilangan yang pasti merupakan prima sedangkan algoritma probabilistik dapat menghsailkan pseudoprimes (prima semu) [11].
2.3.2 The Sieve of Eratosthenes
Metode The Sieve of Eratosthenes merupakan sebuah algoritma deterministik sederhana untuk membangkitan bilangan prima yang ditemukan oleh Eratosthenes seorang matematikawan Yunani kuno [5]. Metode The Sieve of Eratosthenes membangkitkan bilangan prima yang ada di antara bilangan satu sampai dengan batas bilangan maksimum yang ditentukan dengan cara membuat daftar semua bilangan asli dari satu sampai batas kemudian mengeliminasi bilangan komposit hingga tersisa hanya bilangan prima. Bilangan komposit adalah bilangan asli yang lebih besar dari satu dan bukan bilangan prima, memiliki pembagi selain satu dan bilangan itu sendiri.
Disebut The Sieve of Eratosthenes, sieve (saringan) karena bukannya membangun objek yang diinginkan, yaitu bilangan prima, tetapi menyaringnya dari yang bukan prima [5].
Tabel 2.1 Komputasi Running Time Pembangkit Bilangan Prima Metode Standar pada Komputer 3.2 GHz Sistem Operasi Linux [5]
n 103 104 105 106
Time 0.00 s 0.20 s 19.4 s 1934.4 s
Tabel 2.2 Komputasi Running Time Pembangkit Bilangan Prima Metode The Sieve of Eratosthenes pada Komputer 3.2 GHz Sistem Operasi Linux [5]
n 106 107 108 109
Time 0.02 s 0.43 s 5.4 s 66.5 s
Adapun prosedur dari metode standar pembangkitan bilangan prima yang diutarakan oleh Möhring dan Oellrich adalah sebagai berikut.
Tabel 2.3 Prosedur Pembangkit Bilangan Prima Metode Standar [5]
Tabel 2.4 Prosedur Pembangkit Bilangan Prima Metode The Sieve of Eratosthenes [5]
Algoritma The Sieve of Eratosthenes adalah sebagai berikut. 1. Buat daftar bilangan dari 2..n
2. Tandai bilangan pertama dari daftar sebagai bilngan prima pertama, yaitu p = 2.
3. Eliminasi semua kelipatan p yang lebih kecil dari n (untuk 2 eliminasi 4, 6, 8,…), menghitung kelipatan p dimulai dari p2.
4. Tandai bilangan terkecil yang belum dieliminasi dari daftar namun lebih besar dari p sebagai prima selanjutnya, ulangi langkah 3.
5. Sampai tidak ada lagi bilangan yang bisa ditandai sebagai prima karena semua bilangan yang tersisa tidak tereliminasi dari daftar sudah ditandai sebagai prima.
2.3.3 Relatif Prima
Menurut Munir [6], dua buah bilangan bulat a dan b dikatakan relatif prima jika pembagi berasama terbesarnya PBB(a, b) = 1. Jika a dan b relatif prima, maka terdapat bilangan bulat m dan n sedemikian sehingga
2.3.4 Fungsi Totient Euler
Fungsi Totient Euler mendefinisikan (n) untuk n 1 yang menyatakan jumlah bilangan bulat positif < n yang relatif prima dengan n [6]. Sebagai contoh bilangan 8, bilangan bulat positif lebih kecil dari 8 adalah 1...7, diantara bilangan tersebut yang relatif prima dengan 8 adalah 1, 3, 5, dan 7 maka, (8) = 4.
Jika n prima, maka setiap bilangan bulat yang lebih kecil dari n relatif prima terhadap n. Dengan kata lain, (n) = n Ŕ 1 hanya jika n prima [6]. Contoh bilangan prima 11, bilangan yang lebih kecil dari 11 adalah 1…10 dan semua bilangan ini
relatif prima terhadap 11, maka (11) = 10.
Jika n = pq adalah bilangan komposit dengan p dan q prima, maka (n) = (p)
(q) = (p-1) (q-1) [6].
Jika p bilangan prima dan k > 0, maka (pk) = pkŔpk-1 = pk-1 (p-1) [6].
(Euler’s Generalization of Fermat Theorem). Jika PBB(a, n) = 1, maka a(n) mod n = 1 (atau a(n) 1 (mod n)) [6].
2.3.5 Akar Primitif (Primitive Root) dari Bilangan Prima p
Jika r dan n adalah bilangan bulat yang relatif prima dengan n > 0. Dan jika
(n) adalah m eksponen positif paling akhir sehingga rm 1 (mod n), maka r disebut akar primitif modulo n [11].
Secara umum, dapat dikatakan bahwa eksponen tertinggi yang mungkin untuk dimilki sebuah bilangan (mod n) adalah (n). Jika sebuah bilangan merupakan bagian dari urutan ini, maka bilangan tersebut disebut sebagai akar primitif dari n. Pentingnya gagasan ini adalah jika a adalah akar primitif dari n, maka orde-nya
a, a2, ..., a(n)
a, a2, ..., ap1
adalah (mod p) yang berbeda [11]. Untuk bilangan prima 19, akar primitif-nya adalah 2, 3, 10, 13, 14, dan 15.
Tidak semua bilangan bulat memiliki akar primitif. Bahkan, bilangan bulat dengan akar primitif adalah hanya dari bentuk 2, 4, pα, dan 2pα, dimana p adalah prima ganjil setiap dan α adalah bilangan bulat positif [11].
2.3.6 Perpangkatan Modulo
Perhitungan perpangkatan modulo ini sangat penting dalam algoritma kriptografi ElGamal karena perhitungan ini digunakan pada proses pembangkitan kunci, enkripsi maupun dekripsi.
Berikut ini merupakan pemahaman aritmatika modulo menurut Munir [6], misalkan a adalah bilangan bulat dan m adalah bilangan bulat > 0. Operasi (dibaca a modulo m) memberikan sisa jika a dibagi dengan m. Bilangan m disebut modulus atau modulo, dan hasil aritmatika modulo m terletak di dalam himpunan {0, 1, 2, …, m-1}. Notasi: sedemikian sehingga , dengan 0 ≤ r≤ m.
Perhitungan perpangkatan modulo, misalnya menghitung persamaan . Untuk memperjelas perhitungannnya berikut ini merupakan contoh perhitungan modulo.
Berdasarkan persamaan aritmatika modulo :
perhitungan perpangkatan modulo dapat dilakukakan seperti contoh berikut.
( )
Perhitungan ini disebut metode divive conquer atau disebut juga metode addition chainning karena hasil perkalian antara langsung dirangkai dengan operasi modulo [6].
2.4NetBeans IDE
NetBeans IDE adalah sebuah lingkungan pengembangan - sebuah kakas untuk pemrograman, menulis, mengompilasi, mencari kesalahan dan menyebarkan program. Bahasa pemrograman yang didukung oleh NetBeans antara lain Java, JavaScript, PHP, Python (tidak lagi didukung setelah NetBeans 7), Groovy, C, C++, Scala, Clojure, dan lain-lain. Netbeans IDE ditulis dalam Java dan dapat berjalan pada Windows, Mac OS, Linux, Solaris, dan platform lainnya didukung JVM yang sesuai. NetBeans merupakan produk open source dan bebas (free) untuk penggunaan komersial dan non komersial. NetBeans IDE 7.0 dirilis April 2011, pada tanggal 1 agustus 2011, tim NetBeans merilis NetBeans IDE 7.0.1 yang mendukung Java SE 7 platform [7].
Awalnya NetBeans adalah Java IDE yang dikembangkan sebagai projek mahasiswa dibawah bimbingan Faculty of Mathematics and Physics di Charles University di Prague, Republik Czech pada 1996 dengan nama Xelfi. Pada tahun 1997 Roman Staněk membentuk perusahaan dan menghasilkan versi komersial dari NetBeans IDE sampai akhirnya dibeli oleh Sun Microsystems pada 1999. Setahun kemudian pada bulan juni Sun menjadikan NetBeans IDE sebagai projek open source. Sejak itu komunitas NetBeans terus berkembang kemudian pada 2010, Sun dan NetBeans menjadi milik Oracle [7].
Berikut ini merupakan kelebihan dan kekurangan NetBeans dibandingkan Java IDE lain seperti Eclipse dan JCreator.
1. NetBeans memiliki fitur GUI builder dan profiler yang terintegrasi, built-in pada NetBeans itu sendiri sedangkan pada Eclipse diperlukan mengunduh plug-in [8], dan JCreator tidak memiliki fitur tersebut.
3. NetBeans dan Eclipse open source dan gratis sedangkan JCreator berbayar. 4. NetBeans dibangun dengan bahasa Java sehingga ukuran file-nya lebih besar
BAB III
ANALISIS DAN PERANCANGAN SISTEM
Tahap analisis dan perancangan sistem berguna untuk menentukan kebutuhan sistem dan menyesuaikan dengan kebutuhan pengguna sehingga memudahkan proses pembuatan sistem.
3.1 Analisis Sistem
Analisis sistem dilakukan dengan menentukan tujuan pembangunan sistem, memahami cara kerja, dan fungsi-fungsi sistem. Sistem yang akan dibangun ini merupakan sistem kriptografi kunci publik, tujuan pembangunan sistem adalah untuk keamanan data, yaitu mengamankan pesan (plainteks) milik pengguna dari pihak-pihak yang tidak diinginkan dengan mengubahnya ke bentuk yang sama sekali berbeda dengan pesan aslinya (cipherteks) melalui proses enkripsi.
Algoritma kriptografi yang digunakan pada sistem adalah algoritma ElGamal, selain itu sistem juga menerapkan metode The Sieve of Eratosthenes untuk pembangkit bilangan prima. Algoritma kriptografi kunci publik ElGamal terbagi atas tiga aktivitas, yaitu :
1. Pembangkitan kunci
Aktivitas pembangkitan kunci dilakukan oleh penerima pesan. Kunci yang dibangkitkan terdiri dari :
a. Kunci p merupkan sembarang bilangan prima, dalam penelitian ini digunakan metode The Sieve of Eratosthenes untuk membangkitkan bilangan prima.
c. Kunci α merupakan salah satu akar primitif (primitive root) dari bilangan prima p , α ≠ pdan α ≠ a. Sebagaimana yang telah disebutkan pada bab yang sebelumnya, primitive root dari sebuah bilangan prima p adalah sebuah bilangan asli g yang mana orde modulo dari g (mod p) adalah p-1 [10].
d. Kunci y dengan persamaan .
Sehingga keluaran dari aktivitas pembangkitan kunci ini adalah tiga kunci publik (p, α, y) yang akan dibagikan kepada para calon pengirim pesan dan satu kunci privat (a) yang hanya diketahui oleh penerima pesan.
2. Enkripsi
Aktivitas enkripsi dilakukan oleh pengirim pesan dengan masukkan berupa tiga kunci publik (p, α, y) milik penerima pesan dan pesan asli plainteks (m) yang akan dikirimkan. Enkripsi dilakukan dengan menghitung cipherteks pertama dan cipherteks kedua . Hasil keluarannya berupa cipherteks (c1, c2)dikirimkan kepada penerima pesan.
3. Dekripsi
Dekripsi dilakukan oleh penerima pesan dengan masukkan cipherteks (c1, c2), kunci privat (a), dan kunci publik (p) miliknya. Apabila cipherteks dan kunci yang dimasukkan benar maka akan diperoleh keluaran berupa plainteks yang sama dengan pesan aslinya.
Berdasarkan pembahasan di atas, sistem yang akan dibangun memiliki tiga fungsi mengikuti aktivitas yang dimiliki algoritma ElGamal, yaitu pembangkit kunci, enkripsi, dan dekripsi. Di dalam fungsi ini terdapat proses-proses pendukung seperti pembangkit bilangan prima metode The Sieve of Eratosthenes, perhitungan modulo, dan proses pengujian apakah sebuah bilangan merupakan akar primitif dari kunci p.
3.1.1 Pembangkit Bilangan Prima
berdasarkan nilai kunci p oleh karena itu, sebelum aktivitas pembangkitan kunci dilakukan pembangkitan bilangan prima terlebih dahulu.
3.1.1.1The Sieve of Eratosthenes
Dalam penelitian ini, algoritma pembangkit bilangan prima yang digunakan adalah The Sieve of Eratosthenes. Berikut ini merupakan langkah-langkah pembangkitan bilangan prima metode The Sieve of Eratosthenes.
1. Inisialisasi integer 2…N.
2. Tandai bilangan terkecil dari daftar 2…N sebagai prima pertama, p1 = 2. 3. Eliminasi semua bilangan kelipatan p1dari daftar 2…N dimulai dari p12 = 22
= 4 yaitu (4, 6, 8,…).
4. Tandai bilangan integer terkecil berikutnya dari daftar 2…N yang belum
tereliminasi sebagai bilangan prima selanjutnya, pi+1.
5. Eliminasi semua bilangan kelipatan pi+1dari daftar 2…N dimulai dari pi+12. 6. Ulangai angkah e dan g sampai pi+12 > N, maka integer dari daftar 2…N yang
tersisa adalah prima.
Untuk mempermudah pemahaman langkah-langkah di atas, berikut ini merupakan contoh pembangkitan bilangan prima metode The Sieve of Eratosthenes jika nilai batas atas N = 30.
1. Inisialisasi integer 2…Nyaitu 2…30.
2. Tandai bilangan terkecil dari 2…30 sebagai prima pertama, p1 = 2.
3. Eliminasi semua bilangan kelipatan p1dari daftar 2…30 dimulai dari p12 = 22 = 4 yaitu (4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30), maka daftar integer yang belum tereliminasi (2, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29).
4. Tandai bilangan integer terkecil berikutnya dari daftar 2…N yang belum tereliminasi sebagai prima selanjutnya, pi+1 = p2 = 3.
6. Tandai bilangan integer terkecil berikutnya dari daftar 2…N yang belum tereliminasi sebagai prima selanjutnya, pi+1 = p3 = 5.
7. Eliminasi semua bilangan kelipatan pi+1 = p2 = 5 dari daftar 2…N dimulai dari p22 = 52 = 25 yaitu (25, 30), maka daftar integer yang belum tereliminasi (2, 3, 5, 7, 11, 13, 17, 19, 23, 29).
8. Bilangan integer terkecil berikutnya dari daftar 2…N yang belum tereliminasi sebagai prima selanjutnya adalah pi+1 = p4 = 7 namun 72 > N, sehingga dapat dipastikan bilangan yang tersisa dari daftar integer yang belum tereliminasi yaitu (2, 3, 5, 7, 11, 13, 17, 19, 23, 29) adalah bilangan prima.
3.1.2 Algoritma Kriptografi Kunci Publik ElGamal
Algoritma kriptografi kunci publik ElGamal terdiri dari pembangkitan kunci oleh penerima pesan, enkripsi pesan oleh pengirim pesan, dan dekripsi pesan oleh penerima pesan.
3.1.2.1Proses Pembangkitan Kunci Algoritma ElGamal
Berikut ini merupakan langkah-langkah pembangkitan kunci algoritma kriptografi elgamal.
1. Pilih bilangan prima untuk digunakan sebagai kunci p. Plainteks direpresentasikan sebagai bilangan dalam rentang 0…p-1 maka, kunci p harus lebih besar dari pada plainteks. Untuk merepresentasikan plainteks ke
bentuk bilangan digunakan kode ASCII yang berada dalam rentang 0…255
sehingga p harus lebih besar dari 255. Dalam penelitian ini bilangan prima dipilih berdasarkan daftar prima yang telah dibangkitkan melalui proses pembangkitan bilangan prima metode The Sieve of Eratosthenes.
2. Tentukan kunci a dengan syarat a merupakan bilangan bulat dan 2 ≤ a ≤ p-1. 3. Kunci publik α harus merupakan primitive root dari kunci publik p, berikut
ini merupakan cara pembangkitan kunci publik α.
b. Kemudian diuji apakah α primitive root dari p, jika α ternyata bukan primitive root dari p kembali ke langkah sebelumnya. Jika α terbukti primitive root dari p lanjutkan ke langkah no.4.
4. Hitung kunci y dengan persamaan .
5. Hasil pembangkitan kunci berupa kunci publik (p, α, y) disebarkan dan kunci privat (a) disimpan.
3.1.2.2Proses Enkripsi Algoritma ElGamal
Berikut ini merupakan langkah-langkah enkripsi algoritma kriptografi elgamal oleh pengirim pesan.
1. Siapkan kunci publik (p, α, y) milik penerima pesan. 2. Tentukan plainteks m yang akan dienkripsi.
3. Untuk setiap karakter pada plainteks diubah menjadi bilangan bulat, langkah ini dilakukan melalui pengkodean ASCII.
4. Untuk setiap bilangan plainteks dienkripsi dengan langkah sebagai berikut. a. Tentukan sembarang kunci sesi (b), dengan syarat b merupakan
sebuah bilangan asli dan b ≤ p-1. Perlu diperhatikan bahwa penggunaan nilai b acak menghasilkan variasi cipherteks yang berbeda-beda meskipun nilai p, α, y dan m sama.
b. Hitung cipherteks pertama . c. Hitung cipherteks kedua
.
5. Maka setiap karakter akan menghasilkan pasangan cipherteks (c1, c2) sebanyak jumlah karakter dalam plainteks.
3.1.2.3Proses Dekripsi Algoritma ElGamal
Berikut ini merupakan langkah-langkah melakukan dekripsi oleh penerima pesan menggunakan algoritma kriptografi Elgamal.
a. Hitung
b. Dekripsi chiperteks menjadi plainteks,
3. Maka diperoleh plainteks yang masih dalam bentuk bilangan kode ASCII m = ( ,…, ), k = banyaknya blok cipherteks. Untuk setiap plainteks plainteks , i =1…k, diubah kembali menjadi karakter biasa berdasarkan pengkodean ASCII.
4. Sehingga diperoleh plainteks (m) yang jika kunci dan cipherteks benar, plainteks hasil dekripsi sama dengan pesan aslinya.
Untuk mempermudah pemahaman langkah-langkah algoritma di atas berikut ini merupkan contoh rangkaian aktivitas kriptografi algoritma ElGamal meliputi pembangkitan kunci, enkripsi, dan dekripsi.
1. Aktivitas dimulai dengan pembangkitan kunci oleh penerima pesan.
2. Pembangkitan kunci diawali dengan menentukan sembarang bilangan bulat positif N sebagai batas atas bilangan prima yang dibangkitkan menggunakan metode The Sieve of Eratosthenes. Misalnya N = 350, sehingga diperoleh daftar bilangan prima yang dibangkitkan melealui metode The Sieve of Eratosthenes sebagai berikut.
Tabel 3.1Tabel Bilangan Prima di antara Bilangan 1-350
2 3 5 7 11 13 17 19 23 29
31 37 41 43 47 53 59 61 67 73
79 83 89 97 101 103 107 109 113 127
131 137 139 149 151 157 163 167 173 179
181 191 193 197 199 211 223 227 229 233
239 241 251 257 263 269 271 277 281 283
293 307 311 313 317 331 337 347 349
3. Kemudian dipilih sembarang bilangan prima dari daftar bilangan prima yang dihasilkan pada proses sebelumnya (tabel 3.1) sebagai kunci publik p, misalnya p = 317.
4. Pilih kunci privat a dari sembarang bilangan bulat dengan syarat berada dalam rentang 2 ≤ a ≤ p-1, misalnya a = 7.
5. Pilih kunci publik α dari sembarang bilangan bulat dengan syarat α ≤ p-1dan α ≠ a, misalnya α = 166.
6. Kemudian diuji apakah α = 166 primitive root dari p = 317, jika α ternyata bukan primitive root dari p kembali ke langakah no.5. Jika α terbukti primitive root dari p lanjutkan ke langkah no.7. Dalam kasus ini, 166 adalah primitive root dari 317.
7. Hitung kunci publik y dengan persamaan . y = 1667 mod 317
=3473414526672256 mod 317 y = 202
8. Hasil pembangkitan kunci berupa kunci publik (p = 317, α = 166, y = 202) dikirimkan kepada pengirim pesan dan kunci privat (a = 7) disimpan oleh penerima pesan.
9. Pengirim pesan menerima kunci publik (p = 317, α = 166, y = 202) dan menggunakannya untuk mengenkripsi pesan plainteks (m), misalnya m = ŖIlmuŗ.
10.Enkripsi pesan yang dilakukan oleh pengirim pesan diawali dengan mepersiapkan plainteks yang akan dienkripsi, dalam kasus ini plainteks m = ŖIlmuŗ. Kemudian setiap karakter pada plainteks di ubah menjadi bilangan melalui pengkodean ASCII.
m1 = I 73 m2= l 108 m3 = m 109 m4 = u 117
11.Ekripsi pesan untuk menghasilkan cipherteks, diawali dengan menentukan secara acak kunci sesi b kemudian menghitung persamaan dan untuk setiap karakter plainteks mi dengan i = (1…4).
Untuk m1= 73, cipherteks1 = (196, 311) b. Tentukan kunci sesi b = 5,
Untuk m2= 108, cipherteks2 = (5, 228) c. Tentukan kunci sesi b = 8,
Untuk m3= 109, cipherteks3 = (247, 159) d. Tentukan kunci sesi b = 7,
Untuk m4= 117, cipherteks4 = (202, 207)
12.Maka cipherteks yang dihasilkan dari plainteks m = ŖIlmuŗ dengan kunci publik (p = 317, α = 166, y = 202) adalah (196, 311) (5, 228) (247, 159) (202, 207). Cipherteks ini kemudian dikirim kepada penerima pesan.
13.Penerima pesan menerima cipherteks = (196, 311) (5, 228) (247, 159) (202, 207) yang kemudian didekripsi menggunakan kunci p = 317 dan kunci privat a = 7.
14.Dekripsi untuk setiap blok cipherteks (ci1, ci2) i = (1…4) dengan persamaan
b.
c.
d.
15.Diperoleh plainteks m = (73, 108, 109, 117) yang masih dalam bentuk ASCII, kemudian setiap bilangan plainteks diubah ke bentuk karakter.
73 I 108 l 109 m 117 u
16.Plainteks yang diterima oleh penerima pesan adalah ŖIlmuŗ, sesuai dengan
pesan asli sebelum proses enkripsi oleh pengirim pesan.
3.2Perancangan Aplikasi
3.2.1 Perancangan Antarmuka
Antarmuka pada sistem ini dirancang memiliki tampilan yang sederhana sehingga mudah bagi pengguna untuk menggunakannya.
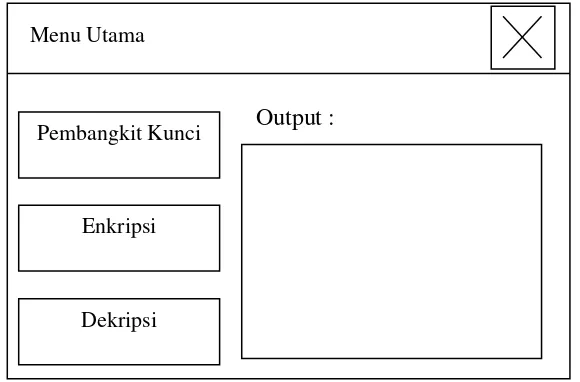
1. Jendela Menu Utama
Jendela menu utama merupakan tampilan yang pertama kali muncul ketika program dijalankan.
Gambar 3.1 Tampilan Rancangan Jendela Menu Utama
Dapat dilihat pada gambar 3.6 pengguna diberikan pilihan menu, yaitu
berupa tombol ŖPembangkit Kunciŗ, ŖEnkripsiŗ, dan ŖDekripsiŗ. Tombol menu
yang dipilih akan menampilkan jendela selanjutnya yang berkaitan dengan fungsi menu yang dipilih. Output dari proses menu apapun yang dipilih pengguna
nantinya juga akan ditampilkan pada jendela ini di bagian ŖOutput :ŗ.
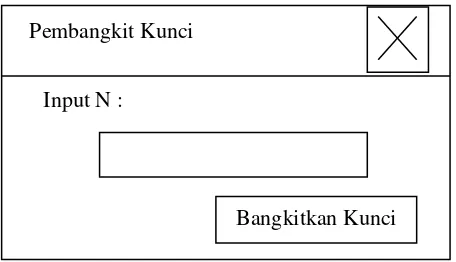
2. Jendela Pembangkit Kunci
Apabila pengguna memilih menu ŖPembangkit Kunciŗ, maka jendela ini akan
ditampilkan.
Menu Utama
Pembangkit Kunci
Enkripsi
Dekripsi
Gambar 3.2 Tampilan Rancangan Jendela Pembangkit Kunci
Dapat dilihat pada gambar 3.7 pengguna akan diminta memberikan input N,
kemudian jika tombol ŖBangkitkan Kunciŗ diklik, maka proses membangkitkan
kunci berdasarkan input N dari pengguna akan dilaksanakan. Hasilnya berupa pasangan kunci publik dan privat ditampilkan pada jendela menu utama pada
bagian ŖOutput :ŗ.
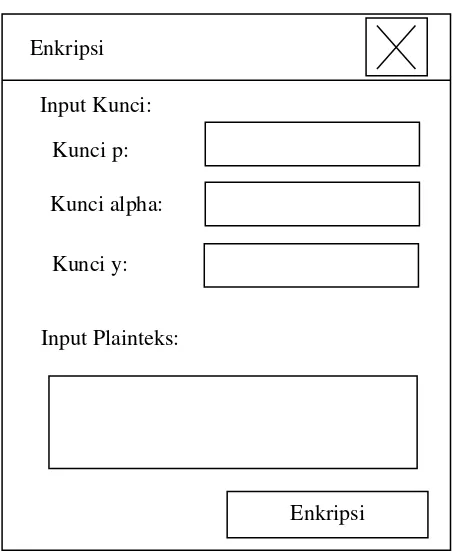
3. Jendela Enkripsi
Jendela ini ditampilkan jika pengguna memilih menu ŖEnkripsiŗ pada jendela
menu utama. Tombol ŖEnkripsiŗ pada jendela ini akan menjalankan proses
enkripsi berdasarkan input kunci publik dan plainteks yang dimasukkan oleh pengguna. Hasil dari proses enkripsi berupa cipherteks yang akan ditampilkan
pada jendela menu utama pada bagian ŖOutput :ŗ. Pembangkit Kunci
Input N :
Gambar 3.3 TampilanRancangan Jendela Enkripsi
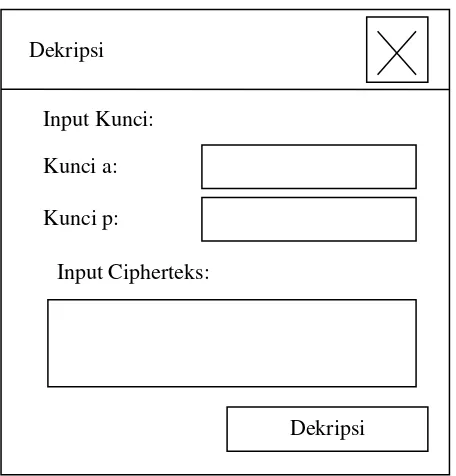
4. Jendela Dekripsi
Jendela dekripsi muncul jika pengguna memilih menu ŖDekripsiŗ pada jendela
menu utama. Pada jendela ini pengguna diminta untuk memasukkan Kunci privat a, kunci p, dan cipherteks. Jika tombol ŖDekripsiŗ pada jendela ini dipilih maka akan dilakukan proses dekripsi berdasarkan input tersebut yang outputnya dapat
dilihat pada jendela utama pada kotak ŖOutput :ŗ Enkripsi
Input Kunci:
Enkripsi Kunci p:
Kunci alpha:
Kunci y:
Gambar 3.4 Tampilan Rancangan Jendela Dekripsi
3.2.2 Flowchart
Berdasarkan aktivitas algoritma yang telah diuraikan sebelumnya pada tahap analisis, sistem dirancang terdiri dari tiga prosedur utama, yaitu prosedur pembangkit kunci, prosedur enkripsi, dan prosedur dekripsi. Dan prosedur pendukung yaitu prosedur pembangkit bilangan prima metode The Sieve of Eratosthenes. Rancangan proses kerja prosedur-prosedur tersebut secara garis besar dapat diilustrasikan malalui flowchart berikut ini.
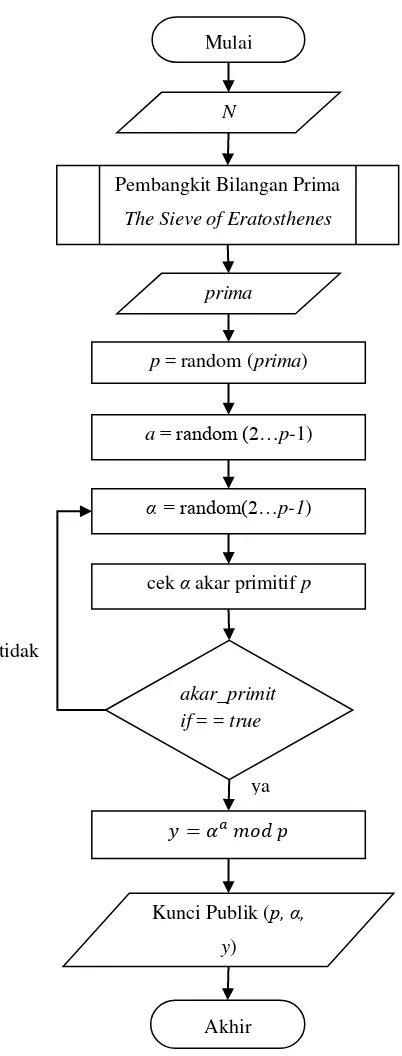
3.2.2.1Flowchart Pembangkit Kunci
Pembangkitan kunci diawali dengan masukan N sebagai batas maksimum nilai bilangan yang dapat dibangkitkan untuk membangkitkan bilangan prima menggunakan The Sieve of Eratosthenes. Bilangan-bilangan prima yang dihasilkan melalui proses pembangkitan bilangan prima kemudian digunakan untuk memilih kunci p yang merupakan bilangan prima. Kemudian nilai kunci p akan menentukan nilai kunci a, α dan y. Gambar 3.5 berikut ini merupakan flowchart prosedur pembangkit kunci.
Dekripsi
Input Kunci:
Dekripsi Kunci a:
Kunci p:
Gambar 3.5 Flowchart Prosedur Pembangkit Kunci
3.2.2.2FlowchartThe Sieve of Eratosthenes
Prosedur pembangkit prima The Sieve of Eratothenes membangkitkan sederetan bilangan prima diantara 1 sampai bilangan batas N yang di input pengguna, kemudian deretan bilangan prima ini digunkan untuk membangkitkan kunci p.
Akhir Mulai
N
Kunci Publik (p, α,
y)
p = random (prima) prima
Pembangkit Bilangan Prima
The Sieve of Eratosthenes
a= random (2…p-1)
α = random(2…p-1)
akar_primit if = = true cekα akar primitif p
Gambar 3.6 Flowchart ProsedurPembangkit Bilangan Prima
The Sieve of Eratosthenes
ya
ya
ya Mulai
Akhir N
i = 2
prima
i*i ≤
prima [i*j] = false
j ++
prima [2…N] = true
prima[i ] ==
j = i
i*j ≤
i ++ tidak
tidak
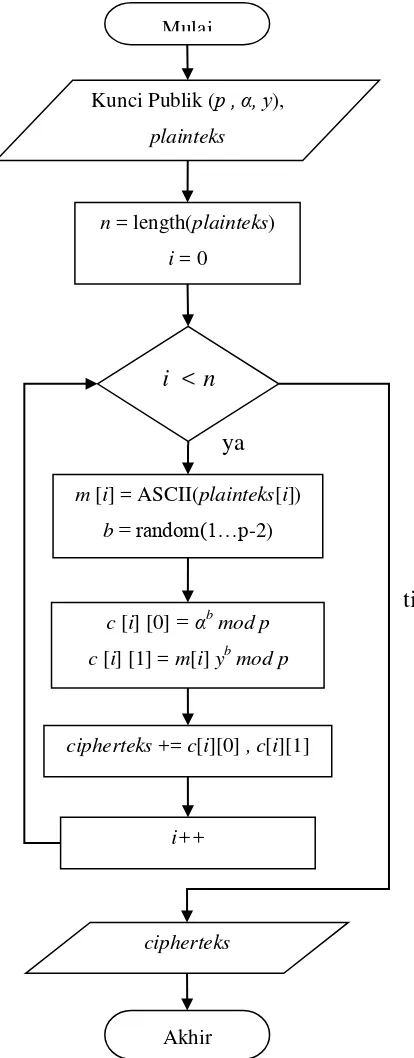
3.2.2.3Flowchart Enkripsi
Prosedur enkripsi akan membagi plainteks ke dalam blok-blok yang setiap blok plainteks berisi satu karakter plainteks, kemudian setiap karakter ini diubah ke dalam bentuk bilangan bulat melalui pengkodean ASCII dan dihitung cipherteksnya.
Gambar 3.7 Flowchart Prosedur Enkripsi tidak Mulai
Akhir
Kunci Publik (p , α, y),
plainteks
c [i] [0]= αb mod p
c [i] [1] = m[i] yb mod p
cipherteks
m [i] = ASCII(plainteks[i])
b= random(1…p-2) n = length(plainteks)
i = 0
i < n
i++ ya
3.2.2.4Flowchart Dekripsi
Pada prosedur dekripsi dilakukan perhitungan untuk memperoleh kembali plainteks (pesan asli) dengan menggunakan input cipherteks, kunci privat a dan kunci publik p milik penerima pesan.
Gambar 3.8 Flowchart Prosedur Dekripsi Mulai
Akhir cipherteks
Kunci privat (a) Kunci publik (p)
(αb) -a = ( c[i][0] ) p-1-a mod p
plainteks
m [i] = (αb) Ŕa c[i][1] mod p
i++
c [n][0..1] = cipherteks i = 0
i < n
plainteks += m[i] ya
BAB IV
IMPLEMENTASI DAN PENGUJIAN SISTEM
Setelah tahap perancangan, sistem diimplementasikan dalam bentuk aplikasi komputer. Aplikasi komputer yang dibangun sebagai pendukung skripsi ini dinamai KriptoElGamal dibuat dengan NetBeans IDE 7.0.1 menggunakan bahasa pemorograman Java. Aplikasi ini dapat berjalan pada komputer dengan sistem operasi Windows Vista 32 bit, prosessor Intel Core2 Duo 2GHz yang sudah diinstal Java Virtual Machine.
4.1. Tampilan Antarmuka
Berdasarkan desain antarmuka pada tahap perancangan, aplikasi komputer pendukung skripsi ini memiliki tampilan antarmuka (interface) yang sengaja dibuat sederhana agar pengguna dapat memanfaatkan fungsi pembangkit kunci, enkripsi, dan dekripsi yang tersedia pada aplikasi ini dengan mudah.
4.1.1. Jendela Menu Utama
Gambar 4.1 Jendela Menu Utama Aplikasi KriptoElGamal
4.1.2. Jendela Pembangkit Kunci
Jendela Pembangkit Kunci fungsinya membangkitkan kunci untuk pengguna, seperti yang terlihat pada gambar 4.2, pengguna diminta memasukkan input bilangan N yang merupakan batas atas dari nilai kunci yang akan dibangkitkan. Jadi, nilai bilangan kunci nantinya tidak akan melebihi nilai input N. Tombol BangkitkanKunci pada jendela Pembangkit Kunci akan menjalankan proses pembangkitan kunci sesuai dengan algoritma The Sieve of Eratosthenes dan algoritma kriptografi ElGamal sebagaimana telah dijelaskan pada tahap perancangan sistem.
Apabila proses pembangkitan kunci berhasil, setelah pengguna menekan tombol PembangkitKunci maka jendela pembangkit kunci akan tertutup dan pengguna akan kembali ke jendela Menu Utama untuk melihat output dari proses pembangkitan kunci pada kotak Output. Proses ini menghasilkan tiga kunci publik yang terdiri dari kunci p, kunci alpha, dan kunci y serta sebuah kunci privat a. Sedangkan tombol Batal akan membawa pengguna kembali kepada jendela Menu Utama tanpa melakukan proses pembangkitan kunci.
4.1.3. Jendela Enkripsi
Pada jendela Enkripsi pengguna diminta menginputkan pesan yang ingin dienkripsi (plainteks) dan kunci publik milik penerima pesan yang dituju oleh pengguna. Berikut ini merupakan tampilan jendela Enkripsi.
Gambar 4.3 Jendela Enkripsi Aplikasi KriptoElGamal
Menu Utama. Sedangkan jika tombol Batal pada jendela ini yang dipilih maka jendela Enkripsi akan tertutup tanpa menjalankan proses enkripsi.
4.1.4. Jendela Dekripsi
Pada jendela ini pengguna diminta menginputkan pesan terenkripsi (cipherteks) yang diterima oleh pengguna berserta kunci privat a dan kunci publik p milik pengguna sebagaimana yang ditunjukkan pada gambar 4.4.
Gambar 4.4 Jendela Dekripsi Aplikasi KriptoElGamal
Setelah semua permintaan input terisi ketika tombol DekripsiPesan ditekan aplikasi akan menjalankan proses dekripsi, menutup jendela Dekripsi, dan menampilkan plainteks hasil proses dekripsi tersebut pada kotak Output di jendela Menu Utama. Sedangkan tombol Batal pada jendela ini jika dipilih akan menutup jendela Dekripsi tanpa menjalankan proses dekripsi. Apabila pesan cipherteks dienkripsi menggunakan kunci yang salah atau berbeda maka pesan plainteks yang dihasilkan tidak akan sama dengan yang aslinya.
![Tabel 2.3 Prosedur Pembangkit Bilangan Prima Metode Standar [5]](https://thumb-ap.123doks.com/thumbv2/123dok/208989.17197/30.595.118.512.392.541/tabel-prosedur-pembangkit-bilangan-prima-metode-standar.webp)