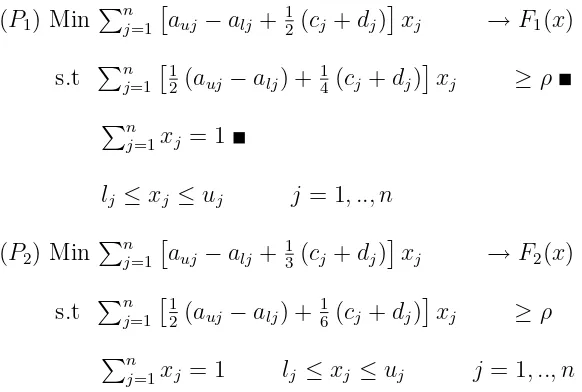Optimasi Fortofolio Dengan Risiko Downside Fuzzy

OPTIMASI PORTOFOLIO DENGAN RISIKO

DOWNSIDE FUZZY

TESIS

Oleh

WILMA HANDAYANI 127021001/MT

OPTIMASI PORTOFOLIO DENGAN RISIKO

DOWNSIDE FUZZY

T E S I S

Diajukan Sebagai Salah Satu Syarat

untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

WILMA HANDAYANI 127021001/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

Judul Tesis : OPTIMASI PORTOFOLIO DENGAN RISIKO DOWNSIDE FUZZY

Nama Mahasiswa : Wilma Handayani Nomor Pokok : 127021001

Program Studi : Magister Matematika

Menyetujui, Komisi Pembimbing

(Dr. Sutarman, M.Sc) (Prof. Dr. Herman Mawengkang)

Ketua Anggota

Ketua Program Studi Dekan

Telah diuji pada Tanggal 4 Juni 2014

PANITIA PENGUJI TESIS

Ketua : Dr. Sutarman, M.Sc

PERNYATAAN

OPTIMASI PORTOFOLIO DENGAN RISIKO DOWNSIDE FUZZY

TESIS

Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa

kutipan dan ringkasan yang masing-masing dituliskan sumbernya

Medan, 4 Juni 2014 Penulis,

ABSTRAK

Pada tesis ini disajikan dua model seleksi portofolio yang tujuannya untuk memi-nimumkan risiko downside berkendala sehingga expected return dapat terca-pai. Diasumsikan tingkat pengembalian dari setiap sekuritas menggunakan pen-dekatan bilanganLR₋f uzzy, danexpected returnserta risiko dievaluasi dengan menggunakan rata-rata interval ₋valued. Dibangun hubungan antara definisi mean₋interval-nya menggunakan hubungan terurut yang sesuai. Akhirnya, di-formulasikan bahwa masalah seleksi portofolio sebagai program linear diamana setiap asetnya berbentuk trapesium.

Kata kunci : Portofolio, Expected return, Bilangan fuzzy, Fuzzy expected return

ABSTRACT

This paper presents two fuzzy portfolio selection models where the objective is to minimize the downside risk constrained so that a given expected return should be achieved. We assume that the rates of returns on securities are approximated as LR-fuzzy numbers of the same shape, and that the expected return and risk are evaluated by interval-valued means. We establish the relationship between those mean-interval definitions for a given fuzzy portfolio by using suitable ordering re-lations. Finally, we formulate the portfolio selection problem as a linear program when the returns on the assets are of trapezoidal form.

KATA PENGANTAR

Setinggi puji dan sedalam syukur penulis serahkan kehadirat Allah SWT yang telah memberikan berkat dan rahmatNya sehingga penulis dapat menyele-saikan tesis yang berjudul ”Optimasi Fortofolio Dengan Risiko Downside Fuzzy”. Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Studi Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Universitas Sumatera Utara.

Pada kesempatan ini, penulis menyampaikan terimakasih kepada :

Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K)selaku Rektor Universitas Sumatera Utara

Dr. Sutarman, M.Sc selaku Dekan Fakultas Matematika dan Ilmu Penge-tahuan Alam (FMIPA) Universitas Sumatera Utara dan selaku Pembimbing Per-tama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

Prof. Dr. Herman Mawengkang selaku Ketua Program Studi Magister Ma-tematika FMIPA USU dan selaku Pembimbing Kedua yang telah banyak mem-berikan bimbingan dan arahan dalam penulisan tesis ini.

Prof. Dr. Saib Suwilo, M.Si selaku Pembanding Pertama yang telah banyak memberikan bimbingan dan arahan dalam penulisan tesis ini.

Prof. Dr Opim Salim Sitompul, M.Si selaku Pembanding Dua yang juga telah banyak memberikan bimbingan kepada penulis dalam penulisan tesis ini. Lembaga Pengelola Dana Pendidikan pada Kementrian keuangan RI yang telah banyak memberikan beasiswa dana penelitian tesis 2014 sehingga penulis dapat menyelesaikan penelitian ini dengan baik.

Seluruh rekan-rekan Mahasiswa Program Studi Magister Matematika FMIPA USU tahun 2012 ganjil (Tiwie-Rini, Romy-Isna, Hari-P’Le-Adi, Arie-Dilla, Ugie, Silvi, P’Mail, Juli, Fitra, Hana, Weni, Sari, Well, Tiur, Soes, Ndi) yang telah memberikan bantuan moril dan dorongan kepada penulis dalam penulisan tesis ini.

Tak lupa penulis mengucapkan terimakasih sebesar-besarnya dan penghar-gaan setinggi-tingginya kepada suami tercinta Ilhamuddin dan Orang Tu-aku tercinta yang mencurahkan kasih sayang dan dukungan kepada penulis ser-ta dengan setia mendampingi dan membantu penulis selama mengikuti perku-liahan hingga sampai penulisan tesis ini. Tak lupa pula kepada anak-anakku Zaky Muhammad Alghifari, Zaida Ramadhani Tasneem, Zia Muham-mad Alqudwah, dan Zulfa RaMuham-madhani Sayyeeda yang telah memberikan semangat selama penulisan tesis ini. Terima kasih kepada sahabat-sahabatku serta rekan-rekan lainnya yang tidak dapat disebutkan satu-persatu. Semoga Al-lah SWT memberikan balasan atas jasa-jasa mereka yang teAl-lah diberikan kepada penulis.

Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya. Terimakasih.

Medan, 4 Juni 2014 Penulis,

RIWAYAT HIDUP

Wilma Handayani dilahirkan di Garut pada tanggal 12 Juni 1976 dari pasang-an Ibu Ido Hindpasang-anih & Bapak Ukab Abdul Mpasang-anaf. Penulis lulus dari pendidikpasang-an Sekolah Dasar Negeri Talun 1 Garut pada tahun 1989, Sekolah Menengah Pertama Negeri 1 Garut pada tahun 1992, Sekolah Menengah Atas Negeri 1 Garut tahun 1995. Pada tahun 1996 memasuki tingkat Perguruan Tinggi di Universitas Pasun-dan Bandung Fakultas Keguruan Pasun-dan Ilmu Pendidikan jurusan(S-I) Matematika lulus tahun 2000. Alhamdulillah penulis sudah menikah dengan Ilhamuddin dan dikaruniai empat orang anak yaitu Zaky Muhammad Alghifari, Zaida Ramadhani Tasneem, Zia Muhammad Alqudwah, dan Zulfa Ramadhani Sayyeeda.

DAFTAR ISI

Halaman

PERNYATAAN i

ABSTRAK ii

ABSTRACT iii

KATA PENGANTAR iv

RIWAYAT HIDUP vi

DAFTAR ISI vii

DAFTAR GAMBAR ix

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Tujuan Penelitian 3

1.4 Manfaat Penelitian 3

BAB 2 TINJAUAN PUSTAKA 4

2.1 Investasi 5

2.2 Portofolio 6

2.3 Risiko 7

2.4 Investasi yang Berisiko 7

2.5 Risiko Downside 11

2.6 Himpunan Fuzzy 12

2.6.1 Fungsi keanggotaan pada himpunan fuzzy 12

2.6.3 Metode penyelesaian program linear 15

BAB 3 PEMBAHASAN 18

3.1 Model Optimisasi Portofolio 18

3.2 Perumusan Fungsi Objektif Model 18

3.3 Perumusan Fungsi Kendala 19

3.4 Fuzzy Expected Return 20

3.5 Risiko Downside Fuzzy 25

3.5.1 Model optimisasi downside fuzzy 28

3.5.2 Proses fuzzyfikasi 29

3.6 Contoh Permasalahan 30

BAB 4 KESIMPULAN DAN SARAN 35

4.1 KESIMPULAN 35

DAFTAR GAMBAR

Nomor Judul

ABSTRAK

Pada tesis ini disajikan dua model seleksi portofolio yang tujuannya untuk memi-nimumkan risiko downside berkendala sehingga expected return dapat terca-pai. Diasumsikan tingkat pengembalian dari setiap sekuritas menggunakan pen-dekatan bilanganLR₋f uzzy, danexpected returnserta risiko dievaluasi dengan menggunakan rata-rata interval ₋valued. Dibangun hubungan antara definisi mean₋interval-nya menggunakan hubungan terurut yang sesuai. Akhirnya, di-formulasikan bahwa masalah seleksi portofolio sebagai program linear diamana setiap asetnya berbentuk trapesium.

Kata kunci : Portofolio, Expected return, Bilangan fuzzy, Fuzzy expected return

ABSTRACT

This paper presents two fuzzy portfolio selection models where the objective is to minimize the downside risk constrained so that a given expected return should be achieved. We assume that the rates of returns on securities are approximated as LR-fuzzy numbers of the same shape, and that the expected return and risk are evaluated by interval-valued means. We establish the relationship between those mean-interval definitions for a given fuzzy portfolio by using suitable ordering re-lations. Finally, we formulate the portfolio selection problem as a linear program when the returns on the assets are of trapezoidal form.

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Pada dasarnya setiap investor dalam menginvestasikan asetnya pasti mengingin-kan tingkat keuntungan tertentu dengan risiko terendah. Setiap investor juga harus bisa mengidentifikasi saham atau sekuritas mana yang akan dipilih dan ditentukan besaran investasinya.

Mengidentifikasi saham atau sekuritas mana yang akan dipilih dan berapa proporsi dana yang akan ditanamkan pada masing-masing saham atau sekuritas tersebut adalah proses pemilihan portofolio. Pemilihan portofolio dari banyak sekuritas dimaksudkan untuk meminimumkan risiko yang ditanggung. Teori op-timisasi sangat aplikatif pada permasalahan yang menyangkut masalah pengop-timalan (Markowitz (1952) dalam Fuller dan Maljender (2003)).

Secara matematis portofolio pertama kali diformulasikan oleh Markowitz (1952). Dengan formula matematika ini membahas permasalahan bagaimana mengalokasikan penanaman modal dengan harapan mendapatkan keuntungan op-timum dengan risiko minimum. Teori manajemen portofolio yang dicetuskan oleh Markowitz menggabungkan teori probabilitas dan teori optimisasi menjadi suatu model yang sesuai dengan perilaku para pelaku ekonomi (Fuller dan Maljender, 2003).

2

Bermudez et al., (2005) berpendapat bahwa untuk membentuk portofo-lio yang optimum, investor harus menentukan portofoportofo-lio efisien terlebih dahulu. Ef f icient f rontier merupakan kumpulan portofolio efisien. Portofolio efisien adalah portofolio yang menghasilkan tingkat keuntungan tertentu dengan risiko terendah, atau risiko tertentu dengan tingkat keuntungan tertinggi. Sedangkan portofolio optimal merupakan portofolio yang dipilih seorang investor dari sekian banyak pilihan yang ada pada kumpulan portofolio yang efisien.

Masalah pemilihan portofolio berhubungan dengan cara membuat portofolio sesuai dengan yang diinginkan. Masalahan seleksi portofolio dalam menentukan sekuritas yang dipilih sulit dilakukan karena ada unsur ketidakpastian pada setiap returnnya. Tujuan umum seleksi portofolio adalah untuk mendapatkan proporsi yang optimum antara return dan risiko. Pemilihan portofolio berpedoman pada optimisasi alokasi aset portofolio. Dalam alokasi asset portofolio akan berkaitan dengan probabilitas penurunan harga asset. Hubungan demikian akan berkaitan dengan apa yang disebut risiko downside.

Selain itu Carlson et al., (2002) berpendapat bahwa asumsi terpenting dari model pemilihan portofolio adalah adanya investsi yang pasti, artinya seorang investor harus mengetahui dengan pasti kapan memulai investasi dan mengakhiri investasi, namun sebagian besar praktik investasi dilakukan tanpa batasan waktu tertentu. Hal ini menjadi salah satu alasan penting bahwa unsur ketidakpastian dimasukkan ke dalam model pemilihan portofolio terkait dengan waktu investasi. Satu cara untuk menyelesaikan pemilihan portofolio dengan unsur ketidak-pastian adalah dengan menggunakan himpunan fuzzy. Kemudian masalah keti-dakpastian return aset yang melibatkan perilaku pasar keuangan dapat menggu-nakan cara fuzzy dan atau kendala fuzzy dan beberapa elemen dapat menjadi fuzzy dalam masalah seleksi portofolio (Bilbaoet al., 2005).

3

1.2 Perumusan Masalah

Permasalahan dalam penelitian ini terkait seleksi portofolio optimum dengan op-timisasi alokasi aset portofolio yang berhubungan dengan risiko downside serta ketidakpastian pengembalian aset yang dimodelkan dengan himpunan fuzzy.

1.3 Tujuan Penelitian

Penelitian ini bertujuan untuk optimisasi portofolio dengan risiko downside fuzzy. Selanjutnya penelitian ini dapat digunakan untuk mengatur masalah pemilihan portofolio dengan menggunakan ekspektasi interval-valued.

1.4 Manfaat Penelitian

BAB 2

TINJAUAN PUSTAKA

Pada bab ini akan diuraikan konsep dan teori yang ada kaitannya dengan optimasi portofolio dengan risiko downside fuzzy. Salah satu konsep yang dibahas adalah f uzzy portf olio optimization downside risk measure (Bermudez et al., 2005). Selanjutnya akan diuraikan juga mengenai investasi, portofolio, risiko, investasi yang berisiko, risiko downside, himpunan fuzzy.

Pada era globalisasi, pasar saham tidak lagi didominasi oleh perusahaan besar dan investor institusi, investor individu juga mulai memasukinya. Hal tersebut disebabkan mudahnya menentukan alokasi aset keuangan sesuai dengan yang diinginkan. Penentukan alokasi aset tersebut, sering berhubungan dengan naik dan turunnya aset. Hal tersebut berakibat juga pada adanya ketidakpastian pengembalian aset. Ketidakpastian pengembalian aset bisa juga berasal dari kon-disi sosial, faktor analisis statistik data historis dan faktor ambigu seperti aspek psikologi investor serta efisiensi informasi.

Persoalan pemilihan alokasi aset keuangan secara umum disebut persoalan pemilihan portofolio. Persoalan tersebut kajiannya terus dilakukan sampai seka-rang. Seperti penelitian pendekatan matematika Markowitz (1952) telah meng-usulkan model mean ₋ variance dalam persoalan pemilihan portofolio. Pen-dekatan ini menjadi pusat kegiatan penelitian di bidang keuangan.

Seperti dikemukakan sebelumnya bahwa dalam menentukan alokasi aset berhubungan dengan naik dan turunya harga aset. Hubungan tersebut berkait-an dengberkait-an risiko downside (Sukono et al., 2008). Peneliti lainnya yang melaku-kan pemilihan portofolio dengan risiko downside diantaranya adalah Postet al., (2002), Nowrochi dan David (1999).

5

Leon et al., (2004) mengemukakan bahwa rata-rata dari sejumlah bilangan fuzzy bisa digunakan untuk mengevaluasi pengembalian yang diharapkan dan risiko portofolio yang diberikan. Dubois dan Prade (1987) memperkenalkan inter-val rata-rata dari bilangan fuzzy sebagai sebuah interinter-val tertutup yang dibatasi oleh beberapa ekspektasi yang dihitung dari probabilitas bawah dan atas.

Popularitas risikodownsidekalangan investor tumbuh dan berkembang da-lam seleksi portofolio. Ukuran risikodownsidehanya mempertimbangkan pengem-balian yang berada di bawah risiko. Ide di balik dunia risiko downside adalah bahwa sisi kiri dari distribusi kembali melibatkan risiko sementara sisi kanan berisi peluang investasi yang lebih baik .

2.1 Investasi

Setiap manusia pernah melakukan kegiatan investasi dalam hidupnya. Kegiatan investasi sebenarnya adalah kegiatan yang penuh dengan ketidakpastian atas sesu-atu yang terjadi pada waktu yang akan datang. Karena investasi merupakan kegiatan investor yang menanamkan modalnya pada saat sekarang dengan hara-pan memperoleh pendapatan atau tingkat keuntungan di waktu yang akan datang selama umur investasi tersebut.

Bilbao-Terol et al., (2006) mengatakan bahwa investasi secara sederhana dapat diartikan sebagai komitmen atas sejumlah dana yang dilakukan pada saat ini agar memperoleh sejumlah keuntungan di masa mendatang. Harapan keun-tungan di masa depan tersebut merupakan konpensasi atas waktu dan risiko yang berkaitan dengan investasi yang dilakukan. Harapan tingkat keuntungan tersebut sering disebut sebagai return, sedangkan risiko merupakan seberapa jauh hasil yang diperoleh atau return yang menyimpang dari nilai yang diharapkan. Dari pengertian investasi tersebut, menunjukkan bahwa tujuan dari investasi tidak lain adalah untuk meningkatkan kesejahteraan investor baik sekarang maupun di masa mendatang.

perusa-6

Dalam melakukan investasi di pasar modal diperlukan pengetahuan yang cukup, pengalaman dan naluri bisnis untuk menganalisa sekuritas atau mana yang akan dibeli, dijual dan mana yang dapat dimiliki. Sebagai seorang investor harus dapat bersikap rasional dalam menghadapi pasar jual beli saham. Selain itu juga investor harus mempunyai ketajaman dalam memperkirakan masa depan saham perusahaan yang akan di beli maupun di jual. Investor yang rasional ten-tunya tidak akan menyukai ketidakpastian atau risiko. Sikap investor terhadap risiko yang sangat bergantung kepada preferensi investor terhadap risiko. In-vestor yang mempunyai sikap enggan terhadap risiko disebut sebagairisk averse investors, yaitu investor yang tidak mau mengambil risiko jika investasi tersebut tidak memberikan harapan return yang layak sebagai kompensasi terhadap risiko yang ditanggung. Sedangkan investor yang berani mengambil risiko disebut seba-gai risk taker investors, yaitu investor yang lebih berani memilih risiko investasi yang tinggi dengan diikuti oleh harapan return yang tinggi juga (Carlsson et al., (2002)).

Pada umumnya investasi dibedakan menjadi dua, yaitu investasi padaf inan₋ cial assets dan investasi pada real assets. Investasi pada f inancial assets dilakukan di pasar uang, misalnya berupa deposito, commercial paper, surat berharga, dan yang lainnya. Atau dilakukan di pasar modal, misalnya berupa saham, obligasi, waran, opsi, dan lainnya. Sedangkan investasi pada real assets diwujudkan dalam bentuk pembelian aset produktif, pendirian pabrik, pembukaan pertambangan, pembukaan perkebunan, dan lainnya.

2.2 Portofolio

7

Dalam pembentukkan portofolio hubungan antar instrumen portofolio per-lu diperhatikan agar risiko yang diperoleh dapat optimum atau terkecil. Dan tahap akhir dalam tindakan portofolio yaitu melakukan evaluasi portofolio inves-tasi. Tahap ini dilakukan bila ada konstruksi portofolio yang dibangun, begitu juga sebaliknya. Dan untuk melakukan pembentukkan portofolio, investor selalu menginginkan return yang maksimum dengan risiko yang minimum.

2.3 Risiko

Risiko adalah segala sesuatu yang dapat mempengaruhi pencapaian tujuan orga-nisasi. Sedangkan manajemen risiko adalah serangkaian prosedur dan metodologi yang digunakan untuk mengidentifikasi, mengukur, memantau, dan menganda-likan risiko yang timbul dari kegiatan usaha.

Model yang berkembang dalam manajemen risiko adalah mengintegrasikan risiko dan pengelolaan usaha. Model tersebut dirancang supaya manajemen risiko memberikan nilai. Ada beberapa jenis risiko yaitu:

1. Risiko lingkungan (eksternal environmental risk), yakni kerugian kare-na bencakare-na alam, perubahan rasa dan preferansi pelanggan, kompetitor, lingkunga politis, dan ketersediaan modal dan tenaga kerja.

2. Risko proses usaha (business process risk), yakni kerugian yang diaki-batkan tidak efektif dan efisien dalam memperoleh, membiayai, mentransfor-masikan, dan memasarkan barang-barang dan jasa, serta ancaman kerugian aktiva, termasuk reputasi perusahaan.

3. Risiko informasi (inf ormation risk), yakni kerugian yang diakibatkan in-formasi yang bermutu rendah untuk pengambilan keputusan usaha dan ke-salahan memberikan informasi kepada pihak luar.

Faktor-faktor keberhasilan dalam pengelolaan risiko terdiri dari komitmen, tang-gung jawab, kesadaran, kebijakan, metodologi, keterampilan, dan pemantauan.

2.4 Investasi yang Berisiko

8

pengembalian yang dicapai secara nyata (actual return). Semakin besar penyim-pangannya maka semakin besar tingkat risikonya. Adapun alat yang digunakan sebagai ukuran dalam menghitung tingkat pengembalian dan risiko dalam porto-folio adalah sebagai berikut:

1. Return, return ekspektasi dan risiko saham (a) Return

Pt−1 : Harga saham periode sebelumnya (b) Return ekspektasi saham

E(Ri) =

PN

j=1Rij

N (2.2)

E(Ri) = Tingkat keuntungan yang diharapakan dari nvestasi Rij = Return saham iperiode j

Dimana N adalah return yang terjadi pada periode pengamatan 2. Return, return ekspekstasi dan risiko pasar

(a) Return pasar (IHSG)

9

Dimana E(Rm) adalah return ekspektasi pasar (c) Risiko pasar 3. Alpha dan beta sekuritas

(a) Alpha sekuritas 4. Kesalahan residu dan varian dari kesalahan residu

(a) Kesalahan residu

Ri =αi+aβi.Rm+̺i (2.10) Dimana ̺i adalah kesalahan residu

(b)Varian dari kesalahan residu

σ_i2 =β_i2σ2_m+σ_ei2 (2.11) Dimana:

σ2

ei : Varian dari kesalahan residu sekuritas kei σ2

10

Beta dari portofolio (βp) yang merupakan rata-rata terimbang dariβp masing-masing sekuritas.

Alpha dari portofolio (αp) yang merupakan rata-rata tertimbang dari αp tiap-tiap sekuritas.

Dengan mensubstitusikan karakteristik antara βp dengan αp maka return ekspektasi portofolio adalah sebagai berikut:

E(Rp) = αp+βp.E(Rm) (2.15) (b) Risiko portofolio varian dari portofolio

σ_p2 =β_p2.σm2+ (Xωi−σei)2 (2.16)

Tanaka dan Guo (1999) mengemukakan sebuah alternatif untuk memilih saham mana yang masuk dalam portofolio dengan menggunakanexcess return to beta (ERB). Dimana ERB merupakan selisih antara tingkat pengembalian saham dengan tingkat pengembalian aset bebas risiko yang selanjutnya dibagi dengan beta saham tersebut. Excess return to beta ini diurutkan dari terbesar sampai yang terkecil. ERB juga mengukur tingkat tambahan pengembalian pada sebuah saham per unit dari risiko yang tidak dapat diversifikasi. Untuk menghitung excess return to beta adalah sebagai berikut:

ERB= (Ri−Rf) βi

(2.17) Dimana:

ERB = Excess return to beta

11

Selanjutnya, Carlson et al., (2000) memberikan rumusan mengenai saham-saham yang masuk dalam portofolio yaitu saham-saham-saham-saham yang memiliki ERB di atas batas tertentu yang disebut dengan cut₋of f ₋rate, yang dapat dihitung sebagai berikut:

m = Varians tingkat pengembalian pasar βj = Beta saham kej

σ2

ej = Varians saham yang tidak dihubungkan dengan pasar ke j Ri = Tingkat pengembalian saham kei

Rf = Tingkat pengembalian aset bebas risiko

Dubois dan Prade (1987) juga memperkenalkan analisis network atau je-jaring yang diaplikasikan kepada model portofolio. Model portofoloio ini selalu dipresentasikan dalam bentuk node yang selalu berhubungan dengan input yang masing-masing sebagai penawaran (supplies) dan permintaan (demands) dan ini merupakan komponen pertama. Komponen kedua yang digunakan dalam mo-del portofolio adalah titik transaksi (point transaction) atau node portofolio (portf olio nodes).

2.5 Risiko Downside

Sebuah estimasi potensi keamanan mengalami penurunan nilai jika kondisi pasar berubah, atau jumlah kerugian yang dapat diderita sebagai akibat dari penu-runan. Pemilihan portofolio berpedoman pada optimisasi alokasi aset portofolio. Dalam alokasi asset portofolio akan berkaitan dengan probabilitas penurunan har-ga asset. Hubunhar-gan demikian akan berkaitan denhar-gan risiko downside.

12

Beberapa investasi memiliki jumlah terbatas risiko downside, sementara yang lain memiliki risiko yang tak terbatas. Pembelian saham, misalnya, memi-liki jumlah terbatas risiko downside; investor dapat kehilangan seluruh inves-tasinya. Penjualan saham, seperti yang dicapai melalui penjualan pendek (atau ”short-selling”) memerlukan risiko downside terbatas, karena harga bisa terus meningkat tanpa batas.

2.6 Himpunan Fuzzy

Tidak semua himpunan yang dijumpai dalam kehidupan sehari-hari terdefinisi se-cara jelas, misalnya himpunan orang miskin, himpunan orang pandai, himpunan orang tinggi, dan sebagainya. Misalnya, pada himpunan orang tinggi, tidak dapat ditentukan secara tegas apakah seseorang adalah tinggi atau tidak tinggi. Anggap bahwa definisi orang tinggi adalah orang yang tingginya lebih besar atau sama dengan 1.75 meter, maka orang yang tingginya 1.74 meter menurut definisi terse-but termasuk orang yang tidak tinggi. Sulit diterima bahwa orang yang tingginya 1.74 meter itu tidak termasuk orang tinggi. Hal ini menunjukkan bahwa batas antara kelompok orang tinggi dan kelompok orang yang tidak tinggi tidak dapat ditentukan secara tegas.

Untuk mengatasi permasalahan himpunan dengan batas yang tidak tegas itu, L.A. Zadeh mengaitkan himpunan tersebut dengan suatu fungsi yang menya-takan nilai keanggotaan pada suatu himpunan tak kosong sebarang dengan menga-itkan pada interval [0,1]. Himpunan tersebut disebut himpunan fuzzy dan fungsi ini disebut fungsi keanggotaan (membershipf unction) dan nilai fungsi itu disebut derajat keanggotaan.

2.6.1 Fungsi keanggotaan pada himpunan fuzzy

13

[0,1] dengan nilai dari fA(x) pada x mewakili derajat keanggotaan x pada A. Maka, semakin dekat nilai fA(x) ke semesta pembicaraan, semakin tinggi dera-jat keanggotaan x pada A. Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk dioperasikan dalam suatu variabel fuzzy.

Semesta pembicaraan merupakan himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri ke kanan dan nilai semesta pem-bicaraan dapat berupa bilangan positif atau negatif. Domain himpunan fuzzy adalah keseluruhan nilai yang diizinkan dalam semesta pembicaraan dan boleh di-operasikan dalam suatu himpunan fuzzy. Fungsi keanggotaan (membership func-tion) adalah suatu kurva yang menunjukkan pemetaan titik titik input data ke dalam nilai keanggotaan yang mempunyai interval antara 0 sampai 1.

Definisi 2.1:

X adalah sebuah himpunan tak kosong. Sebuah himpunan fuzzy A pada Xditan₋ dai oleh f ungsi keanggotaannya:

A:X _→[0,1]

dan A(x) diinterpretasikan sebagai derajat keanggotaan dari elemen x pada

him-punan f uzzy A untuk setiap x_∈X.

Nilai 0 digunakan untuk mewakili bukan anggota, nilai 1 digunakan un-tuk mewakili keanggotaan penuh, dan nilainilai di antaranya digunakan unun-tuk mewakili derajat keanggotaan menengah. PemetaanAjuga disebut sebagai fungsi keanggotaan dari himpunan fuzzyA.

Definisi 2.2:

Sebuah himpunan fuzzy adalah kosong jika dan hanya jika fungsi keanggotaannya

sama dengan 0 pada X Definisi 2.3

Dua himpunan fuzzy A dan B adalah sama, ditulis A=B,

14

2.6.2 Bilangan fuzzy

Sebuah bilangan fuzzy merupakan perluasan dari bilangan biasa, dalam arti bah-wa hal itu tidak mengacu pada suatu nilai tunggal melainkan pada suatu him-punan nilai-nilai yang mungkin berhubungan, dimana setiap nilai kemungkinan memiliki bobot sendiri antara 0 dan 1. Bobot ini disebut sebagai fungsi keang-gotaan. Dengan demikian, sebuah bilangan fuzzy adalah sebuah kasus khusus dari himpunan fuzzy konveks. Sama seperti Logika Fuzzy yang merupakan perluasan dari Logika Boolean (di mana hanya menggunakan ya dan tidak dan tidak ada di antaranya), bilangan fuzzy merupakan perluasan dari bilangan real. Perhitungan dengan menggunakan bilangan fuzzy memungkinkan penggabungan ketidakpas-tian parameter, sifat, geometri, kondisi awal, dan sebagainya.

Sebelum menjelaskan tentang bilangan fuzzy, berikut beberapa hal dan definisi yang penting dalam teori himpunan fuzzy: (Inuiguchi et al., 1990)

1. Sebuah himpunan fuzzy A pada R (barisan bilangan real) didefinisikan se-bagai himpunan pasangan terurut A= _{(x, µA(x))_|x _∈R_}, di mana µ_A˜(x) disebut sebagai fungsi keanggotaan untuk himpunan fuzzy.

2. Sebuah himpunan fuzzyA disebut normal jika terdapat paling sedikit satu titik x_∈R denganµ_A˜(x) = 1

3. Sebuah himpunan fuzzyApadaRadalah konveks jika untuk setiapx, y _∈R setiap λ_∈[0,1] sehingga µA(λx+ (1₋λ)y)_≥min_{µA(x), µA(y)_}.

4. Sebuah bilangan fuzzy adalah sebuah himpunan fuzzy pada barisan bilangan real yang memenuhi kondisi normalitas dan konveksitas.

Definisi 2.4

Bilangan fuzzy A˜ adalah sebuah normalisasi himpunan fuzzy konveks pada barisan

bilangan R sehingga:

15

0, untuk yang lainnya

(2.19)

dimanamA _{adalah nilai rata rata dari ˜A dan α}A _{dan β}A _{adalah penyebaran kiri} dan kanan berturut-turut, ini disebut sebagai bilangan fuzzy triangular. Sebuah bilangan fuzzy triangular ditunjukkan dengan ˜A= (mA_{, α}A_{, β}A_{) danF(R) adalah} himpuanan dari bilangan fuzzy triangular.

Definisi 2.5

2.6.3 Metode penyelesaian program linear

Permasalahan dalam bentuk Fuzzy Linear Programming (FLP) ditransfor-masi ke bentuk Linear Programming (LP), akan dicari solusi yang optimal dari model tersebut dan solusinya digunakan sebagai solusi yang optimal dari FLP.

Linear Programmingadalah sebuah metode matematika yang digunakan un-tuk mencari hasil paling optimum dalam suatu model matematika dengan be-berapa daftar kendala yang direpresentasikan dalam persamaan linear. Sebuah permasalahan LP dapat didefinisikan sebagai berikut:

M aks:z =cx (2.20)

16

dimana: x= (x1, ..., xn)T, c = (c1, ..., cn), b= (x1, ..., xn)T, danA= [aij]mn

Ada beberapa cara untuk menyelesaikan persoalan LP, diantaranya dengan menggunakan metode grafik dan metode simplex. Metode grafik tidak dapat digunakan dalam menyelesaikan persoalan program linear yang memiliki variabel keputusan yang cukup besar atau lebih dari dua, jadi untuk menyelesaikannya digunakan metodesimplex.

Langkah-langkah penyelesaian program linear dengan metode grafik:

1. Bentuk model matematika dari persoalan untuk: a. Fungsi tujuan (objective function)

b. Fungsi kendala (constraint)

2. Ubah bentuk pertidaksamaan pada kendala menjadi persamaan. 3. Gambarkan grafik pada langkah ke-2 dan tentukan daerah layak.

4. Uji titiktitik ekstrim yang diperoleh dengan mensubstitusikan nilai titik ke fungsi tujuan.

Langkah-langkah penyelesaian program linear dengan metode simplex:

1. Formulasikan dan standarisasikan persoalan ke model linear.

2. Tambahkan variabelslackpada masing masingconstraint(pembatas) untuk memperoleh bentuk standar. Model ini digunakan untuk identifikasi solusi

feasible awal dari pembatas bernilai lebih kecil atau sama dengan. 3. Buat tabelsimplex awal.

4. Pilih kolom kunci, yaitu kolom yang memiliki nilai (cj −zj) yang paling positif untuk kasus maksimasi atau yang memiliki nilai (cj−zj) yang paling negatif untuk kasus minimasi.

17

7. Lakukan iterasi dengan menentukan baris kunci baru, baris z baru, dan baris variabel-variabel slack baru.

(a) Baris kunci baru ditentukan dengan membagi baris kunci lama dengan elemencell.

(b) Baris z baru dan barisbaris lainnya ditentukan dengan cara: Baris lama(nilai kolom kunci baris yang sesuai baris kunci baru)

(c) Letakkan nilai nilai baris yang baru diperoleh ke dalam tabel

BAB 3 PEMBAHASAN

Pada bab ini akan disajikan konsep optimasi portofolio dengan risiko downside fuzzy (Bermudez et al., 2005). Untuk melengkapi pembahasan terhadap ap-likasinya akan disajikan salah satu contohnya.

3.1 Model Optimisasi Portofolio

Model optimisasi portofolio terdiri dari dua fungsi objektif yaitu memaksimumkan nilai expected return dan meminimumkan risiko portofolio, risiko dalam hal ini adalah varian. Sedangkan variabel keputusan adalah proporsi dana yang akan diinvestasikan pada masing-masing saham dalam portofolio tersebut.

3.2 Perumusan Fungsi Objektif Model

Penentuan fungsi objektif model portofolio mempertimbangkan dua aspek, yaitu return dan risiko portofolio, sebagai berikut:

1. Fungsi objektif maksimasiexpected return

M aksE(P) = n

X

i=1

E(Pi)(xi) (3.1)

Dimana:

E(P) : Expected returnportofolio

E(Pi) : Expected returndari investasi saham i

xi : Proporsi dana yang diinvestasikan pada sahami 2. Fungsi objektif minimasi risiko

M inσ2_p = n

X

i=1

σ2_ixi + n

X

i−1 n

X

h=1,h6=1

19

3.3 Perumusan Fungsi Kendala

Dalam memenuhi tujuan optimisasi portofolio tersebut ada beberapa kendala, antara lain:

1. Fungsi kendala koefisien risiko

Koefisien risiko mengukur korelasi antara nilai investasi dan gerakan pasar secara keseluruhan. Perumusan fungsi kendala koefisien risiko adalah seba-gai berikut:

Dengan βi yang merupakan nilai koefisien risiko saham i. Karena investor cenderung menghindar risiko, maka koefisien risiko harus kurang dari atau sama dengan satu.

2. Fungsi kendala jumlah proporsi dana yang diinvestasikan

Perumusan fungsi kendala jumlah proporsi dana yang diinvestasikan adalah sebagai berikut:

n

X

i=1

xi = 1 (3.4)

Jumlah proporsi dana yang diinvestasikan pada masing-masing saham adalah satu.

Agar dana yang diinvestasikan dapat terisi untuk semua saham, diasumsikan batas bawah penanaman modal adalah 10 per sen, makaxi ≥0,1. Jadi model optimisasi portofolio dapat diformulasikan sebagai berikut:

20

3.4 Fuzzy Expected Return

Beberapa penulis menggunakan bilangan fuzzy untuk mewakili ketidakpastian

return aset dan mereka menjadikan seleksi portofolio sebagai masalah pemrogra-man matematika untuk memilih alternatif terbaik dalam masalah pengambilan keputusan (Carlsson et al., 2002).

Dalam formulasi standar pemilihan portofolio, investor memilih xj, yang menunjukkan proporsi dari total dana investasi yang ditujukan untuk aset ke j, untuk n aset berisiko, sehingga portofolio dapat dinotasikan dengan P(x) =

{x1, ..., xn}. Diasumsikan bahwa uj mewakili masing-masing maksimum dan lj mewakili masing-masing minimum dari total dana yang dapat diinvestasikan da-lam aset ke-j, maka persamaan anggaran berikut ini berlaku: Pn

j=1xj = 1 dengan lj ≤ lj ≤ uj, j = 1, ..., n. Kendala lj ≥ 0 menyiratkan bahwa short selling dari sekuritas tidak diperbolehkan.

Returnfuzzy dari aset ke-j dalam portofolio P(x), maka rata-rata interval-valuenya didefinisikan sebagai berikut: menunjukkan masing-masing titik ekstrim kiri dan kanan dari level α yang me-motong ˜Pj untuk α∈(0,1).

Dengan menggunakan definisi dari rata-ratainterval-valueduntuk ˜Pj (Carls-son dan Fuller (2001)), maka:

M( ˜Pj) = untuk bilangan LR-Fuzzy dengan penurunan fungsi, maka berlaku:

bergan-21

returndiformulasikan dengan nilai keanggotaan fuzzy yang berbentuk trapesium, karena pada saat tertentu return bisa dalam kondisi naik, turun, atau tetap (Bermudez et al., 2005) Beberapa definisinya sebagai berikut:

Definisi 1. Bilangan f uzzy A dikatakan suatu bilangan LR˜ ₋f uzzy, ˜A =

Khusus saat L dan R berupa fungsi linear ˜A disebut bilangan fuzzy trape-sium, dimana ˜A adalah (al−c, au +d) dan L(1) =R(1) = 0. Jika ditambahkan al =au, maka disebut bilangan fuzzy triangular.

Lemma 1. M isalkan A˜= (al1, au1, c1, d1)LR dan B˜ = (al2, au2, c2, d2)LR adalah

dimana penjumlahan dan perkalian skalar didef inisikan oleh prinsip perpan₋ jangan sup₋min.

Ditunjukkan bahwa return dari aset ke-j dengan R = (alj, auj, cj, dj), de-ngan asumsi bahwa fungsi referensi kiri-kanannya adalah bentuk yang sama untuk j = 1, ..., n yang memenuhi kombinasi linear total return fuzzy pada portofolio P(x) =_{x1, ..., n}:

22

= (Pl(x), Pu(x), C(x), D(x))LR

dimana xij ∈R+ merupakan proporsi aset ke-j pada komposisi portofolio. Hal ini secara luas diakui bahwa ekspektasi interval ₋valued E( ˜A) dan M( ˜A) tetap aditif dalam penambahan bilangan fuzzy (Carlsson dan Fuller (2001), Dubois dan Prade (1987)). Lalu dipertimbangkan portofolio fuzzy ˜P dimana L danRfungsi dengan parameter yang sama yaitup, danL(x) =R(x) =max_{0,1₋

|x_|p_{}, p > 0. Karena fungsi yang kontinu menurun, maka rata-rata} possibilis-tic interval₋valued adalah bagian dari rata-rata possibilitas interval₋valued (Carlsson dan Fuller, 2001).

Kemudian diverifikasi bahwa himpunan α₋level dari ˜P memiliki bentuk sebagai berikut:

23

Definisi 2. M isalkan A dan B adalah dua interval tertutup pada garis real, maka:

1)A_≤LR B ↔aL ≤bL, dan aR ≤bR.

2)A_≤mw B ↔m(A)≤m(B), dan hw(A)≤hw(B).

Hal ini menunjukkan bahwa relasi order pertama tidak bisa diaplikasikan untuk order intervalmean₋valueddan akan dibuktikan bahwa relasi kedua terjadi saat D(x) > C(x). Kemudian akan digunakan relasi order yang diperpanjang, yang diperkenalkan oleh Sengupta dan Pal (2000), untuk membandingkan dua interval alternatif keuntungan dalam masalah memaksimalkan expected return. Ada peringkat dibuat dalam bentuk nilai dan itu hanya sebagian berlaku untuk memilih alternatif terbaik dari setiap pengambilan keputusan yang akan diambil. Definisi 3. M isalkan A dan B dua interval tertutup sehingga m(A)_≤m(B). Dilambangkan dengan_≺sebuah perintah hubungan diperpanjang,sedemikian rupa sehingga A lebih rendah dari B, A _≺B, dalam nilai indeks penerimaan A≺ = _hw(B)+hw(A)m(B)−m(A) , dimana hw(B) +hw(A)6= 0.

Remark 1. Nilai A≺ dapat ditafsirkan sebagai kelas penerimaan dari premis

”Interval pertama lebih rendah dari interval kedua”. Perhatikan bahwa untuk m(A) = m(B), kelas penerimaan dari ”A lebih rendah dari B” adalah nol, dan bahwa kelas ini lebih besar dari satu jika m(A) < m(B) dan A dan B tidak overlap, yaitu aR=bL. Jikam(A)< m(B) dan aR> bL, premis diterima dengan kelas yang berbeda dari nilai yang memuaskan di (0,1).

Propposisi 1. Perhatikan ekspektasi mean-interval dari suatu return fuzzy P˜ = (Pl(x), Pu(x), C(x), D(x))LR dari portofolio P(x) yang diberikan, dengan asumsi bilangan LR-fuzzy dengan bentuk yang sama diberikan dengan p > 0. Lalu dida-patkan:

1. Jika ”lef t₋widht” adalah yang terbesar, yaitu C(x)_≥D(x), maka E( ˜P)_≤mw M( ˜P),

2. Jika tidak, M( ˜P)_≺E( ˜P)dengan nilai penerimaan yang lebih rendah dari

24

Bukti: Beberapa notasi yang digunakan adalah: E( ˜P) = [EL, ER =< m(E)], hw(E)>

Pertama-tama, harus dicatat bahwa urutan hubungan _≤LR tidak dapat dite-rapkan. Selain itu, dari ketidaksamaan 2p < 2p+ 1, dapat membuktikan bahwa hw(E) > hw(M), karena Pu(x) ≥ Pl(x), C(x) ≥ 0 dan D(x) ≥ 0. Tetapi se-hubungan dengan titik tengah, ada dua kasus:

1. JikaC(x)> D(x), menyatakanm(E)< m(M) kemudianE( ˜P)_≤mw M( ˜P). Ketika portofolio fuzzy adalah bilangan fuzzy simetris, C(x) = D(x), titik tengah tepat diatas relasi trivial.

2. Jika penyebaran yang tepat adalah yang terbesar, C(x) < D(x), maka

Dimisalkan jika fungsi referensiLdan R dari semua returnfuzzy adalah li-near,returndari portofolio juga memiliki bentuk trapesium dan ekspektasi mean-intervalnya adalah sebagai berikut:

25

Lalu ditunjukkan bahwa interval ini bertepatan dengan himpunan tingkat λ dari return fuzzy ˜P untuk λ = 1/2 dan λ = 2/3. Di sisi lain, karena bilangan fuzzy trapesium adalah dengan p = 1, proposisi di atas terpenuhi dan ketika C(x) < D(x) kelas dari M( ˜P)_≺E( ˜P) dihitung dengan:

A≺=

1/12(D(x)₋C(x))

Pu(x)₋Pl(x) + 5/12(D(x) +C(x)) <1/5 (3.18) Proposisi 2. M isalkan P˜ adalah bilangan LR-fuzzy dengan fungsi referensi menurun kontinu, seperti L = R. Jika C(x) < D(x) maka M( ˜P) _≺ E( ˜P)

dengan nilai akseptabilitas di (0,1), jika E( ˜P)_≤mw M( ˜P).

Bukti: Dengan asumsi yang dikemukakan oleh Fuller dan Majlender (2003) bah-wa nilai rata-rata posibilitasinterval₋value dari suatu portofolio adalah bagian dari interval nilai rata-rata probabilitas interval₋valued, M( ˜P)_⊆E( ˜P), maka hw(M) =hw(E). Selain itu, dalam Fuller dan Majlender (2003) terbukti bahwa:

Z 1 L₋ 1(α) menjadi kebalikan dari fungsi referensi. Oleh karena itu, tergantung pada tanda perbedaan antara kanan dan kiri penyebaran portofolio,D(x)₋C(x), didapatkan m(E)< m(M) (negatif) atau m(E)> m(M) (positif). Dalam kasus kedua ini _≤mw tidak dapat diterapkan, tetapi titik akhir kanan interval M( ˜P) lebih besar dari titik akhir kiri interval E( ˜P) dan hasil yang diharapkan dari M( ˜P)_≺E( ˜P) tetap di (0,1).

3.5 Risiko Downside Fuzzy

26

penggunakan semi- variance, yang merupakan jumlah kuadrat dari rata-rata de-viasi negatif. Ukuran yang berbeda dari risiko portofolio telah diusulkan nakan baik saat momen parsial tinggi atau rendah. Jika ukuran risiko yang digu-nakan adalah rata-rata deviasi semi-absolut, seperti yang diusulkan oleh Speranza (1993), risiko fungsi dapat dengan mudah dievaluasi, berbeda dengan kompleksi-tas portofolio dengan semi-variance minimum.

Bawa dan Linderberg (1997) mengemukakan bahwa ukuran risikodownside dinyatakan sebagai berikut:

β = cov(Ri, Rm/Rm < µm) var(Rm/Rm < µm)

(3.20) Ri adalah return ke-i,Rmadalah return ke-m, danµmadalah rata-rata surplusnya.

Ri,t =

Pi,t−Pi,t−1 Pi,t−1

(3.21) Ri,t adalah return ke-i pada periode t, Pi,t adalah portofolio ke-i periode t, dan Pi,t−1 adalah portofolio ke-i periode sebelum t. Sehingga:

M axE(P) = n

X

i=1

αiEt[Ri,t+1] (3.22)

Anggap skema optimasi fuzzy untuk memilih portofolio yang optimal, dengan asumsi bahwa tingkat pengembalian aset dimodelkan dengan menggunakan bila-ngan LR-fuzzy trapesium. Leon dan Vercher (2004) mengenalkan risikodownside fuzzy untuk portofolio trapesium menggunakan definisi berikut :

˜

27

c) maxn0, M( ˜P)₋P˜o=0, Pu(x)₋Pl(x) + D(x)₃ ,0, C(x) LR

d) ˜w( ˜P) = Mmax_{0, M( ˜P)₋P˜_}=h0, Pu(x)₋Pl(x) + C(x)+D(x)₃ i

Bukti: Yang dibuktikan hanya (c, d) karena (a, b) dapat dibuktikan dengan cara yang sama. Pertama-tama dievaluasi dulu perbedaan antara crips-interval (rata-rata interval₋valued) dan bilangan LR-fuzzy. Untuk melakukan itu, asumsikan bahwa M( ˜P) adalah bilangan fuzzy trapesium dengan kanan dan kiri menyebar nol, yaitu: Kemudian terapkan Lemma 1 dengan kalkulus langsung kita memperoleh:

M( ˜P)₋P˜=M( ˜P)₋(Pl(x), Pu(x), C(x), D(x))_LR = yang juga merupakan bilangan fuzzy trapesium. Sekarang dihitung maksimal dua bilangan fuzzy trapesium dengan menggunakan definisi dari maksimal dua bilangan fuzzy (Dubois dan Prade, 1980), dan untuk 0 = (0,0,0,0)LR diperoleh:

max_{0, M( ˜P)₋P˜_}= yang merupakan bilangan fuzzy trapesium dipotong ke kiri nilai 0 dengan interval tertutup

0, Pu(x)₋Pl(x) + 1 3D(x)

. Kemudian, dengan menggunakan hasil pada (3.18), kita memperoleh possibilitas rata-rata interval₋valued:

w( ˜P) =

yang merupakan probabilitasrata-rata deviasi semi-absolut dari portofolio trape-sium.

28

3.5.1 Model optimisasi downside fuzzy

Masalah seleksi portofolio berkaitan dengan mencari strategi optimal investor untuk mendapatkan portofolio yang diinginkan, dengan mempertimbangkan ke-seimbangan antarareturn maksimal dan risiko minimal dari suatu investasi. Ke-mudian perlu ditentukan rata-rata yang diharapkan dan risiko portofolio. Model dasar menentukan portofolio yang meminimalkan risiko sementara tingkat ke-untungan yang diharapkan tetap terjamin, sehingga masalah dapat dirumuskan sebagai berikut:

Model yang berbeda untuk memilih portofolio terbaik sesuai dengan masing-masing fungsi tujuan fuzzy dalamrisk₋return trade₋of f. Maka risiko downside fuzzy dapat direpresentasikan sebagai berikut:

˜

jadi masalah di atas dapat dianggap sebagai masalah program linier dengan koe-fisien interval, di mana pengembalian yang diinginkan dinyatakan sebagai berikut:

E( ˜P) =

29

3.5.2 Proses fuzzyfikasi

Proses fuzzyfikasi adalah proses menemukan nilai representatif skalar dari sejum-lah fuzzy dan hal itu dapat dilakukan dengan berbagai cara. Untuk mendapatkan solusi dari model fuzzy, perlu memilih fungsi tujuan krip dan nilai L dari total kendala return. Dalam hal ini meminimalkan risiko downside fuzzy dianggap se-bagai krip obyektif yang akan memaksimalkan hasil yang diharapkan. Pertama kita meminimalkan batas atas interval rata-rata (Proposisi 3), yang sesuai dengan risiko downside fuzzy untuk memastikan pengembalian yang diharapkan. Fungsi tujuan dari model krip tersebut adalah:

F1(x) =

Pemodelan krip dari sejumlah bilangan fuzzy yang mewakili return yang diharap-kan maka dipilih titik tengah yang sesuai dengan interval-valued. Apabila lebar L fuzzy lebih besar dari lebar R, rata-ratanya bergeser ke kiri untuk mencer-minkan dispersi yang lebih besar, jika perpindahan adalah ke kanan. Oleh karena itu usulan defuzzifikasi return fuzzy yang diharapkan dapat dinyatakan sebagai berikut:

di mana ρ adalah return minimum yang diharapkan investor. Di sisi lain, ketika rata-rata possibilistik interval-value digunakan maka:

(P2) Minimalkan: Pn

j=1 auj −alj+ 1₃(cj +dj)

30

Pn

j=1xj = 1

lj ≤xj ≤uj, j = 1, ..., n

Jelas, perbandingan langsung antara kinerja program linear (P1) dan (P2) dan risiko harapan dengan menggunakanE( ˜P) danM( ˜P), masing-masing dapat dibu-at .

3.6 Contoh Permasalahan

Seorang investor memilihxj yaitu total investasi pada aset ke-j, untuknaset-aset beresiko, maka portofolio didenotasikan sebagai P(x) = _{x1, ..., n}. Assumsikan uj/lj merupakan jumlah/total fund maksimum/minimum yang diinvestasikan pa-da aset ke-j, maka persamaan budget Pn

j=1xj = 1 sehingga lj ≤ xj ≤ uj, j = 1, ..., n.

Misalkan terdapat tiga aset yang pengembaliannya mengikuti bilangan fuzzy trape-zoidal:

˜

R1 = (−11; 71; 5; 100) ˜R2 = (−9; 36; 5; 55) ˜R3 = (−6; 29; 12; 85) Kemudian diberikan portofolio sebagai berikut:

P1(x) = _{0,124; 0,373; 0,503_}, P2(x) = _{0,163; 0,837; 0_}, P3(x) = {0,103; 0; 0,897}, P4(x) = _{0; 0; 1_}

Penyelesaian:

Pengembalian pada aset ke-j adalah ˜R = (alj, auj, cj, dj)LR ˜

P =Pn

j=1R˜jxj =

h Pn

j=1aljxj,Pnj=1aujxj,Pnj=1cjxj,Pnj=1djxj

i

LR = (Pl(x), Pu(x), C(x), D(x))_LR

31

= (₋11)(0,124) + (₋9)(0,373) + (₋6)(0,503) =₋1,364₋3,357₋3,018

=₋7,739

Pu(x) = au1x1+au2x2+au3x3

= (71)(0,124) + (36)(0,373) + (29)(0,503) = 8,804 + 13,428 + 14,587

= 36,819

C(x) =C1x1+C2x2+C3x3

= (5)(0,124) + (5)(0,373) + (12)(0,503) = 0,62 + 1,865 + 6,036

= 8,521

D(x) =D1x1+D2x2 +D3x3

= (100)(0,124) + (55)(0,373) + (85)(0,503) = 12,4 + 20,515 + 42,755

= 75,67

Misalkan diberikan parameter p = 1 pada fungsi reference L(x) dan R(x) maka pada P1(x) di dapat:

E(P1) = hPl(x)₋C(x)_p+1p , Pu(x) +D(x)_p+1p i =

−7,739₋(8,521)₁₊₁1 ,36,819 + (75,67)₁₊₁1

= [₋12,000,74,654] M(P1) =

h

Pl(x)−C(x) 2p

2

(p+1)(2p+1), Pu(x) +D(x) 2p2

(p+1)(2p+1)

i

=

−7,738₋(8,521)1

3,36,819 + (75,67) 1 3

32

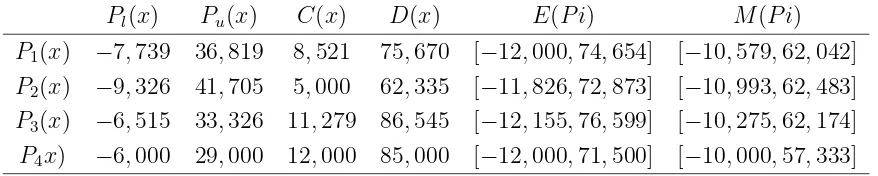
Untuk mencari Pl(x), Pu(x), C(x), C(x), D(x), E(pi), M(pi) pada P2(x), P3(x), P4(x) dilakukan dengan cara yang sama atau dapat dilihat pada tabel di bawah ini:

Tabel 3.1 Portofolio dalam Setiap Titik

Pl(x) Pu(x) C(x) D(x) E(P i) M(P i) P1(x) ₋7,739 36,819 8,521 75,670 [₋12,000,74,654] [₋10,579,62,042] P2(x) ₋9,326 41,705 5,000 62,335 [₋11,826,72,873] [₋10,993,62,483] P3(x) ₋6,515 33,326 11,279 86,545 [₋12,155,76,599] [₋10,275,62,174] P4x) −6,000 29,000 12,000 85,000 [−12,000,71,500] [−10,000,57,333]

Dari hasil yang di dapat dari Tabel 3.1 dapat dilihat bahwa:

E(P4)< E(P2)< E(P1)< E(P3)

Sehingga disarankan pemilihan alternatif yaitu P3(x) yang memilihi nilai maksi-mum. Faktanya, pengambilan keputusan akan puas bahwa E(P1) adalah inferior tehadap E(P3) dengan grade kepuasan A≺ sebesar:

A_≺= plabilitas dalam interval (0,1) terbukti. Dan jikap > 0 (parameter diambilp= 1) maka batas atas bernilaiA _≺= 0,2 terbukti.

33 Tabel 3.2 Portofolio dengan Downside Risk Fuzzy

Upper Bound 0,4 0,5 0,6 0,7 0,8 1

Tabel 3.2 menunjukkan portofolio yang tersedia dengan pemecahan program linear (P1) dibawah kondisi diversifikasi yang sama. Nilai-nilai krisp dari pengembalian (return) dan risiko terlihat pada baris terakhir (F1).

Fungsi objektif dari model krisp adalah: F1(x) = Pn_j=1auj −alj+ 1₂(cj +dj)xj F2(x) = Pnj=1auj −alj+ 1₃(cj +dj)xj

34

Pada tabel 3.2, untuk upper-bound (batas atas)=0,4, maka: F1(x) = 71−(−11) + 1₂(5 + 100)

0,268

+ 36₋(₋9) + 1₂(5 + 55)

0,332

+ 29₋(₋6) + 1₂(12 + 85)

0,4

= 94,346

F2(x) = 71−(−11) + 1₃(5 + 100)0,268+ 36−(−9) + 1₃(5 + 55)0,332 + 29₋(₋6) + 1

3(12 + 85)

0,4

= 80,08

F1(x) dan F2(x) untuk batas atas berikutnya dicari dengan cara yang sama atau terlihat dalam tabel 3.2.

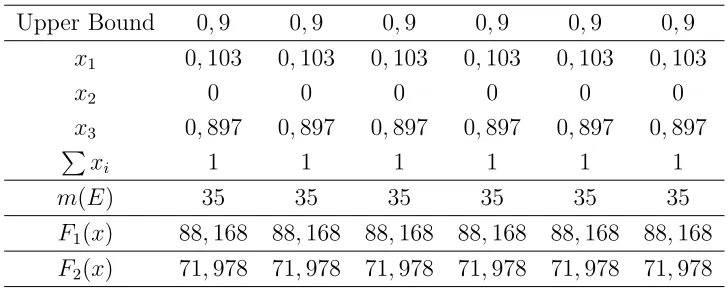
Adapun kalau masalah diatas tidak menggunakan fuzzy maka untukx1,x2, danx3 diambil dari portofolio yang disarankan di tabel 3.1 yaituP3(x) = _{0,103; 0; 0,897_}, sehingga diperoleh F(x) dan F2(x) sebagai berikut:

Tabel 3.3 Portofolio Risiko Downside Tanpa Fuzzy Upper Bound 0,9 0,9 0,9 0,9 0,9 0,9

x1 0,103 0,103 0,103 0,103 0,103 0,103

x2 0 0 0 0 0 0

x3 0,897 0,897 0,897 0,897 0,897 0,897

P

xi 1 1 1 1 1 1

m(E) 35 35 35 35 35 35

F1(x) 88,168 88,168 88,168 88,168 88,168 88,168 F2(x) 71,978 71,978 71,978 71,978 71,978 71,978

BAB 4

KESIMPULAN DAN SARAN

4.1 KESIMPULAN

Sejumlah model pemilihan portofolio menggunakan rata-rata sampel untuk mem-perkirakan return yang diharapkan dari suatu aset yang diberikan. Secara khusus, model mean-variance adalah metode yang dibangun dengan memberikan hasil yang cukup memuaskan. Namun rata-rata sampel tidak selalu menjadi pilihan terbaik untuk menggambarkan satu set data. Pendekatan fuzzy merupakan suatu alternatif yang diambil dalam situasi ini.

Metodologi Fuzzy memungkinkan penggabungan ketidakpastian ke dalam data base dan juga untuk menggabungkan karakteristik subjektif ke dalam model, yang merupakan aspek dasar untuk menetapkan estimasi yang berbeda dari risiko dan keuntungan yang diharapkan.

DAFTAR PUSTAKA

Bawa, V. S., dan Lindenberg E.B., (1997), Capital Market Equilibrium in a Mean-Lower Partial Moment Framework, Journal of Financial Economics, 5, 189-200.

Bermudez J. D., Segura J.V. dan Vercher E., (2005),Fuzzy portofolio optimization under downside risk measures, Centro de Investigacion Operativa, Universi-dad Miguel Hernandez de Elche.

Bilbao, Terol A., Prez-Gladish T, Arenas-Parra M.V., Rodrguez-Ura, (2005),Fuzzy compromise programming for portfolio selection, Applied Mathematics and Computation.doi:10.1016/j.amc.2005.04.003.

Carlsson C., Fuller R., (2001) On possibilistic mean value and variance of fuzzy numbers, Fuzzy Sets and Systems 122, 315-326.

Carlsson C., Fuller R., Majlender P., (2002), A possibilistic approach to selecting portfolios with highest utility score, Fuzzy Sets and Systems 131.2002.13-21. Dubois.D, Prade H., (1980), Systems of linear fuzzy constraints, Fuzzy Sets and

Systems 3 (1980) 37-48.

Dubois D., Prade H., (1987), The mean value of a fuzzy number, Fuzzy Sets and Systems 24 (1987) 279-300.

Fuller R., Majlender P., (2003), On weighted possibilistic mean and variance of fuzzy numbers, Fuzzy Sets and Systems 136 (2003) 363-374.

Inuiguchi M., H. Ichihashi, Tanaka., (1990),Fuzzy Programming-a survey of recent developments, in: R. Slowinski, J. Teghem (ed.), Stochastic versus Fuzzy approaches to multiobjective Mathematical Programming under Uncertainty, Kluwer Academic, Dordretch, 1990, pp 45-68.

Ishibuchi H., Tanaka H. (1990), Multiobjective programming in optimization of the interval objective function, European Journal of Operational Research48 (1990) 219-225.

Jones, C., (1992),A Century of Stock Market Liquidity and Trading Costs, working paper Columbia University.

Konno H., Yamazaki H., (1991)Mean-absolute deviation portfolio optimization mo-del and its applications to Tokyo Stock Market, Management Science 37 (1991) 519-531.

Leon T., Liern V., Marco P., Segura J.V., Vercher E., (2004), A downside risk ap-proach for the portfolio selection problem with fuzzy returns,Fuzzy Economic Review 9 (2004) 61-77.

Leon T., Vercher E, (2004), Solving a class of fuzzy linear programs by using semiinfinite programming techniques,Fuzzy Sets and Systems146 (2004) 235-252.

37

Post, Thierty, Pim Van Vliet, (2002),Downside risk and upside potential, Erasmus Researc Institute of Management(ERIM).

Sengupta A, Pal T.K., (2000), On comparing interval numbers,European Journal of Operational Research 127 (2000) 28-43.

Speranza M.G, (1993), Linear programming model for portfolio optimization, Fi-nance 14 (1993) 107-123.

Sukono, Subanar, Dedi Rosadi, (2008),Model Optimisasi Portofolio dibawah risiko downside , Matematika dan Statistik FMIPA Unair.

Tanaka T., Guo P., (1999), Portfolio selection based on upper and lower exponen-tial possibility distributions, European Journal of Operational Research 114 (1999) 115-126.