PENGEMBANGAN MODEL KALIBRASI
DENGAN PENDEKATAN BAYES
(Kasus Tanaman Obat)
ERFIANI
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI DISERTASI DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa disertasi Pengembangan Model Kalibrasi dengan Pendekatan Bayes (Kasus Tanaman Obat) adalah karya sendiri dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yag diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir disertasi ini.
Bogor, Oktober 2005
ABSTRAK
Erfiani. PENGEMBANGAN MODEL KALIBRASI DENGAN PENDEKATAN BAYES (KASUS TANAMAN OBAT). Dibawah bimbingan Khairil Anwar Notodiputro sebagai ketua, Ahmad Ansori Mattjik, dan Latifah K. Darusman sebagai anggota.
Tanaman obat banyak digunakan di Indonesia, baik dalam bentuk segar atau bentuk olahan sebagai obat tradisional seperti jamu. Produk obat tradisional agar diterima oleh masyarakat dan indusrti harus memiliki jaminan kualitas. Oleh karena itu salah satu hal penting yang harus dilakukan adalah melakukan standarisasi senyawa aktif.
Secara kualitatif dan kuantitatif suatu senyawa aktif dapat diketahui antara lain melalui metode HPLC (High Performance Liquid Chromatography). Pengukuran menggunakan HPLC menghasilkan keluaran konsentrasi senyawa aktif, proses ini memerlukan biaya dan waktu yang cukup besar. Metode kualitatif lain yang juga sering digunakan adalah spektroskopi FTIR (Fourier Transform Infrared). Pengukuran menggunakan FTIR akan menghasilkan pola kromatogram yang tertentu tergantung responnya, proses ini memerlukan biaya dan waktu yang tidak terlalu besar. Penentuan kandungan senyawa aktif tanaman obat perlu dilakukan secara cepat dan akurat. Salah satu pemecahan yang dapat dilakukan adalah mengembangkan model kalibrasi yang menggambarkan hubungan antara konsentrasi senyawa aktif yang dihasilkan oleh HPLC dengan keluaran FTIR. Model ini akan mempercepat waktu proses dan menekan biaya.
Model kalibrasi adalah fungsi yang menghubungkan antara persen transmitan (X) dan konsentrasi senyawa aktif (y). Model kalibrasi lebih baik bila menggunakan spektrum dengan banyak puncak, sehingga disebut model kalibrasi ganda. Model ini merupakan fungsi matematik untuk menduga y yang tidak diketahui menggunakan informasi dari X (Martens & Naes 1989). Pada model kalibrasi ganda ditemukan permasalahan kekolinearan ganda antara peubah bebas (X) serta jumlah pengamatan (n) yang jauh lebih kecil dibandingkan jumlah peubah bebas (p). Pendekatan Bayes dengan penambahan informasi tentang prior dapat mengatasi permasalahan ini.
Model kalibrasi menggunakan pendekatan Bayes berhirarki memiliki sifat statistik yang robust. Model kalibrasi Gingerol dan Kurkumin dengan pendekatan ini memberikan hasil besaran RMSEP yang lebih kecil dibandingkan dengan pendekatan lain. Model Bayes Gingerol dengan memasukkan peubah umur simpan dan menggunakan pendekatan regresi terpenggal menghasilkan RMSEP sebesar 0.0622. Model ini memberikan hasil besaran RMSEP jauh lebih kecil dibandingkan Principal Component Regression (PCR) dengan menggunakan koreksi pencaran pada tahap pre-processing. Model Bayes Kurkumin menggunakan pendekatan regresi terpenggal menghasilkan RMSEP sebesar 0.107.
ABSTRACT
Erfiani. IMPROVEMENT CALIBRATION MODELS WITH BAYESIAN APPROACH (CASES MEDICINAL PLANTS). Advisory committee Khairil Anwar Notodiputro, Ahmad Ansori Mattjik, and Latifah K. Darusman as a co-promotor.
Medicinal plants have been used commonly in Indonesia, either as raw material or as traditional medicine product e.g “jamu”’ standardized extracts and phytopharmaca. To ensure the quality of medicinal plants product to be accepted by community and industry, the standardization of active or market compound is one of important things to be searched and determined.
The active material can be termine qualitatively and quantitatively by HPLC (High Performance Liquid Chromatography). This process produce concentrate of active material and need more time and costly. The other qualitative methods is using by FTIR (Fourier Transform Infra Red). This process produce chromatogram which depend on respons , fastly and cheaper. The contents of active material in medicine herbs need to be determine accurately and faster. To overcome these problem, accurate and cheaper methods are needed. One of the method is calibration model development which shows the relationship between concentration of active material resulted by HPLC and that by FTIR. This model will decrease processing time and cost.
Building calibrations models usually face due to large dimension problem. In the first step needed data reduction. Segmented regression approach is one of method which can be handle this problem. Segmented regression approach is good for reduction percent transmitan resulted by FTIR. This approach has attributes (1) Consist of spread data (2) Solving problem large dimension data (3) Having exact criteria.
independent variables (X) and the number of observations (n) is much less than the number of independent variables (p). Bayesian approaches which add prior information can be utilized to overcome these problems.
Calibration Models using hierarchical Bayes approach have robust statistics. These Models for Gingerol and Kurkumin have smaller RMSEP than others models. Bayes model for Gingerol by using storage time and Segmented Regression for 20 sample produce RMSEP 0.0622. This slightly improves RMSEP produced by PCR using scatter correction as its pre-processing methods. Bayes model for Kurkumin by using Segmented Regression for 40 sample produce RMSEP 0.107
Hak cipta milik Erfiani, tahun 2005 Hak cipta dilindungi
PENGEMBANGAN MODEL KALIBRASI
DENGAN PENDEKATAN BAYES
(Kasus Tanaman Obat)
OLEH :
ERFIANI
Disertasi
sebagai salah satu syarat untuk memperoleh gelar
Doktor pada
Departemen Statistika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Disertasi : Pengembangan Model Kalibrasi dengan Pendekatan Bayes (Kasus Tanaman Obat)
Nama Mahasiswa : Erfiani Nomor Pokok : G326010011
Disetujui Komisi Pembimbing
Dr. Ir. Khairil Anwar Notodiputro, MS Ketua
Prof. Dr. Ir. Ahmad Ansori Mattjik Anggota
Prof. Dr. Ir. Latifah K. Darusman Anggota
Diketahui
Ketua Program Studi Statistika Dekan Sekolah Pascasarjana
Dr. Ir. Budi Susetyo, MS Prof. Dr. Ir. Syafrida Manuwoto, M.Sc
PRAKATA
Alhamdulillah, puji syukur yang sangat dalam penulis sampaikan kepada Illahi Rabbi, atas segala nikmat, rahmat, karunia, pertolongan, dan ridhoNYA yang tidak terhingga yang telah dilimpahkan kepada penulis sehingga penelitian dan penulisan disertasi ini dapat diselesaikan.
Disertasi ini yang berjudul ”PENGEMBANGAN MODEL KALIBRASI DENGAN PENDEKATAN BAYES (KASUS TANAMAN OBAT)” disusun berdasarkan penelitian yang dilakukan di Departemen Statistika Fakultas Matematika dan Ilmu Pengetahuan Alam FMIPA-IPB. Penelitian yang dilakukan penulis merupakan bagian dari payung penelitian Hibah Pasca 2003-2005, yang merupakan kerjasama antara Departemen Statistika dan Biofarmaka, Institut Pertanian Bogor. Payung penelitian tersebut saat ini memasuki tahun ke-tiga, peneliti mengikuti kegiatan penelitian tersebut sejak awal, dan diperkirakan selesai pada semester akhir tahun 2005.
Dengan segala keterbatasan yang ada pada penulis, penulis menyadari masih banyak kekurangan dalam penyusunan disertasi ini. Penulis sangat mengharapkan masukan-masukan guna penyempurnaan dan perbaikan tulisan ini.
Bogor, Oktober 2005
RIWAYAT HIDUP
DAFTAR ISI
Halaman
DAFTAR TABEL xv
DAFTAR GAMBAR xvii
BAB I PENDAHULUAN UMUM
A Latar Belakang ………... 1
B Tujuan Penelitian ………... 4
C Sistematika Disertasi ………... 4 BAB II TINJAUAN PUSTAKA
A Teknik Spektroskopi ………... 8 B Fourier Transform Infrared (FTIR) ………... 8 C High Performance Liquid Chromatography (HPLC)
………
9 D Kandungan Senyawa aktif pada Jahe ... 11 E Kandungan Senyawa aktif pada Temulawak
...
12 F Pentingnya Penentuan Konsentrasi Senyawa Aktif Tanaman
Obat
……… 12
G Model Dasar Kalibrasi ………...… 14
H Pendekatan Bayes ………..…… 16
I Keunggulan Pendekatan Bayes ………..……
17 J Monte Carlo Markov Chain (MCMC)
...
17
BAB III PEMAMPATAN DATA KELUARAN Fourier Transform Infrared (FTIR) MENGGUNAKAN PENDEKATAN REGRESI TERPENGGAL (Segmented Regression)
A Pendahuluan ………. 19
B Sumber Data ………. 20
C Regresi Terpenggal (Segmented Regression) ... 21 D Pendekatan Regresi Terpenggal untuk Pereduksian Data
n<<p DAN TERDAPAT MULTIKOLINIER
A Pendahuluan ………. 27
B Tujuan ……….. 27
C Tinjauan Pustaka ……….. 28
Metode Simulasi ... 28
WinBUGS ... 28
Kriteria Kebaikan Model ... 28
D Bahan dan Metode ……… 29
Tahapan Simulasi Data ……… 30
Tahapan Penyusunan Model Kalibrasi ……….… 32
E Hasil dan Pembahasan ……….. 33
Pendekatan Bayes dengan Model I ... 34
Pendekatan Bayes dengan Model II ... 36
Pendekatan Bayes dengan Model III ... 38
Pendekatan Bayes dengan Model IV ... 39
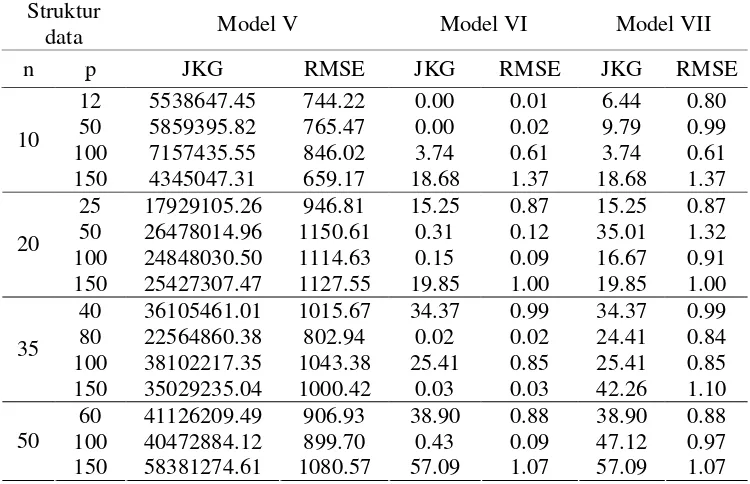
Pendekatan Bayes dengan Model V, VI dan VII ... 40
F Simpulan ... 44
BAB V SIFAT-SIFAT STATISTIK DARI DUGAAN MODEL KALIBRASI DENGAN PENDEKATAN BAYES A Pendahuluan ... 46
B Model Linier Umum Pendekatan Bayes ... 46
C Model Kalibrasi dengan Model Normal Pendekatan Bayes ... 48
D Model Linier Umum Pendekatan Bayes Berhirarki ... 51
E Kuadrat Tengah Galat Penduga Bayes ... 53
F Simpulan ... 55
BAB VI MODEL KALIBRASI GINGEROL DAN KURKUMIN DENGAN MENGGUNAKAN PENDEKATAN BAYES (Studi Kasus Tanaman Temulawak dan Jahe di Daerah Karanganyar, Kulonprogo, Majalengka dan Bogor) A Pendahuluan ... 56
B Tujuan ……….. 56
C Tinjauan Pustaka ……….. 57
Validasi Model ………. 57
Analisis Kesejajaran dengan Pendekatan Uji Ragam ... 58
D Bahan dan Metode ……… 59
E Hasil dan Pembahasan ……….. 65
Eksplorasi Data Gingerol ………. 65
Model Kalibrasi Gingerol ……… 68
Eksplorasi Data Kurkumin ………... 76
Model Kalibrasi Kurkumin ……….. 77
BAB VII PEMBAHASAN UMUM ……… 84
BAB VIII SIMPULAN UMUM ………... 89
LAMPIRAN ……….... ... 91
DAFTAR TABEL
Halaman
1 Daerah identifikasi spektra IR Gingerol ... 9
2 Daerah identifikasi spektra IR Kurkumin ... 9
3 Jumlah titik hasil reduksi ... 25
4 Kombinasi n dan p yang dicobakan ……….. 29
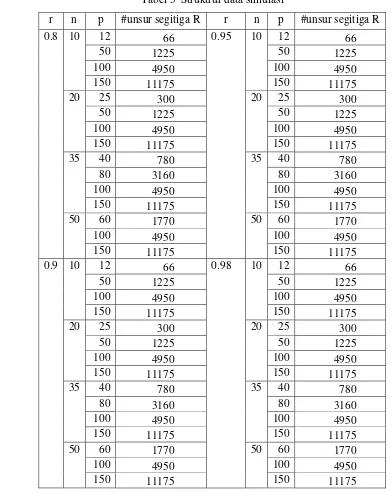
5 Struktur data simulasi ... 31
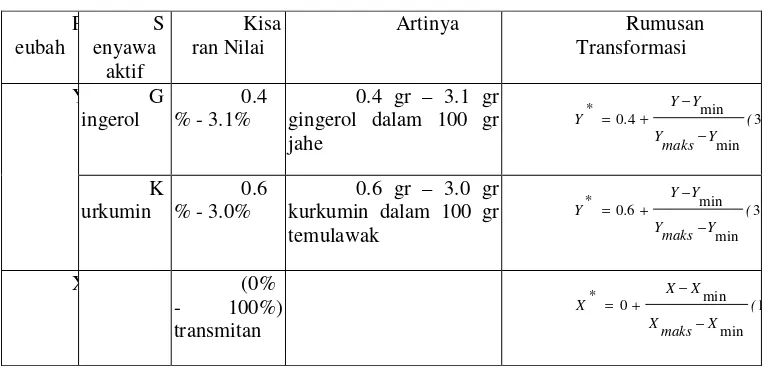
6 Transformasi data Y dan X ………... 32
7 Nilai korelasi antar peubah bebas, n=50, p=100, E(r)=0.1 ... 34
8 Nilai JKG dan RMSE pada berbagai besaran n dan p dengan penentuan nilai awal sembarang ... 40
9 Nilai JKG dan RMSE pada berbagai besaran n dan p menggunakan Model V dengan besaran nilai awal mendekati nilai parameter …... 41
10 Nilai JKG dan RMSE pada berbagai besaran n dan p menggunakan Model V dengan berbagai sebaran prior ……… 42
11 Nilai JKG dan RMSE pada berbagai besaran n dan p menggunakan Model VI dengan berbagai sebaran prior ……….. 42
12 Nilai JKG dan RMSE pada berbagai besaran n dan p menggunakan Model VII dengan berbagai sebaran prior ………. 42
13 Nilai JKG dan RMSE pada Berbagai Besaran n dan p menggunakan Model VI dan VII ……….. 43
14 Jumlah pengamatan rimpang Jahe dan rimpang Temulawak ……… 61
15 Matriks data persentase transmitan keluaran FTIR ... 62
16 Struktur data konsentrasi Gingerol ... 62
17 Rataan dan ragam selisih persentase transmitan Gingerol antar ulangan dalam setiap petani ……… ……….. 66
18 F-hit kesejajaran spektrum Gingerol antar petani dalam daerah yang sama ... 66
20 Konsentrasi Gingerol 20 pengamatan ... 68
21 Jumlah titik persentase transmitan Gingerol hasil reduksi menggunakan pendekatan Regresi Terpenggal ………. 70
22 R2, JKG dan RMSEP model D8, D8k, D8w dan D8kw ……… 72
23 R2, JKG dan RMSE penyusunan model Kalibrasi Gingerol ………. 73
24 Nilai dugaan konsentrasi Gingerol (y-duga) pada validasi model ... 73
25 Rataan dan ragam selisih persentase transmitan Kurkumin antar contoh dalam setiap petani ... 76
26 F-hitung kesejajaran spektrum Kurkumin antar petani dalam daerah yang sama ……….. 77
27 F-hitung kesejajaran spektrum Kurkumin antar daerah ... 77
28 Konsentrasi Kurkumin 16 pengamatan contoh berbagai daerah ... 78
29 Konsentrasi Kurkumin 24 pengamatan hasil percobaan ... 78
30 Jumlah titik persentase transmitan Kurkumin hasil reduksi menggunakan pendekatan Regresi Terpenggal ………. 79
DAFTAR GAMBAR
Halaman
1 Alur metode penyusunan model .………. 3
2 Alur kegiatan penelitian ………... 6 3 Skema keterkaitan hubungan antara topik dalam disertasi ... 7
4 Struktur gingerol pada Jahe ... 11
5 Struktur kurkuminoid pada Temulawak ... 12
6 Ilustrasi Regresi Terpenggal dengan dua buah sekatan ... 21
7 Pemilihan titik pada pendekatan Regresi Terpenggal ... 23
8 Spektrum serbuk Gingerol Kulonprogo ... 25
9 Spektrum serbuk Gingerol Karanganyar ... 25
10 Spektrum serbuk Gingerol sebelum reduksi data ... 26
11 Spektrum serbuk Gingerol sesudah reduksi data ... 26
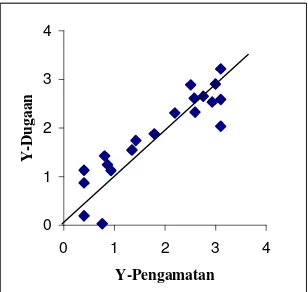
12 Plot antara Y dugaan dan Y pengamatan, n=50, p=150, r=0.7, Nilai awal 100, prior βi ∼ N(0, 0.001) ... 35
13 Plot antara Y dugaan dan Y pengamatan, n=10, p=100, r=0.1, Nilai awal 100, prior βi =1/σ ... 37
14 Model VI, n=10, p=12 ... 43
15 Model VI, n=20, p=100 ... 43
16 Skema penyusunan model kalibrasi ... 64
17 Spektrum serbuk Gingerol untuk 20 contoh ... 65
18 Spektrum serbuk Gingerol Contoh 2 Kulonprogo ... 66
19 Spektrum serbuk Gingerol daerah Jawa Tengah, Majalengka dan Bogor ... 67
20 Spektrum serbuk Gingerol D8 ... 70
22 Spektrum serbuk Gingerol D10 ... 70 23 Spektrum serbuk Gingerol dengan konsentrasi 0.63 ... 71 24 Spektrum serbuk Gingerol 20 contoh setelah dikoreksi pencaran 71 25 Pola JKG pada seluruh model kalibrasi Gingerol ... 75 26 Pola RMSEP pada seluruh model kalibrasi Gingerol ... 75 27 Plot y-duga dan y-(HPLC) Gingerol model D3
...………
75
28 Spektrum serbuk Kurkumin contoh ke-1 daerah Kulonprogo ...
76
29 Spektrum serbuk Kurkumin 40 pengamatan ... 78 30 Spektrum serbuk Kurkumin D8
...
79
31 Spektrum serbuk Kurkumin D9 ...
79
32 Spektrum serbuk Kurkumin D10 ...
80
33 Pola JKG pada seluruh model kalibrasi Kurkumin ... 81 34 Pola RMSEP pada seluruh model kalibrasi Kurkumin ... 82 35 Plot y-duga dan y-(HPLC) Kurkumin model D2 ..………. 82
DAFTAR LAMPIRAN
Halaman 1 Doodle Model I
...
89
2 Doodle Model II ………..… 89
3 Doodle Model III ... 90
4 Doodle Model IV ... 90
5 Doodle Model V ………..………… 91
6 Doodle Model VI ... 91
7 Doodle Model VII ... 92
8 Contoh Program WinBUGS 1.4 Model I ... 93
9 Contoh Program WinBUGS 1.4 Model II ... 94
10 Contoh Program WinBUGS 1.4 Model III ... 95 11 Contoh Program WinBUGS 1.4 Model IV ... 96
12 Contoh Program WinBUGS 1.4 Model V ... 97
13 Contoh Program WinBUGS 1.4 Model VI ... 98
14 Contoh Program WinBUGS 1.4 Model VII ……… ... 99
15 Nilai JKG dan RMSE Model I ... 100
16 Nilai JKG dan RMSE Model II ... 102
17 Nilai JKG dan RMSE Model III ... 104 18 Nilai JKG dan RMSE Model IV
...
BAB I. PENDAHULUAN
A. Latar Belakang
Banyak fenomena yang ada di alam bila diamati dengan seksama ternyata memiliki pola dan perilaku tertentu. Fenomena alam tersebut biasanya dipengaruhi oleh satu atau beberapa kondisi alam atau faktor-faktor lainnya. Sebagai contoh dalam masalah iklim atau cuaca, curah hujan di suatu daerah akan dipengaruhi antara lain oleh temperatur permukaan air laut di sekitarnya, arah mata angin dan tekanan udara. Dalam bidang kesehatan, tinggi badan seorang anak selain disebabkan faktor gizi juga dipengaruhi oleh tinggi badan orang tua, tingkat pendidikan orang tua, penghasilan orang tua dan beberapa faktor lain. Dalam bidang kimia, kandungan senyawa aktif yang dikandung suatu bahan ternyata memiliki pola hubungan dengan panjang gelombang yang dihasilkan bila senyawa aktif tersebut diamati menggunakan alat ukur tertentu. Sehingga bila pola hubungan tersebut diketahui, dapat dilakukan penentuan kandungan senyawa aktif suatu bahan kimia yang belum teridentifikasi. Berdasarkan beberapa contoh kasus tersebut, dapat dibuat suatu gambaran apabila pola hubungan antara peubah dapat diketahui, maka model yang diperoleh dapat digunakan untuk melakukan pendugaan atau perkiraan pada pengamatan lain yang memiliki perilaku sama.
Dalam sebuah model peubah amatan dapat dibedakan menjadi dua, pertama adalah peubah respons yaitu peubah yang dipengaruhi oleh peubah lain, kedua adalah peubah penjelas yaitu peubah yang mempengaruhi peubah lain. Misalkan y adalah peubah respons dan X adalah peubah penjelas, y dapat dipengaruhi oleh satu atau beberapa X dengan banyaknya y yang diamati dapat satu atau beberapa buah. Model hubungan tersebut dapat dirumuskan sebagai berikut:
yi = f(xi,x2, ...,xp) + εi, i=l,2,...,n (1.1) Fungsi f(x) dapat bersifat linier atau non linier. Persamaan (1.1) dapat dituliskan dalam notasi matriks berikut
Y = Xâ + ε
(1.2)
matriks peubah penjelas berukuran nxp, p adalah banyaknya peubah penjelas yang diamati. â adalah matriks koefisien berukuran pxm, sedangkan ε adalah matriks sisaan berukuran nxm.
Bila matriks X’X nonsingular, dengan menggunakan metode kuadrat terkecil, matrik â dapat diperoleh. Sebaliknya bila X’X singular dengan metode kuadrat terkecil tidak akan diperoleh matrik â yang bersifat unik. Dua penyebab X’X singular yaitu:
(1) Adanya kekolinearan ganda yang sempurna antara peubah bebas X
(2) Jumlah pengamatan n, lebih kecil dibandingkan jumlah peubah bebas p (n<p) Kedua kondisi data diatas antara lain banyak dijumpai dalam masalah kalibrasi. Adanya kekolinearan ganda antara peubah bebas X mengakibatkan model dalam keadaan "ill condition" dan menyebabkan galat baku dugaan menjadi sangat besar. Dengan kata lain kekolinearan ini dapat menyebabkan ketelitian (accuracy) dari dugaan parameter sangat rendah (Notodiputro 2003). Permasalahan lain dalam pembentukan model kalibrasi adalah jumlah pengamatan (n) yang jauh lebih kecil dibandingkan jumlah peubah bebas p (n<<p). Kondisi tersebut mengakibatkan matriks X bersifat singular.
Gambar 1. menunjukkan alur metode yang dapat digunakan untuk penyusunan model. Pada pendugaan model kalibrasi apabila terdapat masalah kolinearitas, beberapa metode yang dapat digunakan yaitu metode regresi bertatar, regresi ridge, regresi komponen utama, metode NIPALS (dengan prinsip regresi komponen utama), metode Neural Network Partial Least Square (NNPLS) dan metode Partial Least Square (PLS) (Wold (1984); Martens dan Naes (1989); Qin dan Avoy (1992); Young (1994)). Untuk p>>n beberapa tulisan ilmiah dan metode yang pernah digunakan antara lain regresi stepwise dan regresi linier berganda dengan wavelength, regresi komponen utama, Shrinkage of wavelett coeffisien. Brown (2001) menggunakan Bayesian wavelet regression untuk aplikasi pada permasalahan kalibrasi spektroskopy.
merupakan suatu altematif untuk mengatasi masalah kolinearitas. Hal ini dimungkinkan karena dalam pendekatan ini informasi baru ditambahkan kedalam model dengan cara mengganggap bahwa parameter model berasal dari sebaran tertentu sehingga tidak bersifat deterministik. Sebaran ini dikenal sebagai sebaran prior yang mencerminkan keyakinan kita tentang besarnya parameter tersebut. Berdasarkan kondisi tersebut pendekatan Bayes merupakan salah satu alternatif pendekatan yang dapat digunakan dalam penyusunan model kalibrasi. Pendekatan Bayes dapat mengatasi masalah kolinearitas antar peubah bebas serta besarnya pengamatan yang jauh lebih kecil dari jumlah peubah bebas. Pada pendekatan Bayes hasil yang diperoleh dipengaruhi oleh penentuan sebaran parameter model, sehingga perlu dilakukan kajian tentang sebaran parameter model yang tepat digunakan dalam penyusunan model kalibrasi. Selain itu perlu juga dilakukan kajian tentang sifat statistik dugaan model kalibrasi yang diperoleh melalui pendekatan Bayes.
D A T A n p e n g a m a ta n p p e u b a h b e b a s
p = 1 ?
n < = p ? M o d e l P e u b a h G a n d a
K o lin e a rita s ?
M e to d e P e n a m b a h a n
In fo rm a s i
R e g re s i B a y e s tid a k
tid a k
P e re d u k s ia n P e u b a h B e b a s
?
P e re d u k s ia n P e u b a h B e b a s R e g re s i
P e u b a h T u n g g a l ya
ya ya
P e n d e k a ta n B a ye s ?
R e g re s i P e u b a h G a n d a
tid a k
ya tid a k
ya
B. Tujuan penelitian
Dalam penelitian ini akan dilakukan kajian pengembangan model kalibrasi untuk tanaman obat dengan menggunakan Pendekatan Bayes. Tanaman obat yang akan dikaji adalah jahe dan temulawak. Senyawa aktif yang diamati pada tanaman Jahe adalah Gingerol (5-α Hidroksil-(1-hidroksi-3metoksifenil)-3-dekana), sedangkan pada tanaman Temulawak diamati senyawa aktif Kurkumin (1,7-bis(4-hidroksi-3 metoksipenil)1,6-heptadiena-3,5dione). Kedua tanaman obat tersebut diamati dari beberapa daerah sentra tanaman obat di Jateng (Karanganyar), D.I Yogyakarta (Kulonprogo) dan Jabar (Bogor, majalengka, Sukabumi).
Beberapa tujuan pada penelitian ini, dapat dirumuskan sebagai berikut: 1. Mengkaji pendekatan Bayes secara teori.
2. Melakukan evaluasi pendekatan Bayes menggunakan data empirik maupun data simulasi.
3. Menyusun model yang dapat digunakan untuk penentuan kandungan senyawa aktif gingerol pada tanaman jahe dari beberapa daerah sentra penghasil tanaman obat di propinsi Jawa Tengah, D.I Yogyakarta, dan Jawa Barat. 4. Menyusun model yang dapat digunakan untuk penentuan kandungan senyawa
aktif kurkumin pada tanaman temulawak dari beberapa daerah sentra penghasil tanaman obat di propinsi Jawa Tengah, D.I Yogyakarta, dan Jawa Barat.
C. Sistematika Disertasi
Setiap kajian tentang penyusunan model kalibrasi dituliskan dalam satu bab tertentu. BAB II berisi kajian pustaka aspek kimia dan statistika yang digunakan pada keseluruhan bab. Pada penyusunan model kalibrasi struktur data yang digunakan memiliki dimensi yang sangat besar. Kondisi ini seringkali menimbulkan permasalahan pada tahap analisis data, khususnya berkaitan dengan ketersediaan perangkat keras yang memadai untuk pengolahan data dengan dimensi besar. Dalam BAB III dilakukan kajian pereduksian data keluaran FTIR menggunakan pendekatan Regresi Terpenggal (Segmented Regression). Data contoh yang digunakan adalah data hasil pengukuran Gingerol untuk tanaman jahe yang berasal dari daerah Kulonprogo dan Karanganyar.
Pada penyusunan model kalibrasi dengan pendekatan Bayes, dugaan model yang diperoleh sangat dipengaruhi oleh penetapan sebaran awal parameter model. Oleh karena itu perlu dilakukan kajian tentang sebaran awal parameter yang tepat digunakan untuk penyusunan model kalibrasi. BAB IV berisi tentang kajian penerapan pendekatan Bayes pada data n<<p dan terdapat Kekolinieran ganda. Data yang digunakan adalah data simulasi dengan berbagai kombinasi n dan p (n<<p) dan berbagai struktur korelasi antara peubah bebas. Pendekatan Bayes yang digunakan adalah non hirarki dan hirarki dengan berbagai pemilihan sebaran prior. Hasil akhir yang diperoleh diharapkan dapat menunjukkan Pendekatan Bayes terbaik yang dapat digunakan untuk Model Kalibrasi, yaitu yang bersifat robust, tidak dipengaruhi oleh struktur data dan penentuan prior.
BAB V berisi kajian sifat-sifat statistik penduga Bayes. Pada kajian ini digunakan pendekatan matematis untuk melihat sifat-sifat statistik dari penduga Bayes seperti bias, ragam dan kuadrat tengah galat. Hasil yang diperoleh diharapkan dapat menunjukkan kelebihan penggunaan pendekatan Bayes. Pendekatan yang digunakan adalah pendekatan matematis, dilakukan hanya untuk pendekatan Bayes terbaik yang diperoleh pada BAB IV.
Bayes terbaik yang diperoleh pada BAB IV. Bagian akhir dan merupakan bab penutup dari disertasi ini adalah BAB VII PEMBAHASAN UMUM dan BAB VIII SIMPULAN UMUM.
Alur kegiatan penyusunan model kalibrasi yang dilakukan pada penelitian ini tersaji pada Gambar 2. Keterkaitan antara bab dalam disertasi ini dan hubungan antar masing-masing topik penelitian disajikan pada Gambar 3.
S tu d i L itera tu r
P e n g e m b an g a n M o d e l
S im u la si
M o d e l m em u a sk a n ? P e n a rik an c o n to h
P e ra n c a n g a n P erc o b a a n
P e n g u k u ran R e sp o n s
A n alisis K im ia
P e n g u m p u lan D ata F T IR P e n g u m p u lan D ata H P L C
P e n y u s u n a n M o d e l
m em u a sk a n ?
M o d e l K a lib ra si b elu m
ya
y
a
b elu m n d a n p
S tru k tu r X
S e b a ra n (p rio r d an y )
BAB II. TINJAUAN PUSTAKA
A. TeknikSpektroskopi
Berbagai teknik spektroskopi banyak digunakan dalam analisis kimia biologis, antara lain: spektroskopi UV-VIS, spektroskopi absorpsi atom, spektroskopi infra merah, spektroskopi fluorensi, spektroskopi NMR, dan spektroskopi massa (Nur & Adijuwana 1989).
Dalam melakukan teknik analisis dengan spektroskopi, preparasi contoh merupakan hal yang penting dan adakalanya sulit serta memerlukan waktu yang lama. Preparasi contoh harus dilakukan sesuai dengan tujuan analisis, apakah analisis unsur, analisis protein atau analisis asam amino. Untuk analisis unsur, biasanya sampel didestruksi dalam suatu larutan buffer pada PH tertentu, dan untuk analisis asam amino contoh dihidrolisis misalnya hidrolisis asam kemudian hidrolisatnya setelah ditambah pereaksi tertentu kemudian ditentukan konsentrasinya.
B. Fourier Transform Infrared (FTIR)
FTIR merupakan salah satu teknik spektroskopi infra merah. Pada spektroskopi infra merah, spektrum infra merah terletak pada daerah dengan panjang gelombang dari 0.78 sampai dengan 1000 µm atau bilangan gelombang dari 12800 sampai 1 cm-1. Dilihat dari segi aplikasi dan instrumentasi spektrum infra merah dibagi kedalam tiga jenis radiasi yaitu infra merah dekat (bilangan gelombang 12800-4000 cm-1), infra merah pertengahan (bilangan gelombang 4000-200 cm-1), dan infra merah jauh (bilangan gelombang 200-10 cm-1) (Nur & Adijuwana 1989), FTIR termasuk dalam kategori radiasi infra merah pertengahan (bilangan gelombang 4000-200 cm-1).
dapat menyatakan apakah kedua senyawa tersebut identik atau tidak. Pelacakan tersebut lazim dikenal dengan bentuk sidik jari (Finger Print) dari dua spektrum inframerah. Jika puncak spectrum inframerah kedua senyawa tepat sama maka dalam banyak hal dua senyawa tersebut adalah identik (Sostrohamidjoyo 1990).
Salah satu kegunaan penting dari spektrum infra merah adalah memberikan keterangan tentang gugus fungsi pada suatu molekul. Gugus fungsi yang dihasilkan dapat dibedakan antara daerah identifikasi dan daerah sidik jari. Serapan setiap tipe akan mencerminkan gugus fungsi dan hanya diperoleh dalam bagian-bagian kecil tertentu dari daerah vibrasi inframerah. Kisaran serapan yang kecil dapat digunakan untuk menentukan setiap tipe ikatan. Tabel 1. dan Tabel 2. menyajikan daerah identifikasi untuk gingerol dan kurkumin (Socrates 1994).
Tabel 1 Daerah identifikasi spektra IR Gingerol
Jenis vibrasi Bilangan
gelombang cm-1
intensitas
Ikatan hidrogen O-H 3550-3230 m-s
C-H rentangan asimetri ; CH3-Ar 2935-2925 m-s
Aromatik -C=C- 1625-1590 vs
α-β-keton takjenuh 1700-1660 vs
R-O-Ar 1310-1210
1050-1010
m m C-H ikatan bidang luar
Vinil R- CH=CH2-
990-980 910-230
m s C-H ikatan bidang luar
o-subsitusi benzen
770-735 710-690
Tabel 2. Daerah identifikasi spektra IR Kurkumin No Jenis vibrasi Bilangan
Gelombang cm-1
intensitas
1 Ikatan hidrogen OH 3600-3300 m-s
2 C-H Alkana 3000-2850 s
3 Aromatik -C=C- rentangan
1660-1450 s
4 R-O-Ar 1300-1000 m
5 C=O keton 1820-1660 vs
6 Sidik jari 900-700 s
Keterangan: (s) kuat; (m) medium; (vs) sangat kuat
C. High Performance Liquid Chromatography (HPLC)
Kromatografi adalah suatu metode pemisahan komponen-komponen dari suatu campuran, komponen-komponen tersebut akan terdistribusi diantara dua fase. Salah satu fase dibuat diam dan dinamakan fase diam atau fase stasioner, fase lainnya disebut fase gerak atau fase mobil yang bergerak diantara celah-celah atau pada permukaan fase stasioner. Pergerakan fase mobil ini mengakibatkan pergerakan diferensial dari komponen-komponen contoh (Nur & Adijuwana 1989). Metode pemisahan ini memerlukan waktu sangat singkat dan lebih efektif dibandingkan dengan pemisahan lain. Fase diam pada kromatografi dapat berupa cair atau padatan sedangkan fase gerak dapat berupa cair atau gas. Berdasarkan jenis fasenya kromatografi dapat digolongkan menjadi empat jenis yaitu: cair-padatan, gas-cair-padatan, cair-cair dan gas-cair.
Kromatografi cair adalah semua metode kromatografi yang menggunakan cairan sebagai fase mobil. Kromatografi cair meliputi metode kromatografi sederhana dan kromatografi modern. HPLC adalah salah satu metode kromatografi yang termasuk kromatografi cair modern. HPLC adalah kromatografi yang menggunakan cairan sebagai fasa gerak dan sebagai fasa diam dapat berupa suatu padatan atau senyawa tertentu yang terikat secara kimia dengan padatan pendukungnya.
sehingga tidak mampu melewati kolom dan sampel tidak tahan pada suhu tinggi sehingga akan mengalami dekomposisi pada kondisi pemisahan. HPLC dapat mengatasi permasalahan tersebut, karena HPLC mampu memisahkan senyawa yang tidak mudah menguap dan stabil pada suhu tinggi. Selain itu berbagai macam fase diam dan fase gerak dapat digunakan pada HPLC yang memungkinkan metode ini memisahkan berbagai jenis senyawa.
HPLC pada dasarnya adalah suatu kromatografi kolom yang menggunakan kolom yang terbuat dari bahan kemasan, maka untuk mendapatkan laju alir yang memadai, digunakan tekanan sampai 5000 lb/inci atau sekitar 2000 kg/cm. Teknik pemisahan HPLC dilakukan dengan menginjeksikan sedikit sampel yang berbentuk cairan ke dalam aliran cairan (fase mobil/fase gerak) yang berjalan melalui kolom yang berisi partikel dari suatu fase stasioner. Pemisahan campuran kedalam komponennya tergantung pada tingkat retensi masing-masing komponen di dalam kolom. Kecenderungan suatu komponen ditahan di dalam kolom ditentukan oleh partisinya diantara cairan fase mobil dan fase stasioner.
HPLC digunakan terutama untuk golongan senyawa tak atsiri, misalnya terpenoid tinggi, segala jenis fenol, alkaloid, lipid dan gula. HPLC berhasil paling baik untuk senyawa yang dapat dideteksi pada daerah spektrum UV atau spektrum sinar tampak.
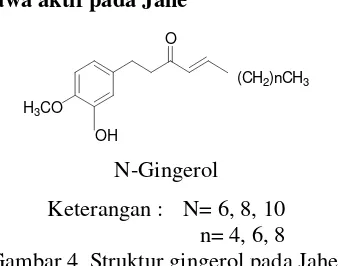
D. Kandungan Senyawa aktif pada Jahe
H3CO
O
OH
(CH2)nCH3
N-Gingerol Keterangan : N= 6, 8, 10
[image:30.612.236.405.87.220.2]n= 4, 6, 8 Gambar 4 Struktur gingerol pada Jahe.
Komponen yang terkandung dalam jahe atara lain air 80.9%; protein 2.3%; lemak 0.9%; mineral 1-2%; serat 2.4% dan karbohidrat 12.3%. Kandungan kimia ini berbeda-beda tergantung dari faktor genetik dan lingkungan tumbuh yang meliputi iklim, ketinggian, cuaca, jenis tanah, pemupukan dan pengolahan pasca panen. Menurut Young et al (2002) rizoma jahe mengandung dua bagian utama yaitu minyak volatil yang memberikan aroma dan gingerol sebagai pembawa rasa pedas. Stuktur gingerol dapat dilihat pada Gambar 4 ( Chan et al 1986)
E. Kandungan Senyawa Aktif pada Temulawak
Menurut Sinambela (1985), komposisi rimpang temulawak dapat dibagi menjadi dua fraksi utama yaitu zat warna kurkuminoid dan minyak atsiri. Warna kekuningan temulawak disebabkan adanya kurkuminoid. Kandungan utama kurkuminoid terdiri dari senyawa kurkumin, desmetoksikurkumin dan bis-desmetoksikurkumin. Rimpang temulawak segar, selain terdiri dari senyawa kurkuminoid dan minyak atsiri juga mengandung lemak, protein, selulosa, pati, dan mineral. Kadar masing-masing zat tersebut tergantung pada umur rimpang yang dipanen juga dipengaruhi letak dan ketinggian tempat temulawak berada. Struktur kurkuminoid dapat dilihat pada Gambar 5
Keterangan:
R1 R2
-OCH3 -OCH3 = kurkumin
-OCH3 -H = desmetoksikurkumin
OH O
R2
OH HO
-H -H = bis-desmetoksikurkumin
Gambar 5 Struktur kurkuminoid pada Temulawak.
F. Pentingnya Penentuan Konsentrasi Senyawa Aktif Tanaman Obat
Indonesia merupakan salah satu negara yang memiliki potensi hayati cukup besar dalam tanaman obat. Di Indonesia, tanaman obat telah lama digunakan oleh masyarakat dan industri dalam pembuatan jamu. Pada akhir-akhir ini, perusahaan farmasi pun telah memanfaatkan tanaman obat tradisional pada produk-produknya. Penggunaannya yang semakin meluas, mengakibatkan kualitas senyawa baku tanaman obat menjadi fokus perhatian, terutama untuk kalangan jamu dan industri farmasi, untuk menjamin agar produknya dapat bersaing dan diterima oleh masyarakat. Ditambah lagi dengan adanya persyaratan ISO9000 dan ISO14000, kualitas bahan baku tanaman obat harus menjadi ukuran baku dalam jaminan kualitas suatu produk industri jamu dan farmasi (Dhanutirto 2001).
Khasiat tanaman obat tidak terlepas dari kandungan kimiawinya, sedangkan kandungan kimia dari masing-masing tanaman obat bisa berbeda disetiap wilayah atau negara karena tergantung pada iklim, ketinggian, jenis tanah, perlakuan terhadap tanaman dan cara pengolahannya seperti infus, dekok, tingtur dan sebagainya (Dhanutirto 2001). Di dalam proses industri kita mengenal adanya senyawa aktif dan senyawa penciri. Senyawa penciri dapat aktif atau tidak aktif, tetapi harus bersifat stabil selama proses.
Oleh karena obat tradisional, baik dalam bentuk simplisia tunggal maupun ramuan, sebagian besar penggunaan dan kegunaannya masih berdasarkan pengalaman maka data yang meliputi kegunaan, dosis dan efek samping sebagian besar belum memiliki landasan ilmiah yang kuat. Demikian pula tentang kandungan senyawa aktif dan penciri dalam tanaman obat belum mendapat perhatian yang baik, padahal pengetahuan tentang kandungan senyawa aktif dan penciri suatu tanaman obat dapat memberi arahan tentang kegunaan dan cara penggunaan tanaman obat tersebut (Hadiwigeno 1993).Penentuan konsentrasi secara kimia dilakukan melalui penentuan kandungan senyawa aktif atau senyawa penciri. Proses penentuan konsentrasi ini dilakukan melalui proses yang panjang meliputi penghancuran bahan, pelarutan, dan pengukuran dengan HPLC dan FTIR. Proses ini memerlukan waktu dan biaya yang relatif mahal. Alternatif cara penentuan lain yang dapat dilakukan adalah dengan mengembangkan model kalibrasi yang menyatakan hubungan antara kandungan senyawa aktif atau penciri hasil pengukuran HPLC dengan data hasil pengukuran FTIR (absorban).
Ketersediaan model ini akan menghemat waktu dan biaya. Proses penentuan kandungan senyawa aktif atau penciri dapat dilakukan melalui sampel secara sederhana dan cepat. Selain itu penentuan ini dapat dilakukan berdasarkan serbuk kasar sehingga tidak perlu proses yang panjang. Hal ini akan menunjang industri dan perdagangan serbuk kasar tanaman obat.
G. Model Dasar Kalibrasi
diketahui. Dalam proses pendugaannya, biasanya parameter ini dianggap konstan dan jika seandainya berbagai respon instrumen tadi tidak bersifat kolinear maka dapat dihasilkan penduga yang optimum.
Secara umum kalibrasi menggunakan suatu fungsi matematik dengan data empirik dan pengetahuan untuk menduga informasi pada y yang tidak diketahui berdasarkan informasi pada X yang tersedia (Martens & Naes 1989). Dalam bidang kimia, model kalibrasi pada spektroskopi merupakan suatu fungsi hubungan antara absorban (X) pada panjang gelombang yang dihasilkan oleh spektrometer dengan konsentrasi (y) larutan unsur atau senyawa yang akan dianalisis (Nur & Adijuwana 1989). Dengan kalibrasi, konsentrasi larutan contoh dapat diketahui berdasarkan absorbannya.
Pendugaan model kalibrasi dapat menggunakan model peubah tunggal atau peubah ganda tergantung pada spektrometer yang digunakan. Spektrometer UV-VIS menghasilkan spektrum yang berbentuk satu puncak absorban, sehingga model kalibrasinya adalah model peubah tunggal. Spektrometer NIR atau FTIR menghasilkan spektrum dengan banyak puncak absorban, sehingga akan terbentuk suatu model kalibrasi peubah ganda. Model kalibrasi suatu senyawa lebih tepat menggunakan spektrum dengan banyak puncak daripada satu puncak absorban (Nur & Adijuwana 1989). Pada pendugaan model kalibrasi ganda sering timbul masalah kolinearitas di antara peubah absorban (Naes 1985), sehingga metode baku seperti Metode Kuadrat Terkecil tidak dapat digunakan. Permasalahan lain yang dijumpai adalah jumlah pengamatan yang relatif kecil dibandingkan jumlah peubah bebas yang ada. Hal ini umumnya dikarenakan permasalahan biaya, waktu atau keterbatasan kemampuan untuk melakukan pengamatan dengan ukuran besar.
penduga model kalibrasi yang lebih baik. Dengan data yang sama hasil metode PLS juga lebih baik dari metode NIPALS (Wigena & Aunuddin, 1997).
du Plessis dan van der Merwe (1995) telah mengkaji metode Bayes dan membandingkannya dengan metode klasik Brown (1982) secara simulasi dan menerapkannya untuk pendugaan kandungan protein dalam gandum. Hasil kajian menunjukkan bahwa metode Bayes lebih baik dari metode Brown. Sebagai analisis pendahuluan dengan data yang sama Wigena dan Aunuddin (1998) menggunakan metode PLS. Hasil analisis menunjukkan bahwa metode Bayes yang dikemukakan oleh du Plessis dan van der Merwe (1995) relatif lebih baik daripada metode PLS.
West (2003) menggunakan pendekatan Bayes untuk menganalisa data spectral dengan p=300 dan n=39. Hasil yang diperoleh menunjukkan tingkat ketepatan pendugaan yang sangat baik dengan R2 yang dihasilkan sebesar 99.995%.
Rahayu (2003), Melakukan pendugaan parameter regresi menggunakan pendekatan Bayes dengan dua model. Model pertama mengasumsikan parameter regresi β saling bebas, sedangkan model kedua mengasumsikan parameter regresi
β berkorelasi. Data yang digunakan adalah data Naes (1985) untuk menduga kadar lemak pada ikan Trout. Hasil pendugaan yang diperoleh menunjukkan bahwa model kedua menghasilkan Jumlah Kuadrat Galat yang lebih kecil daripada model pertama.
Notodiputro (2003), membandingkan antara Regresi Kuadrat Terkecil (RKTP), regresi atas Koefisien Fourier (RKF), Jaringan Syaraf Tiruan (JST) dan pendekatan Bayes. Keempat metode tersebut dicobakan pada data simulasi dan data dari Naes (1985). Kriteria kebaikan model yang diperoleh dilihat dari koefisien Jumlah Kuadrat Galat (JKG) dan R2. Hasil yang diperoleh menunjukkan pendekatan Bayes dan JST lebih unggul dari RKTP, sedangkan performans RKF sangat tergantung pada jenis data yang dihadapi.
H. Pendekatan Bayes
model dengan cara mengganggap bahwa parameter model berasal dari sebaran tertentu sehingga tidak bersifat deterministik. Sebaran ini dikenal sebagai sebaran prior yang mencerminkan keyakinan kita tentang besamya parameter tersebut. Jika parameter model yang ingin diduga adalah β dengan y sebagai peubah acaknya, maka parameter β dipilih yang memaksimumkan fungsi kepekatan bersyarat π(β| y). Fungsi kepekatan bersyarat ini disebut fungsi posterior.
Secara umum, jika h(β) adalah sebaran prior dari β dan statistik w= u(yl, y2,...,yp) maka sebaran posteriornya adalah:
π(β| w)=
) (
) | ( ) ( ) (
) , (
w g
w f h w g
w
f β β β
=
Dalam hal ini f(w|β) adalah fungsi kemungkinan dari w, f(β,w)adalah fungsi kepekatan bersama dari β dan w. Nilai β dipilih sedemikian sehingga diperoleh
π(β|w). Pemilihan h(β) yang tepat akan dapat memperbaiki fungsi f(w|β) sehingga ruang bagi nilai optimum β menjadi terbatas.
Sebaran prior dapat diperoleh melalui dua pendekatan informative prior atau non informative prior. Pada informative prior, parameter ditetapkan memiliki sebaran tertentu dengan kisaran nilai yang dapat diterima. Sedangkan pada non informative prior, tidak ada informasi tambahan tentang parameter. Pada non informative prior apabila prior bernilai konstan maka penduga parameter dengan metode Bayes akan sama dengan penduga dengan metode kemungkinan maksimum.
Metode lain untuk menentukan sebaran prior yang cukup sederhana dan melibatkan data yang ada adalah dengan metode prior sekawan (Conjugate prior). Prior sekawan ditentukan dengan memeriksa fungsi kemungkinan L(β/y) = f(y/β), dan memilih sebagai keluarga sekawan adalah kelompok sebaran yang sama dengan fungsi kemungkinannya. Sebagai contoh bila f(y/β) menyebar normal maka L(β/y) juga akan mengikuti sebaran normal.
I. Keunggulan Pendekatan Bayes
• Dapat digunakan untuk parameter dengan berbagai sebaran peluang
• Dapat digunakan untuk model parameter numerik yang perilakunya berubah-ubah
• Mengatasi salah satu kelemahan pendugaan parameter secara konvensional, yaitu penurunan tingkat efisiensi dengan meningkatnya jumlah parameter yang akan diduga.
• Pada metoda konvensional parameter ditetapkan pada kisaran nilai yang dapat diterima, sedangkan pada pendekatan Bayes penentuan prior dapat diperoleh berdasarkan informasi dari data itu sendiri.
• Dapat dikembangkan suatu model hirarki.
J. Monte carlo Markov Chain (MCMC)
Salah satu metode optimasi yang banyak digunakan dalam metode Bayes adalah metode simulasi Monte Carlo Markov Chain (MCMC). Metode simulasi MCMC sudah ada kurang lebih 50 tahun, dalam empat dekade terakhir metode ini banyak digunakan pada bidang fisika. Sejak tahun 1980 perkembangan metode ini sangat cepat pada pengembangan konsep peluang dan bidang Statistika. Metode simulasi MCMC adalah suatu metode numerik untuk memperoleh fungsi kepekatan bersama. Pendugaan parameter menggunakan MCMC merupakan pendekatan numerik dari fungsi sebaran peluang yang dibangkitkan dari model parameter. Rataan, ragam dan momen lainnya dari parameter dapat diperoleh dari pendekatan numerik fungsi sebaran peluang (Roy 1998). Cheng (1999), menyatakan bahwa pada metode MCMC penghitungan untuk memperoleh P(β/y) diperoleh dengan menyekat kurva menjadi beberapa bagian, karena sulit menghitung
∫
β(
P(y|β)pP(β))
dβ.nW B W n
Rˆ = ( −1) +
(2.2)
W adalah within sequence variance dan B adalah between sequence variance. Konvergensi diperoleh bila Rˆ <1.2.
Pendekatan Bayes dengan menggunakan MCMC merupakan suatu pendekatan yang cukup menjanjikan. Namun demikian diperlukan kehati-hatian dalam pemilihan sebaran prior. West (2001) menggunakan pendekatan Bayes dan MCMC untuk penyusunan model kalibrasi pada p>>n, hasil yang diperoleh sangat baik dengan R2 sebesar 99.995%.
BAB III
PEMAMPATAN DATA KELUARAN Fourier Tansform Infrared (FTIR) MENGGUNAKAN PENDEKATAN REGRESI TERPENGGAL
(Segmented Regression)
A. Pendahuluan
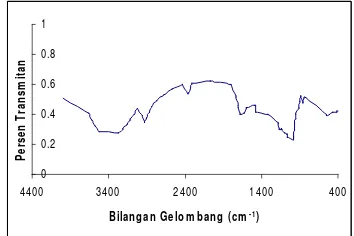
Spektrum keluaran FTIR merupakan data dalam dua dimensi yang merupakan data berpasangan antara persen transmitan (Y) dan bilangan gelombang (X). Data spektrum yang dihasilkan oleh FTIR tersebut adalah data kuantitatif yang umumnya berdimensi besar. Sehingga bila ingin dilakukan analisis data akan dijumpai permasalahan dalam penggunaan paket program pengolah data dan kemampuan hardware yang dimiliki. Oleh karena itu diperlukan suatu metode pendekatan untuk mereduksi data tanpa menghilangkan pola spektrum awal. Bila pendekatan ini diperoleh akan mempermudah untuk melakukan analisis statistika selanjutnya, seperti dalam hal pengelompokan senyawa dan penentuan senyawa yang dianggap memberikan hasil respons terbaik.
aktif gingerol dan kurkumin. Hasil yang diperoleh menunjukkan metode pendekatan ini cukup baik dilakukan untuk mereduksi dimensi data. Penggunaan metode pendekatan titik balik dapat mereduksi dimensi vektor titik persentase transmitan dari 1869 menjadi 27.
Teknik pereduksian data keluaran Near Infrared (NIR), yang diterapkan pada Regresi Komponen Utama, dicobakan pada Erfiani et al. (2004b). Hasil yang diperoleh menunjukkan terdapat banyak metode eksploratif yang relatif sederhana namun memberikan ketepatan pendugaan model yang tinggi. Beberapa metode pendekatan yang digunakan yaitu penyekatan peubah menjadi kelompok-kelompok peubah dengan jumlah peubah pada setiap kelompok-kelompok sama. Jarak lompatan antara kelompok dicobakan pada beberapa jarak lompatan yaitu 2, 5, 10, 20, 30, 50, 75, dan 80. Dari setiap kelompok peubah diambil satu peubah baru yang merupakan fungsi dari peubah-peubah di dalam kelompok tersebut. Fungsi yang digunakan adalah nilai rataan, maksimum, dan peubah pada ujung sekatan. Hasil yang diperoleh menunjukkan bahwa penggunaan fungsi peubah pada ujung masing-masing sekatan dengan berbagai jarak lompatan lebih mudah dan sederhana dilakukan dari dua fungsi lainnya. Penggunaan jarak lompatan kurang dari 10 dapat menggunakan salah satu dari ketiga macam fungsi pereduksian banyak peubah, tetapi penggunaan jarak lompatan lebih dari 10 lebih baik jika menggunakan fungsi nilai rataan pada masing-masing sekatan atau peubah pada ujung masing-masing sekatan. Jarak lompatan tergantung banyaknya peubah bebas. Semakin banyak peubah bebas, maka jarak lompatan masing-masing kelompok sekatan dapat semakin besar. Besaran nilai R2 dan R2(adj) yang dihasilkan oleh regresi dengan menggunakan data hasil reduksi dengan pendekatan lompatan dan Regresi Komponen Utama relatif sama. Oleh karena itu metode pendekatan ini cukup baik penggunaannya dalam mereduksi data keluaran Infrared.
Pada tulisan ini akan dilakukan kajian penerapan pendekatan Regresi Terpenggal (Segmented Regression) untuk pereduksian data keluaran FTIR.
B. Sumber Data
C. Regresi Terpenggal (Segmented Regression)
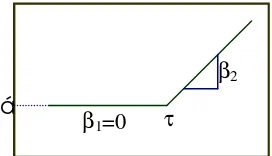
Jika (Xi, Yi), i=1, 2, ..., n adalah pasangan data yang saling bebas dengan Y adalah peubah terikat dan X adalah peubah bebas. Pada Model Regresi Terpenggal wilayah X dibagi menjadi dua atau lebih interval atau sekatan dengan masing-masing sekatan memiliki bentuk fungsi tersendiri Titik akhir dari setiap sekatan disebut changepoints atau breakpoints (Küchenhoff & Wellisch 1997). Ilustrasi sederhana dari model Regresi Terpenggal dengan dua buah sekatan tersaji pada Gambar 6, τ adalah breakpoints.
[image:40.612.265.401.255.333.2]
Gambar 6 Ilustrasi Regresi Terpenggal dengan dua buah sekatan.
Jika fungsi regresinya kontinu, model linear dengan dua sekatan atau satu breakpoints, memiliki persamaan regresi sebagai berikut:
E( Y | X=x ) = G( á + â1(x-ô)- + â2(x-ô)+ ) (3.1)
− +
=exp ( ) ( , )
) , |
( ξ
ξ ϑ ϑ ξ
ϑ y b c y
y
f (3.2)
Keterangan: t+ = maks (0,t) t- = min (0,t)
G adalah fungsi penghubung Natural, ϑ = á + â1(x-ô)- + â2(x-ô)+ ô adalah parameter breakpoints
ξ adalah nuisance parameter )
(
' ϑ
b = E( Y | X=x )
Vektor parameter yang akan diduga adalah θ = (á, â1, â2, ô). Perilaku θˆ , dapat diperoleh dengan menggunakan beberapa regularity assumptions berikut: (Fahrmeir & Kaufmann 1985)
τ β1=0
(1) Jika (Xi, Yi), i=1, 2, ..., n adalah contoh yang saling bebas dari model persamaan (3.1) dan (3.2) dengan fungsi penghubung natural, maka penciri model persamaan (3.1) akan dipenuhi bila â1 ≠â2.
(2) Momen pertama dan momen kedua dari X ada atau E(X) dan E(X2) ada. (3) (i) E(G(Y, á + â1(x-ô)- + â2(x-ô)+), ada. G adalah fungsi log-kemungkinan. (ii) E(S(Y, X, θ)2) ada. S adalah score function.
Berdasarkan (1) dan (3) diperoleh perilaku θˆ sebagai berikut: (a) θˆ bersifat konsisten. Plim θˆ = θ untuk n →∞.
(b) θˆ adalah asymptotic solution dari score equation. 0
) ˆ , , (
1 2 1
→
∑
= −
P n
i
i i X Y S
n θ , untuk n →∞.
D. Pendekatan Regresi Terpenggal untuk Pereduksian Data Keluaran FTIR Setiap pola spektrum terdiri dari titik yang menunjukkan hubungan antara bilangan gelombang (cm-1) dengan persentase transmittan yang dihasilkan oleh FTIR. Banyaknya titik yang dihasilkan mengakibatkan dimensi yang dihasilkan oleh setiap spektrum sangat besar. Setiap pola spektrum yang dapat disekat menjadi beberapa sekatan garis, dengan setiap sekatan memilliki pola spektrum tertentu. Berdasarkan pola yang diperoleh pada setiap sekatan, dapat dilakukan pereduksian jumlah titik dalam partisi tersebut. Sebagai contoh pada suatu partisi yang terdiri dari 20 titik dan membentuk suatu pola garis lurus, maka sesungguhnya cukup hanya diambil sedikitnya dua titik saja dari partisi tersebut. Sehingga jumlah data yang semula 20 titik dapat direduksi menjadi dua titik. Pendekatan ini memiliki konsep yang relatif sama dengan Regresi Terpenggal, hanya tujuan dari pendekatan ini bukan untuk menduga besaran vektor parameter
Algoritma pereduksian data menggunakan pendekatan Regresi Terpenggal, yaitu:
1. Tetapkan 2 0
R , yaitu besaran koefisien determinasi standar untuk persamaan garis lurus pada semua sekatan.
2. Tetapkan i = 1, j = 2, dan k =1
i = titik ujung awal sekatan, j = titik ujung akhir sekatan, k = sekatan 3. Ambil dua pasang titik pertama (Xi, Yi) dan (Xj, Yj) sebagai titik awal. 4. Buat regresi linier Yˆ = á + âX. dan hitung nilai R2.
5. Bila R2 • 2 0
R , j = j + 1, gabungkan pasangan data (Xj, Yj) dan kembali kerjakan 4.
6. Bila R2 < R02,
a. Catat nilai pasangan data pertama (Xi, Yi) dan data terakhir (Xj, Yj) sebagai titik ujung awal dan titik ujung akhir sekatan ke-k.
[image:42.612.233.427.380.499.2]b. Hitung i=j+1, j=j+2, dan k=k+1. Jika j < n kembali ke 4, selainnya stop.
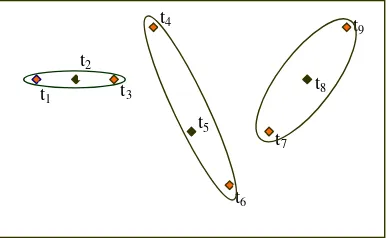
Gambar 7 Pemilihan titik pada pendekatan Regresi Terpenggal.
Ilustrasi pendekatan Regresi Terpenggal untuk pereduksian data tersaji pada Gambar 7. Pada Gambar 7 terdapat sembilan titik yang membentuk tiga daerah sekatan. Daerah sekatan pertama terdiri dari tiga titik t1, t2 dan t3, daerah sekatan kedua terdiri dari titik t4, t5 dan t6, sedangkan daerah sekatan ketiga terdiri dari titik t7, t8 dan t9. Pada setiap sekatan diambil dua titik yang merupakan titik ujung setiap sekatan, sehingga jumlah titik hasil pereduksian sebanyak enam yaitu t1, t3, t4, t6, t7 dan t9. Bila jumlah sekatan yang dihasilkan adalah k, maka jumlah titik yang digunakan sebanyak 2k.
t2
t3
t4
t5
t6
t7
t8
t9
Keuntungan menggunakan pendekatan Regresi Terpenggal untuk mereduksi data keluaran FTIR, yaitu:
1. Pereduksian data dilakukan dengan tidak menghilangkan pola sebaran data. Hal ini diperlukan karena untuk setiap senyawa aktif akan memiliki daerah identifikasi tertentu. Pada daerah identifikasi tersebut, yaitu daerah bilangan gelombang tertentu akan ditemukan lonjakan-lonjakan nilai persentase transmitan. Hasil pereduksian data menggunakan pendekatan Regresi Terpenggal ini, akan berupa pasangan titik data bilangan gelombang dan persentase transmitan dengan pola spektrum yang sama dengan pola spektrum data awal.
2. Menanggulangi permasalahan dimensi data yang besar. Pada beberapa perangkat lunak dimensi data yang besar kadang menimbulkan permasalahan tersendiri dalam pengolahan data, misalkan dalam hal waktu proses. Oleh karena itu diawal proses diperlukan tahapan pereduksian data. Pereduksian data menggunakan pendekatan Regresi Terpenggal, merupakan salah satu alternatip metode yang cukup mudah dan efisien penggunaannya. Hal ini terlihat dari algoritma yang sederhana sehingga tidak ditemukan masalah dalam hal komputasi, dalam pengadaan perangkat lunak maupun perangkat keras.
3. Pengukuran kebaikan hasil menggunakan acuan yang pasti. Pada pendekatan ini digunakan besaran koefisien determinasi (R02) untuk menentukan banyaknya daerah sekatan bilangan gelombang. Semakin besar acuan nilai
2 0
R yang digunakan, akan semakin banyak jumlah sekatan dan jumlah titik hasil reduksi yang dihasilkan.
E. Studi Kasus Penerapan Pendekatan Regresi Terpengga
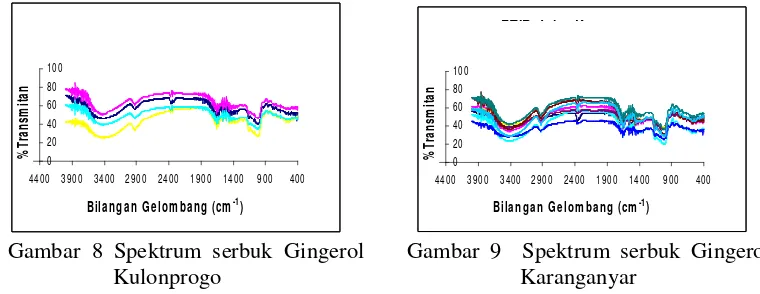
daerah identifikasi. Pada Spektrum IR Gingerol, pada daerah bilangan gelombang 3550-3230 cm-1 akan terdapat ikatan hidrogen O-H, pada daerah bilangan gelombang 2935-2925 cm-1 terdapat C-H rentangan asimetri; CH3-Ar, dst (Socratesg 1994). Gambar 8 dan Gambar 9. memperjelas kondisi tersebut, bahwa untuk senyawa aktif tertentu meskipun berasal dari sumber berbeda (pada kasus ini berasal dari daerah dan teknik budidaya yang berbeda), akan memiliki pola spektrum yang sama. Oleh karena itu untuk tahap pereduksian data selanjutnya, hanya akan diambil salah satu spektrum saja.
Gambar 8 Spektrum serbuk Gingerol
Kulonprogo
Gambar 9 Spektrum serbuk Gingerol Karanganyar
Kriteria penentuan jumlah titik pada setiap sekatan yaitu berdasarkan besaran koefisien determinasi (R2) yang diperoleh dengan menggunakan regresi linier sederhana. Jumlah titik yang berada dalam satu sekatan akan ditentukan oleh besaran R2 yang ditetapkan ( 2
0
R ). Semakin tinggi nilai penetapan 2 0
[image:44.612.129.509.237.384.2]R , akan semakin sedikit jumlah titik yang dihasilkan untuk setiap partisi. Pada penelitian ini pereduksian data dicobakan pada beberapa besaran R02 yaitu 0.95, 0.98, 0.99 dan 0.999. Hasil pereduksian jumlah pasangan data persentase transmitan dan bilangan gelombang dengan empat kriteria R02yang digunakan tertera pada Tabel 3.
Tabel 3 Jumlah titik hasil reduksi
2 0
R Jumlah Titik Hasil Persentase Data Tereduksi
0.95 14 99 %
0.98 26 99 %
0.99 46 98 %
0.999 86 90 %
FTIR Jahe-K aranganyar
0 20 40 60 80 100 400 900 1400 1900 2400 2900 3400 3900 4400
Bila nga n G e lom ba ng (cm-1)
% T ra n sm it an
FTIR Jahe-K ulonprogo
0 20 40 60 80 100 400 900 1400 1900 2400 2900 3400 3900 4400
Bila nga n G e lom ba ng (cm-1)
Penerapan pendekatan Regresi Terpenggal untuk data diatas, ternyata memberikan hasil yang cukup baik. Pada pendekatan ini hanya akan diambil dua titik dari sekumpulan titik yang membentuk persamaan regresi linier. Pada R02 sebesar 0.999, jumlah titik awal sebanyak 1868 ternyata dapat direduksi menjadi 86 titik tanpa merubah pola titik yang dihasilkan seperti tampak pada Gambar 10 dan Gambar 11.
0 0.2 0.4 0.6 0.8 1
400 1400
2400 3400
4400
Bilangan Gelombang (cm-1)
P
e
rse
n
T
ra
n
s
m
it
a
n
0 0.2 0.4 0.6 0.8 1
400 1400
2400 3400
4400
Bilan g an Ge lo m b an g (cm-1)
P
e
rs
en Tr
a
ns
m
it
an
[image:45.612.328.505.204.322.2]Gambar 10 Spektrum serbuk Gingerol sebelum reduksi data Gambar 11 Spektrum serbuk Gingerol
F. Simpulan
Beberapa kelebihan pendekatan Regresi Terpenggal untuk pereduksian data adalah tetap mempertahankan pola data awal, mudah dalam pengerjaannya dan tidak menghadapi kendala dalam penyediaan perangkat lunak maupun perangkat keras.
BAB IV
KAJIAN SIMULASI: PENDEKATAN BAYES PADA DATA
n<<p DAN TERDAPAT KEKOLINEARAN-GANDA
A. Pendahuluan
Pada pendugaan model kalibrasi peubah ganda, sering timbul masalah kekolinieran ganda. Kekolinieran ganda ditandai dengan adanya korelasi antar peubah-peubah bebasnya. Solusi untuk melakukan pendugaan parameter dengan data berkorelasi diantaranya dapat digunakan Analisis Komponen Utama, Regresi Kuadrat Terkecil Parsial, Regresi atas Koefisien Fourier, Jaringan Syaraf Tiruan dan Pendekatan Bayes (Notodiputro 2003).
Menurut penelitian yang telah dilakukan sebelumnya dengan membandingkan metode yang disebutkan di atas ternyata pendekatan Bayes mempunyai hasil yang lebih baik dibanding dengan metode lain dalam pendugaan parameter (du Plessis (1995); Wigena dan Aunuddin (1998); West (2003); Rahayu (2003); Notodiputro (2003)). Hal ini dikarenakan dalam pendekatan Bayes ditambahkan informasi tambahan terhadap model yang dibangun, informasi tambahan ini disebut dengan informasi prior. Penelitian yang dilakukan oleh Rahayu (2003) menunjukkan pemilihan penggunaan sebaran prior sangat berpengaruh terhadap hasil dugaan. Oleh karena itu diperlukan ketepatan pemilihan prior agar model mempunyai tingkat keakuratan yang tinggi.
B. Tujuan
C. Tinjauan Pustaka Metode Simulasi
Simulasi adalah suatu model matematika yang dapat menerangkan perilaku suatu sistem dari waktu ke waktu. Metode simulasi dapat memberikan efisiensi dan kemudahan dalam menganalisis suatu model matematika. Simulasi berbasis komputer saat ini lebih banyak diterapkan dalam penelitian-penelitian dibandingkan dengan simulasi secara manual (Watson & Blackstone 1989).
WinBUGS
WinBUGS merupakan suatu perangkat lunak yang berbasis Windows yang digunakan untuk analisis statistika dengan metode bayes. Software ini menggunakan Markov Chain Monte Carlo (MCMC) untuk menemukan sebaran posteriornya (Spiegelhater et al 2002). Pada penggunaan program WinBUGS perlu dituliskan nilai awal untuk parameter, terutama parameter ragam. Hal ini dikarenakan software WinBUGS dapat memberikan nilai default negatif untuk nilai awal parameter ragamnya (Anonim, 2004).
Kriteria Kebaikan Model
Menurut Mattjik dan Sumertajaya (2002) kriteria untuk melihat keterandalan model antara lain adalah Jumlah Kuadrat Galat (JKG) dan Koefisien Determinasi (R2). Model yang baik mempunyai JKG yang kecil dan R2 yang besar. Rumus untuk mencari R2 adalah sebagai berikut:
JKT JKG JKT
JKR
R2 = =1− di mana :
Ukuran kebaikan model lainnya yang dapat digunakan antara lain adalah akar kuadrat tengah galat (RMSE = Root Mean Square Error). Model dikatakan baik jika memiliki nilai RMSE yang kecil (Naes et al. 2002). Rumusan RMSE dapat dituliskan dalam persamaan berikut:
RMSE = MSE = E
(
yˆ−y)
2
MSE adalah Mean Square Error (Kuadrat Tengah Galat / KTG).
D. Bahan dan Metode
Data yang digunakan dalam penelitian ini merupakan data simulasi atau data bangkitan. Data hasil bangkitan berupa data peubah Y dan peubah X, dimana peubah Y merupakan fungsi dari peubah X. Fungsi peubah Y adalah sebagai berikut:
Y = f(X1, X2, X3, …, Xp)
Dalam penelitian ini, pembangkitan nilai data Y mengikuti interval data senyawa gingerol pada jahe dengan kisaran nilai antara 0.4 sampai dengan 3.1. Sedangkan peubah X yang dibangkitkan, nilainya mengikuti kisaran nilai %transmitan. Nilai peubah X berkisar antara 0 sampai dengan 100 dan peubah-peubah X dalam matriks data X tersebut dikondisikan saling berkorelasi. Korelasi yang dicobakan adalah 0.1, 0.3, 0.5, 0.7, 0.8, 0.9, 0.95, 0.98. Sedangkan kombinasi jumlah pengamatan (n) dan jumlah peubah (p) dalam matriks data X tersaji pada Tabel 4.
Tabel 4 Kombinasi n dan p yang dicobakan n
10 20 35 50
Alur kerja yang dilakukan dalam penelitian ini adalah sebagai berikut: Tahapan Simulasi Data
1. Pembangkitan ( , 2,..., )
1 *
p nxp x x x
X = ~ N(µ, Σ), dengan korelasi antar peubah tinggi dengan langkah-langkah sebagai berikut:
1.1.Membangkitkan matriks korelasi R
= pp p p p p r r r r r r r r r R ... ... ... ... ... ... ... 2 1 2 22 21 1 12 11
Matriks R dicobakan pada beberapa kondisi yaitu: rij ∼ Uniform (0.75, 0.85)
rij ∼ Uniform (0.85, 0.95) rij ∼ Uniform (0.95, 1)
rij ∼ Uniform (0.96, 1), i = 1, 2, ....p dan j = 1, 2, ....p
Untuk setiap gugus r, dibangkitkan data berdasarkan p maks (p=150 buah). Jumlah data yang dibangkitkan untuk setiap gugus: 0.5(p-1)p = 11.175 buah
1.2. Membangkitkan matriks Xnxp = (x1, x2, ..., xp)∼ N(µ, Iσ2), untuk berbagai
nilai n dan p seperti tertera pada tabel 4 (contoh yang digunakan µ=0 dan
σ2
=9). Struktur data hasil tahap 1.1 dan 1.2 tersaji pada tabel 5.
1.3. Menyusun Matriks peragam Σ dengan menggunakan hasil yang diperoleh pada 1.1. dan 1.2. σij2 =rijσiσj,
1.4. Dengan menggunakan SVD dekomposisi Σ menjadi L’L
Σ = ADF, Apxn, A' A = I
D = Diagonal (d1, d2, ..., dn), d1≥d2≥ ...≥dn≥0
Fnxn,F' F=FF' =I = AD1D1F, D = D12
= L' L Catatan : Untuk matriks yang simetrik A = F.
1.5. Hitung :X*=XS*L, S*=Diag
p σ σ σ 1 ,..., 1 , 1 2 1
2.1. Tetapkan β 2.2. Hitung E(y) = Xβ
2.3. Bangkitkan ε (contoh yang digunakan ε∼ N(0, σ=2)) 2.4. Hitung nilai pengamatan y = E(y)+ ε
[image:51.612.107.499.209.701.2]3. Transformasi Y dan X sehingga interval data yang digunakan sesuai dengan sesungguhnya. Bentuk transformasi data tersaji pada Tabel 6.
Tabel 5 Struktrur data simulasi
r n p #unsur segitiga R r n p #unsur segitiga R
12 66 12 66
50 1225 50 1225
100 4950 100 4950
10
150 11175
10
150 11175
25 300 25 300
50 1225 50 1225
100 4950 100 4950
20
150 11175
20
150 11175
40 780 40 780
80 3160 80 3160
100 4950 100 4950
35
150 11175
35
150 11175
60 1770 60 1770
100 4950 100 4950
0.8
50
150 11175
0.95
50
150 11175
12 66 12 66
50 1225 50 1225
100 4950 100 4950
10
150 11175
10
150 11175
25 300 25 300
50 1225 50 1225
100 4950 100 4950
20
150 11175
20
150 11175
40 780 40 780
80 3160 80 3160
100 4950 100 4950
35
150 11175
35
150 11175
60 1770 60 1770
100 4950 100 4950
0.9
50
150 11175
0.98
50
Tabel 6 Transformasi data Y dan X P eubah S enyawa aktif Kisa ran Nilai
Artinya Rumusan
Transformasi
G ingerol
0.4 % - 3.1%
0.4 gr – 3.1 gr gingerol dalam 100 gr jahe ( Y maks Y Y Y . *
Y 3.
min min 4 0 − − + = Y K urkumin 0.6 % - 3.0%
0.6 gr – 3.0 gr kurkumin dalam 100 gr temulawak ( Y maks Y Y Y . * Y 3 min min 6 0 − − + = X (0% - 100%) transmitan ( X maks X X X * X 100 min min 0 − − + =
Tahapan Penyusunan Model Kalibrasi
Model kalibrasi dibangun dengan pendekatan Bayes non hirarki dan Bayes hirarki. Pendekatan Bayes non hirarki yang dicobakan yaitu:
y ∼ N(Xβ , σ2),
y adalah vektor berukuran nx1, X adalah matriks berukuran nxp dan β adalah vektor berukuran px1, beberapa sebaran prior β yang dicobakan dirumuskan dalam model dibawah ini:
a. Model I : Prior β ~ N (0, 0.001) b. Model II : Prior β = 1/ó
c. Model III : Prior β ~ Gamma (2,5) d. Model IV : Prior β ~ Eksponensial (1)
Pada model I, III dan IV βi, i = 1, 2, ..., p bersifat saling bebas dan identik. Pada keseluruhan model dicobakan beberapa kemungkinan nilai awal bagi ragam (σ2) yaitu : 1, 10, 50, 100.
Y ∼ N(Xβ , σ2)
Beberapa sebaran prior β yang dicobakan dirumuskan dalam model dibawah ini:
a. Model V : β berhirarki dan σ konstan b. Model VI : β berhirarki dan σ acak c. Model VII : β berhirarki, σ berhirarki.
Pada perilaku β berhirarki, dicobakan berbagai kemungkinan kombinasi sebaran prior dan hiperprior, yaitu sebaran Normal, Eksponensial dan Gamma. Sehingga akan dapat diketahui model pendekatan yang relatif tidak dipengaruhi oleh penetapan sebaran awal β atau bersifat robust. Pemilihan bentuk sebaran prior dan hiperprior ditentukan secara subyektif, dengan anggapan keseluruhan sebaran yang dipilih telah mewakili bentuk sebaran keluarga eksponensial. Pada keseluruhan model juga dicobakan berbagai kondisi penetapan nilai awal σ2.
Ketepatan model yang dihasilkan dilihat dari beberapa kriteria yaitu besaran nilai Jumlah Kuadrat Galat (JKG) dan Root Mean Square Error (RMSE). Perangkat lunak yang digunakan adalah Winbugs14.
E. Hasil dan Pembahasan
Setiap matriks data X bangkitan mempunyai nilai korelasi antar peubah yang tertentu. Tabel 7 merupakan contoh yang menunjukkan korelasi antar peubah bebas dimana korelasi yang dicobakan adalah 0.1 dengan kombinasi jumlah pengamatan (n) 50 dan jumlah pebah bebas (p) 150. Pada tabel 7 hanya ditampilkan sebagian saja korelasi antar peubah, hasil dari pembangkitan matriks data X.
Tabel 7 Nilai korelasi antar peubah bebas.n=50, p=100, E(r)=0.1
x1 x2 x3 x4 x5 x6
x2
-0.310
x3
-0.040
-0.243
x4
-0.052
0.042
0.033 x5
0.248
-0.044
-0.067
0.020 x6
0.042
0.113 0.060
-0.016
0.181
….. ….. ….. ….. ….. ….. …..
x150
-0.108
0.006 0.031
-0.157
0.197 0.092
Pendekatan Bayes dengan Model I
Model I merupakan model pendekatan bayes dengan menggunakan prior
βi~N(0, 0.001). Tabel Lampiran 1 merupakan hasil dari pengolahan data dengan model I. Pada matriks data 10x12 dapat dilihat bahwa peningkatan nilai awal menyebabkan nilai JKG dan nilai RMSE menurun. Sebagai contoh data pada korelasi 0.1 untuk n=10 dan p=12, pada nilai awal 1 nilai JKG sebesar 6.114 dan nilai RMSE sebesar 0.782. Saat nilai awal sebesar 100 nilai JKG mnurun menjadi 0.061 dan nilai RMSE menurun menjadi sebesar 0.078. Jika dilihat lebih jauh perubahan nilai JKG dan RMSE pada nilai awal 1 ke nilai awal 10 lebih besar dibandingkan perubahan nilai JKG dan RMSE dari nilai awal 50 ke 100.
Bila dilihat dari nilai korelasi yang dicobakan pada matriks data 10x12 perubahan nilai JKG dan RMSE untuk setiap kenaikan korelasi sangatlah kecil. Pada nilai awal 100 untuk semua nilai korelasi, nilai RMSE masih cenderung sama.
0 1 2 3 1
2 3
y p e n g a ma ta n
y
d
u
g
a
a
n
Secara umum pada n=10 dengan p=100 dan p=150 masih memiliki sifat yang sama dengan p=12 dan p=50. Peningkatan nilai awal menyebabkan nilai JKG dan RMSE menurun. Persentase perubahan nilai JKG dan RMSE dari nilai awal 1 ke nilai awal 10 lebih besar daripada perubahan nilai JKG dan RMSE pada nilai awal 50 ke nilai awal 100. Nilai ketepatan model pada p=100 dan p=150 cenderung menurun pada saat nilai korelasi datanya tinggi.
Penambahan jumlah peubah bebas pada n=10 dengan berbagai kombinasi besaran korelasi yang dicobakan, belum menunjukkan suatu pola tertentu. Hal ini dapat dilihat pada matriks data dengan korelasi yang sama, nilai JKG dan RMSE mengalami peningkatan saat jumlah peubah bebasnya bertambah menjadi 50, tetapi nilai JKG dan RMSE kembali menurun saat jumlah peubah bebasnya 100 dan kemudian meningkat kembali saat jumlah peubah bebasnya 150.
Perilaku JKG dan RMSE untuk ukuran matriks data yang lebih besar masih sama dengan matriks data sebelumnya. Nilai JKG dan RMSE menurun seiring peningkatan nilai awal. Perubahan nilai JKG dan RMSE pada nilai awal 1 ke 10 lebih besar dari pada perubahan nilai JKG dan RMSE pada nilai awal 50 ke 100.
Gambar 12 Plot antara Y dugaan dan Y pengamatan,n=50, p=150, r=0.7, Nilai awal 100 prior βi ~ N (0, 0.001).
Secara umum nilai ketepatan model I untuk semua ukuran matriks sangat tinggi saat nilai awalnya 100. Gambar 12 merupa