! ! ! " " # $ %
& ' ( ) # * ( * # # & & *
& * # * * # ! # & * & + ' &
# & # * * # ! ! # * * ! ! * # # & ,
& & ' ( ) # # - #
# ! ." # & # ! ! / # &
& * # & / * * ! ! * # & # # ! !
( ! ! # * ! & # # ! ! * &
& # ! ! & # # * # ! & " * *0 1
* * * ! 0 & # ! ! !
# ! # & ' ( ) # ." # ! # # & #
# ! ! & + & # # * # * * *
2 * ! * +3 454556 # * ! * ! & # 7 / 58
# & / ! 0 # & ! # " * *0 & & # +
" ( 9 & ' ( ) , & # ! ! , #
! " #$ $
% & '()
&*
* !
*
*
*/
&
*
& #
#
9
!
9
*
#/
9 %:3;5<=>4
/
9
9
"
&
,
'
/
,
9 :6?5;3<::66;;<:;;:
1
@
* 9
!
!
,
!
!
,
" *
# ,
,
9 :6?6;6:<:66>;<:;;:
,
,
*
* # # " # @ & & # <3 :64> * !
# ! * # , # & * / A # $ # ' / *
* / * & # # * # * # B # @ & & #
:666 # & # * * & * # << # @ &
& # <;;< # & # # * # < # @ &
/ # * * & * & # <;;5 # <;;5, & * * ( * # * !
* *0 * # * * , #
! # <;;? & * # # * *0 & * * *
! * & ! $
& & # # # , & * 7 * ! & * * *
* *0 C / * ! # - * # & # <;;? # <;;> #
<;;4, & * ! & 7 * ! ! # & # & &
* *0 ! * 33 * # C & & * *0 !
35 & # <;;4 * & # * * & * *
" & # <;;6+<;:; " & & # & * #
# */ & * & # '1 * * & ,
, , , # + / * / # & # * * 0
* * * * # & & # ! # ', ! * , * ! ,
* & / / * * * D ! * # /
# E ! E " /
& * * */ * / * # & * *0 # &
* & # & * , A * #
, *
& * * & ! / & * # & ! / , *& * , #
& / ! ! , * & * ( & ! / * ,
# / & # 9
: & " * # # ! * ! & ! ! # & ! !
/ ! 0 # * / & # & *
< # * & * * * # / ! 7
= * 7 & * , / , , 1 /, , *,
# , # , # , # $# * ! #
/
3 ! , / , " 1 , # ! 1 / * # & * & *
/ * & # # # & *
5 1 + ' * 9 $ 0 , , , ! , # F * & * !
# * / # !
? + * 3< * ! * /
> + & * / * ! # & *
4 & / # ! * # * ! & * * & *
, <;:;
+ #
A1 1 $@
-A1 %
-A1 @ )
$ @
@ :
1 :
1 1 "
' ( ) & ' ( ) :
<
." =
" * =
$1 $
3
# 5
@ $
* 5
# >
"$ @
" * & 4
6
A1 1 " 6
+ #
: " * ' ( ) , + , # ." & # ! 7 "
" % & # % ! 1 5
< " * ' ( ) , + , # ." , , dan "
% & # % ! 1 ?
= " * ' ( ) , + , # ." , , dan
" % & # % ! 1 ?
3 " * ' ( ) , + , # ." , , dan "
% & # % ! 1 ?
5 " * ' ( ) , + , # ." dan " % &
# % ! # >
? 1 ! * " * *0 1 3= >
> & + & # " 1 3= 4
+ #
: * # & * % & # % ! 3
< * # # / % & / # * # ! 5
= )& " * *0 1 3= & " * >
+ #
: / ) + ::
< / ) ." :<
= / ) " * & * " # % & # % !
! :=
3 / ) " * # % & / # * #
% ! :5
5 " * ' ( ) , + , # ." & * " # % & #
% ! ! :>
? " * ' ( ) , + , # ." # % & / # *
# % ! :4
1
Uji nonparametrik telah mendapat perhatian di tahun tahun terakhir ini karena beberapa kelebihan yang dimilikinya dibanding uji parametrik. Beberapa kelebihan tersebut adalah perhitungan uji nonparametrik relatif sederhana sehingga dapat dikerjakan dengan cepat, dapat menggunakan data dengan skala ordinal, dan menggunakan lebih sedikit asumsi dibandingkan uji parametrik padanannya.
Uji jumlah peringkat Wilcoxon adalah suatu uji nonparametrik yang membandingkan dua grup dan telah menjadi prosedur standar diantara para statistikawan. Uji jumlah peringkat Wilcoxon menggabungkan observasi dari kedua grup, memeringkatkan gabungan observasi tersebut, lalu menghitung jumlah peringkat berdasarkan observasi dari salah satu grup. Asumsi umum yang digunakan dalam uji jumlah peringkat Wilcoxon adalah semua observasi dalam penelitian saling bebas. Walaupun demikian, dalam banyak situasi ada observasi observasi yang berkorelasi sehingga membentuk gerombol. Contoh dari data bergerombol adalah pengukuran tekanan darah secara berulang dari seseorang, respon dari grup anak binatang yang baru lahir dari percobaan yamg menggunakan tikus, atau berat tubuh dari saudara kandung (Datta dan Satten 2005).
Xiong, Krushkal, dan Boerwinkle (1998) telah memperkenalkan suatu uji yang digunakan dalam data loci yang berbentuk gerombol. Uji ini diperkenalkan sebelum Datta dan Satten memperkenalkan ujinya. Untuk selanjutnya dalam makalah ini, uji yang diperkenalkan Xiong et al. (1998) akan disebut uji XKB.
Datta dan Satten memperkenalkan uji jumlah peringkat untuk membandingkan dua grup ketika data berbentuk gerombol. Untuk selanjutnya dalam makalah ini, uji jumlah peringkat Wilcoxon akan disebut uji Wilcoxon dan uji jumlah peringkatuntuk data gerombol akan disebut uji Datta Satten. Datta dan Satten menyertakan pengaruh gerombol dalam perhitungan statistik uji yang digunakan dalam uji Datta Satten sehingga diharapkan mampu mengatasi masalah yang terdapat dalam data bergerombol. Untuk melihat perbedaan hasil yang dikeluarkan dari uji Wilcoxon, uji XKB, dan uji Datta Satten perlu dilakukan suatu studi simulasi sehingga dapat dibandingkan hasil ketiga uji tersebut.
Sebagai contoh, pada penelitian ini juga akan diakukan pengujian pada data sekunder berupa IPK mahasiswa TPB IPB angkatan 43. Pada pengujian ini grup yang dibandingkan adalah mahasiswa perempuan dan laki laki. Penggerombolan terbentuk berdasarkan kelas dimana ada korelasi kuat antara mahasiswa dalam satu kelas yang bisa diakibatkan karena sering terjadinya interaksi antara mahasiswa dalam satu kelas serta lingkungan pembelajaran yang sama.
Tujuan dari penelitian ini adalah:
1. Mengkaji metode uji jumlah peringkat untuk data bergerombol (uji Datta Satten). 2. Membandingkan hasil dari uji Wilcoxon,
uji XKB, dan uji Datta Satten pada data bergerombol.
3. Menerapkan uji Datta Satten dengan membandingkan IPK mahasiswa perempuan dan laki laki pada data IPK TPB IPB angkatan 43.
! "
Uji Wilcoxon adalah salah satu uji nonparametrik. Uji parametrik padanan dari uji Wilcoxon adalah uji t. Uji Wilcoxon digunakan untuk mengetahui apakah ada perbedaan antara dua populasi yang ingin diuji. Data yang dipakai dalam uji ini berjumlah observasi dimana m
adalah jumlah amatan pada sampel X(0) dengan
X(0) beranggotakan X(0)1,….,X(0)m dan n adalah jumlah amatan pada sampel X(1) dengan X(1) beranggotakan X(1)1,….,X(1)n dimana X(0)l adalah observasi ke l dari grup 0 dan X(1)l adalah observasi ke l dari grup 1.
# #
Asumsi yang dipakai dalam uji Wilcoxon adalah (Wolfe 1973):
1. Model yang dipakai adalah:
Xi = ei, i=1,…,m; dan
Yj = em+j + , j = 1,…,n,
dimana X dan Y merupakan peubah yang dapat dicari, em+1,…,em+n adalah peubah acak yang tidak dapat dicari, dan adalah selang yang tidak diketahui karena perlakuan.
2
3. Setiap e berasal dari populasi kontinu yang sama.
$ # #
Hipotesis yang dipakai dalam uji Wilcoxon adalah (Daniel 1990):
dimana adalah jumlah peringkat contoh dari grup 1. Pemeringkatan ini dilakukan dengan menggabungkan kedua contoh terlebih dahulu.
% $ #
Proses pengambilan keputusan bergantung kepada hipotesis awal yang dipakai.
a) Ketika menguji hipotesis awal a, tolak ketika nilai W yang didapat lebih dari
c) Ketika menguji hipotesis awal c, tolak ketika nilai W yang didapat kurang dari atau sama dengan & # $
! ! '.
&
Uji Datta Satten digunakan untuk membandingkan dua grup pada data yang bergerombol. Data bergerombol yang dimaksud bukan data yang digerombolkan dengan analisis gerombol melainkan digerombolkan berdasarkan peubah yang telah ditentukan. Asumsi asumsi yang digunakan pada uji ini sama dengan asumsi asumsi pada uji jumlah peringkat Wilcoxon, hanya saja tidak terdapat asumsi kebebasan pada data yang diamati, sehingga asumsinya adalah:
1. Setiap contoh dipilih secara acak dari populasi yang diwakilkannya,
2. Peubah awal dari observasi adalah peubah acak kontinu.
#
Notasi yang dipakai adalah sebagai berikut:
1. M adalah banyak gerombol,
2. ni merupakan banyaknya observasi pada Datta Satten adalah observasi dari kedua grup mengikuti sebaran yang sama, dengan kata
3
dimana persamaan yang digunakan untuk menghitung ( dan ? ( adalah sebagai
Untuk kepentingan simulasi dan analisis telah dibuat syntax uji Datta Satten dua arah dalam bahasa R. Syntax tersebut dapat dilihat pada Lampiran 1.
(
Uji XKB diperkenalkan oleh M. M. Xiong, J. Krushkal, dan E. Boerwinkle (1998). Uji ini adalah pengembangan dari uji TDT yang telah ada sebelumnya. XKB menggunakan statistik uji TDT yang dapat dihitung menggunakan
adalah jumlah anggota grup 1, adalah jumlah anggota grup 0.
Seperti uji lain yang menggunakan distribusi F dalam pengambilan keputusannya, dalam uji XKB hanya terdapat hipotesis dua
Untuk kepentingan simulasi dan analisis telah dibuat syntax uji XKB dua arah dalam bahasa R. Syntax tersebut dapat dilihat pada Lampiran 2.
# "
Kendall & Stuart (1973) menyatakan bahwa untuk menguji suatu hipotesis yang berbasis contoh acak diperlukan pembagian ruang contoh (W) menjadi dua daerah. Jika contoh yang teramati x jatuh pada salah satu daerah ini, katakan w, maka hipotesis akan ditolak; jika x jatuh pada daerah komplemennya, W)w, maka hipotesis harus diterima. W)w dikenal sebagai daerah penerimaan dan w dikenal sebagai daerah kritik dari suatu uji.
Jika sebaran peluang dari pengamatan dibawah hipotesis yang diuji (H0) diketahui, nilai w dapat ditentukan. Jika H0 diketahui benar, peluang untuk menolak H0 sama dengan nilai α, dapat ditulis sebagai berikut:
0,1 g 2 /
Nilai α disebut juga sebagai ukuran dari suatu uji atau juga tingkat nyata (level of
significance), merupakan kesalah tipe I yang
yang mungkin dilakukan. Sedangkan kesalahan tipe II disebut sebagai β merupakan fungsi dari H1 (hipotesis alternatif), yaitu:
h 0,1 g $ 2 /
Peluang komplemen dari h yang juga merupakan fungsi dari H1 disebut kuasa uji
(power of test), yaitu # $ h 0,1 g 2 /
Jika kuasa pengujian rendah maka kemungkinan besar percobaan yang dilakukan memberikan kesimpulan yang salah.
4
) *
!
Bahan yang digunakan dalam penelitian ini adalah data simulasi dan data sekunder berupa IPK mahasiswa TPB IPB angkatan 43 dengan grup yang dibandingkan adalah mahasiswa perempuan dan laki laki.
Model umum dari uji Datta Satten adalah
i adalah nilai intersep j adalah pengaruh grup
)(* adalah grup pada observasi kek dan gerombol kei.
k adalah besar pengaruh gerombol i adalah pembobot peubah kej
m( adalah peubah kej yang berpengaruh terhadap observasi dalam gerombol ke i. p(* adalah pengaruh acak.
Sebagai perbandingan dengan model umum, berikut ini adalah penjelasan peubah yang digunakan dalam uji Datta Sattern untuk data sekunder IPK mahasiswa TPB IPB angkatan 43:
+(* adalah IPK mahasiswa kek pada kelasi.
i adalah nilai intersep
j adalah pengaruh jenis kelamin
)(* adalah jenis kelamin mahasiswa kek
dan kelasi.
k adalah besar pengaruh kelas i adalah pembobot peubah kej
m( adalah peubah kej yang berpengaruh pada mahasiswa kelas i.
p(* adalah pengaruh acak.
Uji Datta Satten hanya menggunakan peubah +(* (IPK mahasiswa kek pada kelas
i) dan )(* (jenis kelamin mahasiswa kek dan kelasi). Dalam data sekunder terdapat data nama kelas yang berformat tulisan sehingga harus diubah terlebih dahulu menjadi data berformat angka agar dapat digunakan dalam uji Datta Satten. Selain itu terdapat juga data jenis kelamin yang berformat tulisan sehingga harus diubah menjadi data berformat angka yang bernilai 0 dan 1.
Data simulasi dalam penelitian ini dibangkitkan menggunakan perangkat lunak R versi 2.9.1. Data simulasi tersebut dibangkitkan menggunakan nilai intersep nol dan hanya menggunakan dua peubah (m( dan m(J) yang berpengaruh pada gerombol kei. Dengan kondisi demikian, model data simulasi yang digunakan dapat dituliskan sebagai
γ adalah besar pengaruh grup,
)(* adalah grup dari observasi kek dan gerombol kei,
k adalah besar pengaruh gerombol, m( dan m(J adalah peubah peubah yang menyebar tertentu dalam gerombol kei
yang berpengaruh terhadap observasi dalam gerombol kei,
p(* adalah pengaruh acak yang menyebar tertentu.
Dalam penentuan grup, pembangkitan data dibagi menjadi dua berdasarkan proporsi kedua grup dalam gerombol, yaitu:
1. Pembangkitan data bergerombol dimana proporsi kedua grup dalam tiap gerombol merata (berimbang). Ilustrasi pembangkitan pertama ini dapat dilihat pada Gambar 1.
Gambar 1 Simulasi dengan Proporsi Grup dalam Gerombol Merata.
5
Gambar 2 Simulasi dengan adanya Grup yang Mendominasi dalam Suatu Serombol.
Populasi yang dibangkitkan dalam tiap simulasi berukuran 100.000 dengan menggunakan tiga kombinasi nilai γ, k, dan lima sebaran yang berbeda. Nilai γ dan k yang digunakan adalah 0, 0.5, dan 1. Dengan menggunakan ketiga kombinasi tersebut, jumlah populasi yang dibangkitkan adalah sebanyak 45. Sebaran yang dipakai adalah Normal (0,1), Lognormal (0,1), F (1,2), Uniform (0,2), dan Exponensial (1). Ukuran contoh yang dipakai dalam simulasi adalah 20 dengan ulangan sebanyak 1000. Nilai kuasa uji diperoleh dengan persamaan:
qrAsA rtu vw ;x [y ;* zvw ;x v ; F;
vw ;x [y ;* z
(14)
Syntax perhitungan kuasa uji ketika
proporsi kedua grup dalam gerombol berimbang dapat dilihat pada Lampiran 3. Sedangkan untuk syntax perhitungan kuasa uji ketika ada grup yang mendominasi dalam gerombol dapat dilihat pada Lampiran 4.
) '
Penelitian ini dilakukan dengan langkah langkah:
1. Membangkitkan data simulasi seperti yang telah dijelaskan pada bahan, 2. Menghitung kuasa uji Wilcoxon, uji
XKB, dan uji Datta Satten, 3. Membandingkan ketiga kuasa uji, 4. Menguji perbandingan IPK TPB IPB
angkatan 43 mahasiswa perempuan dan laki laki menggunakan uji Datta Satten, 5. Membuat kesimpulan dari hasil
pengujian perbandingan IPK TPB IPB angkatan 43 mahasiswa perempuan dan laki laki yang diperoleh.
)
#
Pada penelitian ini ada empat kriteria yang mempengaruhi kuasa uji yaitu γ, k, sebaran D, dan tingkat keragaman grup dalam suatu gerombol. Data simulasi dikatakan memiliki keragaman grup yang tinggi apabila proporsi grup 0 dan grup 1 dalam tiap gerombol relatif berimbang. Sebaliknya, data simulasi dikatakan memiliki keragaman grup yang rendah apabila ada grup yang mendominasi pada tiap gerombol.
Nilai kuasa uji seharusnya memberikan nilai yang sekecil kecilnya ketika nilaij 3 karena nilai j 3 menunjukkan bahwa tidak ada pengaruh grup dalam data bangkitan sehingga dalam uji perbandingan dua grup diharapkan nilai kuasa uji yang sekecil kecilnya. Sebaliknya, untuk nilai j 3 diharapkan nilai kuasa uji yang sebesar besarnya.
! + %
Pengaruh gerombol terhadap nilai kuasa uji dilihat berdasarkan nilai k ketika nilai γ yang digunakan sama dan sebaran yang digunakan juga sama. Pada Tabel 1 dapat kita lihat bahwa pengaruh k tidak begitu besar terhadap nilai kuasa uji ketika tidak ada perbedaan pengaruh grup (nilai j 3). Untuk nilai j 3, nilai k memberikan pengaruh negatif terhadap nilai kuasa uji ketiga metode. dimana semakin besar nilai k maka semakin besar penurunan nilai kuasa uji.
6
! %
Nilai kuasa uji yang diperoleh pada tiap sebaran dapat dibandingkan dengan melihat kuasa uji pada nilai γ yang sama dan nilai k
yang sama. Pembahasan ini hanya akan ditampilkan nilai kuasa uji ketika j 3 dan k 3 yang dapat dilihat pada Tabel 2, nilai kuasa uji ketika j 3{| dan k 3{| yang dapat dilihat pada Tabel 3, dan nilai kuasa uji ketika j # dan k # yang dapat dilihat pada Tabel 4.
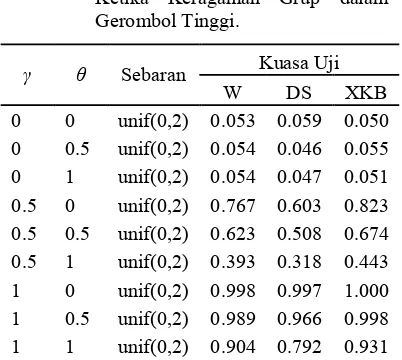
Tabel 2 memperlihatkan bahwa nilai kuasa uji terbesar ketika j 3 (tidak ada pengaruh grup), k 3 (tidak ada pengaruh gerombol), dan keragaman grup dalam gerombol tinggi diperoleh ketika data dibangkitkan dengan sebaran Uniform(0,2). Nilai kuasa uji terkecil pada Tabel 2 diperoleh ketika data dibangkitkan dengan sebaran F(1,2), kecuali untuk uji Datta Satten dimana kuasa uji terkecil didapat ketika data dibangkitkan menggunakan sebaran Lognormal(0,1).
Tabel 2 Kuasa Uji Wilcoxon, Datta Satten, dan XKB ketika j 3, k 3, dan
Keragaman Grup dalam Gerombol Tinggi.
Tabel 3 memperlihatkan bahwa nilai kuasa uji terbesar ketika j 3{|, k 3{|, dan
keragaman grup dalam gerombol tinggi diperoleh ketika data dibangkitkan dengan sebaran Uniform(0,2). Nilai kuasa uji terkecil pada Tabel 3 diperoleh ketika data dibangkitkan dengan sebaran F(1,2).
Tabel 3 Kuasa Uji Wilcoxon, Datta Satten,
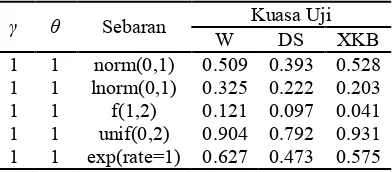
Tabel 4 memperlihatkan bahwa nilai kuasa uji terbesar ketika j #, k #, dan
keragaman grup dalam gerombol tinggi diperoleh ketika data dibangkitkan dengan sebaran Uniform(0,2). Nilai kuasa uji terkecil pada Tabel 4 diperoleh ketika data dibangkitkan dengan sebaran F(1,2).
Tabel 4 Kuasa Uji Wilcoxon, Datta Satten, dan XKB ketika j #, k #, dan
Keragaman Grup dalam Gerombol Tinggi. memperlihatkan bahwa nilai kuasa uji terbesar diperoleh ketika data dibangkitkan dengan sebaran Uniform(0,2). Besarnya nilai kuasa uji yang diperoleh ketika data dibangkitkan menggunakan sebaran Uniform(0,2) kemungkinan disebabkan karena nilai tengah sebaran Uniform(0,2) lebih kecil dibandingkan sebaran lain dalam simulasi.
Secara keseluruhan, Tabel 2, 3, dan 4 memperlihatkan bahwa nilai kuasa uji terkecil diperoleh ketika data dibangkitkan dengan sebaran F(1,2), kecuali pada kuasa uji Datta Satten ketika γ dan θ bernilai nol (Tabel 2). Kecilnya nilai kuasa uji yang diperoleh ketika data dibangkitkan menggunakan sebaran F kemungkinan disebabkan karena nilai tengah sebaran F(1,2) lebih besar dibandingkan sebaran lain yang digunakan dalam simulasi. Adapun penyimpangan yang terjadi pada kuasa uji Datta Satten pada Tabel 2 kemungkinan disababkan pengaruh acak.
7
Selain data yang dibangkitkan dengan sebaran Normal dan Uniform, uji Wilcoxon memiliki nilai kuasa uji yang terbesar dibandingkan kedua uji lainnya. Sedangkan untuk uji Datta Satten, secara keseluruhan tidak menghasilkan kuasa uji terbaik pada sebaran tertentu, akan tetapi nilai kuasa uji Datta Satten tidak terlalu jauh dibandingkan kedua metode lainnya.
! + $
+ %
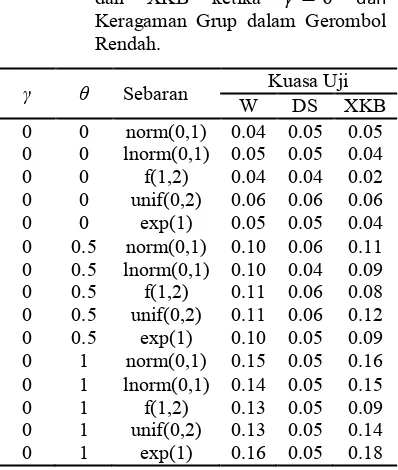
Tabel 5 menampilkan kuasa uji ketika keragaman grup dalam gerombol rendah (proporsi kedua grup dalam gerombol berimbang). Ketika k 3, nilai kuasa uji pada ketiga uji masih belum menampakkan kejanggalan karena nilai kuasa uji yang j 3 ini berarti resiko yang kita hadapi ketika menolak padahal benar juga besar. Oleh karena itu kita sebaiknya tidak memakai uji XKB dan Wilcoxon untuk data dimana ada grup yang mendominasi dalam suatu gerombol. Tidak seperti kedua uji lainnya, uji Datta Satten mendapatkan nilai kuasa uji yang mendekati 0.05 ketika j 3, k 3 dan keragaman grup dalam gerombol rendah. Dengan demikian, untuk data dimana ada grup yang mendominasi dalam suatu gerombol lebih baik menggunakan uji Datta Satten.
Tabel 5 Kuasa Uji Wilcoxon, Datta Satten, dan XKB ketika j 3 dan
Keragaman Grup dalam Gerombol Rendah.
Gambar 3 memperlihatkan bahwa sebaran data IPK pada tiap kelas berbeda. Hal ini menunjukkan adanya pengaruh kelas terhadap IPK mahasiswa. Pengaruh kelas tersebut bisa disebabkan beberapa faktor seperti perbedaan dosen yang mengajar, perbedaan teman sekelas, dan beberapa faktor lainnya.
Boxplot pada Gambar 3 menunjukkan bahwa kelas yang memiliki rata rata IPK terbesar adalah kelas B01 dengan rata rata IPK 3.135. Sebaliknya, kelas yang memiliki rata rata IPK terkecil adalah kelas B09 dengan rata rata IPK 2.6548.
8
Gambar 4 memperlihatkan bahwa proporsi mahasiswa laki laki dan perempuan tidak merata, dimana banyak kelas didominasi oleh mahasiswa perempuan. Walaupun demikian ada pula kelas yang didominasi mahasiswa laki laki, seperti kelas A3, A12, dan B28. Karena ada banyak kelas yang didominasi grup tertentu maka kita sebaiknya menggunakan uji Datta Satten.
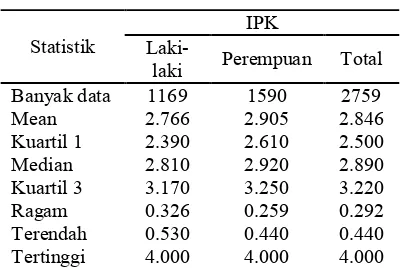
Tabel 6 memperlihatkan bahwa jumlah perempuan pada Mahasiswa TPB IPB Angkatan 43 lebih banyak dibandingkan dengan jumlah laki laki. Ukuran pemusatan (diwakili oleh mean dan median) mahasiswa perempuan lebih besar dibandingkan laki laki. Sebaliknya, ukuran keragaman (diwakili oleh ragam) mahasiswa perempuan lebih kecil
dibandingkan laki laki. Nilai statistika deskriptif lainnya dapat dilihat pada Tabel 6.
Tabel 6 Tabel Ringkasan IPK Mahasiswa TPB IPB Angkatan 43.
Statistik
IPK Laki
laki Perempuan Total Banyak data 1169 1590 2759
Gambar 4 Histogram Jumlah Mahasiswa Laki Laki dan Perempuan disetiap Kelas.
# # ) &
Syntax R yang digunakan dalam uji Datta
Satten dua arah pada data TPB IPB angkatan 43 dapat dilihat pada Lampiran 7. Keluaran perangkat lunak R 2.91 dengan menggunakan
syntax tersebut ditampilkan pada Tabel 4.
Tabel 7 Output Uji Datta Satten pada Data IPK TPB IPB Angkatan 43.
Statistik Nilai Datta Satten sebesar 4.858559 dan p)value
sebesar #{#} ~ • E #37€. P)value yang sangat kecil ini menandakan adanya perbedaan IPK TPB antara laki laki dan perempuan pada mahasiswa IPB angkatan 43. Dengan menggunakan uji Datta Satten satu arah diketahui bahwa IPK mahasiswa perempuan lebih tinggi dibandingkan IPK laki laki.
) ,
)
9
Analisis dengan data sekunder menghasilkan p)value sebesar #{#} ~ • E #37€. Hal ini berarti pada taraf nyata 5% kita dapat menyatakan bahwa nilai IPK TPB mahasiswa perempuan berbeda dengan nilai IPK TPB mahasiswa laki laki. Dengan menggunakan uji Datta Satten satu arah diketahui bahwa IPK mahasiswa perempuan lebih tinggi dibandingkan IPK laki laki.
,
Simulasi yang dilakukan masih memiliki beberapa kekurangan. Kekurangan tersebut yaitu simulasi belum melihat pengaruh jumlah contoh yang diambil dari populasi dan terbatasnya sebaran yang digunakan. Keterbatasan tersebut perlu dikembangkan agar diperoleh hasil yang lebih baik.
Seringkali dalam kenyataan kita temui data yang memiliki lebih dari tiga grup dalam suatu populasi. Oleh karena itu sebaiknya dilakukan penelitian lanjutan yang membahas uji Datta Satten untuk grup sebanyak m.
- ,
Daniel, W. W. 1990. Applied Nonparametic
Statistics. Boston: PWS KENT.
Datta, S., & Satten, G. A. 2005. Rank)Sum
Test for Clustered Data. JASA , 908.
Kendall, M., & Stuart, A. 1973. The Advanced
Theory of Statistics. New York: Hafner
Publishing Company.
Walpole. 1988. Pengantar Statistika. Jakarta: PT Gramedia Pustaka Utama.
Wolfe, H. 1973. Nonparametric Statistical
Methods. Canada: John Wiley & Sons,
Inc.
Xiong, M. M., Krushkal, J., & Boerwinkle, E. 1998. TDT statistics for mapping
quantitative trait loci. Annals of Human
11
$ . / & !
##### menghitung F.hat {1/2(F(X_ik )+F(X_ik ))} n< length(X)
F.hat< numeric(n) for (i in 1:n){
F.hat[i]< (sum(X<=X[i])+sum(X<X[i]))/(2*n) }
##### menghitung F.prop {1/2 Sigma_(j|=i) {F_j (X_ik )+F_j (X_ik ) } )
#### M adalah banyak gerombol, n.i merupakan banyaknya observasi pada gerombol i M< length(unique(Cluster))
n.i=numeric(max(Cluster)) for(i in 1:max(Cluster)) n.i[i]=sum(Cluster==i) F.prop< numeric(n) for(ii in 1:n){
F.j< numeric(M) for (i in 1:M){
F.j[i]< (sum(X[Cluster==i]<X[ii])+0.5*sum(X[Cluster==i]==X[ii]))/(n.i[i]) }
F.prop[ii]< sum(F.j[ Cluster[ii]]) }
########### menghitung persamaan 3 { S=E(W*|X,g) } a< numeric(M)
b< 1+F.prop for (i in 1:M){
a[i]< sum((grp[Cluster==i]*b[Cluster==i])/(n.i[i])) }
c< 1/(M+1) S< c*sum(a)
#########menghitung persamaan 4 { E(S)=E(W*) } n.i1=numeric(max(Cluster))
for(i in 1:max(Cluster))
n.i1[i]=sum(Cluster==i&grp==1) d< n.i1/n.i
E.S< (1/2)*sum(d)
####### menghitung persamaan 5 { penduga var(S) }
W.hat< numeric(M) ##### pertama tama menghitung persamaan 6 { W.hat tiap gerombol} a< n.i1/n.i
for (i in 1:M){ b< 1/(n.i[i]*(M+1)) c< (grp[Cluster==i])*(M 1) d< sum(a[ i])
W.hat[i]< b*sum((c d)*F.hat[Cluster==i]) }
a< n.i1/n.i
E.W< (M/(2*(M+1)))*(a sum(a)/M) ## kedua, menghitung persamaan 7 { E(W) }
var.s< sum((W.hat E.W)^2) #menghitung var(s)
####### menghitung persamaan 2 { statistik uji Z } stat< (S E.S)/sqrt(var.s)
p.value< 2*pnorm(abs(stat),lower.tail=F)
12
$ 0 / (
TDT< function(X,grp) { n1=sum(grp==1) n0=sum(grp==0)
#menghitung persamaan 9 X1=sum(X[grp==1])/n1
#menghitung persamaan 10 X0=sum(X[grp==0])/n0
#menghitung persamaan 11
Ssqr=(sum((X[grp==1] X1)^2)+sum((X[grp==0] X0)^2))/(n1+n0 2)
#menghitung persamaan 8 T=(X1 X0)^2/((1/n1+1/n0)*Ssqr)
#menghitung p value
p.value=pf(T,1,n1+n0 2,,lower.tail=F) p.value
13
$ 1 / ! # $ # ' + $ ' + %
%
sebaran< function(M,seb)
{switch(seb,"1"=rnorm(M,0,1),"2"=rlnorm(M,0,1),"3"=rf(M,1,2),"4"=runif(M,0,2),"5"=rexp(M, rate = 1))
}
powwil=numeric(45) powdat=numeric(45) powtdt=numeric(45) npow=1
M=20 rep=1000
tdt=datta=wilcox=numeric(rep) for(seb in 1:5)
{
ni=ceiling(runif(100000,0,4)) sni=sum(ni)
v1=sebaran(100000,seb) v2=sebaran(100000,seb) p.v1=rep(v1,ni)
p.v2=rep(v2,ni) p.v1v2=p.v1+p.v2 Cluster=rep(1:100000,ni) E=sebaran(sni,seb) grp=rbinom(sni,1,0.5)
for(alpha in c(0,0.5,1)) {
for(betta in c(0,0.5,1)) {
X=numeric(sni)
X=alpha*grp+betta*(p.v1v2)+E for(ul in 1:rep)
{
sampel=sort(sample(1:100000,20)) nisam=ni[sampel]
Clustersam=rep(1:20,nisam) grpsam=grp[Cluster %in% sampel] Xsam=X[Cluster %in% sampel]
datta[ul]=clus.rank.sum(Clustersam,Xsam,grpsam)[[5]] wilcox[ul]=wilcox.test(Xsam[grpsam==1],Xsam[grpsam==0],
alternative="t",exact= FALSE)[[3]] tdt[ul]=TDT(Xsam,grpsam)
}
powdat[npow]=sum(datta<0.05)/rep powwil[npow]=sum(wilcox<0.05)/rep powtdt[npow]=sum(tdt<0.05)/rep npow=npow+1
} }
14
###SAVE KE EXEL### sebaran< function(seb)
{switch(seb,"1"="norm(0,1)","2"="lnorm(0,1)","3"="f(1,2)","4"="unif(0,2)","5"="exp(rate = 1)") }
a=numeric(45) b=numeric(45) i=1
dis=0
for(seb in 1:5){
for(alpha in c(0,0.5,1)){ for(betta in c(0,0.5,1)){ a[i]=alpha
b[i]=betta
dis[i]=sebaran(seb) i=i+1
}}}
dimas< data.frame(a,b,dis,powwil,powdat,powtdt) library(xlsReadWrite)
15
$ 2 / ! # ' + $ / ) ' # '
+ %
sebaran< function(M,seb)
{switch(seb,"1"=rnorm(M,0,1),"2"=rlnorm(M,0,1),"3"=rf(M,1,2),"4"=runif(M,0,2),"5"=rexp(M, rate = 1))}
powwil=numeric(45) powdat=numeric(45) powtdt=numeric(45) npow=1
M=20 rep=1000
tdt=datta=wilcox=numeric(rep) for(seb in 1:5)
{
ni=ceiling(runif(100000,0,4)) sni=sum(ni)
v1=sebaran(100000, seb) v2=sebaran(100000, seb) p.v1=rep(v1,ni)
p.v2=rep(v2,ni) p.v1v2=p.v1+p.v2 X=numeric(sni) Cluster=numeric(sni)
grpdom=rbinom(100000,1,0.5) ##grup yang mendominasi pada suatu kluster grp=numeric(sni)
Cluster=rep(1:100000,ni)
grp[Cluster %in% c(1:100000)[grpdom==1]]=rbinom(sum(Cluster %in% c(1:100000)[grpdom==1]), 1, 0.90)
grp[Cluster %in% c(1:100000)[grpdom==0]]=rbinom(sum(Cluster %in% c(1:100000)[grpdom==0]), 1, 0.10)
E=sebaran(sni,seb) for(alpha in c(0,0.5,1))
{
for(betta in c(0,0.5,1)) {
X=numeric(sni)
X=alpha*grp+betta*(p.v1v2)+E for(ul in 1:rep)
{
sampel=sort(sample(1:100000,20)) nisam=ni[sampel]
Clustersam=rep(1:20,nisam) grpsam=grp[Cluster %in% sampel] Xsam=X[Cluster %in% sampel]
datta[ul]=clus.rank.sum(Clustersam,Xsam,grpsam)[[5]] wilcox[ul]=wilcox.test(Xsam[grpsam==1],Xsam[grpsam==0],
alternative="t",exact= FALSE)[[3]] tdt[ul]=TDT(Xsam,grpsam)
}
powdat[npow]=sum(datta<0.05)/rep powwil[npow]=sum(wilcox<0.05)/rep powtdt[npow]=sum(tdt<0.05)/rep npow=npow+1
} }
16
###SAVE KE EXEL### sebaran< function(seb)
{switch(seb,"1"="norm(0,1)","2"="lnorm(0,1)","3"="f(1,2)","4"="unif(0,2)","5"="exp(rate = 1)") }
a=numeric(45) b=numeric(45) i=1
dis=0
for(seb in 1:5){
for(alpha in c(0,0.5,1)){ for(betta in c(0,0.5,1)){ a[i]=alpha
b[i]=betta
dis[i]=sebaran(seb) i=i+1
}}}
dimas< data.frame(a,b,dis,powwil,powdat,powtdt) library(xlsReadWrite)
17
$ 3 # 4 & 4 ' ( $ # ' + $
' + % %
γ θ Sebaran Kuasa Uji
W DS XKB
0 0 Normal(0,1) 0.051 0.054 0.051 0 0 Lognormal(0,1) 0.039 0.043 0.037
0 0 F(1,2) 0.039 0.050 0.014
0 0 Uniform(0,2) 0.053 0.059 0.050 0 0 Exponensial(1) 0.049 0.047 0.047 0 0.5 Normal(0,1) 0.042 0.056 0.043 0 0.5 Lognormal(0,1) 0.050 0.055 0.049 0 0.5 F(1,2) 0.062 0.061 0.031 0 0.5 Uniform(0,2) 0.054 0.046 0.055 0 0.5 Exponensial(1) 0.051 0.046 0.048 0 1 Normal(0,1) 0.045 0.046 0.045 0 1 Lognormal(0,1) 0.054 0.057 0.045
0 1 F(1,2) 0.040 0.041 0.030
0 1 Uniform(0,2) 0.054 0.047 0.051 0 1 Exponensial(1) 0.054 0.050 0.046 0.5 0 Normal(0,1) 0.366 0.301 0.407 0.5 0 Lognormal(0,1) 0.484 0.374 0.180 0.5 0 F(1,2) 0.390 0.334 0.026 0.5 0 Uniform(0,2) 0.767 0.603 0.823 0.5 0 Exponensial(1) 0.659 0.525 0.416 0.5 0.5 Normal(0,1) 0.280 0.230 0.304 0.5 0.5 Lognormal(0,1) 0.192 0.148 0.123 0.5 0.5 F(1,2) 0.100 0.074 0.034 0.5 0.5 Uniform(0,2) 0.623 0.508 0.674 0.5 0.5 Exponensial(1) 0.373 0.287 0.319 0.5 1 Normal(0,1) 0.177 0.149 0.194 0.5 1 Lognormal(0,1) 0.111 0.074 0.086 0.5 1 F(1,2) 0.067 0.072 0.032 0.5 1 Uniform(0,2) 0.393 0.318 0.443 0.5 1 Exponensial(1) 0.191 0.149 0.152 1 0 Normal(0,1) 0.913 0.804 0.928 1 0 Lognormal(0,1) 0.900 0.812 0.505
1 0 F(1,2) 0.739 0.603 0.054
1 0 Uniform(0,2) 0.998 0.997 1.000 1 0 Exponensial(1) 0.987 0.924 0.922 1 0.5 Normal(0,1) 0.795 0.640 0.814 1 0.5 Lognormal(0,1) 0.575 0.447 0.352 1 0.5 F(1,2) 0.222 0.164 0.041 1 0.5 Uniform(0,2) 0.989 0.966 0.998 1 0.5 Exponensial(1) 0.869 0.752 0.781 1 1 Normal(0,1) 0.509 0.393 0.528 1 1 Lognormal(0,1) 0.325 0.222 0.203
1 1 F(1,2) 0.121 0.097 0.041
18
$ 5 # 4 & 4 ' ( ' + $ /
) ' # ' + %
γ θ Sebaran Kuasa Uji
W DS XKB
0 0 Normal(0,1) 0.044 0.050 0.051 0 0 Lognormal(0,1) 0.048 0.048 0.044
0 0 F(1,2) 0.043 0.042 0.020
0 0 Uniform(0,2) 0.055 0.063 0.057 0 0 Exponensial(1) 0.045 0.054 0.041 0 0.5 Normal(0,1) 0.101 0.058 0.107 0 0.5 Lognormal(0,1) 0.099 0.043 0.092
0 0.5 F(1,2) 0.111 0.055 0.077
0 0.5 Uniform(0,2) 0.106 0.057 0.119 0 0.5 Exponensial(1) 0.099 0.054 0.093 0 1 Normal(0,1) 0.149 0.053 0.157 0 1 Lognormal(0,1) 0.143 0.051 0.146
0 1 F(1,2) 0.125 0.053 0.091
0 1 Uniform(0,2) 0.130 0.051 0.136 0 1 Exponensial(1) 0.156 0.049 0.175 0.5 0 Normal(0,1) 0.376 0.292 0.398 0.5 0 Lognormal(0,1) 0.447 0.361 0.160
0.5 0 F(1,2) 0.424 0.342 0.028
0.5 0 Uniform(0,2) 0.757 0.627 0.816 0.5 0 Exponensial(1) 0.678 0.544 0.418 0.5 0.5 Normal(0,1) 0.308 0.208 0.337 0.5 0.5 Lognormal(0,1) 0.258 0.135 0.165 0.5 0.5 F(1,2) 0.161 0.055 0.073 0.5 0.5 Uniform(0,2) 0.584 0.439 0.635 0.5 0.5 Exponensial(1) 0.392 0.252 0.351 0.5 1 Normal(0,1) 0.235 0.100 0.258 0.5 1 Lognormal(0,1) 0.195 0.082 0.162
0.5 1 F(1,2) 0.164 0.057 0.112
0.5 1 Uniform(0,2) 0.396 0.234 0.432 0.5 1 Exponensial(1) 0.267 0.119 0.253 1 0 Normal(0,1) 0.897 0.805 0.913 1 0 Lognormal(0,1) 0.870 0.780 0.452
1 0 F(1,2) 0.740 0.629 0.062
1 0 Uniform(0,2) 0.997 0.992 1.000 1 0 Exponensial(1) 0.964 0.909 0.886 1 0.5 Normal(0,1) 0.711 0.557 0.742 1 0.5 Lognormal(0,1) 0.543 0.369 0.336
1 0.5 F(1,2) 0.270 0.144 0.106
1 0.5 Uniform(0,2) 0.983 0.932 0.991 1 0.5 Exponensial(1) 0.852 0.683 0.781 1 1 Normal(0,1) 0.457 0.262 0.483 1 1 Lognormal(0,1) 0.386 0.218 0.288
1 1 F(1,2) 0.214 0.081 0.109
19
$ 6 / # # ) & $ ' '
###membaca data berbentuk spreadsheet ke aplikasi R data1< read.csv("E:\\My Document\\datafix.csv",header=T)
###merubah format data list ke format data vektor NAMA=as.vector(data1[[1]])
NIM=as.vector(data1[[2]]) IPK=as.vector(data1[[3]]) KEL=as.vector(data1[[4]]) LP=as.vector(data1[[5]])
###transformasi vektor KEL ke ke dalam bentuk angka tabel=table(KEL)
tmp=0 Cluster=0 for(i in 1:56)
{Cluster[tmp+1:tabel[[i]]]=i tmp=tmp+tabel[[i]]}
###transformasi vektor LP ke bentuk angka 0(nol) dan 1(satu) agar bisa dianalisis grp=0
for(i in 1:2759)
{if(LP[i]=="P") grp[i]=0 else if(LP[i]=="L") grp[i]=1}
###analisis X=IPK