TUGAS AKHIR
Program Studi S1 Sistem Komputer
Oleh :
ANGGI TIARA CITRA EKINASTI 13.41020.0122
FAKULTAS TEKNOLOGI DAN INFORMATIKA
HALAMAN JUDUL... i
HALAMAN SYARAT ... ii
MOTTO ... iii
HALAMAN PERSEMBAHAN ... iv
HALAMAN PENGESAHAN... v
HALAMAN PERNYATAAN ... vi
ABSTRAK ... vii
KATA PENGANTAR ... viii
DAFTAR ISI ... x
DAFTAR GAMBAR ... xiii
DAFTAR TABEL ... xvi
BAB I PENDAHULUAN ... 1
1.1 Latar Belakang Masalah ... 1
1.2 Rumusan Masalah ... 4
1.3 Batasan Masalah ... 4
1.4 Tujuan ... 5
1.5 Sistematika Penulisan ... 5
BAB II LANDASAN TEORI ... 7
2.1 Sinyal Suara Jantung (PCG) ... 7
2.2 Wavelet ... 8
2.3.3 TransformasiWaveletDiskrit ... 12
2.3.4Mother Wavelet... 14
2.3.4.1WaveletDaubechies... 15
2.3.4.2WaveletCoiflet ... 17
2.3.4.3WaveletSymlet ... 17
2.3.4.4WaveletBiorthogonal ... 18
2.4 Parameter... 19
2.4.1 Standar Deviasi ... 19
2.4.2 Energi ... 19
2.4.3 Normalisasi Energi... 20
2.5Denoising Wavelet... 20
BAB III METODE PENELITIAN DAN PERANCANGAN SISTEM ... 24
3.1. Metode Penelitian ... 24
3.2. Prosedur Penelitian ... 26
3.3. Analisis TransformasiWaveletDiskrit ... 28
3.3.1 Denoising ... 33
3.3.2 Energi Dekomposisi dan Normalisasi Energi Dekomposisi ... 33
3.3.3FlowchartProgram Energi Dekomposisi dan Normalisasi Energi Dekomposisi ... 36
4.2. Pengujian Program ... 44
4.2.1 Tujuan ... 44
4.2.2 Prosedur Pengujian Program Energi dan Normalisasi Energi... 44
4.2.3 Hasil Pengujian Program Energi dan Normalisasi Energi... 45
4.2.4 Prosedur Pengujian Program Standar Deviasi... 46
4.2.5 Hasil Pengujian Program Standar Deviasi... 47
4.3 Pengambilan Data... 48
4.4 Denoising Sinyal PCG ... 52
4.5 Dekomposisi Sinyal PCG ... 58
4.6 Analisis Hasil Dekomposisi Energi ... 58
4.6.1 Frekuensi Cuplik 8 KHz ... 58
4.6.2 Frekuensi Cuplik 44,1 KHz ... 60
4.6.3 Frekuensi Cuplik 48 KHz ... 62
4.6.4 Database Sinyal PCG Michigan ... 65
BAB V PENUTUP ... 69
5.1. Kesimpulan ... 69
5.2. Saran ... 71
DAFTAR PUSTAKA ... 72
LAMPIRAN ... 75
1.1 Latar Belakang Masalah
Penyakit jantung menduduki peringkat teratas penyebab kematian di
dunia. Proporsi penyebab kematian penyakit tidak menular (PTM) pada
orang-orang berusia kurang dari 70 tahun, penyakit jantung merupakan penyebab
terbesar (39%), diikuti kanker (27%), sedangkan penyakit pernafasan kronis,
penyakit pencernaan dan PTM yang lain bersama-sama menyebabkan sekitar 30%
kematian, serta 4% kematian disebabkan diabetes (Kristomo, 2014).
Untuk alasan ini, auskultasi adalah tes utama yang dilakukan oleh dokter
untuk mengevaluasi keadaan jantung dengan cara mendengarkan suara jantung
melalui stetoskop, auskultasi merupakan komponen dasar dalam diagnosis jantung
dan merupakan teknik yang paling umum digunakan untuk diagnosis dalam
perawatan kesehatan. Di beberapa keadaan, terutama di daerah terpencil daerah
atau negara-negara berkembang, auskultasi mungkin satu-satunya cara yang
tersedia. Akan Tetapi, mendeteksi gejala yang relevan dan membentuk suatu
diagnosis berdasarkan suara yang terdengar melalui stetoskop adalah keterampilan
yang sangat lama untuk dipelajari, selain itu diagnosis dengan mendengarkan
suara jantung memiliki kelebihan dibandingan dengan diagnosis berbasis EKG,
diantaranya dari sisi kemudahan (Nazeran, 2007).
Oleh karena alasan diatas, maka diperlukan suatu cara untuk
memudahkan diagnosis dengan merekam suara jantung lalu menganalisis sinyal
sinyal suara jantung, pada penelitian ini sinyal suara jantung (PCG) pada ranah
waktu akan ditransformasikan ke dalam ranah waktu-frekuensi untuk diamati pola
serta ciri-cirinya, pada ranah waktu-frekuensi isyarat PCG memiliki pola yang
menggambarkan unsur-unsur frekuensi yang terkandung di dalam sinyal (Ruth,
2014).
Sebelumnya telah dilakukan penelitian oleh oleh Nazeran pada tahun
2007dengan judul “Wavelet-based Segmentation and Feature Extraction of Heart Sounds for Intelligent PDA-based Phonocardiography” yang mengolah sinyal suara jantung dengan ektraksi ciri menggunakan analisis Wavelet Diskrit Daubechies dengan dekomposisi level 4 (250–500 Hz) dan level 6(62.5-125Hz)
pada frekuensi cuplik 8012 Hz dimana metode tersebut digunakan untuk
mendeteksi ciri-ciri antara sinyal jantung normal dan abnormal, hasil dari
penelitian ini menunjukan bahwa metode ekstraksi ciri terbukti efektif digunakan
untuk mengetahui ciri sinyal suara jantung normal yang memiliki energi terbesar
berada diantara 50Hz dan 150-200 Hz serta abnormal yang energi terbesarnya
berada pada 250-500 Hz.
Pada tahun 2014 telah diakukan penelitian oleh Ruth dengan judul
“Analisis Sinyal Ekg Menggunakan Transformasi Wavelet”, penelitian ini menganalisis sinyal EKG dengan menggunakan Transformasi Wavelet untuk mendapatkan pola dan ciri sinyal EKG dengan sinyal EKG yang lainya. Mother Wavelet yang digunakan adalah Coiflet 5. Analisis dilakukan berdasarkan hasil grafik skalogram dan energi dekomposisi, dan didapatkan bahwa Transformasi
D3 dengan jangkauan frekuensi 8 – 16 Hz. Pada sinyal EKG abnormal kondisi
Atrial Fibrillation, energi dekomposisi tertinggi semua subyek terdapat pada komponen aproksimasi A4 dengan jangkauan frekuensi 0-4. Untuk
Supraventricular Arrhytmia memiliki energi tertinggi yang bervariasi pada jangkauan frekuensi 0-4 Hz dan 4-8 Hz.
Pada tahun 2013 dilakukan penelitian berjudul“Performance Analysis of DWT at different levels for Feature Extraction of PCG Signals” oleh Devi, Bhisiek, serta Sinha, yang menganalisis pengaruh beberapa parameter yaitu
energi, standar deviasi, serta energi pada koefisien aproksimaksi dan detail dari
sebuah dekomposisi sinyal Diskrit Wavelet. Dalam penelitian tersebut, menggunakan transformasi Wavelet Diskrit Daubechies 4 lalu dilakukan penelitian pada sepuluh level dekomposisi, dengan berbagai macam sinyal PCG
(murmur dan normal), adapun kesimpulanya menunjukan bahwa energi terbaik
untuk normal heart sound berada pada level 9, Aortic Stenosis pada level 9, Mitral Regurgation berada pada level 9 sedangkan Aortic Regurgation dan Mitral
Stenosis pada level 6 karena memiliki amplitude yang rendah dan durasi sinyal
yang panjang.
Pada tahun 2015 dilakukan penelitian oleh Venkatta dan Dr. Kumar
dengan judul “Analysis of Various DWT Methods for Feature Extracted PCG Signals” yang menganalisis sinyal PCG untuk ekstraksi ciri dengan beberapa
Mother Wavelet yaitu Biorthogonal, Symlet, Coiflet, Haar yang menggunakan beberapa parameter yaitu standar deviasi, energi, variansi, entropi, SNR (Signal to Noise Ratio), penelitian ini difokuskan pada level dekomposisi dari setiap tipe
DWT Coiflet merupakan metode terbaik dari beberapa metode Wavelet yang diteliti.
Dengan acuan empat penelitian tersebut maka akan dilakukan analisis
dan ekstraksi ciri dari data real sinyal suara jantung yang didapat dengan
auskultasi (menggunakan stetoskop digital). Adapun metode yang akan digunakan
adalah dekomposisi transformasi Wavelet Diskrit dengan menggunakan beberapa tipe Mother Wavelet dengan berbagai macam orde, berbagai macam level pada setiap orde nya serta berbagai macam frekuensi cuplik, adapun parameter yang
akan digunakan adalah energi, dan standard deviasi.
1.2. Rumusan Masalah
Berdasarkan latar belakang diatas maka dapat dirumuskan permasalahan:
Bagaimana melakukan analisis ciri sinyal jantung untuk menentukan Mother Waveletyang mengandung energi tertinggi dalam dekomposisi sinyal PCG dalam penentuan energi tersebut digunakan variable-variabel bebas yaitu frekuensi
cuplik, tipeMother, berbagai ordeMother Wavelet, dan level dekomposisi. Selain itu juga digunakan parameter uji yaitu standar deviasi dan energi normalisasi.
1.3 Batasan Masalah
Dalam perancangan dan pembuatan simulasi ini, terdapat beberapa batasan
masalah, antara lain :
1. Sampel penelitian ini suara berasal dari 3 subject yang diambil secara random
dan realtime menggunakandigital sthetoscopedarithinkslabone.
3. Menggunakan transformasiWaveletDiskrit.
4. Tipe Mother Wavelet yang digunakan adalah Coiflet 2, Coiflet 5 Symlet 2, Symlet 5, Symlet 7, Daubechies 2, Daubechies 5, Daubechies 7, Biorthogonal
2.8, Biorthogonal 3.9, Biorthogonal 6.8.
5. Data yang diamati adalah satu siklus (0,8 detik).
6. Jumlah pengambilan data untuk setiap subyek adalah 30 kali.
7. Kondisi subyek adalah orang normal dalamrelaxdan kondisi lingkungan yang tenang.
1.4 Tujuan
Berdasarkan rumusan masalah yang diuraikan diatas, maka tujuan
penelitian ini adalah sebagai berikut :
Melakukan analisis ciri sinyal jantung untuk menentukan Mother Wavelet yang mengandung energi tertinggi dalam dekomposisi sinyal PCG dalam penentuan
energi tersebut digunakan variable-variabel bebas yaitu frekuensi cuplik, tipe
Mother, berbagai orde Mother Wavelet, dan level dekomposisi. Selain itu juga digunakan parameter uji yaitu standar deviasi dan energi normalisasi.
1.2 Sistematika Penulisan
Pembahasan Tugas Akhir ini secara Garis besar tersusun dari 5 (lima)
bab, yaitu diuraikan sebagai berikut:
1. BAB I PENDAHULUAN
Pada Bab ini akan dibahas mengenai latar belakang masalah, batasan masalah,
2. BAB II LANDASAN TEORI
Pada Bab ini akan dibahas teori penunjang dari permasalahan, yaitu mengenai
Sinyal suara jantung (PCG), Wavelet, Dekomposisi Wavelet, Transformasi
Wavelet, Transformasi Wavelet Kontinyu, Transformasi Wavelet Diskrit,
Mother Wavelet, Biorthogonal, Symlet, Coiflet, Daubechies, Energi Dekomposisi, Normalisasi Energi dan Standar Deviasi, danDenoising Wavelet.
3. BAB III METODE PENELITIAN DAN PERANCANGAN SISTEM
Pada Bab ini akan dibahas tentang blok diagram rancangan penelitian, proses
penelitian yang akan dilakukan, denoising sinyal PCG, analisis dengan
transformasi Wavelet Diskrit, cara mengolah data hasil dekomposisi untuk mendapatkan energi serta normalisasi energi meliputi flowchart algoritma
program untuk mengolah data agar didapatkan pola energi dekomposisi, energi
normalisasi, serta standard deviasi.
4. BAB IV HASIL DAN PEMBAHASAN
Pada Bab ini akan dibahas mengenai pengujian program energi dan normalisasi
energi, program standar deviasi, dan hasil yang diperoleh dari pengolahan
energi dekomposisi pada frekuensi cuplik 8KHz, 44,1KHz, 48KHz, dengan
empat macam Mother Wavelet dengan berbagai orde. Parameter – parameter yang akan dianalisa adalah hasil normalisasi energi dekomposisi, rata-rata
normalisasi enegi dekomposisi, dan standar deviasi.
5. BAB V KESIMPULAN DAN SARAN
Berisi kesimpulan yang didapat dari hasil penelitian berdasarkan rumusan
2.1 Sinyal Suara Jantung (PCG)
Jantung adalah organ tubuh yang berfungsi untuk memompa darah dan
terdiri dari bagian atas yang disebut serambi (atrium) dan bagian bawah yang
disebut dengan bilik (ventricle). Otot-otot jantung memompa darah dari satu ruangan ke ruangan lainnya. Setiap kali terjadi proses pemompaan, katup jantung
membuka sehingga darah dapat mengalir ke ruangan yang dituju. Selanjutnya
katup menutup untuk mencegah aliran balik darah (Setiaji, 2011).
Pada detak jantung dihasilkan dua suara yang berbeda yang dapat
didengarkan pada stetoskop, yang sering dinyatakan dengan lub-dub. Suara lub
disebabkan oleh penutupan katup triscupid dan mitral (atrioventrikular) yang
memungkinkan aliran darah dari atrium (serambi jantung) ke ventricle (bilik jantung) dan mencegah aliran balik dan dapat disebut dengan suara jantung
pertama (S1) yang terjadi pada awal systole (periode jantung berkontraksi). Suara dub disebut suara jantung kedua (S2) yang terjadi pada akhir systole atau awal
diastole dan disebabkan oleh penutupan katup semilunar (aortic dan pulmonary) yang membebaskan darah ke sistem sirkulasi paru-paru dan seluruh tubuh (Rizal,
2007). Sinyal suara jantung merupakan sinyal gelombang suara yang lemah, dan
biasanya sinyal ini berada di range antara 10 Hz hingga 250 Hertz (Adinarayana,
Gambar 2.1 Bunyi Jantung Normal. (Setiaji, 2011)
Gambar 2.2 Anatomi Jantung. (Anonim, 2015).
2.2 Wavelet
Wavelet adalah sebuah gelombang kecil, yang dimana energinya terkonsentrasi dalam waktu untuk menyediakan alat bantu analisis non-stationer
yang fleksibel. Hal ini diilustrasikan dalam Gambar 2.3 dimana wave (kurva
sinus) bergerak dengan amplitudo sama pada -∞ ≤ t ≤ ∞ sehingga memiliki energi
yang tak berhingga, dengan Wavelet yang memiliki energi berhingga terkonsentrasi pada suatu titik. (Burrus, Gopinath, Guo, 1998)
Gambar 2.3 Bentuk Sebuah Wave dan Wavelet. (Burrus, Gopinath, Guo, 1998)
2.3 Transformasi Wavelet
Sinyal suara jantung merupakan jenis sinyal non-stationer. Sinyal non-stasioner memiliki frekuensi yang bervariasi di dalam waktu, sehingga untuk
menganalisisnya dibutuhkan metode transformasi yang dapat memberikan
resolusi frekuensi dan waktu secara bersamaan maka metode yang cocok adalah
Transformasi Wavelet dikarenakan Transfromasi Wavelet dapat
mempresentasikan informasi suatu sinyal dalam kawasan waktu dan frekuensi
2.3.1 Dekomposisi Wavelet
Wavelet dapat digunakan untuk melakukan analisis multi resolusi yang akan menghasilkan informasi dalam ranah waktu dan frekuensi. Skala atau
resolusi yang biasanya dilihat pada data merupakan peranan yang penting.
Algoritma Wavelet memproses data pada skala atau resolusi yang berbeda-beda. Pada Gambar menunjukan dekomposisi pada sinyal PCG berdasarkan pendekatan
Wavelet. Pada Gambar 2.4 dapat dilihat jika sebuah sinyal dengan jendela yang besar, maka seseorang hanya akan memperhatikan informasi sinyal secara
general, begitu juga saat sinyal dengan jendela yang kecil maka seseorang hanya
akan memperhatikan sinyal pada detailnya saja, sehingga penggunaan resolusi
yang bervariasi sangat diperlukan. Dasar dari prosedur analisis Wavelet adalah pemilihan fungsi prototype yang disebut Mother Wavelet. Analisis sementara dilakukan dengan frekuensi tinggi yang merupakan versi dari prototype Wavelet, sedangkan untuk analisis frekuensi dilakukan dengan dilatasi pada frekuensi
Gambar 2.4 Dekomposisi Sinyal PCG Dengan Menggunakan Wavelet. (Abbas, Bassam, 2009)
2.3.2 Transformasi Wavelet Kontinyu
Transformasi Wavelet kontinyu didefinisikan secara matematis dengan persamaan sebagai berikut
(2.1)
dimana ψ*(t) adalah konjugat komplek fungsi Wavelet penganalisa ψ(t). persamaan ini menunjukan bagaimana fungsi f(t) di dekomposisikan ke dalam
sebuah set dari fungsi basis s, ψ(t) disebut dengan Wavelet. Variabel s dan τ yang
merupakan skala dan translasi adalah dimensi baru setelah di transformasi.
2.3.3 Transformasi Wavelet Diskrit
Pada transformasi Wavelet kontinyu yang telah di jelaskan pada subab sebelumnya bahwa Continue Transform Wavelet (CWT) dihitung dengan menggeser skala yang dapat diubah secara kontinyu. Pada Transformasi Wavelet
Diskrit (TWD) skalanya dan translasinya tidak berubah secara kontinyu tapi
berubah secara diskrit, sehingga menghasilkan rumus sebagai berikut
(2.2)
s dan τ adalah integer dan adalah step dilatasi yang telah baku sesuai dengan aturan dyadic dan nilainya harus lebih besar dari satu. τ0 adalah parameter
translasi yang nilainya harus besar dari nol dan tergantung pada perubahan
dilatasi. Efek dari mendiskritkan Wavelet berdampak pada waktu-skala yang menjadi interval-interval diskrit. Jika sampel dari axis frekuensi yang
berhubungan dengan dyadic sampel yaitu s0 = 2, dan jika nilai translasi yang
dipilih adalah 1 berarti τ0 = 1, maka akan persamaan 2.2 akan menjadi
(2.3)
(Abbas, Bassam, 2009)
Dengan menggunakan fungsi Wavelet diskrit diatas sehingga diperoleh transformasi Wavelet diskrit sebagai berikut
,� dikenal sebagai koefisien detil Wavelet pada indek skala s dan lokasi τ. Wavelet diskrit dyadic orthonormal berkaitan dengan fungsi penskala dan persamaan dilatasinya. Fungsi penskala berkenaan dengan penghalusan sinyal dan memiliki bentuk yang sama seperti fungsi Wavelet adalah
� ,� =√ ��
−� �
� (2.5)
Lalu fungsi penskala di konvolusi dengan sinyal sehingga menghasilkan koefisien approksimasi
,� = ∫−∞∞ � ,� (2.6)
Akhirnya sinyal x(t) dapat disajikan sebagai kombinasi deret ekspansi dengan menggunakan koefisien aproksimasi dan koefisien detil sebagai berikut :
= ∑∞�= −∞ ,� � ,� + ∑∞= −∞∑∞�= −∞ ,�ψ ,� (2.7)
Gambar 2.5 Lokalisasi Wavelet Diskrit di Dalam Ruang Waktu-Skala Pada
Dyadic Grid. (Vallens,1999)
Untuk pengaplikasian transformasi Wavelet diskrit, sinyal masukan diproses dengan melewatkan sinyal yang akan dianalisis menggunakan filter
frekuensi rendah identik dengan informasi global yang terdapat pada sinyal input, sedangkan sinyal frekuensi tinggi identik dengan informasi detil dari sinyal input. Sinyal frekuensi rendah ini dapat dimanfaatkan untuk mengenali pola umum pada
sinyal input. (Alfatwa, 2009)
Contoh untuk dekomposisi pada Wavelet diskrit transform satu dimensi ditunjukan pada gambar 2.3 yang merupakan pohon dekomposisi, dimana S
merupakan sebuah sinyal yang di dekomposisi dengan orde 3 dan menghasilkan
koefisien detail cD1, cD2, cD3, serta koefisien aproksimasi cA1. (Ruth, 2014)
Gambar 2.6 Dekomposisi Orde 3 Untuk Sinyal S. (Matlab, 2013)
2.3.4 Mother Wavelet
Mother Wavelet merujuk pada arti kata small wave (gelombang kecil) yang berarti memiliki panjang yang terbatas. (Ruth, 2014) Mother Wavelet
)
b = parameter translasi
a = parameter skala
� = MotherWavelet
(Surtono, 2012)
Gambar 2.7 Illustrasi Transformasi Wavelet. (Kauhsoik, 2014)
2.3.4.1Wavelet Daubechies
Ingrid Daubechies merupakan salah satu dari bintang paling cemerlang
jenis Wavelet ini didapat dari penurunan persamaan Wavelet secara matematis oleh Igrid Daubechies. (Napitupulu, 2012).
Hasil akhir dari persamaan yang digunakan untuk menetukan koefisien filter
adalah sebagai berikut :
(2.9)
Daubechies membangun Wavelet yang mempunyai karakteristik compact support
(mempunyai panjang yang terbatas, Nk ) dan diperhasul hingga beberapa derajat.
Smoothness dari Wavelet berhubungan dengan kondisi momen yang merupakan
pengaruh dari fungsi skala. Untuk m = 0,1,2,…..,Nk/2 – 1. Wavelet Daubechies
memiliki Nk/2 vanishing moments yang berarti sinyal dapat diperhalus hingga polynomial dengan derajat Nk/2 – 1. Wavelet Daubechies sangat bagus untuk
merepresentasikan sifat-sifat polynomial di dalam sinyal. Panjang support dari
Wavelet Daubechies adalah Nk-1, contohnya adalah D2 (Wavelet Haar)
mempunyai support length sama dengan 1, D4 mempunyai support length sama dengan 3, D5 mempunyai support length sama dengan 4.
2.3.4.2 Wavelet Coiflet
`Wavelet Daubechies mempunyai bentuk yang tidak simetris, untuk meningkatkan
bentuk simetrisnya makan Daubechies membangun Wavelet Coiflet. Jenis Waveletfilter
ini tidak jauh berbeda dengan Daubechies filter. Filter Coiflet ini juga di design oleh Igrid Daubechies sama halnya dengan filter Daubechies. (Napitupulu, 2012)
Gambar 2.9 Wavelet Coiflet. (Venkatta, Kumar, 2014)
2.3.4.3 Wavelet Symlet
Symlet Wavelet merupakan bentuk singkat dari symmetrics Wavelet. Memang tidak secara sempurna simetris, namun filter ini di design dengan cara agar memiliki sedikit bentuk asimetris, Symlet juga dirancang oleh inggrid Daubechies
Gambar 2.10 Wavelet Symlet. (Venkatta, Kumar, 2014)
2.3.4.4 Wavelet Biorthogonal
Wavelet Biorthogonal menggunakan dua Wavelet, satu untuk dekomposisi (di sisi kiri) dan yang lainnya untuk rekonstruksi (di sebelah kanan sisi). Istilah
‘Biorthogonal’ merujuk pada adanya 2 fungsi skala yang orthogonal satu sama lain.
(Napitupulu, 2012).
2.4 Parameter 2.4.1 Standar Deviasi
Standar deviasi digunakan untuk mengukur besar dari variasi atau
penyebaran dari rata-rata. Semakin rendah nilai suatu standar deviasi
mengindikasikan bahwa titik data cenderung sangat dekat dengan rata-rata (nilai
yang diharapkan), begitu juga ketika nilai standard deviasi tinggi mengindikasikan
bahwa jangkauan titik data yang tersebar sangat besar.
= √� = √
�− ∑��= ��−� (2.10)S = standar deviasi, N = nomor sample, Xi= input sinyal jantung, µ= rata-rata
2.4.2 Energi
Energi berarti sesuatu memiliki kemampuan untuk menyebabkan
perubahan, energi biasanya digunakan untuk menggambarkan berapa banyak
potensi sistem yang harus berubah. Pada sinyal suara jantung, Energi total di
setiap komponen detail dan approksimasi memberikan informasi yang berguna
tentang lokasi artefak di sinyal. Artefak merupakan variasi sinyal yang tidak
diinginkan. Artefak ini termasuk instrumen suara, suara dari suara tubuh, suara
karena gerakan subjek dan gerakan diafragma stetoskop. Semakin rendah range
frekuensi hasil dekomposisi maka memiliki Energi normalisasi yang besar
dikarenakan mengandung suara jantung, sedangkan semakin tinggi range
frekuensi hasil dekomposisi maka memiliki Energi normalisasi yang kecil
Energi dekomposisi rerata di setiap EDi dihitung dengan persamanaan (diasumsikan akan didekomposisi hingga level 10) :
EDi= ∑
�ℎ � � , K= 1,2,……. Panjang Di (2.11)
i = 1,2,…. N=10
Energi dekomposisi rerata di EA10 dihitung dengan persamanaan (diasumsikan akan didekomposisi hingga level 10) :
EA10= ∑ �
�ℎ � � � , K= 1,2,…….Jumlah cuplik A10 (2.12)
2.4.3 Normalisasi Energi
Energi dekomposisi rerata perlu dinormalisasi agar energi terendah berada
pada nilai 0 dan energi tertinggi berada pada nilai 1 sehingga rentang nilai grafik
normalisasi energi akan berada diantara range 0 dan 1.
ENj = ��
� � , � , j = 1,2,3….n (2.13)
ENj = Energi rerata normalisasi pada dekomposisi ke –j (j= 1,2,3…N=10)
EDi = Energi rerata sinyal detail ke- I (i= 1,2,3….N=10)
EA10= Energi rerata sinyal aproksimasi A10
2.5 Denoising Wavelet
Denoising sinyal adalah memperkirakan nilai sinyal yang sebenarnya dari sinyal yang memiliki noise dan dapat digambarkan dengan persamaan sebagai berikut :
y(n) adalah sinyal yang berderau, x(n) adalah sinyal asli, dan s(n) merupakan
derau sinyal. (Sundararajan, 2015)
Pada umumnya, DenoisingWavelet memiliki prosedur sebagai berikut :
Menggunakan transformasi Wavelet ke sinyal yang berderau untuk
memproduksi koefisien Wavelet pada setiap level dekomposisi.
Memilih batas nilai threshold yang tepat pada setiap level dekomposisi dan
metode threshold yang diinginkan (hard atau soft tresholding)
Merekonstruksi sinyal dengan transformasi Waveletinverse.
Seperti yang telah disebutkan diatas bahwa prosedur Denoising memiliki tiga proses yaitu mendekomposisikan sinyal, memberikan batas nilai threshold, dan merekonstruksi sinyal. Denoising memiliki metode yang disebut Shrinkage yang dapat diimplementasikan dengan hard tresholding ataupun soft tresholding. Pada
hard tresholding, koifisien Wavelet yang memiliki nilai dibawah ambang batas yang telah ditentukan akan diubah menjadi nol, sedangkan pada soft tresholding
koifisien Wavelet akan di reduksi mendekati nilai ambang batas yang telah ditentukan. Nilai ambang batas merupakan nilai perkiraan dari tingkatan derau
yang didapatkan dengan menghitung nilai standar deviasi dari koefisien detail.
2.12 serta dapat dilihat pada gambar 2.13 yang merupakan contoh penerapan soft tresholding dimana nilai threshold � = 0.4 sehingga pada Gambar 2.13(b) semua nilai antar 0.4 hingga -0.4 akan dibuat menjadi nol, sedangkan nilai yang lebih
besar dari 0.4 dan lebih kecil dari -0.4 akan diubah mendekati axis- oleh 0.4.
(Sundararajan, 2015)
Gambar 2.12 Tipe Threshold Yaitu (a) Hard dan (b) Soft. (Ergen, 2012)
Gambar 2.13 (a) Sebuah Sinyal Sinusoidal (b) Sinyal Sinusoidal Dengan Soft
Metode hard tresholding tidak mempengaruhi koefisien detail yang lebih besar dari ambang batas atau threshold. Metode hard tresholding memiliki karakterstik yang tidak stabil dan sensitif terhadap perubahan yang kecil pada sinyal,
sedangkan metode soft tresholding dapat menimbulkan bias ketika koefisien terlalu besar, meskipun beberapa metode yang baru telah diusulkan untuk
mengatasi kekurangan metode shrinkage ini, namun metode shrinkage merupakan metode yang masih lebih efisien untuk digunakan. (Donoho, 1995)
Hal yang penting didalam metode tresholding adalah mencari nilai yang tepat untuk nilai ambang batas yang akan digunakan. Pada kenyataanya telah banyak
teknik ataupun metode yang diusulkan untuk menghitung nilai threshold, namun
pada kenyataanya semua teknik tersebut membutuhkan perkiraan tingkat derau.
Standar deviasi dari nilai data dapat digunakan untuk menentukan nilai perkiraan
tingkat derau, Donoho mengusulkan teknik untuk mendapatkan nilai estimator
yang cukup baik pada Denoising Wavelet yang persamaanya dijelaskan sebagai berikut :
(2.17)
Dimana L merupakan jumlah dari tingkatan dekomposisi, median dipilih dari nilai
koefisien detail pada sinyal yang dianalisis. (Donoho and Johnstone 1994;
3.1 Metode Penelitian
Gambar 3.1 Diagram Blok Rancangan Penelitian.
Sinyal PCG
Denoising
Dekomposisi
Frekuensi cuplik 8Khz
Frekuensi cuplik
44,1Khz
Frekuensi cuplik 48Khz
Daubechies Biorthogonal Symlet
Coiflet
Orde 2 Orde 5 Orde 2,5,7 Orde 2.8 Orde 3.9 Orde 6.8
Level n
Metode penelitian yang digunakan meliputi studi kepustakaan, pembuatan
program, dan analisis. Studi kepustakaan dilakukan untuk mencari teori atau
informasi dari buku, jurnal, dan artikel-artikel yang berkaitan dengan dekomposisi
sinyal PCG, Dari informasi studi kepustakaan yang diperoleh, maka dilakukan
pembuatan program pada matlab untuk membantu analisis.
Penelitian ini menggunakan data real yang didapat menggunakan stetoskop digital dari thinkslabone. Berdasarkan blok diagram pada Gambar 3.1,
dijelaskan bahwa sinyal PCG yang masuk akan di pecah dan Denoising untuk menghapus sinyal yang tidak diperlukan dari sinyal suara jantung yang telah
direkam. Setelah sinyal yang tidak diperlukan dihapus maka akan di dekomposisi
kedalam bentuk gelombang yang disebut Mother Wavelet, yang mana sinyal tersebut akan di pecah menjadi sinyal yang berfrekuensi tinggi (aproksimasi) dan
sinyal yang berfrekuensi rendah (detail), parameter yang mempengaruhi antara
lain sinyal PCG dari subyek, frekuensi cuplik, Mother Wavelet, dan tingkat dekomposisi. Dari hasil dekomposisi akan didapatkan beberapa sinyal detail dan
sinyal aproksimasi yang terakhir sehingga akan dihitung energi dekomposisi yang
telah dinormalisasi dan standard deviasi untuk ciri dari sinyal PCG
masing-masing subyek. Hasil perhitungan parameter yang telah ditentukan akan dianalisis
untuk menjadi ciri antara satu jenis sinyal PCG dengan jenis sinyal PCG yang
3.2 Prosedur Penelitian
Prosedur ini menjelaskan tentang langkah-langkah yang dilakukan dalam
penelitian seperti pada Gambar 3.2. dan Gambar 3.3
.
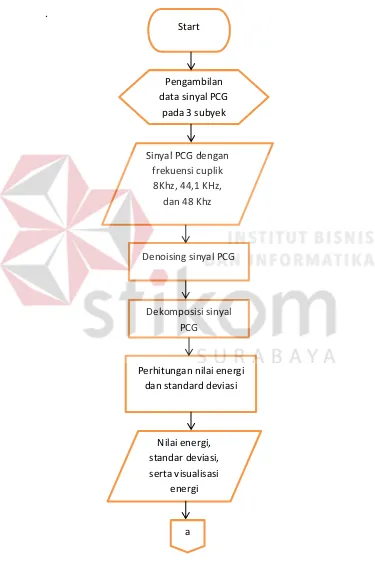
Gambar 3.2 Flowchart Proses Penelitian Sinyal Suara Jantung.
Pengambilan
Denoising sinyal PCG
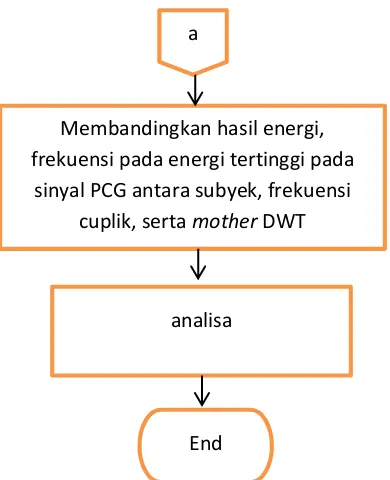
Gambar 3.3 Flowchart Proses Penelitian Sinyal Suara Jantung (Lanjutan Gambar 3.2).
Dari Gambar 3.2 dan Gambar 3.3 yang merupakan flowchart proses penelitian sinyal PCG yang akan dijelaskan sebagai berikut:
Data sinyal suara jantung persiklus diambil dari 3 subyek dalam keadaan
normal dan relaks, pada setiap subyek dilakukan pengambilan data sebanyak 30
kali dengan tiga macam frekuensi cuplik yaitu 8KHz, 44,1KHz, dan 48KHz.
Pengambilan data dilakukan dengan stetoskop digital thinkslabone.
Setelah pengambilan data sinyal PCG lengkap maka akan dipecah-pecah
dan didenoising untuk menghapus data sinyal yang tidak diperlukan, yang
terekam pada saat proses perekaman sinyal jantung, selanjutnya sinyal PCG akan
didekomposisi dengan sebelas Mother Wavelet diskrit yaitu symlet 2, symlet 5, symlet 7, daubechies 2, daubechies 5, daubechies 7, coiflet 2, coiflet 5,
biorthogonal 2.8, biorthogonal 3.9, dan biorthogonal 6.8. Setelah didekomposisi
maka akan dihitung nilai energi normalisasinya, serta standar deviasi.
a
Membandingkan hasil energi,
frekuensi pada energi tertinggi pada sinyal PCG antara subyek, frekuensi
cuplik, serta mother DWT
analisa
Hasil perhitungan dari normalisasi energi akan di visualisasikan berupa
grafik bar, lalu dilakukan analisis hasil normalisasi energi, serta standar deviasi.
Analisis dilakukan dengan membandingkan hasil energi, range frekuensi pada
energi tertinggi pada sinyal PCG antara subyek, frekuensi cuplik, serta mother
DWT.
3.3 Analisis Transformasi Wavelet Diskrit
Transformasi Wavelet diskrit digunakan untuk mendekomposisikan sinyal masukan PCG ke dalam bentuk gelombang seusai dengan Mother Wavelet yang digunakan, dekomposisi dilakukan dengan memisahkan sinyal masukan ke dalam
frekuensi rendah dan frekuensi tinggi, hasil dari dekomposisi adalah komponen
approximation yang merupakan scaling function (lowpass filter) dan komponen
detail yang merupakan Wavelet function. (Sundararajan, 2015).
Level dekomposisi ditetapkan berdasarkan frekuensi cuplik yang
digunakan. (Venkatta, 2015). Penelitian ini dipengaruhi beberapa parameter yaitu
sinyal PCG dari setiap subyek, frekuensi cuplik, Mother Wavelet, dan level dekomposisi. Sinyal PCG akan didekomposisikan menjadi A yang merupakan
approksimasi dan D yang merupakan detail, serta akan didekomposisikan sesuai
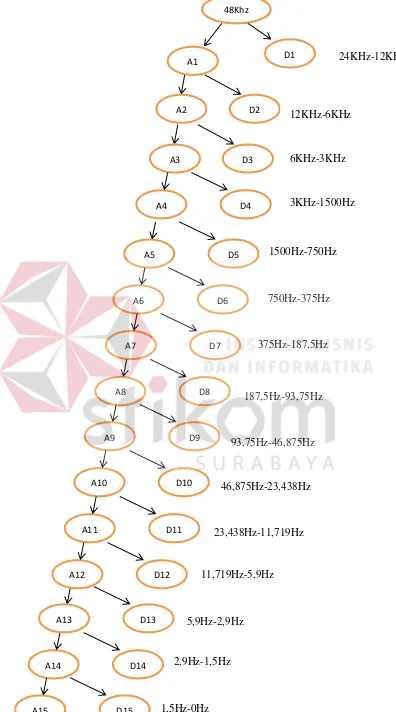
dengan frekuensi cupliknya, pada frekuensi cuplik 48Khz dan 44,1KHz akan
didekomposisikan sebanyak 15 tingkat yang dapat dilihat pada Gambar 3.4 dan
3.5, sedangakan frekuensi cuplik 8Khz akan didekomposisikan sebanyak 10
Analisis transformasi Wavelet diskrit dilakukan dengan mendekomposisi sinyal PCG menggunakan Matlab, untuk mendekomposisi sinyal satu dimensi
maka digunakan fungsi wavedec, cuplikan program proses dekomposisi dapat
dilihat pada Gambar 3.7
Gambar 3.7 Cuplikan Program Proses Dekomposisi.
Fungsi wavedec(‘x’,N,’Wname’) pada matlab memiliki parameter input x
untuk sinyal masukan, N untuk tingkat level, dan Wname untuk Mother Wavelet, sedangkan parameter outputnya adalah hasil dekomposisi dan panjang data dari
setiap komponen dapat dilihat pada Gambar 3.8
3.3.1 Denoising
Denoising sinyal bertujuan untuk menghapus data yang tidak diperlukan, yang terekam pada saat proses perekaman suara sinyal jantung. Setelah sinyal
suara jantung diambil maka sinyal harus di Denoising terlebih dahulu, metode
Denoising yang digunakan adalah soft tresholding, dimana metode ini akan membuat nilai yang berada antara threshold –T< X < T menjadi 0, sedangkan
nilai yang lebih dari T telah diubah untuk mendekati axis X. Denoising pada penelitian ini dilakukan secara manual dan Mother Wavelet yang digunakan untuk
Denoising adalah daubechies 5, hal ini dikarenakan pada penelitian yang dilakukan oleh Mishra tahun 2013 dengan judul Denoising Of Heart Sound Signal Using Wavelet Transform didapatkan bahwa daubechies 5 memiliki nilai presentase rekonstruksi yang maksimum dan nilai SNR(Signal to Noise Ratio) yang maksimum dimana SNR merupakan metode untuk mengukur kekuatan
sinyal terhadap derau, yang berarti bahwa semakin besar nilai SNR maka akan
semakin baik hasil produk yang didapat dari Denoising tersebut.
3.3.2 Energi Dekomposisi dan Normalisasi Energi Dekomposisi
Energi Dekomposisi digunakan untuk mengetahui ciri atau pola sinyal
PCG dengan yang lainya, pada penelitian ini digunakan tiga frekuensi cuplik yang
akan menghasilkan dua macam level yaitu dekomposisi 15 level untuk 48KHz
dan 44,1KHz, serta dekomposisi 10 level untuk 8Khz. Berdasarkan level maka
dapat dihitung energi dekomposisinya pada setiap komponen detail dan
approksimasi terakhir. Energi dekomposisi rerata pada sinyal detail dapat dihitung
Energi dekomposisi rerata level 10
EDi= ∑
� �ℎ ��� , K= 1,2,……. Panjang Di (3.1)
i = 1,2,…. N=10
Energi dekomposisi rerata level 15
EDi= ∑
� �ℎ ��� , K= 1,2,……. Panjang Di (3.2)
i = 1,2,…. N=15
Energi dekomposisi rerata sinyal aproksimasi dihitung dengan persamaan sebagi
berikut:
Energi dekomposisi rerata level 10
EA10= � �ℎ ��� �∑ � , K= 1,2,…….Jumlah cuplik A10 (3.3)
Eenergi dekomposisi rerata level 15
EA15= ∑ � 5
� �ℎ ��� � 5, K= 1,2,…….Jumlah cuplik A15 (3.4)
Setelah energi didekomposisi rerata dihitung maka akan dilakukan normalisasi
energi agar nilai energi berada diantara nilai 0 dan 1. Energi normalisasi dihitung
dengan persamaan sebagai berikut:
Normalisasi Energi dekomposisi level 10
ENj = ��
� � �� , � (3.5)
EDi = Energi rerata sinyal detail ke- I (i= 1,2,3….N=10)
EA10= Energi rerata sinyal aproksimasi A10
Normalisasi Energi dekomposisi level 15
ENj = � � ��
�� , � 5 (3.6)
ENj = Energi rerata normalisasi pada dekomposisi ke –j (j= 1,2,3…N=15)
EDi = Energi rerata sinyal detail ke- I (i= 1,2,3….N=15)
3.3.3 Flowchart Program Energi Dekomposisi dan Normalisasi Energi Flowchart program untuk mendapatkan nilai energi dekomposisi dan normalisasi energi, serta visualisasi normalisasi energi adalah sebagai
berikut:
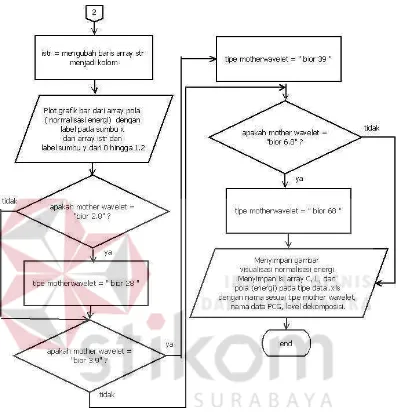
Gambar 3.10 Flowchart Program Perhitungan Energi Dekomposisi dan Normalisasi Energi (Lanjutan Gambar 3.9).
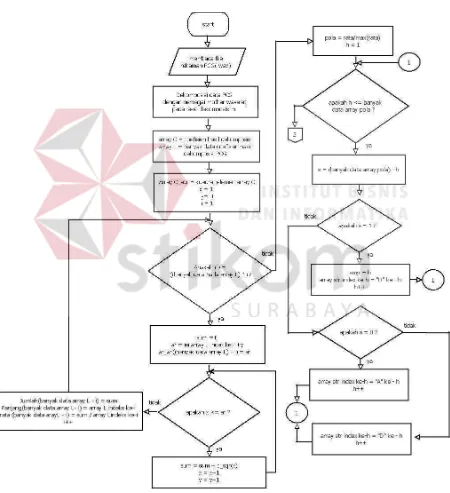
Gambar 3.9 dan Gambar 3.10 merupakan gambar flowchart dari program perhitungan energi dan normalisasi energi yang akan dijelaskan sebagai berikut :
2. Program menyimpan data rekaman ke dalam bentuk array dan
mendekomposisikanya dengan transformasi Wavelet descrete menggunkanan berbagai Mother Wavelet dan berbagai orde ke dalam bentuk data-data integer yang tersimpan pada array C, selain itu hasil dekomposisi juga menyimpan
banyak data hasil yang disimpan pada array L.
3. Semua elemen pada array C di kuadratkan.
4. Pemecahan data pada array C yang di sesuaikan dengan nilai dari setiap index
dari array L yang merupakan array untuk menampung banyak data pada setiap
detail dan aproksimasi hasil dekomposisi.
5. Data yang sudah dipecah pada array C dijumlahkan sesuai dengan tingkat
detail dan aproksimasinya untuk mendapatkan nilai energi pada setiap
tingkatan detail dan aproksimasi.
6. Data pada array C yang telah di jumlah usesuai dengan tingkat detail dan
aproksimasi untuk mendapatkan nilai energi akan di hitung nilai rata-ratanya.
7. Menghitung normalisasi energi dari setiap aproksimasi dan detail dengan
membagi nilai rata-rata energi dari setiap tingkatan detail dan aproksimasi
dengan nilai rata-rata yang terbesar lalu hasilnya akan disimpan pada array
pola.
8. Hasil dari normalisasi energi di visualisasikan dengan grafik bar.
9. Data koifisien pada array C, banyak data pada setiap detail dan aproksimasi
pada array L, dan nilai normalisasi energi yang disimpan pada array pola akan
penamaan file yang sesuai dengan Mother Wavelet, urutan data sampel, dan level dekomposisi yang digunakan.
3.3.4 Standard Deviasi
Standar deviasi digunakan untuk mengukur variasi atau penyebaran data
dari rata-rata, Jika nilai standar deviasi semakin rendah maka dapat diartikan
bahwa data cenderung sangat dekat dengan rata-rata, namun ketika nilai standar
deviasi tinggi mengindikasikan bahwa jangkauan data yang tersebar sangat besar.
Dalam pengukuran energi, standar deviasi digunakan untuk mengetahui tingkat
persebaran data dari nilai rata-rata energi normalisasi maupun energi dekomposisi
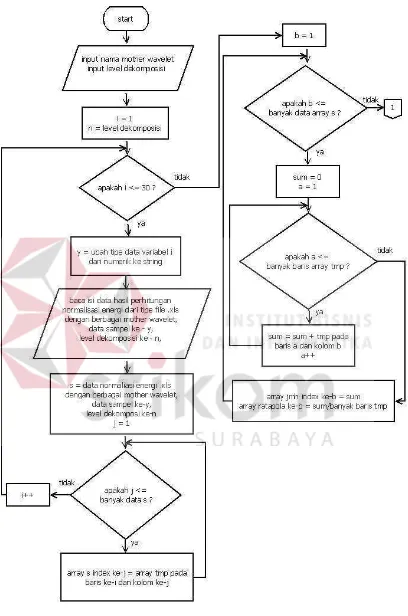
dari setiap komponen detail ataupun aproksimasi. Adapun flowchart program yang digunakan untuk menghitung rata-rata, dan standar deviasi akan di jelaskan
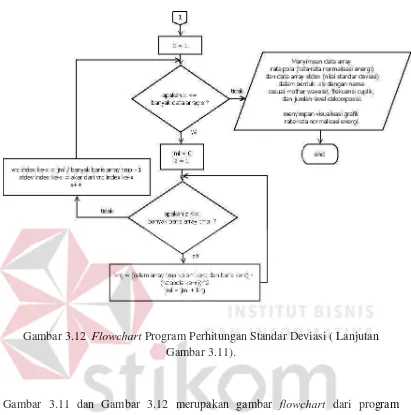
Gambar 3.12 Flowchart Program Perhitungan Standar Deviasi ( Lanjutan Gambar 3.11).
Gambar 3.11 dan Gambar 3.12 merupakan gambar flowchart dari program perhitungan energi dan normalisasi energi yang akan dijelaskan sebagai berikut :
1. Nama Mother Wavelet dan level dekomposisi di inputkan untuk memanggil file
normalisasi energi yang bertipe .xls yang sesuai dengan nama Mother Wavelet
dan level dekomposisi.
3. Menghitung rata-rata normalisasi energi dengan cara menjumlahkan dan
manghitung rata-rata isi baris array tmp yang merupakan tingkatan detail dan
aproksimasi.
4. Menyimpan hasil rata-rata normalisasi energi pada setiap aproksimasi dan
detail ke array ratapola.
5. Menghitung standar deviasi normalisasi energi pada setiap aproksimasi dan
detail dan disimpan pada array stdev.
6. Menyimpan data array ratapola yang merupakan nilai rata-rata normalisasi
energi dan data array stdev yang merupakan nilai standar deviasi normalisasi
energi dalam format Microsoft excel dengan nama sesuai Mother Wavelet, level dekomposisi, serta frekuensi cuplik.
7. Menyimpan secara otomatis dan menampilkan visualisasi nilai rata-rata
BAB IV
HASIL DAN PEMBAHASAN
4.1 Kebutuhan Sistem
Sebelum melakukan perbandingan sinyal suara jantung dibutuhkan
perangkat lunak yang dapat menunjang penelitian. Perangkat keras dan lunak
yang digunakan dapat dilihat pada Tabel 4.1 dan Tabel 4.2.
Tabel 4.1 Kebutuhan Perangkat Keras.
Perangkat Keras Spesifikasi
Processor Intel Core i3
Memori 4 Gb
Sistem Operasi Windows 7
Tabel 4.2 Kebutuhan Perangkat Lunak.
Perangkat Lunak Uraian
Matlab
Aplikasi yang digunakan untuk mengolah sinyal suara
jantung menjadi energi dan energi normalisasi.
Audacity
Aplikasi yang digunakan untuk merekam suara sinyal
jantung dari digital stetoskop thinkslabone ke
4.2 Pengujian Program
Pengujian program untuk meghitung nilai energi serta energi normalisasi
dan standar deviasi dilakukan dengan membandingkan perhitungan rumus secara
manual pada microsoft excel dan hasil perhitungan program yang akan disimpan
secara otomatis didalam format Microsoft excel.
4.2.1 Tujuan
Pengujian ini dilakukan untuk mengetahui apakah program yang telah
dibuat sesuai dengan dasar teori rumus yang ada.
4.2.2 Prosedur Pengujian Program Energi dan Normalisasi Energi
Prosedur pengujian program energi dan normalisasi energi :
a. Mendapatkan nilai hasil dekomposisi dari matlab yaitu berupa koifisien dan
banyak data pada setiap detail dan aproksimasi dalam bentuk format Microsoft
excel (.xls).
b. Memecah data koifisien sesuai dengan banyak data yang ada pada setiap detail
dan aproksimasi.
c. Menghitung energi dekomposisi sinyal detail dengan rumus sebagai berikut:
Energi dekomposisi rerata level 10
EDi= ∑
� �ℎ ��� , K= 1,2,……. Panjang Di (4.1)
Energi dekomposisi rerata level 15
EDi= ∑
� �ℎ ��� , K= 1,2,……. Panjang Di (4.2)
i = 1,2,…. N=15
d. Menghitung energi dekomposisi rerata sinyal aproksimasi dihitung dengan
persamaan sebagi berikut:
Energi dekomposisi rerata level 10
EA10= ∑ �
� �ℎ ��� � , K= 1,2,…….Jumlah cuplik A10 (4.3)
Energi dekomposisi rerata level 15
EA15= � �ℎ ��� �∑ � 5
5, K= 1,2,…….Jumlah cuplik A15
e. Menghitung normalisasi energi dekomposisi rerata sinyal aproksimasi dan
detail dihitung dengan persamaan sebagi berikut:
ENj = � � ��
�� , � (4.4)
ENj = Energi rerata normalisasi pada dekomposisi ke –j (j= 1,2,3…N=10)
4.2.3 Hasil Pengujian Program Energi dan Normalisasi Energi
Hasil dari pengujian dengan menghitung secara manual di Microsoft
Excel dapat dilihat pada Gambar 4.1, sedangkan hasil dari program energi dan
Gambar 4.1. Hasil Perhitungan Energi dan Normalisasi Energi Dengan
Menggunakan Microsoft Excel.
Gambar 4.2. Hasil Perhitungan Program Energi dan Normalisasi Energi.
4.2.4 Prosedur Pengujian Program Standar Deviasi
Prosedur pengujian program standar deviasi :
a. Mendapatkan nilai normalisasi energi dalam format .xls pada data ke-1 hingga
data ke-30.
b. Program secara otomatis membaca nilai normalisasi energi pada data ke-1
c. Menghitung standar deviasi dari energi normalisasi secara manual
menggunakan Microsoft excel dengan rumus sebagai berikut :
� = √�2 = √
�− ∑��= ��−� (4.5)
S = standar deviasi, N = nomor sample, Xi= input sinyal jantung, µ= rata-rata
4.2.5 Hasil Pengujian Program Standar Deviasi
Hasil dari pengujian dengan menghitung standar deviasi normalisasi
energi pada setiap detail dan aproksimasi secara manual di Microsoft Excel dapat
dilihat pada Gambar 4.3, dan hasil perhitungan nilai rata-rata normalisasi energi
secara manual pada setiap detail dan aproksimasi manual di Microsoft excel dapat
dilihat pada Gambar 4.5, sedangkan hasil perhitung standar deviasi normalisasi
energi pada setiap detail dan aproksimasi dari program dapat dilihat pada Gambar
4.4, serta rata-rata normalisasi energi pada setiap detail dan aproksimasi dari
program dapat dilihat pada Gambar 4.6. Pada Gambar 4.3 dan Gambar 4.4 dapat
dilihat hasil pengujian dengan perhitungan nilai standar deviasi normalisasi energi
secara manual dan perhitungan program secara otomatis menghasilkan hasil
perhitungan yang sama, begitu juga pada Gambar 4.5 dan 4.6 dapat dilihat hasil
pengujian dengan perhitungan nilai rata-rata normalisasi energi secara manual dan
Gambar 4.3 Hasil Perhitungan Standar Deviasi Normalisasi Energi Secara Manual
Dengan Menggunakan Microsoft Excel.
Gambar 4.4 Hasil Perhitungan Program Standar Deviasi Normalisasi Energi.
Gambar 4.5 Hasil Perhitungan Rata-Rata Normalisasi Energi Secara Manual
Dengan Menggunakan Microsoft Excel.
Gambar 4.6 Hasil Perhitungan Program Rata-Rata Normalisasi Energi.
4.3 Pengambilan Data
Data diambil menggunakan stetoskop digital thinkslab dengan
menggunakan tiga macam frekuensi cuplik yaitu 8KHz, 44,1KHz, 48KHz untuk
setiap subyek. Pada setiap subyek dan setiap frekuensi cuplik dilakukan
pengambilan 30 siklus data dimana persiklusnya memiliki waktu rata-rata sekitar
Gambar 4.7, untuk subyek dua dapat dilihat pada Gambar Gambar 4.8, untuk
subyek dua dapat dilihat pada Gambar 4.9.
(a)
(b)
(c)
Gambar 4.7 Sinyal Hasil Pengambilan Dengan Stetoskop Digital Thinkslabone di
Subyek Satu Pada (A) Frekuensi 8KHz, (B) Frekuensi 44,1KHz, (C) Frekeunsi
(a)
(b)
(c)
Gambar 4.8 Sinyal Hasil Pengambilan Dengan Stetoskop Digital Thinkslabone di
Subyek Dua Pada (A) Frekuensi 8KHz, (B) Frekuensi 48KHz, (C) Frekeunsi 44,1
(a)
(b)
(c)
Gambar 4.9 Sinyal Hasil Pengambilan Dengan Stetoskop Digital Thinkslabone di
Subyek Tiga Pada (A) Frekuensi 8KHz, (B) Frekuensi 48KHz, (C) Frekeunsi
4.4 Denoising Sinyal PCG
Pada Gambar 4.7, Gambar 4.8, dan Gambar 4.9 dapat dilihat bahwa sinyal
hasil pengambilan dengan digital stetoskop thinkslabone masih memiliki artefak,
sehingga sebelum di olah lebih jauh maka sinyal yang tidak dibutuhkan, yang
terekam pada saat proses perekaman sinyal suara jantung harus dihapus. Pada
Denoising ini digunakan Mother Wavelet Daubechies 5 dan Soft Tresholding
dimana nilai threshold di dapatkan secara manual. Hasil dari Denoising sinyal suara jantung dari subyek satu dapat dilihat pada Gambar 4.10, Hasil dari
Denoising sinyal suara jantung dari subyek dua dapat dilihat pada Gambar 4.11, dan Hasil dari Denoising sinyal suara jantung dari subyek tiga dapat dilihat pada Gambar 4.12.
(a)
(c)
(d)
(e)
(f)
Gambar 4.10 Hasil Denoising Pada Subyek Satu (A) Sinyal Pada Frekuensi Cuplik 8 KHz Sebelum Didenoising (B) Sinyal Pada Frekuensi Cuplik 8 KHz
Didenoising (D) Sinyal Pada Frekuensi Cuplik 44,1 KHz Setelah Didenoising (E)
Sinyal Pada Frekuensi Cuplik 48 KHz Sebelum Didenoising (F) Sinyal Pada
Frekuensi Cuplik 48 KHz Setelah Di Denoising.
(a)
(b)
(d)
(e)
(f)
Gambar 4.11 Hasil Denoising Pada Subyek Dua (A) Sinyal Pada Frekuensi Cuplik 8 KHz Sebelum Didenoising (B) Sinyal Pada Frekuensi Cuplik 8 KHz
Setelah Didenoising (C) Sinyal Pada Frekuensi Cuplik 44,1 KHz Sebelum
Didenoising (D) Sinyal Pada Frekuensi Cuplik 44,1 KHz Setelah Didenoising (E)
Sinyal Pada Frekuensi Cuplik 48 KHz Sebelum Didenoising (F) Sinyal Pada
(a)
(b)
(d)
(e)
(f)
Gambar 4.12 Hasil Denoising Pada Subyek Tiga (A) Sinyal Pada Frekuensi Cuplik 8 KHz Sebelum Didenoising (B) Sinyal Pada Frekuensi Cuplik 8 KHz
Setelah Didenoising (C) Sinyal Pada Frekuensi Cuplik 44,1 KHz Sebelum
Didenoising (D) Sinyal Pada Frekuensi Cuplik 44,1 KHz Setelah Didenoising (E)
Sinyal Pada Frekuensi Cuplik 48 KHz Sebelum Didenoising (F) Sinyal Pada
4.5 Dekomposisi Sinyal PCG
Setelah di Denoising maka sinyal akan di dekomposisi menggunakan matlab. Dekomposisi dilakukan dengan menggunakan beberapa Mother Wavelet
yaitu Symlet 2, Symlet 5, Symlet 7, Daubechies 2, Daubechies 5, Daubechies 7,
Coiflet 2, Coiflet 5, Biorthogonal 2.8, Biorthogonal 3.9, Biorthogonal 6.8. Level
dekomposisi tergantung dengan frekuensi cuplik, jika frekuensi cuplik 8KHz
maka akan didekomposisi hingga 10 level, namun jika frekuensi cuplik 44,1 KHz,
dan 48KHz maka akan didekomposisi hingga 15 level. Setelah didekomposisi
maka akan mendapatkan dua koefisien yang ditampung di dalam array variabel C
dan variabel L, dimana isi variabel C adalah koefisien hasil dekomposisi yaitu
approksimasi dan detail sedangkan variabel L digunakan untuk menampun
panjang setiap komponen approksimasi dan detail.
4.6 Analisis Hasil Dekomposisi Energi
Pada tahap ini akan dijelaskan tentang hasil pengolahan energi dan
normalisas energi untuk mendapatakan pola pada setiap PCG.
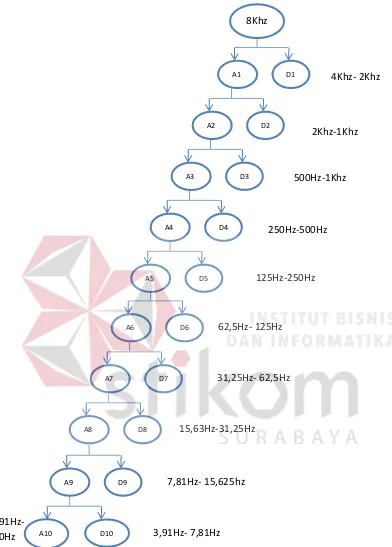
4.6.1. Frekuensi cuplik 8KHz
Hasil pengolahan sinyal PCG yang dengan frekuensi cuplik 8KHz akan
menghasilkan dekomposisi 10 level, dimana pada level satu akan menghasilkan
komponen detail D1 dengan jangkauan frekuensi 2KHz hingga 4KHz dan
komponen aproksimasi A1 dengan jangkauan frekuensi 2KHz hingga 0Hz,
selanjutnya akan dipecah lagi menjadi D2 (2KHz – 1KHz), A2(1KHz-0KHz),
Begitu seterusnya hingga D10(7,813HZ- 3,9Hz) dan A10 (3,9Hz-0Hz) untuk
Setelah didekomposisi maka akan dihitung nilai normalisasi energi
dekomposisi, Hasil normalisasi energi dekomposisi pada frekuensi 8KHz dari
ketiga subyek normal dengan menggunakan 11 Mother Wavelet dapat dilihat pada Tabel 4.3, untuk visualisasi pola normalisasi energi dekomposisi rata-rata dapat
dilihat pada Gambar 4.13.
Tabel 4.3 Normalisasi Energi Dekomposisi, Rata-Rata Energi, & Standar Deviasi
Pada Frekuensi Cuplik 8KHz
Wavelet
Coiflet 2 0.73938
15.625-62.5 0.90325 62.5-125 0.94933 62.5-125 0.86399 0.11035 Coiflet 5 0.75826
0
Gambar 4.13. Normalisasi Energi Rata-Rata Dekomposisi Dengan Frekuensi Cuplik 8KHz.
Dari hasil Tabel 4.3 dan Gambar 4.13 dapat dilihat bahwa Biorthogonal 3.9
memiliki rata-rata normalisasi energi dekomposisi yang paling tinggi yaitu
0,950361 dengan standar deviasi yang paling rendah pada sampling 8KHz,
standar deviasi menandakan bahwa range persebaran data dari rata-rata tidak
terlalu jauh, mendekati akurat, selain itu 63.6% dari seluruh Mother Wavelet menghasilkan energi dekomposisi terbesar pada D6 dengan range frekuensi 62.5
hingga 125Hz
.
4.6.2. Frekuensi cuplik 44,1 KHz
Hasil pengolahan sinyal PCG yang dengan frekuensi cuplik 44,1 KHz
akan menghasilkan dekomposisi 15 level, dimana pada level satu akan
menghasilkan komponen detail D1 dengan jangkauan frekuensi 11025Hz hingga
hingga 0Hz, selanjutnya akan dipecah lagi menjadi D2 (11025Hz – 551,25Hz),
A2(551,25Hz-0KHz), Begitu seterusnya hingga D10(1,35HZ- 0 Hz) dan A10
(0Hz) untuk Gambar dekomposisi 15 tingkat dapat dilihat pada Gambar 3.5.
Setelah didekomposisi maka akan dihitung nilai normalisasi energi dekomposisi,
Hasil normalisasi energi dekomposisi pada frekuensi 44,1 KHz dari ketiga subyek
normal dengan menggunakan 11 Mother Wavelet dapat dilihat pada Tabel 4.4, untuk visualisasi pola normalisasi energi dekomposisi rata-rata dapat dilihat pada
Gambar 4.14.
Tabel 4.4 Normaliasi Energi Dekomposisi, Rata-Rata Energi, & Standar Deviasi
Pada Frekuensi Cuplik 44,1KHz.
Wavelet
Symlet 2 1.00000
43.066-86.133 0.97609
43.066-86.133 1.00000
43.066-86.133 0.99203 0.01381
Symlet 5 1.00000
43.066-86.133 0.94966
43.066-86.133 1.00000
43.066-86.133 0.98322 0.02906
Symlet 7 1.00000
43.066-86.133 0.93679
Coiflet 2 1.00000
43.066-86.133 0.92389
43.066-86.133 1.00000
43.066-86.133 0.97463 0.04394
Coiflet 5 1.00000
0.86
Gambar 4.14. Normalisasi energi rata-rata dekomposisi dengan frekuensi cuplik 44,1 KHz.
Dari hasil Tabel 4.4 dan Gambar 4.14 dapat dilihat bahwa Biorthogonal 3.9
memiliki rata-rata normalisasi energi dekomposisi yang paling tinggi yaitu 1
dengan standar deviasi yang paling rendah yaitu 0 pada sampling 44,1 KHz,
standar deviasi menandakan bahwa range persebaran data dari rata-rata tidak ada
karena nilai standar deviasi menghasilkan 0 yang berarti akurat dan presisi, selain
itu data menunjukan hasil yang konsisten karena 100% dari 990 data (11 Mother
Wavelet pada subyek satu, dau, dan tiga pada frekuensi cuplik 44,1 KHz)
menghasilkan energi dekomposisi terbesar pada D9 dengan range frekuensi
43.066Hz hingga 86.133Hz.
4.6.3. Frekuensi cuplik 48KHz
Hasil pengolahan sinyal PCG yang dengan frekuensi cuplik 48KHz akan
menghasilkan dekomposisi 15 level, dimana pada level satu akan menghasilkan
komponen detail D1 dengan jangkauan frekuensi 12KHz hingga 24KHz dan
komponen aproksimasi A1 dengan jangkauan frekuensi 12KHz hingga 0Hz,
selanjutnya akan dipecah lagi menjadi D2 (12KHz – 6KHz), A2(6KHz-0KHz),
Begitu seterusnya hingga D10(1,5HZ-0Hz) dan A10(0Hz) untuk Gambar
dekomposisi 15 tingkat dapat dilihat pada Gambar 3.4. Setelah didekomposisi
maka akan dihitung nilai normalisasi energi dekomposisi, Hasil normalisasi energi
dekomposisi pada frekuensi 48KHz dari ketiga subyek normal dengan
menggunakan 11 Mother Wavelet dapat dilihat pada Tabel 4.5, untuk visualisasi pola normalisasi energi dekomposisi rata-rata dapat dilihat pada Gambar 4.15.
Tabel 4.5 Normaliasi Energi Dekomposisi, Rata-Rata Energi, & Standar Deviasi
Pada Frekuensi Cuplik 48KHz.
Wavelet
Symlet 2 0.99412
46.875-93.75 0.88977
93.75-187.5 1.00000
46.875-93.75 0.96130 0.06202
Symlet 5 1.00000
46.875-93.75 0.89698
93.75-187.5 1.00000
46.875-93.75 0.96566 0.05948
Symlet 7 1.00000
46.875-93.75 0.91276
Coiflet 2 1.00000
46.875-93.75 0.92772
93.75-187.5 1.00000
46.875-93.75 0.97591 0.04173
Coiflet 5 1.00000
Gambar 4.15. Normalisasi energi rata-rata dekomposisi dengan frekuensi cuplik 48KHz
Dari hasil Tabel 4.5 dan Gambar 4.15 dapat dilihat bahwa Coiflet 2 memiliki
rata-rata normalisasi energi dekomposisi yang paling tinggi yaitu 0.97590 dengan
standar deviasi yang paling rendah yaitu 0,41729 pada sampling 48KHz, namun
hasil energi dekomposisi dengan Mother Wavelet yang lain tidak terlalu jauh berbeda, dan cenderung konsisten pada nilai 0.9. Selain itu 69,7% data dari 990
data (11 Mother Wavelet pada subyek satu, dua, dan tiga pada frekuensi cuplik 48KHz) menghasilkan energi dekomposisi terbesar pada D9 dengan range
frekuensi 46.88Hz hingga 93.75Hz. 0
0.2 0.4 0.6 0.8 1 1.2
Normalisasi Energi Dekomposisi
4.6.4. Database sinyal PCG Michigan
Database sinyal PCG normal dari Michigan University di gunakan untuk membandingkan sinyal PCG dari tiga subyek normal yang diambil menggunakan
stetoskop digital. Database sinyal PCG normal dari Michigan University dalam keadaan tanpa noise, sehingga didapat hasil pada Tabel 4.6 dan visualisasi pola
dengan frekuensi cuplik 8KHz, 44,1KHz, 48KHz. dapat dilihat pada Gambar 4.16
sedangkan visualisasi rata-rata normalisasi energi dapat dilihat pada Gambar 4.17.
Tabel 4.6 Normaliasi Energi Dekomposisi, Rata-Rata Energi, & Standar Deviasi
Pada Frekuensi Database Michigan University Pada Sampling 8 KHz, 44,1 KHz, dan 48 KHz.
Symlet 2 1.00000 62.5-125 0.99840
43.066-172.27 1.00000
46.875-93.75 0.99947 0.00093
Symlet 5 1.00000 62.5-125 0.92180
43.066-172.27 1.00000
46.875-93.75 0.97393 0.04515
Symlet 7 1.00000 62.5-125 1.00000
43.066-86.133 1.00000
Coiflet 2 1.00000 62.5-125 1.00000
43.066-86.133 1.00000
46.875-93.75 1.00000 0.00000
Coiflet 5 1.00000 62.5-125 1.00000
(a)
(b) 0
0.2 0.4 0.6 0.8 1 1.2
Normalisasi Energi 8KHz
0.88 0.9 0.92 0.94 0.96 0.98 1 1.02
(c)
Gambar 4.16. Normalisasi Energi Rata-Rata Dekomposisi Dari Sinyal PCG
Michigan University Pada (A) Frekuensi Cuplik 8KHz (B) Frekuensi Cuplik 44,1KHz (C) Frekuensi Cuplik 48KHz.
Gambar 4.17. Rata-Rata Normalisasi Energi Dekomposisi Dari Sinyal PCG
Pada Gambar 4.16, Gambar 4.17 dan Tabel 4.6 dapat dilihat bahwa pada Mother
Wavelet dan frekuensi cuplik yang berbeda sebagian besar hasil pola energi tidak
terlalu jauh satu sama lain yaitu berada pada energi dekomposisi dengan nilai 1.
Untuk frekuensi cuplik 8KHz pada semua Mother Wavelet energi tertinggi berada pada D6 dengan range frekuensi 62.5Hz hingga 125Hz, untuk frekuensi 44,1KHz
pada 63.6% Mother Wavelet energi tertinggi berada pada D9 dengan range frekuensi 43.066Hz hingga 86.133Hz, untuk frekuensi 48KHz pada semua Mother
Wavelet energi tertinggi berada pada D9 yaitu dengan range frekuensi 46.88Hz
hingga 93.75Hz.
Secara keseluruhan dapat disimpulkan bahwa hasil pengolahan sinyal PCG
yang didapat dari pengambilan data secara langsung dan data dari Michigan University didapatkan bahwa untuk sampling 8KHz, terdapat kesesuaian range frekuensi pada energi dekomposisi terbesar berada di D6 yaitu dengan range
frekuensi 62.5 Hz hingga 125 Hz. Untuk sampling 44,1KHz terdapat kesesuaian
range frekuensi pada energi dekomposisi terbesar berada di D9 yaitu dengan
frekuensi range 43.066 Hz hingga 86.133 Hz. Untuk sampling 48KHz terdapat
kesesuaian range frekuensi pada energi dekomposisi terbesar berada di D9 yaitu
dengan frekuensi range 46.88 Hz hingga 93.75 Hz.
Dari berbagai frekuensi cuplik dalam pengujian ini didapatkan bahwa
sinyal jantung normal memiliki energi dekomposisi terbesar pada range 62.5 Hz
5.1 Kesimpulan
Berdasarkan seluruh hasil analisa dari pola berdasarkan enrgi
dekomposisi sinyal PCG dari tiga subyek, dengan tiga frekuensi, empat Mother Wavelet dengan berbagai orde maka dapat diambil beberapa kesimpulan sebagai berikut.
1. Range frekuensi hasil dekomposisi dengan energi normalisasi terbesar untuk
4 Mother Wavelet dengan orde yang berbeda memberikan hasil range frekuensi yang tidak terlalu jauhantara satu dengan yang lainya.
2. Pada frekuensi cuplik 8KHz sebanyak 63.6% dari seluruh Mother Wavelet
dalam uji coba menghasilkan energi dekomposisi terbesar pada D6 dengan
range frekuensi 62.5Hz hingga 125Hz, sedangkan pengujian yang dilakukan
pada data sinyal PCG yang berasal dari Michigan University menunjukan bahwa seluruh data uji coba (100%) menghasilkan energi tertinggi pada D6
(62.5-125Hz), hal ini berarti bahwa pada kedua pengujian menunjukkan
adanya kesesuaian range frekuensi berada pada D6.
3. Pada frekuensi cuplik 44,1KHz data menunjukan hasil yang konsisten
karena 100% dari 990 data (11 Mother Wavelet pada subyek satu, dua, dan tiga) menghasilkan energi dekomposisi terbesar pada D9 dengan range
frekuensi 43.066Hz hingga 86.133Hz, sedangkan pengujian yang dilakukan
hal ini berarti bahwa pada kedua pengujian menunjukkan adanya kesesuaian
range frekuensi berada pada D9.
4. Pada frekuensi cuplik 48KHz hasil energi dekomposisi dengan Mother Wavelet yang lain tidak terlalu jauh berbeda, dan cenderung konsisten pada nilai 0.9, selain itu 69,7% data dari 990 data (4 Mother Wavelet dengan berbagai Mother pada subyek satu, dua, dan tiga) menghasilkan energi
dekomposisi terbesar pada D9 dengan range frekuensi 46.88Hz hingga
93.75Hz, sedangkan pengujian yang dilakukan pada sinyal PCG dari
Michigan University menunjukan bahwa seluruh data uji coba (100%) menghasilkan energi tertinggi pada D9 (46.88Hz-93.75Hz) hal ini berarti
bahwa pada kedua pengujian menunjukkan adanya kesesuaian range
frekuensi berada pada D9.
5. Pada berbagai frekuensi cuplik didapatkan bahwa sinyal jantung normal
memiliki energi dekomposisi terbesar pada range 62.5 Hz hingga 125 Hz
untuk pengujian dengan berbagai Mother Wavelet.
6. Pola sinyal PCG normal berdasarkan frekuensi cuplik 8KHz, 44100Hz,
48KHz, dengan Mother Wavelet Symlet 2, Symlet 5, Symlet 7, Daubechies 2, Daubechies 5, Daubechies 7, Coiflet 2, Coiflet 5, Biorthogonal 2.8,
Biorthogonal 3.9, Biorthogonal 6.8 dapat digunakan sebagai referensi untuk
5.2 Saran
Dari kesimpulan yang telah dibuat, agar didapat hasil pengolahan energi
yang lebih akurat maka dibutuhkan metode denoising yang lebih baik
Abbas, K., Rasha, B. 2009. Phonocardiography Signal Processing. Morgan & calypool publisher.
Alfatwa, Dean Fathony. 2009. Watermarking pada Citra Digital Menggunakan Discrete Wavelet Transform. Bandung : Institute Teknologi Bandung. Ardinaraya, K., 2014, Heart Sounds Analysis for PCG Signal in Under
Bio-Orthogonal Wavelets Compared to Other Wavelets, International Journal of Engineering and Technology Research, Vol. 3, Issues 30, October-2014, Mylavaram, India.
Anonim. 2015. Bagaimana Cara Kerja Jantung Pada Tubuh Manusia? http://sehatjantungku.com/bagaimana-cara-kerja-jantung-pada-tubuh-manusia/bagaimana-cara-kerja-jantung-normal/. Diakses pada tanggal 12 Desember 2015.
Burrus, S., Gopinath, A., Guo, H. 1998. Introduction to Wavelets and Wavelets Transform A Primer. New Jersey: Prentice-Hall.
Devi, A. 2013.Performance Analysis of DWT at Different Level for Extraction of PCG Signal. IEEE International Conference on Microelectronics. Communication and Renewable Energy (ICMiCR). India.
Donoho, D. L. 1995. Denoising by soft-thresholding. IEEE Trans. Inform. Theory 41(3): 613-627.
Donoho, D. L. and I. M. Johnstone .1994.Ideal spatial adaptation via wavelet shrinkage. Biometrika 81(3): 425-455.
Donoho, D. L. and I. M. Johnstone . 1998.Minimax estimation via wavelet shrinkage. Annals of statistics: 879-921.
Donoho, D. L. and J. M. Johnstone 1994.Ideal spatial adaptation by wavelet shrinkage. Biometrika 81(3): 425.
Ergen, B. 2012.Signal and Image Denoising Using Wavelet Transform. Firat University. Turkey