SKRIP SI
AZWAR SYARIF 090823006
PROGRAM STUDI SARJANA MATEMATIKA DEP ARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENG ETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN
STUDI MENGENAI KURVA PARAMETRIK CATMULL-ROM SPLINES
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
AZWAR SYARIF 090823006
PROGRAM STUDI SARJANA MATEMATIKA DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : STUDI MENGENAI KURVA PARAMETRIK
CATMULL-ROM SPLINES
Kategori : SKRIPSI
Nama : AZWAR SYARIF
Nomor Induk Mahasiswa : 090823006
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juni 2011
Komisi Pembimbing :
Pembimbing II Pembimbing I
Drs. Marwan Harahap, M.Eng Drs. Bambang Irawan, M.Sc NIP 19461225 197403 1 001 NIP 19470421 197603 1 001
Diketahui Oleh:
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
STUDI MENGENAI KURVA PARAMETRIK CATMULL-ROM SPLINES
SKRIPSI
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa
kutipan dan ringkasan yang masing- masing disebutkan sumbernya.
Medan, Juni 2011
PENGHARGAAN
Puji dan syukur penulis panjatkan kepada Tuhan Yang Maha Pemurah dan Maha Penyayang, dengan limpah kurnia-Nya kertas kajian ini berhasil diselesaikan dalam waktu yang telah ditetapkan.
ABSTRAK
Kurva secara luas digunakan dalam setiap aspek komputer grafis, terutama splines yang merupakan sepenggal polinomial kurva parametrik. Splines populer dalam Computer Aided Design (CAD)karena kesederhanaan konstruksi, kemudahan dan akurasi evaluasi, serta kapasitas untuk menentukan bentuk kompleks suatu permukaan. Bentuk permukaan objek nyata dapat direpresentasikan di layar komputer dengan menggunakan kurva parametrik. Teknik ini menggunakan fungsi parametrik, di mana bentuk dari kurva parametrik ini akan bergantung pada nilai parameter pembentuk kurvanya. Fungsi parametrik Kubik Bezier, dan B-Splines adalah beberapa fungsi parametrik yang dapat digunakan untuk merepresentasikan objek. Dalam penelitian ini, penulis menggunakan fungsi parametrik Catmull-Rom spline.
STUDY ON PARAMETRIC CURVE CATMULL-ROM SPLINES
ABSTRACT
The curves are widely used in every aspect of computer graphics, especially a piece of polynomial splines are parametric curves. Splines popular in Computer Aided Design (CAD) because of the simplicity of construction, ease and accuracy evaluation, and capacity to determine the shape of a surface complex. Real object surface shape can be represented on a computer screen by using parametric curves. This technique uses parametric functions, where this form of parametric curves will depend on the parameter value forming the curve. Cubic Bezier parametric function, and B-Splines are parametric functions which can be used to represent objects. In this study, the authors use a parametric function of Catmull-Rom spline.
DAFTAR ISI
2.1.1 Pemanfaatan Grafika Komputer 6
2.1 Kurva 8
3.1.Catmull- Rom Splines 19
3.2.Kurva Parametrik 20
3.2.1 Kurva Parametrik Catmull- Rom Splines 21 3.3 Pemrograman GDI+ (Grafik Device Interface) 27
3.3.1 Area Menggambar 29
3.3.2 Sistem Koordinat 31
3.3.3 Menggambar Garis Pada Form 32
BAB 4. KESIMPULAN DAN SARAN 44
4.1 Kesimpulan 44
4.2 Saran 45
DAFTAR GAMBAR
Halaman
Gambar 2.1 Kerangka Grafik Komputer Interatif 7 Gambar 2.2 Elemen-Elemen Pembentuk Grafik 8 Gambar 2.3 Kurva Polinomial derajat satu 11 Gambar 2.4 Kurva Polinomial derajat dua 11
Gambar 2.5 Kurva Polinomial derajat tiga 12
Gambar 2.6 Koordinat Kurva Spline 13
Gambar 2.7 Kontinuitas Pada Kurva 15
Gambar 2.8 Kurva Dengan Titik Kontrol 16
Gambar 3.9 Kurva Catmull- Rom Spline 17
Gambar 3.10 Perubahan Kurva Pada Nilai 17
Gambar 3.11 Derivasi Kurva Catmull- Rom Splines 18 Gambar 3.12 Garis Singgung Kurva Catmull-Rom spline 22 Gambar 3.13 Interpolasi Kurva Catmull- Rom spline 23 Gambar 3.14 Model Interpolasi Catmull- Rom Splines 23 Gambar 3.15 (a) hasil perubahan dalam Persamaan (1),
(b) hasil dari perubahan dalam Persamaan (3) 25
Gambar 3.16 Fungsi Lokal Kontrol Catmull-Rom Saplines 25 Gambar 3.17 Dua Segmen Kurva B-Spline Kubik Seragam 26
Gambar 3.18 Arsitektur GDI+ 28
Gambar 3.19 GDI+ Namespaces dan Class dalam .NET 29
Gambar 3.20 Bit Daerah Gambar 30
Gambar 3.21 Koordinat Kartesian 31
Gambar 3.22 Koordinat Display GDI+ 32
Gambar 3.23 Menggambar Garis dari titik (0,0) sampai (120,80) 32
Gambar 3.24 Garis Pada Form 34
Gambar 3.25 Garis Pada Form Dengan Pen 36
Gambar 3.26 Ellipse Pada Form Dengan Pen 37
Gambar 3.27 Arc Pada Form Dengan Pen 38
Gambar 3.29 Garis Pada Form Dengan Structure Point 39
Gambar 3.30 Poligon 40
Gambar 3.31 Poligon Pada Form Dengan Structure Point 40
Gambar 3.32 Cardinal Splines 41
Gambar 3.33 Cardinal Pada Form Dengan Structure Point 41 Gambar 3.34 Cardinal Tertutup Pada Form Dengan Structure Point 42
Gambar 3.35 Berzier Splines 42
DAFTAR ISTILAH
Aerospace, cabang ilmu yang mempelajari tentang angkasa luar.
Automotive, sesuatu hal/kegitan yang berhubungan dengan mobil.
Approksimasi, untuk menghitung lebih dekat dan mendekati ke nilai yang
benar.
memotong hanya dalam ke dua titik.
Dimensi, mengacu pada properti-properti yang disebut panjang, luas, dan
volume. Hanya memiliki konfigurasi panjang dikatakan menjadi satu dimensi
Diinkremen, ditambahkan.
Drop-off, pengurangan.
Eksplisit, gamblang.
F orward difference, perbedaan maju.
F leksibel, mudah disesuaikan.
Geometri, ilmu yang menangani tentang bentuk dan ukuran pada sesuatu
benda.
Grafik, berkaitan dengan grafik, atau skala gambar.
Grafika, gambar yang menunjukkan relasi antara angka set tertentu.
Grid, jaringan.
Implisit, mutlak
Interval, adalah himpunan yang berisi semua angka antara ke dua angka yang
diberikan.
Interpolasi, proses mencari nilai fungsi antara dua nilai yang dikenal dengan
prosedur lainnya dalam membandingkan hukum yang diberikan oleh fungsi
itu sendiri.
Koordinat, salah satu bilangan mengatur penempatan titik dalam ruang.
Komputasi, tindakan melaksanakan proses matematika. Digunakan terutama
dengan mengacu pada aritmatika dan bukan bekerja secara aljabar.
Linear, yang berhubungan dengan garis-garis lurus.
Matriks, sebuah array segi empat yang memiliki elemen baris dan kolom.
Numerik, terdiri dari bilangan, bukan huruf, tentang sifat angka.
Parametrik, merupakan keluarga kurva yang memiliki ketentuan, u = konstan
dan v = konstan di mana x = x(u,v), y = y(u,v), dan z = z(u,v).
Permukaan = Surface, adalah bentuk geometris yang terdiri pada titik-titik
koordinat yang memenuhi persamaan apa pun.
Polinomial, fungsi yang nilainya dapat dihitung dengan mensubstitusi nilai
tentang variabel independen.
Poligon, suatu bidang yang terdiri dari titik n.
Presisi, ketelitian.
Spasial, tata ruang.
Step, langkah.
Software, perangkat lunak.
Shipbuilding, pembuatan kapal.
Spline, didefinisikan sebagai gabungan potongan-potongan polynomial yang
didefinisikan sepanjang interval tertentu.
Tangen, jarak dari titik kontak ke persimpangan pada garis singgung.
Tension, ketegangan.
Topologi, bahwa cabang geometri yang berkaitan dengan sifat topologi.
Vektor, dalam ruang Euclid tiga dimensi, suatu entitas yang dapat
digambarkan oleh segmen garis terarah dan tunduk pada operasi tertentu
ABSTRAK
Kurva secara luas digunakan dalam setiap aspek komputer grafis, terutama splines yang merupakan sepenggal polinomial kurva parametrik. Splines populer dalam Computer Aided Design (CAD)karena kesederhanaan konstruksi, kemudahan dan akurasi evaluasi, serta kapasitas untuk menentukan bentuk kompleks suatu permukaan. Bentuk permukaan objek nyata dapat direpresentasikan di layar komputer dengan menggunakan kurva parametrik. Teknik ini menggunakan fungsi parametrik, di mana bentuk dari kurva parametrik ini akan bergantung pada nilai parameter pembentuk kurvanya. Fungsi parametrik Kubik Bezier, dan B-Splines adalah beberapa fungsi parametrik yang dapat digunakan untuk merepresentasikan objek. Dalam penelitian ini, penulis menggunakan fungsi parametrik Catmull-Rom spline.
STUDY ON PARAMETRIC CURVE CATMULL-ROM SPLINES
ABSTRACT
The curves are widely used in every aspect of computer graphics, especially a piece of polynomial splines are parametric curves. Splines popular in Computer Aided Design (CAD) because of the simplicity of construction, ease and accuracy evaluation, and capacity to determine the shape of a surface complex. Real object surface shape can be represented on a computer screen by using parametric curves. This technique uses parametric functions, where this form of parametric curves will depend on the parameter value forming the curve. Cubic Bezier parametric function, and B-Splines are parametric functions which can be used to represent objects. In this study, the authors use a parametric function of Catmull-Rom spline.
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Grafika komputer tengah menjadi teknologi masa kini. Segala proses
perancangan model- model objek saat ini telah banyak menggunakan
bantuan komputer. Industri automotive misalnya, sebelum mulai
mengeluarkan model bodi mobil terbaru, para desainer terlebih dahulu
merancang kerangka bodi tersebut dengan bantuan komputer. Dari
rancangan ini, para ahli teknik dapat memperhitungkan segala sesuatunya
sedemikian hingga bodi mobil tersebut pada akhirnya memiliki kualitas
maksimal. Bantuan komputer tadi dikenal dengan istilah CAD (Computer
Aided Design).
Ekplorasi lebih jauh dari CAD mengenai penggunaan kurva dan
permukaan sebagai alat bantu perancangan model terdapat pada CAGD
(Computer Aided Geometric Design). Kurva dan permukaan
Catmul-Rom Splines menjadi salah satu objek penting dalam CAGD dan banyak
digunakan dalam industry automotive, aerospace, dan shipbuilding.
Dalam merancang kerangka suatu model (mobil, pesawat, kapal),
desainer memerlukan permodelan matematika untuk menghasilkan kurva
atau permukaan yang halus. Kurva atau permukaan ini harus dapat diatur
secara bebas dan fleksibel. Selain itu, kriteria yang penting bagi desainer
adalah apabila mereka melakukan modifikasi pada suatu daerah kurva
atau permukaan, idealnya adalah yang terpengaruh hanya sebatas daerah
sekitar modifikasi dilakukan. Dengan demikian rancangan yang telah
pada daerah lain. Kurva parametrik Catmull-Rom splines memenuhi
semua kriteria perancangan. K urva parametrik Catmull-Rom splines
sebagai objek dasar yang paling populer di CAGD, selain karena
kestabilan dan keefisienan perhitungan numeriknya.
Kurva parametrik merupakan kurva dua dimensi yang dihasilkan dari
himpunan kurva yang berasal dari suatu fungsi parametrik. Beberapa
jenis kurva dapat digunakan untuk menghasilkan permukaan parametrik,
seperti B-Splines, Hermite, dan Catmull-Rom splines. Pada penelitian ini,
penulis menggunakan Catmull-Rom splines yang ditemukan ilmuan
Edwin Catmull dan Raphael Rom (2003). Kurva ini memiliki
karakteristik istimewa, yaitu kurva yang dihasilkan selalu melalui titik
kontrol dari kurva.
Berdasarkan karakteristik kurva ini, pengguna dapat menentukan bentuk
dari kurva yang dihasilkan dengan menentukan nilai titik kontrol kurva
tersebut. Dengan demikian kurva parametrik yang dihasilkan dari kurva
ini juga akan memiliki karakteristik. Dengan karakteristik ini, kurva
parametrik akan lebih mudah untuk diinterpretasikan ke dalam suatu
perangkat lunak. Dalam hal ini peranan dari bidang ilmu Grafika
Komputer akan sangat dibutuhkan.
1.2 Perumusan Masalah
Permasalahan dalam tulisan ini adalah bagaimana memvisualisasikan
kurva parametrik Catmull-Rom splines secara komputerisasi.
1.3 Tinjauan Pustaka
Menurut Jhon P ontas Simbolon & dkk (2010) Permukaan merupakan
setiap titik terdapat bagian kecil dari sistem koordinat yang didefenisikan
dari sistem koordinat dua dimensi. Sehingga permukaan parametrik
merupakan generalisasi dari kurva-kurva parametrik. Kurva merupakan
garis yang dihasilkan dari suatu fungsi matematika yang bentuknya
disesuaikan dengan titik kontrol (control point) yang merupakan
parameter dari fungsi tersebut. Dalam Grafika Komputer, kurva sering
digunakan untuk menggambarkan grafik dan permukaan suatu ob jek.
Menurut Achmad Basuki dan Ramadijanti (2006) Grafika Komputer
merupakan perangkat (tool) dasar yang digunakan untuk membuat kurva,
grafik, ataupun gambar dengan komputer. Dengan menggunakan
perangkat ini, penciptaan gambar ataupun permukaan parametrik dapat
dilakukan, bahkan dimudahkan. Ada beberapa program sederhana sampai
program yang sangat kompleks guna membuat gambar ataupun
permukaan parametrik antara lain; Adobe photoshop, Autocad, Visual
Basic 2008 (VB.NET).
Menurut Janner Simarmata (2010) Perangkat lunak adalah instruksi
langsung komputer untuk melakukan pekerjaan dan dapat ditemukan di
setiap aspek kehidupan modern, seperti perangkat lunak pemantau media,
perangkat hiburan, sampai perangkat untuk membuat kurva, grafik,
ataupun gambar.
1.4 Tujuan Penelitian
Tujuan penelitian ini adalah untuk dapat memvisualisasikan kurva
parametrik Catmull-Rom splines secara komputerisasi dengan bentuk
yang dapat disesuaikan, agar menghasilkan kurva parametrik yang
1.5 Kontribusi Penelitian
Setelah melakukan penelitian ini, penulis berharap bahwa yang
dihasilkan dari penelitian ini dapat bermanfaat di dalam dunia industri.
Karena melalui kurva parametrik ini suatu bentuk permukaan objek nyata
dapat direpresentasikan di layar komputer.
1.6 Metode Penelitian
Dalam metode penelitian ini penulis melakukan 3 (tiga) tahapan, yaitu:
Menentukan bentuk kurva Catmull-Rom splines
Kurva ini merupakan keluarga kurva kubik interpolasi,
kelengkungan kurva ini selalu dipengaruhi dua titik sebelumnya
dan titik sesudahnya. Kemudian sebuah parameter u bernilai dari 0
sampai 1 digunakan untuk menentukan jumlah step dari kurva, dan
kelengkungan yang dibentuk dipengaruhi oleh tension (t).
Membentuk pola kurva parametrik Catmull-Rom splines
Dalam pembentukan kurva parametrik Catmull-Rom splines
dibutuhkan sejumlah titik yang dapat mengatur bentuk kurva yang
dihasilkan, biasanya disebut titik ko ntrol. Setiap titik kontrol
mempengaruhi bentuk dari kurva yang dihasilkan.
Adapun nilai-nilai yang dapat di-input terhadap parameternya
adalah:
Tension = bilangan riil
Step = bilangan riil
Manipulasi dan modifikasi kurva Catmull-Rom splines yang
ditelaah terbatas pada menambah, menyisipkan dan menghapus
titik kontrol, menggeser posisi titik kontrol, menggeser nilai
tension, menyisipkan satu buah nilai tension, dan meningkatkan
derajat dengan tetap mempertahankan bentuk kurva.
Merepresentasikan hasil dari kurva parametrik ke dalam perangkat lunak GDI+ (Graphic Device Interface) yang merupakan bagian
dari sistem operasi XP.
1.7 Sistematika Penulisan
Sistematika penulisan skripsi ini adalah sebagai berikut:
BAB I PENDAHULUAN membahas tentang Latar Belakang,
Perumusan Masalah, Tujuan Penelitian, Kontribusi Penelitian, Metode
Penelitian, serta Sistematika Penulisan.
BAB 2 LANDASAN TEORI menguraikan tentang Grafika Komputer
dan mengenai kurva parametrik serta non-parametrik. Bab ini juga
menyinggung mengenai pemograman yang digunakan.
BAB 3 PEMBAHASAN menjelasakan tentang penerapan Catmull-Rom
splines dengan prinsip-prinsipnya, karakteristik, dan modifikasinya
dengan mengugunakan program komputer.
BAB 4 KESIMPULAN berisikan kesimpulan umum dan saran untuk
BAB 2
LANDASAN TEORI
2.1 Pengertian Grafika Komputer
Grafika komputer adalah suatu bidang yang mempelajari penggambaran
suatu gambar dengan menggunakan komputer. Sehingga di dalam grafika
computer dibahas teknik-teknik pembuatan, penyimpanan, dan
manipulasi model dalam bentuk data gambar. Grafika komputer
menghasilkan software-software desain grafis yang saat ini sudah sangat
canggih, yang disebut GUI (Graphics User Interface) yang memudahkan
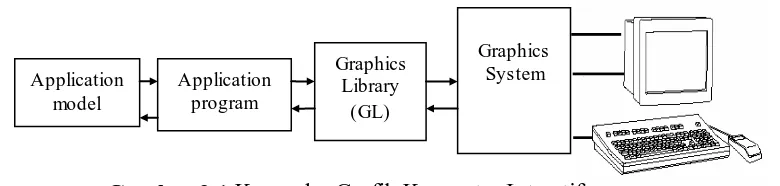
dan menyenangkan. Berikut ini merupakan kerangka Grafik Komputer
Interaktif.
Gambar 2.1 Kerangka Grafik Komputer Interatif
2.1.1 Pemanfaatan Grafika Komputer
Dalam pemanfaatan grafika komputer, hal yang dibahas adalah
mengenai spesifikasi bidang-bidang yang memanfaatkan grafika
komputer. Bidang-bidang tersebut di antaranya:
a. Computer-Aided Design (CAD)
CAD adalah suatu metode yang digunakan untuk
merancang suatu model 3D yang sekarang sudah rutin Graphics
System Graphics
Library (GL) Application
program Application
digunakan untuk merancang gedung, mobil, model pesawat,
komputer, tekstil dan banyak produk lainnya.
b. Hiburan
Industri filem dan televisi merasakan sekali pentingnya
grafika komputer. Selain itu, grafika komputer juga
dimanfaatkan pada pengembangan game di seluruh dunia.
c. P endidikan dan P elatihan
Pemodelan fisika, keuangan, dan sistem ekonomi sering
digunakan sebagai tujuan pendidikan. Pemodelan dari
sistem fisika, sistem fisilogis dan perkembangan populasi
bisa membantu untuk memahami jalannya suatu sistem.
d. Visualisasi
Ilmuwan, teknisi, personil medis, analis bisnis dan lainnya
sering membutuhkan untuk menganalisa banyaknya
informasi atau melakukan studi atas kelakuan dari proses
penting. Dengan menggunakan visualisasi semakin
mempermudah mempelajari, memahami dan melakukan
analisa terhadap suatu permasalahan.
e. P engolahan Citra
Suatu citra yang telah rusak dapat diperbaiki kembali
sehingga kualitasnya hampir menyamai citra yang masih
baru.
f. Graphical User Interface
GUI (Graphical User Interface) adalah perangkat lunak
atau program yang tersedia jadi lebih interaktif dan mudah
mengoperasikannya. Adapun bahasa pemrograman yang
Sedangkan kegiatan pemograman yang berkaitan dengan grafika
komputer, adalah:
Pemodelan Geometris: menciptakan model matematika dari objek objek 2D dan 3D.
Rendering: memproduksi citra yang lebih solid dari model yang telah dibentuk.
Animasi: menetapkan/menampilkan kembali tingkahlaku objek bergantung waktu.
Pemodelan geometris merupakan transformasi dari suatu konsep
(atau suatu benda nyata) ke suatu model geometris yang bisa
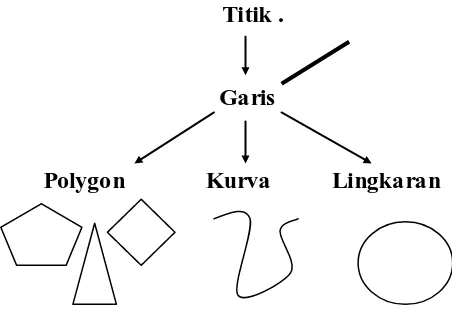
ditampilkan pada suatu komputer. Berikut merupakan
elemen-elemen pembentuk grafik pada geometri:
Titik .
Garis
Polygon Kurva Lingkaran
Gambar 2.2 Elemen-elemen pembentuk grafik
2.2 Kurva
Kurva merupakan garis yang yang dihasilkan dari sesuatu fungsi
matematika yang bentuknya disesuaikan dengan titik kontrol (control
point) yang merupakan parameter dari fungsi tersebut. Kurva dapat
direpresentasikan sebagai kumpulan titik-titik persamaan berbentuk
non-parametrik ataupun non-parametrik. Persamaan menggunakan dua koordinat
(x dan y) untuk kurva bidang (2D) dan tiga koordinat (x, y, dan z) untuk
Persamaan kurva pada bidang non-parametrik secara umum adalah:
• Kurva eksplisit
Fungsi: y = f (x)
Contoh:
- Persamaan garis lurus: y = 3x + 1
- Persamaan parabola: y = x2
Kesulitan yang ditemui dari persamaan ini adalah:
1. Tidak mungkin mendapatkan lebih dari satu nilai y untuk setiap
satu nilai x. Dengan demikian kurva berbentuk lingkaran dan
elipse harus direpresentasikan dengan beberapa segmen kurva.
2. Kurva hasil persamaan ini tidak mudah untuk dilakukan rotasi.
3. Sulit merepresentasikan kurva dengan tangen vertikal karena
kemiringannya yang tak terhingga.
• Kurva implisit
Fungsi: f (x, y) = 0
Contoh:
- Persamaan lingkaran: x2 + y2− 1 = 0 - Persamaan elipse:
Persamaan ini memang dapat mengatasi masalah nilai tunggal y untuk
setiap satu nilai x, seperti yang dialami persamaan kurva eksplisit.
Namun kesulitan akan muncul apabila hanya memerlukan nilai tunggal y.
Bayangkan bagaimana menggambar setengah lingkaran dengan
menggunakan persamaan implisit. Jika ingin menggabungkan dua
segmen kurva implisit menjadi satu, maka sulit untuk menentukan
Persamaan kurva pada bidang parametrik secara umum adalah:
• x = f (t), y = g(t)
dengan t adalah parameter independent dalam interval tertentu ([t1, t2]).
Contoh:
- Persamaan garis: x(t) = 2t + 7 , y(t) = 4t + 11
dengan 0 ≤ t ≤ 1
- Persamaan lingkaran kuadran I: dengan 0 ≤ t ≤ 1
Representasi dengan menggunakan persamaan parametrik mengatasi
masalah yang dihadapi bentuk eksplisit maupun implisit. Karena itulah
kurva parametrik lebih umum digunakan dalam CAGD (Computer Aided
Geometric Design).
Baik representasi parametrik maupun non-parametrik memiliki
keunggulan dan kelemahan masing- masing. Misalnya pada representasi
non-parametrik, dapat dengan mudah mengetahui apakah suatu titik (x,y)
terletak pada kurva atau tidak. Sedangkan pada representasi parametrik,
hal ini menjadi sesuatu yang sulit. Ke dua representasi ini berguna dalam
aplikasi grafika komputer. Semuanya relatif dari tujuan penggambaran
kurva. Untuk kurva ruang persamaannya sama, hanya saja perlu
menambahkan satu koordinat z, dengan demikian titik-titik kurva terdiri
atas koordinat x, y, dan z.
2.2.1 Kurva Polinomial
Representasi yang umumnya digunakan adalah parametrik.
Diharapkan adanya suatu fungsi yang perhitungannya sederhana
namun dapat menggambarkan berbagai variasi kurva. Fungsi
polinomial dikatakan cukup memenuhi kriteria ini, karena itu
Bentuk umum fungsi polinomial adalah sebagai berikut:
= a0+ a1t+ a2t2+…+antn
dengan ketentuan n adalah derajat polinomial tersebut.
Berbagai variasi kurva dapat disajikan tergantung pada derajat
polinomial yang digunakan, misalnya:
Polinomial derajat satu (linea r) hanya dapat menggambarkan garis lurus.
Gambar 2.3 Kurva Polinomial derajat satu
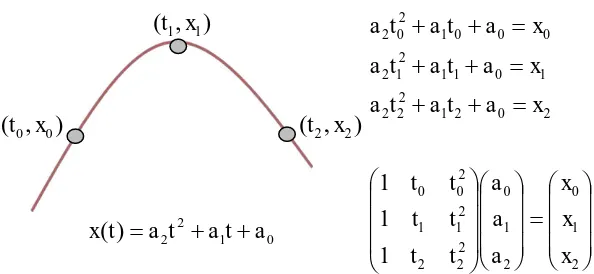
Polinomial derajat dua (kuadratik) dapat menggambarkan parabola. Fungsi ini belum memiliki titik belok (point of
inflection), suatu titik di mana kurva berubah dari cembung
ke cekung atau sebaliknya. Namun titik ini dapat diperoleh
dengan menggabungkan beberapa polinomial derajat dua
menjadi satu kurva utuh.
Gambar 2.4 Kurva Polinomial derajat dua
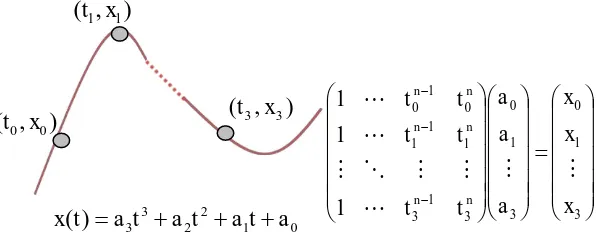
Polinomial derajat tiga (kubik) adalah polinomial yang dapat dikatakan sebagai standar dalam penyajian kurva.
Karena polinomial ini cukup fleksibel dan mampu
merepresentasikan bermacam- macam bentuk kurva.
Semakin tinggi suatu derajat polinomial, memang semakin
baik hasil gambar yang direpresentasikan, namun
perhitungan yang dilakukan juga semakin besar da n rumit.
Karena itulah, umumnya polinomial kubik yang digunakan
dalam penyajian kurva.
Gambar 2.5 Kurva Polinomial derajat tiga
2.2.2 Kurva Spline
Kurva yang merupakan hasil gabungan polinomial-polinomial
berderajat n. Kurva spline dapat didefinisikan sebagai gabungan
potongan-potongan polinomial (piecewise polynomial function)
yang didefinisikan sepanjang interval tertentu. Berikut merupakan
bentuk persamaan umumnya:
Secara alamiah spline kubik merupakan model matematis untuk
sejenis thin strip, yang mana melalui semua titik kontrol yang dapat
meminimalkan energi dasar. Spline kubik alami (natural cubic
spline) mempunyai kontinuitas C2 (terdiri C1, C0) dan lebih halus dibandingkan dengan kurva Hermite ataupun Bezier.
Contoh kurva spline:
x(t) = 2t + 7 , y(t) = 4t + 11 0 ≤ t ≤ 1
x(t) = t2 + 7t+ 1, y(t) = t2+ 5t + 9 1 ≤ t ≤ 2
Gambar 2.6 Koordinat Kurva Spline
2.2.3 Kontinuitas
Walaupun polinomial sudah dikatakan cukup sederhana dan mudah
digunakan merepresentasikan grafik, namun sulit menyajikan
bentuk kurva yang diharapkan hanya dengan menggunak an satu
fungsi polinomial untuk x = f (t) dan y = g (t). Hal yang dilakukan
adalah membagi bentuk kurva tersebut menjadi beberapa bagian
yang kemudian disebut sebagai segmen kurva. Setiap segmen
kurva didefinisikan dari polinomial terpisah yang berlaku pada
suatu interval parameter, kemudian digabungkan menjadi satu
membentuk suatu kurva polinomial utuh. Dengan membagi ke
dalam bentuk segmen-segmen kurva, objek grafik yang ingin
digambar dapat direpresentasikan dengan polinomial berderajat
Karena adanya penggabungan segmen-segmen kurva
polinomial kecil, tentunya harus memperhatikan kontinuitas dari
fungsi polinomial tersebut. Supaya kurva hasil gabungan
segmen-segmen tadi tersambung mulus dan tidak terputus, fungsi tersebut
harus kontinu.
Misalkan f(t) dan g(t) merupakan dua buah kurva polinomial kubik,
f(a) adalah ujung kanan kurva f dan g(b) adalah ujung kiri kurva g.
Jika f(a)= g(b), maka ke dua kurva ini memiliki kontinuitas C0 atau kontinu pada posisi. Sehingga f'(a)= g'(b), dikatakan kurva yang
memiliki kontinuitas C1 atau kontinuitas tangen (velocity). Jika
f''(a)= g''(b), maka kurva memiliki kontinuitas C2 atau kontinuitas turunan ke dua (acceleration). Secara umum kurva yang bertemu di
satu titik akan memiliki kontinuitas Cn, dengan ketentuan nilainya sama sampai dengan turunan ke n.
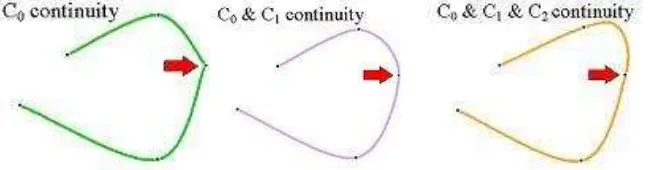
Kurva dengan kontinuitas C2 akan lebih mulus daripada kurva dengan kontinuitas C1 dan kurva dengan kontinuitas C1 akan lebih mulus daripada kurva dengan kontinuitas C0. Kurva dengan kontinuitas C0 atau kontinu pada posisi hanya memperlihatkan bahwa kurva tersebut tersambung dan tidak terputus, namun tidak
mulus. Kurva Catmull-Rom splines kubik yang akan dibahas pada
bab berikutnya adalah kurva dengan kontinuitas C2.
Kontinuitas C adalah kontinuitas parametrik. Selain kontinuitas C
terdapat suatu kontinuitas G yang dikenal dengan kontinuitas
geometri. Kontinuitas G0 memiliki arti sama dengan C0 yakni kontinu pada posisi. Kontinuitas G1 adalah kontinuitas vektor tangen. Untuk mendapatkan kontinuitas C1 (kontinuitas tangen), kedua kurva harus memenuhi f'(a)= g'(b). Namun untuk
sama (sejajar), kurva yang tersambung dikatakan memiliki
kontinuitas G1 (kontinuitas vektor tangen). Kontinuitas G2 adalah kelengkungan kontinuitas vektor.
Kelengkungan kurva pada suatu titik (Curvature sebuah garis lurus
adalah nol). Kurva dapat dikatakan memiliki kontinuitas G2 tanpa harus memiliki kontinuitas C2. G. Neilson (2000) memberikan formula mudah untuk kontinuitas G2 sebagai kontinuitas geometri pada titik temu jika dan hanya jika vektor f''(a) − g''(b) paralel dengan vektor tangen di titik temunya. Berikut ini adalah contoh
gambar kurva yang memilikikontinuitas C0, C1, C2:
Gambar 2.7 Kontinuitas pada kurva
2.2.4 Titik Kontrol Kurva
Kurva adalah bentuk primitif dari suatu objek grafik. Bentuk
primitif ini, dapat membuat objek yang rumit dan kompleks.
Pembahasan sebelumnya, telah mengetahui bahwa kurva di sini
akan menggunakan persamaan polinomial. Namun persamaan
polinomial seperti x(t) = axt2+ bxt + cx, y(t) = ayt2+ byt + cy tidak
banyak berarti bagi seorang desainer yang ingin membuat
representasi grafik dengan kurva tersebut.
Setiap persamaan polinomial memiliki sejumlah titik kontrol.
Dinamakan titik kontrol karena titik ini berkaitan dengan fungsi
kurva. Hal ini dapat memanipulasi bentuk kurva secara bebas
Gambar 2.8 Kurva dengan titik kontrol
Perhatikan Gambar 2.8. Dengan tiga titik kontrol (x1, y1), (x2, y2),
dan (x3, y3), dapat membentuk satu segmen kurva polinomial
kuadratik yang didefinisikan sepanjang interval tertentu. Jadi bagi
seorang desainer, menyimpan tiga titik kontrol ini jauh lebih efisien
daripada menyimpan fungsi polinomial untuk satu segmen kurva.
Contoh yang umum digunakan adalah kurva Bézier dan kurva
Catmull- Rom splines.
Ada beberapa cara untuk mendefinisikan kurva tertentu dengan
menggunakan titik kontrol. Masing- masing dapat diklasifikasikan
sebagai kurva hasil interpolasi atau approksimasi. Pada kasus
interpolasi, kurva melewati semua titik kontrol yang diberikan.
Sedangkan pada kasus approksimasi, kurva hanya perlu mendekati
sekumpulan titik kontrol yang diberikan. Seberapa dekat antara
kurva dan titik kontrol tergantung dari teknik approksimasi yang
digunakan.
Gambar 2.8 Kurva dengan titik kontrol
Perhatikan Gambar 2.8. Dengan tiga titik kontrol (x1, y1), (x2, y2),
dan (x3, y3), dapat membentuk satu segmen kurva polinomial
kuadratik yang didefinisikan sepanjang interval tertentu. Jadi bagi
seorang desainer, menyimpan tiga titik kontrol ini jauh lebih efisien
daripada menyimpan fungsi polinomial untuk satu segmen kurva.
Contoh yang umum digunakan adalah kurva Bézier dan kurva
Catmull- Rom splines.
Ada beberapa cara untuk mendefinisikan kurva tertentu dengan
menggunakan titik kontrol. Masing- masing dapat diklasifikasikan
sebagai kurva hasil interpolasi atau approksimasi. Pada kasus
interpolasi, kurva melewati semua titik kontrol yang diberikan.
Sedangkan pada kasus approksimasi, kurva hanya perlu mendekati
sekumpulan titik kontrol yang diberikan. Seberapa dekat antara
kurva dan titik kontrol tergantung dari teknik approksimasi yang
digunakan.
BAB 3
PEMBAHASAN
3.1 Catmull-Rom Splines
Catmull- Rom splines adalah interpolasi spline lokal yang dikembangkan
untuk keperluan komputer grafis. Skripsi ini menyajikan pengembangan
sederhana dari bentuk matriks spline. Matriks formulir timbul dari
sebuah argumen geometris sederhana yang mencoba untuk memperbaiki
garis singgung pada titik-titik kontrol tertentu menjadi rata-rata dari
kemiringan dua segmen garis kontrol poligon berdekatan dengan setiap
titik kontrol.
P1
P0
P3
P2
Gambar 3.9 Kurva Catmull-Rom spline
Catmull- Rom splines memiliki kontinuitas C1, kontrol lokal, dan interpolasi, dalam kehalusan titik kontrolnya. Garis singgung pada titik
P0 adalah tidak secara jelas didefinisikan, seringkali menetapkan ini
untuk (P1-P0). Parameter tersebut dikenal sebagai tension yang
mempengaruhi kurva melengkung tajam (interpolasi) di titik kontrol.
Berikut adalah gambarannya:
= 0.2 = 0.5 = 0.75
Dalam persamaan matriksnya, Catmull-Rom splines adalah keluarga
splines interpolasi kubik yang dirumuskan sedemikian rupa sehingga
garis singgung di masing- masing titik Pi dihitung dengan menggunakan
titik sebelumnya dan berikutnya pada spline, (Pi+1-Pi-1). Bentuk
geometri matriksnya adalah:
(1)
(2)
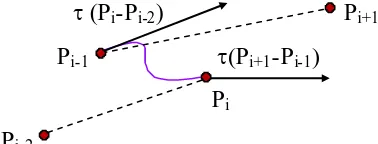
Perhatikan suatu segmen Catmull- Rom spline tunggal, P(s) dimisalkan
oleh 4 (empat) titik kontrol, Pi-2, Pi-1, Pi, dan Pi+1, seperti pada Gambar
3.11.
(Pi-Pi-2) Pi+1
Pi-1 Pi+1-Pi-1
Pi
Pi-2
Gambar 3.11 Derivasi kurva Catmull- Rom spline
Dari hasil pemeriksaan Gambar 3.11, ditemukan:
P (0) = Pi-1
P (1) = Pi
P’ (0) = (Pi – Pi-2)
P’ (1) = (Pi+1– Pi-1)
Setelah itu bisa digabungkan kendala di atas dengan (2) untuk
mendapatkan berikut:
C0 = Pi-1 (3)
C0 + C1 + C2 + C3 = Pi (4)
C1 = (Pi– Pi-2) (5)
Seterusnya, untuk menggantikan (3) dan (5) ke (4) dan (6) agar
mendapatkan persamaan di mana C2 dan C3 adalah satu-satunya variabel.
C2 + C3 = (Pi– Pi-1) – (Pi– Pi-2)
2C2 + 3C3 = (Pi+1– Pi-1) – (Pi– Pi-2)
Kemudian, jelas bahwa dengan mengurangi ke dua persamaan dapat
dengan mudah memperoleh C2 dan C3:
C0 = Pi-1
C1 = (Pi– Pi-2)
C2 = 3 (Pi– Pi-1) − (Pi+1– Pi-1) – 2 (Pi– Pi-2)
C3 = -2 (Pi– Pi-1) + (Pi+1– Pi-1) + (Pi– Pi-2)
Jika ingin membentuk dasar matriks ini, maka harus mengkelompokkan
semua secara bersamaan hingga diperoleh:
C0 = Pi-1
C1 = ( - )Pi-2 + ( )Pi
C2 = ( 2)Pi-2 + ( − 3 )Pi-1 + ( 3 – 2)Pi + ( -)Pi+1
C3 = ( -)Pi-2 + ( 2 − )Pi-1 + ( − 2 )Pi + ( )Pi+1
Dari hal ini cukup jelas untuk mengisi geometri matriks,
3.2 Kurva Prametrik
Representasi poligon dalam beberapa hal amatlah memakan ruang
penyimpanan. Suatu permukaan yang penuh dengan lekukan apabila
direpresentasikan dengan poligon bisa memerlukan begitu banyak
poligon. Semakin mengharapkan representasi yang tepat dengan
bentuknya semakin halus ukuran tiap poligon.
Fungsi parametrik dapat digunakan untuk merepresentasikan
obyek-obyek permukaan atau kurva demikian. Suatu kurva dapat dipandang
sebagai sejumlah titik yang memenuhi fungsi persamaan P (t) dengan
parameter t yang berharga dalam range . Kurva dinyatakan dalam
persamaan parametrik polinomial berderajat tiga (kubik). Sehingga
titik-titik pada kurva direpresentasikan P (t) = at3 + bt2 + ct + d dengan
berada dalam range [0, 1]. P (t) untuk suatu adalah koordinat titik pada
kurva dan koefisien tersebut masing- masing juga adalah vektor a = (ax,
ay, az), b = (bx, by, bz), c = (cx, cy, cz), dan d = (dx, dy, dz).
x(t) = axt3 + bxt2 + cxt + dx
y(t) = ayt3 + byt2 + cyt + dy
z(t) = azt3 + bzt2 + czt + dz
Bentuk pesamaan dapat dituliskan dalam notasi perkalian matriks
sebagai:
Dalam memaparkan fungsi kurva parametrik dengan polinomial
berderajat tiga atau disebut fungsi kurva parametrik kubik. Derajat yang
lebih tinggi dari tiga bisa lebih tepat, bisa juga terlalu tepat sehingga
terbentuk kerutan yang tidak diharapkan. Sementara, derajat yang
Dalam penggambaran kurva tersebut t diinkremen dari 0.0 hingga 1.0
dengan inkremen = 1/n, jika n jumlah sampling pada kurva.
Harga-harga x(t), y(t) dan z(t) dapat dihitung secara naif dari fungsi
polinomialnya tersebut tetapi untuk efisiensi dapat menggunakan
metoda “forward difference” P(t) sebagai berikut:
P(t+) = a(t+)3 + b(t+)2 + c(t+) + d
= P(t) + 3at2+ 3a2t + a3 + 2bt + b2 + c = P(t) + P(t)
dengan P(t) = 3at2+ (3a2+ 2b)t + (a3 + b2 + c ) yang masih merupakan polinomial berderajat dua. Dengan Forward difference
diperoleh:
P(t+) = 3a(t+)2+ (3a2+ 2b)(t+) + (a3 + b2 + c) = P(t) + 6a2t + 6a3 + 2b2
= P(t) + 2P(t)
dengan 2P(t) = 6a2t + 6a3 + 2b2 yang masih merupakan polinomial berderajat satu. Dengan forward difference diperoleh:
2
P(t+) = 6a2(t+) + 6a3 + 2b2
= 2P(t) + 6a3
= 2P(t) + 3P(t) dengan 3P(t) = 6a3 suatu konstanta.
Pada saat t = 0 diperoleh:
P(0) = d
P(0) = a3 + b2 + c
P2(0) =6a3 + 2b2 dan
3
3.2.1 Kurva Parametrik Catmull-Rom Splines
Kurva secara luas digunakan dalam setiap aspek komputer grafis,
terutama splines yang merupakan sepenggal polinomial kurva
parametrik. Splines populer dalam Computer-Aided Design (CAD)
karena kesederhanaan konstruksi, kemudahan dan akurasi evaluasi,
serta kapasitas untuk menentukan bentuk kompleks permukaan.
Catmull- Rom (C-R) splines adalah keluarga interpolasi kubik
kurva yang dirumuskan sedemikian rupa sehingga garis singgung
disetiap titik kontrol dihitung dengan menggunakan titik kontrol
sebelumnya dan berikutnya pada spline.
Gambar 3.12 Garis Singgung Kurva Catmull-Rom spline
Catmull- Rom splines memiliki kontinuitas C1, kontrol lokal, dan interpolasi titik kontrol, tetapi tidak terletak dalam titik kontrol.
Berikut adalah rumusan interpolasinya:
Penulis menggunakan jenis spline di permukaan interaktif
karena kemampuannya untuk setiap interpolasi titik kontrol. Dalam
operasi manipulasi titik kontrol, tidak dapat menerapkan
modifikasi bentuk spline yang mempengaruhi lebih dari sebuah
lingkungan kecil di spline dan rentang antara tetangga titik kontrol.
Bisa dilihat pada Gambar 3.13 bahwa Catmull-Rom splines tidak
interpolasi titik kontrol pertama dan terakhir.
V0 = P1
V1 = P1 + (P2 – P0)
V2 = P2 + (P3 – P1)
V3 = P2
Gambar 3.13 Interpolasi Kurva Catmull- Rom spline
Kemampuan C-R spline untuk interpolasi titik kontrol adalah fitur
penting, yang memungkinkan untuk secara akurat menerjemahkan
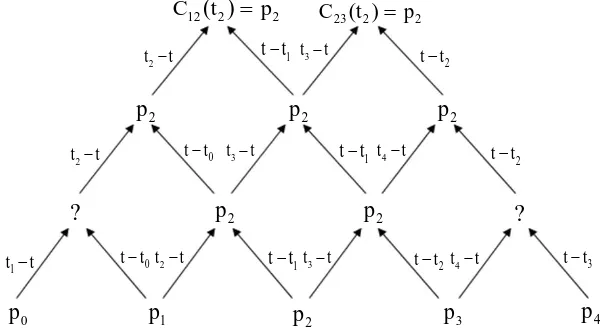
input pengguna ke dalam matematika representasi.
Gambar 3.14 Model interpolasi Catmull- Rom splines
Pendekatan pertama yang dilakukan untuk menyelesaikan masalah
perpindahan kontrol penyebaran titik dalam jendela aktif,
menetapkan arah perpindahan yang sama untuk semua titik kontrol
dalam jendela. Besarnya perpindahan monoton menurun dari titik
kontrol yang dimodifikasi untuk batas-batas jendela. Drop off
Penulis telah menguji beberapa fungsi tersebut dan menemukan
tiga yang menyediakan transisi mulus ya ng diinginkan (Persamaan
1, 2, dan 3), yaitu:
Linear: (1)
Gaussian: (2)
Sinusoidial: (3)
Persamaan linier, gaussian dan sinusoidial memiliki semua
penurunan dalam rentang 1-0. Persamaan (2) menggunakan fungsi
kedua (f (d)) untuk memastikan kondisi batas yang tepat, karena
Gaussian tidak pergi ke nol dalam rentang terbatas.
dengan ketentuan d adalah jarak (melengkung ke atas) ke pusat
jendela, yaitu titik kontrol yang dimodifikasi oleh pengguna, dan W
adalah sebuah ukuran jendela yang ditetapkan untuk setiap sisi
jendela yang aktif, baik WR atau WL . f adalah fungsi yang
menjamin persamaan seluruh pergi ke nol.
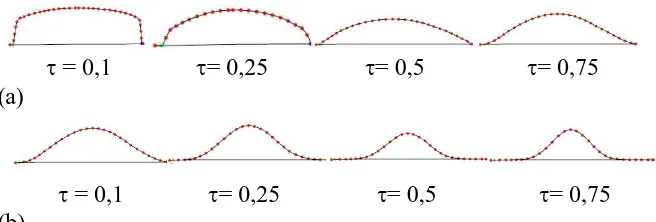
Parameter t eksponen dari kosinus dalam Persamaan (3).
Pengaturan parameter untuk sesuatu selain 1 mengubah bentuk
kurva dalam jendela aktif. Seperti yang terlihat pada Gambar 3.15,
= 0,1 = 0,25 = 0,5 = 0,75 (a)
= 0,1 = 0,25 = 0,5 = 0,75
(b)
Gambar 3.15 (a) hasil perubahan dalam Persamaan (1), (b) hasil dari perubahan dalam Persamaan (3)
Untuk memberikan fleksibilitas yang lebih besar, kontrol dan
ekspresif, dalam hal ini telah dikembangkan teknik yang
memperluas dan generalisasi hasil modifikasi satu titik kontrol C-R
spline. Teknik yang memungkinkan pengguna untuk menentukan
dan berbagai jenis pengaruh yang manipulasi dari sebuah titik
kendali tunggal dapat menghasilkan pada kurva C-R spline,
sehingga menciptakan kemampuan pengeditan kurva fleksibel dan
kurva fungsi lokal.
Gambar 3.16 Fungsi lokal kontrol Catmull-Rom splines
Pengeditan fungsi lokal memberikan kontrol pengguna lebih besar
atas bentuk spline ketika bergerak dari satu titik kontrol. Hal ini
memungkinkan pengguna untuk meningkatkan densitas dari titik
kontrol di mana detail lebih dibutuhkan, dan membuat bagian dari
kurva lebih terkendali. Namun, karena lokalitas Catmull- Rom
splines, perubahan apapun pada satu titik kontrol hanya perubahan
porsi kurva antara titik kontrol dan tetangganya titik kontrol.
Elber dan Gotsman (2007), memperpanjang pendekatan
non-seragam-B-spline dan menyediakan mekanisme untuk lokal
perbaikan dan manipulasi kurva adaptif lokal. Namun, metode ini
menggunakan kuadrat-terkecil pendekatan untuk dekomposisi
multi-resolusi dari kurva bebas-bentuk dan tidak mampu
menyediakan kontinu resolusi kontrol. Kemudian bekerja
menyajikan sebuah skema yang menggabungkan kontrol
multi-resolusi dengan kendala linier ke dalam satu kerangka, yang
memungkinkan seseorang untuk melakukan manipulasi
multi-resolusi kurva B-spline tidak seragam.
Kontrol multi-resolusi dikombinasikan dengan kendala linier
mengatur geometri yang tepat, dan menciptakan kerangka kerja
untuk mengedit interaktif kurva B-spline tidak seragam. Untuk
menambahkan satu segmen kurva yang tersambung mulus, hanya
perlu menambahkan satu titik kontrol dan satu buah knot. Di mana
pun titik kontrol tambahan itu diletakkan, hasil kurva B-spline yang
terbentuk akan tersambung mulus. Melihat hasil kurva yang
tergambar sungguh merupakan hal yang mengagumkan.
Kurva ini cocok untuk set baru titik kontrol setelah setiap langkah
mengedit, dan pengguna disediakan dengan langsung umpan balik
dari keseluruhan bentuk kurva ketika mengedit. Jumlah titik
kontrol dalam jendela aktif dapat diubah oleh pengguna untuk
menyediakan lebih rinci, dan lebih tinggi resolusi mengedit.
Jumlah titik kontrol dapat dikurangi dalam jendela.
Gerakan dari titik kontrol dalam jendela aktif dapat digambarkan
melalui serangkaian skema yang memodifikasi semua kontrol poin
lainnya dalam jendela sebagai fungsi dari perpindahan dari titik
kontrol yang dipilih. Dua alternatif ide: interpolasi perpindahan
yang dipilih titik kontrol dalam jendela aktif, dan interpolasi vektor
pergeseran dengan vektor ortogonal untuk kurva.
3.3 Pemrograman GDI + (Graphic Device Interface)
Dalam hal ini, perangkat lunak yang penulis gunakan adalah Visual Basic
2008 (VB.NET). Untuk pemrograman Grafik VB.NET dibutuhkan GDI+
(Graphic Device Interface) yang merupakan bagian dari sistem operasi
XP. GDI+ yang memiliki kemampuan untuk mengolah grafik vektor dua
dimensi (gar is), imaging (bitmap) dan typography (font) pada layar
maupun Printer.
Dengan GDI+, programmer tidak perlu mengetahui detail dari
masing- masing peralatan untuk menampilkan grafik diatasnya, tetapi
cukup menggunakan fasilitas yang telah disediakan oleh GDI+ class.
GDI+ adalah library pada .NET yang digunakan untuk membuat aplikasi
grafis berbasis Windows dan Web yang dapat berinteraksi dengan
perangkat grafis berupa printer atau monitor. Graphical User Interface
(GUI) berinteraksi dengan perangkat hardware seperti monitor, printer,
tetapi tidak ada program yang dapat mengakses perangkat hardware
tersebut secara langsung, dibuat user interface agar pengguna dapat
berinteraksi dengan perangkat-perangkat tersebut.
Untuk membuat user interface tersebut harus digunakan third component
sebagai jembatan antara program dan perangkat keras, dibuatlah
komponen GDI+ library, dengan komponen tersebut dapat menampilkan
output berupa text dan gambar ke perangkat hardware.
Pada aplikasi .NET dapat menggunakan GDI+ untuk membuat aplikasi
grafis baik untuk aplikasi berbasis windows maupun aplikasi web.
Library GDI+ sudah tersinstall secara default pada sistem operasi
Windows XP, Vista, dan Windows 2003 yang berlokasi di class library
dengan nama Gdiplus.dll.
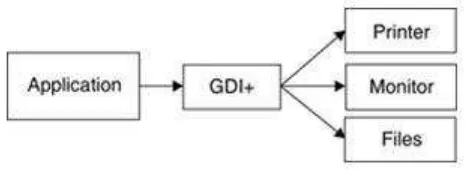
Gambar 3.18 Arsitektur GDI+
Fitur GDI+ dapat kategorikan dalam 3 (tiga) fungsi utama yaitu:
a) 2D Vektor Graphic P rogramming
Vektor Graphic merupakan komponen pembentuk bentuk gambar
mis (kotak, lingkaran) yang dibentuk dari kumpulan titik pada sistem
koordinat. Pada.NET Framework library 2D vektor graphic
programming dibagi menjadi dua kategori yaitu general dan
advanced. General 2D vektor graphic didefinisikan dalam library
System.Drawing namespace dan advance function didefinisikan
b) Imaging
Imaging digunakan untuk memanipulasi image. Image file yang
dapat dimanipulasi misalnya; .bmp, .jpg, .gif, dan .png.
Fungsi-fungsi untuk memanipulasi images ada dalam Image class yang
digunakan untuk create, save, dan load images.
c) Typography
Typography digunakan untuk mendesign dan merepresentasikan
text. GDI+ menyediakan class untuk membuat dan menggunakan
font.
Gambar 3.19 GDI+ Namespaces dan Class dalam .NET
3.3.1 Area Menggambar
Setiap aplikasi menggambar paling tidak terdiri dari 3 (tiga)
komponen yaitu canvas, brush, pen, dan process:
• Canvas: adalah area di mana object akan digambar, pada aplikasi Windows, Windows Form adalah canvasnya.
• Brush atau Pen merepresentasikan tekstur, warna, dan ukuran dari objek yang digambar pada canvas.
Gambar 3.20 Bit Daerah Gambar
Setiap area gambaran memiliki 4 (empat) properti utama yaitu:
lebar, tinggi, resolution dan warna depth.
• Lebar dan tinggi properti digunakan untuk menentukan ukuran area menggambar secara vertikal dan horizontal
• Resolution adalah satuan untuk mengukur output kualitas dari grafik objek atau gambar dalam satuan dot per inchi
(dpi). Sebagai contoh resolusi 72 dpi berarti 1 inchi dari
area tersebut terdiri dari 72 horizontal dan 72 vertikal
pixel. Untuk monitor resolusi 1280x1024 berarti pada area
monitor tersebut terdiri dari 1280 horizontal pixel dan
1024 vertikal pixel.
• Warna depth adalah jumlah warna yang digunakan untuk merepresentasikan setiap pixel.
Definisi: Pixel adalah elemen terkecil pada proses menggambar
untuk menampilkan graphic object atau images pada layar.
Struktur warna pada GDI+ mempunyai 4 (empat) komponen warna
yaitu: alpha, red, green, dan blue. Red green blue (RGB) komponen
mewakili kombinasi warna yang muncul. Setiap komponen dalam
RGB mempunyai 256 (28) kombinasi warna, sehingga kombinasi
tiga komponen RGB tersebut mempunyai kemungkinan warna
256x256x256. Alpha komponen mewakili aspek transparan dari
3.3.2 Sistem Koordinat
Memahami sistem koordinat sangat penting untuk pemrograman
grafik, sistem koordinat merepresentasikan letak grafik objek pada
perangkat tampilan seperti monitor dan printer.
a) Sistem Koordinat Kartesian
Ini adalah koordinat umum yang dipelajari pada pelajaran
matematika dasar, terdiri dari sumbu x dan y
Gambar 3.21 Koordinat Kartesian
Posisi sitem koordinat Kartesian dibagi menjadi beberapa kuadran:
• Kuadran I: x > 0 dan y > 0
• Kuadran II: x < 0 dan y > 0
• Kuadran III: x < 0 dan y < 0
• Kuadran IV: x > 0 dan y < 0
b) Sistem Koordinat Standar GDI+
Tidak seperti sistem Kartesian, pada perangkat tampilan seperti
Gambar 3.22 Koordinat Display GDI+
Gambar 3.23 Menggambar Garis dari titik (0,0) sampai (120,80)
3.3.3 Menggambar Garis Pada Form
Penggambaran Grafik form dapat dilakukan melalui Objek Grafik
yang dapat dideklarasikan sebagai berikut:
Dim MyGraphics As System.Drawing.Graphics = Me.CreateGraphics
Objek Grafik menyediakan berbagai metode untuk menggambar seperti DrawLine, DrawRectangle, dll
Dalam penggambaran, membutuhkan Objek Pen penyedia
atribut Warna dan Ketebalan garis dalam ukuran pixel.
Objek Pen dapat dideklarasikan sebagai berikut:
Warna adalah warna yang diinginkan, dan tebal adalah tebal pen
dalam ukuran point.
Contoh program GDI+ yang pertama:
Option Explicit On Imports System
Imports System.Windows.Forms
Imports Microsoft.VisualBasic
Public Class MyForm :Inherits Form<System.STAThread()> _
Public Shared Sub Main()
Application.Run(New MyForm)
End Sub
Public Sub New() 'Constructor
Me.Text = "Mengambar garis pada Form"
End Sub
Private Sub MyForm_Click(Sender As Object, e As
System.EventArgs)
Handles MyBase.Click
Dim MyPen As New
System.Drawing.Pen(System.Drawing.Color.Red,3)
Dim MyGraphic As System.Drawing.Graphics =
Me.CreateGraphics
MyGraphic.DrawLine(MyPen,10,10,200,100)
End Sub End Class
Kemudian simpan program di atas dengan mana grafik.vb
a) Proses Kompilasi
Proses kompilasi dengan menggunakan perintah:
Vbcgrafik.vb/r:System.dll/r:System.Windows.For
Ketika dijalankan, dan klik pada form akan menghasilkan
tampilan:
Gambar 3.24 Garis Pada Form
Catatan:
Mengenai pemrogram form pada VB.NET dapat dibaca di
ebook pemrogram form pada VB.NET
Salah satu kelemahan dari cara di atas adalah, kalau form mengalami refresh, garis yang telah digambarkan tersebut akan hilang (VB.NET tidak menyediakan property AutoRedraw seperti yang terdapat pada VB6)
Untuk membuktikannya minimize dan maximize kembali form diatas, garis tersebut akan hilang.
b) Melakukan Overriding Te rhadap Metoda Onpaint
OnPaint Event Handle adalah event yang dibangkitkan setiap
kali form mengalami refresh (pada saat minimize, maximize
maupun ditimpa oleh form lain). Jika dilakukan overriding
terhadap Event ini dan menempatkan perintah penggambaran
garis di dalamnya ini, maka garis tersebut digambar setiap
Parameter PaintEventArgs pada Sub OnPaint merupakan
Protected Overrides Sub OnPaint(ByVal e As
PaintEventArgs)
Kalau program di atas dijalankan, akan menampilkan garis
pada form dan tetap akan ada walaupun form direfresh.
Catatan:
Pada contoh diatas melakukan overriding terhadap metoda OnPaint yang ada pada Base class dengan Metoda baru yang dibuat di dalamnya mengambarkan garis, sehingga setiap kejadian OnPaint akan menjalankan Event baru tersebut.
3.3.4 Menggambar Grafik Vektor 2 Dimensi
Grafik vektor merupakan kemampuan menggambar bentuk-bentuk
tradisional seperti garis, kurva dan bentuk berdasarkan sekumpulan
titik tertentu.
Untuk penggambaran grafik vektor dapat menggunakan objek Pen
dan Brush, dimana objek Pen untuk penggambaran bentuk garis,
dan Brush untuk objek isian.
3.3.4.1 Menggambar Garis Dengan Pen
Perintah DrawLine (pen, x1, y1, x2, y2) digunakan menggambar
garis dari koordinat awal (x1, y1) ke koordinat akhir (x2, y2).
Contoh:
Dim MyPen As New
System.Drawing.Pen(System.Drawing.Color.Red,3) e.Graphics.DrawLine(MyPen,10,10,200,100)
akan menghasilkan:
a) Menggambar Ellipse Pada Form Dengan Pen
Dapat digunakan metoda DrawEllipse (Pen, x, y, lebar,
tinggi) pada objek grafik untuk menggambar ellipse pada
koordinat x, y dengan ukuran lebar dan tinggi tertentu.
Contoh:
e.Graphics.DrawEllipse(MyPen,10,10,200,100)
akan menghasilkan:
Gambar 3.26 Ellipse Pada Form Dengan Pen
b) Menggambar Arc Pada Form Dengan Pen
Dapat digunakan metoda DrawArc (Pen, x, y, lebar,
tinggi, sudutawal, sudutakhir) untuk menggambar arcus,
adapun perbedaan antara Ellipse dengan Arc adalah, kalau
ellipse adalah gambar kurva tertutup, sedangkan Arc
ditentukan oleh sudut awal dan akhir penggambaran
kurva.
Contoh:
akan menghasilkan:
Gambar 3.27 Arc Pada Form Dengan Pen
c) Menggambar Pie pada Form dengan Pen
Kalau Arc adalah kurva dengan sudut awal dan akhir,
demikian juga pie, bedanya adalah pie merupakan kurva
tertutup. Untuk menggambar pie dapat digunakan metoda
DrawEllipse(Pen,x,y,lebar,tinggi).
Contoh:
e.Graphics.DrawPie(MyPen,10,10,200,100,0,90)
akan menghasilkan:
3.3.4.2 Menggunakan Structure Point
Dapat juga menggunakan structure point untuk penentuan
koordinat (x, y) awal dan akhir pada perintah DrawLine(pen,
point1, point2).
Catatan:
DrawLine(pen, point1, point2) merupakan metode overloading
terhadap DrawLine(pen,x1,y1,x2,y2)
Contoh:
Dim Point1 As New System.Drawing.Point(10,10)
Dim Point2 As New System.Drawing.Point(200,100) e.Graphics.DrawLine(MyPen,Point1,Point2)
ketika dijalankan akan menghasilkan garis yang sama dengan
perintah:
e.Graphics.DrawLine(MyPen,10,10,200,100)
akan menghasilkan:
a) Menggambar Poligon Dengan Array Dari Point
DrawPolygons(Pen,PointArray) merupakan kurva tertutup
yang dibentuk oleh garis-garis, untuk menggambar
poligon perlu menyediakan array yang berisi koord inat
(x,y) dari sudut-sudut poligon.
Gambar 3.30 Poligon
Contoh:
Dim MyPen As New
System.Drawing.Pen(System.Drawing.Color.Red, 3)
Dim MyArr As System.Drawing.Point() = _ {new System.Drawing.Point(0,0), _
new System.Drawing.Point(250,130), _
new System.Drawing.Point(190,160)} e.Graphics.DrawPolygon(MyPen,MyArr)
akan menghasilkan:
b) Menggambar Cardinal Splines Dengan Array Point Jika poligon merupakan kurva tertutup yang dihubungan
oleh garis lurus pada setiap koordinat (x,y) sudutnya,
maka DrawCurve(Pen, PointArray, Tangen) merupakan
kurva terbuka yang dibentuk dengan garis lengkung yang
memiliki nilai tangent tertentu, berikut ini adalah contoh
gambar cardinal splines yang memiliki tiga titik dengan
nilai tangent yang berbeda (0, 1, 1.5, dan 2).
Gambar 3.32 Cardinal Splines
Contoh:
Dim MyPen As New
System.Drawing.Pen(System.Drawing.Color.Red, 3)
Dim MyArr As System.Drawing.Point() = _ {new System.Drawing.Point(0,0), _
new System.Drawing.Point(250,130), _
new System.Drawing.Point(190,160)} e.Graphics.DrawCurve(MyPen,MyArr,1.5F)
akan menghasilkan:
Kemudian dapat juga menggunakan DrawClosedCurve
(pen, PointArray) untuk menghasilkan kurva tertutup.
Contoh:
Dim MyPen As New
System.Drawing.Pen(System.Drawing.Color.Red, 3)
Dim MyArr As System.Drawing.Point() = _ {new System.Drawing.Point(0,0), _
new System.Drawing.Point(250,130), _
new System.Drawing.Point(190,160)} e.Graphics.DrawClosedCurve(MyPen,MyArr)
akan menghasilkan:
Gambar 3.34 Cardinal Tertutup Pada Form Structure Point
c) Menggambar Bezier Splines Dengan Array Dari Point DrawBezier(pen, x1, y1, x2, y2, x3, y3, x4, y4) merupakan
kurva dengan dari koordinat (x1, y1) awal ke koordinat (x2,
y2), dengan dua koordinat kontrol (x3, y3) dan (x4, y4).
Pada Gambar. 3.35 P1 awal koordinat awal, P2 adalah
koordinat akhir, dan C1, C2 adalah koordinat kontrol
Bezier.
Contoh:
Dim MyPen As New
System.Drawing.Pen(System.Drawing.Color.Red, 3) e.Graphics.DrawBezier(MyPen,0,0,200,200,70,50, 150, 40)
akan menghasilkan:
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan hasil pengujian dan pembahasan, dapat disimpulkan
beberapa hal tentang pembentukkan permukaan Catmull-Rom spline,
yaitu:
1. Kurva parametrik Catmull-Rom splines yang dihasilkan memiliki
keterbatasan dalam pembentukannya sebatas titik kontrol yang
digunakan pada permukaan.
2. Kelengkungan kurva parametrik Catmull- Rom splines dipengaruhi
parameter kelengkungan (tension). Semakin kecil nilai tension, kurva
yang dihasilkan semakin tegak lurus sebaliknya semakin besar nilai
tension, kurva yang dihasilkan semakin melengkung.
3. Ketika terdapat dua titik maksimum dan minimum yang berdekatan,
kurva akan mengalami kelengkungan yang kasar.
4. Kurva parametrik Catmull- Rom splines yang dihasilkan dapat
digunakan untuk memodelkan permukaan datar maupun
bergelombang, hal ini dipengaruhi nilai titik kontrol dan parameter
4.2 Saran
Untuk pengembangan permukaan parametrik Catmull- Rom splines ini
ada beberapa saran yang dapat penulis berikan, diantaranya:
1. Sebaiknya penerapan kurva parametrik Catmull- Rom splines dengan
menggunakan aplikasi lain, misalnya: CAD (Computer-Aided
Design) dan CAGD (Computer Aided Geometric Design).
2. Agar pengembangan kurva parametrik Catmull-Rom splines
dilakukan dengan cara membandingkan dengan kurva lain, misalnya:
LAMPIRAN
a) Kurva parametrik Catmull-Rom splines yang dipengaruhi oleh titik kontrol:
1. Berikut ini merupakan kurva yang memiliki 4 (empat) titik kontrol dan 1(satu) titik maksimum serta 1(satu) titik minimum dengan nilai = 0.
b) Kelengkungan kurva parametrik Catmull-Rom splines yang dipengaruhi oleh nilai tension:
1. Berikut ini merupakan kurva yang memiliki 4 (empat) titik kontro l dan 1(satu) titik maksimum serta 1(satu) titik minimum dengan nilai = 0.5.
c) Kelengkungan kurva yang kasar akan terjadi, ketika terdapat dua titik maksimum dan minimum yang berdekatan:
1. Berikut ini merupakan kurva yang memiliki 6 (empat) titik kontrol dengan 1(satu) titik maksimum serta 1(satu) titik minimum yang berdekatan dengan nilai = 0.