Penentuan Ambang Batas Curah Hujan Ekstrim dengan Mean Residual Life dan Threshold Choice (Studi Kasus : Curah Hujan Periode 1977-2010 di Stasiun Pondok Betung)

(1)

PENENTUAN AMBANG BATAS CURAH HUJAN EKSTRIM

DENGAN MEAN RESIDUAL LIFE DAN

THRESHOLD CHOICE

(Studi Kasus : Curah Hujan Periode 1977–2010 di Stasiun Pondok Betung)

IMAM WIDYANTO

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(2)

(3)

PERNYATAAN MENGENAI SKRIPSI DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa skripsi berjudul Penentuan Ambang Batas Curah Hujan Ekstrim dengan Mean Residual Life dan Threshold Choice (Studi Kasus : Curah Hujan Periode 1977-2010 pada Stasiun Pondok Betung) adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

(4)

ABSTRAK

IMAM WIDYANTO. Penentuan Ambang Batas Curah Hujan Ekstrim dengan Mean Residual Life dan Threshold Choice (Studi Kasus : Curah Hujan Periode 1977-2010 di Stasiun Pondok Betung). Dibimbing oleh AJI HAMIM WIGENA dan FARIT MOCHAMAD AFENDI.

Curah hujan memiliki keragaman tinggi dan berpotensi terjadi curah hujan ekstrim yang pada umumnya dapat mengakibatkan banjir. Informasi curah hujan ekstrim perlu diketahui lebih awal untuk mengantisipasi kemungkinan banjir dengan cara menentukan nilai ambang batas. Nilai ambang batas ini dapat ditentukan dengan persentil 90, Mean Residual Life (MRL), dan Threshold Choice (TC) berdasarkan Sebaran Pareto Terampat (Generalized Pareto Distribution, GPD). Nilai ambang batas di Pondok Betung adalah 61 mm berdasarkan data curah hujan harian pada peiode 1977-2010. Secara umum kejadian banjir terjadi ketika curah hujan harian di stasiun Pondok Betung melebihi 61 mm.

Kata Kunci : GPD, MRL, TC

ABSTRACT

IMAM WIDYANTO. Threshold Determination of Extreme Rainfall with Mean Residual Life and Threshold Choice (Case Study : Rainfall in 1977-2010 period at Pondok Betung Station). Supervised by AJI HAMIM WIGENA and FARIT MOCHAMAD AFENDI.

Rainfall has a high diversity and potentially extreme rainfall which can cause flood. Extreme rainfall information needs to be known early to anticipate the possibility of flooding by determining the threshold value. This threshold value can be determined by the 90th percentile, Mean Residual Life (MRL), and Threshold Choice (TC) based on Generalized Pareto Distribution (GPD). Threshold value in Pondok Betung station is 61 mm, based on daily rainfall data in 1977-2010. In general, the majority of flood events occur when daily rainfall at Pondok Betung station above 61 mm.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Statistika

pada

Departemen Statistika

PENENTUAN AMBANG BATAS CURAH HUJAN EKSTRIM

DENGAN MEAN RESIDUAL LIFE DAN

THRESHOLD CHOICE

(Studi Kasus : Curah Hujan Periode 1977–2010 di Stasiun Pondok Betung)

IMAM WIDYANTO

DEPARTEMEN STATISTIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR

(6)

(7)

(8)

Judul Skripsi : Penentuan Ambang Batas Curah Hujan Ekstrim dengan Mean Residual Life dan Threshold Choice (Studi Kasus : Curah Hujan Periode 1977-2010 di Stasiun Pondok Betung)

Nama : Imam Widyanto NIM : G14090026

Disetujui oleh

Dr Ir Aji Hamim Wigena, MSc Pembimbing I

Dr Farit Mochamad Afendi, MSi Pembimbing II

Diketahui oleh

Dr Ir Hari Wijayanto, MSi Ketua Departemen

(9)

PRAKATA

Alhamdulillah, puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia Nya sehingga penelitian ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan April 2013 sampai September 2013 ini ialah ambang batas curah hujan ekstrim, dengan judul Penentuan Ambang Batas Curah Hujan Ekstrim dengan Mean Residual Life dan Threshold Choice (Studi Kasus : Curah Hujan Periode 1977-2010 di Stasiun Pondok Betung).

Terima kasih penulis ucapkan kepada Bapak Dr Ir Aji Hamim Wigena, MSc dan Bapak Dr Farit Mochammad Afendi MSi selaku pembimbing, serta Bapak Wido Hanggoro, SSi dan keluarga besar dari Badan Meteorologi Klimatologi dan Geofisika yang telah banyak memberi saran. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, keluarga, dan keluarga besar Statistika IPB atas dukungan, doa, dan kasih sayangnya.

Akhirnya penulis berharap semoga tulisan ini bermanfaat dalam pengembangan ilmu Statistika khususnya di bidang Meteorologi.

(10)

DAFTAR ISI

DAFTAR TABEL viii

DAFTAR GAMBAR viii

DAFTAR LAMPIRAN viii

PENDAHULUAN 1

Latar Belakang 1

Tujuan Penelitian 2

METODE 2

Data 2

Prosedur Analisis Data 2

HASIL DAN PEMBAHASAN 5

Eksplorasi Data Curah Hujan Harian 5

Penentuan Ambang Batas 7

Pendugaan Parameter GPD 11

Peramalan Tingkat Pengembalian 12

Penentuan Ambang Batas u Terbaik Berdasarkan MAPE 14

SIMPULAN DAN SARAN 17

Simpulan 17

Saran 17

DAFTAR PUSTAKA 17

LAMPIRAN 20

(11)

DAFTAR TABEL

1 Ukuran pemusatan dan penyebaran data curah hujan harian periode

bulanan tahun 1977–2010 (mm) 7

2 Nilai dugaan parameter GPD periode analisis 1 Januari 1977–31

Desember 2009 11

3 Uji Kolmogorov-Smirnov untuk tiap calon ambang batas u 12 4 Ramalan tingkat pengembalian curah hujan untuk tiap calon ambang

batas u 13

5 Nilai MAPE untuk tiap calon ambang batas u 15 6 Kejadian banjir dan longsor periode 1977-2013 di Jakarta 16 7 Ramalan banyaknya hari dengan curah hujan ekstrim periode ramalan

tahun 2010 16

DAFTAR GAMBAR

1 Histogram curah hujan harian tahun 1977-2010 6 2 Diagram kotak garis curah hujan harian periode bulanan 1977-2010 6 3 Grafik MRL curah hujan harian selang ambang batas 0–330 8 4 Grafik MRL curah hujan harian selang ambang batas 30–90 9 5 Grafik MRL curah hujan harian selang ambang batas 70–125 9 6 Grafik TC untuk reparameterisasi parameter skala curah hujan harian

selang ambang batas 0-125 10

7 Grafik TC untuk parameter bentuk curah hujan harian selang ambang

batas 0-125 10

8 Plot peluang untuk ambang batas u = 61 12

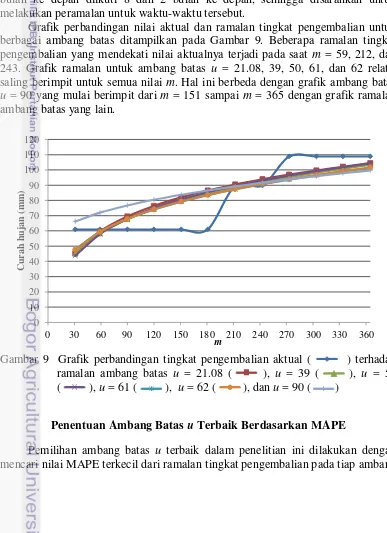
9 Grafik perbandingan tingkat pengembalian aktual dengan ramalan tiap

ambang batas 14

DAFTAR LAMPIRAN

1 Ukuran pemusatan dan penyebaran data curah hujan harian periode

tahunan 1977–2010 di stasiun Pondok Betung 20

(12)

9 Grafik MRL curah hujan harian untuk stasiun Tanjung Priok tahun

1973-2009 24

10 Grafik MRL curah hujan harian untuk stasiun Cengkareng tahun

1986-2009 24

11 Grafik TC untuk reparameterisasi parameter skala dan parameter bentuk curah hujan harian untuk stasiun Kemayoran tahun 1980-2009 25 12 Grafik TC untuk reparameterisasi parameter skala dan parameter

bentuk curah hujan harian untuk stasiun Tanjung Priok tahun

1973-2009 25

13 Grafik TC untuk reparameterisasi parameter skala dan parameter bentuk curah hujan harian untuk stasiun Cengkareng tahun

1986-2009 26

(13)

(14)

PENDAHULUAN

Latar Belakang

Salah satu unsur cuaca yang memiliki keragaman cukup tinggi adalah curah hujan. Hal ini dipengaruhi salah satunya oleh pola musim di Indonesia. Curah hujan akan rendah saat musim kemarau dan akan tinggi saat musim hujan. Tingginya curah hujan pada musim hujan akan cenderung menghasilkan curah hujan yang ekstrim.

Curah hujan ekstrim dapat mengakibatkan tanah longsor dan banjir. Jakarta merupakan salah satu wilayah yang sering dilanda banjir. Banyak faktor yang menyebabkan banjir di Jakarta selain curah hujan ekstrim, di antaranya adalah perubahan tutupan lahan, Jakarta yang merupakan hilir dari 13 aliran sungai, banyaknya sampah di saluran air, dan lain-lain. Berdasarkan kondisi di atas, banjir disebabkan oleh banyak faktor dan merupakan suatu fenomena yang kompleks.

Informasi ambang batas curah hujan ekstrim di Jakarta perlu diketahui lebih awal dalam mewaspadai terjadinya banjir. Ambang batas curah hujan ekstrim menurut BMKG (2008) adalah 50 mm/hari. Ambang batas tersebut tentu tidak sama untuk tiap daerah begitu pula dengan di Jakarta, karena karakteristik curah hujan yang berbeda-beda tiap daerah, sehingga diperlukan suatu pendekatan lain dalam menentukan curah hujan ekstrim di suatu daerah. Menurut Gilli dan K llezi (2006), penentuan nilai-nilai ekstrim dapat dilakukan dengan dua cara yaitu Block Maxima dan Peaks Over Threshold (POT). Block Maxima yaitu mengambil nilai-nilai maksimum dari setiap periode atau blok sebagai nilai-nilai ekstrim yang selanjutnya didekati dengan Generalized Extreme Value (GEV). POT yaitu mengambil nilai-nilai yang melampaui suatu nilai ambang batas (threshold) sebagai nilai ekstrim yang selanjutnya didekati dengan Sebaran Pareto Terampat (Generalized Pareto Distribution, GPD).

(15)

2

Tujuan Penelitian

Tujuan penelitian ini adalah mengeksplorasi curah hujan harian dan menentukan ambang batas curah hujan harian ekstrim dengan persentil 90, MRL, dan TC.

METODE

Data

Data dalam penelitian ini diperoleh dari Badan Meteorologi, Klimatologi, dan Geofisika (BMKG). Data ini merupakan data curah hujan harian periode 1977–2010 pada stasiun Pondok Betung, Jakarta Selatan. Data tahun 1977-2009 digunakan sebagai data analisis, sedangkan data tahun 2010 digunakan sebagai data validasi. Satuan curah hujan adalah milimeter. Curah hujan satu milimeter (1 mm) artinya adalah air hujan yang jatuh pada setiap permukaan seluas 1 m2 setinggi 1 mm dengan tidak menguap, meresap atau mengalir (BMKG 2008).

Prosedur Analisis Data

Langkah-langkah dalam penelitian ini adalah :

1. Eksplorasi data curah hujan harian dengan histogram dan diagram kotak garis

2. Penentuan calon ambang batas menggunakan persentil 90, MRL dan TC a. Persentil 90

b. Mean Residual Life (MRL)

Mean Residual Life (MRL) merupakan suatu metode yang berlandaskan pada rata-rata pelampauan ambang batas. Metode ini sering digunakan di berbagai bidang seperti reliabilitas, analisis survival, studi aktuaria, dan lain-lain. Omey et al.(2009) menggunakan MRL untuk menentukan ambang batas kecepatan angin di Schiphol, Belanda. MRL sering juga dikenal dengan Expected Remaining Life atau Mean Excess.

Misalkan X merupakan peubah acak yang merepresentasikan amatan yang melebihi ambang batas dengan parameter skala  dan parameter bentuk

(16)

3 Plot MRL dilengkapi dengan selang kepercayaan. Selang kepercayaan pada plot MRL dapat dihitung melalui pendekatan normal dari rataan contoh. Selain uraian di atas, Abdous dan Berred (2004) melakukan pendekatan kernel untuk menduga fungsi MRL.

c. Threshold Choice (TC)

Threshold Choice (TC) dikenal juga dengan Parameter Stability atau Threshold Stability yang merupakan metode dalam menentukan ambang batas. Menurut Coles (2001), TC merupakan metode lain dalam GPD untuk suatu rentang ambang batas dan mencari kestabilan dugaan parameter.

Misalkan X menyebar GPD pada maka akan menyebar GPD juga pada

. Parameter skala diparameterisasi untuk mempermudah Plot TC direpresentasikan dengan titik sebagai berikut :

 dan 

dengan adalah nilai maksimum dari amatan x. Penentuan selang kepercayaan untuk  dapat menggunakan matriks ragam peragam V, sedangkan untuk mendapatkan selang kepercayaan  diperlukan metode delta yang menyatakan bahwa  bergantung pada  dan . Ragam dari

 adalah

  _ _, dengan  _ _ .

3. Pendugaan parameter GPD menggunakan metode kemungkinan maksimum untuk tiap calon ambang batas

Misalkan adalah peubah acak dan misalkan

(17)

4

Misal adalah banyaknya nilai yang melebihi ambang batas maka pelampauan ambang batas akan memiliki fungsi kepekatan peluang (fkp) sebagai berikut :

Pendugaan parameter dapat dilakukan dengan metode kemungkinan maksimum. Fungsi log kemungkinan menurut Coles (2001) dari

Pemaksimuman fungsi log kemungkinan tidak dapat dilakukan secara analitik, maka diperlukan pendekatan numerik dalam penyelesainnya. 4. Pemeriksaan model menggunakan plot peluang dan uji

Kolmogorov-Smirnov

a. Plot Peluang

Menurut Coles (2001) misal ada suatu ambang batas , suatu pelampauan ambang ... , dan model dugaan , maka plot peluang :

dimana dapat dilihat pada persamaan (1).

b. Uji Kolmogorov-Smirnov

Menurut Daniel (1990) hipotesis pada uji ini adalah

5. Peramalan tingkat pengembalian curah hujan untuk tiap calon ambang batas

Peramalan tingkat pengembalian (return level) merupakan salah satu aplikasi dalam GPD. GPD dengan parameter  dan  adalah sebaran yang tepat untuk pelampauan suatu ambang batas dari variabel . Menurut Coles (2001) untuk maka

(18)

5 Selanjutnya didapatkan persamaan peluang di bawah ini

 _ Banyaknya pelampauan ambang batas mengikuti sebaran binomial ( , ). Tingkat pengembalian dinotasikan dengan yang merupakan nilai maksimum yang diharapkan akan dilampaui satu kali secara rata-rata dalam setiap pengamatan. Persamaannya adalah

 _  ramalan tingkat pengembalian yang dapat dilihat pada persamaan (3). 6. Penentuan ambang batas terbaik berdasarkan nilai MAPE dari suatu

ramalan tingkat pengembalian

Metode dalam mengukur nilai kesalahan antara nilai ramalan dengan nilai aktual, menurut Montgomery et al. (2008) dapat menggunakan Mean Absolute Percentage Error (MAPE) sebagai berikut

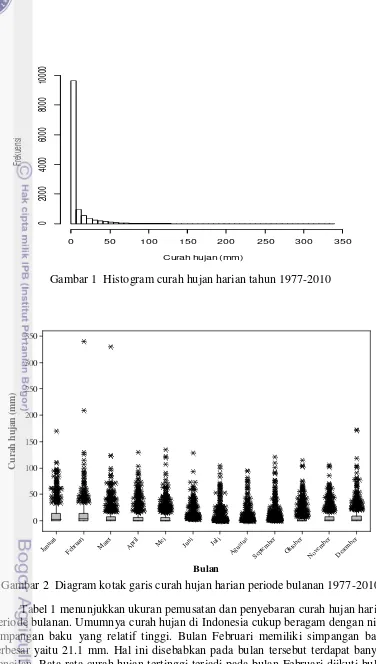
Eksplorasi dengan histogram curah hujan harian tahun 1977-2010 ditampilkan pada Gambar 1. Histogram tersebut memiliki ekor kanan yang panjang, sehingga diindikasikan terdapat nilai-nilai curah hujan ekstrim pada ekor.

(19)

6

Gambar 1 Histogram curah hujan harian tahun 1977-2010

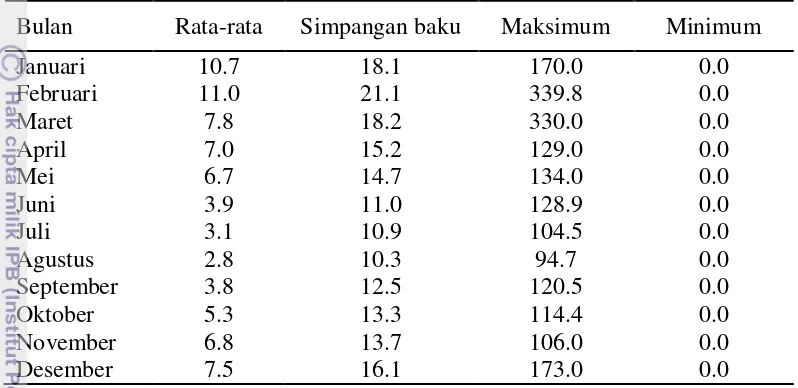
Gambar 2 Diagram kotak garis curah hujan harian periode bulanan 1977-2010 Tabel 1 menunjukkan ukuran pemusatan dan penyebaran curah hujan harian periode bulanan. Umumnya curah hujan di Indonesia cukup beragam dengan nilai simpangan baku yang relatif tinggi. Bulan Februari memiliki simpangan baku terbesar yaitu 21.1 mm. Hal ini disebabkan pada bulan tersebut terdapat banyak pencilan. Rata-rata curah hujan tertinggi terjadi pada bulan Februari diikuti bulan Januari. Bulan Februari memiliki nilai curah hujan tertinggi sebesar 339.8 mm diikuti bulan Maret, Desember, dan Januari. Tiap bulan memiliki nilai minimum sebesar 0 mm, yang artinya ada hari pada tiap bulan yang tidak terjadi hujan. Nilai

(20)

7 rata-rata, simpangan baku, maksimum dan minimum curah hujan, dan banyaknya hujan per tahun dapat dilihat pada Lampiran 1. Jumlah hari hujan berdasarkan kategori hujan harian (BMKG 2008) dapat dilihat pada Lampiran 2.

Tabel 1 Ukuran pemusatan dan penyebaran data curah hujan harian periode bulanan tahun 1977–2010 (mm)

Bulan Rata-rata Simpangan baku Maksimum Minimum

Januari 10.7 18.1 170.0 0.0

Nilai ambang batas ditentukan berdasarkan data curah hujan harian tahun 1977–2009. Scarrot dan MacDonald (2012) melakukan pendugaan ambang batas menggunakan MRL dan TC dengan menetapkan beberapa calon ambang batas terlebih dahulu.

Persentil 90

Data curah hujan harian di stasiun Pondok Betung tahun 1977-2009 memiliki persentil 90 sebesar 21.08. Amatan yang melebihi ambang batas tersebut berjumlah 1206 amatan dan sudah cukup baik untuk pendugaan parameter GPD. Nilai tersebut dijadikan salah satu calon ambang batas curah hujan ekstrim.

Mean Residual Life (MRL)

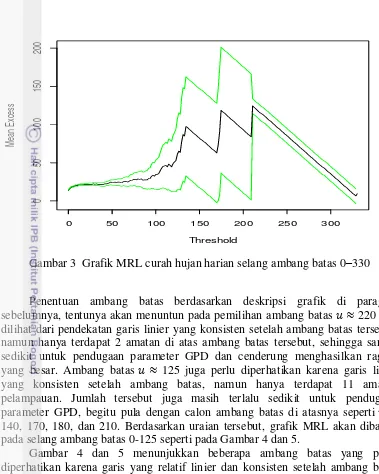
Intrepretasi MRL dalam praktik tidak selalu sederhana. Penentuan ambang batas harus memerhatikan terhadap banyaknya amatan yang melampaui ambang batas dan pendekatan garis linier yang konsisten setelah ambang batas. Grafik MRL curah hujan harian selang ambang batas 0–330 yang dilengkapi selang kepercayaan 95% ditampilkan pada Gambar 3.

(21)

8

Gambar 3 Grafik MRL curah hujan harian selang ambang batas 0–330

Penentuan ambang batas berdasarkan deskripsi grafik di paragraf sebelumnya, tentunya akan menuntun pada pemilihan ambang batas 220 jika dilihat dari pendekatan garis linier yang konsisten setelah ambang batas tersebut, namun hanya terdapat 2 amatan di atas ambang batas tersebut, sehingga sangat sedikit untuk pendugaan parameter GPD dan cenderung menghasilkan ragam yang besar. Ambang batas 125 juga perlu diperhatikan karena garis linier yang konsisten setelah ambang batas, namun hanya terdapat 11 amatan pelampauan. Jumlah tersebut juga masih terlalu sedikit untuk pendugaan parameter GPD, begitu pula dengan calon ambang batas di atasnya seperti 140, 170, 180, dan 210. Berdasarkan uraian tersebut, grafik MRL akan dibatasi pada selang ambang batas 0-125 seperti pada Gambar 4 dan 5.

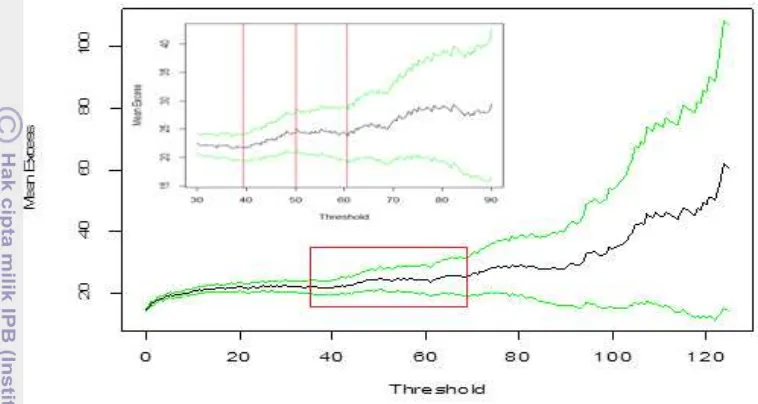
Gambar 4 dan 5 menunjukkan beberapa ambang batas yang perlu diperhatikan karena garis yang relatif linier dan konsisten setelah ambang batas yaitu ambang batas 40, 60, dan 90. Ambang batas tersebut berturut-turut memiliki pelampauan sebanyak 507, 198, dan 54 amatan dan cukup untuk pendugaan parameter GPD. Langkah selanjutnya adalah menentukan lebih detail dari nilai ambang batas tersebut dengan cara memperkecil selang ambang batas grafik MRL untuk tiap calon ambang batas tersebut. Ambang batas u 40 dan 60 dijelaskan oleh Gambar 4 dan ambang batas u 90 dijelaskan oleh Gambar 5.

Gambar 4 menunjukkan setelah nilai ambang batas 39, 50, dan 61 grafik mendekati garis relatif linier dan konsisten. Amatan di atas ambang batas

39, 50, dan 61 berturut-turut sebanyak 535, 291, dan 189 amatan. Banyaknya amatan yang melampaui ketiga ambang batas tersebut sudah cukup untuk pendugaan parameter GPD sehingga ketiga nilai tersebut dijadikan calon ambang batas.

(22)

9 amatan dan sudah cukup untuk pendugaan parameter GPD. Ambang batas 90 kemudian dipilih menjadi salah satu calon ambang batas. Penentuan ambang batas curah hujan ekstrim dengan MRL untuk stasiun Kemayoran, Tanjung Priok, dan Cengkareng dapat dilihat pada Lampiran 8, 9, dan 10.

Threshold Choice (TC)

(23)

10

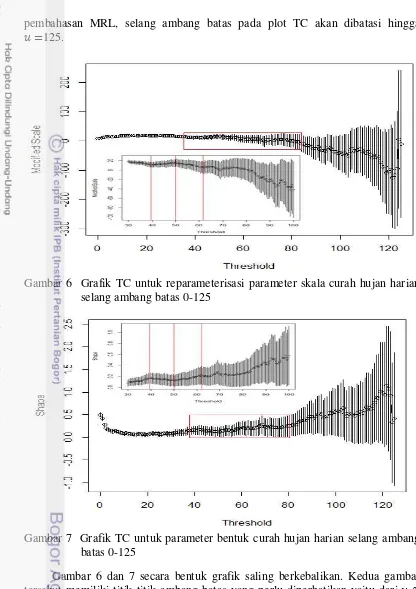
pembahasan MRL, selang ambang batas pada plot TC akan dibatasi hingga

125.

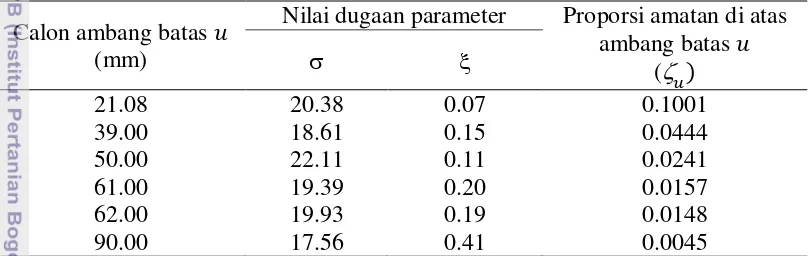
Gambar 6 Grafik TC untuk reparameterisasi parameter skala curah hujan harian selang ambang batas 0-125

Gambar 7 Grafik TC untuk parameter bentuk curah hujan harian selang ambang batas 0-125

(24)

11 parameter skala dan bentuk yang dihasilkan relatif stabil. Masing-masing ambang batas tersebut memiliki berturut-turut 535, 291, dan 178 amatan di atas ambang batas, sehingga cukup untuk pendugaan parameter GPD. Penentuan ambang batas curah hujan ekstrim dengan TC untuk stasiun Kemayoran, Tanjung Priok, dan Cengkareng dapat dilihat pada Lampiran 11, 12, dan 13.

Pendugaan Parameter GPD

Pendugaan parameter GPD harus didahului dengan penentuan nilai ambang batas. Nilai-nilai calon ambang batas yang didapat adalah 21.08,39, 50, 61, 62, dan 90 yang telah ditentukan pada subbab sebelumnya. Penelitian ini menduga parameter GPD dengan metode kemungkinan maksimum.

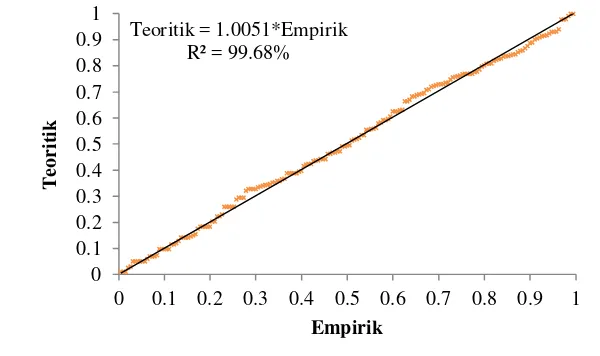
Tabel 2 Nilai dugaan parameter GPD periode analisis 1 Januari 1977–31 Desember 2009

Calon ambang batas (mm)

Nilai dugaan parameter Proporsi amatan di atas ambang batas

Tabel 2 menunjukkan nilai dugaan parameter dan proporsi pelampauan tiap calon ambang batas. Keragaman amatan di atas ambang batas berbanding lurus dengan parameter skala. Keragaman terbesar dan terendah adalah pada 50 dan u = 90 dengan nilai parameter skala  = 22.11 dan  = 17.56. Ambang batas

21.08, 39, 50, 61, dan 62 memiliki nilai parameter bentuk yang saling berdekatan, namun berbeda jauh dengan ambang batas u = 90. Semakin besar nilai ambang batas maka semakin kecil proporsi amatan pelampauannya. Nilai dugaan parameter GPD tiap calon ambang batas untuk stasiun Kemayoran, Tanjung Priok, dan Cengkareng dapat dilihat pada Lampiran 14.

Pemeriksaan Model

(25)

12

Gambar 8 Plot peluang untuk ambang batas u = 61

Hasil pemeriksaan dengan plot peluang dan plot kuantil-kuantil menghasilkan interpretasi yang terkesan subjektif, sehingga diperlukan suatu uji formal yaitu uji Kolmogorov-Smirnov. Uji ini memiliki hipotesis nol:

. merupakan sebaran empirik sedangkan merupakan sebaran teoritis yaitu GPD. Tabel 3 menunjukkan hasil uji Kolmogorov-Smirnov untuk tiap calon ambang batas u. Tabel tersebut menunjukkan semua ambang batas u menyebar GPD. Hal ini membenarkan teori bahwa jika suatu pelampauan ambang batas menyebar GPD, maka untuk ambang batas pun menyebar GPD. Semua calon ambang batas menyebar GPD sehingga dapat dilakukan analisis lebih lanjut.

Tabel 3 Uji Kolmogorov-Smirnov untuk tiap calon ambang batas u Calon ambang batas u

(26)

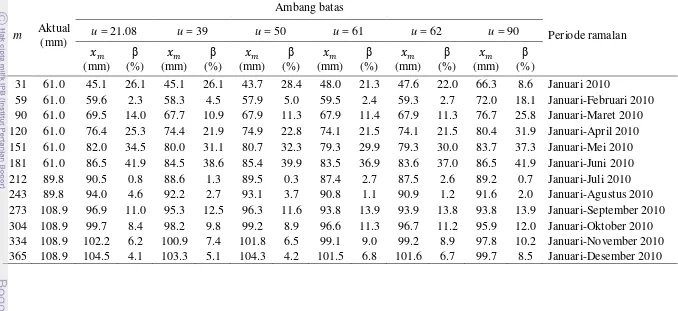
Tabel 4 Ramalan tingkat pengembalian curah hujan untuk tiap calon ambang batas u

m Aktual (mm)

Ambang batas

Periode ramalan

u = 21.08 u = 39 u = 50 u = 61 u = 62 u = 90

(mm)

β

(%) (mm)

β

(%) (mm)

β

(%) (mm)

β

(%) (mm)

β

(%) (mm)

β

(%)

31 61.0 45.1 26.1 45.1 26.1 43.7 28.4 48.0 21.3 47.6 22.0 66.3 8.6 Januari 2010

(27)

(28)

Tabel 4 menunjukkan ramalan tingkat pengembalian untuk tiap ambang batas. Tabel tersebut menunjukkan terdapat nilai ramalan yang berada dibawah ambang batas, padahal seharusnya nilai > u. Berdasarkan persamaan (3) maka perlu ditambah kendala yaitu _  , sehingga dapat ditentukan minimal nilai m agar > u. Ramalan terbaik secara umum terjadi pada m = 212 atau 7 bulan ke depan dengan nilai ramalan yang mendekati nilai aktualnya.Tabel tersebut juga menyajikan kesalahan relatif (β) dari peramalan tingkat pengembalian untuk berbagai ambang batas. Berdasarkan informasi BMKG dalam Prang (2006), adanya perbedaan nilai antara dugaan dengan di lapangan sebesar 25-30%, dugaan atau ramalan yang diberikan masih cukup baik. Kesalahan relatif terbesar terjadi pada peramalan 181 atau 6 bulan ke depan yaitu sekitar 36.9-41.9% dan kesalahan relatif terkecil terjadi pada peramalan 212 atau 7 bulan ke depan yaitu sekitar 1.1-4.6%. Ramalan terbaik terjadi pada periode ramalan 7 bulan ke depan diikuti 8 dan 2 bulan ke depan, sehingga disarankan untuk melakukan peramalan untuk waktu-waktu tersebut.

Grafik perbandingan nilai aktual dan ramalan tingkat pengembalian untuk berbagai ambang batas ditampilkan pada Gambar 9. Beberapa ramalan tingkat pengembalian yang mendekati nilai aktualnya terjadi pada saat m = 59, 212, dan 243. Grafik ramalan untuk ambang batas u = 21.08, 39, 50, 61, dan 62 relatif saling berimpit untuk semua nilai m. Hal ini berbeda dengan grafik ambang batas u = 90 yang mulai berimpit dari m = 151 sampai m = 365 dengan grafik ramalan ambang batas yang lain.

Gambar 9 Grafik perbandingan tingkat pengembalian aktual ( ) terhadap ramalan ambang batas u = 21.08 ( ), u = 39 ( ), u = 50 ( ), u = 61 ( ), u = 62 ( ), dan u = 90 ( )

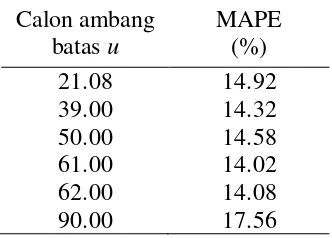
Penentuan Ambang Batas u Terbaik Berdasarkan MAPE

Pemilihan ambang batas u terbaik dalam penelitian ini dilakukan dengan mencari nilai MAPE terkecil dari ramalan tingkat pengembalian pada tiap ambang

(29)

2

batas u. Nilai MAPE pada penelitian ini dihitung dari rata-rata kesalahan relatif peramalan tingkat pengembalian dari beberapa periode tahun 2010 untuk tiap ambang batas u yang telah dijelaskan pada subbab per tingkat pengembalian. Nilai MAPE untuk tiap calon ambang batas u ditampilkan pada Tabel 5.

Tabel 5 Nilai MAPE untuk tiap calon ambang batas u Calon ambang

Tabel 5 menunjukkan ambang batas u = 21.08, 39, 50, 61, dan 62 memiliki nilai MAPE yang tidak jauh berbeda, lain halnya dengan ambang batas u = 90 yang memiliki nilai MAPE terbesar. Ambang batas terbaik dipilih berdasarkan nilai MAPE terkecil. Selain nilai MAPE, hal yang perlu menjadi pertimbangan adalah ragam atau parameter skala. Tabel 2 menunjukkan ambang batas u = 61 memiliki parameter skala sebesar 19.39. Nilai tersebut merupakan ketiga terkecil setelah ambang batas u = 90 dan 39. Ambang batas u = 90 tentulah tidak disarankan untuk dipilih karena nilai MAPE yang besar, sedangkan ambang batas u = 39 memiliki nilai MAPE yang lebih besar dari ambang batas u = 61 tetapi memiliki ragam yang lebih kecil. Menurut BMKG (2008), curah hujan ekstrim harian nilainya lebih dari 50 mm/hari. Hal ini menuntun untuk memilih ambang batas u = 61 sebagai ambang batas yang lebih baik dibanding ambang batas yang lain dengan pertimbangan nilai MAPE terkecil dan besarnya ragam masih relatif kecil. Ambang batas terbaik berdasarkan nilai MAPE tiap calon ambang batas untuk stasiun Kemayoran (55 mm), Tanjung Priok (80 mm), dan Cengkareng (65 mm) dapat dilihat pada Lampiran 14.

Ambang batas u = 61 akan diverifikasi dengan kejadian banjir di Jakarta. Hasil yang diperoleh pada Tabel 6 menunjukkan mayoritas kejadian banjir periode 1977-2013 terjadi ketika curah hujan harian di stasiun Pondok Betung lebih dari ambang batas u = 61 mm. Nilai curah hujan pada kejadian banjir tanggal 20 Januari 1977, 23 September 2010, 6 Oktober 2010, dan 14 Oktober 2010 tidak melebihi ambang batas 61 mm, sehingga POT mendefinisikan curah hujan untuk keempat kejadian banjir tersebut bukan sebagai nilai ekstrim, namun berdasarkan klasifikasi curah hujan ekstrim BMKG (2008), dua kejadian banjir yang disebutkan pertama termasuk curah hujan ekstrim karena nilai curah hujannya lebih dari 50 mm, sedangkan dua kejadian banjir yang disebutkan terakhir tidak tergolong ekstrim baik menurut POT maupun BMKG (2008). Persentil curah hujan saat kejadian banjir 3 April 2012 dan 17 Januari 2013 tidak dapat diketahui karena data curah hujan pada tahun tersebut tidak dimiliki oleh penulis. Rata-rata persentil curah hujan saat terjadi banjir adalah 99 yang nilainya di atas persentil ambang batas u = 61 yaitu 98.43, sehingga secara umum curah hujan saat kejadian banjir merupakan curah hujan yang ekstrim.

(30)

3 Tabel 6 Kejadian banjir dan longsor periode 1977-2013 di Jakarta

Tanggal Jakarta(2008); gBMKG (2010a, 2010b, 2010c, 2010d, 2010e); hBMKG (2012); iBMKG (2013)

Tabel 7 Ramalan banyaknya hari dengan curah hujan ekstrim periode ramalan

59 0 1 (0.955) 0.3675 0.6150 Jan-Feb 2010

90 0 1 (1.432) 0.3420 0.7611 Jan-Mar 2010

120 0 2 (1.909) 0.2701 0.8518 Jan-Apr 2010

151 0 2 (2.392) 0.2616 0.9086 Jan-Mei 2010

181 0 3 (2.864) 0.2233 0.9429 Jan-Jun 2010

212 2 3 (3.316) 0.2206 0.9637 Jan-Jul 2010

243 3 4 (3.780) 0.1941 0.9772 Jan-Agu 2010

273 4 4 (4.295) 0.1933 0.9864 Jan-Sep 2010

304 5 5 (4.725) 0.1741 0.9911 Jan-Okt 2010

334 5 5 (5.250) 0.1744 0.9948 Jan-Nov 2010

365 5 6 (5.727) 0.1596 0.9967 Jan-Des 2010

Tabel 7 menunjukkan banyaknya hari dengan curah hujan ekstrim (> 61 mm/hari) yang didekati dengan sebaran Poisson. Peluang terjadi hujan ekstrim sebanyak ramalan (x) didekati dengan persamaan , dengan

(31)

4

λ d l h t -rata banyaknya hari dengan hujan ekstrim dalam selang waktu m. Peluang terjadi hujan ekstrim dapat dicari dengan persamaan berikut

_{. Hasil nilai ramalan untuk}_m_{= 31 sampai}_m_{= 181 jauh berbeda} dengan nilai aktual, sedangkan ramalan terbaik adalah saat m = 273, 304, dan 334, dengan nilai ramalan sama dengan nilai aktual. Peluang tidak terjadi hujan ekstrim pada Januari tahun 2010 cukup besar yaitu sebesar 0.6205. Selama tahun 2010 hampir dipastikan terjadi hujan ekstrim yang ditunjukkan dengan nilai peluang sebesar 0.9967.

SIMPULAN DAN SARAN

Simpulan

Curah hujan harian di stasiun Pondok Betung menunjukkan banyak pencilan di tiap bulan. Hal ini mengindikasikan adanya nilai-nilai curah hujan yang ekstrim. Nilai-nilai ekstrim tersebut dapat dikaji dengan baik oleh GPD. Penentuan ambang batas curah hujan ekstrim dapat diduga dengan MRL dan TC dalam GPD. Selain dengan MRL dan TC, ambang batas juga dapat didekati dengan persentil 90. Ramalan tingkat pengembalian terbaik terjadi pada periode ramalan 7 bulan ke depan. Ambang batas u = 61 menjadi ambang batas terbaik karena menghasilkan nilai MAPE terkecil dari suatu ramalan tingkat pengembalian dan memiliki ragam yang masih relatif kecil dibanding ambang batas yang lain. Nilai ambang batas curah hujan ekstrim di tiap daerah di Jakarta tidak sama. Hasil verifikasi menunjukkan mayoritas kejadian banjir periode 1977-2013 terjadi ketika curah hujan harian di stasiun Pondok Betung di atas ambang batas 61 mm.

Saran

Penentuan ambang batas curah hujan ekstrim menggunakan persentil 90, MRL, dan TC memiliki kelemahan yaitu intrepetasi hasil yang terkesan subjektif, sehingga penulis menyarankan untuk menggunakan suatu metode yang objektif dalam menentukan ambang batas. Selain itu, dalam penentuan tingkat pengembalian diharapkan periode ramalan yang digunakan harus cukup panjang sehingga nilai tingkat pengembalian melebihi nilai ambang batas.

DAFTAR PUSTAKA

Abdous B, Berred A. 2004. Mean residual life estimation. Journal of Statistical Planning and Inference [Internet]. [diunduh 2013 Mei 1];132 (2005) : 3-19.

Tersedia pada :

(32)

5 Berita BPDAS. Tersedia pada : http://bpdasctw.info/?p=300 [diakses 2013 Juni 14].

Jakarta dilanda banjir besar sejak 1621. 2011 Feb. Kumpul Berita. Tersedia pada : http://www.kumpulberita.com/2011/02/jakarta-dilanda-banjir-besar-sejak-1621.html [diakses pada 2013 Juni 14].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2008. Curah Hujan dan Potensi Bencana Gerakan Tanah. Jakarta : BMKG (ID). Tersedia pada

http://pirba.hrdp-network.com/e5781/e5795/e6331/e15201/eventReport15215/CurahHujan_P otensiGertan_BMKG.pdf [diakses pada 2013 Mei 6].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2010a. Analisis Cuaca Ekstrim Wilayah DKI Jakarta Tanggal 14 September 2010. Jakarta :

BMKG (ID). Tersedia pada

www.staklimpondokbetung.net/publikasi/curah%20hujan%20ekstrim.pdf [diakses pada 2013 Juni 23].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2010b. Analisis Cuaca Ekstrim Wilayah DKI Jakarta Tanggal 23 September 2010. Jakarta :

www.staklimpondokbetung.net/publikasi/banjir%20bintaro.pdf [diakses pada 2013 Juli 14].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2010c. Analisis Cuaca Ekstrim Wilayah Jabodetabek Tanggal 06 Oktober 2010. Jakarta :

www.staklimpondokbetung.net/publikasi/Analisis%20Cuaca%20Ekstrim% 20Jabodetabek.pdf [diakses pada 2013 Juli 14].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2010d. Analisis Cuaca Ekstrim Wilayah Jakarta Tanggal 14 Oktober 2010. Jakarta : BMKG

(ID). Tersedia pada

www.staklimpondokbetung.net/publikasi/Cuaca%20Ekstrim%20Jakarta%2 014%20Oktober%202010.pdf [diakses pada 2013 Juli 14].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2010e. Analisis Cuaca Ekstrim Wilayah Jabodetabek Tanggal 25 Oktober 2010. Jakarta :

(33)

6

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2012. Analisis Kejadian Banjir Wilayah Jakarta Tanggal 2-3 April 2012. Jakarta : BMKG

(ID). Tersedia pada

www.staklimpondokbetung.net/publikasi/Banjir%20Jakarta.pdf [diakses pada 2013 Juni 23].

[BMKG] Badan Meteorologi Klimatologi dan Geofisika (ID). 2013. Analisis Kejadian Banjir DKI Jakarta (17 Januari 2013). Jakarta : BMKG (ID).

Tersedia pada

www.staklimpondokbetung.net/publikasi/Banjir%20Jakarta%2017%20Janu ari%202013.pdf [diakses pada 2013 Juni 23].

Coles S. 2001. An Introduction to Statistical Modelling of Extreme Values. London : Springer.

Daniel WW. 1990. Applied Nonparametric Statistics. Boston : PWS-KENT. Gilli M, K llezi E. 2006. An application of extreme value theory for measuring

financial risk. Computational Economics [Internet]. [diunduh 2013 Mar 19];

27(1) : 1-23. Tersedia pada :

Irfan M. 2011. Sebaran Pareto Terampat untuk Menentukan Curah Hujan Ekstrim (Studi Kasus : Curah Hujan Periode 2001-2010 pada Stasiun Dramaga).[Skripsi]. Bogor : Institut Pertanian Bogor.

Jaya A. 2012 Jul 13. Jakarta bebas banjir : mungkinkah ?. Kompasiana. Rubrik

Green. Tersedia pada :

http://green.kompasiana.com/iklim/2012/07/13/jakarta-bebas-banjir-mungkinkah-476575.html [diakses 2013 Juni 14].

Montgomery DC, Jennings CL, Kulahci M. 2008. Introduction to Time Series Analysis and Forecasting. New Jersey : John Wiley & Sons, Inc.

Omey E, Mallor F, Nualart E. 2009. An Introduction to Statistical Modelling of Extreme Values Application to Calculate Extreme Wind Speeds. Hogeschool Universiteit Brussel [Internet]. [diunduh 2013 Mei 1]. Tersedia pada: https://lirias.hubrussel.be/bitstream/123456789/2841/1/09HRP36.pdf. Scarrott C, MacDonald A. 2012. A review of extreme value threshold estimation

and uncertainty quantification. Statistical Journal [Internet]. [diunduh 2013

(34)

7 Lampiran 1 Ukuran pemusatan dan penyebaran data curah hujan harian periode

tahunan 1977–2010 di stasiun Pondok Betung

(35)

8

Lampiran 2 Jumlah hari hujan berdasarkan kategori hujan harian (BMKG 2008) periode tahunan 1977–2010 di stasiun Pondok Betung

(36)

(37)

(38)

11 Lampiran 8 Grafik MRL curah hujan harian untuk stasiun Kemayoran tahun

1980-2009

Lampiran 9 Grafik MRL curah hujan harian untuk stasiun Tanjung Priok tahun 1973-2009

Lampiran 10 Grafik MRL curah hujan harian untuk stasiun Cengkareng tahun 1986-2009

(39)

12

Lampiran 11 Grafik TC untuk reparameterisasi parameter skala (atas) dan parameter bentuk (bawah) curah hujan harian untuk stasiun Kemayoran tahun 1980-2009

Lampiran 12 Grafik TC untuk reparameterisasi parameter skala (atas) dan parameter bentuk (bawah) curah hujan harian untuk stasiun Tanjung Priok tahun 1973-2009

(40)

13 Lampiran 13 Grafik TC untuk reparameterisasi parameter skala (atas) dan parameter bentuk (bawah) curah hujan harian untuk stasiun Cengkareng tahun 1986-2009

Lampiran 14 Nilai dugaan parameter GPD dan nilai MAPE tiap calon ambang batas untuk stasiun Kemayoran, Tanjung Priok, dan Cengkareng

Stasiun

Calon ambang batas u

(mm)

Nilai dugaan parameter

Proporsi amatan di atas ambang

batas u (

MAPE (%)

 

Kemayoran

21 20.5227 0.1035 0.0752 13.79

40 22.0439 0.1341 0.0300 14.19

55 17.9623 0.3033 0.0166 12.67

68 21.9921 0.2965 0.0087 12.64

80 31.9295 0.1671 0.0049 17.64

Tanjung Priok

25 23.3672 0.0779 0.0597 17.62

40 28.4604 -0.0031 0.0303 18.12

61 27.8016 0.0197 0.0141 18.02

80 20.2739 0.2144 0.0077 13.07

Cengkareng

38 20.6972 0.1387 0.0314 20.21

62 27.3315 0.0747 0.0103 20.37

65 22.6138 0.1561 0.0102 18.86

(41)

14

RIWAYAT HIDUP

Penulis dilahirkan di Bogor pada tanggal 3 Juni 1991 dari ayah Setyono dan Ibu Rahina Rosmawati. Penulis adalah putra pertama dari dua bersaudara. Tahun 2009 penulis lulus dari SMA Negeri 1 Bogor dan pada tahun yang sama penulis lulus seleksi masuk Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB dan diterima di Departemen Statistika, Fakultas Matematika dan Ilmu Pengetahuan Alam. Selama mengikuti perkuliahan, penulis pernah menjadi asisten responsi Metode Statistika pada tahun ajaran 2011/2012 dan 2012/2013 dan asisten responsi Perancangan Percobaan I tahun ajaran 2011/2012. Penulis juga sempat aktif mengajar mata kuliah Fisika TPB di bimbingan belajar Expert. Bulan Februari-Maret 2013 penulis melaksanakan Praktik Lapangan di Badan Meteorologi Klimatologi dan Geofisika (BMKG) pusat, Kemayoran, Jakarta Pusat. Penulis juga aktif dalam organisasi Gamma Sigma Beta (GSB) periode tahun 2012 sebagai staf departemen Data Base Center (DBC). Selain itu juga penulis pernah mengikuti kepanitiaan Statistika Ria tahun 2010 sebagai anggota divisi Sponsorship dan tahun 2011 sebagai ketua divisi Humas.