BAB 2 LANDASAN TEORI

BAB 2

LANDASAN TEORI

2.1 Kriptografi

2.1.1 Definisi Kriptografi

Kata kriptografi berasal dari bahasa Yunani, “kryptós” yang berarti tersembunyi dan “gráphein” yang berarti tulisan. Sehingga kata kriptografi dapat diartikan berupa frase “tulisan tersembunyi”. Menurut Request for Comments (RFC), kriptografi merupakan ilmu matematika yang berhubungan dengan transformasi data untuk membuat artinya tidak dapat dipahami (untuk menyembunyikan maknanya), mencegahnya dari

perubahan tanpa izin, atau mencegahnya dari penggunaan yang tidak sah. Jika transformasinya dapat dikembalikan, kriptografi juga bisa diartikan sebagai proses mengubah kembali data yang terenkripsi menjadi bentuk yang dapat dipahami. Artinya, kriptografi dapat diartikan sebagai proses untuk melindungi data dalam arti yang luas (Oppliger, 2005).

Dalam kamus bahasa Inggris Oxford diberikan pengertian kriptografi sebgai berikut :

“ Sebuah teknik rahasia dalam penulisan, dengan karakter khusus, dengan mengguanakan huruf dan karakter di luar bentuk aslinya, atau dengan metode-metode lain yang hanya dapat dipahami oleh pihak-pihak yang memproses kunci, juga semua hal yang ditulis dengan cara seperti ini.”

Jadi, secara umun dapat diartikan sebagai seni menulis atau memecahkan cipher (Talbot dan welsh, 2006).

Menezes, van Oorschot dan Vanstone (1996) menyatakan bahwa kriptografi adalah suatu studi teknik matematika yang berhubungan dengan aspek keamanan informasi seperi kerahasiaan, integritas data, otentikasi entitas dan otentikasi keaslian

data. Kriptografi tidak hanya berarti penyediaan keamanan informasi, melainkan sebuah himpunan teknik-teknik.

Selain defenisi di atas, Scheiner (1996) mengemukakan pendapatnya tentang defenisi kriptografi yaitu : ilmu dan seni untuk menjaga keamanan pesan. Penggunaan kata “seni” di dalam definisi di atas berasal dari fakta sejarah bahwa pada masa-masa awal sejarah kriptografi, setiap orang mungkin mempunyai cara yang unik untuk merahasiakan pesan. Cara-cara unik tersebut mungkin berbeda-beda pada setiap pelaku kriptografi sehingga setiap cara menulis pesan rahasia pesan mempunyai nilai estetika tersendiri sehingga kriptografi berkembang menjadi sebuah seni merahasiakan pesan (kata “graphy” di dalam “cryptography” itu sendiri sudah menyiratkan sebuah seni) (Munir, 2006).

2.1.2 Sejarah Kriptografi

Kriptografi mempunyai sejarah yang panjang dan menakjubkan. Informasi yang lengkap mengenai sejarah kriptografi dapat ditemukan di dalam buku David Kahn yang berjudul The Codebreakers. Buku yang tebalnya 1000 halaman ini menulis secara rinci sejarah kriptografi mulai dari penggunaan kriptografi oleh Bangsa Mesir 4000 tahun yang lalu (berupa hieroglyph yang terdapat pada piramid) hingga penggunaan kriptografi pada abad ke-20 (Menezes, van Oorschot dan Vanstone, 1996).

Secara historis ada empat kelompok yang berkontribusi terhadap perkembangan kriptografi, dimana mereka menggunakan kriptografi untuk menjamin kerahasiaan dalam komunikasi pesan penting, yaitu kalangan militer (termasuk intelijen dan mata-mata), kalangan diplomatik, penulis buku harian, dan pencinta (lovers). Di antara keempat kelompok ini, kalangan militer yang memberikan kontribusi paling penting karena pengiriman pesan di dalam suasana perang membutuhkan teknik enkripsi dan dekripsi yang rumit.

Sejarah kriptografi sebagian besar merupakan sejarah kriptografi klasik, yaitu metode enkripsi yang menggunakan kertas dan pensil atau mungkin dengan bantuan alat mekanik sederhana. Secara umum algoritma kriptografi klasik dikelompokkan menjadi dua kategori, yaitu algoritma transposisi (transposition cipher) dan algoritma substitusi (substitution cipher). Cipher transposisi mengubah susunan huruf-huruf di dalam pesan, sedangkan cipher substitusi mengganti setiap huruf atau kelompok huruf dengan sebuah huruf atau kelompok huruf lain.

Sejarah kriptografi klasik mencatat penggunaan cipher transposisi oleh tentara Sparta di Yunani pada permulaan tahun 400 SM. Mereka menggunakan alat yang namanya scytale (Gambar 2.1(a)). Scytale terdiri dari sebuah kertas panjang dari daun papyrus yang dililitkan pada sebuah silinder dari diameter tertentu (diameter silender menyatakan kunci penyandian). Pesan ditulis secara horizontal, baris per baris (Gambar 2.1(b)). Bila pita dilepaskan, maka huruf-huruf di dalamnya telah tersusun secara acak membentuk pesan rahasia. Untuk membaca pesan, penerima pesan harus melilitkan kembali melilitkan kembali kertas tersebut ke silinder yang diameternya sama dengan diameter silinder pengirim.

Sedangkan algoritma substitusi paling awal dan paling sederhana adalah Caesar cipher, yang digunakan oleh raja Yunani kuno, Julius Caesar. Caranya adalah dengan mengganti setiap karakter di dalam alfabet dengan karakter yang terletak pada tiga posisi berikutnya di dalam susunan alfabet (Munir, 2006).

(a) (b)

Gambar 2.1. (a) Sebuah scytale; (b) Pesan ditulis secara horizontal, baris per baris. Bila kertas dilepaskan, maka pesan yang terbentuk adalah cipherteks.

Kriptografi juga digunakan untuk tujuan keamanan. Kalangan gereja pada masa awal agama Kristen menggunakan kriptografi untuk menjaga tulisan relijius dari gangguan otoritas politik atau budaya yang dominan saat itu. Mungkin yang sangat terkenal adalah “Angka si Buruk Rupa (Number of the Beast) di dalam Kitab Perjanjian Baru. Angka “666” menyatakan cara kriptografik (yaitu dienkripsi) untuk menyembunyikan pesan berbahaya, para ahli percaya bahwa pesan tersebut mengacu pada Kerajaan Romawi.

Di India, kriptografi digunakan oleh pencinta (lovers) untuk berkomunikasi tanpa diketahui orang. Bukti ini ditemukan di dalam buku Kama Sutra yang merekomendasikan wanita seharusnya mempelajari seni memahami tulisan dengan cipher. Pada Abad ke-17, sejarah kriptografi mencatat korban ketika ratu Skotlandia, Queen Mary, dipancung setelah surat rahasianya dari balik penjara (surat terenkrpsi yang isinya rencana membunuh Ratu Elizabeth I) berhasil dipecahkan oleh seorang pemecah kode (Munir, 2006).

Seperti yang telah disebutkan di atas bahwa kriptografi umum digunakan di kalangan militer. Pada Perang Dunia ke II, Pemerintah Nazi Jerman membuat mesin enkripsi yang dinamakan Enigma. (Gambar 2.2). Mesin yang menggunakan beberapa buah rotor (roda berputar) ini melakukan enkripsi dengan cara yang sangat rumit. Namun Enigma cipher berhasil dipecahkan oleh pihak Sekutu dan keberhasilan memecahkan Enigma sering dikatakan sebagai faktor yang memperpendek perang dunia ke-2 (Churchhouse, 2004).

Gambar 2.2. Mesin enkripsi Enigma yang digunakan oleh tentara Jerman pada masa Perang Dunia ke-2. Enigma cipher berhasil dipecahkan oleh Sekutu.

Kriptografi modern dipicu oleh perkembangan peralatan komputer digital. Dimulai dari usaha Feistel dari IBM di awal tahun 70-an dan mencapai puncaknya pada 1977 dengan pengangkatan DES (Data Encryption Standard) sebagai standar pemrosesan informasi federal Amerika Serikat untuk mengenkripsi informasi yang tidak belum diklasifikasi. DES merupakan mekanisme kriptografi yang paling dikenal sepanjang sejarah.

Pengembangan paling mengejutkan dalam sejarah kriptografi terjadi pada 1976 saat Diffie dan Hellman mempublikasikan ”New Directions in Cryptography”. Tulisan ini memperkenalkan konsep revolusioner kriptografi kunci publik dan juga memberikan metode baru untuk pertukaran kunci, keamanan yang berdasar pada kekuatan masalah logaritma diskret. Meskipun Diffie dan Hellman tidak memiliki realisasi praktis pada ide enkripsi kunci publik saat itu, idenya sangat jelas dan menumbuhkan ketertarikan yang luas pada komunitas kriptografi.

Pada 1978 Rivest, Shamir dan Adleman menemukan rancangan enkripsi kunci publik yang sekarang disebut RSA. Rancangan RSA berdasar pada masalah faktorisasi bilangan yang sulit, dan menggiatkan kembali usaha untuk menemukan metode yang lebih efisien untuk pemfaktoran. Tahun 80-an terjadi peningkatan luas di area ini, sistem RSA masih aman. Sistem lain yang merupakan rancangan kunci publik ditemukan oleh Taher ElGamal pada tahun 1984. Rancangan ini berdasar pada masalah logaritma diskret.

Salah satu kontribusi penting dari kriptografi kunci publik adalah tanda tangan digital. Pada 1991 standar internasional pertama untuk tanda tangan digital diadopsi.

Standar ini berdasar pada rancangan kunci publik RSA. Pada 1994 pemerintah Amerika Serikat mengadopsi Digital Signature Standard, sebuah mekanisme kriptografi yang berdasar pada algoritma ElGamal (Menezes, van Oorschot dan Vanstone, 1996).

2.1.3 Tujuan Kriptografi

Tujuan dari kriptografi yang juga merupakan aspek keamanan informasi adalah sebagai berikut (Menezes, van Oorschot dan Vanstone, 1996)(Scheiner, 1996) :

a) Kerahasiaan (confidentiality) adalah layanan yang digunakan untuk menjaga isi informasi dari semua pihak kecuali pihak yang memiliki otoritas terhadap informasi. Ada beberapa pendekatan untuk menjaga kerahasiaan, dari pengamanan secara fisik hingga penggunaan algoritma matematika yang membuat data tidak dapat dipahami. Istilah lain yang senada dengan confidentiality adalah secrecy dan privacy.

b) Integritas data adalah layanan penjagaan pengubahan data dari pihak yang tidak berwenang. Untuk menjaga integritas data, sistem harus memiliki kemampuan untuk mendeteksi manipulasi pesan oleh pihak-pihak yang tidak berhak, antara lain penyisipan, penghapusan, dan pensubsitusian data lain kedalam pesan yang sebenarnya. Di dalam kriptografi, layanan ini direalisasikan dengan menggunakan tanda-tangan digital (digital signature). Pesan yang telah ditandatangani menyiratkan bahwa pesan yang dikirim adalah asli.

c) Otentikasi adalah layanan yang berhubungan dengan identifikasi, baik mengidentifikasi kebenaran pihak-pihak yang berkomunikasi (user

authentication atau entity authentication) maupun mengidentifikasi kebenaran sumber pesan (data origin authentication). Dua pihak yang saling berkomunikasi harus dapat mengotentikasi satu sama lain sehingga ia dapat memastikan sumber pesan. Pesan yang dikirim melalui saluran komunikasi juga harus diotentikasi asalnya. Otentikasi sumber pesan secara implisit juga memberikan kepastian integritas data, sebab jika pesan telah dimodifikasi berarti sumber pesan sudah tidak benar. Oleh karena itu, layanan integritas data selalu dikombinasikan dengan layanan otentikasi sumber pesan. Di dalam kriptografi, layanan ini direalisasikan dengan menggunakan tanda-tangan digital (digital signature). Tanda-tangan digital menyatakan sumber pesan.

d) Nirpenyangkalan adalah layanan untuk mencegah entitas yang berkomunikasi melakukan penyangkalan, yaitu pengirim pesan menyangkal melakukan pengiriman atau penerima pesan menyangkal telah menerima pesan.

Tujuan dasar dari kriptografi adalah mewujudkan keempat aspek keamanan informasi tersebut dalam teori dan praktek

2.1.4 Terminologi dan Konsep Dasar Kriptografi

Di dalam kriptografi kita akan sering menemukan berbagai istilah atau terminologi. Beberapa istilah yang penting untuk diketahui diberikan di bawah ini:

2.1.4.1 Pesan, Plainteks, dan Cipherteks

Pesan (message) adalah data atau informasi yang dapat dibaca dan dimengerti maknanya. Nama lain untuk pesan adalah plainteks atau teks jelas (cleartext)

(Scheiner, 1996). Pesan dapat berupa data atau informasi yang dikirim (melalui kurir, saluran telekomunikasi, dsb) atau yang disimpan di dalam media perekaman (kertas, storage, dan sebagainya). Pesan yang tersimpan tidak hanya berupa teks, tetapi juga dapat berbentuk citra (image), suara/bunyi (audio), dan video, atau berkas biner lainnya.

Agar pesan tidak dapat dimengerti maknanya oleh pihak lain, maka pesan perlu disandikan ke bentuk lain yang tidak dapat dipahami (enkripsi). Bentuk pesan yang tersandi disebut cipherteks atau kriptogram. Proses pembalikan dimana cipherteks diubah kembali menjadi plainteks di sebut dekripsi (Stamp , 2007).

(a) Plainteks (teks) (b) Cipherteks dari (a) Gambar 2.3. Contoh-contoh plainteks dan cipherteksnya.

2.1.4.2 Peserta Komunikasi

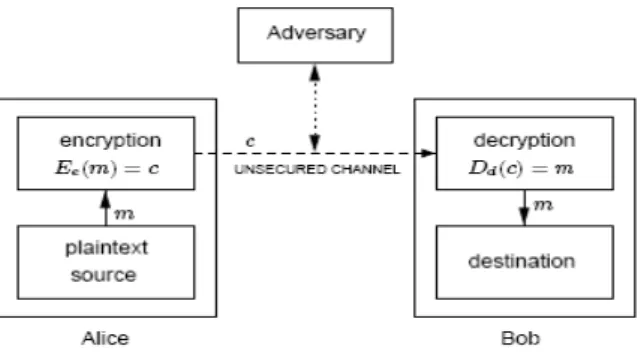
a) Entitas atau peserta adalah orang atau sesuatu yang mengirim, menerima, atau memanipulasi informasi. Entitas bisa berupa orang, terminal komputer, kartu kredit, dan sebagainya. Jadi, orang bisa bertukar pesan dengan orang lainnya (contoh: Alice berkomunikasi dengan Bob) sedangkan di dalam jaringan komputer, mesin (komputer) berkomunikasi dengan mesin (contoh: mesin ATM berkomunikasi dengan komputer server di bank).

b) Pengirim adalah entitas dalam komunikasi yang mengirimkan informasi kepada entitas lainnya lainnya.

c) Penerima adalah entitas dalam komunikasi yang diharapkan menerima informasi.

d) Penyusup (adversary) adalah entitas diluar pengirim dan penerima yang mencoba untuk membobol keamanan informasi. Penyusup biasanya bertindak seolah-olah sebagai pengirim yang sah ataupun penerima yang sah.

2.1.4.3. Kriptologi

Kriptologi berasal dari bahasa Yunani, “kryptós” yang berarti “tersembunyi” dan “lógos” yang berarti “kata”. Jadi, kriptologi dapat diartikan sebagai frase kata yang tersembunyi (Oppliger, 2005). Kriptologi dapat juga diartikan sebagai seni dan ilmu untuk membuat dan memecahkan kode rahasia. Kriptologi dibagi menjadi kriptografi (seni dan ilmu membuat kode rahasia), kriptanalisis (ilmu dan seni untuk memecahkan chiperteks menjadi plainteks tanpa mengetahui kunci yang digunakan)( Stamp, 2007) dan steganografi (metoda menyembunyikan pesan atau data lainnya)(Oppliger, 2005).

Pelaku kriptanalisis disebut kriptanalis. Jika seorang kriptografer mentransformasikan plainteks menjadi cipherteks dengan suatu algoritma dan kunci

maka sebaliknya seorang kriptanalis berusaha untuk memecahkan cipherteks tersebut untuk menemukan plainteks atau kunci.

.

Gambar 2.5. Hubungan kritografi, kriptanalisis dan steganografi

2.1.5 Algoritma dan Kunci

Algoritma menggambarkan sebuah prosedur komputasi yang terdiri dari variabel input dan menghasilkan output yang berhubungan (Oppliger, 2005). Algoritma kriptografi atau sering disebut dengan cipher adalah suatu fungsi matematis yang digunakan untuk melakukan enkripsi dan dekripsi (Schneier, 1996). Algoritma kriptografi ini bekerja dalam kombinasi dengan menggunakan kunci (key) seperti kata, nomor atau frase tertentu.

Bila keamanan algoritma bergantung pada kerahasian algoritma yang bekerja, maka algoritma tersebut dikatakan sebagai algoritma terbatas (terbatas kemampuannya). Algoritma terbatas mempunyai sejarah yang menarik. Algoritma terbatas biasanya digunakan oleh sekelompok orang untuk bertukar pesan satu sama lain. Mereka membuat suatu algoritma enkripsi dan algoritma enkripsi tersebut hanya diketahui oleh anggota kelompok itu saja. Tetapi, algoritma terbatas tidak cocok lagi saat ini, sebab setiap kali ada anggota kelompok keluar, maka algoritma kriptografi

harus diganti lagi. Kerahasian algoritmanya menjadi titik kelemahan karena tidak mengijinkan adanya kontrol kualitas atau standarisasi.

Kriptografi modern mengatasi masalah di atas dengan penggunaan kunci, dimana algoritma yang diguakan tidak lagi dirahasiakan, tetapi kunci harus dijaga kerahasiaannya. Kunci adalah parameter yang digunakan untuk transformasi enciphering dan dechipering. Kunci biasanya berupa string atau deretan bilangan. Dengan menggunakan kunci K, maka fungsi enkripsi dan dekripsi dapat ditulis sebagai

EK(P) = C dan DK(C) = P

dan kedua fungsi ini memenuhi DK(EK(P)) = P

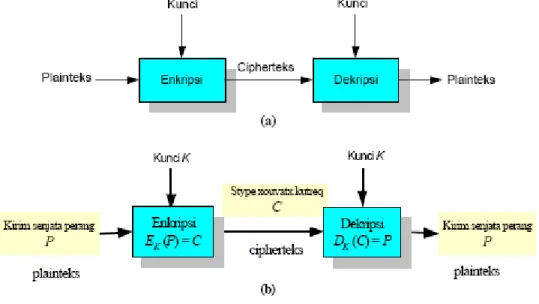
Gambar 2.6. (a) Skema enkripsi dan dekripsi, (b) contoh ilustrasi enkripsi dan dekripsi pesan.

Gambar 2.6(a) memperlihatkan skema enkripsi dan dekripsi dengan menggunakan kunci, sedangkan Gambar 2.6(b) mengilustrasikan enkripsi dan dekripsi terhadap sebuah pesan (Schneier, 1996).

2.1.6 Jenis Algoritma Kriptografi

Berdasarkan jenis kunci yang digunakannya, algoritma .kriptografi dikelompokan menjadi dua bagian, yaitu : algoritma simetris (algoritma konvensional) dan algoritma asimetris (algoritma kunci publik) (Scheiner, 1996) (Kurniawan, 2004) (Munir, 2006) (Menezes, van Oorschot dan Vanstone, 1996).

2.1.6.1 Algoritma Simetris

Algoritma simetris adalah algoritma kriptografi yang menggunakan kunci enkripsi yang sama dengan kunci dekripsinya. Istilah lain untuk kriptografi kunci-simetri adalah kriptografi kunci privat (private-key cryptography), kriptografi kunci rahasia (secret-key cryptography), atau kriptografi konvensional (conventional cryptography). Sistem kriptografi kunci-simetri (atau disingkat menjadi “kriptografi simetri” saja), mengasumsikan pengirim dan penerima pesan sudah berbagi kunci yang sama sebelum bertukar pesan. Keamanan sistem kriptografi simetri terletak pada kerahasiaan kuncinya.

Kriptografi simetri merupakan satu-satunya jenis kriptografi yang dikenal dalam catatan sejarah hingga tahun 1976. Semua algoritma kriptografi klasik termasuk ke dalam sistem kriptografi simetri.

Gambar 2.7. Skema kriptografi simetri. Kunci enkripsi sama dengan kunci dekripsi, yaitu K.

Kelebihan algoritma simetris ini adalah proses enkripsi dan deskripsinya yang jauh lebih cepat dibandingkan dengan algoritma asimetris. Sedangkan kelemahan algoritma ini adalah permasalahan distribusi kunci (key distribution). Seperti yang telah dibahas, proses enkripsi dan deskripsi menggunakan kunci yang sama. Sehingga muncul persoalan menjaga kerahasian kunci, yaitu pada saat pengiriman kunci pada media yang tidak aman seperti internet. Tentunya jika kunci ini sampai hilang atau sudah dapat ditebak oleh orang lain (orang yang tidak berhak), maka kriptosistem ini sudah tidak aman lagi.

Kelemahan lain adalah masalah efisiensi jumlah kunci. Jika terdapat n user, maka diperlukan n(n-1)/2 kunci, sehingga untuk jumlah user yang sangat banyak, sistem ini tidak efisien lagi (Menezes, van Oorschot dan Vanstone, 1996).

2.1.6.2. Algoritma Asimetris

Algoritma asimetris atau kunci publik didesain sehingga kunci yang digunakan untuk enkripsi berbeda dengan kunci untuk dekripsi dimana kunci untuk enkripsi tidak rahasia dan dapat diketahui oleh siapapun (diumumkan ke publik), sementara kunci untuk dekripsi hanya diketahui oleh penerima pesan (rahasia).

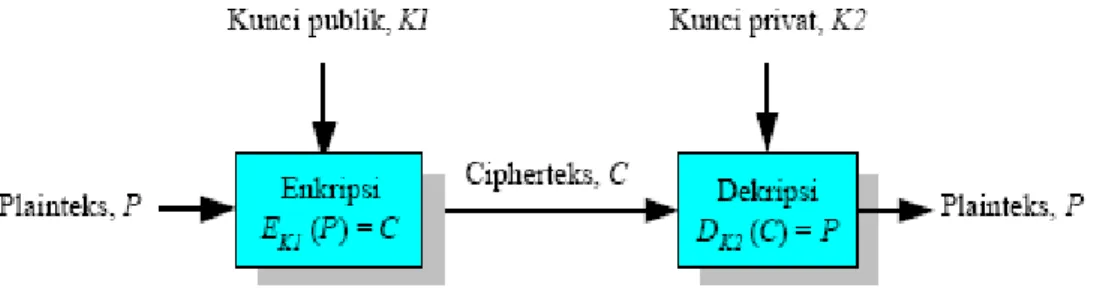
Pada kriptografi jenis ini, setiap orang yang berkomunikasi mempunyai sepasang kunci, yaitu kunci privat dan kunci publik. Pengirim mengenkripsi pesan dengan menggunakan kunci publik si penerima pesan. Hanya penerima pesan yang dapat mendekripsi pesan karena hanya ia yang mengetahui kunci privatnya sendiri

(Gambar 2.8). Contoh algoritma kriptografi kunci-publik diantaranya RSA, Elgamal, DSA, dan sebagainya.

Gambar 2.8. Skema kriptografi Asimetri. Kunci enkripsi tidak sama dengan kunci dekripsi. Kunci enkripsi bersifat publik (tidak rahasia), sedangkan kunci dekripsi

privat (rahasia).

Kriptografi kunci-publik dapat dianalogikan seperti kotak surat yang terkunci dan memiliki lubang untuk memasukkan surat. Setiap orang dapat memasukkan surat ke dalam kotak surat tersebut, tetapi hanya pemilik kotak yang dapat membuka kotak dan membaca surat di dalamnya karena ia yang memiliki kunci. Keuntungan sistem ini ada dua. Pertama, tidak ada kebutuhan untuk mendistribusikan kunci privat sebagaimana pada sistem kriptografi simetri. Kunci publik dapat dikirim ke penerima melalui saluran yang sama dengan saluran yang digunakan untuk mengirim pesan. Saluran untuk mengirim pesan umumnya tidak aman.

Kedua, jumlah kunci dapat ditekan. Untuk berkomunikasi secara rahasia dengan banyak orang tidak perlu kunci rahasia sebanyak jumlah orang tersebut, cukup membuat dua buah kunci, yaitu kunci publik bagi para koresponden untuk mengenkripsi pesan, dan kunci privat untuk mendekripsi pesan. Berbeda dengan

kriptografi kunci-simetris dimana jumlah kunci yang dibuat adalah sebanyak jumlah pihak yang diajak berkorespondensi.

Contoh penggunaan, misalkan jaringan komputer menghubungkan komputer karyawan di kantor cabang dengan komputer manejer di kantor pusat. Seluruh kepala cabang diberitahu bahwa kalau mereka mengirim laporan ke manejer di kantor pusat, mereka harus mengenkripsi laporan tersebut dengan kunci publik manejer (kunci publik menejer diumumkan kepada seluruh kepala cabang). Untuk mengembalikan laporan tersandi ke laporan semula, hanya manejer yang dapat melakukan dekripsi, karena hanya dialah yang memegang kunci privat. Selama proses transmisi cipherteks dari kantor cabang ke kantor pusat melalui saluran komunikasi mungkin saja data yang dikirim disadap oleh pihak ketiga, namun pihak ketiga ini tidak dapat mengembalikan cipherteks ke plainteksnya karena ia tidak mengetahui kunci untuk dekripsi.

Meski berusia relatif muda (sejak 1976), kriptografi kunci-publik mempunyai kontribusi yang luar biasa dibandingkan dengan sistem kriptografi simetri. Kontribusi yang paling penting adalah tanda-tangan digital pada pesan untuk memberikan aspek keamanan otentikasi, integritas data, dan nirpenyangkalan. Tanda-tangan digital adalah nilai kriptografis yang bergantung pada isi pesan dan kunci yang digunakan. Pengirim pesan mengenkripsi pesan (yang sudah diringkas) dengan kunci privatnya, hasil enkripsi inilah yang dinamakan tanda-tangan digital. Tanda-tangan digital dilekatkan (embed) pada pesan asli. Penerima pesan memverifikasi tanda-tangan digital dengan menggunaklan kunci publik.

Baik kriptografi simetri maupun kriptografi asimetri (kuncipublik), keduanya mempunyai kelebihan dan kelemahan.

a. Kelebihan kriptografi simetri:

1. Algoritma kriptografi simetri dirancang sehingga proses enkripsi/dekripsi membutuhkan waktu yang singkat.

2. Ukuran kunci simetri relatif pendek.

3. Algorima kriptografi simetri dapat disusun untuk menghasilkan cipher yang lebih kuat.

4. Otentikasi pengirim pesan langsung diketahui dari cipherteks yang diterima, karena kunci hanya diketahui oleh pengirim dan penerima pesan saja.

b. Kelemahan kriptografi simetri:

1. Kunci simetri harus dikirim melalui saluran yang aman. Kedua entitas yang berkomunikasi harus menjaga kerahasisan kunci ini.

2. Kunci harus sering diubah, mungkin pada setiap sesi komunikasi.

c. Kelebihan kriptografi kunci-publik (asimetri):

1. Hanya kunci privat yang perlu dijaga kerahasiaannya oleh setiap entitas yang berkomuniaksi (tetapi, otentikasi kunci publik tetap harus terjamin). Tidak ada kebutuhan mengirim kunci privat sebagaimana pada sistem simetri.

2. Pasangan kunci publik/kunci privat tidak perlu diubah, bahkan dalam periode waktu yang panjang.

3. Dapat digunakan untuk mengamankan pengiriman kunci simetri.

4. Beberapa algoritma kunci-publik dapat digunakan untuk memberi tanda tangan digital pada pesan.

d. Kelemahan kriptografi kunci-publik (asimetri):

1. Enkripsi dan dekripsi data umumnya lebih lambat daripada sistem simetri, karena enkripsi dan dekripsi menggunakan bilangan yang besar dan melibatkan operasi perpangkatan yang besar.

2. Ukuran cipherteks lebih besar daripada plainteks (bisa dua sampai empat kali ukuran plainteks).

3. Ukuran kunci relatif lebih besar daripada ukuran kunci simetri.

4. Karena kunci publik diketahui secara luas dan dapat digunakan setiap orang, maka cipherteks tidak memberikan informasi mengenai otentikasi pengirim. 5. Tidak ada algoritma kunci-publik yang terbukti aman (sama seperti block

cipher). Kebanyakan algoritma mendasarkan keamanannya pada sulitnya memecahkan persoalan-persoalan aritmetik (pemfaktoran, logaritmik, dan sebagainya) yang menjadi dasar pembangkitan kunci.

2.1.7 Keamanan Sistem Kriptografi

Suatu sistem kriptografi merupakan sebuah himpunan algoritma, seluruh kemungkinan plainteks, cipherteks, kunci, dan proses manajemen kunci yang digunakan(Oppliger, 2005) .

2.1.7.1 Jenis-Jenis Ancaman Keamanan

Terdapat banyak faktor yang mengancam keamanan data. Ancaman-ancaman tersebut menjadi masalah terutama dengan semakin meningkatnya komunikasi data yang bersifat rahasia seperti: pemindahan dana secara elektronik pada dunia perbankan atau pengiriman dokumen rahasia pada instansi pemerintah. Untuk mengantisipasi

ancaman-ancaman tersebut perlu dilakukan usaha untuk melindungi data yag dikirim melalui saluran komunikasi. Salah satunya adalah dengan teknik enkripsi.

Dari sekian banyak faktor-faktor yang dapat mengancam keamanan dari suatu data, maka berdasarkan tekniknya, faktor-faktor tersebut dapat dikelompokkan ke dalam empat jenis ancaman, yaitu:

a) Interruption

Interruption terjadi bila data yang dikirimkan dari A tidak sampai pada orang yang berhak (B). Interruption merupakan pola penyerangan terhadap sifat availability (ketersediaan data), yaitu data dan informasi yang berada dalam sistem komputer dirusak atau dibuang, sehinggga menjadi tidak ada dan tidak berguna. Contohnya, hard disk yang dirusak atau memotong jalur komunikasi.

Gambar 2.9 Interruption b) Interception

Serangan ini terjadi jika pihak ketiga berhasil mendapatkan akses informasi dari dalam sistem komputer. Contohnya, dengan menyadap data yang melalui jaringan public (wiretapping) atau menyalin secara tidak sah file atau program Interception merupakan pola penyerangan terhadap sifat confidentially/secrecy (kerahasiaan data).

Sumber Tujuan Normal Flow Interception Sumber Tujuan Normal Flow Interruption

Gambar 2.10 Interception

c) Modification

Pada serangan ini pihak ketiga yang tidak hanya berhasil mendapatkan akses informasi dari dalam sistem komputer, tetapi juga dapat melakukan perubahan terhadap informasi. Contohnya, merubah program berhasil merubah pesan yang dikirimkan. Modification merupakan pola penyerangan terhadap sifat integrity (keaslian data).

Gambar 2.11 Modification

d) Fabrication

Fabrication merupakan ancaman terhadap integritas, yaitu orang yang tidak berhak yang meniru atau memalsukan suatu objek ke dalam sistem. Contohnya, dengan menambahkan suatu record ke dalam file.

Gambar 2.12 Fabrication Sumber Tujuan Normal Flow Modification Sumber Tujuan Normal Flow Fabrication

2.1.7.2 Serangan Pada Sistem Kriptografi

Pada dasarnya serangan terhadap sistem kriptografi dapat dibedakan menjadi dua jenis yaitu:

a) Serangan pasif adalah serangan dimana penyerang hanya memonitor saluran komunikasi. Penyerang pasif hanya mengancam kerahasiaan data.

b) Serangan aktif adalah serangan dimana penyerang mencoba untuk menghapus, menambahkan, atau dengan cara yang lain mengubah transmisi pada saluran. Penyerang aktif mengancam integritas data dan otentikasi, juga kerahasiaan.

2.1.7.3 Kualitas Keamanan Algoritma

Suatu algoritma dikatakan aman, bila tidak ada cara menemukan plaintextnya, berapapun banyaknya ciphertext yang dimiliki cryptanalyst. Sampai saat ini hanya OTP (one-time-pad) yang dinyatakan tidak dapat dipecahkan meskipun diberikan sumber daya yang tidak terbatas. Seluruh algoritma lainnya selalu dapat dipecahkan dengan Ciphertext only attack, dan dengan teknik brute-force attack (memeriksa satu-persatu seluruh kemungkinan kunci dan memeriksa apakah plaintext yang dihasilkan memiliki arti yang sesuai). Harap diingat, komputer DNA yang sedang diteliti sekarang memiliki kemampuan yang mampu melakukan perhitungan milyaran kali lebih cepat daripada komputer yang ada sekarang ini. Dengan peningkatan kecepatan komputasi, maka keamanan algoritma kriptografi akan semakin terancam tentunya.

Karenanya selalu terdapat kemungkinan ditemukannya cara baru untuk menembus suatu algoritma kriptografi, maka algoritma kriptografi yang dikatakan “cukup“ atau “mungkin” aman, bisa memiliki keadaan sebagai berikut:

a) Bila harga untuk membobol algoritma lebih besar daripada nilai informasi yang dibuka, maka algoritma tersebut cukup aman. Misalkan, diperlukan komputer

senilai 1 juta dollar untuk menjebol algoritma senilai 100 ribu dollar, maka algoritma tersebut dapat dikatakan aman.

b) Bila waktu yang diperlukan untuk menjebol algoritma tersebut lebih lama daripada lamanya waktu yang diperlukan oleh informasi tersebut harus tetap aman, maka algoritma tersebut mungkin aman. Misalnya waktu untuk membobol sebuah kartu kredit 1 tahun, sedangkan sebelum setahun, kartu tersebut sudah tidak berlaku lagi, maka algoritma tersebut cukup aman.

c) Bila jumlah data yang dienkrip dengan kunci dan algoritma yang sama laebih sedikit dari jumlah data yang diperlukan untuk menembus algoritma tersebut, maka algoritma tersebut aman. Misalkan diperlukan 100 ciphertext untuk menebak kunci yang digunakan pada algoritma X. Sedangkan satu kunci hanya digunakan untuk satu pesan ( Kurniawan, 2004).

2.2 Konsep Dasar Matematis Kriptografi 2.2.1 Teori Bilangan

Teori bilangan ( Number Theory) adalah teori mendasar dalam memahami kriptografi, khususnya sistem kriptografi kunci publik. Bilangan yang digunakan disini adalah bilangan bulat (integer). Bilangan bulat adalah bilangan yang tidak mempunyai pecahan desimal, misalnya 8, 21, 8765, -89, dan 0. Himpunan semua bilangan bulat yang dinotasikan dengan Z adalah himpunan {...,-3,-2,-1,0,1,2,3,...}. Himpunan ini berperan sangat penting karena banyak algoritma kriptografi yang menggunakan sifat-sifat himpunan semua bilangan bulat dalam melakukan prosesnya. Pada himpunan bilangan bulat berlaku sifat asosiatif, komutatif dan distributif terhadap operasi penjumlahan dan pergandaan biasa

a. Sifat Pembagian Pada Bilangan Bulat

Misalkan a, b adalah bilangan bulat dengan syarat a ≠ 0. Kita dapat menyatakan a habis membagi b ( a divides b) jika terdapat bilangan bulat c, sedemikian hingga b = ac. Jika a membagi b, maka a disebut pembagi (divisior) b, dan b disebut kelipatan (multiple) a. Bilangan bulat a yang membagi b ditulis a|b (Menezes, van Oorschot dan Vanstone, 1996) .

Contoh : 4 | 12 karena 12 ÷ 4 = 3 (bilangan bulat) atau 12 = 4 x 3

b. Pembagi Persekutuan Terbesar

Misalkan a dan b adalah dua buah bilangan bulat tidak nol. Pembagi persekutuan terbesar (PBB - gratest common divisor atau gcd) dari a dan b adalah bilangan bulat terbesar d sedikian hingga d|a dan d|b. Dapat dinyatakan bahwa PBB atau gcd(a, b) = d (Menezes, van Oorschot dan Vanstone, 1996).

Contoh : Faktor pembagi 45 : 1, 3, 5, 15, 30, 45; Faktor pembagi 36 : 1, 2, 3, 4, 9, 12, 36; Faktor pembagi bersama dari 45 dan 36 adalah 1, 3, 9 sehingga PBB(45,36) = 9.

c. Algoritma Euclidean

Algoritma Euclidean adalah algoritma untuk mencari PBB dari dua buah bilangan bulat. Penemu algoritma Euclidean adalah seorang matematikawan Yunani yang menuliskan algoritmanya tersebut dalam bukunya yang terkenal, Element (Scheiner, 1996).

Diberikan dua buah bilangan bulat tak negatif m dan n (m ≥ n). Algoritma Euclidean berikut mencari pembagi persekutuan terbesar dari m dan n.

Algoritma Euclidean (Menezes, van Oorschot dan Vanstone, 1996) : 1) Jika n = 0 maka m adalah PBB(m,n); stop.

Kalau tidak (yaitu n ≠ 0) lanjutkan ke langkah 2. 2) Bagilah m dengan n dan misalkan sisanya adalah r.

3) Ganti nilai m dengan n dan nilai n dengan r lalu ulanh kembali ke langkah 1.

Contoh : Misalkan m = 80, n = 12 dan dipenuhi syarat m ≥ n, maka PBB(80, 12) dihitung dengan algoritma Euclidean sebagai berikut :

80 = 6.12 + 8

12 = 1.8 + 4

8 = 2.4 + 0

Sisa pembagian terakhir sebelum 0 adalah 4, maka PBB(80,12) = 4.

d. Relatif Prima

Dua buah bilangan bulat a dan b dikatakan relatif prima jika PBB(a, m) =1. Jika a dan m relatif prima, maka terdapat bilangan bulat p dan q sedemikian hingga

pa + qm = 1 (1)

Contoh : 20 dan 3 relaif prima sebab PBB(20,3) = 1. Dengan juga 7 dan 11 relatif prima karena PBB(7, 11) = 1. Tetapi, 20 dan 5 tidak relatif prima sebab PBB(20, 5) = 5 ≠ 1 (Munir, 2006).

e. Aritmatika Modulo

Misalkan a adalah bilangan bulat dan m adalah bilangan bulat > 0. Operasi a mod m (dibaca “a modulo m”) memberikan sisa jika a dibagi dengan m. Bilangan m disebut

modulus atau modulo, dan hasil aritmetika modulo m terletak di dalam himpunan {0, 1, 2,..., m-1} (Scheiner, 1996).

Notasi : a mod m = r sedemikian hingga a = mq + r, dengan 0 ≤ r < m.

Contoh : 23 mod 4 = 3 (23 = 5 . 4 + 3) 27 mod 3 = 0 (27 = 3 . 9 + 0) 6 mod 8 = 6 (6 = 8 . 0 + 6) 0 mod 12 = 0 (0 = 12.0 + 0) -41 mod 9 = 4 (-41 = 9 (-5) + 4) f. Kekongruenan

Misalkan a dan b adalah bilangan bulat dan m adalah bilangan bulat > 0, maka a ≡ b (mod m) jika m habis membagi a – b ditulis (m|a − b). Jika a tidak kongruen dengan b dalam modulus m, maka di tulis a ≡/ b (mod m) (Oppliger, 2005).

Contoh : 17 ≡ 2 (mod 3) (3 habis membagi 17 - 2 = 15) -7 ≡ 15 (mod 11) (11 habis membagi -7 - 15= -22) 12 ≡ / 2 (mod 7) (7 tidak habis membagi 12-2 = 10)

Kekongruenan a ≡ b (mod m) dapat juga di tuliskan hubungan a = b + km

yang dalam hal ini k adalah bilangan bulat. Berdasarkan definisi aritmetika modulo, dapat dituliskan a ≡ b mod m

Contoh : 17 ≡ 2 (mod 3), dapat ditulis sebagai 17 = 2 + 5 . 3 -7 ≡ 15 (mod 11), dapat ditulis sebagai -7 = 15 + (-2) .11.

Persamaan kongruen modulo n merupakan relasi ekuivalensi pada bilangan bulat. Hal ini berarti untuk setiap n ∈ N dan a, b, c ∈ Z

1. a ≡ a (mod n) (relasi refleksif);

2. Jika a ≡ b (mod n), maka b ≡ a (mod n) (relasi simetris);

3. Jika a ≡ b (mod n) dan b ≡ c (mod n), maka a ≡ c (mod n) (relasi transitif).

g. Inversi Modulo

Jika a dan m relatif prima dan m > 1, maka kita dapat menemukan invers dari a modulo m. Invers dari a (mod m), disebut juga invers perkalian, adalah bilangan bulat a-1 sedemikian hingga :

a a-1 ≡ 1 (mod m)

Bukti :

Dari defenisi relatif prima diketahui bahwa PBB(a,m) = 1, dan menurut persamaan (1) terdapat bilangan bulat p dan q sedemikian hingga

pa + qm = 1

yang mengimplikasikan bahwa pa + qm ≡ 1 (mod m) karena qm ≡ 0 (mod m) maka :

pa ≡ 1 (mod m)

p ≡ a-1 ▄

Untuk mencari invers dari a (mod m), haruslah dibuat kombinasi lanjar dari a dan m sama dengan 1. Koefisien a dari kombinasi lanjar tersebut merupakan invers dari a modulo m.

Contoh : Tentukan invers dari 4 (mod 9).

Karena PBB(4,9) = 1, maka invers dari 4 (mod 9) ada. Dari algoritma Euclidean diperoleh bahwa

9 = 2 . 4 + 1

susun persamaan di atas menjadi : -2 . 4 + 1.9 = 1

Dari persamaan terakhir ini kita peroleh -2 dari 4 (mod 9). Jadi 4-1≡ -2 (mod 9) (9 habis membagi -2 . 4 – 1 = -9)

Invers modulo dapat juga diselesaikan dengan pendekatan kekongruenen lanjar. Sebagaimana telah diketahui bahwa invers dari a (mod m) adalah bilangan bulat a-1,sedemikian hingga :

a a-1 ≡ 1 (mod m)

maka a a-1 ≡ 1 (mod m) dapat ditulis dalam hubungan a a-1 = 1 + km yang dapat disusun menjadi : a-1 = a km + 1 dimana k = 0, 1, 2, ... dan k = -1, -2, ...

Contoh : Hitung 4 (mod 9)

Penyelesaian : 4. 4-1≡ 1 (mod 9), atau dapat juga ditulis sebagai 4-1 =

4 . 9 1+ k

dengan mencoba semua kemungkinan nilai k = 0, 1, 2, ... dan k = -1, -2, ..., diperoleh nilai pembagian yang bulat untuk k = -1, k = 3, dan seterusnya. Untuk k = -1 diperoleh 4-1≡ -2 (mod 9), untuk k = 3 diperoleh 4-1≡ 7 (mod 9) dan seterusnya.

h. Aritmetika Modulo dan Kriptografi

Aritmetika modulo cocok digunakan untuk kriptografi karena (Munir, 2006) :

1. Nilai-nilai aritmetika modulo berada dalam himpunan berhingga (0 sampai modulus m – 1), maka tidak perlu khawatir hasil perhitungan berada di luar himpunan.

2. Jika bekerja dengan bilangan bulat, maka tidak perlu khawatir kehilangan informasi akibat pembulatan (round off), sebagaimana pada operasi bilangan riil.

j. Bilangan Prima

Sebuah bilangan prima adalah bilangan bulat yang besar dari 1 yang hanya mempunyai faktor 1 dan bilangan itu sendiri. Tidak ada bilangan pembagi lainnya. 2 (dua) adalah bilangan prima (Scheineir, 1996).

Contoh : 73, 2521, 2365347734339, dan 2756839 _{- 1.}

Kriptografi, khususnya kunci publik biasanya menggunakan bilangan prima yang besar (512 bits atau lebih besar). Bilangan selain bilangan bilangan prima disebut bilangan komposit. Misalnya, 20 adalah bilangan komposit karena 20 dapat dibagi oleh 2, 4, 5, 10, selain 1 dan 20 sendiri.

2.2.2 Aljabar Abstrak

Aljabar adalah bidang matematika yang berhubungan dengan himpunan elemen (seperti himpunan bilangan) dan operasi yang dilakukan pada elemen tersebut (Churchhouse, 2004). Aljabar abstrak adalah cabang matematika yang mempelajari struktur aljabar. Struktur aljabar adalah satu atau lebih himpunan dengan sejumlah

operasi yang didefenisikan didalamnya serta memenuhi beberapa aksioma. Di dalam struktur aljabar terdapat grup, ring dan grup berhingga yang penting dalam kriptografi pada umumnya dan kriptografi kunci publik khususnya (Churchhouse, 2004).

Himpunan adalah sekumpulan objek atau unsur dengan kriteria atau syarat tertentu. Unsur-unsur dalam elemen S disebut anggota (elemen) dari S. Himpunan yang tidak memiliki anggota disebut himpunan kosong dan ditulis

{ }

atau Φ .

2.2.2.1 Operasi biner

1) Operasi biner * pada himpunan S adalah aturan yang diberikan pada masing-masing urutan pasangan ( a, b) dari elemen S.

Contoh : Operasi penjumlahan + adalah sebuah operasi biner pada himpunan R. Operasi perkalian (.) adalah operasi biner pada R. R bisa juga digantikan dengan himpunan C, Z+_{, Z, atau R}+ _{(Fraleigh, 2000).}

2) Sebuah operasi biner pada himpunan S bersifat komutatif jika dan hanya jika a * b = b * a untuk setiap a, b Є S (Fraleigh, 2000).

3) Sebuah operasi biner pada himpunan S bersifat assosiatif jika (a * b) * c = a * (b * c) untuk setiap a, b, c Є S (Fraleigh, 2000).

4) Misalkan S adalah sebuah himpunan dan * merupakan operasi biner pada S, sebuah elemen e Є S disebut elemen identitas kiri jika e * a = a untuk setiap a Є S (Oppliger, 2005).

5) Misalkan S adalah sebuah himpunan dan * merupakan operasi biner pada S, sebuah elemen e Є S disebut elemen identitas kanan jika a * e = a untuk setiap a Є S (Oppliger, 2005).

6) Misalkan S adalah sebuah himpunan dan * merupakan operasi biner pada S, sebuah elemen e Є S disebut elemen identitas jika merupakan elemen identitas kiri dan elemen identitas kanan (e * a = a * e = a) untuk setiap a Є S (Oppliger, 2005).

7) Misalkan S adalah sebuah himpunan dan * merupakan operasi biner dengan elemen identitas e dan a merupakan sebuah elemen pada S. Jika terdapat sebuah elemen b Є S dengan a * b = b * a = e, maka a dapat diinverskan dan b merupakan elemen invers dari a (Oppliger, 2005).

2.2.2.2 Grup

Diberikan sebarang himpunan tidak kosong G dan operasi biner “*” pada G, maka G disebut grup terhadap operasi biner “*” dan ditulis (G,*) jika dipenuhi :

1. Tertutup (closure) : operasi biner * menghasilkan nilai di dalam G, yaitu untuk semua a dan b di dalam G, a * b juga berada di dalam G.

2 a * (b * c) = (a * b) * c untuk a,b,c Є G (asosiatif).

3. Terdapat sebuah elemen e Є G sedemikian hingga e * a = a * e = a untuk setiap a .

4. Untuk setiap a Є G terdapat sebuah elemen b Є G sehingga b * a = a * b = e. b disebut dengan invers a.

Notasi (G,*) menyatakan sebuah grup dengan operasi grup *. Notasi (G,+) disebut dengan grup penjumlahan dan (G,•) disebut grup perkalian. Pada grup

penjumlahan, elemen netral disimbolkan dengan 0 dan invers dari a dinyatakan sebagai –a. Sedangkan grup perkalian elemen netral disimbolkan dengan 1 dan invers a dinyatakan sebagai a-1. Sebagai contoh integer modulo n, ditulis sebagai Zn = {0,1,2, … , n-1} merupakan bentuk sebuah grup pada operasi penjumlahan modulo n. Jika p adalah bilangan prima, maka elemen-elemen bukan nol Zp dapat ditulis sebagai Z*p={1,2, … , p-1}, merupakan bentuk sebuah grup pada operasi perkalian modulo p. Nilai elemen grup g Є G adalah bilangan integer positif n sehingga gn = 1. Sebagai

contoh untuk grup Z*11 dengan elemen = 3 memiliki 5 buah nilai, yaitu : 31≡ 3 (mod 11),

32≡ 9 (mod 11), 33≡ 5 (mod 11), 34≡ 4 (mod 11), 35 ≡ 1 (mod 11).

Suatu grup (G,*) disebut Abelian jika operasi binernya bersifat komutatif. Selanjutnya, grup (G,*) dapat dituliskan dengan G apabila operasi binernya telah diketahui (Oppliger, 2005).

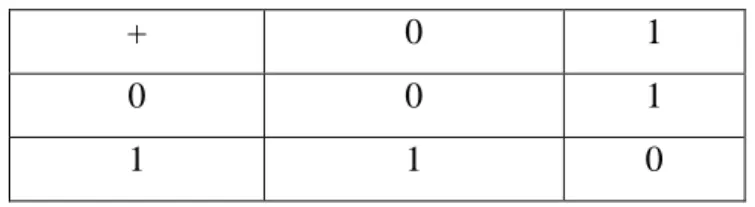
Contoh : Penjumlahan dalam modulo 2 dengan G = {0, 1} dan operator biner + adalah sebuah grup. Operasi biner penjumlahan dalam modulo 2 didefenisikan sebagai tabel Cayley berikut :

Tabel 2.1 Tabel Cayley

+ 0 1

0 0 1

1 1 0

(G, +) adalah sebuah grup karena memenuhi keempat aksioma di atas yaitu :

i. Closure : Perhatikan bahwa semua hasil operasi penjumlahan selalu menghasilkan nilai yang terdapat di dalam G (0 atau 1).

ii. Asosiatif : Operasi penjumlahan modulo 2 bersifat asosiatif yang berarti bahwa (a + b) + c = a + (b + c) untuk semua a, b, c elemen dari {0, 1}.

iii. Elemen 0 adalah elemen identitas dan mempunyai sifat bahwa a + 0 = 0 + a = a . iv. Untuk semua elemen a di dalam G, elemen 0-1 adalah 0 dan elemen 1-1 adalah1 sehingga 0 + 0 = 0 dan 1 + 1 = 0 (pada kebanyakan kasus elemen invers tidak selalu dirinya sendiri). Karena operatornya adalah +, maka inversnya dinamakan juga elemen invers penjumlahan ( sering disimbolkan dengan –a).

1) Diberikan grup G dan subset tak kosong H ⊆ G. Subset H disebut subgrup G jika terhadap operasi biner yang sama pada G, maka H membentuk grup, ditulis H < G (Fraleigh, 2000).

2) Subset tak kosong H merupakan subgrup G jika dan hanya a *b-1 ∈ H, untuk setiap a, b ∈ H (Fraleigh, 2000).

3) Jika G mempunyai banyak elemen yang berhingga, maka G disebut grup berhingga (finite group) dan banyaknya elemen G disebut order G, ditulisG (Fraleigh, 2000).

4) Diberikan H subgrup G dan a ∈ G. Didefinisikan himpunan Ha = {h*a : h ∈ H} dan aH = {a *h : h ∈ H} , maka Ha disebut dengan koset kanan dan aH disebut dengan koset kiri. Jika aH = Ha, maka H disebut subgrup normal dan ditulis H <G (Fraleigh, 2000).

5) Jika terdapat a ∈ G sedemikian hingga x = a*a*a*...*a sebanyak k faktor untuk setiap x∈G maka G disebut grup siklis yng dibangun oleh a. Selanjutnya, a disebut pembangun G dan k disebut dengan eksponen, ditulis G = {ak: k ∈ Z} =

a (Fraleigh, 2000).

2.2.2.3 Ring (Gelanggang)

Suatu gelanggang (ring)

(

R,+,.

)

adalah himpunan R tak kosong yang dilengkapi dengan dua operasi biner yaitu operasi penjumlahan “+” dan operasi pergandaan “× ” yang memenuhi :

1)

( )

R,+ merupakan grup Abelian, 2) Operasi pergandaan bersifat assosiatif,

3) Untuk setiap a,b,c Є R berlaku sifat distributif kiri, yaitu a.(b + c) = a.b + a.c dan sifat distributif kanan yaitu (a + b).c = a.c + b.c .

4) Terdapat elemen identitas perkalian yang dinyatakan dengan 1, dimana 1≠0, sedemikian hingga 1×a = a ×1 = a.

Gelanggang (R,+,×) dapat dituliskan dengan R apabila operasi binernya diketahui.

Suatu gelanggang R yang operasi pergandaannya bersifat komutatif disebut gelanggang komutatif. Elemen identitas pada operasi pergandaan yaitu 1ЄR disebut dengan uniti. Suatu gelanggang yang mempunyai elemen identitas terhadap pergandaan disebut gelanggang dengan uniti (Fraleigh, 2000).

Contoh : Himpunan bilangan Z bersama–sama dengan operasi penjumlahan + dan perkalian × membentuk sebuah gelanggang. Semua penjumlahan selalu menghasilkan

bilangan bulat pula. Dimana elemen identitas pada operasi penjumlahan adalah 0. Himpunan biner dengan operasi penjumlahan modulo 2 dan 3 juga membentuk sebuah gelanggang. Operasi penjumlahan dan perkalian pada modulo 2 dan 3 dinyatakan dengan tabel Cayley berikut :

Modulo 2 Modulo 3

2.2.2.4 Lapangan (Field)

Suatu gelanggang yang bersifat komutatif dimana setiap elemen tidak nol mempunyai invers perkalian disebut dengan lapangan (field). Yang dimaksud dengan invers perkalian adalah untuk setiap a ≠ 0 yang termasuk dalam F, terdapat a-1 Є F sedemikian hingga a × a-1 = 1 (Fraleigh, 2000).

Himpunan bilangan bulat dengan operasi penjumlahan dan perkalian tidak membentuk lapangan, karena hanya 1 dan -1 yang mempunyai invers perkalian (yaitu 1 × 1 = 1 dan (-1) × (-1) = 1). Tetapi himpunan bilangan rasional Q dan himpunan bilangan riil R dengan operasi penjumlahan dan perkalian membentuk lapangan. × 0 1 0 0 0 1 0 1 × 0 1 2 0 0 0 0 1 0 1 2 2 0 2 1

Secara sederhana lapangan adalah tempat dimana kita dapat melakukan operasi seperti penjumlahan dan perkalian (pengurangan a – b dipandang sebagai a + (-b), dimana –b merupakan elemen invers penjumlahan dari b, sedangkan pembagian

b

a dipandang sebagai a × b-1

, dimana b-1 adalah elemen invers perkalian dari b.

2.2.2.5 Gelanggang Bilangan Bulat Modulo

Diberikan bilangan bulat m>1, didefinisikan himpunan Z =

{

xmodm:xεZ

}

, maka

Zm merupakan himpunan sisa pembangian semua bilangan bulat dengan m. Selanjutnya, elemen-elemen himpunan Zm dapat dipandang sebagai klas-klas asing yang menyatakan himpunan bilangan bulat yang mempunyai sisa yang sama apabila dibagi dengan m yaitu Zm =

{

0,1,2,...,m−1

}

. Himpunan Zm seperti ini disebut dengan himpunan bilangan bulat modulo m.

Pada himpunan Zm berlaku operasi penjumlahan dan pergandaan dan modulo m,

yaitu untuk setiap a,b∈ Zm maka a+b=(a+b) mod m dan a.b = (a.b)mod m. Jelas bahwa kedua operasi tersebut merupakan operasi biner pada Zm. Selanjutnya,

himpunan Zm yang dilengkapi dengan operasi penjumlahan modulo dapat membentuk

grup (Zm,+) dengan 0∈ Zm adalah elemen identitas Zm.

2.2.2.6 Grup Pergandaan Bilangan Bulat Modulo

Himpunan semua unit dalam Zm yang dilengkapi dengan operasi pergandaan membentuk suatu grup belian berhingga. Grup seperti ini disebuat dengan grup

pergandaan bilangan bulat modulo m dan dinotasikan dengan Zm*. Dengan

demikian dapat ditulis bahwa Zm* =

{

a,εΖm:gcd(a,m)=1

}

.

Contoh :

Diberikan gelanggang ℤ5 . Karena 5 adalah bilangan prima, maka ℤ5 adalah lapangan. Selanjutnya, menggunakan sifat lapangan diperoleh bahwa setiap elemen dalam ℤ5 kecuali nol pasti mempunyai invers. Dengan kata lain, setiap elemen ℤ5 kecuali nol merupakan unit. Jadi, ℤ5 * = {1,2,3,4}.

2.2.2.7 Grup Pergandaan Bilangan Bulat Modulo Prima

Diberikan bilangan prima p, maka Z*p =

{

1,2,..,p−1

}

merupakan grup terhadap

operasi pergandaan, sebab berlaku : 1) Untuk setiap a,b∈ Z*

p,maka a×b∈ Z*p.

2) a×(b×c) = (a×b)×c, untuk setiap a,b∈ Z*

p.

3) Terdapat 1∈ Z*

p sedemikian hingga 1×a = a×1, untuk setiap a,b∈ Z*p.

4) Untuk setiap a∈ Z*

p, terdapat elemen inversnya yaitu b∈ Z*p, sedemikian

hingga a×b = (b×a) = 1. Artinya, untuk setiap elemen kecuali nol mempunyai elemen invers, atau dengan kata lain setiap elemen Z*p=

{

1,2,..,p−1

}

mempunyai invers. Dimana a.a-1 = 1 mod p.

Contoh : Z*7

Bukti : Z*

7 merupakan grup pergandaan bilangan bulat modulo 7 dengan Z*7=

x 0 1 2 3 4 5 6 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 2 0 2 4 6 1 3 5 3 0 3 6 2 5 1 4 4 0 4 1 5 2 6 3 5 0 5 3 1 6 4 2 6 0 6 5 4 3 2 1

1) Closure : jelas terlihat hasil pergandaan pada Z*7 terdapat pada Z*7=

{

1,2,3,4,5,6

}

.

2) Pergandaan elemen Z*

7 bersifat asosiatif. Contoh : 1×(2×3) = (1×2)×3=6.

3) Elemen identitas pada Z*7 adalah 1.

4) Setiap elemen kecuali 0 mempunyai invers, yaitu : a. 1-1 = 1 sebab 1 x 1 mod 7 = 1 b. 2-1 = 4 sebab 2 x 4 mod 7 = 1 c. 3-1 = 5 sebab 3 x 5 mod 7 = 1 d. 4-1 = 2 sebab 4 x 2 mod 7 = 1 e. 5-1 = 3 sebab 5 x 3 mod 7 = 1 f. 6-1 = 6 sebab 6 x 6 mod 7 = 1 2.2.3. Logaritma Diskret

Misalkan G adalah grup siklik dengan order n, α adalah pembangun G dan 1 adalah elemen identitas G. Diberikan β € G. Permasalahan yang dimunculkan adalah bagaimana menentukan suatu bilangan bulat nonnegatif terkecil a sedemikian hingga :

β = α a

Bilangan bulat a seperti ini disebut dengan logaritma diskret (discrete logarithm) dari β dengan basis α . Selanjutnya, masalah bagaimana menentukan bilangan bulat a seperti ini disebut dengan masalah logaritma diskret (discrete logarithm problem). Masalah logaritma diskret ini menjadi sulit apabila digunakan grup dengan order yang besar (Buchmann, 2000).

2.2.3.2 Masalah Logaritma Diskret pada Grup Pergandaan Bilangan Bulat Modulo Prima

Diberikan bilangan prima p, dan Z*p adalah grup siklik yang mempunyai order p −1.

Akibatnya terdapat suatu elemen yang membangun Z*p yang disebut dengan elemen

primitif. Misalkan α € Z*p adalah elemen primitif, maka untuk sebarang β € Z*p,

terdapat suatu eksponen a €

{

0,1,2,..,p−2

}

sedemikian hingga : β = α a

(mod p)

Eksponen a merupakan logaritma diskret dari β dengan basis α . Untuk menentukan logaritma diskret tersebut bukanlah permasalahan yang mudah, apalagi bila digunakan bilangan prima dan logaritma diskret yang besar (Buchmann, 2000). Salah satu metode yang dapat digunakan untuk mencari nilai logaritma diskret adalah metode enumerasi, yaitu dengan mengecek seluruh kemungkinan, mulai dari 0, 1, 2, dan seterusnya sampai akhirnya ditemukan nilai a yang tepat. Metode enumerasi membutuhkan sebanyak a −1 proses pergandaan modulo dan sebanyak a

perbandingan. Apabila digunakan nilai a yang lebih besar, maka metode ini membutuhkan proses perhitungan dan waktu yang lebih banyak lagi.

2.3 Algoritma ElGamal

Algoritma ElGamal merupakan algoritma enkripsi kunci asimetris yang berdasarkan pada pertukaran kunci Diffe-Hellman. Algoritma ini diusulkan Taher Elgamal pada tahun 1984. Keamanan algoritma ini didasarkan pada kesulitan memecahkan masalah logaritma diskret dalam grup.

Logaritma ini disebut logaritma diskret karena nilainya berhingga dan bergantung pada bilangan prima yang digunakan. Karena bilangan prima yang digunakan adalah bilangan prima yang besar, maka sangat sulit bahkan tidak mungkin menurunkan kunci privat dari kunci publik yang diketahui walaupun serangan dilakukan dengan menggunakan sumberdaya komputer yang sangat besar.

Algoritma ElGamal terdiri dari tiga proses, yaitu proses pembentukan kunci, proses enkripsi dan proses dekripsi. Plainteks yang akan dienkripsi dipecah menjadi blok-blok plainteks, selanjutnya proses enkripsi pada blok-blok plainteks dan menghasilkan blok-blok cipherteks yang kemudian dilakukan proses dekripsi dan hasilnya digabungkan kembali menjadi pesan yang utuh dan dapat dimengerti.

2.3.1 Proses Pembentukan kunci

Proses pertama pada algoritma ElGamal adalah pembentukan kunci yang terdiri dari kunci rahasia dan kunci publik. Pada proses ini dibutuhkan sebuah bilangan prima aman p yang digunakan untuk membentuk grup Z*p, elemen primitif α yang

merupakan elemen pembangun grup dan sebarang a Є {0,1,..., p − 2}. Kunci publik algoritma ElGamal berupa pasangan 3 bilangan, yaitu (p, α , β ), dengan:

β = α a

(mod p), (2.1)

dimana a merupakan kunci rahasia.

2.3.1.1 Bilangan Prima Aman

Untuk memperoleh keamanan pada algoritma ElGamal, maka bilangan prima yang digunakan haruslah bilangan prima yang aman. Untuk melakukan pengujian apakah suatu bilangan merupakan bilangan prima yang aman atau tidak dapat dilakukan dengan langkah-langkah berikut:

a. Input bilangan prima p ≥ 5. b. Hitung q = 2 1 − p .

c. Jika q adalah bilangan prima, maka output (”prima aman”). d. Jika q komposit, maka output (”bukan prima aman”).

Sementara untuk mengetahui apakah suatu bilangan merupakan bilangan prima atau bukan dapat dilakukan pengujian. Ada pun langkah – langkah tes untuk menentukan suatu bilangan merupakan bilangan prima atau tidak adalah sebagai berikut : a. Input p ≥ 3. b. b = 1; c. Repeat b = b+1; c = p mod b Until c = 0.

d. Jika p = b maka output(”prima”).

e. Jik tidak, maka output (”bukan bilangan prima”).

2.3.1.2 Elemen Primitif

Selain bilangan prima, dalam kriptografi ElGamal juga digunakan elemen primitif yang merupakan elemen pembangun dari grup. Elemen primitif adalah elemen pembangun grup Zp. Untuk mencari elemen ini digunakan p = 2q +1, dimana q

merupakan bilangan prima. Jika elemen α memenuhi α2 mod p ≠ 1 dan α q mod p ≠ 1, maka α merupakan elemen primitif.

Untuk mengetahui suatu bilangan merupakan elemen primitif atau tidak dapat dilakukan langkah-langkah sebagai berikut :

1. Input bilangan prima aman p ≥ 5. 2. Hitung q = 2 1 − p . 3. Hitung α2 _{mod p dan α}q

mod p.

4. Jika α2 _{mod p= 1, maka α bukan elemen primitif.} 5. Jika αq _{mod p= 1, maka α bukan elemen primitif.}

6. Jika tidak terpenuhi dua persyaratan di atas maka q merupakan elemen primitif.

2.3.1.3 Proses Pembentukan Kunci

Langkah-langkah dalam pembentukan kunci sebagai berikut: a) Input bilangan prima aman p > 255

c) Input sebuah bilangan a Є {0,1,..., p − 2} d) Hitung β = α a (mod p)

e) Publikasikan nilai p, α , dan β , serta rahasiakan nilai a.

Pihak yang membuat kunci publik dan kunci rahasia adalah penerima, sedangkan pihak pengirim hanya mengetahui kunci publik yang diberikan oleh penerima, dan kunci publik tersebut digunakan untuk mengenkripsi pesan. Jadi, kentungan menggunakan algoritma kriptografi kunci publik adalah tidak ada permasalahan pada distribusi kunci apabila jumlah pengirim sangat banyak serta tidak ada kepastian keamanan jalur yang digunakan.

Contoh :

Misalkan Andi dan Budi saling berkomunikasi. Pada suatu saat, Andi akan mengirimkan pesan rahasia kepada Budi. Oleh karena itu, Budi harus membuat kunci publik dan kunci rahasia. Misalkan Budi ingin membangkitkan pasangan kuncinya. Budi memilih bilangan prima p = 2099, α = 975 sebagai elemen pembangun dan kunci rahasia a = 225. Andi menghitung:

β = α a

mod p = 975225 mod 2099 = 469

Jadi, kunci publik Budi adalah (p = 2099, α = 975 dan β = 469) dan kunci rahasianya 225. Budi mengirimkan pasangan kunci publik (2099, 975, 469) pada Andi dan menyimpan kunci rahasianya.

2.3.2. Proses Enkripsi

Karena pada algoritma ElGamal menggunakan bilangan bulat dalam proses perhitungannya, maka pesan harus dikonversi ke dalam suatu bilangan bulat. Untuk

mengubah pesan menjadi bilangan bulat, digunakan kode ASCII (American Standard for Information Interchange). Kode ASCII merupakan representasi numerik dari karakter-karakter yang digunakan pada komputer, serta mempunyai nilai minimal 0 dan maksimal 255. Oleh karena itu, berdasarkan sistem kriptografi ElGamal di atas maka harus digunakan bilangan prima yang lebih besar dari 255 sehingga kode ASCII berkorespondensi 1-1 dengan karakter pesan.

Pada proses enkripsi pesan dienkripsi menggunakan kunci publik (p,α , β ) dan sembarang bilangan acak rahasia k Є {0,1,..., p − 2}. Misalkan m adalah pesan yang akan dikirim. Selanjutnya, m diubah ke dalam blok-blok karakter dan setiap karakter dikonversikan ke dalam kode ASCII, sehingga diperoleh plainteks m1, m2, m3, ..., mn dengan mi Є {1, 2,..., p-1} dan i =1, 2,..., n .

Proses enkripsi pada algoritma ElGamal dilakukan dengan menghitung

γ i = α ki (mod p) (2.2)

dan

δ i= βki × m (mod p) (2.3)

dengan k Є {0,1,..., p − 2} acak. Diperoleh cipherteks (γ , δ ) .

Bilangan acak k ditentukan oleh pihak pengirim dan harus dirahasiakan, jadi hanya pengirim saja yang mengetahuinya, tetapi nilai k hanya digunakan saat melakukan enkripsi saja dan tidak perlu disimpan.

Langkah-langkah proses enkripsi :

a) Pesan dipotong-potong ke dalam bentuk blok-blok pesan dengan setiap blok adalah satu karakter pesan.

b) Konversikan masing-masing karakter ke dalam kode ASCII, maka diperoleh plainteks sebanyak n bilangan, yaitu m1, m2, ..., mn.

c) Untuk i dari 1 sampai n kerjakan:

- Pilih bilangan acak ki dimana 1 < k ≤ p-2 - Hitung γ i = α ki (mod p)

- Hitung δ i = βki × mi (mod p)

d) Diperoleh cipherteks (γi,δ i), dimana i = 1,2,...,n.

Contoh :

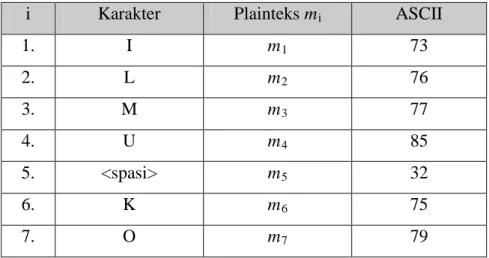
Andi memperoleh kunci publik ( p,α ,β ) = (2099, 975,469) . Pada suatu hari, Andi akan mengirimkan pesan rahasia ”ILMU KOMPUTER” kepada Budi. Oleh karena sifat pesan yang rahasia, maka pesan tersebut harus dienkripsi, dan Andi akan mengenkripsi menggunakan kunci publik (2099, 975,469) yang telah diberikan Budi. Selanjutnya, Andi melakukan proses berikut. Pertama, pesan dipotong-potong menjadi blok-blok karakter dan setiap karakter dikonversi ke dalam kode ASCII. Perhatikan tabel di bawah ini :

Tabel 2.2 Konversi karakter pesan ke kode ASCII

i Karakter Plainteks mi ASCII

1. I m1 73 2. L m2 76 3. M m3 77 4. U m4 85 5. <spasi> m5 32 6. K m6 75 7. O m7 79

8. M m8 77 9. P m9 80 10. U m10 85 11. T m11 84 12. E m12 69 13. R m13 82

Berdasarkan Tabel 2.2, diperoleh bahwa banyaknya karakter pada pesan tersebut adalah n = 13. Proses selanjutnya adalah menentukan bilangan acak rahasia ki €

{0,1,...,2097}, i =1, 2,...,13 . Kemudian dihitung γ i = 975ki (mod 2099) dan δ i = 469ki × mi (mod 2099).

Perhatikan tabel di bawah ini :

Tabel 2.3 Proses enkripsi

i mi ki γ i = 975ki (mod 2099) 469ki × mi (mod 2099). 1. 73 1414 61 121 2. 76 1527 228 349 3. 77 1843 1480 1836 4. 85 2175 2040 1185

Tabel 2.3 Proses enkripsi (lanjutan)

i mi ki γ i = 975ki (mod 2099) 469ki × mi (mod

2099).

5. 32 1553 395 980

7. 79 1404 534 1676 8. 77 2183 1005 209 9. 80 1091 1686 521 10. 85 1606 1566 1524 11. 84 1664 2004 736 12. 69 990 474 1734 13 82 1127 852 83

Berdasarkan Tabel 2.3, diperoleh cipherteks (γ i , δ i ), i =1, 2,...,13 sebagai berikut : (61, 121) (228, 349) (1480, 1836) (2040, 1185)

(395, 980) (908, 1582) (534, 1676) (1005,209) (1686, 521) (1566, 1524) (2004, 736) (474, 1734) (852, 83).

Selanjutnya, Andi mengirimkan cipherteks ini kepada Budi.

Salah satu kelebihan algoritma ElGamal adalah bahwa suatu plainteks yang sama akan dienkripsi menjadi cipherteks yang berbeda-beda. Hal ini dikarenakan pemilihan bilangan k yang acak. Akan tetapi, walaupun cipherteks yang diperoleh berbeda-beda, tetapi pada proses dekripsi akan diperoleh plainteks yang sama, seperti dijelaskan berikut ini.

2.3.3 Proses Dekripsi

Setelah menerima cipherteks (γ ,δ ), proses selanjutnya adalah mendekripsikan cipherteks menggunakan kunci publik p dan kunci rahasia a. Dapat ditunjukkan bahwa plainteks m dapat diperoleh dari cipherteks menggunakan kunci rahasia a.

Diberikan (p, α , β ) sebagai kunci publik dan a sebagai kunci rahasia pada algoritma ElGamal. Jika diberikan cipherteks (γ,δ ), maka:

m = (γa)-1× (mod p) dengan m adalah plainteks.

Bukti :

Diketahui kunci publik (p, α , β ) dan kunci rahasia a pada algoritma ElGamal. Diberikan cipherteks (γ,δ ), dari persamaan (2.1), (2.2), dan (2.3) diperoleh bahwa:

δ (γ a)-1 ≡ (βk×m) (γ a)-1 (mod p) ≡ βk _{× m ×}γ -a (mod p) ≡ (α a )k× m (α k)-a (mod p) ≡ αak _{× m ×}α-ak (mod p) ≡ m ×α 0 (mod p) ≡ m (mod p)

Dengan demikian terbukti bahwa: m = (γa)-1(mod p)

Langakah-langkah proses dekripsi: a) Input cipherteks.

b) Potong cipherteks ke dalam blok-blok cipherteks. c) Untuk i dari 1 sampai n kerjakan:

• Hitung γ ip-1-a (mod p)

• Hitung mi = δ iγ ip-1-a (mod p) d) Diperoleh plainteks m1, m2, ..., mn

e) Konversikan masing-masing bilangan m1, m2, ..., mn ke dalam karakter sesuai dengan kode ASCII-nya, kemudian hasilnya digabungkan kembali

Contoh :

Andi telah mengirimkan cipherteks kepada Budi. Cipherteks yang diperoleh Budi adalah sebagai berikut :

(61, 121) (228, 349) (1480, 1836) (2040, 1185) (395, 980) (908, 1582) (534, 1676) (1005,209) (1686, 521) (1566, 1524) (2004, 736) (474, 1734) (852, 83).

Budi mempunyai kunci publik p = 2099 dan kunci rahasia a = 225 Selanjutnya, untuk mendapatkan pesan asli yang dikirimkan Andi Budi melakukan perhitungan sebagai berikut :

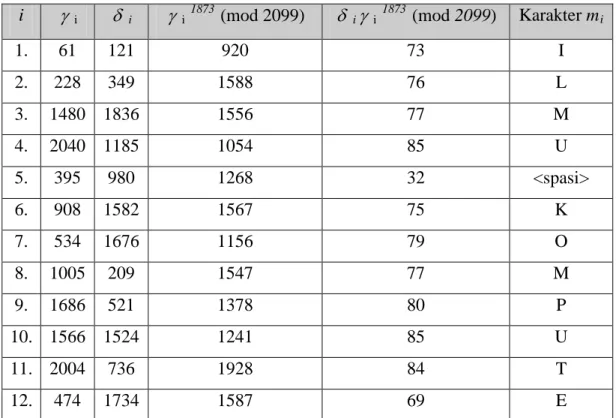
Tabel 2.4. Proses dekripsi

i γ i δ i γ i 1873 (mod 2099) δ iγ i 1873 (mod 2099) Karakter mi

1. 61 121 920 73 I 2. 228 349 1588 76 L 3. 1480 1836 1556 77 M 4. 2040 1185 1054 85 U 5. 395 980 1268 32 <spasi> 6. 908 1582 1567 75 K 7. 534 1676 1156 79 O 8. 1005 209 1547 77 M 9. 1686 521 1378 80 P 10. 1566 1524 1241 85 U 11. 2004 736 1928 84 T 12. 474 1734 1587 69 E

13. 852 83 1139 82 R

Berdasarkan perhitungan pada Tabel 2.4, Andi mengetahui pesan rahasia yang dikirimkan oleh Budi, yaitu ”ILMU KOMPUTER”.