KHUSUS DALAM ALJABAR KUATERNION REAL DAN
PENERAPANNYA DALAM STRUKTUR PERSAMAAN DIRAC
Latief Rahmawati 01/147328/PA/08613
Departemen Pendidikan Nasional Universitas Gadjah Mada
Fakultas Matematika dan Ilmu Pengetahuan Alam
YogyakartaKHUSUS DALAM ALJABAR KUATERNION REAL DAN
PENERAPANNYA DALAM STRUKTUR PERSAMAAN DIRAC
Latief Rahmawati 01/147328/PA/08613
Sebagai salah satu syarat untuk memperoleh
derajat Sarjana S1 Program Studi Fisika pada Jurusan Fisika
Departemen Pendidikan Nasional Universitas Gadjah Mada
Fakultas Matematika dan Ilmu Pengetahuan Alam
YogyakartaPENERAPANNYA DALAM STRUKTUR PERSAMAAN DIRAC
Latief Rahmawati 01/147328/PA/08613
Dinyatakan lulus ujian skripsi oleh tim penguji pada tanggal 17 Juli 2007
Tim Penguji
Dr.rer.nat. M. Farchani Rosyid Dr.Arief Hermanto
Pembimbing Penguji I
❞
beliau ini, penulis telah menyusun hingga bab 5.Namun sampai beliau wafat, penulis belum sempat mendiskusikan bab 4 dan bab 5 dengan
beliau.Penulisan skripsi ini selanjutnya hingga selesai dilanjutkan bersama Dr.rer.nat.Muhammad Farchani Rosyid.
Keterangan ini merupakan salah satu wujud penghargaan penulis kepada mendiang Prof.Drs.Muslim Ph.D (Rahimahullahu)atas jasa− jasa beliau ,khususnya dalam pembimbingan skripsi ini.
❛❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❜❝ ❞
❞ ❞ ❞ ❞ ❞ ❞ ❞
Karya ini saya persembahkan untuk yang tersayang :
Bapak dan Ibu
Mas Yusron, mbak Ami dan dd Bening serta Uda Ardhi
❞
tidak kamu ketahui. Sesungguhnya dalam proses tanya jawab tersebut akan diberikan pahala oleh Allah pada 4 golongan: orang yang bertanya, orang yang menjawab, orang yang mendengarkan dan orang yang mencintai mere-ka. (HR. Abu Na’im dari Ali bin Abi Thalib)
❡
to hear is to forget to see is to remember to do is to understand to elaborate is to be master
to communicate is to build self confidence to give experience is the best of all
Nya yang diturunkan, lewat lisan Nabi Muhammad saw. utusan-Nya. Melalui kitab itu dinyatakan, bahwa Dia adalah Esa dalam Dzat-Nya, tiada sekutu bagi-Nya; Ma-ha Tunggal yang tiada misal bagi-Nya, waMa-hana bergantungnya makhluk yang tiada tandingan-Nya, Maha Dahulu tiada permulaan bagi-Nya, Maha Kekal tiada akhir. Shalawat serta salam semoga tetap tercurah bagi junjungan kita Nabi Muhammad shallallahu alaihi wa sallam beserta segenap sahabat dan keluarganya serta para pengikutnya yang setia hingga hari kiamat nanti.
Alhamdulillah, akhirnya setelah melalui perjalanan yang cukup berliku yang syarat dengan tantangan (hambatan), penulis dengan izin Allah dapat menyelesaikan skripsi ini. Penulis merasa bersyukur kepada Allah atas rahmat-Nya memberikan ke-sempatan kepada penulis untuk menempuh pendidikan di jenjang universitas, khusus-nya program studi fisika. Apa yang telah diperoleh penulis selama berada di bangku perkuliahan jika dibandingkan dengan ilmu fiska yang sudah ada adalah bagaikan setetes air dan lautan luas, dan tahap ini barulah titian awal bagi penulis jika ingin terjun dalam dunia fisika.
KepadaProf.Drs. Muslim Ph.D (Rahimahullahu)penulis mengucapkan ter-imakasih yang sebesar-besarnya atas teladan yang diberikan, atas segala perhatian, atas waktu dan kesempatan dalam tanya jawab yang diberikan serta kesabaran beli-au kepada penulis selama ini. Belibeli-aulah yang mengenalkan fisika dan menanamkan semangat penulis untuk berada dalam lingkungan fisika teori ini. Beliau juga yang telah membimbing penulis dalam menyelesaikan skripsi ini, dalam pembimbingan skripsi ini bersama beliau penulis sudah menyusun hingga 5 bab selama kurang lebih 2 tahun bahkan setelah gempa melanda keluarga penulis, sehingga berbulan-bulan
penulis tidak aktif dalam penyusunan skripsi ini beliau tetap bersedia membimbing dan menyediakan waktunya. Komunitas fisika teoretik Indonesia amat kehilangan dengan kepergian beliau. Semoga Allah membalas semua amal baik beliau pada penulis dan semoga beliau tenang dan bahagia di alamnya yang sekarang.
KepadaDr.rer.nat. Muhammad Farchani Rosyidpenulis juga merasa bert-erimakasih sekali atas kuliah dan nasehat-nasehat yang beliau sampaikan, untuk men-gubah pola pikir penulis dalam mempelajari matematika dan fisika kearah yang lebih maju. Serta kesediannya meluangkan waktu untuk melanjutkan pembimbingan skrip-si ini.
KepadaProf. Stefano De Leodi Dipartimento di Fisica Universita´di Lecce, Instituto Nazionale di Fisica Nucleare, sezione di Lecce, Lecce Italy, terimakasih atas kesediannya mengirimkan jurnal-jurnalnya dan menjawab pertanyaan-pertanyaan yang penulis sampaikan.
Adalah kedua orang tua penulis, Bapak Muryadi dan ibunda Sutari, yang telah mencurahkan seluruh kasih sayangnya yang takkan mampu penulis memba-yarnya meskipun dengan nyawa sekalipun dan memberikan restu sehingga penulis da-pat menyelesaikan studi sebagai bekal perjalanan selanjutnya. Hanya do’a tulus yang mampu ananda panjatkan pada Allah, "Ya Allah, kasihilah kedua orang tua ham-ba seham-bagaimana mereka telah mengasihi hamham-ba semenjak hamham-ba dalam rahim.
Berikanlah perlindungan-Mu dalam setiap langkah keduanya dan muliakanlah
keduanya di dunia maupun di akhirat. Amin...".
Kepada Mas Yusron, kakakku semata wayang, mba Ami serta dd Bening terimakasih atas segala dukungannya. Penulis bersyukur kepada Allah memiliki kelu-arga ini. Smoga Allah merahmati kita semua
Kepada keluargadr. Muslim M, terimakasih atas doa restunya dan sambutan manisnya. Semoga Allah selalu membimbing kita.
Kepadakeluarga Lik Sri, terimakasih atas perhatian dan kesediannya untuk meminjamkan printer hingga terselesaikannya skripsi ini. Juga kepadakeluarga be-sardi Jogomangsan, terimakasih atas perhatian yang diberikan kepada penulis.
Kepada Kepada teman-teman di kelompok"underground"mathematical physics, terimakasih atas semua bantuan dan dukungannya kepada penulis. Teruslah berse-mangat, agar bendera mathematical physics yang ditancapkan pak Rosyid di UGM tetap berkibar.
Kepada teman-teman fisika,Duwi,Maya, Lisa, maupun di F8A Karang Wu-ni;Endah,Markum,Lilik,Eso, Dian,Anik,Etik,Lindya, Lindadll, terimakasih atas suasana kehangatan dan senyuman manieznya.
KepadaAgungdandd Mittul, terimakasih atas hiburannya dan kesediannya menemani ibu di rumah, belajar ya..
Kepada pihak-pihak lain yang tidak tersebutkan satu-persatu dalam halaman ini yang telah membantu terselesaikannya skripsi ini, penulis ucapkan terimakasih yang sebesar-besarnya. Semoga Allah selalu membimbing kita semua.
Akhirnya, penulis memohon maaf atas kekurangan-kekurangan yang ada dalam skripsi ini. Semoga di balik kekurangan yang tampak masih ada manfaat bagi kita se-mua.
Yogyakarta, 17 Juli 2007
Halaman Judul i
Halaman Pengesahan ii
Halaman Persembahan iii
Halaman Motto v
PRAKATA vi
INTISARI xii
ABSTRACT xiii
I PENDAHULUAN 1
I.1 Latar Belakang Masalah . . . 1
I.2 Perumusan Masalah . . . 3
I.3 Ruang Lingkup Kajian . . . 3
I.4 Tujuan Penelitian . . . 4
I.5 Tinjauan Pustaka . . . 4
I.6 Sistematika Penulisan . . . 5
I.7 Metode Penelitian . . . 6
II TEORI RELATIVITAS KHUSUS 7 II.1 Asas-Asas Teori Relativitas Khusus dan Transformasi Lorentz . . . . 7
II.2 Ruang Minkowski . . . 12
II.3 Grup Lorentz . . . 18
II.4 GrupSL(2, C) . . . 28
III DASAR-DASAR ALJABAR KUATERNION 36
III.1 Aljabar Kuaternion Real . . . 37
III.1.1 Aljabar Kuaternion Kompleks . . . 41
IV OPERATOR-OPERATOR KUATERNIONIK 44 IV.1 Operator-OperatorR,C,H-Linear Kanan . . . . 44
IV.2 Operasi Konjugasi,TransposedanTrace . . . 47
V PENYAJIAN TRK MENGGUNAKAN KUATERNION 53 V.1 GrupU(1,HL) . . . . 53
V.2 GrupSL(1,HL⊗CR) . . . . 59
V.3 GrupO˜(1,HL⊗HR)danSOfo(1,HL⊗HR) . . . . 63
VI PERSAMAAN DIRAC DAN PENYAJIANNYA DENGAN ALJABAR KU-ATERNION 70 VI.1 Stuktur Persamaan Dirac . . . 71
VI.1.1 Kovariansi Lorentz Persamaan Dirac . . . 75
VI.1.2 Transformasi Similar antar Wakilan . . . 78
VI.1.3 Wakilan Chiral . . . 79
VI.1.4 Wakilan Standar . . . 82
VI.1.5 Penyelesaian Persamaan Dirac untuk Partikel Bebas . . . 84
VI.2 Persamaan Dirac dalam Aljabar Kuaternion . . . 90
VI.2.1 Wakilan Chiral Kuaternionik . . . 90
VI.2.2 Wakilan Standar Kuaternionik . . . 96
VI.3 Penyelesaian Persamaan Dirac untuk Partikel Bebas . . . 98
VII.2 Saran . . . 108
A PEMBUKTIAN PERSAMAAN 112
I.1 Pembuktian Persamaan Dalam Bab II . . . 112 I.2 Pembuktian Persamaan Dalam Bab V . . . 113
B HubunganSU(2)danSO(3) 121
KHUSUS DALAM ALJABAR KUATERNION REAL DAN
PENERAPANNYA DALAM STRUKTUR PERSAMAAN DIRAC
Oleh :
Latief Rahmawati 01/147328/PA/08613
Telah dikaji penerapan aljabar kuaternion real dalam teori relativitas khusus dan struk-tur persamaan Dirac. Dengan mendefinisikan operator-operator R,C dan H-linear
kanan, pembangkit transformasiboostdan rotasi dapat diperoleh sehingga pada gili-rannya, dapat di bentuk grup-grup simetri kuaternionik dalam teori relativitas khusus. Grup simetri itu berupaSO˜o(1,HL⊗HR)danSL(1,HL⊗CR)yang masing-masing
berpadanan dengan grupSOo(3,1)danSL(2,C). Dipelajari peranan yang dimainkan
olehSL(1,HL⊗HR)dalam pembahasan persamaan Dirac kuaternionik.
Kata kunci : Aljabar kuaternion real, grup simetri, relativitas khusus, persamaan Dirac.
SPECIAL THEORY OF RELATIVITY IN REAL
QUATERNION ALGEBRA AND ITS APPLICATION IN THE
STRUCTURES OF DIRAC EQUATION
By :
Latief Rahmawati 01/147328/PA/08613
The applications of real quaternion algebra in special theory of relativity and the structure of Dirac equation has been studied. By defining right R,C and H-linear
operators, generators of boosts and rotations can be constructed and in turn, the sym-metry groups of special theory of relativity can be formed. The symsym-metry group are SO˜o(1,HL⊗HR) and SL(1,HL⊗CR) which is the counterpart of SOo(3,1)and
SL(2,C)in quaternionic versies respectivelly. The role ofSL(1,HL⊗HR)in
quater-nionic Dirac equation has been studied.
Keywords: Real quaternion algebra, symmetry groups, special theory of relativity, Dirac equation.
I.1 Latar Belakang Masalah
Teori Relativitas Khusus (TRK) muncul secara utuh dalam makalah Albert Einstein yang berjudul (dalam terjemahan bahasa Inggris) "On the Electrodynamics of Moving Bodies"1pada 30 Juni 1905. Sebelum Einstein memunculkan makalahnya, beberapa ide yang tercakup dalam TRK pernah disinggung dalam artikel tokoh-tokoh lain. Pada tahun 1904 Poincaré hampir tiba pada gagasan TRK, seperti yang per-nah diungkapkannya "...as demanded by the relativity principle the observer cannot know whether he is at rest or in absolute motion." 2. Dalam makalahnya, Einstein membangun TRK di atas dua asas dan transformasi Lorentz yang diperoleh Einstein melalui caranya sendiri yang sebenarnya telah diungkapkan oleh H.A. Lorentz pada tahun 1899.3
Pada tahun 1908 melalui gagasan Herman Minkowski,4 TRK menjadi dapat ditelaah secara geometris. Dalam telaah itu ditinjau entitas yang invarian terhadap transformasi Lorentz dalam TRK dan selanjutnya dicari pula grup simetrinya. Untuk mencari entitas yang invarian itu, didefinisikan metrik tak-definit yang kini dikenal dengan nama metrik Minkowski. Grup simetri yang digunakan dalam TRK meru-pakan suatu subgrup dari grup Lorentz O(3,1) yang disebut sebagai grup Lorentz proper, orthochronousSOo(3,1).
Dengan berkembangnya penerapan teori grup dalam fisika, grupSL(2,C)pun
1Judul asli dari makalah ini adalah "Zur Elektrodynamik bewegter Körper". Makalah ini diterbitkan dalam jurnal Annalen der Physik, 17, 1905.
2www.Nobelprice.History of Special Relativity.org 3
Pada tahun 1887 selama mempelajari efek Doppler, Woldemar Voigt juga menuliskan transformasi yang sama dengan transformasi Lorentz dan tahun 1898 transformasi Lorentz juga dituliskan kembali oleh Joseph Larmor.
4
Seorang guru besar matematika yang pernah mengajari Einstein.
dapat digunakan untuk menyatakan transformasi Lorentz. Hal ini karena terdapat homomorfisme dariSL(2,C)keSOo(3,1). Sebagai padanan ruang Minkowski bagi
SL(2,C)adalah himpunan semua matriks Hermitian2×2 (Q). Besaran yang
inva-rian dalam teori ini adalah detX, X ∈ Q.
Di lain pihak, persamaan Dirac5yang menggambarkan partikel berspin 12 rel-ativistik, kovarian terhadap transformasi Lorentz. Dalam kasus ini, ditinjau waki-lan transformasi Lorentz di ruang spinor Dirac sebagai pemenuhan asas kovariansi6 dalam TRK. Salah satu bentuk wakilan transformasi Lorentz yang ada berbentuk ma-triks 4× 4 blok diagonal7 yang entri masing-masing blok diagonalnya merupakan unsur-unsur dari grupSL(2,C).
Aljabar kuaternion ditemukan oleh Sir William Rowan Hamilton pada 16 Ok-tober 1843. Hamilton berusaha memperluas medan kompleks untuk menggambarkan rotasi dalam ruang tiga dimensi. Pada awal kemunculannya, aljabar kuternion diang-gap memiliki manfaat yang cukup berarti dalam fisika dan selama periode ini Hamil-ton sempat menulis buku yang berjudul Lecture on Quaternion (1844) yang dipub-likasikan tahun 1853 dan Element of Quaternion yang dipublikasikan tahun 1866 setahun setelah kematiannya.
Sekitar tahun 1845-1879 William Kingdom Clifford memperkenalkan suatu aljabar Geometris yang merupakan perluasan dari aljabarkuaternion. Namun dalam perkembangan selanjutnya, dalam dunia fisika, baik aljabar kuaternion maupun al-jabar geometris sedikit memberikan kemajuan dan kurang mendapat perhatian. Hal ini terlihat dari sangat jarangnya buku teks atau jurnal yang membahas penerapan aljabar kuaternion dalam dunia fisika. Permasalahan yang membuat operasi dalam
al-5Persamaan ini dirumuskan oleh P.A.M Dirac. 6
Asas kovariansi sering pula disebut sebagai asas relativitas (Friedman,1983). 7
jabar kuaternion berbeda dengan yang lainnya (RataupunC) adalah sifat tak-komutatifnya.
Meskipun perkembangan aljabar kuaternion dalam dunia fisika sempat sepi, beberapa tahun terakhir ini aljabar kuaternion mulai dilirik dan menjadi salah satu topik yang hangat.
Atas dasar masih jarangnya penggunaan aljabar kuaternion dalam dunia fisi-ka, maka usaha menyajikan TRK dan struktur persamaan Dirac dengan aljabar ku-aternion merupakan usaha pelebaran penggunaan matematika dalam fisika.
I.2 Perumusan Masalah
Penerapan aljabar kuaternion dalan TRK akan dipusatkan pada pencarian grup-grup simetri yang berpadanan denganSOo(3,1)danSL(2,C)khususnya akan dicari
bentuk transformasiboostdan rotasi khusus, pembangkit-pembangkit dan kaitan ko-mutasi pembangkit-pembangkit grup itu.
Sedangkan dalam penerapan aljabar kuaternion untuk menampilkan struktur persamaan Dirac, akan dicari bentuk wakilan8untuk transformasi Lorentz, swafungn-si bagi operator spin dan operator spin itu dalam verswafungn-si kuaternionik.
I.3 Ruang Lingkup Kajian
Kajian skripsi ini dibatasi hanya pada penyajian TRK dalam aljabar kuater-nion real. Topik mengenai Presesi Thomas dalam TRK tidak menjadi bagian dalam skripsi ini. Pembahasan grup simetri dalam TRK hanya dibatasi pada grupSOO(3,1),
sehingga tidak membahas sampai pada grup Poincar´e. Pembahasan dalam stuktur persamaan Dirac hanya dipusatkan pada pencarian bentuk transformasi Lorentz, op-erator spin dan swafungsi bagi opop-erator spin itu. Kajian lanjutan terhadap persamaan Dirac dalam dunia fisika partikel tidak dibahas dalam skripsi ini. Kemudian baik
8
didalam TRK maupun dalam struktur persamaan Dirac, tidak dibahas mengenai in-teraksi antara dua partikel maupun antara partikel dengan medan.
I.4 Tujuan Penelitian
1. Mencari bentuk metrik Minkowski di TRK dalam penyajian aljabar kuaternion.
2. Mencari grup simetri yang terkait dengan metrik Minkowski itu.
3. Mencari pembangkit transformasi Lorentz murni (boost) dan rotasi dalam al-jabar kuaternion .
4. Mencari kaitan komutasi bagi pembangkit-pembangkit itu.
5. Mencari bentuk eksplisit wakilan transformasi Lorentz di ruang spinor Dirac versi kuaternionik.
6. Mencari operator spin versi kuaternionik.
7. Mencari swafungsi bagi operator spin dalam ruang spinor Dirac versi kuater-nionik.
I.5 Tinjauan Pustaka
Pada tahu 1905 dalam makalahnya yang berjudul "On the Electrodynamics of Moving Bodies Einstein berhasil merumuskan TRK secara utuh walaupun TRK secara langsung bukanlah satu-satunya hal yang melatarbelakangi makalahnya itu.
Jauh sebelum Einstein menemukan TRK nya, Sir W.R.Hamilton menemukan aljabar kuaternion, tepatnya pada 16 Oktober 1843, yang pada awal kemunculannya diprediksi akan memberikan manfaat dalam dunia fisika. Namun dalam perkemban-gannya, aljabar kuaternion sempat berhenti dan kurang memberi kemajuan dalam dunia fisika.
Setelah sekian lama tenggelam, beberapa tahun terakhir penerapan aljabar ku-aternion dalam dunia fisika mulai dikembangkan. Salah satu tokoh yang berkecim-pung di bidang ini adalah Stefano de Leo yang pada tahun 1996 mempublikasikan makalahnya yang berjudul Quaternion and Special Relativity. Dalam makalahnya ini Stefano menyajikan TRK dengan menggunakan aljabar kuaternion. Pada tahun 2001 Stefano de Leo kembali mempublikasikan makalahnya yang berjudul Quater-nionic Lorentz Group And Dirac Equation, makalahnya ini menyajikan grup simetri dalam kuaternion yang berkaitan dengan grup Lorentz dan menyajikan persamaan Dirac versi kuaternion.
I.6 Sistematika Penulisan
Skripsi ini ditulis dalam 6 bab, dengan penjelasan bab demi bab adalah sebagai berikut:
• Pada BAB 1 dikemukakan latar belakang penelitian yang dilakukan, tujuan penelitian, tinjauan pustaka, sistematika penulisan, serta penjelasan mengenai metode pelaksanaan penelitian.
dis-ajikan grup Lorentz yang melestarikan∆s2. Terakhir disajikan grupSL(2,C)
sebagai grup yang homomorfis dengan grup Lorentz yang melestarikan nilai determinan matriks Hermitian2×2yang berkaitan dengan∆s2.
• BAB 3 memaparkan dasar-dasar aljabar kuaternion yang terdiri dari aljabar kuaternion real dan kuaternion kompleks.
• BAB 4 membahas operator-operator kuaternionik, yang dimulai dari pendefin-isian operator kiri dan operator kanan. Selanjutnya dari kedua operator itu dapat dibentuk operator yang linear dari kanan terhadap "lapangan" R(OR),
opera-tor linear dari kanan terhadap lapanganC (OC) dan operator linear dari kanan
terhadap lapanganH(OH).9
• BAB 5 menyajikan grup-grup simetri versi kuaternionSOfo(1,HL⊗HR)dan
SL(1,HL ⊗CR) yang masing-masing berpadanan dengan grup-grup simetri
dalam TRK yaituSOO(3,1)danSL(2,C).
• BAB 6 menyajikan tinjauan singkat mengenai struktur persamaan Dirac dan peranan grupSL(1,HL⊗CR)untuk menyajikan struktur persamaan Dirac versi
kuaternion.
• BAB 7 memberikan kesimpulan dan saran untuk pengembangan kajian.
I.7 Metode Penelitian
Metode yang digunakan dalam penelitian ini adalah kajian teoretis terhadap konsep TRK, struktur persamaan Dirac dan aljabar kuaternion serta penerapan aljabar kuaternion dalam menyajikan TRK dan struktur persamaan Dirac melalui peninjauan grup simetrinya.
9
Telah digunakan istilah yang tidak tepat ketika menyebutHsebagai suatu jenis lapangan karena
II.1 Asas-Asas Teori Relativitas Khusus dan Transformasi Lorentz
Teori relativitas khusus (TRK) dimunculkan oleh Einstein pada tahun 19051 dibangun di atas dua asas, yaitu
1. Semua kerangka inersial (lembam) sama baiknya untuk merumuskan hukum-hukum alam.
2. Cahaya memiliki kelajuan konstan sebesarcdi semua kerangka acuan inersial.
Asas yang dituliskan pertama di atas sering disebut sebagai asas relativitas atau asas kovariansi (keseragaman bentuk bagi semua kerangka inersial), sedangkan asas yang dituliskan kedua terkait dengan invariansi kelajuan cahaya.2 Asas pertama dimak-sudkan untuk menegaskan bahwa tidak ada kerangka inersial yang istimewa di dalam TRK. Berbeda dengan elektrodinamika berbasiskan mekanika Newton, di dalam TRK persamaan-persamaan Maxwell berlaku untuk semua kerangka inersial. Asas ked-ua berimplikasi bahwa kelajked-uan cahaya tidak bergantung pada kelajked-uan sumbernya (Friedman,1983).
Kerangka acuan dimaksudkan sebagai suatu wadah yang digunakan untuk me-nentukan sistem koordinat (Breithoupt,2001). Pemberian koordinat terhadap suatu peristiwa tidak hanya dikaitkan dengan pelabelan koordinat ruang tempat suatu peri-1Sebenarnya, di dalam makalahnya pada tahun itu, Einstein belum menamakannya sebagai teori relativitas khusus.
2Baik asas relativitas maupun asas yang terkait dengan invariansi laju cahaya memiliki bentuk pernyataan yang beragam dalam berbagai buku mengenai teori relativitas atau teori ruang-waktu. Tetapi tidak semua varian bentuk masing-masing asas itu ekivalen satu dengan yang lainnya. Kajian mengenai varian bentuk masing-masing asas itu tidak termasuk dalam skripsi ini.
stiwa terjadi, melainkan juga dikaitkan dengan pelabelan waktu ketika peristiwa itu terjadi. Pelabelan koordinat ruang bergantung pada pusat koordinat ruang yang dip-ilih. Sedangkan pelabelan koordinat waktu suatu peristiwa di suatu lokasi diberikan oleh nilai yang ditunjukkan oleh jam yang terletak di sekitar lokasi peristiwa itu ter-jadi. Jadi dalam suatu kerangka acuan telah tersebar jam dimana-mana. Agar hasil pencatatan waktu oleh jam-jam yang berbeda lokasinya saling terkait, maka jam-jam itu harus saling sinkron satu dengan yang lainnya. Sehingga pemberian koordinat su-atu peristiwa dilakukan dengan melabelkan peristiwa itu dengan tiga koordinat ruang (yang bergantung pada pemilihan pusat koordinat) yang terkait dengan posisi peris-tiwa itu terjadi dan satu koordinat waktu saat perisperis-tiwa itu terjadi. Pengamat dalam suatu kerangka diidentikkan dengan suatu himpunan tak berhingga dari jam-jam pen-catat yang tersinkronkan satu terhadap lainnya yang terdistribusi di seluruh ruang (Resnick,1968).
Kerangka acuan disebutinersialjika benda yang tidak dipengaruhi oleh gaya luar akan teramati tetap diam atau bergerak dengan kecepatan konstan relatif terhadap pengamat yang diam di kerangka itu; bergantung pada kondisi awal gerakan benda. Dari sini, kerangka inersial dapat dibedakan secara eksperimen dengan kerangka yang dipercepat terhadap sembarang kerangka inersial. Kajian dalam TRK dibatasi pada penggunaan kerangka-kerangka acuan yang bersifat inersial saja, yaitu kerangka yang di dalamnya berlaku hukum kelembaman (hukum Newton I) yang tetap berlaku dalam teori relativistas.
ke-serentakan menjadi tidak mutlak, pengukuran selang waktu dua buah peristiwa juga dapat bergantung pada pengamat (kerangka acuan).
Asas relativitas bersama dengan asas invariansi laju cahaya digunakan untuk menurunkan bentuk transformasi yang mengaitkan perpindahan peninjauan berba-gai observabel fisika suatu peristiwa antar dua buah kerangka inersial. Dalam penu-runan transformasi itu, digunakan asumsi homogenitas dan isotropi ruang-waktu. Ho-mogenitas ruang-waktu memiliki arti bahwa hasil pengukuran panjang dan interval waktu antara dua peristiwa tidak bergantung pada dimana atau kapan interval itu ter-jadi. Hal ini berarti pula bahwa semua tempat atau lokasi dan saat kapanpun masing-masing memiliki prioritas yang sama dalam pengukuran panjang suatu benda dan pengukuran selang waktu dua buah peristiwa. Secara matematis, homogenitas ruang-waktu berakibat bahwa transformasi yang mengaitkan perpindahan peninjauan suatu peristiwa antara dua buah kerangka harus merupakan transformasi linear. Transfor-masi linear ini berakibat bahwa semua titik dalam himpunan ruang-waktu dapat di-gunakan sebagai pusat koordinat (Resnick,1968). Sedangkan isotropi ruang berakibat bahwa ke arah manapun pengukuran di dalam ruang dilakukan, hasil yang diperoleh tidak bergantung pada arah pengukuran itu.
Transformasi yang diperoleh dari kedua asas dalam TRK itu beserta asumsi homogenitas ruang-waktu dan isotropi ruang disebut sebagaitransformasi Lorentz.3 Untuk perpindahan peninjauan suatu peristiwa dari suatu kerangka inersialK(t, x, y, z)4ke kerangka inersial lainK′ (t′, x′, y′, z′)yang bergerak relatif terhadap kerangka
K sepanjang sumbux di kerangkaK dengan kelajuan sebesar V, diperoleh bentuk 3Transformasi ini telah dimunculkan oleh H. A. Lorentz sebelum makalah TRK Einstein muncul. Namun demukian, Lorentz menafsirkan transformasi itu secara berbeda dengan tafsiran yang kini dilekatkan pada transformasi itu dalam TRK.
4
transformasi Lorentz (khusus)5
t′ = t− V c2x
q
1− V2
c2
,
x′ = qx−V t
1− V2
c2
,
y′ =y,
z′ =z.
(II.1)
Dalam bentuk umumnya, transformasi Lorentz untuk koordinat waktu menjadi (Mus-lim,1997)
t′ = Γ(t−V~ · ~r
c2), (II.2)
sedangkan untuk koordinat ruang menjadi (Muslim,1997)
r′k =~r′ ·nˆ = Γ(rk−V t) = Γ(~r·nˆ −V t) (II.3)
dan
~r′⊥ =~r⊥, (II.4)
dengan rk dan r⊥ masing-masing merupakan komponen vektor ~r yang sejajar dan
tegak lurus terhadapV~. Dalam hal ini tentunya~r⊥, ~r, ~V dan~rk terletak dalam satu
bidang yang sama. Penggabungan pers.(II.3) dan (II.4) menghasilkan bentuk
~r′ =~r+ (Γ−1)(~r·V~ )V~
V2 −ΓV~t, (II.5)
dengan komponen-komponen Cartesannya berbentuk
x′ =x+ (Γ−1)(n2xx+nxnyy+nxnzz)−ΓV nxt,
y′ =y+ (Γ−1)(nynzx+n2yy+nynzz)−ΓV nyt,
z′ =z+ (Γ−1)(nznxx+nznyy+n2zz)−ΓV nzt,
(II.6)
dengannx, ny,dannzmerupakan kompenen Cartesan vektor satuannˆ pada arahV~.
Pengukuran panjang suatu benda yang rehat di suatu kerangka inersialK′
da-pat dilakukan seperti lazimnya mengukur panjang suatu benda. Dalam hal ini, dada-pat dilakukan dengan langsung mengukur panjang benda yang rehat itu dengan menggu-nakan batang pengukur. Jika benda yang akan diukur rehat terhadap suatu kerangka inersial K′ yang bergerak relatif dengan kecepatan konstan terhadap K, maka
pe-ngukuran panjang di kerangka K dilakukan dengan konsep sebagai berikut. Ten-tukan dua buah titik ujung benda itu pada saat bersamaan menurut jam di kerangka K, kemudian dengan menggunakan batang pengukur, diukur jarak antara kedua titik
tadi. Pengukuran diKdengan mengunakan konsep itu akan memberikan nilai seperti yang diperoleh melalui transformasi Lorentz yang terkait dengan perpindahan penin-jauan dari K′ ke K jika koordinat waktu untuk kedua titik ujung benda itu dibuat
sama. Jika kerangkaK′ bergerak relatif terhadapK sepanjang sumbuxdengan
ke-cepatan relatif sebesarV, maka nilai pengukuran yang diperoleh dari pengukuran itu akan menunjukkan bahwa panjang dalam arah gerak benda yang diukur oleh kerang-kaK (dimana benda itu teramati bergerak) akan lebih pendek daripada panjang yang diukur di kerangkaK′(dimana benda itu rehat), sedangkan panjang dalam arah tegak
oleh faktorΓ ≡ 1
q
1−V2
c2
dalam transformasi Lorentz yang terkait. Efek pemendekan panjang suatu benda itu dikenal dengan namakontraksi Lorentz-Fitzgerald. Pan-jang benda yang diukur di kerangka K′ (dimana benda itu rehat) disebut sebagai panjang sejati(proper length) dari benda itu. Dengan mengasumsikan bahwa semua besaran panjang dan waktu bernilai real, maka berlaku0< V < csehinggaΓ>1.
Pengukuran selang waktu antara dua buah peristiwa yang dilakukan oleh berba-gai kerangka inersial dengan jam-jam sinkronnya masing-masing tidak akan mem-berikan hasil yang sama. Hal ini merupakan konsekuensi langsung dari bentuk trans-formasi Lorentz. Jika dua buah peristiwa terjadi pada suatu lokasi yang sama menurut suatu kerangka inersial, maka pengukuran selang waktu dengan menggunakan jam yang rehat di kerangka itu dan terletak di lokasi tempat peristiwa itu terjadi dise-but sebagaiselang waktu sejati(proper time interval). Untuk kerangka inersial lain yang mengamati kedua peristiwa itu tidak terjadi di satu lokasi yang sama, maka pengukuran selang waktu dua peristiwa itu akan lebih besar daripada selang waktu sejati. Efek ini dikenal dengan namadilatasi waktu(time dilation). Pengamatan se-lang waktu sejati(∆τ) dan selang waktu lainnya(∆t)terhadap dua peristiwa yang sama terkait oleh transformasi berikut
∆t= q∆τ 1− V2
c2
. (II.7)
Dalam pers.(II.7), V menyatakan besarnya kecepatan relatif kerangka inersial yang mengamati∆tterhadap kerangka inersial yang memiliki∆τ.
II.2 Ruang Minkowski
ruang-waktu yang kini dikenal sebagairuang Minkowski. Ruang Minkowski merupakan suatu himpunan6 Myang berunsurkan semua peristiwa di alam ini. Pemberian nilai koordinat(ct, x, y, z)7pada suatu peristiwa diidentikkan dengan mengamati peristiwa itu dari suatu kerangka acuanK (t, x, y, z). Perjalanan atau sejarah suatu partikel di alam ini dilukiskan dalam ruang MinkowskiM sebagai kurva dengan karakteristik tertentu. Kurva itu nantinya akan disebut sebagaigaris dunia(world line).
Dari pers.(II.2) dan (II.5), untuk dua buah peristiwa, diperoleh interval waktu
∆t′ = Γ(∆t−V~ · ∆~r
c2 ) (II.8)
dan interval ruang
∆~r′ = ∆~r+ (Γ−1)(∆~r·V~)V~
V2 −ΓV~∆t. (II.9)
Kemudian dari pers.(II.8) dan (II.9) dengan mengalikancpada kedua sisi pers.(II.8) dapat diperoleh kaitan berikut
(c∆t′)2 −∆~r′2 = (c∆t)2 −∆~r2, (II.10)
atau dalam bentuk uraian komponen-komponen Cartesannya
(c∆t′)2−(∆x′)2−(∆y′)2−(∆z′)2 = (c∆t)2−(∆x)2−(∆y)2−(∆z)2. (II.11)
Dari pers.(II.11) terlihat bahwa bentuk∆s2 ≡(c∆t)2−∆x2−∆y2−∆z2yang
dinyatakan oleh K dalam(ct, x, y, z)sama dengan yang dinyatakan oleh K′ dalam
6Dari tinjauan geometri diferensial, himpunan
Mini merupakan manifold yang dilengkapi dengan objek metrik absolut tertentu. Metrik ini dikenal dengan nama metrik Minkowski dan tergolong dalam metrik Lorentzian.
7
(ct′, x′, y′, z′). KarenaK danK′ sembarang kerangka inersial, maka∆s2merupakan
besaran yang invarian terhadap transformasi Lorentz dan ditafsirkan sebagaiselang ruang-waktuantara dua peristiwa (Carroll,1997).
Dengan menuliskan
ct=x0, x=x1, y =x2, danz =x3, (II.12)
∆s2 dalam sistem koordinat(x0, x1, x2, x3)dapat diberikan dalam bentuk yang lebih
ringkas8
∆s2 =η
µν∆xµ∆xν, (II.13)
dengan
ηµν =
+1 µ=ν= 1,2,atau3
−1 µ=ν= 0
0 µ6=ν.
(II.14)
Obyek-obyekηµν merupakan komponen suatu tensor metrikηtak-definit
(in-definite) bersignature (3,1) yang disebut sebagai (tensor) metrik Minkowski. Ben-tuk ηµν dalam pers.(II.13) merupakan komponen tensor η dalam sistem koordinat (x0, x1, x2, x3).
komponen metrik Minkowski bernilai seperti dalam pers.(II.14).9 Hal ini juga berarti bahwa pada ruang MinkowskiM dapat dibentuk struktur ruang vektor yang diper-oleh dari R4 melalui sistem koordinat itu. Dari sini, peristiwa-peristiwa di ruang
MinkowskiMdapat dipandang sebagai suatu vektor. Sebenarnya, yang disebut se-bagai ruang Minkowski adalah manifold ruang-waktu M yang dilengkapi dengan metrik Minkowskiηdan sering dituliskan sebagai(M, η). Untuk selanjutnya dalam skripsi ini, ruang Minkowski akan dituliskan sebagaiM.
Andaikan(a, b)suatu interval terbuka diR. Suatu lintasanσ di dalam ruang
Myang diparameteri oleh¯t, dengana < ¯t < b, dituliskan sebagai σ(¯t). Nilai-nilai koordinat dari lintasan itu menurut(x0, x1, x2, x3)dituliskan sebagai
Penyematan setiap titik dengan vektor singgungnya di lintasan itu disebut sebagai medan vektor singgunglintasan itu.
Jika ¯t = t = x0
c dan lintasan σ menggambarkan garis dunia suatu partikel
bermassa, maka vektor singgung di titikpdari lintasan itu ,
vp ≡ d(x◦σ)(t)
pakan kecepatan dari partikel itu menurutK(x0, x1, x2, x3), maka pers.(II.17) dapat
dituliskan dalam bentuk
vp = (c, ~vp). (II.18)
Kemudian jika¯t =τ, maka
u≡ d(x◦σ)(τ)
dτ
p
(II.19)
disebut sebagaivektor-4 swa kecepatanbagi lintasanσdip.
Syarat yang harus dipenuhi oleh garis dunia suatu partikel bermassa adalah nilai turunannya di setiap titik di lintasan itu harus memenuhi
η(vp,vp) =c2−~v2
p >0. (II.20)
Vektorvpyang demikian disebut sebagaivektor bak-waktu(time-like). Untuk garis
dunia cahaya, vektor singgungnya harus memenuhi
η(vp,vp) = c2−c2 = 0. (II.21)
Vektorvp yang demikian disebut sebagaivektor bak-cahaya(light-like) atau vektor
null. Vektor singgung yang memenuhi syarat
η(vp,vp)<0 (II.22)
Andaikan kerangkaK′bergerak terhadapKsepanjang sumbux′diKdengan
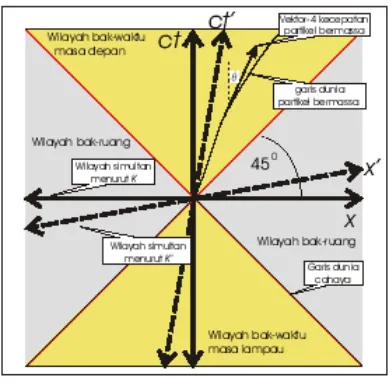
kecepatan relatif sebesarV. Penggambaran (2-D) diagram ruang-waktu Minkowski untuk kedua kerangka itu diberikan oleh gambar berikut
Gambar II.1: Diagram ruang-waktu
Dalam Gb.(II.1), sumbu x′ dan ct′ terlihat tidak tegak lurus. Dengan
me-ngatur x′0 = 0 di dalam pers.(II.1) diperoleh x0 = βx1, dengan β = V
c. Karena
x′0 = 0 merupakan sumbux′1 di K′, maka sumbux′1 digambarkan oleh garis yang
membentuk sudut sebesarφ = tan−1β <450 terhadap sumbux1. Kemudian dengan
mengaturx′1 = 0di dalam pers.(II.1) diperoleh x1 = βx0 yang merupakan sumbu
x′0 =ct′ dariK′. Sudut yang dibentuk oleh sumbux′0 denganx0 juga sebesarφ.
Karena titik di sumbu x1 memiliki koordinat kenol ct = 0, maka sumbu x
merupakanwilayah keserentakan untuk kerangkaK. Kemudian titik di sumbux′1
memiliki koordinat ke nolct′ = 0, maka sumbux′1 merupakan wilayah keserentakan
untuk kerangkaK′.
Titik perpotongan semua sumbu dapat diartikan sebagai peristiwa yang terjadi saat sekarang (t =t′ = 0) dan berada di pusat koordinat yang sama bagiK danK′.
maka garis dunianya harus membentuk sudut sebesar tan−1(ct′
ct) = tan
−1(1) = 450
terhadap sumbu ct. Kemudian karena adanya pembatasan kecepatan untuk partikel bermassa, maka lintasan/garis dunia partikel bermassa yang melintasi titik perpoto-ngan sumbu itu akan selalu berada di dalam wilayah yang dibatasi oleh garis dunia cahaya bagian atas. Wilayah itu disebut sebagaiwilayah bak-waktu masa depan. Wilayah yang dibatasai oleh garis dunia cahaya bagian bawah merupakan wilayah yang dapat dilalui oleh partikel bermassa yang (akan) melintas di titik perpotongan sumbu-sumbu. Wilayah ini disebut sebagai wilayah bak-waktu lampau. Untuk sembarang titik di kedua wilayah bak-waktu dapat dihubungkan dengan titik perpo-tongan sumbu-sumbu oleh suatu garis lurus yang merupakan sumbu x˜0 dari suatu
kerangka K˜ yang bergerak relatif dengan kecepatan sebesar V˜ relatif terhadap K sepanjang sumbux1.
Wilayah di luar wilayah bak-waktu masa depan dan lampau disebut sebagai wilayah bak-ruang. Untuk sembarang titik di dalam wilayah ini dapat dihubungkan dengan titik perpotongan sumbu-sumbu oleh garis lurus yang merupakan sumbu x¯1
dari suatu kerangkaK¯ yang bergerak relatif dengan kecepatan sebesarV¯ terhadapK sepanjang sumbux1.
Meskipun berada di dalam wilayah bak-waktu (lampau dan masa depan), tidak semua lintasan yang demikian merupakan garis dunia partikel bermassa. Adanya pembatasan kecepatan untuk partikel bermassa juga memberikan syarat bahwa lin-tasan itu tidak boleh memiliki vektor singgung yang tergolong vektor bak-ruang.
II.3 Grup Lorentz
Transformasi antara sistem koordinat inersial
denganΛα
β danaαkonstanta, yang memenuhi
ΛαγΛβδηαβ =ηγδ, (II.24)
atau dalam bentuk matriks
ΛTηΛ =η, (II.25)
melestarikan bentuk ∆s2. Transformasi itu disebut sebagai transformasi Lorentz
tak-homogenatautransformasi Poincaré dan disimbolkan sebagaig(Λ, a). Trans-formasi yang berbentuk g(Λ,0) ≡ Λ disebut sebagai transformasi Lorentz ho-mogenatau singkatnyatransformasi Lorentzsedangkan transformasi yang berben-tukg(I, a)≡T(a)disebut sebagaitransformasi translasi.
Dari pers.(II.23), kombinasi dua transformasi Lorentz tak homogeng(Λ1, a1)
dang(Λ2, a2)dapat dituliskan sebagai
g(Λ1, a1)g(Λ2, a2) =g(Λ1Λ2,Λ1a2+a1). (II.26)
Transformasi balikan (invers) darig(Λ, a)berbentukg(Λ−1,−Λ−1a). Dari sini,
him-punan semua transformasi Poincaré dapat membentuk grup yang disebut sebagai grup Poincaré, dengan unsur identitas berbentukg(I,0)dan aturan perkaliannya diberikan
Dengan menuliskan
dapat diverifikasi dekomposisi transformasi Poincaré
g(Λ, a) = T(a)Λ. (II.28)
Dari sini dapat disimpulkan bahwa grup Poincaré merupakan hasil perkalian antara grup translasi (T) dan grup Lorentz (L).
AndaikanΛsembarang transformasi Lorentz homogen danT(a)suatu translasi
dalam ruang MinkowskiM. Suatu translasiT(a)yang tertransformasi Lorentz
(sim-ilar) merupakan translasi lainnya, yakni berlaku
ΛT(a)Λ−1 =T(Λa). (II.29)
Secara umum, dengan menggunakan pers.(II.28) dan (II.29), berlaku
g(Λ, a)T(b)g(Λ−1, a) = T(Λb). (II.30)
Persamaan terakhir yang menunjukkan bahwa grup translasi merupakan subgrup in-varian grup Poincaré.
Dari pers.(II.25), diperoleh (detΛ)2 = 1 sehingga determinan sembarang
disebut sebagai transformasi Lorentzproper, sedangkan yang berdeterminan−1 dise-but sebagai transformasi Lorentz improper. Kumpulan semua transformasi proper membentuk suatu subgrup grup Lorentz.
Dari pers.(II.25) dan pers.(II.14), dengan memilihγ =δ = 0, diperoleh
(Λ00)2−(Λ10)2−(Λ20)2 −(Λ30)2 = 1. (II.31)
Dari sini,(Λ0
0)2 >1, sehingga diperoleh
Λ00 >1 atau Λ00 6−1. (II.32)
Transformasi Lorentz yang memiliki unsur Λ0
0 > 1 disebut sebagai transformasi
Lorentzorthochronous. Kumpulan semua transformasi Lorentzorthochronous mem-bentuk suatu subgrup dari grup Lorentz.
Empat bagian dari grup Lorentz diberikan sebagai berikut (Carmeli,1977):
(1) L↑+: detΛ = 1,Λ0
0 >1. Bagian ini memuat unsur identitas grup.
Kumpu-lan semua transformasi Lorentz, proper, orthocronous membentuk suatu subgrup dalam grup Lorentz yang disebut sebagaigrup Lorentz orthochronous proper.
(2) L↑−: detΛ =−1,Λ0
0 >1. Bagian ini memuat unsur pembalikan ruangS
yang menggambarkan pencerminan relatif terhadap cacah gasal sumbu ru-ang:
x′0 =x0, x′1 =−x1 x′2 =−x2 x′3 =−x3
(3) L↓−: detΛ =−1,Λ0
menggambarkan pencerminan relatif terhadap sumbu waktu:
x′0 =−x0, x′1 =x1, x′2 =x2, x′3 =x3.
(4) L↓+: detΛ = +1,Λ0
0 6−1. Bagian ini memuat unsur pembalikan sumbu
waktu dan pembalikan sumbu ruangST.
Dari empat bagian di atas, L↑ ≡ L↑+∪ L↑− merupakan subgrup grup Lorentz yang akan disebut sebagai grup Lorentz orthochronous, sedangkan L+ ≡ L↑+ ∪
L↓+ merupakan subgrup yang lain dan akan disebut sebagai grup Lorentz proper.
Dalam literatur matematika, grup L+ sering dituliskan sebagai SO(3,1) dan grup
L↑+ disimbolkan sebagai SOo(3,1)(Prugove˘cki, 1995). Setiap transformasi Lorentz
improperberbentukΛ =SΛ1, denganΛ1 merupakan transformasi Lorentzproper.
Secara umum matriksΛmemiliki 16 unsur. Dengan adanya pers.(II.24), yang terdiri dari 10 persamaan pembatasan/kendala, maka dari keenam belas unsur itu hanya ada 6 unsur yang independen. Hal ini menunjukkan bahwa grup Lorentz memi-liki 6 parameter sehingga berdimensi 6. Pada gilirannya, keenam parameter itu terdiri dari 3 parameterboostdan 3 parameter rotasi .
Dengan menggunakan notasi seperti dalam (II.12), pers.(2.1) dapat dituliskan dalam bentuk
x′0 = Γ(x0−βx1)
x′1 = Γ(x1−βx0)
x′2 =x2
x′3 =x3.
denganΓ = 1
q
1−V2 c2
danβ = V
c. Agar pers.(II.11) berlaku, maka harus dipenuhi
Matriks-matriks transformasi Lorentz khusus sepanjang sumbux2danx3 masing-Transformasi Lorentz yang mengaitkan perpindahan peninjauan dari suatu kerangka inersial K ke kerangka inersial K′ yang bergerak dengan kecepatan V~
relatif terhadap K disebut sebagi transformasi Lorentz murni atau transformasi boost. Oleh karena itu, baik transformasi Lorentz khusus maupun transformasi Lorentz umum keduanya merupakan transformasiboost. MatriksB1(ξ),B2(ξ)danB3(ξ)pun
tergolong transformasiboost. Ketiganya merupakan unsur dariSOo(3,1). Terhadap
nilai-nilai0≤ξ < ∞, baikB1(ξ), B2(ξ)maupunB3(ξ)akan tetap merupakan unsur
Selain transformasiboost, transformasi rotasi juga melestarikan∆s2. Bentuk
matriks transformasi rotasi di sekitar sumbu-idiberikan oleh
Ai =
dengan Ri merupakan matriks-matriks rotasi dalam R3, seperti dalam pers.(B.11),
(B.12) dan (B.13). Rotasi dalam ruang Minkowski merupakan perluasan rotasi dalam
R3. Himpunan semua matriks transformasi rotasi membentuk grup dan merupakan
subgrup dariSOo(3,1).
Matriks-matriks dalam pers.(II.37), (II.38) dan (II.39) akan menjadi I4 jika
ξ = 0. Begitu juga dengan matriks-matriks dalam pers.(II.40) akan menjadi I4 jika
ˆ
Keenam matriks terakhir akan menjadi basis bagi aljabar Lie bagi grup SOo(3,1).
Keenam matriks itu disebut sebagaipembangkituntuk masing-masing transformasi yang terkait dengannya. Keenam pembangkit itu memenuhi kaitan komutasi berikut
Transformasiboostinfinitesimal disajikan oleh
Λ(δξ) =I4 +δξmBˆm, m = 1,2,3, (II.48)
dengan δξ parameter boost infinitesimal. Transformasi boost berhingga sebesar ξ dinyatakan dalam bentuk
Λ(ξ) = eξmBmˆ , (II.49)
yang dapat diperoleh dengan melakukan transformasiboostinfinitesimal secara bertu-rutan sebanyakN =ξm¯/dξm¯ kali kearah yang tetap (ke sumbuxm).
Serupa dengan transformasiboost, transformasi rotasi infinitesimal disajikan oleh
Λ(δθ) =I4+δθmAˆm, (II.50)
denganδθmerupakan parameter rotasi infinitesimal. Secara umum, bentuk transfor-masi rotasi diberikan oleh
dan
Dengan menggunakanδωµν danJ
µν, pers.(II.48) dan (II.50) dapat dituliskan dalam
bentuk yang lebih kompak, yaitu
Λ(δω) = I4+1
2δω µνJ
µν, µ, ν = 0,1,2,3. (II.54)
Sedangkan pers.(II.49) dan (II.51) dapat dirangkum dalam bentuk
Λ(ω) = e12ω
µνJµν
, µ, ν = 0,1,2,3. (II.55)
Dari sini,δωµν danJ
µν masing masing dapat diartikan sebagai rotasi/boost
infintesi-mal dan pembangkit rotasi/boostpada bidang(µ−ν).
II.4 GrupSL(2, C)
Ditinjau matriks-matriks kompleks hermitan berbentuk
Matriks-matriks yang demikian memenuhi
detX(x) = (x0)2−(x1)2−(x2)2−(x3)2. (II.57)
Himpunan semua matriks kompleks2×2yang berbentuk seperti dalam pers.(II.56) akan dinyatakan sebagaiQ. Untuk setiapA∈ SL(2,C)≡ {G ∈GL(2,C)|detG=
1}, pemetaanA:Q → Qyang diberikan oleh
X 7→X′ =AXA† (II.58)
jelas melestarikan sifat Hermitan matriksX, karena
X′†= (AXA†)†= (A†)†X†A† =AXA†=X′, (II.59)
dan detX. Pers.(II.56) juga dapat dinyatakan dalam bentuk
X(x) = σµxµ, (II.60)
dengan σ0 = I2 dan σi (i = 1,2,3) merupakan matriks-matriks Pauli.
Matriks-matriks ini memenuhi kaitan-kaitan berikut
detσµ= 1
trσi = 0, i= 1,2,3
σ0σi =σiσ0 =σi, i= 1,2,3
(II.61)
dan
Dengan menggunakan kaitan di atas, komponen untuk vektorxµdapat diperoleh dari
matriksX dengan menggunakan rumus berikut
xµ= 1
2tr(σµX). (II.63)
Relasi antaraMdanQdalam pers.(II.60) merupakan isomorfisme.
Dari sini, nilai koordinat suatu peristiwa yang teramati oleh suatu kerangka K, selain dapat dinyatakan sebagai x = (x0, x1, x2, x3), dapat pula disajikan dalam
bentukX(x) = σµxµ dengan pemetaan balikannya diberikan oleh pers.(II.63).
De-ngan melihat pada pers.(II.57), (II.60) dan (II.63), hal ini berarti bahwa pemetaan olehA ∈SL(2,C)diQ(II.58) menginduksi suatu transformasi Lorentz.
JikaX′ =σ
αx′α =AXA†, maka
x′α = 1
2tr(σαX
′)
= 1
2tr(σαAXA
†)
= 1
2tr(σαAσβA
†)xβ.
(II.64)
Dengan demikian dari sini dapat disimpulkan bahwa A ∈ SL(2,C)menginduksiΛ
yang entrinya diberikan oleh
Λ(A)αβ = 1
2tr(σαAσβA
Pemetaan dalam pers.(II.65) bersifat homomorfis, karena berlaku
Pada baris keenam dalam pers.(II.66) di atas telah digunakan kenyataan berikut ini
Ξαβγδ =
A,−A∈SL(2,C)akan memberikanΛ(A) = Λ(−A). JikaA =I2, maka pers.(II.65)
memberikan
Λ(I2) =I4. (II.68)
Pada kenyataannya, peta bayangan proses pemetaan dalam pers.(II.65) merupakan SOo(3,1)(Carmeli,1977). Pemetaan itu bersifat 2-1 dariSL(2,C)keSOo(3,1).
Matriks-matriks kompleks2×2secara umum didefinisikan dengan menggu-nakan 4 bilangan kompleks atau 8 bilangan real. Tetapi karena fungsi det:GL(n,C)→ Cmemberikan dua batasan bagi entri bilangan real dalamSL(2,C), makaSL(2,C)
sebagai subhimpunan dari GL(2,C) hanya didefinisikan oleh 6 bilangan real yang
bebas. Hal ini menunjukkan bahwaSL(2,C)(sebagai grup Lie) berdimensi 6. Oleh
karena itu, aljabar Lie dariSL(2,C)juga berdimensi 6.
Suatu transformasiboostinfinitesimalδξsepanjang sumbux1dapat disajikan
oleh
x′0 =x0−δξx1, x′1 =x1−δξx0, x′2 =x2, x′3 =x3. (II.69)
TransformasiA ∈ SL(2,C)yang berkaitan dengan transformasiboostinfinitesimal
(II.69) dituliskan sebagai
A=I2+δξˆκ1, (II.70)
dengan κˆ1 matriks kompleks 2×2 sebagai pembangkit boost akan ditentukan
ke-mudian. Dengan memasukkan pers.(II.69) ke sebelah kiri dari pers X′ = AXA†,
yaitu
X′ =σµx′µ
=X−δξσ0x1−δξ1x0
=X−δξ(σ0x1+σ1x0)
dan pers.(II.70) ke sebelah kanan dariX′ =AXA†, yaitu
X′ =AXA†= (I2+δξκˆ1)X(I2+δξˆκ†
1)
=X+δξκˆ1X+δξXκˆ†1
=X+δξ(ˆκ1X+Xˆκ†1)
(II.72)
maka dengan menyamakan pers.(II.71) dan (II.72), diperoleh
−σ0x1−σ1x0 = ˆκ1X+Xκˆ†1. (II.73)
Dari sini dapat disimpulkan bahwaκˆ1harus memenuhi kaitan berikut ini
ˆ
κ1σ0 +σ0κˆ†1 =−σ1;
ˆ
κ1σ1 +σ1κˆ†1 =−σ0;
ˆ
κ1σ2 +σ2κˆ†1 = 0;
ˆ
κ1σ3 +σ3κˆ†1 = 0.
(II.74)
Penyelesaian untuk persamaan di atas adalah
ˆ
κ1 =−
1
2σ1. (II.75)
Dengan cara yang identik, pembangkitboostsepanjang sumbux2 yaituˆκ
2 dan
sepa-njang sumbux3 yaituκˆ
3 masing-masing diberikan oleh
ˆ
κ2 =−
1
2σ2 dan κˆ3 =− 1
2σ3. (II.76)
de-ngan
x′0 =x0, x′1 =x1, x′2 =x2−δθx3, x′3 =x3+δθx2. (II.77)
Pembangkit dari rotasi ini di dalamQakan dinyatakan sebagaiˆλ1, dan transformasi
rotasi infinitesimalnya dinyatakan dengan rumusan berikut
A=I+δθλˆ1. (II.78)
Bentukλˆ1dapat dicari dengan langkah yang sama seperti pada kasus untuk penelusuran
pembangkit boost ˆκi. Dengan memasukkan pers.(II.77) ke sisi kiri dari persamaan
X′ =AXA†, dan pers.(II.78) ke sisi kanan dari persamaanX′ =AXA†diperoleh
σ3x2−σ2x3 = ˆλ1X+Xλˆ†1. (II.79)
Dari sini dapat disimpulkan bahwaλˆ1harus memenuhi empat persamaan berikut
ˆ
λ1σ0 +σ0λˆ†1 = 0,
ˆ
λ1σ1 +σ1λˆ†1 = 0,
ˆ
λ1σ2 +σ2λˆ†1 =σ3,
ˆ
λ1σ3 +σ3λˆ†1 =−σ2.
(II.80)
Penyelesaian untuk persamaan di atas diberikan oleh
ˆ
λ1 =−
i
2σ1. (II.81)
x2 danx3 masing-masing dinyatakan dengan
ˆ
λ2 =−
i
2σ2 dan λˆ3 =−
i
2σ3. (II.82)
Dari sifat-sifat matriks Pauli, keenam pembangkit itu jelas saling bebas linear. Oleh karena itu, keenam pembangkit itu dapat digunakan sebagai basis dalam aljabar Lie bagiSL(2,C). Keenam pembangkit itu memenuhi kaitan komutasi berikut
[ˆλi,λˆj] =ǫijkλˆk, [ˆκi,ˆκj] =−ǫijkˆλk, [ˆλi,ˆκj] =ǫijkˆλk. (II.83)
Dari sini, transformasiboost dan rotasi dalamQdengan menggunakan grup SL(2,C)dinyatakan oleh
Kuaternion ditemukan oleh Hamilton pada 16 Okteber 1843. Penemuannya ini dilatarbelakangi oleh keinginannya untuk mengetahui cara mengalikan pasangan 3 bilangan real triplet (a, b, c) sehingga dapat menggambarkan sistem bilangan 3-dimensi, seperti halnya dalam bilangan kompleks yang dapat dinyatakan sebagai pasangan bilangan real(a, b)dapat menggambarkan sistem bilangan 2-dimensi.
Setelah melakukan banyak usaha, akhirnya yang ditemukan oleh Hamilton bukanlah suatu sistem bilangan 3-dimensi melainkan sistem bilangan 4 dimensi yang disebut dengan kuaternion. Sistem bilangan ini dinyatakan dalam 1, i, j, k, dengan i, j, kmerupakan bilangan imajinernya, yang memenuhi kaitan berikut
i2 =j2 =k2 =−1. (III.1)
Konon, rumusan ini datang tiba-tiba ketika Hamilton berjalan bersama istrinya untuk menghadiri pertemuan yang dipimpinnya di Akademi Kerajaan Irlandia di Dublin. Rumusan dasar tersebut ia tulis di atas batu di jembatan Brougham, Dublin.
Gambar III.1: Rumusan quaternion yang ditulis oleh Hamilton diatas batu di jembat-an Brougham
III.1 Aljabar Kuaternion Real
Aljabar kuaternion realHRmerupakan ruang vektor real berdimensi 4 yang
di dalamnya didefinisikan perkalian(q1, q2)→q1q2 yang memenuhi hukum
distribu-tif dan asosiadistribu-tif berikut, untuk setiapq1, q2, q3 ∈HRdan setiapa ∈R,
(q1q2)q3 =q1(q2q3)
q1(q2+q3) =q1q2+q1q3
(q1+q2)q3 =q1q3+q2q3
a(q1q2) =q1(aq2)
(III.2)
dan terdapat basis{1, i, j, k}yang memenuhi sejumlah kaitan komutasi produk berikut:
ii=jj=kk =−1 (III.3)
ij =−ji=k, jk =−kj =i, ki=−ik =j, ijk =kk=−1, (III.4)
serta untuk setiapq∈HRdipenuhi
1q =q1 =q. (III.5)
Secara umum setiapq∈HRdisebut sebagai kuaternion real yang dapat ditulis
dalam kombinasi linear berikut ini
q= 1a0+ia1+ja2+ka3 (III.6)
dengan a0, a1, a2a3 ∈ R. Karena 1 merupakan unsur identitas terhadap perkalian
persamaan (III.6) menjadi
q=a0+ia1+ja2+ka3. (III.7)
qterdiri dari bagian realℜ(q)≡a0 dan bagian imajinerℑ(q)≡ia1+ja2+ka3.
Himpunan semua kuaternion dengan bagian imajinernya sama dengan nol di-tulis sebagaiℜ[HR]. Sedangkan himpunan semua kuaternion dengan bagian realnya
sama dengan nol ditulis sebagaiℑ[HR]. Dengan demikian setiapq ∈ HR dapat
dit-uliskan dalam bentuk
q= (ℜ(q),ℑ(q)). (III.8)
Kemudian penulisan untukqjuga dapat berbentuk
q = (t, ~q). (III.9)
Dengan menggunakan kaitan komutasi pada pers.(III.3) dan (III.4), perkalian antara dua buah kuaternionq = a0+ia1+ja2+ka3 = (t, ~q)danq′ = a′0 +ia′1+
ja′
2+ka′3 = (t′, ~q′)disajikan secara eksplisit seperti berikut ini
qq′ =[a0a′0−a1a1′ −a2a′2−a3a′3]+
i[a0a′1+a1a′0+a2a′3−a3a′2]+
j[a0a′2 +a2a′0+a3a′1−a1a′3]+
k[a0a′3+a3a′0+a1a′2−a2a′1].
(III.10)
Kemudian dengan menuliskana0a′0 =tt′, a1a′1 +a2a′2 +a3a′3 =~q·~q′, ia0a′1+
a1a′3) +k(a1a′2−a2a′1) =~q×~q′, pers.(III.10) dapat disajikan dalam bentuk
qq′ =tt′ −~q·~q′+t~q′+~qt′ +~q×~q′, (III.11)
atau
(t, ~q)(t′, ~q′) = (tt′−~q·~q′, t~q′+~qt′+~q×~q′). (III.12)
Perkalian ini disebut juga sebagaiperkalian Grassmann. Perkalian dua buah kuater-nion ini dapat dibagi menjadi dua komponen yaitu komponen simetris yang disebut sebagaiperkalian dalam Grassmann(The Grassmann Inner product) dan kompo-nen antisimetris yang disebut sebagai perkalian luar Grassmann(The Grassmann Outer product). Perkalian dalam antara dua buah kuaternion didefinisikan sebagai
(t, ~q)(t′, ~q′)≡ (t, ~q)(t
′, ~q′) + (t′, ~q′)(t, ~q)
2 = (tt
′−~q·~q′, t~q′+~qt′), (III.13)
sedangkan perkalian luar antara dua buah kuaternion didefinisikan sebagai
(t, ~q)(t′, ~q′)≡ (t, ~q)(t
′, ~q′)−(t′, ~q′)(t, ~q)
2 = (0, ~q×~q
′). (III.14)
Konjugat kuaterniondidefinisikan sebagai
q†≡a0−ia1−ja2−ka3 (III.15)
dengan sifat
(q†)† =q dan (pq)† =q†p†. (III.16)
Normasuatu kuaternion didefinisikan sebagai
Dari sini,inversiterhadap perkalian dari suatu kuaternionqdiberikan oleh
q−1 = q
†
N(q) =
q†
qq†. (III.18)
Suatu perbedaan yang penting antara kuaternion dan bilangan kompleks yang berhubungan dengan definisi operasi konjugasi yaitu bahwa dalam bilangan kompleks hanya terdapat satu jenis konjugasi misalnya:
i→ −i
Sedangkan dalam sistem bilangan kuaternion, terdapat operasi konjugasi yang berbe-da dengan operasi konjugasi stanberbe-dar seperti paberbe-da pers.(III.15). Dengan aberbe-danya tiga buah imajiner satuan terdapat beberapa kemungkinan untuk mendefinisikan operasi-operasi konjugasi baru yang berbeda, yaitu
(i, j, k)→(−i,+j,+k),(+i,−j,+k),(+i,+j,−k)
(i, j, k)→(+i,−j,−k),(−i,+j,−k),(−i,−j,+k).
(III.19)
Keenam operasi konjugasi di atas secara ringkas dapat dinyatakan dalam q dan q†
sebagai berikut
q → −iq†i,−jq†j,−kq†k
q→ −iqi,−jqj,−kqk
(III.20)
Sedangkanq†dapat juga dinyatakan dalamqdalam bentuk:
q†=−1
2(q+iqi+jqj+kqk). (III.21)
jika dikalikan dengan q secara umum akan menghasilkan kuaternion lain dengan bagian imajinernya tidak sama dengan nol. Hal ini berarti perkalian itu secara umum tidak akan komutatif. Sehingga dari keenam bentuk konjugasi itu tidak ada yang dapat digunakan untuk mendefinisikan invers perkalian dari suatu kuaternion.
III.1.1 Aljabar Kuaternion Kompleks
Aljabar kuaternion kompleksHCmerupakan aljabar kuaternion H(1,~h)di
atas lapangan/medan kompleksC(1,I)
Hc =nc0+~c·~h |~h ≡(i, j, k) dan c0, c1, c2, c3 ∈C(1,I)o, (III.22)
yang memenuhi pers.(III.2), (III.3), (III.4) dan (III.5), dengana∈C, serta dipenuhinya
syarat berikut
[I, i] = [I, j] = [I, k] = 0. (III.23)
Karena perkalian sembarang dua buah bilangan kompleks bersifat komutatif, maka definisi perkalian dalam Grassmann dan perkalian luar Grassmann dalam al-jabar kuaternion kompleks serupa seperti yang diberikan dalam alal-jabar kuaternion real, yakni pada pers.(III.13) dam (III.14).
Untuk kuaternion kompleks terdapat banyak kemungkinan dalam mendefin-isikan operasi konjugasi. Tiga macam di antaranya diberikan sebagai berikut:
1. Konjugat kompleksunsurqc adalah
Dibawah operasi ini
(I, i, j, k) → (−I, i, j, k), (III.25)
dan
(qcpc)∗ =qc∗pc∗. (III.26)
2. Konjugat kuaternionunsurqcadalah
qc⋆ =c0−ic1−jc2−kc3. (III.27)
Dibawah operasi ini
(I, i, j, k) → (I,−i,−j,−k), (III.28)
dan
(qcpc)⋆ =pc⋆qc⋆. (III.29)
3. Konjugat keseluruhan (dengan mengkombinasi operasi-operasi tersebut di atas)
qc† =c0∗−ic1∗−jc2∗−kc3∗. (III.30)
Dibawah operasi ini
(I, i, j, k) → −(I, i, j, k), (III.31)
dan
Dari berbagai operasi konjugasi yang mungkin dalam aljabar kuaternion kom-pleks, hanya bentuk konjugasi dalam pers.(III.27) yang jika dikalikan denganqcakan
selalu menghasilkan kuaternion kompleks yang bagian imajinernya sama dengan nol. Sehingganormadariqcdapat diberikan oleh
N(qc) =N(c0+c1i+c2j +c3k) =c0c0−c1c1 −c2c2−c3c3, (III.33)
daninversperkalian dariqc diberikan oleh
(qc)−1 =
qc⋆
qcqc⋆
IV.1 Operator-OperatorR,C,H-Linear Kanan
Berkaitan dengan sifat alamiah tak komutatif dari kuaternion, maka harus dibedakan antara aksi kiri dan aksi kanan dari satuan imajiner i, j, k pada objek ku-aternion real q. Untuk menyatakan aksi kiri dan aksi kanan dari satuan-satuan ima-jiner kuaternion, diperkenalkan operator-operator
Lµ ≡(1, ~L), L~ = (Li, Lj, Lk), (IV.1)
yang dinamakan sebagai operator kiri, dan
Rµ ≡(1, ~R), R~ = (Ri, Rj, Rk), (IV.2)
yang dinamakan operator kanan yang masing-masing bertindak pada kuaternion q menurut cara sebagai berikut
Lµ:H−→H, Lµq≡hµq∈H
Rµ:H−→H, Rµq≡qhµ ∈H
(IV.3)
denganhµ ≡(1,~h) = (1, i, j, k). Operator-operator ini memenuhi sifat
L2i =L2j =Lk2 =LiLjLk =R2i =R2j =R2k =RkRjRi =−1 (IV.4)
dan kaitan komutasi berikut
[Li, Ri] = 0, [Lj, Rj] = 0, [Lk, Rk] = 0. (IV.5)
Selain itu diperkenalkan pulaoperator halang(barred operator) yang didefinisikan sebagai operator yang berbentukA|B dan bekerja padaq∈Hmenurut
(A|B)q≡AqB, A, B, q∈H. (IV.6)
Selain dengan menggunakan notasi operator halang, aksi kiri dan kanan secara sekali-gus dari satuan-satuan imajiner kuaternion akan dinyatakan juga dengan
Mµν ≡Lµ⊗Rν,
Mµνq ≡(Lµ⊗Rν)q=hµqhµ.
(IV.7)
Selanjutnya, didefinisikan himpunan-himpunan berikut ini
HL ≡ {aµLµ|aµ∈R} HR ≡ {bµRµ|bµ∈R}
HL⊗HR ≡ {aµνLµ⊗Rν|aµν ∈R}.
(IV.8)
Dari definisi terakhir, diperoleh bahwa
HL ∼= HL⊗ {1} HR ∼= {1} ⊗HR.
(IV.9)
Kemudian, didefinisikan operasi penjumlahan diHL⊗HRsebagai
dan operasi perkalian dengan setiapa ∈Rsebagai
a(aµνLµ⊗Rν)q = (aaµνLµ⊗Rν)q. (IV.11)
Dari sini, dapat diperoleh bahwaHL ⊗HR merupakan ruang vektor berdimensi 16
di atasR. Sedangkan HL maupunHRmerupakan ruang vektor berdimensi 4 di atas R. Himpunan{Lµ⊗Rν}dapat berperan sebagai basis diHL⊗HR, sedangkan{Lµ}
dan{Rν}masing-masing dapat digunakan sebagai basis diHLdanHR.
Selanjutnya, untuk kesederhanaan, diperkenalkan notasi
OX:H−→H (IV.12)
untuk menyatakan unsur-unsur diHL⊗HRyang linear dari kanan terhadap lapangan X. Dari sini, makaORdiHL⊗HRyang berbentuk
OR=aµνLµ⊗Rν ∈HL⊗HR (IV.13)
merupakan operator-operator yangR-linear dari kanan karena dipenuhi
Mµν(qρ) = (Mµνq)ρ =ρ(Mµνq), ρ∈R. (IV.14)
Himpunan semua OR seperti dalam pers.(IV.13) jelas merupakan HL ⊗ HR. Jika
X=C, makaOCdiHL⊗HRberbentuk
OC =aµnLµ⊗Rn, n= 0,1 (IV.15)
karena dipenuhi
Himpunan semua O seperti pada pers.(IV.15) akan dinyatakan sebagai HL ⊗CR.
Kemudian karena perkalian kuaternion bersifat asosiatif, makaOHyang didefinisikan
sebagai
OH =aµLµ∈HL, (IV.17)
merupakan operator yang linear kanan terhadapHdiHkarena berlaku
Lµ(q1q2) = (Lµq1)q2, q1, q2 ∈H. (IV.18)
Untuk definisi terakhir ini telah digunakan penyalahgunaan notasi karena H bukan
merupakan lapangan. Dari sini dapat disimpulkan bahwa
HL ⊂HL⊗CR⊂HL⊗RR. (IV.19)
Dengan menggunakan notasi operator halangOR,OC danOH masing-masing dapat
dinyatakan sebagai
OR =q0+q1|i+q2|j +q3|k
OC =q0+q1|i
OH =q
(IV.20)
denganq, q0, q1, q2, q3 ∈HR.
IV.2 Operasi Konjugasi,TransposedanTrace
Hasil kali langsung dua operatorR-linear dari kanan
ORa =a
µνM
µν, dan ORb =b
τ σM