PENYELESAIAN MASALAH OPTIMASI LINEAR MENGGUNAKAN
METODE TITIK-INTERIOR PRIMAL-DUAL
DENGAN LANGKAH NEWTON-PENUH
BRAMMANTO PRATAMA BASKARA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
BRAMMANTO PRATAMA BASKARA. Penyelesaian Masalah Optimasi Linear Menggunakan Metode Titik-Interior Primal-Dual dengan Langkah Newton-Penuh. Dibimbing oleh BIB PARUHUM SILALAHI dan FARIDA HANUM.
Optimasi adalah suatu ilmu dari matematika terapan yang mempelajari masalah-masalah dengan tujuan mencari nilai maksimum atau minimum dari suatu fungsi yang memenuhi kendala-kendala. Sedangkan optimasi linear khusus mempelajari hal-hal yang berkaitan dengan memaksimumkan atau meminimumkan fungsi linear dengan kendala linear. Salah satu cara penyelesaian masalah optimasi linear adalah dengan menggunakan metode-metode titik-interior. Terdapat beberapa variasi dari metode titik-interior, dalam karya ilmiah ini dibahas mengenai metode titik-interior primal-dual dengan langkah Newton-penuh. Metode ini mengikuti suatu lintasan yang disebut dengan central path. Pergerakan central path akan dianalisis berdasarkan metode ini dan diimplementasikan dengan MATLAB. Dari hasil simulasi yang dilakukan, central path mendekati solusi optimal dari masalah optimasi linear.
Kata Kunci: central path, langkah Newton-penuh, metode titik-interior, optimasi linear, masalah primal-dual.
ABSTRACT
BRAMMANTO PRATAMA BASKARA. Linear Optimization Problem Solving Using Primal-Dual Interior-Point Method with Full-Newton Steps. Supervised by BIB PARUHUM SILALAHI and FARIDA HANUM.
Optimization is a branch of applied mathematics, which studies problems in order to find the maximum or minimum value of a function that satisfies certain constraints. Especially, a linear optimization studies things that maximizes or minimizes a linear function with linear constraints. One of the ways for solving linear optimization problems is by using interior-point method. There are several variations of the point method, but the aim this paper is to discuss the interior-point method with primal-dual full-Newton steps. This method follows a guideline called the central path. The movement of the central path are analyzed by this method and implemented with MATLAB. Simulation result shows that the central path approaches the optimal solution of a linear optimization problem.
Keywords: central path, full-Newton steps, interior-point method, linear optimization, primal-dual problems.
PENYELESAIAN MASALAH OPTIMASI LINEAR MENGGUNAKAN
METODE TITIK-INTERIOR PRIMAL-DUAL
DENGAN LANGKAH NEWTON-PENUH
BRAMMANTO PRATAMA BASKARA
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi : Penyelesaian Masalah Optimasi Linear Menggunakan Metode
Titik-Interior Primal-Dual dengan Langkah Newton-Penuh
Nama
: Brammanto Pratama Baskara
NIM
: G54080056
Menyetujui
Pembimbing I,
Dr. Ir. Bib Paruhum Silalahi, M.Kom.
NIP: 19670101 199203 1 004
Pembimbing II,
Dra. Farida Hanum, M.Si.
NIP: 19651019 199103 2 002
Mengetahui:
Ketua Departemen,
Dr. Berlian Setiawaty, M.S.
NIP: 19650505 198903 2 004
Tanggal Lulus :
KATA PENGANTAR
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala rahmat dan karunia-Nya serta selawat dan salam kepada Nabi Muhammad SAW sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini tidak lepas dari peranan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang setinggi-tingginya kepada:
1. Keluargaku tersayang: Bunda Neneng Suprihatin dan Ayah Dwi Heriyanto (terima kasih atas doa, cinta yang tulus, dukungan, kesabaran, dan kepercayaannya), ketiga adikku (terima kasih atas doa, dukungan, dan motivasinya), serta keluarga besar baik dari Bunda maupun Ayah (terima kasih atas doanya),
2. Para donatur dan staf program beasiswa Yayasan Karya Salemba Empat, terima kasih atas doa, motivasi, dan bantuan finansial selama perkuliahan,
3. Dr. Ir. Bib Paruhum Silalahi, M.Kom.selaku dosen pembimbing I yang telah mencurahkan segala ilmu, motivasi, kesabaran, dan bantuannya untuk menyelesaikan karya ilmiah ini, 4. Dra. Farida Hanum, M.Si. selaku dosen pembimbing II (terima kasih atas ilmu, kesabaran,
kritik, saran, dan dukungannya),
5. Dr. Ir. Fahren Bukhari, M.Sc.selaku penguji (terima kasih atas dorongan semangat, ilmu, dan sarannya),
6. segenap dosen Departemen Matematika: Bu Anggi, Pak Kutha, Pak Wayan, Pak Amril, Pak Prapto, Pak Jahar, Bu Endar, Bu Sri, dan lainnya (terima kasih atas semua ilmu yang telah diberikan),
7. staf Departemen Matematika: Pak Yono, Bu Susi, Mas Heri, Alm. Pak Bono, Bu Ade, Pak Deni, dan lainnya (terima kasih atas bantuan dan motivasinya),
8. kakak-kakak Matematika angkatan 42, 43, dan 44 yang memberikan inspirasi untuk menjadi pribadi yang lebih baik,
9. teman-teman seperjuangan, Matematika angkatan 45: Haya, Irwan, Rini, Arbi, Ari, Chastro, Dimas, Dini, Dono, Fenny, Fikri, Tiwi, Fina, Fuka, Haryanto, Herlan, Heru, Ijun, Irma, Khafidz, Kunedi, Mega, Prama, Rian, Ridwan, Roni, Yunda, dan yang lainnya yang selalu mengisi semangat,
10. adik-adik Matematika angkatan 46, 47, dan 48 yang terus mendukung agar berkembang, 11. Gugus Mahasiswa Matematika (Gumatika) yang memberikan pengalaman baru, 12. dan semua pihak yang membantu dalam penyusunan skripsi ini.
Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan khususnya matematika dan menjadi inspirasi bagi penelitian-penelitian selanjutnya.
Bogor, Maret 2013
RIWAYAT HIDUP
Penulis dilahirkan di Bogor pada tanggal 5 Desember 1989 dari pasangan Bapak Dwi Heriyanto dan Ibu Neneng Suprihatin. Penulis merupakan putra pertama dari empat bersaudara.
Tahun 2002 penulis lulus dari SD Negeri Polisi 5 Bogor, tahun 2005 lulus dari SMP Negeri 7 Bogor, tahun 2008 penulis lulus dari SMA Negeri 5 Bogor, dan pada tahun yang sama diterima sebagai mahasiswa IPB melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis memilih mayor Matematika minor Kewirausahaan Agribisnis, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Pengantar Metode Komputasi (S1) pada semester ganjil tahun akademik 2010-2011, 2011-2012, dan 2012-2013 serta asisten mata kuliah Pemrograman Linear (S1) pada semester genap tahun akademik 2010-2011. Pada tahun 2010-2013 penulis mendapatkan beasiswa dari Yayasan Karya Salemba Empat.
Penulis aktif dalam berbagai kegiatan kemahasiswaan. Penulis pernah menjabat sebagai Sekretaris Umum di Himpunan Profesi Gugus Mahasiswa Matematika (Gumatika) Institut Pertanian Bogor pada tahun 2010-2011. Pada tahun 2011-2012 penulis menjabat sebagai Staf Divisi Forum Silaturahmi Civitas Matematika di Gumatika. Penulis pernah menjadi tutor Wolfram
Mathematica untuk semifinalis Matematika-Ria Pesta Sains 2011. Penulis juga pernah menjadi
DAFTAR ISI
Halaman DAFTAR GAMBAR ... ix DAFTAR LAMPIRAN ... ix I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan Penelitian ... 1 II TINJAUAN PUSTAKA 2.1 Maksimum dan Minimum Lokal ... 22.2 Metode Pengali Lagrange ... 2
2.3 Metode Newton ... 2
2.4 Aljabar Linear ... 3
2.5 Matriks ... 5
2.6 Matriks Diagonal ... 5
2.7 Sistem Persamaan Linear ... 5
2.8 Ortogonalitas ... 6
2.9 Optimasi Linear ... 6
2.10 Bentuk Standar Primal dan Bentuk Standar Dual ... 7
III HASIL DAN PEMBAHASAN 3.1 Pendekatan Barrier dan Kondisi Fisibel Titik-Interior ... 7
3.2 Central Path ... 9
3.3 Langkah Newton-Penuh ... 10
3.4 Transformasi Vektor , dan ke Vektor dan dalam Sistem (3.5) ... 11
3.5 Langkah Newton-Penuh dari Titik di Daerah Fisibel ke -center ... 12
3.6 Algoritme untuk Metode Titik-Interior Primal-Dual ... 13
IV APLIKASI DAN IMPLEMENTASI ... 14
V SIMPULAN DAN SARAN 5.1 Simpulan ... 16
5.2 Saran ... 16
DAFTAR PUSTAKA ... 16
LAMPIRAN ... 17
DAFTAR GAMBAR
Halaman
1 Central path ... 7
2 Pola titik di sekitar central path ketika dari contoh kasus ke-1 ... 14
3 Pola titik di sekitar central path ketika dari contoh kasus ke-1 ... 14
4 Pola titik di sekitar central path ketika dari contoh kasus ke-1 ... 14
5 Pola titik di sekitar central path ketika dari contoh kasus ke-2 ... 15
6 Pola titik di sekitar central path ketika dari contoh kasus ke-2 ... 15
7 Pola titik di sekitar central path ketika dari contoh kasus ke-2 ... 15
DAFTAR LAMPIRAN
Halaman 1 Transformasi Persamaan (10) menjadi Persamaan (11)... 182 Transformasi Sistem (3.5) menjadi Sistem (3.7) ... 18
3 Penentuan Solusi , , dan ... 21
4 Program MATLAB untuk contoh kasus ke-1 ... 23
5 Program MATLAB untuk contoh kasus ke-2 ... 25
6 Program MATLAB untuk Newton_step ... 27
I PENDAHULUAN
1.1 Latar BelakangOptimasi adalah suatu bidang dari matematika terapan yang mempelajari masalah-masalah yang bertujuan mencari nilai minimum atau maksimum suatu fungsi, dengan memenuhi kendala-kendala yang ada.
Optimasi linear khusus mempelajari hal-hal yang berkaitan dengan meminimumkan atau memaksimumkan fungsi-fungsi linear, dengan kendala yang juga linear (berupa persamaan atau pertidaksamaan).
Optimasi linear muncul menjadi suatu model matematika pada situasi perang dunia II, ketika Dantzig (1947) mengajukan penggunaan metode simpleks untuk menyelesaikan masalah pemrograman linear. Saat itu kata pemrograman tidak berarti penulisan program komputer, seperti penggunaan secara umum kata pemrograman saat ini. Untuk menghindarkan kerancuan, pada saat ini makin banyak orang yang lebih senang menggunakan kata optimasi daripada pemrograman (Silalahi 2011). Sebuah organisasi dalam bidang matematika optimasi, Mathematical Programming Society, sekarang telah berubah nama menjadi Mathematical Optimization Society.
Daerah fisibel dari masalah optimasi linear adalah suatu polihedron. Metode simpleks bergerak dari verteks ke verteks untuk memperoleh solusi optimal. Metode ini dirancang sedemikian rupa sehingga nilai dari fungsi objektif berubah secara monoton ke arah nilai optimal. Penemuan Dantzig telah menginspirasi banyak penelitian dalam matematika, khususnya bidang optimasi. Metode simpleks merupakan suatu algoritme yang efisien untuk menyelesaikan masalah optimasi linear (Nematollahi & Terlaky 2008). Terdapat banyak variasi dari metode simpleks. Variasi-variasi tersebut dibedakan oleh aturan untuk memilih verteks yang akan dikunjungi yang biasa disebut aturan pivot.
Keefisienan metode simpleks untuk menyelesaikan banyak problem optimasi linear, memunculkan pertanyaan saat itu: apakah ada masalah optimasi linear yang memerlukan iterasi yang eksponensial bila diselesaikan dengan metode simpleks. Per-tanyaan ini dijawab oleh Klee dan Minty pada tahun 1972, dengan memberikan suatu contoh masalah optimasi linear yang memiliki
pertidaksamaan dan memerlukan iterasi (Silalahi 2011). Hal ini memacu penelitian-penelitian untuk menemukan algoritme optimasi linear yang memerlukan iterasi yang polinomial (Silalahi 2011).
Metode elipsoid yang diusulkan oleh Khachiyan pada tahun 1979 dapat menyelesaikan masalah optimasi linear dengan kompleksitas polinomial. Meskipun metode elipsoid memiliki kompleksitas polinomial, namun dalam penerapan secara komputasi metode ini tidak efisien. Kekonvergenan metode ini lebih lambat dari metode simpleks (Silalahi 2011).
Metode proyektif yang dipaparkan oleh Karmarkar pada tahun 1984 dapat menyelesaikan masalah optimasi linear dengan kompleksitas yang lebih efisien daripada metode elipsoid. Metode proyektif Karmarkar memulai revolusi dalam bidang optimasi karena memunculkan sesuatu yang disebut interior-point methods (metode– metode titik-interior). Berbeda dengan metode simpleks yang bergerak dari verteks ke verteks, metode–metode titik-interior bergerak di interior dari domain untuk menemukan nilai optimal (Silalahi 2011). Ada beberapa variasi dari metode titik-interior, di antaranya metode path-following, dengan penentuan solusi optimal menggunakan central path.
Dalam karya ilmiah ini akan dibahas algoritme primal-dual Newton-penuh dengan central path untuk menentukan solusi optimal dari masalah optimasi linear. Sumber utama karya ilmiah ini adalah buku berjudul Interior Point Methods for Linear Optimization (Roos et al. 2006).
1.2 Tujuan Penelitian
Tujuan dari karya ilmiah ini ialah sebagai berikut:
1. menjelaskan dan mengonstruksi kembali langkah Newton-penuh pada metode titik-interior primal-dual,
2. menganalisis pergerakan central path terhadap masalah optimasi linear berdasarkan metode titik-interior primal-dual dengan ..langkah-lnNewton-penuh dan mengimplementasikannya dengan MATLAB...
II TINJAUAN PUSTAKA
2.1 Maksimum dan Minimum LokalSalah satu penggunaan turunan adalah penentuan nilai maksimum dan minimum dari suatu fungsi. Pada subbab ini, turunan parsial akan digunakan untuk menentukan nilai maksimum dan nilai minimum dari fungsi dua variabel. Misalkan fungsi adalah fungsi dua variabel yang memuat variabel dan . Andaikan nilai variabel berubah-ubah sedangkan nilai variabel tetap, dapat dikatakan dengan adalah konstanta sehingga fungsi dapat dipandang sebagai fungsi dengan variabel tunggal , yaitu ( ) ( ). Andaikan juga fungsi mempunyai turunan di sehingga dapat dinotasikan ( ) ( ) yang berarti turunan parsial dari terhadap di ( ). Definisi 1 (Maksimum Lokal)
Fungsi dua variabel mempunyai maksi-mum lokal di ( ) jika ( ) ( ) ketika ( ) dekat ( ) untuk semua titik ( ) di dalam suatu cakram dengan pusat ( ).
(Stewart 2000) Definisi 2 (Minimum Lokal)
Fungsi dua variabel mempunyai minimum lokal di ( ) jika ( ) ( ) ketika ( ) dekat ( ) untuk semua titik ( ) di dalam suatu cakram dengan pusat ( ).
(Stewart 2000) Teorema 1
Jika mempunyai maksimum atau minimum lokal di ( ) dan turunan parsial orde pertama dari ada di ( ) maka
( ) dan ( ) .
(Stewart 2000) Teorema 2 (Uji Turunan Kedua)
Misalkan turunan parsial kedua dari kontinu pada cakram dengan pusat ( ) serta
( ) dan ( ) . Misalkan ( ) ( ) ( ) ( ( )) 1. Jika ( ) dengan ( )
maka ( ) adalah nilai minimum lokal. 2. Jika ( ) dengan ( )
maka ( ) adalah nilai maksimum lokal.
3. Jika ( ) maka ( ) bukan nilai maksimum lokal atau nilai minimum lokal. (Stewart 2000)
2.2 Metode Pengali Lagrange
Metode pengali Lagrange adalah suatu prosedur untuk menentukan maksimum atau minimum fungsi objektif terhadap kendala persamaan. Misalkan diberikan masalah pengoptimuman sebagai berikut
maks ( )
terhadap ( ) ,
dengan ( ) dan ( ) adalah fungsi dari vektor berukuran .
Fungsi Lagrange dari masalah ini ialah ( ) ( ) ∑ ( )
dengan variabel adalah pengali Lagrange. Syarat perlu untuk titik stasioner dari ( ) adalah turunan parsial pertama dari fungsi Lagrange sama dengan nol
(Jensen & Bard 2002) 2.3 Metode Newton
Metode Newton adalah salah satu prosedur iteratif untuk menyelesaikan masalah tak-linear. Misalkan persamaan ( ) adalah persamaan taklinear dengan merupakan penyelesaian dari persamaan tersebut. Fungsi adalah fungsi yang kontinu dan terturunkan. Pada solusi eksak , nilai fungsi dapat dinyatakan sebagai ( ) dan nilai dari fungsi turunan pertama adalah ( ). Nilai adalah solusi yang diperoleh pada iterasi . Misalkan ( ), turunan dapat diartikan sebagai laju perubahan terhadap . Andaikan berubah dari ke maka perubahan pada adalah . Perubahan ini diperlukan untuk mengubah nilai fungsi menuju nol. Selanjutnya, metode Newton dapat diturunkan dari ekspansi deret Taylor orde pertama dari ( ) di sekitar , sebagai berikut
( ) ( ) ( ) ( ) sehingga
( ) ( ) ( )
Tetapkan pendekatan ( ) sama dengan 0 sehingga didapat
3
( ) ( )
Titik adalah solusi pendekatan fungsi ( ). Jika titik awal cukup dekat dengan maka nilai dari akan mendekati
dengan .
Metode Newton dapat juga digunakan untuk mengubah bentuk suatu fungsi taklinear menjadi bentuk fungsi linear dari fungsi multivariabel. Misalkan persamaan ( ) adalah persamaan taklinear dengan vektor dari persamaan multivariabel tersebut dan matriks Jacobi pada dinyatakan sebagai berikut ( ) ( ) kemudian dengan menggunakan deret Taylor orde pertama di sekitar titik dan dengan menetapkan ( ) diperoleh
( ) ( ) ( ) ( ) ( )
dengan dan . Titik adalah solusi pendekatan fungsi ( ). Jika titik cukup dekat dengan titik maka nilai dari akan mendekati dengan (Jensen & Bard 2002). Contoh 1
Diketahui suatu fungsi taklinear ( ) dengan hampiran awal . Metode Newton dapat digunakan untuk mengubah bentuk fungsi taklinear menjadi fungsi linear sebagai berikut ( ) ( ) ( ) dengan ( ) ( ) dan ( ) saat sehingga diperoleh ( ) ( ) ( ) ( )
Jadi fungsi taklinear dapat diubah menjadi fungsi linear .
2.4 Aljabar Linear Definisi 3 (Ruang Vektor)
Misalkan adalah himpunan dengan pendefinisian operasi penjumlahan dan operasi perkalian dengan skalar. Setiap pasangan elemen dan di dalam terdapat suatu elemen yang tunggal juga berada di dalam serta setiap elemen di dalam dan setiap skalar terdapat yang tunggal juga berada di dalam . Himpunan dengan operasi penjumlahan dan operasi perkalian dengan skalar ini dinamakan ruang vektor jika memenuhi aksioma berikut
1. , .
2. ( ) ( ), . 3. Terdapat sehingga
( ), .
4. Untuk setiap , terdapat ( ) sehingga ( ) . 5. ( ) , dan skalar . 6. ( ) , dan skalar serta skalar . 7. ( ) ( ), dengan skalar dan skalar . 8. , .
Elemen dalam adalah vektor sedangkan simbol menyatakan vektor nol.
(Leon 1998) Contoh 2
Misalkan dengan menyatakan himpunan vektor berukuran dengan entri bilangan real. Misalkan vektor
[ ], [ ] elemen dari . Didefinisikan operasi penjumlahan
4 [ ] dan operasi perkalian dengan skalar
[ ] [
] maka himpunan adalah ruang vektor. Contoh 3
Misalkan menyatakan himpunan matriks berukuran dengan entri bilangan real. Misalkan matriks , dengan [ ] [ ] Didefinisikan operasi penjumlahan
[ ] dan operasi perkalian dengan skalar
[
] maka himpunan adalah ruang vektor. Definisi 4 (Ruang Bagian)
Jika adalah himpunan bagian takkosong dari suatu ruang vektor dan memenuhi syarat-syarat berikut
1. jika untuk sembarang skalar ,
2. jika dan , maka disebut ruang bagian dari .
(Leon 1998) Definisi 5 (Kombinasi Linear)
Misalkan adalah vektor-vektor dalam suatu ruang vektor-vektor . Jumlah vektor-vektor yang berbentuk
dengan skalar-skalar disebut kombinasi linear dari .
(Leon 1998)
Definisi 6 (Rentang)
Misalkan adalah vektor-vektor dalam suatu ruang vektor-vektor . Himpunan semua kombinasi linear dari disebut rentang (span) dari vektor-vektor
yang dituliskan sebagai Rentang ( ).
(Leon 1998) Definisi 7 (Himpunan Perentang)
Himpunan { } disebut himpunan perentang untuk jika dan hanya jika setiap vektor dalam dapat ditulis sebagai kombinasi linear dari . (Leon 1998) Definisi 8 (Bebas Linear)
Vektor-vektor dalam ruang vektor disebut bebas linear jika
mengakibatkan semua skalar-skalar
harus sama dengan nol. (Leon 1998) Definisi 9 (Basis)
Vektor-vektor mem-bentuk basis untuk ruang vektor jika dan hanya jika
1. bebas linear, 2. merentang .
(Leon 1998) Definisi 10 (Dimensi)
Misalkan adalah ruang vektor. Jika memiliki basis yang terdiri atas vektor, maka dikatakan memiliki dimensi .
(Leon 1998) Definisi 11 (Ruang Baris)
Misalkan matriks berukuran dan diketahui ruang vektor menyatakan himpunan semua vektor berukuran dengan entri bilangan real. Ruang bagian dari yang direntang oleh vektor-vektor baris dari disebut ruang baris dari .
(Leon 1998) Definisi 12 (Pangkat)
Pangkat dari matriks adalah dimensi dari ruang baris .
5
Definisi 13 (Pangkat Penuh dan Pangkat Baris Penuh)
Pangkat penuh dari suatu matriks dengan baris dan kolom adalah ( ) sedangkan pangkat baris penuh dari matriks adalah .
(Leon 1998) 2.5 Matriks
Definisi 14 (Matriks Identitas)
Matriks identitas adalah matriks ( ) yang berukuran , dengan
{
(Leon 1998) Definisi 15 (Invers dari Suatu Matriks)
Suatu matriks yang berukuran dikatakan taksingular jika terdapat matriks sehingga . Matriks dikatakan invers multiplikatif dari matriks . Invers multiplikatif dari matriks taksingular secara sederhana disebut juga sebagai invers dari matriks dan dinotasikan dengan .
(Leon 1998) Definisi 16 (Transpos dari suatu Matriks)
Transpos dari suatu matriks ( ) yang berukuran adalah matriks ( ) yang berukuran yang didefinisikan oleh
untuk setiap dan . Transpos dari dinotasikan oleh .
(Leon 1998) Definisi 17 (Matriks Simetris)
Suatu matriks berukuran disebut matriks simetris jika .
(Leon 1998) 2.6 Matriks Diagonal
Matriks diagonal adalah matriks berukuran yang semua unsur selain diagonal utama ialah nol. Matriks diagonal berukuran dapat ditulis sebagai
[ ]
dengan , , , disebut unsur diagonal utama. Matriks diagonal memiliki invers yang dapat dinyatakan sebagai
( )
dengan semua unsur diagonal utama adalah taknol sehingga . Matriks dapat dikatakan matriks simetris karena
(Anton & Rorres 2005). 2.7 Sistem Persamaan Linear Definisi 18 (Persamaan Linear)
Suatu persamaan linear dalam variabel adalah persamaan dengan bentuk
dengan , , …, , dan adalah bilangan-bilangan real dan , , …, adalah variabel.
(Leon 1998) Definisi 19 (Sistem Persamaan Linear)
Suatu sistem persamaan linear (SPL) dari persamaan dalam variabel adalah suatu sistem berbentuk dengan dan ( , ) adalah bilangan-bilangan real dan , , …, adalah variabel. SPL tersebut disebut sebagai SPL berukuran .
Penyelesaian SPL berukuran adalah sebuah vektor kolom berukuran , yaitu
[ ],
yang memenuhi semua persamaan linear dalam sistem. Vektor yang demikian disebut sebagai vektor penyelesaian.
(Leon 1998) Selain itu, SPL berukuran tersebut juga dapat ditulis dalam bentuk
dengan matriks dan vektor kolom (masing-masing berukuran dan ) adalah
6 [ ] [ ]
Matriks disebut sebagai matriks koefisien, sedangkan vektor kolom disebut sebagai vektor konstanta.
(Leon 1998) Definisi 20 (Kekonsistenan suatu Sistem
Persamaan Linear)
Suatu SPL dikatakan konsisten jika mempunyai paling sedikit satu penyelesaian, sedangkan suatu SPL yang tidak mempunyai penyelesaian dikatakan takkonsisten.
(Leon 1998) 2.8 Ortogonalitas
Definisi 21 (Hasil Kali Skalar di ) Misalkan dengan
[ ] [ ] maka hasil kali skalar dari dan adalah
(Leon 1998) Definisi 22 (Hasil Kali Hadamard)
Diketahui dan adalah ruang vektor. Vektor dan matriks
. Jika dan didefinisikan sebagai
[ ] [ ]
dan ( ) adalah matriks diagonal dengan unsur diagonal utama ialah elemen vektor sehingga
( ) [ ]
( ) [ ]
maka hasil kali Hadamard dari dan adalah
Dengan perkataan lain, hasil kali Hadamard adalah perkalian antara unsur dengan unsur yang seletak (componentwise) dari dua buah vektor yang berukuran sama. Selanjutnya dalam karya ilmiah ini, hasil kali Hadamard dinotasikan sebagai (Roos et al. 2006).
Contoh 4 (Hasil Kali Hadamard)
Misalkan serta dengan [ ], [ ], ( ), ( ). Hasil kali Hadamard dari dan dinyatakan sebagai
[ ] [ ] [ ] [ ] [ ] [ ] . Dapat juga ditulis sebagai berikut
[ ] [ ] [ ] [ ] [ ] [ ]
Definisi 23 (Norm dari suatu Vektor di ) Misalkan dengan
[ ]
maka norm dari vektor di adalah ‖ ‖ √ √
(Leon 1998) 2.9 Optimasi Linear
Optimasi adalah suatu bidang dari matematika terapan yang mempelajari masalah-masalah yang bertujuan mencari nilai minimum atau maksimum suatu fungsi, dengan memenuhi kendala-kendala yang ada.
Optimasi linear khusus mempelajari hal-hal yang berkaitan dengan meminimumkan atau memaksimumkan fungsi-fungsi linear, dengan kendala yang juga linear (berupa persamaan atau pertidaksamaan).
7
Definisi 24 (Daerah Fisibel)
Daerah fisibel dari masalah optimasi linear adalah himpunan titik-titik yang memenuhi semua kendala dan pembatasan tanda pada optimasi linear tersebut.
(Winston 2004) Definisi 25 (Solusi Optimal)
Untuk masalah maksimisasi, solusi optimal pada optimasi linear adalah suatu titik pada daerah fisibel dengan nilai fungsi objektif paling besar sedangkan untuk masalah minimisasi, solusi optimal pada optimasi linear adalah suatu titik pada daerah fisibel dengan nilai fungsi objektif paling kecil.
(Winston 2004) 2.10 Bentuk Standar Primal dan Bentuk
Standar Dual
Masalah optimasi linear dalam bentuk standar diberikan sebagai berikut
min{ } ( ) dengan vektor , serta adalah matriks berpangkat baris penuh. Masalah ( ) disebut masalah primal.
Masalah dual dari masalah primal ( ) diberikan sebagai berikut
maks { } ( ) dengan dan . Masalah ( ) disebut masalah dual.
Daerah fisibel dari masalah ( ) didefinisi-kan sebagai
{ }
sedangkan daerah fisibel dari ( ) didefinisi-kan sebagai
{( ) } Daerah interior masalah ( ) didefinisikan sebagai berikut
{ }
sedangkan daerah interior dari masalah ( ) didefinisikan sebagai
{( ) } (Silalahi 2011) Proposisi 1 (Dualitas Lemah)
Misalkan adalah solusi fisibel untuk ( ) dan ( ) adalah solusi fisibel untuk ( ) maka . disebut kesenjangan dualitas. Akibatnya, adalah batas atas untuk nilai optimal dari ( ), jika ada, serta adalah batas bawah untuk nilai optimal dari ( ), jika ada. Selanjutnya, jika kesenjangan dualitas adalah nol maka adalah solusi optimal dari ( ) dan ( ) adalah solusi optimal dari ( ).
(Roos et al. 2006) Teorema 3 (Dualitas)
Jika ( ) dan ( ) fisibel maka kedua masalah tersebut mempunyai solusi optimal; kemudian, dan ( ) adalah solusi optimal jika dan hanya jika .
(Roos et al. 2006) Definisi 26 (Central Path)
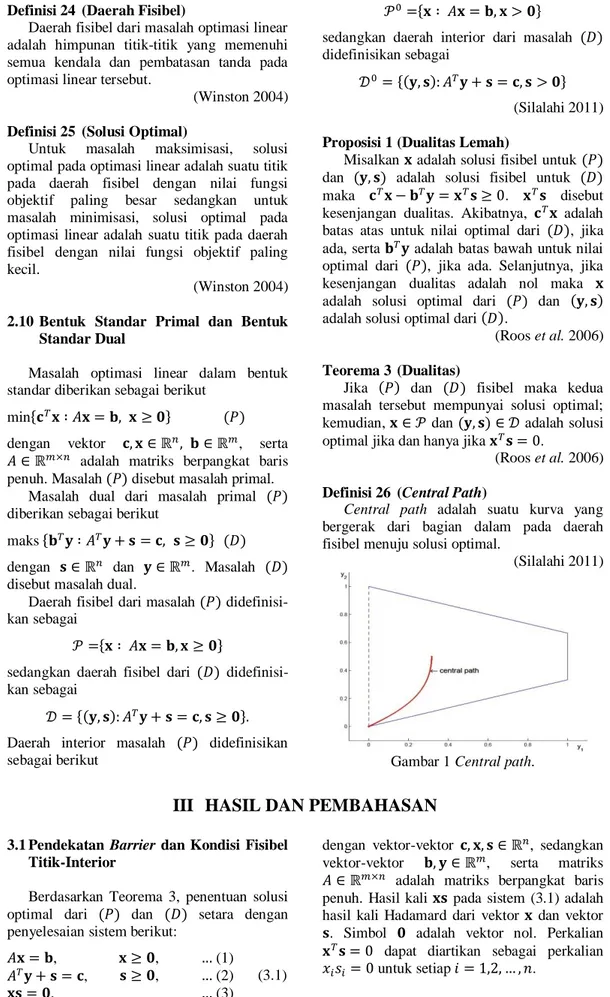
Central path adalah suatu kurva yang bergerak dari bagian dalam pada daerah fisibel menuju solusi optimal.
(Silalahi 2011)
Gambar 1 Central path.
III HASIL DAN PEMBAHASAN
3.1 Pendekatan Barrier dan Kondisi Fisibel Titik-Interior
Berdasarkan Teorema 3, penentuan solusi optimal dari ( ) dan ( ) setara dengan penyelesaian sistem berikut:
, , (1)
, , (2) (3.1)
, (3)
dengan vektor-vektor , sedangkan vektor-vektor , serta matriks adalah matriks berpangkat baris penuh. Hasil kali pada sistem (3.1) adalah hasil kali Hadamard dari vektor dan vektor . Simbol adalah vektor nol. Perkalian dapat diartikan sebagai perkalian
8
Sistem (3.1) adalah kondisi optimal untuk masalah primal-dual. Persamaan (1) pada sistem (3.1) adalah kendala fisibel untuk masalah primal ( ) dan persamaan (2) merupakan kendala fisibel untuk masalah dual ( ). Persamaan (3) dari sistem (3.1) adalah kendala pelengkap. Kendala taknegatif dalam kondisi fisibel membuat penyelesaian dari masalah menjadi taktrivial, hanya metode iteratif yang dapat memperoleh solusi dari sistem linear yang melibatkan kendala pertaksamaan (Silalahi 2011).
Persamaan (3) dari sistem (3.1) merupakan persamaan taklinear sehingga diperlukan suatu pendekatan untuk menentukan solusi agar sistem (3.1) menjadi optimal. Salah satu pendekatan yang dapat digunakan adalah pendekatan barrier. Ide pendekatan barrier diperkenalkan oleh Frisch pada tahun 1955 (Roos et al. 2006). Metode ini bermula dari suatu titik di interior dari pertidaksamaan dan , lalu dikonstruksi barrier sedemikian rupa sehingga variabel tidak menyentuh batas daerah fisibel.
Penambahan ke fungsi objektif merupakan salah satu cara dari pendekatan barrier ini. Penambahan menyebabkan nilai fungsi objektif mengalami kenaikan atau penurunan tanpa batas (apabila atau ). Kesulitan dari ide ini ialah jika titik optimal berada pada batas, misalnya satu atau lebih . Untuk mengatasi kesulitan ini, digunakan parameter untuk menentukan nilai maksimum atau minimum fungsi objektif dari bentuk barrier.
Masalah primal-barrier ditulis sebagai berikut
minimumkan ∑ ( ) terhadap
dan masalah dual-barrier dapat ditulis sebagai berikut
maksimumkan ∑ ( ) terhadap .
Masalah tersebut memiliki fungsi objektif yang taklinear dengan kendala persamaan linear, sehingga dapat diselesaikan dengan metode Lagrange untuk tetap.
Misalkan adalah fungsi Lagrange masalah primal.
∑ ( )
( ) Fungsi diturunkan secara parsial terhadap
dan dengan . Pertama, fungsi diturunkan terhadap dengan ∑ ∑
Kemudian fungsi diturunkan terhadap dengan ∑
Fungsi adalah fungsi Lagrange masalah dual.
∑ ( )
( )
Fungsi diturunkan secara parsial terhadap , , dan dengan . Pertama, fungsi diturunkan terhadap dengan
Selanjutnya fungsi diturunkan terhadap dengan
9
∑
Kemudian fungsi diturunkan terhadap dengan ∑
Variabel dual merupakan pengali Lagrange untuk masalah primal dan variabel primal merupakan pengali Lagrange untuk masalah dual.
Kendala pelengkap diganti menjadi , agar solusi sistem dari sistem yang baru mendekati solusi sistem (3.1), dengan parameter adalah sembarang bilangan positif dan adalah vektor yang semua unsurnya bernilai satu. Kendala ini disebut juga kondisi-pemusat pada (Silalahi 2011).
Dengan demikian, sistem (3.1) menjadi sistem yang baru
, ,
, , (3.2)
, (4)
dengan vektor-vektor , sedangkan vektor-vektor , serta matriks adalah matriks berpangkat baris penuh. Vektor adalah vektor yang semua unsurnya bernilai satu dengan . Sistem ini merupakan kondisi optimal untuk masalah minimisasi (Silalahi 2011).
Jika sistem (3.2) memiliki solusi untuk beberapa nilai positif dari parameter maka daerah fisibel primal mengandung vektor positif, dan daerah fisibel dual mengandung pasangan ( ) dengan vektor positif sehingga daerah fisibel dan daerah fisibel mengandung vektor positif. Hal tersebut merupakan kondisi fisibel titik-interior. Demikian juga sebaliknya, jika daerah fisibel dan mengandung vektor positif maka sistem (3.2) memiliki solusi untuk setiap positif. Hal ini merupakan konsekuensi dari teorema berikut.
Teorema 4
Misalkan . Daerah fisibel dan mengandung vektor positif jika dan hanya jika sistem (3.2) memiliki solusi yang tunggal.
(Roos et al. 2006). 3.2 Central Path
Pada kondisi fisibel titik-interior, sistem (3.2) memiliki solusi tunggal untuk setiap nilai positif dari . Solusi ini dinotasikan sebagai ( ) ( ), dan ( ). Solusi ( ) adalah -center dari ( ) dan solusi ( ( ) ( )) adalah -center dari ( ). Himpunan { ( ) } merupakan suatu kurva di ( ) yang disebut central path dari ( ). Demikian pula dengan himpunan {( ( ) ( )) } merupakan suatu kurva di ( ) yang disebut central path dari ( ) (Silalahi 2011).
Jika maka ( ) ( ( ) ( )) masing-masing konvergen ke analytic center dari ( ) dan ( ).Definisi dari analytic center adalah sebagai berikut.
Definisi 27 (Analytic Center)
Misalkan notasi { ( )} adalah yang memaksimumkan nilai fungsi ( ). Analytic center primal adalah
{ ( ) } sedangkan analytic center dual adalah { ( ) }
(Silalahi 2011) Contoh 5
Misalkan diberikan masalah optimasi linear berikut:
minimumkan
terhadap
Masalah pada Contoh 5 dapat ditulis dalam bentuk standar dual sebagai berikut: maksimumkan
terhadap ...
Penentuan analytic center dual adalah sebagai berikut
{ ( ) } dengan
10 ( ) [ ( ) ( )] {( ) [ ] [ ] [ ] [ ] } sehingga { ( ) } menjadi ( ( ) ( )) dengan ( ) ( ) ( ).
Berdasarkan Teorema 1 untuk menentukan nilai maksimum diperoleh
Titik kritis fungsi adalah ( ). Selanjutnya uji titik kritis dengan uji turunan kedua sebagai berikut
( ) ( )
dan . Kemudian ditentukan ( ) ( ) ( ) ( ( )) . ( ) ( ( ) ( ) ) ( ( ) ( ) ) ( ) ( )( ) lalu ditentukan ( ), ( ) ( ) ( ) sehingga dari Teorema 2 titik ( ) adalah titik maksimum lokal.
Jadi nilai analytic center dual dari Contoh 5 adalah ( ).
3.3 Langkah Newton-Penuh
Langkah Newton-penuh merupakan metode yang dapat digunakan untuk mencari pendekatan penyelesaian sistem (3.2), untuk suatu yang tetap. Misalkan diberikan pasangan solusi fisibel primal-dual ( ( )). Akan didefinisikan, pencarian arah , , dan sehingga ( ) memenuhi (3.2). Dengan perkataan lain, ( ) (5)
( ) ( ) (6) (3.3) ( )( ) (7)
dengan , , , , , , , , dan . Pada persamaan (7) berlaku hasil kali Hadamard. Diketahui dan
. Dari persamaan (5) diperoleh, ( ) Dari persamaan (6), ( ) ( ) Dari persamaan (7),
11
sehingga sistem (3.3) setara dengan
.(8)
.(9) (3.4) (10)
Pada sistem (3.4), persamaan (10) adalah persamaan taklinear karena mengandung bentuk sehingga metode Newton diperlukan untuk mengubah bentuk persamaan (10) menjadi persamaan linear sebagai berikut (penghitungan lengkap lihat Lampiran 1)
Jadi sistem (3.4) dapat ditulis kembali sebagai sistem berikut
(11) (3.5) Sedangkan solusi sistem (3.5) dapat diketahui dari teorema berikut.
Teorema 5 (Solusi Sistem (3.5))
Sistem (3.5) memiliki solusi yang tunggal, yaitu
( ) ( )
(Roos et al. 2006) Solusi , , dan dinamakan arah Newton primal-dual. Dengan mengambil langkah sepanjang arah Newton primal-dual, diperoleh nilai , , dan yang baru dengan notasi , , dan sehingga diperoleh solusi yang baru sebagai berikut
(3.6) Solusi , , dan disebut langkah Newton-penuh.
3.4 Transformasi Vektor , dan ke Vektor dan dalam Sistem (3.5) Pada proses central path menuju solusi optimal, transformasi vektor , dan menjadi dan diperlukan untuk membangkitkan suatu urutan titik dalam lingkungan central path. Dalam melakukan transformasi ini, berlaku hasil kali Hadamard. Sama halnya dengan hasil kali Hadamard, yaitu perkalian unsur dengan unsur yang seletak (componentwise) antara dua vektor, hasil bagi dari dua vektor berukuran sama juga berlaku pembagian unsur dengan unsur
yang seletak (componentwise) antara dua vektor. Sebelum melakukan transformasi pada sistem (3.5), terlebih dahulu akan didefinisikan vektor-vektor , , , dan matriks (√ ⁄ ). Pendefinisian vektor-vektor ini berdasarkan Roos et al. tahun 2006. √ √ ...(12) √ √ √ √ ...(13) √ √ ...(14) Persamaan (12) dapat ditulis sebagai √ √ √
kemudian √ √ disubstitusi ke per-samaan (13), diperoleh √ √ √ √ √ √ √ Misalkan , kemudian substitusi persamaan (12), vektor menjadi
√ √ √ √ Misalkan
√ dinotasikan sebagai vektor . Dengan manipulasi aljabar diperoleh
√ √ √ √
...(15) Persamaan (12) dapat ditulis kembali sebagai
√ √ √
Kemudian √ √ disubstitusi ke per-samaan (13), diperoleh
√ √ √
√
Misalkan , kemudian substitusi persamaan (12), vektor menjadi
√ √ √ √ Misalkan
√ dinotasikan sebagai vektor . Dengan manipulasi aljabar diperoleh
12 √ √ √ √ ...(16) Dari persamaan (8) dengan substitusi persamaan (15) diperoleh
( )
Kemudian substitusi persamaan (13) menjadi
√
Dari persamaan (9) dengan substitusi persamaan (14) dan persamaan (16) diperoleh,
√
√
Kemudian substitusi persamaan (13)menjadi √
√ ( )
Selanjutnya persamaan (11) dengan substitusi persamaan (15) dan persamaan (16) diperoleh,
Lalu substitusi vektor menjadi
√
sehingga sistem (3.5) setara dengan sistem hasil transformasi berikut (bukti Lampiran 2)
( )
(3.7)
3.5 Langkah Newton-Penuh dari Titik di Daerah Fisibel ke -center
Solusi , , dan dapat ditentukan berdasarkan pemisalan berikut.
Misalkan persamaan ketiga pada sistem (3.7) dapat ditulis sebagai (bukti Lampiran 3) ...(17) persamaan (1) dapat ditulis sebagai
...(18) dan persamaan (3) menjadi
...(19) Selanjutnya, akan ditentukan solusi , , dan sebagai berikut.
Dari persamaan (5) diperoleh, ( )
Kemudian substitusi persamaan (18) diperoleh
Lalu substitusi persamaan (15) diperoleh √ √
Dari persamaan (6) diperoleh, ( ) Kemudian substitusi persamaan (19),
√
( ) ...(20) ( )
Selanjutnya substitusi dari persamaan (17) diperoleh ( ) ( ) ( ) ( ) √ ( ( ) ) ( √ ) ...(21) sehingga diperoleh solusi , , dan yang tunggal sebagai berikut
13 √ √ (( ( ) ) ( √ )) ( ) ( ( ) (( ( ) ) ( √ ))) ( ( ) ) ( ( ) (( ( ) ) ( √ )))
Solusi , , dan ini yang akan digunakan dalam algoritme dan program MATLAB pada subbab selanjutnya. Serupa dengan solusi (3.6), sistem solusi (3.8) menggunakan solusi , , dan seperti penurunan langkah Newton-penuh dari titik di daerah fisibel ke -center sehingga diperoleh solusi baru sebagai berikut
(3.8)
Solusi , , dan disebut langkah Newtonpenuh dari titik di daerah fisibel ke -center.
3.6 Algoritme untuk Metode Titik-Interior Primal-Dual
Metode titik-interior primal-dual merupa-kan salah satu metode iteratif untuk menyelesaikan masalah optimasi linear. Proses iterasi pada algoritme untuk metode interior primal-dual menghasilkan titik-titik pada interior daerah fisibel yang akan membentuk central path menuju solusi optimal.
Lema 1
Langkah Newton primal-dual adalah fisibel jika dan hanya jika serta langkah Newton primal-dual adalah fisibel strictly jika dan hanya jika
(Roos et al. 2006) Teorema 6
Jika langkah Newton primal-dual adalah fisibel maka ( ) .
(Roos et al. 2006) Vektor dan merupakan langkah se-panjang arah Newton primal-dual dan adalah banyaknya variabel dari masalah primal-dual.
Sebelum itu, akan diperkenalkan notasi-notasi untuk iterasi-iterasi yang berurutan ini.
Misalkan vektor ( ) adalah titik yang terletak pada daerah fisibel yang dihasilkan saat iterasi ke- . Vektor ( ) dan ( ) adalah titik yang terletak pada daerah fisibel yang dihasilkan saat iterasi ke- . Parameter ( ) adalah bilangan positif yang dihasilkan saat iterasi ke- . , , dan berturut-turut adalah selisih antara ( ) ke ( ), ( ) ke ( ), dan ( ) ke ( ). Simbol dan adalah parameter.
Algoritme atau langkah-langkah untuk mendapatkan solusi optimal dengan metode titik-interior primal-dual adalah sebagai berikut.
Input : Matriks , vektor untuk masalah primal, vektor , vektor untuk masalah dual, ( ) , , dan . Output : Gambar central path, banyaknya
ite-rasi, dan nilai solusi optimal.
Langkah 1. Pilih titik sembarang pada daerah fisibel yang ditandai dengan dan di , di , ( ) positif, , , dan .
Langkah 2. Dengan langkah Newton-penuh untuk ( ) positif. Tentukan ( ) dan ( ) sehingga ( ) ( ) ( ).
Langkah 3. Selama lanjut ke Langkah 4; selainnya, STOP.
Langkah 4. Hitung langkah Newton-penuh pada solusi (3.8)
Langkah 5. Perbarui solusi, ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
Selanjutnya , kembali ke Langkah 3.
14
IV APLIKASI DAN IMPLEMENTASI
Algoritme untuk metode titik-interiorprimal-dual diimplementasikan dengan mem-buat program pada MATLAB. Program MATLAB dari algoritme untuk metode titik-interior primal-dual terdapat pada Lampiran 4, Lampiran 5, dan Lampiran 6. Input dari program ini adalah matriks koefisien dari kendala, vektor pembatas dari kendala, vektor fungsi objektif, titik awal sembarang di interior, dan sembarang nilai , sedangkan outputnya adalah banyak iterasi dan gambar dari central path. Pembangkitan metode titik-interior primal-dual mengguna-kan fasilitas penulisan program M-File pada MATLAB yang telah disediakan oleh Silalahi tahun 2011.
Untuk contoh kasus ke-1, misalkan diberikan masalah optimasi linear berikut: Min
terhadap .
Masalah pada contoh ke-1 dapat juga ditulis dalam bentuk masalah standar dual berikut: Maks
terhadap . Kendala dapat ditulis dalam matriks sebagai
[
] [ ] [ ] [ ]
Lalu inputkan ke dalam program serta titik awal sembarang di interior diberikan [ ] , , dan . Selanjutnya, akan dibandingkan untuk nilai , , dapat dilihat pada Gambar 2, Gambar 3, dan Gambar 4 berikut
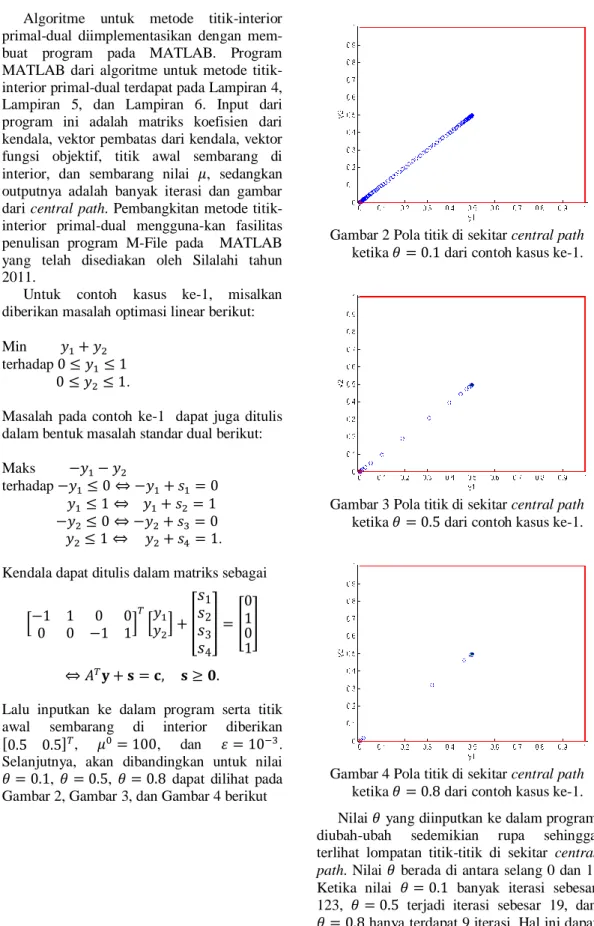
Gambar 2 Pola titik di sekitar central path ketika dari contoh kasus ke-1.
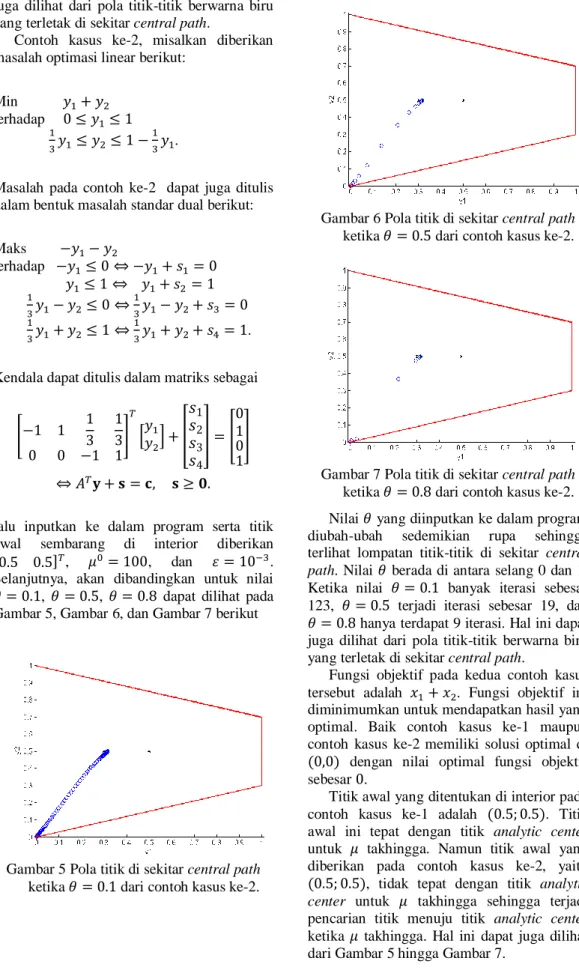
Gambar 3 Pola titik di sekitar central path ketika dari contoh kasus ke-1.
Gambar 4 Pola titik di sekitar central path ketika dari contoh kasus ke-1. Nilai yang diinputkan ke dalam program diubah-ubah sedemikian rupa sehingga terlihat lompatan titik-titik di sekitar central path. Nilai berada di antara selang 0 dan 1. Ketika nilai banyak iterasi sebesar 123, terjadi iterasi sebesar 19, dan hanya terdapat 9 iterasi. Hal ini dapat
15
juga dilihat dari pola titik-titik berwarna biru yang terletak di sekitar central path.
Contoh kasus ke-2, misalkan diberikan masalah optimasi linear berikut:
Min terhadap .
Masalah pada contoh ke-2 dapat juga ditulis dalam bentuk masalah standar dual berikut: Maks
terhadap .
Kendala dapat ditulis dalam matriks sebagai
[
] [ ] [ ] [ ]
lalu inputkan ke dalam program serta titik awal sembarang di interior diberikan [ ] , , dan . Selanjutnya, akan dibandingkan untuk nilai , , dapat dilihat pada Gambar 5, Gambar 6, dan Gambar 7 berikut
Gambar 5 Pola titik di sekitar central path ketika dari contoh kasus ke-2.
Gambar 6 Pola titik di sekitar central path ketika dari contoh kasus ke-2.
Gambar 7 Pola titik di sekitar central path ketika dari contoh kasus ke-2. Nilai yang diinputkan ke dalam program diubah-ubah sedemikian rupa sehingga terlihat lompatan titik-titik di sekitar central path. Nilai berada di antara selang 0 dan 1. Ketika nilai banyak iterasi sebesar 123, terjadi iterasi sebesar 19, dan hanya terdapat 9 iterasi. Hal ini dapat juga dilihat dari pola titik-titik berwarna biru yang terletak di sekitar central path.
Fungsi objektif pada kedua contoh kasus tersebut adalah . Fungsi objektif ini diminimumkan untuk mendapatkan hasil yang optimal. Baik contoh kasus ke-1 maupun contoh kasus ke-2 memiliki solusi optimal di ( ) dengan nilai optimal fungsi objektif sebesar .
Titik awal yang ditentukan di interior pada contoh kasus ke-1 adalah ( ). Titik awal ini tepat dengan titik analytic center untuk takhingga. Namun titik awal yang diberikan pada contoh kasus ke-2, yaitu ( ), tidak tepat dengan titik analytic center untuk takhingga sehingga terjadi pencarian titik menuju titik analytic center ketika takhingga. Hal ini dapat juga dilihat dari Gambar 5 hingga Gambar 7...
16
V SIMPULAN DAN SARAN
5.1 SimpulanMetode titik-interior primal-dual dapat dikonstruksi kembali dengan langkah Newton-penuh. Dengan metode titik-interior primal-dual, solusi optimal diperoleh melalui pergerakan titik di sekitar central path. Nilai yang berbeda akan mengakibatkan pergerakan titik yang berbeda pula di sekitar central path. Ketika nilai mendekati nol, titik di sekitar central path menjadi rapat sedangkan bila
nilai mendekati satu maka titik di sekitar central path menjadi renggang.
5.2 Saran
Untuk penelitian selanjutnya, nilai yang terbaik agar mendapatkan iterasi minimum dapat ditentukan dengan memperhatikan lompatan titik di sekitar central path. Perlu dilakukan analisis algoritme metode titik-interior primal-dual berdasarkan kompleksitas komputasi yang terbaik.
DAFTAR PUSTAKA
Anton H, Rorres C. 2005. Elementary Linear Algebra. Ed ke-9. New Jersey: John Wiley and Sons.
Jensen PA, Bard JF. 2002. Operations Research: Models and Methods. New York: John Wiley and Sons.
Leon SJ. 1998. Linear Algebra with Applications. Ed ke-5. New Jersey: Prentice Hall.
Nematollahi E, Terlaky T. 2008. A Simpler and Tighter Redundant Klee-Minty Construction. Optimization Letters 2(3):403-414.
Roos C, Terlaky T, Vial J-Ph. 2006. Interior Point Methods for Linear Optimization. New York: Springer.
Silalahi BP. 2011. On the Central Path of Redundant Klee-Minty Problems. PhD thesis. Roos C (promotor). Delft University of Technology. The Netherlands: TU Delft.
Stewart J. 2000. Calculus: Concepts and Contexts. Edisi ke-2. California: Brooks/Cole Publishing.
Winston WL. 2004. Operations Research: Applications and Algorithms. Ed ke-4. New York: Duxbury.
18
Lampiran 1
Transformasi Persamaan (10) menjadi Persamaan (11)
Misalkan fungsi taklinear ( ) dengan hampiran awal . Kemudian menggunakan metode Newton sebagi berikut
( ) ( ) ( ) dengan ( ) ( ) dan ( ) untuk , diperoleh ( ) ( ) ( ) ( ) ( ) dengan substitusi diperoleh
( ) ( )
sehingga fungsi taklinear dapat diubah menjadi fungsi linear
Lampiran 2
Transformasi Sistem (3.5) menjadi Sistem (3.7)
√ √ ...(12)
√ √ √
√ ...(13)
√ √ ...(14) Persamaan (12) dapat ditulis sebagai √ √
√ √ √
kemudian √ √ disubstitusi ke persamaan (13), diperoleh √ √ √ √ √ √ √
Misalkan , kemudian substitusi persamaan (12) vektor menjadi √ √ √ √ √ Misalkan
√ dinotasikan sebagai vektor . Dengan manipulasi aljabar diperoleh √ √ √ √ √ √ √
19
Kedua ruas dari persamaan √
√ √ dikalikan √ √ menjadi √ √ √ √ √ √ ...(15) Persamaan (12) dapat ditulis kembali sebagai √ √
√ √ √
kemudian √ √ disubstitusi ke persamaan (13), diperoleh √ √ √ √ √ √ √ Misalkan , kemudian substitusi persamaan (12) vektor menjadi √ √ √ √ √ Misalkan
√ dinotasikan sebagai vektor . Dengan manipulasi aljabar diperoleh √ √ √ √ √ √ √
Kedua ruas dari persamaan √ √
√ dikalikan √ √ menjadi √ √ √ √ √ √ √ √ √ ...(16)
Dari persamaan (8) dengan substitusi persamaan (15) diperoleh
( )
Substitusi persamaan (13) menjadi √ √ √ √ √ √ √ √ √ √ √ √
20
Dari persamaan (9) dengan substitusi persamaan (14) dan persamaan (16) diperoleh,
√
Kedua ruas dari persamaan √ dikalikan menjadi √
Substitusi persamaan (13) menjadi √ √ √ √ ( )
Kemudian persamaan (11) dengan substitusi persamaan (15) dan persamaan (16) diperoleh,
Substitusi vektor menjadi √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ √ ( ) √ √ √ √ √
21
Lampiran 3
Penentuan Solusi , , dan Dari persamaan (5) diperoleh, ( )
Substitusi persamaan (18) diperoleh
Substitusi persamaan (15) diperoleh √ √ √ √ √
Dari persamaan (6) diperoleh, ( ) Substitusi persamaan (19) diperoleh,
√
Kedua ruas dari persamaan √ dikalikan dengan menjadi √
√
(√ )
( ) ...(20)
Kedua ruas persamaan (20) dikalikan dengan matriks sehingga ( )
( )
22 ( ) ( ) ( ) ( ) √ Dari persamaan ( )
√ , diperoleh dengan mengalikan kedua ruas dengan ( ( ) )
( ( ) ) (
√ ) ...(21)
sehingga diperoleh solusi , , dan yang tunggal sebagai berikut √ √ (( ( ) ) ( √ )) ( ) ( ( ) (( ( ) ) ( √ ))) ( ( ) ) ( ( ) (( ( ) ) ( √ )))
23
Lampiran 4
Program MATLAB untuk contoh kasus ke-1
function [A,b,c,x,y,s,mu,opt] = zigzag_Nematollahi(n)
n=4 A=[-1 1 0 0; 0 0 -1 1] b=[-1;-1] c=[0;1;0;1] % figures figure(3) clf %draw_feas_region(A,b,c) % pause y = [0.5 0.5]'; %zeros(size(b)); % A' % d=A'*y % d(1) % d(2) s = c - A'*y mu = 100; x = mu./s rb = A*x-b
% compute (feasible!) 1-center figure(3)
axis([0 1 0 1])
line('color',[0 0
0],'linestyle','*','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',5);%gambar titik awal di daerah fisibel
for i = 1:250,
[x,y,s] = Newton_step(A,b,c,x,y,s,mu); line('color',[0 0
0],'linestyle','*','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',5); end rb = A*x-b rc = c - A'*y - s [x s] x y x.*s mu=(x'*s)/(n); %xsu=(sqrt(x.*s/mu)-sqrt(ones(size(x))*mu./(x.*s))); %delta=normest(xsu)/2
24
Lanjutan Lampiran 4
Program MATLAB untuk contoh kasus ke-1 theta = 0.1 %pilih 0.5 %pilih 0.8
%hilangkan tanda persen jika digunakan eps = 10^(-3) %seberapa dekat dgn solusi optimal figure(3)
line('color',[0 1
0],'linestyle','o','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',5.8);%gambar fix titik analitik center
it=0
while n*mu>eps,
mu = (1-theta)*mu;
[x,y,s] = Newton_step(A,b,c,x,y,s,mu); line('color',[0 0
1],'linestyle','o','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',6);%tebal garis central path
it=it+1 % pause(0.2)
end
line('color',[1 0
0],'linestyle','*','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',8);%titik solusi optimal
axis([-0.02 0.02 0 10^(0)]) %set(gca,'yscale','log'); axis([-0.3 0.3 0 1]) axis([-0.01 1.01 0 1.01]) xx=[0 1 1 0] yy=[0 0 1 1]
line('color',[1 0 0],'linestyle',
'-','erase','none','xdata',xx,'ydata',yy,'linewidth',2); y
25
Lampiran 5
Program MATLAB untuk contoh kasus ke-2
function [A,b,c,x,y,s,mu,opt] = zigzag_Nematollahi(n)
n=4 A=[-1 1 1/3 1/3 ; 0 0 -1 1 ] b=[-1;-1] c=[0;1;0;1] % figures figure(3) clf %draw_feas_region(A,b,c) % pause y = [0.5 0.5]'; %zeros(size(b)); s = c - A'*y mu = 100; x = mu./s rb = A*x-b
% compute (feasible!) 1-center figure(3)
axis([0 1 0 1])
line('color',[0 0
0],'linestyle','*','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',5);%gambar titik awal di daerah fisibel
for i = 1:250,
[x,y,s] = Newton_step(A,b,c,x,y,s,mu); line('color',[0 0
0],'linestyle','*','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',5); end rb = A*x-b rc = c - A'*y - s [x s] x y x.*s mu=(x'*s)/(n); %xsu=(sqrt(x.*s/mu)-sqrt(ones(size(x))*mu./(x.*s))); %delta=normest(xsu)/2
theta = 0.1 %pilih 0.5 %pilih 0.8
26
Lanjutan Lampiran 5
Program MATLAB untuk contoh kasus ke-2 eps = 10^(-3)
figure(3)
line('color',[0 1
0],'linestyle','o','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',5.8);%gambar fix titik analitik center
it=0
while n*mu>eps,
mu = (1-theta)*mu;
[x,y,s] = Newton_step(A,b,c,x,y,s,mu); line('color',[0 0
1],'linestyle','o','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',6);%tebal garis central path
it=it+1 % pause(0.2)
end
line('color',[1 0
0],'linestyle','*','erase','none','xdata',y(1),'ydata',y(2),'marke
rsize',8);%titik solusi optimal
axis([-0.02 0.02 0 10^(0)]) %set(gca,'yscale','log'); axis([-0.3 0.3 0 1]) axis([-0.01 1.01 0 1.01]) xx=[0 1 1 0] yy=[0 0.3 0.7 1]
line('color',[1 0 0],'linestyle',
'-','erase','none','xdata',xx,'ydata',yy,'linewidth',2); y
27
Lampiran 6
Program MATLAB untuk Newton_step
function [x,y,s]= Newton_step(A,b,c,x,y,s,mu);
rb = b - A*x; rc = c - A'*y - s; v = sqrt(x.*s/mu); r = v.^(-1)-v; D = diag(sqrt(x./s)); AA=A*D; M=AA*AA'; % MM=M\A; % MM1=MM*r; % ds=D*A'*MM1; % dx=r-ds; rhs = rb/sqrt(mu)+AA*(diag(v./s)*rc - r); dy=M\rhs; Dy = sqrt(mu)*dy; ds = diag(v./s)*rc - AA'*dy; dx = r - ds; Dx = x.*dx./v; Ds = s.*ds./v; alpha = 1; x = x + alpha*Dx; y = y + alpha*Dy; s = s + alpha*Ds; % return