MODUL 1 – PENGENALAN MATLAB Ibrahim Amyas Aksar Tarigan (S2112002)
Asisten: Zahrotul Aulia Ulfah / 132 11 077 Tanggal Percobaan: 22/09/2014 EL3110-Praktikum Pengolahan Sinyal Digital
Laboratorium Dasar Teknik Elektro - Sekolah Teknik Elektro dan
Informatika ITB
Abstrak
Praktikum kali ini praktikan diminta untuk mengenal MATLAB dan kapabilitasnya sebagai sebuah alat pemrograman untuk analisis dan komputasi numerik. Aspek-aspek yang diperhatikan adalah membuat sinyal input filter berupa superposisi beberapa sinyal sinusoidal dengan frekuensi berbeda, desain dan simulasi filter FIR1 dan FIR2 untuk mencari respon frekuensi, serta membuat m-file untuk melakukan pem-filteran FIR. Hasil yang didapatkan adalah berupa sebuah grafik sinyal yang berbeda untuk setiap jenis filter dan frekuensi yang digunakan.
Kata kunci: MATLAB, FIR1, FIR2, respon frekuensi.
1. PENDAHULUAN
MATLAB (Matrix Laboratory) pada awalnya merupakan interface untuk koleksi rutin-rutin numerik dari proyek LINPACK dan EISPACK, namun sekarang merupakan produk komersial dari perusahaan Mathworks, Inc; MATLAB kini telah berkembang menjadi sebuah
environment pemrograman canggih
yang berisi fungsi-fungsi built-in untuk melakukan tugas pengolahan sinyal, aljabar linier, dan kalkulasi matematis lainnya. Kemampuan pemrograman yang dibutuhkan tidak terlalu sulit bila telah
memiliki pengalaman dalam
pemrograman bahasa lain seperti C, PASCAL, atau FORTRAN. Adapun tujuan dari praktikum kali ini adalah sebagai berikut:
- Mempelajari penggunanan sistem
help untuk mengetahui
commands dan syntax dasar
MATLAB;
- Dapat menggunakan MATLAB untuk desain filter;
- Mempelajari bagaimana menulis fungsi dan m-file pada MATLAB; - Merancang dan memahami
pem-filter-an FIR dengan MATLAB
secara mendalam.
2. STUDI PUSTAKA
2.1 MATLAB HELP
MATLAB menyediakan sistem help
on-line yang dapat diakses dengan perintah help.
>> help filter
Contoh diatas adalah preintah yang kita lakukan apabila ingin memperoleh informasi mengenai filter dalam bentuk teks pada layar MATLAB. Terdapat juga banyak program demonstrasi yang mengilustrasikan berbagai kapabilitas MATLAB, yang dapat dimulai dengan perintah demo.
2.2 VARIABELDAN OPERASI MATRIKS
Tipe variabel dasar pada MATLAB adalah matriks. Untuk mendeklarasikan sebuah variabel, kita hanya perlu memberikan nilai tertentu pada MATLAB prompt. Contoh:
>> M = [ 1 2 6; 5 2 1 ] M = 1 2 6
5 2 1
Jika matriks yang kita gunakan ternyata menggunakan rumus yang panjang atau banyak entri, maka perintah pada MATLAB nya dapat kita pecahkan menjadi dua (atau lebih) dengan menggunakan tanda (...) pada akhir sebuah baris yang ingin dilanjutkan. Contoh:
P = [ 1, 2, 4, 6, 8 ] + [ pi, 4, exp(1), 0, -1 ] + ...
[cos(0.1*pi),sin(pi/3),tan(3),atan( 2),sqrt(pi)];
Ekspresi perintah atau pernyataan yang diakhiri dengan tanda semicolon (;), maka hasilnya tidak akan ditampilkan di layar.
Ukuran dari sebuah matriks dapat diketahui dengan operator size:
>> Msize = size(M) Msize = 2 3
Kita tidak perlu menggunakan variabel khusus untuk melacak jumlah baris dan kolom suatu matriks. Ada dua jenis variabel matriks pada MATLAB, yakni skalar dan vektor. Sebuah skalar adalah sebuah matriks yang hanya berisi satu elemen, jadi berukuran 1 × 1. Sebuah vektor adalah sebuah matriks yang hanya berisi satu baris atau kolom. Elemen individu dari sebuah variabel matriks dapat diakses dengan memberikan indeks baris dan kolom, sebagai contoh:
>> M13 = M(1,3) M13 = 6
2.2.1 OPERATOR COLON (:)
Operator ini sangat berguna untuk membuat index array. Notasi colon didasarkan pada ide bahwa sebuah selang indeks dapat dihasilkan dengan memberikan sebuah nilai awal, interval, dan sebuah nilai akhir. Karena itu, sebuah vektor yang terpartisi dapat diperoleh dengan perintah:
iii = nilai awal : interval : nilai akhir
Tanpa parameter interval, nilai default-nya adalah 1. Metode perhitungan ini mirip dengan notasi loop DO pada FORTRAN, namun untuk MATLABS selangkah lebih maju dengan cara
menggabungkannya dengan
pengindeksian matriks. Tanda colon juga berfungsi sebagai wild card, misalnya, A(2,:) adalah baris kedua matriks A.
Pengindeksian mundur akan
membalikkan sebuah vektor, misal X(9:-1:1). Jika kita membutuhkan sebuah daftar yang berisi semua nilai elemen pada matriks, jadi A(:) memberikan sebuah vektor kolom 72 × 1, merupakan hasil concatenation elemen setiap kolom matriks A, yang juga merupakan contoh
reshaping matriks. Teknik reshaping
yang lebih umum dapat dilakukan dengan fungsi reshape(A,M,N).
2.2.2 OPERASI MATRIKS DAN ARRAY
a.) Tinjauan Perkalian Matriks Opersi perkalian matriks AB hanya dapat dilakukan bila kedua matriks tersebut memiliki dimensi yang kompatibel, yakni jumlah kolom matriks A harus sama dengan jumlah baris matriks B. Bila A adalah “m × n”, maka B haruslah “n × p”, dan hasil perkalian AB akan memiliki dimensi “m × p”. Umumnya perkalian matriks tidak bersifat komutatif, yakni “AB ≠ BA”. Bila “p ≠ m”, maka perkalian AB tidak terdefinisi.
Ada kasus khusus untuk perkalian matriks, yakni outer product dan inner
product. Pada outer product, sebuah
vektor kolom mengalikan sebuah vektor baris untuk menghasilan sebuah matriks. Bila kita membiarkan semua elemen salah satu vektor tersebut berupa ‘1’, maka kita akan memperoleh hasil yang berulang.
Untuk inner product, sebuah vektor baris mengalikan sebuah vektor kolom, jadi hasilnya berupa skalar. Bila kita membiarkan semua elemen salah satu vektor tersebut berupa ‘1’, maka kita akan memperoleh semua elemen vektor lainnya.
b.) Operasi Pointwise Array
Jika kita ingin mengalikan matriks secara elemen per elemen, mereka harus memiliki dimensi yang sama. Untuk melakukan perkalian pointwise pada MATLAB, kita menggunakan operator “point-star”A.*B. Misal, bila A dan B keduanya adalah matriks 3 × 2 maka:
Perkalian semacam ini kita sebut dengan istilah perkalian array. Perkalian array bersifat komutatif karena kita akan memperoleh hasil yang sama bila kita menghitung D = B.*A.
Dalam MATLAB, sebuah “titik” digunakan dengan operator aritmetik, maka ia akan mengubah definisi operator tersebut ke operasi pointwise. Jadi operator “./” berarti pembagian pointwise, “.^” berarti pemangkatan pointwise. Misal, xx = (0.9).^(0:49) akan menghasilkan suatu vektor yang nilainya sama dengan (0.9)n untuk n = 0, 1, 2, ... 49.
c.) Operasi Concatenation Array Operasi ini digunakan untuk menempelkan dua atau lebih array dengan syarat tertentu sesuai dengan operasi concatenation (penempelan) yang diinginkan. Pada MATLAB terdapat dua buah fungsi yang dapat digunakan untuk melakukan proses concatenation
arrays. Fungsi tersebut adalah vertcat
dan horzcat.
2.3 PLOTDAN GRAFIK
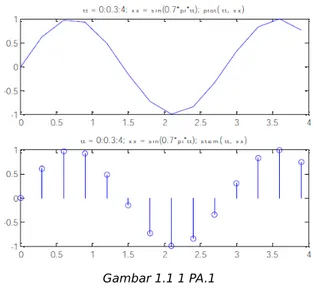
MATLAB dapat menghasilkan plot dua dimensi x-y dan plot tiga dimensi, menayangkan citra dan bahkan membuat dan memutar video. Dua fungsi yang sering digunakan dalam praktikum ini adalah plot dan stem. Untuk memanggil fungsi ini, umumnya kita membutuhkan dua vektor, untuk sumbu x dan sumbu y. Pemanggilan fungsi plot(x,y) akan menghasilkan suatu plot yang terkoneksi dengan garus lurus untuk setiap dua titik.
{ (x(1), y(1)), (x(2),y(2)), (x(3),y(3)), ..., (x(N),y(N)) } seperti yang ditunjukkan pada PA.1. Pemanggilan fungsi stem(x,y) akan menghasilkan presentasi seperti berikut,
Gambar 1.1 1 PA.1
2.3.1 FIGURE WINDOWS
Ketika MATLAB membuat sebuah plot, grafiknya akan dituliskan ke figure
windows. Setiap perintah plot pada command window akan mengalihkan
keluarannya ke window yang aktif. Perintah figure(n) akan menampilkan sebuah figure window yang baru yang ditandai dengan bilangan n, atau membuatnya aktif kemabli bila telah ada sebelumnya. Pengendalian terhadap berbagai atribut window (ukuran, lokasi, warna) juga mungkin dilakukan dengan perintah figure, yang melakukan inisialisasi terhadap window plot.
2.3.2 MEM-PLOT BEBERAPA GRAFIK
Kita dapat membuat beberapa grafik/plot pada satu window dengan menggunakan fungsi subplot. Fungsi ini tidak melakukan proses plotting, namun hanya membagi window menjadi beberapa segmen. Misal, perintah subplot(3,2,3) akan membagi figure
window menjadi tiga baris dan dua
kolom (jadi terdapat enam segmen) dan mengarahkan plot berikutnya ke segmen kiri baris kedua. Grafik PA.1 (gambar 1)
diperoleh dengan perintah
subplot(2,1,1) dan subplot(2,1,2).
2.4 KONSTRUK PEMROGRAMAN MATLAB mendukung paradigma pemrograman fungsional, dimana kita dapat menyusun fungsi-fungsi secara
∑
n=1 Llog
(
|
x
n|
)
Yang dapat diimplementasikan dengan hanya menggunakan satu baris kode MATLAB, yakni:
>> sum(log (abs (x) ) )
Dimana x adalah sebuah vektor yang berisi elemen-elemen xn.
Penulisan kode-kode MATLAB yang efisien memerlukan gaya pemrograman yang menghasilkan fungsi-fungsi kecil yang divektorisasi. Loop-loop harus dihindari. Caranya adalah dengan memanggil fungsi-fungsi toolbox sebanyak/sesering mungkin.
2.4.1 FUNGSI-FUNGSI BUILT-IN MATLAB
Banyak fungsi-fungsi MATLAB yang dapat beroperasi pada skalar sama mudahnya dengan operasi pada array. Misal, bila x adalah sebuah array, maka cos(x) mengembalikan sebuah array dengan ukuran yang sama seandainya x berisi kosinus dari setiap elemen x.
Lihat bahwa tidak ada loop yang diperlukan, meski cos(x) melakukan operasi kosinus pada setiap elemen
array. Kebanyakan fungsi transcendental
mengikuti aturan pointwise ini. Pada beberapa kasus khusus, sangat penting membedakan eksponensial matriks (expm) dengan eksponensial pointwise (exp).
2.4.2 ALIRAN PROGRAM (PROGRAM FLOW)
Aliran program dapat dikendalikan pada MATLAB menggunakan pernyataan ir,
loop while, loop for. Untuk versi yang
terbaru, ada juga pernyataan switch, yang mana mirip seperti bahasa C++ atau PASCAL.
2.5 MATLAB SCRIPTS
Setiap perintah /pernyataan yang dapat dimasukkan pada window prompt dapat disimpan pada sebuah file teks yang dieksekusi sebagai sebuah script.File teks tersebut dapat dibuat dengan menggunakan sembarang editor ASCII seperti program Notepad atau pada
editor teks MATLAB. Ekstensi file harus
berupa “.m” dan script tersebut dieksekusi pada MATLAB dengan hanya mengetikkan nama file (dengna atau tanpa ekstensi). Program-program tersebut umumnya dikenal dengan istilah m-file.
Bila perintah-perintah ini disimpan dengan file bernama plotstem.m maka pengetikan pada plotstem pada
command prompt akan menkalankan file
tersebut, dan kedelapan baris perintah akan dieksekusi sam halnya bila mereka diketikkan baris per baris pada
command prompt.
2.6 MENULIS FUNGSI MATLAB Kita dapat menulis fungsi sendiri lalu ditambahkan pada MATLAB. Fungsi-fungsi ini merupakan enis lain dari
m-file, dan dibuat sebagai sebuah file ASCII
menggunakan editor teks. Kata pertama pada m-file tersebut haruslah keyword function untuk memberitahu MATLAB bahwa file tersebut diperlakukan sebagai sebuah fungsi dengan argumen. Pada baris yang sama juga berisi calling
template yang menyatakan argumen input dan output dari fungsi. Nama file
berekstensi “.m” dan nama fungsi tersebut akan menjadi nama dari perintah baru pada MATLAB.
2.6.1 MEMBUAT SEBUAH FUNGSI CLIP
Perhatikan sebuah fungsi m-file clip yang mengambil dua buah argumen (sebuah vektor sinyal dan nilai skalar
pembatas/threshold) dan
mengembalikan sebuah vektor sinyal keluaran. Kita dapat menggunakan sebuah editor untuk menghasilkan file ASCII dari clip.m yang berisi pernyataan-pernyataan berikut:
Kita dapat memecah m-file clip.m menjadi empat bagian:
a.) Definisi input-output b.) Dokumentasi
c.) Pengujian ukuran (size) dan kesalahan (error)
d.) Operasi fungsi yang sebenarnya
2.6.2 DEBUGGING MATLAB M -FILE
MATLAB adalah sebuah environment yang interaktif, debugging dapat
dilakukan dengan cara menguji variabel-variabel pada workspace. Karena fungsi yang berbeda dapat menggunakan nama variabel yang samam, sangat penting untuk melacak konteks lokal ketika menguji variabel. Beberapa perintah debugging yang berguna didaftarkan di sini, dan yang lainnya dapat anda temukan di help debug. dbstop digunakan untuk mengeset sebuah breakpoint pada sebuah m-file. Ia juga dapat digunakan untuk memberikan sebuah peringatan ketika sebuah kesalahan terjadi dengan mengetikkan dbstop if error sebelum mengeksekusi m-file tersebut.
dbup digunakan untuk menguji variabel didalam fungsi dan workspace.
dbstep akan mengembalikan sebuah peringatan (prompt) ketika setiap baris perintah dieksekusi.
dbcont menyebabkan sebuah eksekusi program yang normal berhenti, atau bila ada kesalahan, mengembalikan status ke MATLAB command prompt.
dbquit membuat keluar dari modebug dan kembali ke MATLAB command
prompt.
keyboard dapat disisipkan ke m-file untuk menghentikan sementara eksekusi program, yang memberikan sebuah MATLAB prompt dalam bentuk K> untuk mengindikasikan bahwa itu bukan
command-line prompt.
2.7 TIPS PEMROGRAMAN
Beberapa gaya penulisan pada m-file (built-in function) yang tersedia pada
toolbox MATLAB:
type angle type conv type trapz
Mempelajari gaya pemrograman orang lain merupakan cara yang efisien untuk memahami suatu bahasa pemrograman komputer. Berikut beberapa petunjuknya:
Menghindari loop;
Pengulangan baris atau kolom; Vektorisasi operasi logika; Membuat sinyal impuls;
Fungsi find; Vektorisasi;
Gaya pemrograman;
3. METODOLOGI
Berikut adalah peralatan yang digunakan selama percobaan berlangsung:
1. Komputer beserta seluruh
hardware-nya
2. Software MATLAB 3. Software DEV-C++
3.1 Percobaan membuat sinyal input
filter berupa superposisi beberapa sinyal
sinusoidal dengan frekuensi berbeda
3.2 Percobaan desain dan simulasi filter
FIR
3.3 Percobaan desain dan simulasi filter
FIR2
Gambar 1.2 Respon Frekuensi Filter
3.4 Percobaan membuat m-file untuk
melakukan pem-filter-an FIR
Laporan Praktikum - Laboratorium Dasar Teknik Elektro – STEI ITB
7
Pada MATLAB, representasikan sinyal dalam vektor (matriks 1xN,
N panjang vektor). Sumbu waktu 0<t<2π.
Beri panjang vektor 100 sampel dengan perintah >>i=1 : 100;
Buat 3 sinyal sinusoidal dengan fs=16000Hz, f1=200Hz, f2=1000Hz, f4=5000Hz. Ketikkan
>>sin1=sin(2*pi*i*f1/fs);sin2=sin(2*pi*i*f2/f s);sin3=sin(2*pi*i*f3/fs);
Jumlahkan ketiga sinyal dengan perintah
>>sintot=(sin1+sin2+sin3)/3;
Plot gambarnya dengan perintah
>>plot(sintot); lalu lihat respon frekuensinya
dengan perintah freqz
Dengan sinyal input pada percobaan sebelumnya, coba beberapa filter berikut:
Low-Pass orde 32 fcut-off 800Hz
Band-Pass orde 32 fcut-off 1000-3000Hz
High-Pass orde 32 fcut-off 6000Hz
Rancang ketiga filter di atas, cari koefisien filter-nya dengan perintah fir1.
Lihat juga frekuensi respon
masing-Desain filter FIR dengan metoda frekuensi
sampling dengan respon frekunesi seperti
pada gambar dibawah, kemudian rancang desain filter-nya, cari filter-nya dengan
perintah fir2. Catat koefisien filter, gunakan orde 16.
Lihat frekuensi respon filter dengan perintah freqz. Gambarkan hasilnya.
Lakukan kembali untuk orde 128, kemudian bandingkan dengan hasil
sebelumnya.
Pada bagian ini anda diminta untuk membuat m-file untuk melakukan pemfilteran FIR saja, untuk m-file anda
tidak diperbolehkan memanggil fungsi internal MATLAB.
Bandingkan hasilnya dengan percobaan menggunakan perintah filter dari MATLAB. Catatan: Koefisien filter FIR adalah merupakan respon impuls dari
4. HASIL DAN ANALISIS
Berikut data-data yang kami kumpulkan selama percobaan berlangsung.
1. Percobaan membuat sinyal input filter berupa superposisi beberapa sinyal sinusoidal dengan frekuensi berbeda.
Diketahui besar frekuensi sinyal sebagai berikut:
fs = 16000 Hz f1 = 200 Hz f2 = 1000 Hz f3 = 5000 Hz
Untuk mendapatkan besar nilai tiap sinyal kita masukkan perintah rumusnya pada MATLAB sebagai berikut:
sin1 = sin(2*pi*i*f1/fs) ; sin2 = sin(2*pi*i*f2/fs) ; sin3 = sin(2*pi*i*f3/fs) ;
Kemudian untuk mendapatkan sintot yang merupakan gabungan ketiga sinyal tersebut, masukkan perintah berikut:
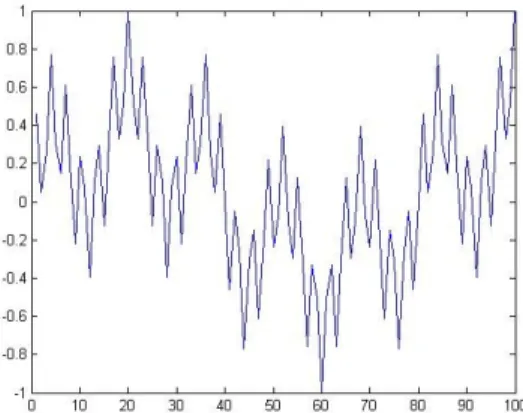
sintot=(sin1+sin2+sin3)/3; sintot sendiri merupakan satu sinyal sinusoidal yang rusak. Kemudian dengan menggunakan perintah plot(sintot), maka akan menghasilkan gambar output berikut:
Gambar 1.3 Plot gambar sintot
Respon frekuensinya kita dapatkan dengan memasukkan perintah freqz. Hasil output-nya:
Gambar 1.4 Plot gambar sintot
Hasil output-output di atas seusai dengan yang diharapkan.
2. Percobaan desain dan simulasi filter FIR 1
Koefisien filter untuk low-pass:
Gambar 1.5 Koefisien Filter Low-pass Gambar respon frekuensinya:
Kemudian untuk band-pass, koefisien
filter-nya:
Gambar 1.7 Koefisien Filter Band-pass Gambar respon frekuensinya:
Gambar 1.8 Respon frekuensi Band-pass Dan yang terakhir high-pass, koefisien
filter-nya:
Gambar 1.9 Koefisien Filter High-pass Respon frekuensinya:
Gambar 1.10 Respon frekuensi High-pass Hasil gambar output-output di atas menandakan bahwa hasil plot yang dilakukan telah sesuai dengan yang diinginkan.
3. Percobaan desain dan simulasi filter FIR 2
Dari data-data grafik respon frekuensi
filter pada modul, maka didapat hasil
respon frekuensinya adalah sebagai berikut:
a.) Untuk orde 16
Gambar 1.11 Respon frekuensi orde 16 b.) Untuk orde 128
Hasil gambar output di atas
memperlihatkan, bahwa ketika ordenya jauh dinaikkan, maka kerapatan getaran frekuensinya semakin rapat. Plot dan pencarian respon frekuensi di atas juga membuktikan bahwa hasilnya sesuai dengan yang diinginkan.
4. Percobaan membuat m-file untuk melakukan pem-filter-an FIR Berikut peritntah yang kami masukkan: Function y=filters(x,I)
[lebar_I panjang_I]= size (I); [lebar_x panjang_x]= size (x); For k=1:panjang_x+1 Y(k)=0; End for i=1:panjang_x for j=1 : panjang_I if j<= i y(i)=y(i) + x(i-j+1)*I(j); end; end; end; end;
Pada percobaan ini kita
mengimplementasikan cara perhitungan convolusi kedalam bentuk MATLAB. Ingat bahwa persamaan untuk konvolusi adalah:
Y(n) = x(0)h(n) + x(1)h(n-1) + ... + x(n)h(0)
Kita definisikan Y(n) sebagai Y(k) dan bernilai 0. k sendiri sudah didefinisikan bernilai 1, dan akan terus bertambah sebesar panjang_x+1. Ini artinya nilai Y(k) nanti akan terus terupdate hingga proses perhitungan berakhir.
Selanjutnya kita harus menentukan besar nilai panjang_I dan panjang_x. Lakukan proses looping di dalam looping yakni syarat i dan j. Nilai yang dihasilkan dalam perhitungan ini gunanya adalah untuk memberikan nilai update kepada Y(k) untuk setiap koefisiennya.
5. KESIMPULAN
Berikut adalah kesimpulan dari percobaan 1 ini:
1. Sistem help sangat bermanfaat sekali bagi siapapun yang memulai menggunakan MATLAB. Gunakan perintah ini apabila kita merasa lupa/ingin tahu commands atau
syntax dasar ketika menggunakan
MATLAB
2. Percobaan 2 dan 3 memperdalam praktikan untuk lebih memahami
penggunaan MATLAB dalam
mendesain filter.
3. Praktikan juga telah mampu melakukan desain dan simulasi filter FIR melalui percobaan 2 dan 3. 4. Praktikan telah mampu memahami
secara mendalam serta merancang pem-filter-an FIR dengan MATLAB.
DAFTAR PUSTAKA
1 McClellan, James. Schafer Ronald. Yoder Mark, DSP First, A Multimedia Approach, Prentice Hall, 1998
2 Proakis, Jhon. Manolakis, Dimitris, Digital Signal Processing, principles, algorithm, and Aplication, Prentice Hall, 1998